Thermal Infrared Radiation and Laser Ultrasound for Deformation and Water Saturation Effects Testing in Limestone
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples and Their Preparation
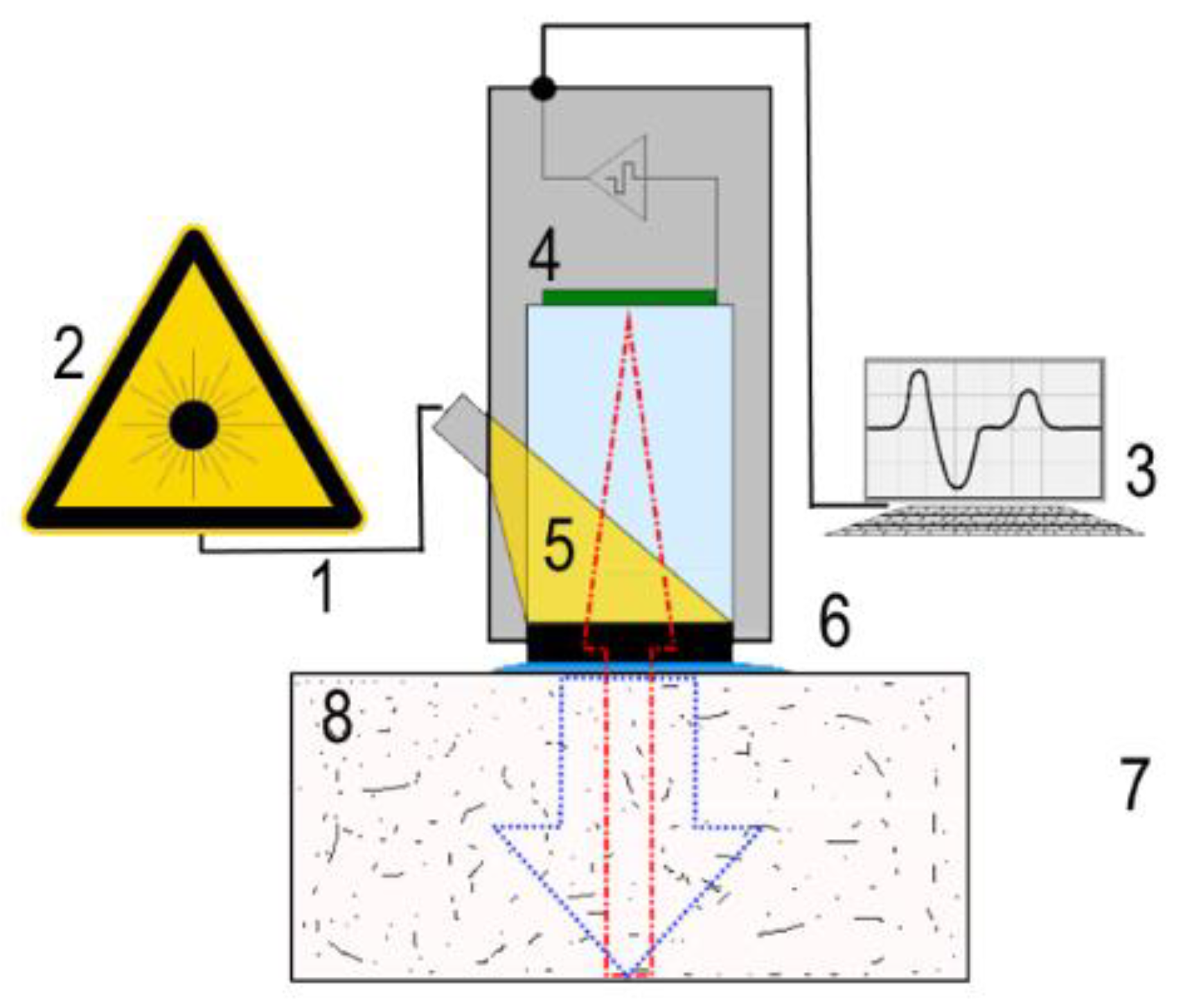
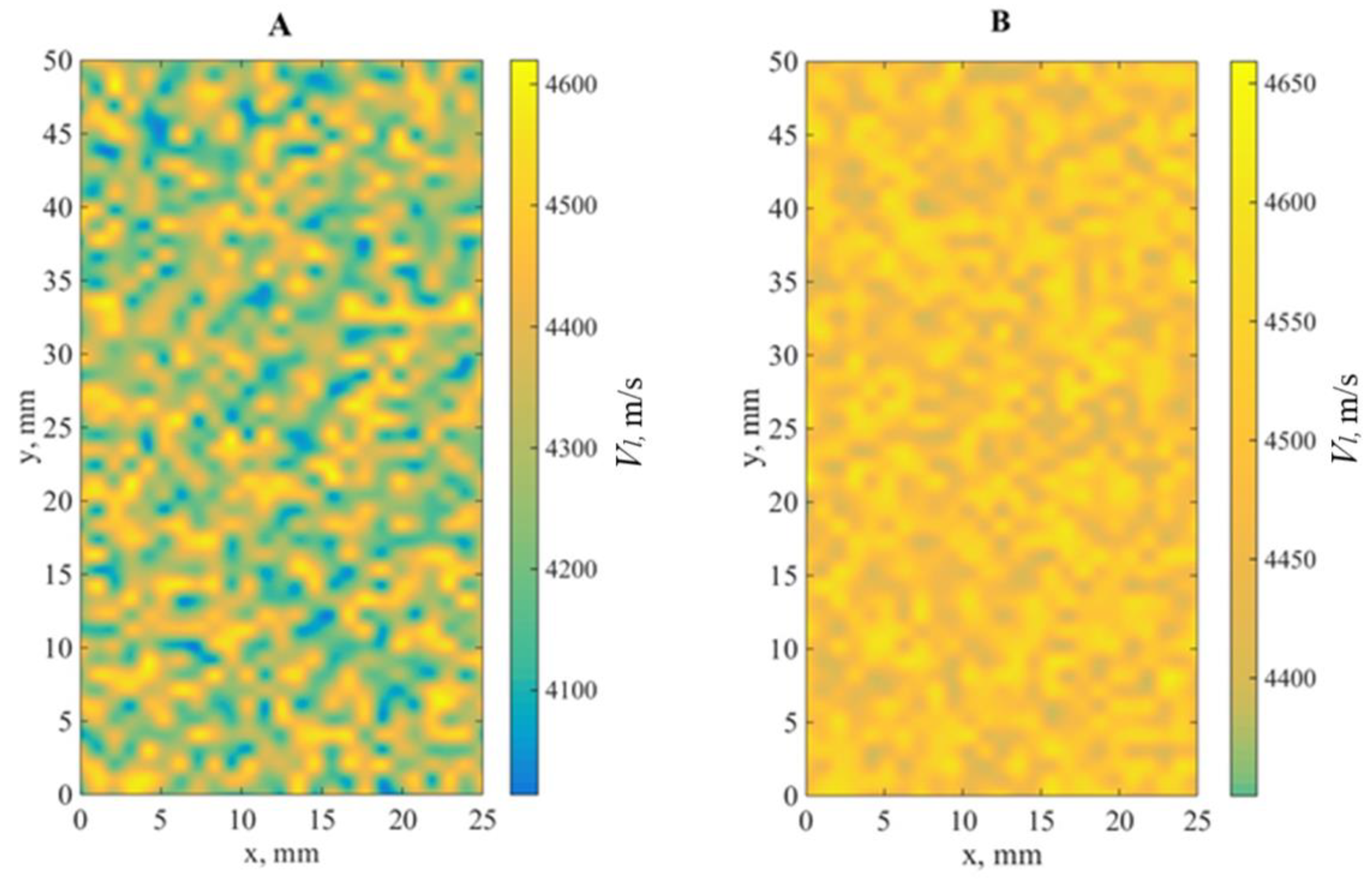
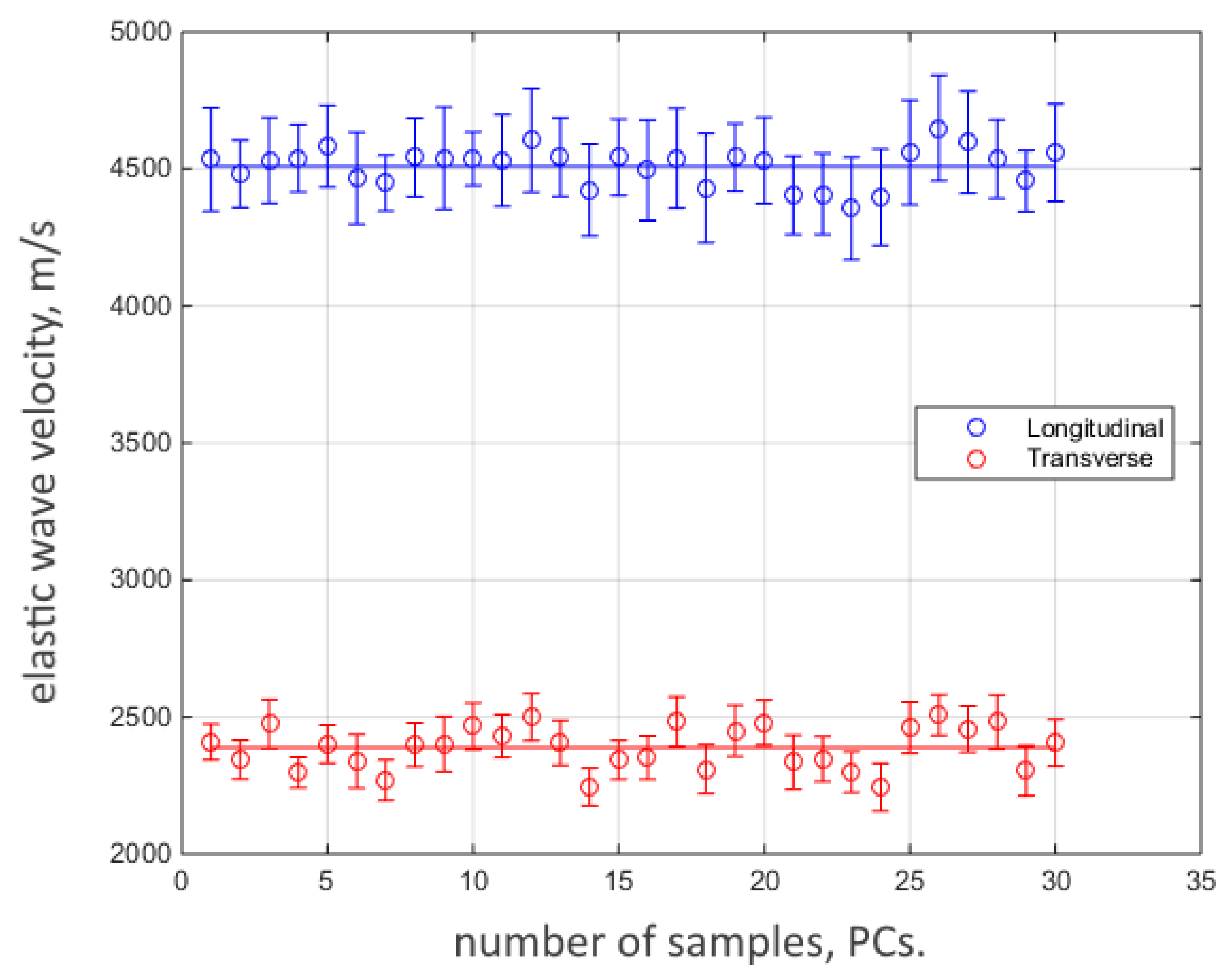
2.2. Measurement of Local Elastic Wave Velocities in Samples by Laser Ultrasonic Structuroscopy
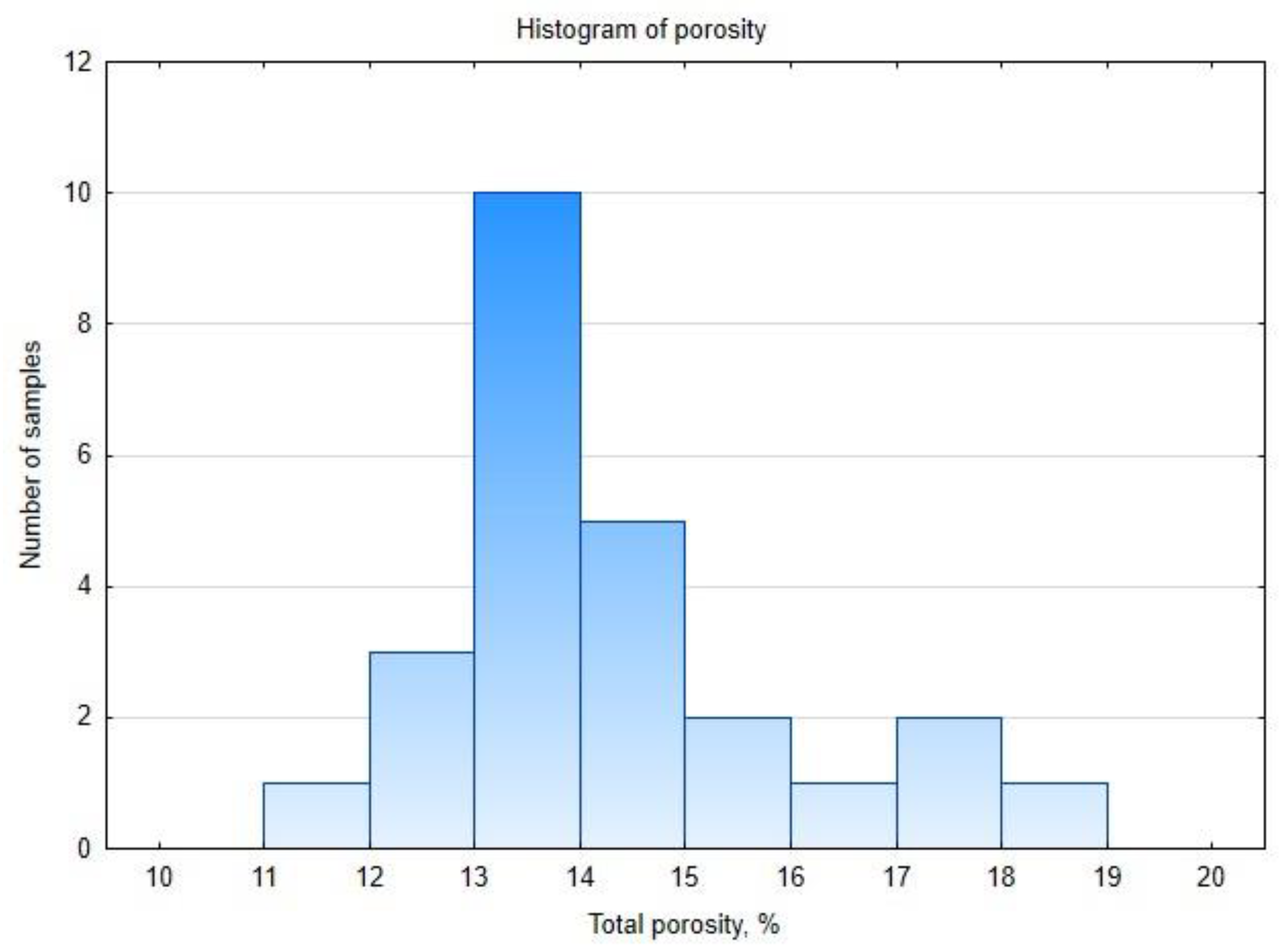
2.3. Calculation of the Total Porosity in Limestone Samples
2.4. Determination of Open Porosity
2.5. Mechanical Tests Accompanied by Infrared Radiation Measurements
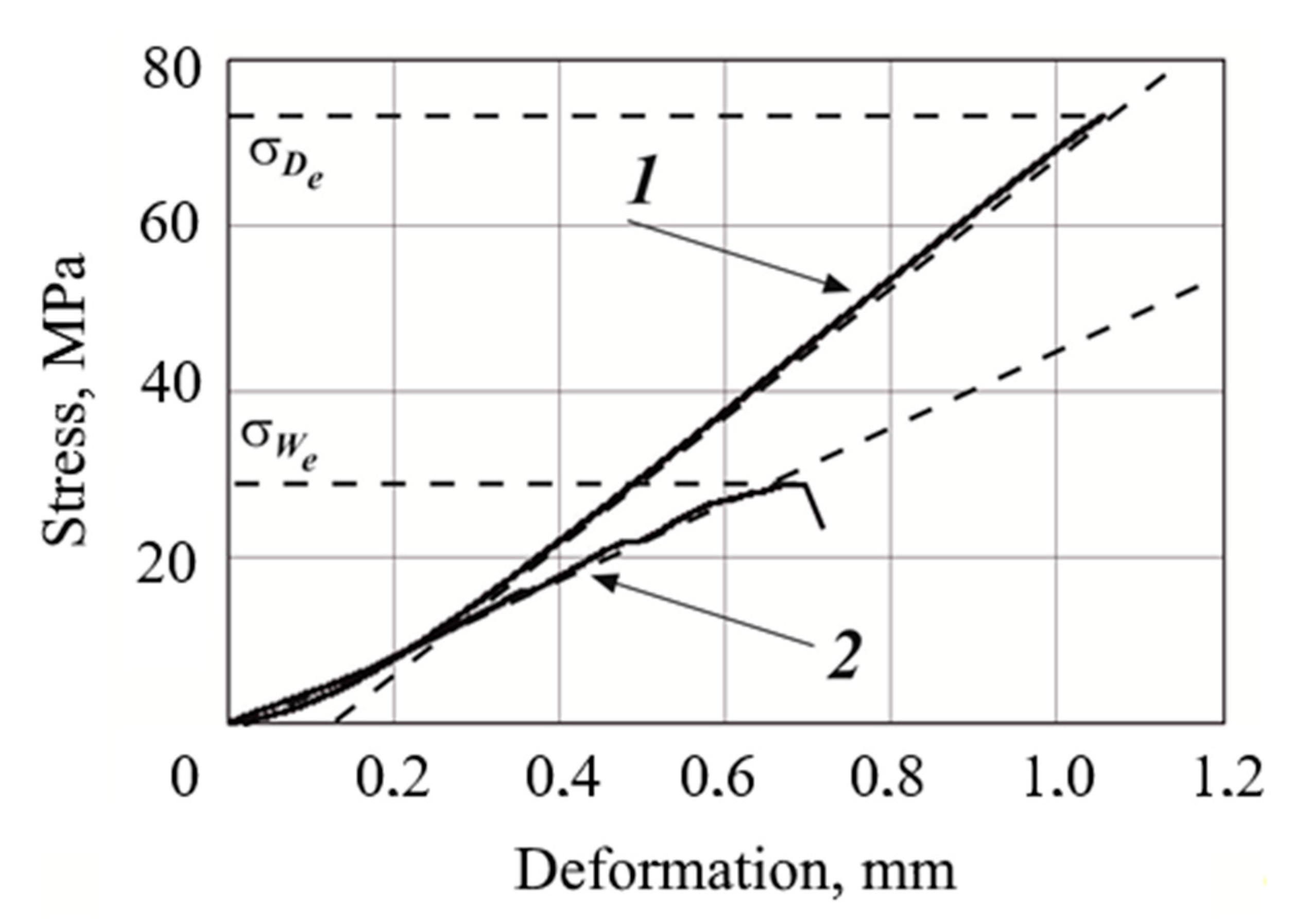
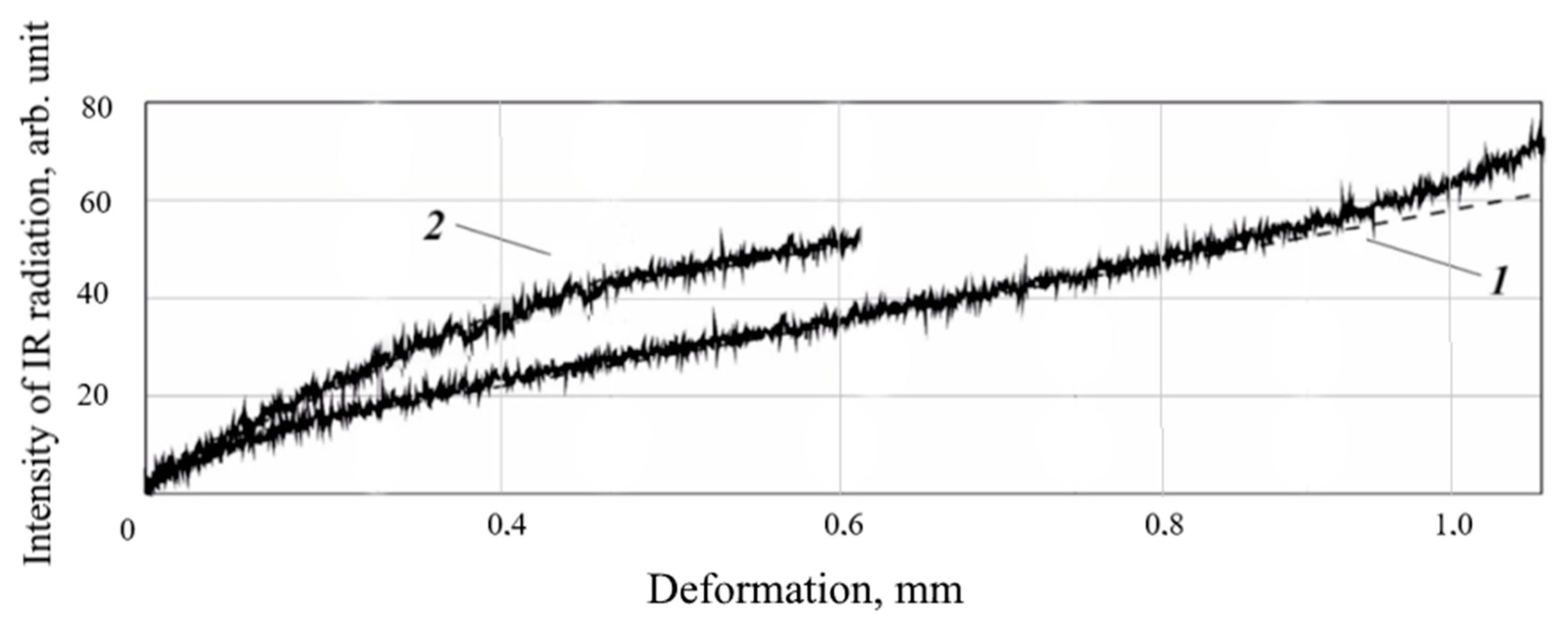
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Calculation of Quasi-Longitudinal Wave Velocities in Calcite
References
- Cassar, J.; Winter, M.G.; Marker, B.R.; Walton, N.R.G.; Entwisle, D.C.; Bromhead, E.N.; Smith, J.W.N. Introduction to stone in historic buildings: Characterization and performance. Geol. Soc. 2014, 391, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Roberti, F.; Oberegger, U.F.; Lucchi, E.; Troi, A. Energy retrofit and conservation of a historic building using multi-objective optimization and an analytic hierarchy process. Energy Build. 2017, 138, 1–10. [Google Scholar] [CrossRef]
- Frodella, W.; Elashvili, M.; Spizzichino, D.; Gigli, G.; Adikashvili, L.; Vacheishvili, N.; Kirkitadze, G.; Nadaraia, A.; Margottini, C.; Casagli, N. Combining infrared thermography and uav digital photogrammetry for the protection and conservation of rupestrian cultural heritage sites in Georgia: A methodological application. Remote Sens. 2020, 12, 892. [Google Scholar] [CrossRef] [Green Version]
- Manohar, S.; Bala, K.; Santhanam, M.; Menon, A. Characteristics and deterioration mechanisms in coral stones used in a historical monument in a saline environment. Constr. Build. Mater. 2020, 241, 7–19. [Google Scholar] [CrossRef]
- Vahaaho, I. Underground space planning in Helsinki. J. Rock Mech. Geotech. Eng. 2014, 387–398. [Google Scholar] [CrossRef]
- Tiennot, M.; Bourgès, A. Evaluation of small core-based specimens for characterization of stone deterioration. Int. J. Rock Mech. Min. Sci. 2016, 84, 69–73. [Google Scholar] [CrossRef]
- Ascione, F.; Ceroni, F.; De Masi, R.F.; de’Rossi, F.; Pecce, M.R. Historical buildings: Multidisciplinary approach to structural/energy diagnosis and performance assessment. Appl. Energy 2017, 185, 1517–1528. [Google Scholar] [CrossRef]
- La Russa, M.F.; Belfiore, C.M.; Fichera, G.V.; Maniscalco, R.; Calabro, C.; Ruffolo, S.A.; Pezzino, A. The behavior to weathering of the Hynlean limestone in the Baroque architecture of the Val di Noto (SE Sicily) an experimental study on the “calcare a lumachella” stone. Constr. Build. Mater. 2014, 77, 7–19. [Google Scholar] [CrossRef]
- Li, L.; Tan, Y.; Huang, B.; Deng, X. Pore property as an indicator of marco-deterioration in slightly weathered tuffs. Eng. Geol. 2020, 267, 105492. [Google Scholar] [CrossRef]
- Scrivano, S.; Gaggero, L.; Gisbert Aguilar, J. An Experimental Investigation of the Effects of Grain Size and Pore Network on the Durability if Vicenza Stone. Rock Mech. Rock Eng. 2019, 52, 2935–2948. [Google Scholar] [CrossRef]
- Shao, Z.; Wang, Y.; Tang, X. The influences of heating and uniaxial loading on granite subjected to liquid nitrogen cooling. Eng. Geol. 2020, 271, 105614. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, D.; Chen, Z.; Liu, A. Deformation and failure characteristics of sandstone under uniaxial compression using distributed fiber optic strain sensing. J. Rock Mech. Geotech. Eng. 2020, 12, 1046–1055. [Google Scholar] [CrossRef]
- Lotidis, M.A.; Nomikos, P.P.; Sofianos, A.I. Laboratory study of the fracturing process in marble and plaster hollow plates subjected to uniaxial compression by combined acoustic emission and digital image correlation techniques. Rock Mech. Rock Eng. 2020, 53, 1953–1971. [Google Scholar] [CrossRef]
- Stoeckhert, F.; Molenda, M.; Brenne, S.; Alber, M. Fracture propagation in sandstone and slate—Laboratory experiments, acoustic emissions and fracture mechanics. J. Rock Mech. Geotech. Eng. 2015, 7, 237–249. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Gracia, V.; Caselles, J.O.; Clapés, J.; Martinez, G.; Osorio, R. Non-destructive analysis in cultural heritage buildings: Evaluating the Mallorca cathedral supporting structures. NDT E Int. 2013, 59, 40–47. [Google Scholar] [CrossRef]
- Bisegna, F.; Ambrosini, D.; Paoletti, D.; Sfarra, S.; Gugliermetii, F. A qualitative method for combining thermal imprints to emerging weak point of ancient wall structures by passive infrared thermography. A Case Study J. Cult. Herit. 2014, 15, 199–202. [Google Scholar] [CrossRef]
- Suzuki, S.; Ogasawara, N. Infrared thermographic test for removing background reflection based on polarization theory. NDT E Int. 2019, 103, 19–25. [Google Scholar] [CrossRef]
- Cong, L.; Zhang, Y.; Xiao, F.; Wei, Q. Laboratory and field investigations of permeability and surface temperature of asphalt pavement by infrared thermal method. Constr. Build. Mater. 2016, 113, 442–448. [Google Scholar] [CrossRef]
- Hill, A.C.; Laugier, E.J.; Casana, J. Archaeological Remote Sensing Using Multi-Temporal, Drone-Acquired Thermal and Near Infrared (NIR) Imagery: A Case Study at the Enfield Shaker Village, New Hampshire. Remote Sens. 2020, 12, 690. [Google Scholar] [CrossRef] [Green Version]
- Vavilov, V.P.; Burleigh, D.D. Review of pulsed thermal NDT: Physical principles, theory and data processing. NDT E Int. 2015, 73, 28–52. [Google Scholar] [CrossRef]
- Sousa, F.J.; Sousa, D.J. Spatial patterns of chemical weathering at the basal tertiary nonconformity in california from multispectral and hyperspectral optical remote sensing. Remote Sens. 2019, 11, 2528. [Google Scholar] [CrossRef] [Green Version]
- Wai-Lok Lai, W.; Dérobert, X.; Annan, P. A review of Ground Penetrating Radar application in civil engineering: A 30-year journey from Locating and Testing to Imaging and Diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar] [CrossRef]
- Solla, M.; Asorey-Cacheda, R.; Núñez-Nieto, X.; Conde-Carnero, B. Evaluation of historical bridges through recreation of GPR models with the FDTD algorithm. NDT E Int. 2016, 77, 19–27. [Google Scholar] [CrossRef]
- Shirole, D.; Hedayat, A.; Ghazanfari, E.; Walton, G. Evaluation of an Ultrasonic Method for Damage Characterization of Brittle Rocks. Rock Mech. Rock Eng. 2020, 53, 2077–2094. [Google Scholar] [CrossRef]
- Chawre, B. Correlations between ultrasonic pulse wave velocities and rock properties of quartz-mica schist. J. Rock Mech. Geotech. Eng. 2020, 10, 594–602. [Google Scholar] [CrossRef]
- Wróblewski, R.; Stawiski, B. Ultrasonic assessment of the concrete residual strength after a real fire exposure. Buildings 2020, 10, 154. [Google Scholar] [CrossRef]
- Skupio, R.; Kubik, B.; Wolański, K. Archival gamma ray logs standardization by nondestructive core measurements of the low-radioactivity rocks. Acta Geophys. 2019, 67, 1835–1844. [Google Scholar] [CrossRef] [Green Version]
- Leng, W.X.; Li, Q.Y.; Bao, R.M.; Zhao, K.; Miao, X.Y.; Li, Y.Z. Characterizing the rock geological time by terahertz spectrum. Sci. China Phys. Mech. Astron. 2019, 62, 14221. [Google Scholar] [CrossRef]
- Mao, L.; Zuo, J.; Yuan, Z.; Chiang, F.-P. Full-field mapping of internal strain distribution in red sandstone specimen under compression using digital volumetric speckle photography and X-ray computed tomography. J. Rock Mech. Geotech. Eng. 2015, 7, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Gibeaux, S.; Vázquez, P.; De Kock, T.; Cnudde, V.; Thomachot-Schneider, C. Weathering assessment under X-ray tomography of building stones exposed to acid atmospheres atcurrent pollution rate. Constr. Build. Mater. 2018, 168, 187–198. [Google Scholar] [CrossRef]
- Winkler, B.; Knorr, K.; Kahle, A.; Vontobel, P.; Lehmann, E.; Hennion, B.; Bayon, G. Neutron imaging and neutron tomography as non-destructive tools to study bulk-rock samples. Eur. J. Miner. 2002, 14, 349–354. [Google Scholar] [CrossRef]
- Kang, T.; Han, S.-J.; Moon, S.; Han, S.; Jeon, J.Y.; Park, G. Lamb-wave sparse-frequency interdigital-transducer-based scanning laser Doppler vibrometry for quantitative depth-wise visualization of defects in plates. NDT E Int. 2019, 107, 102137. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Aria, D.M.D. Emissivity of terrestrial materials in the 8–16 µm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Seo, H.; Choi, H.; Park, J. Crack detection in pillars using infrared thermographic imaging. Geotech. Test. J. 2017, 40, 371–380. [Google Scholar] [CrossRef]
- Imran, M.; Nick, H.M.; Schotting, R.J. Application of infrared thermography for temperature distributions in fluid-saturated porous media. Arab. J. Geosci. 2016, 9, 318. [Google Scholar] [CrossRef]
- Spodek, J.; Rosina, E. Application of Infrared Thermography to Historic Buiding Investigation. J. Archit. Conserv. 2015, 15, 65–81. [Google Scholar] [CrossRef]
- Cui, C.Y.; Deng, M.D.; Geng, N.G. Rock spectral radiation signatures under different pressures. Sci. Bull. 1993, 38, 1377–1382. [Google Scholar] [CrossRef] [Green Version]
- Freund, F. Change generation and propagation in igneous rocks. J. Geodyn. 2002, 33, 543–570. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.Q.; Lin, W.R.; Tadai, O.; Zeng, X.; Yu, C.H.; Ye, H.C.; Li, H.B.; Wang, H. Experimental and numerical investigation of the temperature repose to stress changes of rocks. J. Geophys. Res. Solid Earth 2017, 122, 5107–5117. [Google Scholar] [CrossRef] [Green Version]
- Lui, S.J.; Wu, L.X.; Feng, Z.; Xu, Z.Y. Thermal infrared spectral variation and sensitive waveband of quartzy sandstone under pressure. Spectrosc. Spectr. Anal. 2012, 32, 78–82. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, Y.; Cao, K.; Wang, Z. An experimental study on infrared radiation characteristics of sandstone samples under uniaxial loading. Rock Mech. Rock Eng. 2019, 52, 3493–3500. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Gao, X.; Yang, Z.; Ni, Q.; Wu, L. Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significate. Remote Sens. 2018, 10, 818. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Zhou, Z.; Tan, L.; Zang, H.; Song, Z. Water Saturation Effects on Thermal Infrared Radiation Features of Rock Materials During Deformation and Fracturing. Rock Mech. Eng. 2020. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Liu, S.J.; Wu, L.X.; Feng, Z. Stress-related thermal infrared spectral variation and sensitive waveband of granite. J. Infrared Millim. Waves 2013, 32, 44–49. [Google Scholar] [CrossRef]
- Bychkov, A.; Simonova, V.; Zarubin, V.; Cherepetskaya, E.; Karabutov, A. The progress in photoacoustic and laser ultrasonic tomographic imaging for biomedicine and industry: A review. Appl. Sci. 2018, 8, 1931. [Google Scholar] [CrossRef] [Green Version]
- Shibaev, I.A.; Cherepetskaya, E.B.; Bychkov, A.S.; Zarubin, V.P.; Ivanov, P.N. Evaluation of the internal structure of dolerite specimens using X-ray and laser ultrasonic tomography. Int. J. Civ. Eng. Technol. 2018, 8, 84–92. [Google Scholar]
- Kravcov, A.; Kluczynski, J.; Śnieżek, L.; Svoboda, P.; Grzelak, K.; Morozov, N.; Franek, O.; Kubeček, P. The examination of restrained joints created in the process of multi-material FFF additive manufacturing technology. Materials 2020, 13, 903–918. [Google Scholar]
- Zarubin, V.; Bychkov, A.; Zhigarkov, V.; Karabutov, A.; Cherepetskaya, E. Model-based measurement of internal geometry of solid parts with sub-PSF accuracy using laser-ultrasonic imaging. NDT E Int. 2019, 105, 56–63. [Google Scholar] [CrossRef]
- Aleksandrov, K.S.; Prodayvoda, G.T. Anisotropy of Elastic Properties of Minerals and Rocks; Publishing House SO RAN: Novosibirsk, Russia, 2000; 354p. [Google Scholar]
- Anderson, O.L.; Liebermann, R.C. Sound Velocities in Rocks and Minerals; The Institute of Science and Technologe: Ann Arbor, MI, USA, 1968; 178p. [Google Scholar]
- Sheinin, V.I.; Blokhin, D.I. Features of thermomechanical effects in rock salt samples under uniaxial compression. J. Min. Sci. 2012, 48, 39–45. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1959; 163p. [Google Scholar]




| Mineral | |||||||
|---|---|---|---|---|---|---|---|
| Calcite | 137 | 45.2 | 34.2 | 79.2 | 44.8 | 45.9 | 2980 |
| Quartz | 86.8 | 7.1 | 58.3 | 105.9 | −11.9 | 39.9 | 2650 |
| Dry Limestone Samples | Water-Saturated Limestone Samples | ||
|---|---|---|---|
| No. | c, J/(kg∙K) | No. | c, J/(kg∙K) |
| 1d | 1059 | 1w | 1149 |
| 2d | 1023 | 2w | 1177 |
| 3d | 1015 | 3w | 1131 |
| 4d | 1021 | 4w | 1182 |
| 5d | 1044 | 5w | 1185 |
| Average | 1032 | Average | 1165 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kravcov, A.; Cherepetskaya, E.; Svoboda, P.; Blokhin, D.; Ivanov, P.; Shibaev, I. Thermal Infrared Radiation and Laser Ultrasound for Deformation and Water Saturation Effects Testing in Limestone. Remote Sens. 2020, 12, 4036. https://doi.org/10.3390/rs12244036
Kravcov A, Cherepetskaya E, Svoboda P, Blokhin D, Ivanov P, Shibaev I. Thermal Infrared Radiation and Laser Ultrasound for Deformation and Water Saturation Effects Testing in Limestone. Remote Sensing. 2020; 12(24):4036. https://doi.org/10.3390/rs12244036
Chicago/Turabian StyleKravcov, Alexander, Elena Cherepetskaya, Pavel Svoboda, Dmitry Blokhin, Pavel Ivanov, and Ivan Shibaev. 2020. "Thermal Infrared Radiation and Laser Ultrasound for Deformation and Water Saturation Effects Testing in Limestone" Remote Sensing 12, no. 24: 4036. https://doi.org/10.3390/rs12244036
APA StyleKravcov, A., Cherepetskaya, E., Svoboda, P., Blokhin, D., Ivanov, P., & Shibaev, I. (2020). Thermal Infrared Radiation and Laser Ultrasound for Deformation and Water Saturation Effects Testing in Limestone. Remote Sensing, 12(24), 4036. https://doi.org/10.3390/rs12244036






