Learning Rotation Domain Deep Mutual Information Using Convolutional LSTM for Unsupervised PolSAR Image Classification

Abstract

Deep learning can archive state-of-the-art performance in polarimetric synthetic aperture radar (PolSAR) image classification with plenty of labeled data. However, obtaining large number of accurately labeled samples of PolSAR data is very hard, which limits the practical use of deep learning. Therefore, unsupervised PolSAR image classification is worthy of further investigation that is based on deep learning. Inspired by the superior performance of deep mutual information in natural image feature learning and clustering, an end-to-end Convolutional Long Short Term Memory (ConvLSTM) network is used in order to learn the deep mutual information of polarimetric coherent matrices in the rotation domain with different polarimetric orientation angles (POAs) for unsupervised PolSAR image classification. First, for each pixel, paired “POA-spatio” samples are generated from the polarimetric coherent matrices with different POAs. Second, a special designed ConvLSTM network, along with deep mutual information losses, is used in order to learn the discriminative deep mutual information feature representation of the paired data. Finally, the classification results can be output directly from the trained network model. The proposed method is trained in an end-to-end manner and does not have cumbersome pipelines. Experiments on four real PolSAR datasets show that the performance of proposed method surpasses some state-of-the-art deep learning unsupervised classification methods.

1. Introduction

Polarimetric synthetic aperture radar (PolSAR) is a side-looking active imaging system and it has the advantages of working all day and night, working under all weather conditions, large scope, and certain penetration capacity. PolSAR has developed rapidly recent years, and it plays a significant role in Earth observation, such as land use planning, disaster prevention, environment monitoring, target detection, and so on [1,2,3].

PolSAR image classification is one of the fundamental applications in PolSAR image interpretation. Supervised PolSAR image classification has achieved excellent performance. Many traditional statistical model-based methods and non-neural machine learning [4] methods can achieve good results, such as the CoAS model [5], random forest (RF) [6], support vector machine (SVM) [7], and XGBoost [8]. In [9], two mixture models were proposed for modeling heterogeneous regions in single-look and multi-look polarimetric SAR images, along with their corresponding maximum likelihood classifiers for land cover classification. Feng et al. [10] proposed a classification scheme for forest growth stage types and other cover types while using a SVM that was based on the Polarimetric SAR Interferometric (PolInSAR) data. The interferometric polarimetric SAR multi-chromatic analysis (MCA-PolInSAR) signal processing method that was proposed in [11] can confirm the feasibility to resolve the volume-oriented indetermination problem. Deep learning is a branch of machine learning and it provides the state-of-the-art solutions to many problems in natural image processing field [12,13]. It also shows excellent performance in supervised PolSAR image classification [14,15,16]. Chen et al. [17] used the roll-invariant polarimetric features and hidden polarimetric features in the rotation domain in order to drive deep convolutional neural network and improved the classification performance. Liu et al. [18] proposed a polarimetric convolutional neural network that was based on a new polarimetric scattering coding method to classify PolSAR images by making full use of polarimetric information. Deep learning can automatically learn the discriminative feature representation of input data. With sufficient labeled training samples, the performance of deep learning based PolSAR image classification methods far surpass traditional machine learning methods [17,19].

Labeled PolSAR data are often insufficient and labeling PolSAR data accurately is expensive and time consuming [20]. Unsupervised image classification is one of the fundamental problems in information processing and it does not need labeled data. Central grouping approaches, such as k-means, were popular in early computer versions, since they could be computed efficiently. Lee et al. [21] proposed the iterative Wishart classifier, which is the most widely used classifier for PolSAR covariance matrix data. Spectral clustering, which is based on eigendecomposition of matrices, has good performance on arbitrary shape cluster and it is also often used for unsupervised SAR image classification [22,23]. Song et al. [24] designed a computationally tractable and memory-saving affinity matrix for spectral clustering and could be used for large size PolSAR image clustering. With the development of machine learning, increasing methods have been proposed based on machine learning for unsupervised PolSAR image classification. Hua et al. [25] presented an unsupervised classification algorithm with an adaptive number of classes for PolSAR data, which is capable of automatically estimating the class numbers. Zou et al. [26] proposed an unsupervised classification framework for PolSAR images by combining the superpixel segmentation, Gaussian kernels, consensus similarity network fusion, spectral clustering, and a new post-processing procedure. The non-neural machine learning based methods have achieved promising results for unsupervised PolSAR image classification [27,28], but the current methods still suffer some problems. First, some methods have cumbersome pipelines, such as pre-processing, feature extraction, clustering, post processing, and so on. For example, superpixel segmentation is usually used to take advantage of the spatial information of pixels [24,26,28,29]. Some methods over-cluster PolSAR images and manually merge the similar classes to improve the performance [24]. Second, the separation of feature extraction and clustering will make the solution sub-optimal [30]. Third, some methods require huge computing resources and they cannot classify large size PolSAR images [31].

Image clustering methods that are based on deep learning develop rapidly in natural image processing and they can be coarsely divided to three categories: (1) the combination of traditional clustering algorithms and deep learning. Deep Subspace Clustering (DSC) [32] introduced a novel self-expressive layer between the encoder and decoder of a deep auto-encoder to mimic the “self-expressiveness” property. Subsequently, from the parameters of the self-expressive layer, an affinity matrix was constructed in order to perform spectral clustering to obtain the final clusters. Zhou et al. [33] combined DSC with Generative Adversarial Networks (GAN) to faithfully evaluate the clustering quality. However, these methods often lead to degenerate solutions and they have cumbersome pipelines, such as pre-training, feature post-processing, and clustering mechanisms external to the network [34]. (2) Deep discriminative feature representation learning methods. Donahue et al. [35] added an encoder to GANs for better visual feature extraction. Hjelm et al. [36] performed unsupervised learning of representations by maximizing mutual information between an input and the output of a deep neural network encode. DeepCluster [37] used the pseudo-label that was computed by k-means as supervision to train the deep neural networks. These methods still require extra classifiers or clustering algorithms to output classification results. (3) Deep mutual information based methods. Invariant Information Clustering (IIC) [34] involved a simple mutual information objective function for paired data in a neural network, which was end-to-end and without any labels. An end-to-end classification method in deep learning can classify images by a single neural network model. The input of the model is the image or low level feature and the output is the classification result. For exploring and taking full advantage of various kinds of correlations behind the unlabeled data, Deep Comprehensive Correlation Mining (DCCM) [30] combined the Deep Adaptive Clustering (DAC) [38] architecture with pseudo-graph supervision, pseudo-label supervision, and triplet mutual information for unsupervised image clustering. Deep learning provides a new way for unsupervised PolSAR image classification. Bi et al. [39] proposed an unsupervised PolSAR image classification method that incorporated polarimetric image factorization and deep convolutional networks into a principled framework. At present, deep learning has great potential to further improve the performance of unsupervised PolSAR image classification. Deep learning based unsupervised PolSAR image classification methods are worthy of further investigation. Some methods [25,40] can obtain the optimal number of clusters in the cluster algorithms. Most unsupervised classification methods use a predefined number of classes in both natural image processing and remote sensing image interpretation fields [24,26,30,34,41]. In this paper, we also focus on the unsupervised PolSAR image classification method with a predefined number of classes.

The mutual information based methods IIC and DCCM are end-to-end deep clustering frameworks, which could be used for unsupervised PolSAR image classification. Different methods use different deep features in order to compute mutual information. IIC used the deep prediction features—the output feature of the softmax layer for classification task—of sample $\mathit{x}$ and its randomly geometry transformed version ${\mathit{x}}^{\prime }$ in order to compute mutual information. DCCM constructed the positive pairs and negative pairs based on the pseudo-graph and extracted the shallow layer and deep layer features to compute the triplet mutual information. The geometry transformations, which are suitable for natural image processing, are used in both DCCM and IIC. However, because of the image mechanism of SAR, it is hard to learn the deep mutual information representation of PolSAR data only via geometry transformations. For unsupervised PolSAR image classification, IIC is hard to converge with the use of mutual information alone. DCCM also cannot learn discriminative feature representation of PolSAR images and the performance is unsatisfactory.

This paper aims to propose an end-to-end unsupervised PolSAR image classification method, which does not have cumbersome pipelines and it is simple to apply to practical applications. In order to further improve the unsupervised classification performance, the state-of-the-art unsupervised deep learning algorithms are adopted to unsupervised PolSAR image classification. Therefore, an unsupervised PolSAR image classification method that is based on Convolution Long Short Term Memory (ConvLSTM) [42] network while using Rotation Domain Deep Mutual Information(RDDMI) of polarimetric coherent matrix is proposed in this paper. Two improvements are introduced in proposed method in order to better learn the deep mutual information of PolSAR data. First, the mutual information algorithms of IIC and DCCM are combined to better learn the PolSAR image feature representation and improve the unsupervised PolSAR image classification performance. Second, as a unique data transformation algorithm in PolSAR data interpretation field, the polarimetric matrix rotation is used in order to improve the deep mutual information learning. The polarimetric response of a target is related to the orientation of the target. The hide features in rotation domain can provide useful polarimetric information and be used to improve the classification performance [43,44,45]. Different Polarimetric Orientation Angles (POAs) are used in order to generate a sequence of polarimetric coherent matrices and then the ConvLSTM is used to learn the rotation domain features of the sequence. ConvLSTM can process long-term dependent sequential data with spatial-temporal information and it has been applied to remote sensing image interpretation [46,47,48]. The advantages of proposed method are summarized, as follows: (1) the deep mutual information in rotation domain is introduced for unsupervised PolSAR image classification. (2) Proposed method is an end-to-end model and do not have cumbersome pipelines. The input is the low level polarimetric features and the output is the class label of a pixel in a PolSAR image. Extra preprocessing or post-processing is not required. By introducing the mutual information algorithms of IIC and DCCM and the unique polarimetric matrix rotation, the proposed method can extract more discriminative feature representation and the performance of unsupervised PolSAR image classification is improved.

2. Methods

Figure 1 shows the proposed architecture and it consists of three modules: the first one is the input module, the second one is the network module, and the latter one is the loss function module.

The input data are the sequence of polarimetric coherent matrices in rotation domain, which is one of the most common used low level features for PolSAR image classification. For each pixel in a PolSAR image, the polarimetric matrix rotation along with geometry transformations is used in order to generate paired sequences of polarimetric coherent matrices, $\mathit{x}$ and ${\mathit{x}}^{\prime }$, as the inputs of deep neural network.

The network used in proposed method is a convolutional LSTM network. It mainly contains two ConvLSTM layers (CL${}_1$ and CL${}_2$), three convolutional layers (C${}_1$, C${}_2$, and C${}_3$), three max-pooling layers (M${}_1$, M${}_2$ and M${}_3$), two fully connected layers (FC${}_1$ and FC${}_2$), a softmax layer, and other auxiliary layers, such as ReLU and batch normalization [49].

The loss functions are pseudo-label loss, pseudo-graph loss, and two mutual information losses, which are used to guide the network training. The computation of the IIC mutual information is based on the prediction features of $\mathit{x}$ and ${\mathit{x}}^{\prime }$. The pseudo-label supervision loss, pseudo-graph supervision loss, and triplet mutual information loss were first introduced in DCCM for image clustering. The prediction features of the network are used in order to compute the similarity matrix among samples. Subsequently, the similarity matrix is used to construct pseudo-graph and pseudo-label to guide the network training. Based on the pseudo-graph, the positive pairs and negative pairs are selected to construct triplet correlations. Finally, the shallow layer and deep layer features of samples, which have triplet correlations, are used in order to compute the triplet mutual information loss. The following sections introduce the detailed information.

2.1. Input Polarimetric Features

The deep mutual information learning of each pixel in a PolSAR image requires paired data $\mathit{x}$ and ${\mathit{x}}^{\prime }$, which are both the low level features of the pixel. A simple way to generate paired features for a pixel is to transform the low level feature $\mathit{x}$ to ${\mathit{x}}^{\prime }$ by two transformation algorithms. One is the random geometry transformation algorithm, which is used in IIC and DCCM. The other one is the unique polarimetric matrix rotation algorithm of PolSAR data. It can further improve the deep mutual learning and improve the performance of unsupervised PolSAR image classification. In this paper, $\mathit{x}$ and ${\mathit{x}}^{\prime }$ are two sequences of polarimetric coherent matrices in rotation domain with different POAs.

Polarimetric information of PolSAR data can be expressed by polarimetric coherent matrix $\mathit{T}$. The polarimetric matrix rotation on $\mathit{T}$ is defined, as follows [43]:

$$\mathit{T}\left(\theta \right)=R_3\left(\theta \right)\mathit{T}{R}_3^H\left(\theta \right)$$

(1)

where $\theta$ denotes POA and rotation matrix $R_3\left(\theta \right)$ = $\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\left(2\theta \right)& sin\left(2\theta \right)\\ 0& -sin\left(2\theta \right)& cos\left(2\theta \right)\end{array}\right]$.

According to Equation (1), the elements $T_{ij}\left(\theta \right),i,j=1,2,3$ in $\mathit{T}\left(\theta \right)$ are

$$\begin{array}{cc}\hfill & T_{11}\left(\theta \right)=T_{11}\hfill \\ \hfill & T_{12}\left(\theta \right)=T_{12}cos2\theta +T_{13}sin2\theta \hfill \\ \hfill & T_{13}\left(\theta \right)=-T_{12}sin2\theta +T_{13}cos2\theta \hfill \\ \hfill & T_{23}\left(\theta \right)=\frac{1}{2}(T_{33}-T_{22})sin4\theta +Re\left[T_{23}\right]cos4\theta +jIm\left[T_{23}\right]\hfill \\ \hfill & T_{22}\left(\theta \right)=T_{22}{cos}^{2}2\theta +T_{33}{sin}^{2}2\theta +Re\left[T_{23}\right]sin4\theta \hfill \\ \hfill & T_{33}\left(\theta \right)=T_{22}{sin}^{2}2\theta +T_{33}{cos}^{2}2\theta -Re\left[T_{23}\right]sin4\theta \hfill \end{array}$$

(2)

where $Re[·]$ and $Im[·]$ denote the real part and imaginary part of a complex $T_{ij}$, respectively. We change the POA from 0 to $\pi /2$ with step $\pi /18$ and obtain nine POAs ${\mathit{\theta }}_x$. Subsequently, ${\mathit{\theta }}_x$ are used to generate nine polarimetric coherent matrices. The polarimetric coherent matrices have different POAs and contain spatial information, so it is named “POA-spatio” sequences. For example, Figure 2 shows the Pauli pseudo-color images of the polarimetric coherent matrices of RADARSAT-2 Flevoland dataset. The polarimetric coherent matrices in the rotation domain have different polarimetric properties, which can be used to improve the PolSAR image classification performance.

The rotation domain polarimetric data of each pixel can be defined as a vector ${\mathit{t}}_p$,

$$\begin{array}{c}\hfill {\mathit{t}}_p\left(\theta \right)=[T_{11}\left(\theta \right),T_{22}\left(\theta \right),T_{33}\left(\theta \right),Re\left[T_{12}\left(\theta \right)\right],Im\left[T_{12}\left(\theta \right)\right],\\ \hfill Re\left[T_{13}\left(\theta \right)\right],Im\left[T_{13}\left(\theta \right)\right],Re\left[T_{23}\left(\theta \right)\right],Im\left[T_{23}\left(\theta \right)\right]]\end{array}$$

(3)

For each pixel, the neighborhood window data are used to better reserve the spatial information. The vectors of all pixels in a neighborhood window are used in order to generate the sample $\mathit{x}$ from the nine polarimetric coherent matrices. The size of each sample $\mathit{x}$ is $9\times 9\times w\times w$, where w denotes the window size, the first nine is the number of POAs, and the second nine is number of channels, as shown in Figure 3. Each pseudo-color image patch presented in Figure 3 is generated from $\mathit{T}\left(\theta \right)$, and it denotes the neighborhood window data of a pixel. The deep mutual information learning requires paired data, so the other sample ${\mathit{x}}^{\prime }$ is also shown in Figure 3. There are two steps to generate sample ${\mathit{x}}^{\prime }$. First, sample ${\mathit{x}}^{\prime }$ is also generated from polarimetric coherent matrices with nine POAs ${\mathit{\theta }}_{x^{\prime }}$, which are different from ${\mathit{\theta }}_x$. Sample ${\mathit{x}}^{\prime }$ should be similar to $\mathit{x}$, so the nine POAs ${\mathit{\theta }}_{x^{\prime }}$ of ${\mathit{x}}^{\prime }$ are close to ${\mathit{\theta }}_x$. We make small changes to ${\mathit{\theta }}_x$, and then the POAs ${\mathit{\theta }}_{x^{\prime }}={\mathit{\theta }}_x+\mathsf{\Delta }\mathit{\theta }$, where $\mathsf{\Delta }\mathit{\theta }=[\mathsf{\Delta }{\theta }_0,\mathsf{\Delta }{\theta }_1,\cdots ,\mathsf{\Delta }{\theta }_8]$. For each training epoch, the value of $\mathsf{\Delta }{\theta }_i,i=0,1,\cdots ,8$ is randomly selected in the range $[-5\pi /180,4\pi /180]$. Second, the random geometry transformations are applied to ${\mathit{x}}^{\prime }$. The geometry transformations include rotation, skewing, scaling, flipping, channel shifting, and so on.

In other words, for each pixel, sample $\mathit{x}$ is generated from the rotation domain polarimetric coherent matrices, and then $\mathit{x}$ is converted to ${\mathit{x}}^{\prime }$ by two procedures, which are the polarimetric matrix rotation and random geometry transformations. The network can better learn the deep mutual information of PolSAR data by introducing the unique polarimetric matrix rotation.

2.2. Network Architecture

Figure 4 shows the network used in our method, where N denotes the number of classes. The input sample $\mathit{x}$ or ${\mathit{x}}^{\prime }$ is sequence data and it has spatial information, so the first two ConvLSTM layers are used in order to capture the rotation domain features from the sequence of polarimetric coherent matrices. Subsequently, some convolution layers, as well as fully connected layers, are used in order to further learn deep features of the input sample. Finally, the softmax layer outputs a one-hot vector and the argmax function is used in order to compute the class of the sample. The shallow and deep layer features, which are used to compute the triplet mutual formation loss, are the outputs of the first max-pooling layer and second fully-connected layer, respectively.

LSTM can model long-range dependencies, but it contains too much redundancy for spatial data [42]. ConvLSTM is proposed in order to solve this problem. ConvLSTM replaces the fully connected gate layers of the LSTM with convolutional layers, so it is capable of encoding sequence data that have spatial information [47]. The main equations of ConvLSTM are shown below:

$$\begin{array}{cc}\hfill & i_t=\sigma (W_{xi}\ast x_t+W_{hi}\ast h_{t-1}+W_{ci}\circ C_{t-1}+b_i)\hfill \\ \hfill & f_t=\sigma (W_{xf}\ast x_t+W_{hf}\ast h_{t-1}+W_{cf}\circ C_{t-1}+b_f)\hfill \\ \hfill & C_t=f_t\circ C_{t-1}+i_t\circ tanh(W_{xc}\ast x_t+W_{hc}\ast h_{t-1}+b_c)\hfill \\ \hfill & o_t=\sigma (W_{xo}\ast x_t+W_{ho}\ast h_{t-1}+W_{co}\circ C_t+b_o)\hfill \\ \hfill & h_t=o_t\circ tanh\left(C_t\right)\hfill \end{array}$$

(4)

where * denotes the convolution operation, ∘ denotes the Hadamard product, W denotes learnable weights, b denotes the bias, $x_t$ denotes the input of time t, $f_t$ and $C_t$ denote the hidden state, $o_t$ denotes the output gate, and $h_t$ denotes the final output state of time t. $\sigma$ and tanh are the activation functions.

The “POA-spatio” polarimetric coherent matrices can be regarded as the time steps of ConvLSTM, and sample $\mathit{x}$ or ${\mathit{x}}^{\prime }$ is “POA-spatio” sequence data. Therefore, ConvLSTM fits well with the deep feature representation learning of the PolSAR “POA-spatio” sequence data.

2.3. Loss Functions

2.3.1. IIC Mutual Information

Let $\mathcal{X}={\left\{{\mathit{x}}_i\right\}}_{i=1}^K$ and ${\mathcal{X}}^{\prime }={\left\{{\mathit{x}}_i^{\prime }\right\}}_{i=1}^K$ be paired samples in a PolSAR image, where ${\mathit{x}}_i$ or ${\mathit{x}}_i^{\prime }$ is the i-th sample and K is the number of total sample pairs. IIC aims to learn a representation $\mathsf{\Phi }$ that preserves what is in common between paired data $\mathit{x}$ and ${\mathit{x}}^{\prime }$, while discarding instance-specific details [34], which can be achieved by maximizing the mutual information (MI):

$$\underset{\mathsf{\Phi }}{max}I(\mathsf{\Phi }\left(\mathit{x}\right),\mathsf{\Phi }\left({\mathit{x}}^{\prime }\right)))$$

(5)

where $\mathsf{\Phi }$ is a neural network. The output of the softmax layer $\mathit{z}=\mathsf{\Phi }\left(\mathit{x}\right)$, which is the prediction feature of sample $\mathit{x}$, can be interpreted as the distribution of a discrete random variable y over N classes, formally given by $P(y=n|\mathit{x})={\mathsf{\Phi }}_n\left(\mathit{x}\right)$ [34]. Let y and $y^{\prime }$ be the cluster assignment variables of $\mathit{x}$ and ${\mathit{x}}^{\prime }$, respectively. Because y and $y^{\prime }$ are not independent after marginalization over the dataset [34], the joint probability distribution of y and $y^{\prime }$ is given by a $N\times N$ matrix $\mathit{P}$. Each element at row n and column $n^{\prime }$ of the matrix $\mathit{P}$ is ${\mathit{P}}_{n{n}^{\prime }}=P(y=n,y^{\prime }=n^{\prime })$. Subsequently, $\mathit{P}$ has the following form:

$$\mathit{P}=\frac{1}{K}\sum _{i=1}^K\mathsf{\Phi }\left({\mathit{x}}_i\right)·\mathsf{\Phi }{\left({\mathit{x}}_i^{\prime }\right)}^{\mathsf{T}}$$

(6)

The marginals ${\mathit{P}}_n=P(y=n)$ and ${\mathit{P}}_n^{\prime }=P(y^{\prime }=n^{\prime })$ can be computed by summing the elements of the rows and columns of the matrix $\mathit{P}$ [34]. Plugging the matrix $\mathit{P}$ into the mutual information expression [50] and Equation (5) can be computed equivalently:

$$I(y,y^{\prime })=I\left(\mathit{P}\right)=\sum _{n=1}^N\sum _{n^{\prime }=1}^N{\mathit{P}}_{n{n}^{\prime }}ln\frac{{\mathit{P}}_{n{n}^{\prime }}}{{\mathit{P}}_n{\mathit{P}}_{n^{\prime }}}$$

(7)

Subsequently, the IIC mutual information loss can be formulated as:

$$\underset{\mathsf{\Phi }}{min}{L}_{IIC\underline{}MI}=-I(y,y^{\prime })$$

(8)

2.3.2. Pseudo Graph and Pseudo Label Supervision Loss

The pseudo graph and pseudo label are used in order to guide the network training and the computation of triplet mutual information. The pseudo-graph is used to explore the binary correlation between samples and the pseudo-label loss is used to make full use of category information behind the data [30].

The neural network $\mathsf{\Phi }\left(\mathit{x}\right)$ can output the prediction feature of the input data $\mathit{x}$. Based on the prediction feature vector $\mathit{z}$ of the softmax layer, the cosine similarity of two samples can be calculated by the following equation:

$$S_{ij}=\frac{{\mathit{z}}_{\mathit{i}}·{\mathit{z}}_{\mathit{j}}}{\left|\right|{\mathit{z}}_{\mathit{i}}{\left|\right|}_2·\left|\right|{\mathit{z}}_{\mathit{j}}{\left|\right|}_2}$$

(9)

In [30], a large $thres{h}_w$ is set to the similarity matrix $\mathit{S}$ in order to construct pseudo-graph $\mathit{W}$:

$$W_{ij}=\left\{\begin{array}{cc}1,\hfill & if{s}_{ij}>thres{h}_w,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(10)

If the cosine similarity of two samples is larger than $thres{h}_w$, then the two samples are considered to be the same class. During the network training, the cosine similarity of these samples will be maximized. Otherwise, the samples are thought to be different classes and the cosine similarity will be minimized. The pseudo-graph supervision loss has the following form:

$$\underset{\mathsf{\Phi }}{min}{L}_{PG}\left(\mathsf{\Phi }\right)=\sum _{{\mathit{x}}_i,{\mathit{x}}_j\in \mathcal{X}}{l}_g(\mathsf{\Phi }\left({\mathit{x}}_i\right),\mathsf{\Phi }\left({\mathit{x}}_j\right);W_{ij})$$

(11)

where $l_g$ is the binary cross-entropy loss [38].

If $S_{ij}$ is assumed to be distinctive to each other in similarity matrix $\mathit{S}$, then $\mathcal{X}$ can be divided into exactly N partitions $\{P^1,P^2,⋮,P^N\}$ by a threshold t [30]. The samples that have high cosine similarity will be in the same partition and partition n can be set as the pseudo-label of each $\mathit{x}$. The pseudo-label can be formulated as:

$$y_i=arg\underset{n}{max}{\left[\mathsf{\Phi }\left({\mathit{x}}_i\right)\right]}_n$$

(12)

where ${[·]}_n$ denotes the n-th component of the prediction vector. The probability of the predicted pseudo-label is $p_i=max{\left[\mathsf{\Phi }\left({\mathit{x}}_i\right)\right]}_n$. Because of the optimization problem, by setting a large threshold $thres{h}_l$, only a highly confident pseudo-label is selected to train the network [30].

$$V_i=\left\{\begin{array}{cc}1,\hfill & if{p}_i>thres{h}_l,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(13)

The pseudo-label supervision loss is formulated as:

$$\underset{\mathsf{\Phi }}{min}{L}_{PL}\left(\mathsf{\Phi }\right)=\sum _{{\mathit{x}}_i\in \mathcal{X}}{V}_i·l_l(\mathsf{\Phi }\left(\mathit{x}\right),y_i)$$

(14)

where $l_l$ is the cross-entropy loss.

The local robustness assumption is used in [30]. The feature representations between $\mathit{x}$ and the transformed version ${\mathit{x}}^{\prime }$ should be invariant, which means $\mathsf{\Phi }\left(\mathit{x}\right)\approx \mathsf{\Phi }\left({\mathit{x}}^{\prime }\right)$ and the labels of $\mathit{x}$ and ${\mathit{x}}^{\prime }$ should be the same. Accordingly, the feature invariant loss has the following form:

$$\underset{\mathsf{\Phi }}{min}\sum _{i=1}^N{l}_r(\mathsf{\Phi }\left(\mathit{x}\right),\mathsf{\Phi }\left({\mathit{x}}^{\prime }\right))$$

(15)

where $l_r$ denotes the $l_2$-norm, which measures the distance between the deep features of $\mathit{x}$ and ${\mathit{x}}^{\prime }$. Subsequently, the pseudo-graph and pseudo-label information computed based on transformed samples should be consistent with the original samples. The loss function can be formulated as:

$$\underset{\mathsf{\Phi }}{min}{L}_{PG}^{\prime }\left(\mathsf{\Phi }\right)=\sum _{{\mathit{x}}_i^{\prime },{\mathit{x}}_j^{\prime }\in {\mathcal{X}}^{\prime }}{l}_g(\mathsf{\Phi }\left({\mathit{x}}_i^{\prime }\right),\mathsf{\Phi }\left({\mathit{x}}_j^{\prime }\right);W_{ij})$$

(16)

$$\underset{\mathsf{\Phi }}{min}{L}_{PL}^{\prime }\left(\mathsf{\Phi }\right)=\sum _{{\mathit{x}}_i^{\prime }\in {\mathcal{X}}^{\prime }}{V}_i·l_l(\mathsf{\Phi }\left({\mathit{x}}^{\prime }\right),y_i)$$

(17)

2.3.3. Triplet Mutual Information

The instance-level mutual information between the shallow layer and deep layer features of the same sample should be maximized. The instance-level mutual information of two random variables (D, S) is equal to the Jensen–Shannon divergence (JSD) between samples coming from the joint distribution $\mathbb{J}$ and their product of marginals $\mathbb{M}$ [36,51]. Different layer features of the same sample should follow the joint distribution. If the features are from different samples, then they should follow the marginal product distribution [36]. The JSD version mutual information is defined as:

$${\mathcal{MI}}^{\left(JSD\right)}(D,S)={\mathbb{E}}_{\mathbb{J}}[-sp(-T(d,s))]-{\mathbb{E}}_{\mathbb{M}}\left[sp\left(T(d,s)\right)\right]$$

(18)

where d denotes the deep layer features, s denotes the shallow layer features, and $sp\left(z\right)$ is the softplus function $sp\left(z\right)=log(1+e^z)$. The discriminator T is used to distinguish whether d and s are sampled from the joint distribution or not. It is a convolutional neural network, which uses the deep layer and shallow layer features of samples as input. The output feature maps of T are the inputs of $sp\left(z\right)$. The detailed implementation of the discriminator T is introduced in [36].

For two different samples, ${\mathit{x}}_1$ and ${\mathit{x}}_2$, which belong to the same class, the mutual information between ${\mathit{x}}_1$’s shallow-layer representation and ${\mathit{x}}_2$’s deep-layer representation should also be maximized. Therefore, in [30], the pseudo-graph $\mathit{W}$ in Equation (10) is used to select positive pairs and negative pairs to construct triplet correlations. When two samples are the same class, their features are positive pairs; otherwise, the features are negative pairs. In this way, the deep neural network can learn triplet-level mutual information other than instance-level mutual information. The Equation (18) can be expanded in order to calculate the triplet mutual information. Let $d_j^i$ and $s_j^i$ denote the deep layer features and shallow layer features of sample j and the class of the sample is i. Subsequently, $D^i=\{d_1^i,d_2^i,\cdots ,d_n^i\}$ and $S^i=\{s_1^i,s_2^i,\cdots ,s_n^i\}$ are the features sets of class i. Variables $\mathbb{D}$ and $\mathbb{S}$ are defined by $\mathbb{D}=\{D^1,D^2,\cdots ,D^N\}$ and $\mathbb{S}=\{S^1,S^2,\cdots ,S^N\}$, respectively. Triplet mutual information can be formulated as:

$${\mathcal{MI}}_{set}^{\left(JSD\right)}(D,S)={\mathbb{E}}_{(\mathbb{D},\mathbb{S})=\mathbb{J}}[-sp(-T(d,s))]-{\mathbb{E}}_{\mathbb{D}\times \mathbb{S}=\mathbb{M}}\left[sp\left(T(d,s)\right)\right]$$

(19)

Afterwards, the triplet mutual information loss has the following form:

$$\underset{\mathsf{\Phi }}{min}{L}_{TRI\underline{}MI}=-{\mathcal{MI}}_{set}^{\left(JSD\right)}(D,S)$$

(20)

The triplet mutual information has the advantage that, for two different samples ${\mathit{x}}_1$ and ${\mathit{x}}_2$, which are the same class, the mutual information between ${\mathit{x}}_1$’s shallow layer representation and ${\mathit{x}}_2$’s deep layer representation is also maximized. Subsequently, the deep neural network can learn more discriminative representations through the triplet mutual information.

2.4. Model Optimization

By combining the investigations of IIC and DCCM, the final objective of proposed method can be formulated as:

$$\underset{\mathsf{\Phi }}{min}L=L_{IIC\underline{}MI}+\alpha \widehat{L_{PG}}+\beta \widehat{L_{PL}}+\gamma L_{TRI\underline{}MI}$$

(21)

where $\alpha$, $\beta$, and $\gamma$ control the importance of corresponding loss functions, $\widehat{L_{PG}}=L_{PG}+L_{PG}^{\prime }$, and $\widehat{L_{PL}}=L_{PL}+L_{PL}^{\prime }$.

The proposed method is trained in a minibatch based end-to-end manner. After the model is trained, the cluster label can be computed by Equation (12) while using the output one-hot vector of the softmax layer. The overall training steps are similar to [30], as shown below:

• generate paired “POA-spatio” samples $\mathcal{X}$ and ${\mathcal{X}}^{\prime }$ from the polarimetric coherent matrices in rotation domain.
• initialize the parameters of network $\mathsf{\Phi }$ randomly;
• for each randomly selected minibatch ${\mathcal{X}}_{\mathcal{B}}$ and ${\mathcal{X}}_{\mathcal{B}}^{\prime }$, compute the shadow layer, deep layer, and softmax layer features of $\mathsf{\Phi }\left({\mathit{x}}_i\right)$ and $\mathsf{\Phi }\left({\mathit{x}}_i^{\prime }\right)$;
• compute the similarity matrix $\mathit{S}$, pseudo-graph $\mathit{W}$, and the pseudo-labels;
• select positive and negative pairs based on $\mathit{W}$;
• compute the final loss by Equation (21);
• update the parameters of $\mathsf{\Phi }$; and,
• calculate the unsupervised classification label by Equation (12) after the network is well trained.

3. Datasets

An airborne PolSAR image and three spaceborne PolSAR images are used as the experiment datasets in this section in order to fully demonstrate the performance of proposed method. The detailed data information is presented in

Table 1. The detailed information of four real PolSAR datasets.

Parameter	GF-3 Wuhan	RS-2 Flevoland	AIRSAR Flevoland	RS-2 Wuhan
Sensor	Gaofen-3	RADARSAT-2	NASA/JPL AIRSAR	RADARSAT-2
Band	C	C	L	C
Imaging Area	Wuhan	Flevoland	Flevoland	Wuhan
Imaging Mode	QPSI	Quad-pol	∖	Quad-pol
Imaging time	1-4-2017	2008	16-8-1989	12-2011
Spatial resolution [Range Azimuth] (m)	$5.20\times 2.25$	$12\times 8$	$6\times 12$	$12\times 8$
Image size [Range Azimuth] (pixel)	$976\times 603$	$1400\times 1200$	$750\times 1024$	$5500\times 2400$
Image number	Figure 5	Figure 6	Figure 7	Figure 8

. For each pixel in a PolSAR image, a paired data $\mathit{x}$ and ${\mathit{x}}^{\prime }$ with size of $9\times 9\times w\times w$ are generated as the training samples. Except the pixels from the edge areas of a PolSAR image, all other pixels are used for training.

3.1. Gaofen-3 Wuhan Dataset

The Gaofen-3 (GF-3) Wuhan dataset is a C-band GF-3 spaceborne PolSAR data. It covers the scene of Hannan district, Wuhan, China. The spatial resolution is 5.20 m in range direction and 2.25 m in azimuth direction. The image size is $976\times 603$ pixels. There are five land cover classes identified in this dataset, which are water, building, farmland, vegetation 1, and vegetation 2. According to the backscattering responses and vegetation types, vegetation areas are divided into two classes. Figure 5 shows the Pauli pseudo-color image and ground truth map. The scattering power of vegetation 1 is stronger than that of vegetation 2. Vegetation 1 is shrubs or trees, and vegetation 2 is grasslands or reeds. The ground truth map was first used in [8].

3.2. RADARSAT-2 Flevoland Dataset

The other spaceborne dataset is a C-band RADARSAT-2 (RS-2) PolSAR dataset, which is famous and widely used for classification performance evaluation. It covers the scene of Flevoland in Netherlands, with an image size of $1400\times 1200$ pixels. The spatial resolution is 12 m in range direction and 8 m in azimuth direction. According to high resolution optical images, this dataset contains four land cover classes, which are water, farmland, building, and forest. Figure 6 shows the ground truth map and Pauli pseudo-color image.

3.3. AIRSAR Flevoland Dataset

The airborne dataset is acquired by the NASA/JPL AIRSAR L-band system and it is a four-look fully polarimetric image. This dataset also covers over the scene of Flevoland, Netherlands. The spatial resolution is 6m in range direction and 12 m in azimuth direction. The image size is $750\times 1024$ pixels. This dataset has a well-established ground truth map [52] and it is widely used for supervised PolSAR image classification. It contains 11 land cover types, which are forest, water, bare soil, and other eight crop types. Figure 7 shows the ground truth map and Pauli pseudo-color image.

3.4. RADARSAT-2 Wuhan Dataset

The last spaceborne dataset is acquired by RADARSAT-2 C-band PolSAR system at fine quad-pol mode and it covers over the scene of central area of Wuhan city, China. The image size is 5500 × 2400 and the spatial resolution is 12 m in range direction and 8 m in azimuth direction. A total of three main land cover types are identified in this scene, which are water, building, and forest. The Pauli pseudo-color image and ground truth map are shown in Figure 8a,b, respectively. Wuhan is a big city and it contains high density buildings with different orientations. For example, the two red boxes in the Pauli pseudo-color image are building areas and the corresponding optical images are shown in Figure 8c,d. The optical images show high density buildings with different orientations clearly. This dataset and ground truth map were first used in [20].

4. Experiments

The implementation of proposed method is based on the Pytorch implementation of DCCM (https://github.com/Cory-M/DCCM) and IIC (https://github.com/xu-ji/IIC), and most of the training parameters are not changed. The RMSprop optimizer with $lr=1e-4$ is used. The thresholds $thres{h}_l$ and $thres{h}_w$ are set to 0.9. The parameters that control the importance of different losses are $\alpha =1$, $\beta =5$, and $\gamma =0.05$. The probability outputs of softmax layer are used in order to compute IIC mutual information and the similarity matrix $\mathit{S}$. The shallow layer feature and deep layer feature that are used to compute triplet mutual information are the outputs of M${}_1$ and FC${}_2$. The discriminator of triplet mutual information estimation is the same to DCCM. For all of the PolSAR dataset, the neighborhood window size w is 15.

The overall accuracy (OA), kappa coefficient, purity, and entropy [28,41] are used in order to evaluate the classification performances.

• OA is one of the most common used measures for classification performance evaluation and it can be formulated as

  $$OA=\frac{\widehat{n}}{K}$$

  (22)

  where K denotes the number of total samples and $\widehat{n}$ denotes the correctly classified samples.
• Kappa is an indicator of consistency and it can be computed by the following equation

  $$kappa=\frac{p_o-p_e}{1-p_e}$$

  (23)

  where $p_o$ is OA, $p_e=\frac{\sum _i{n}_i\ast {\tilde{n}}_i}{K\times K}$, $n_i$ is the number of samples that belong to class i, and ${\tilde{n}}_i$ is the number of samples that are classified to class i.
• Purity and entropy are two commonly used measures for clustering performance evaluation. The purity is the higher the better and the entropy is the lower the better. The two measures are defined, as follows [53]

  $$Purity=\sum _{r=1}^k\frac{1}{n}\underset{i}{max}\left(n_r^i\right)$$

  (24)

  $$Entropy=\sum _{r=1}^k\frac{n_r}{n}\left(-\frac{1}{logq}\sum _{i=1}^q\frac{n_r^i}{n_r}log\frac{n_r^i}{n_r}\right)$$

  (25)

  where q is the number of classes, k the number of clusters, $n_r$ is the size of cluster r, and $n_r^i$ is the number of data points in class i clustered in cluster r.

DAC [38], DCCM, DCCM+IIC, and three traditional unsupervised PolSAR image classification methods, which are k-means, wishart cluster, and ASC-S [31], are used to compare the performance with proposed method. The original implementation of ASC-S over-clustered PolSAR images and merged similar classes manually. In this paper, ASC-S clusters the PolSAR image to the number of classes that are defined in the ground truth map directly. DCCM+IIC just combines the DCCM with IIC mutual information loss. The input data of DCCM+IIC are generated from polarimetric coherent matrix $\mathit{T}$, and only random geometry transformations are used to generate paired samples. No rotation domain data are used. In this way, we can more clearly show that the polarimetric matrix rotation in the proposed method can improve deep mutual information learning and the performance of unsupervised PolSAR image classification. The random forest (RF) is used as baseline and it is trained in a supervised manner. For each PolSAR data, 25,000 labeled samples are randomly selected in order to train RF. We run all of the methods multiple times and choose the best classification results.

4.1. Results of GF-3 Wuhan

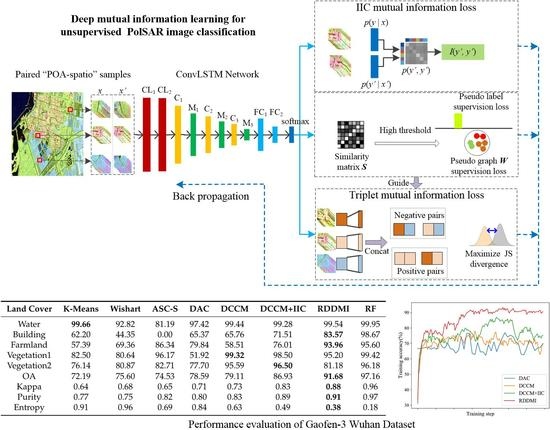
Figure 9 shows the classification results of GF-3 Wuhan dataset and

Table 2. Performance evaluation of GF-3 Wuhan classification results. The numbers in bold denote the best unsupervised classification performance.

Land Cover	K-Means	Wishart	ASC-S	DAC	DCCM	DCCM+IIC	RDDMI	RF
Water	99.66	92.82	81.19	97.42	99.44	99.28	99.54	99.95
Building	62.20	44.35	0.00	65.37	65.76	71.51	83.57	98.67
Farmland	57.39	69.36	86.34	79.84	58.51	76.01	93.96	95.60
Vegetation1	82.50	80.64	96.17	51.92	99.32	98.50	95.20	99.42
Vegetation2	76.14	80.87	82.71	77.70	95.59	96.50	81.18	96.18
OA	72.19	75.60	74.53	78.59	79.11	86.93	91.68	97.16
Kappa	0.64	0.68	0.65	0.71	0.73	0.83	0.88	0.96
Purity	0.77	0.75	0.82	0.80	0.83	0.89	0.91	0.97
Entropy	0.91	0.96	0.69	0.84	0.63	0.49	0.38	0.18

shows the performance evaluation. Because the backscattering property of some pixels in the farmland area is similar to the building type, so the farmland and building areas are difficult to cluster in this dataset. The classification accuracies of k-means, wishart, and ASC-S are low. ASC-S classifies water area to two land cover types and cannot distinguish farmland and building types. The results of DAC and DCCM are comparable. The result of DCCM+IIC is much better. The proposed RDDMI achieves the best classification result, especially the classification accuracies of farmland and building types are both good, and the OA is 4.75% higher than DCCM+IIC. The kappa coefficient, purity, and entropy of the proposed method are also the best. Therefore, the polarimetric features in rotation domain can improve the unsupervised PolSAR data classification.

4.2. Results of RS-2 Flevoland

In the RS-2 Flevoland dataset, the farmland type has different backscattering properties. The backscattering property of some small farmland areas is similar to the forest type. Besides, some small forest areas are interspersed among the building areas, and the forest and building types are hard to cluster. Figure 10 and

Table 3. Performance evaluation of RS-2 Flevoland classification results. The numbers in bold denote the best unsupervised classification performance.

Land Cover	K-Means	Wishart	ASC-S	DAC	DCCM	DCCM+IIC	RDDMI	RF
Water	95.12	90.63	90.77	95.81	93.98	91.28	92.49	95.85
Forest	49.73	77.77	87.14	77.51	76.81	79.63	82.14	87.77
Farmland	38.93	65.65	54.41	80.60	83.74	84.47	86.42	85.60
Building	57.49	55.31	65.04	69.84	94.83	95.90	94.16	82.39
OA	54.70	71.35	72.35	80.15	85.87	86.79	87.86	88.10
Kappa	0.39	0.61	0.62	0.73	0.81	0.82	0.83	0.83
Purity	0.57	0.71	0.72	0.80	0.85	0.86	0.87	0.87
Entropy	1.29	1.12	1.02	0.93	0.72	0.70	0.67	0.68

illustrate that k-means, wishart, ASC-S, and DAC achieve bad results for farmland, forest, or building types. The classification accuracies of DCCM, DCCM+IIC, and proposed method are much better than the above four methods and the OA of proposed method is 1.07% high than DCCM+IIC. Furthermore, the performance of proposed method is very close to the supervised RF, which shows the superiority of proposed method.

4.3. Results of AIRSAR Flevoland

A total of 11 land cover types are identified in the AIRSAR Flevoland dataset and it is a challenge for unsupervised classification. This dataset contains too many unidentified areas, which may contain new land cover types; hence, only the labeled areas are used for training and evaluation. In this dataset, some land cover types have similar backscattering properties. Besides, the observed polarimetric matrices from the same land cover type may also be quite different. The seven methods all do not achieve impressive classification results, as shown in Figure 11 and

Table 4. Performance evaluation of AIRSAR Flevoland classification results. The numbers in bold denote the best unsupervised classification performance.

Land Cover	K-Means	Wishart	ASC-S	DAC	DCCM	DCCM+IIC	RDDMI	RF
Stem bean	73.20	65.15	0.00	93.45	69.51	69.59	94.88	96.69
Forest	77.57	31.13	87.75	79.69	98.30	98.09	97.19	90.18
Potatoes	10.55	87.70	90.35	87.75	43.12	70.97	65.48	89.62
Lucerne	0.62	67.49	72.59	73.93	78.45	77.84	75.78	89.17
Wheat	45.55	57.71	50.40	54.19	34.67	39.27	82.18	77.94
Bare soil	94.08	82.38	75.82	98.52	92.44	94.37	82.88	95.57
Beet	75.12	71.59	82.78	67.45	2.35	93.37	53.32	89.00
Rape seed	59.98	79.90	22.09	59.17	56.78	60.84	35.07	90.38
Peas	67.59	57.95	65.79	66.79	74.30	65.28	78.80	73.50
Grass	0.00	50.36	18.98	1.53	17.55	89.99	91.58	93.56
Water	0.00	0.00	79.96	0.00	0.00	0.00	0.00	99.97
OA	46.73	59.34	58.90	64.91	60.62	67.73	72.84	86.81
Kappa	0.41	0.54	0.53	0.61	0.55	0.64	0.69	0.85
Purity	0.65	0.61	0.66	0.72	0.72	0.77	0.79	0.86
Entropy	1.21	1.58	1.35	1.12	0.96	0.86	0.83	0.73

. The classification accuracies of many land cover types in the results of k-means, wishart, ASC-S, DAC, and DCCM are zero or very low. The backscattering property of water type is similar to other types, so DCCM+IIC and proposed method also do not classify water types correctly. However, the OA, kappa, purity, and entropy of proposed method are still much better than the other six methods. The OA of RDDMI is 5.11% higher than DCCM+IIC. It again shows that the polarimetric matrix rotation is helpful for deep mutual information learning and it can improve the performance of unsupervised PolSAR image classification.

4.4. Results of RS-2 Wuhan

The RS-2 Wuhan dataset contains buildings with different orientations, and it is difficult to classify building type correctly. Figure 12 and

Table 5. Performance evaluation of RS-2 Wuhan classification results. The numbers in bold denote the best unsupervised classification performance.

Land Cover	K-Means	Wishart	ASC-S	DAC	DCCM	DCCM+IIC	RDDMI	RF
Water	97.37	88.10	81.30	90.25	97.19	97.46	92.26	94.01
Building	52.32	67.89	70.30	74.25	58.15	70.16	88.49	88.34
Forest	19.63	74.02	80.90	80.37	75.01	64.26	75.83	81.44
OA	52.31	74.55	76.26	79.93	72.63	74.61	85.31	87.45
Kappa	0.30	0.60	0.63	0.69	0.59	0.62	0.77	0.80
Purity	0.63	0.75	0.76	0.80	0.73	0.75	0.85	0.87
Entropy	1.10	0.88	0.85	0.76	0.92	0.91	0.68	0.59

illustrate the classification results and the performance evaluation, respectively. The result of k-means is very bad. The results of Wishart, DAC, DCCM, and DCCM+IIC are better, but the accuracy of building type or forest type is not high. The OA of RDDMI is the best and the accuracies of building and forest types are both high. The kappa, purity, and entropy of RDDMI are also the best. The proposed method uses rotation domain polarimetric coherent matrices and it shows high robustness to buildings with different orientations. Besides, the OA of the proposed method is close to supervised RF, only 2.14% lower than RF, and it again shows that the proposed method has high performance for unsupervised PolSAR image classification.

5. Discussion

5.1. Semi-Supervised Classification

The proposed method can learn discriminative feature representation, which can be used for semi-supervised classification. The RF is used as the classifier of the semi-supervised classification. Three kinds of data are used as the input of RF. One is the polarimetric coherent matrix $\mathit{T}$, and the other two are the features from the two fully connected layers FC${}_1$ and FC${}_2$ on the top of the network. The output of FC${}_1$ is a 64 dimension vector and the output of FC${}_2$ is a N dimension vector, where N is the number of classes. The GF-3 Wuhan, RS-2 Flevoland, and AIRSAR Flevoland datasets are used for the semi-supervised classification performance evaluation. For each dataset, the classification results with different numbers of labeled training samples are illustrated. When the labeled training samples are less than 1000, the experiments are thought to be semi-supervised classification [54]. We run all of the experiments multiple times and choose the best results.

Table 6. The semi-supervised classification accuracies of GF-3 Wuhan (%).

Number of Samples	Input	Water	Building	Farmland	Vegetation1	Vegetation2	OA
100	$\mathit{T}$	99.79	80.12	90.35	92.70	90.12	91.58
	FC${}_1$	99.32	79.22	94.96	95.27	90.81	93.82
	FC${}_2$	99.68	75.17	93.56	95.44	85.15	91.81
1000	$\mathit{T}$	99.94	88.45	91.64	97.39	92.39	93.80
	FC${}_1$	99.53	81.82	96.51	95.91	90.87	94.77
	FC${}_2$	99.48	81.88	95.61	94.15	88.24	93.62
25,000	$\mathit{T}$	99.95	98.67	95.60	99.42	96.18	97.16
	FC${}_1$	99.73	95.94	96.84	98.58	96.48	97.42
	FC${}_2$	99.60	87.53	95.54	96.28	90.76	94.78

shows the semi-supervised classification results of GF-3 Wuhan dataset. When the number of labeled training samples is 25,000, the OA of FC${}_1$ is the best and the OA of $\mathit{T}$ is a little lower. When the number of samples reduces to 1000, the OA of $\mathit{T}$ decreases a lot. The OA of FC${}_1$ is the best and the OA of FC${}_2$ is the lowest. When the number of samples is 100, the OAs of $\mathit{T}$ and FC${}_2$ are closed to each other, and the OA of FC${}_1$ is the best.

Table 7. The semi-supervised classification accuracies of RS-2 Flevoland (%).

Number of Samples	Input	Water	Forest	Farmland	Building	OA
100	$\mathit{T}$	97.12	67.32	59.69	52.74	66.98
	FC${}_1$	90.08	88.13	89.58	88.81	89.08
	FC${}_2$	92.18	83.16	87.18	90.45	87.57
1000	$\mathit{T}$	95.25	81.06	83.21	73.35	82.66
	FC${}_1$	91.24	87.67	90.01	92.84	90.16
	FC${}_2$	90.83	83.93	88.92	93.54	88.81
25,000	$\mathit{T}$	95.85	87.77	85.60	82.39	88.10
	FC${}_1$	94.03	90.89	91.63	95.12	92.58
	FC${}_2$	91.40	85.60	89.50	93.14	89.48

shows the classification results of the RS-2 Flevoland dataset. When the number of samples is 25,000, the OA of FC${}_1$ is high, and the OAs of $\mathit{T}$ and FC${}_2$ are also good. When the number of samples reduces to 1000 and 100, the OA of $\mathit{T}$ decrease a lot. Especially, when only 100 labeled training samples are used, the OA $\mathit{T}$ is very low, only 66.98%. The OAs of FC${}_1$ and FC${}_2$ decrease a little and the performance of FC${}_1$ is the best.

For ARISAR dataset, the classification result of FC${}_1$ is very good when the number of samples is 25,000, and the OAs of $\mathit{T}$ and FC${}_2$ are much lower, as shown in

Table 8. The semi-supervised classification accuracies of AIRSAR Flevoland (%).

Land Cover	110			1100			25,000
	T	FC${}_1$	FC${}_2$	T	FC${}_1$	FC${}_2$	T	FC${}_1$	FC${}_2$
Stem bean	97.95	95.53	94.75	91.79	99.09	96.52	96.69	99.79	99.42
Forest	48.13	94.51	96.36	80.64	97.10	95.50	90.18	99.15	98.01
Potatoes	43.45	86.95	77.01	77.12	91.78	84.54	89.62	97.00	91.77
Lucerne	67.13	90.82	62.98	74.90	96.35	90.61	89.17	99.07	96.70
Wheat	26.81	81.12	83.59	62.74	94.77	92.01	77.94	96.73	95.07
Bare soil	95.32	85.96	79.88	98.60	94.93	88.25	95.57	99.72	97.60
Beet	49.14	80.01	61.39	82.42	88.95	86.32	89.00	96.72	92.75
Rape seed	76.34	85.40	70.34	88.01	90.34	88.88	90.38	97.73	93.12
Peas	20.20	60.63	52.91	63.15	85.52	67.82	73.50	97.11	88.60
Grass	29.62	86.56	89.60	78.45	96.97	92.31	93.56	99.81	98.04
Water	93.32	95.37	86.36	97.88	99.82	95.58	99.97	99.97	99.59
OA	49.44	84.52	77.81	76.58	93.55	88.84	86.81	97.91	94.80

. When the number of samples reduces to 110, all of the classification accuracies are decreased. However, the OA of FC${}_1$ is still good enough, but the OA of $\mathit{T}$ decreases to 49.44% and it is very low.

The above analysis shows that the feature representation of FC${}_1$ can achieve good results in semi-supervised classification for all three datasets with a commonly used RF classifier. The classification results of FC${}_2$ feature representation are also considerable. When the number of samples is very low, the performance of low level polarimetric feature $\mathit{T}$ is low, and it is not suitable for semi-supervised PolSAR image classification. Therefore, the proposed method can learn discriminative feature representation in an unsupervised manner and improve the performance of semi-supervised PolSAR image classification.

5.2. Training Accuracy Trend

In this section, the classification accuracies of the four datasets during the training process are discussed, as shown in Figure 13. As the number of training steps increases, the cluster accuracy also increases, and it can achieve a relatively stable value. For the GF-3 Wuhan, AIRSAR Flevoland, and RS-2 Wuhan datasets, the accuracies of proposed methods are always higher than DAC, DCCM and DCCM+IIC during training. For the RS-2 Flevoland dataset, the accuracies of DCCM, DCCM+IIC, and the proposed method are closed to each other, but the accuracy of proposed method still a litter higher than DCCM+IIC. Besides, for the four datasets, the performance of DCCM+IIC is better than DCCM, and the performances of DCCM and DAC are comparable. The combination of the deep mutual information algorithms of IIC and DCCM can improve the classification accuracies. By learning the rotation domain deep mutual information while using IIC and DCCM mutual information algorithms, the proposed method is superior to DAC, DCCM, and DCCM+IIC, and it can achieve good performance for unsupervised PolSAR image classification.

As shown in Figure 13, the proposed method also has a disadvantage. As with other unsupervised methods, the cluster accuracies of the proposed method still change in a small range after long time training. However, the range of such accuracy variation is very small and rather smaller than the other methods. It has limited impact on the cluster performance. Therefore, the proposed method has promising value in practical applications.

6. Conclusions

In this paper, the convolutional LSTM and two mutual information losses are used in order to learn the rotation domain deep mutual information of “POA-spatio” polarimetric coherent matrices for unsupervised PolSAR image classification. The proposed method achieves good performance on four real PolSAR image datasets. When compared to six unsupervised classification methods, the performance of proposed method is the best. The proposed method is end-to-end, and no extra preprocessing or post-processing is needed. The deep mutual information of PolSAR image in rotation domain is very helpful for discriminative feature representation learning, and the proposed method also shows good performance in semi-supervised PolSAR image classification.