Satellite-Based Evapotranspiration in Hydrological Model Calibration
Abstract
1. Introduction
2. Methodology
2.1. Hydrological Model
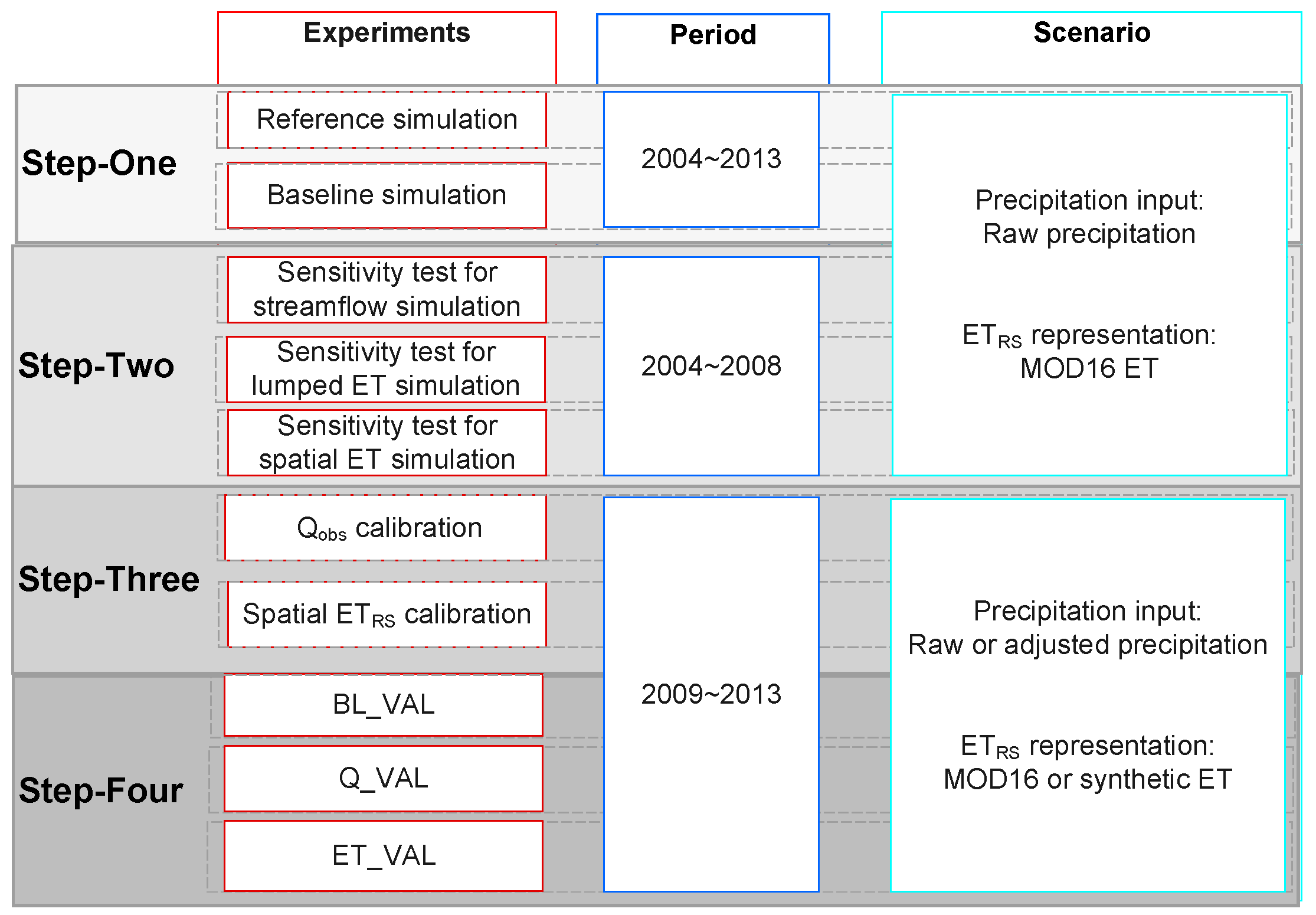
2.2. Model Calibration Experiments
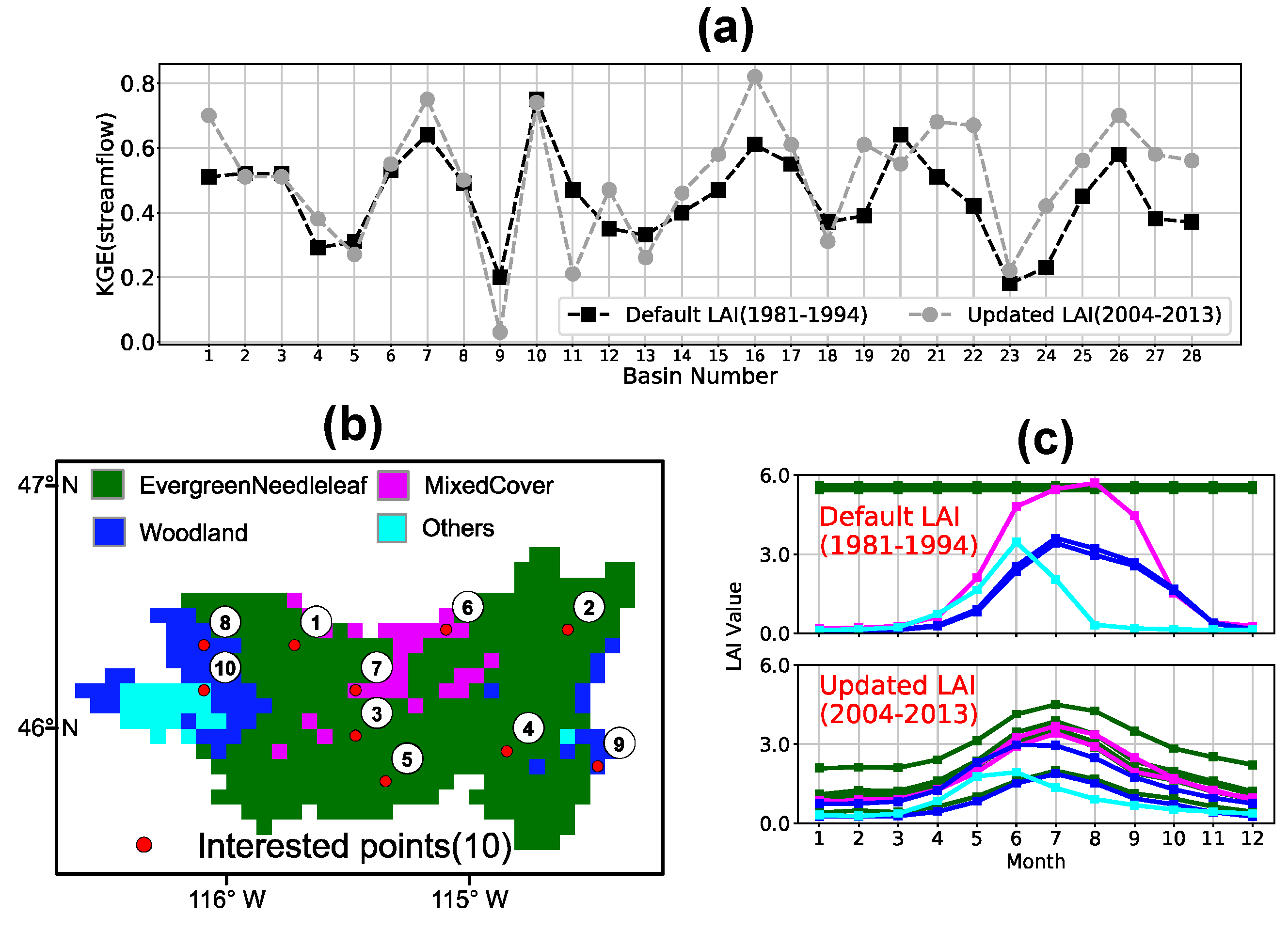
2.2.1. Updating Model Vegetation Inputs
2.2.2. Identifying Sensitive Parameters for Model Calibration
2.2.3. Calibration Model
2.2.4. Model Validation and Evaluation
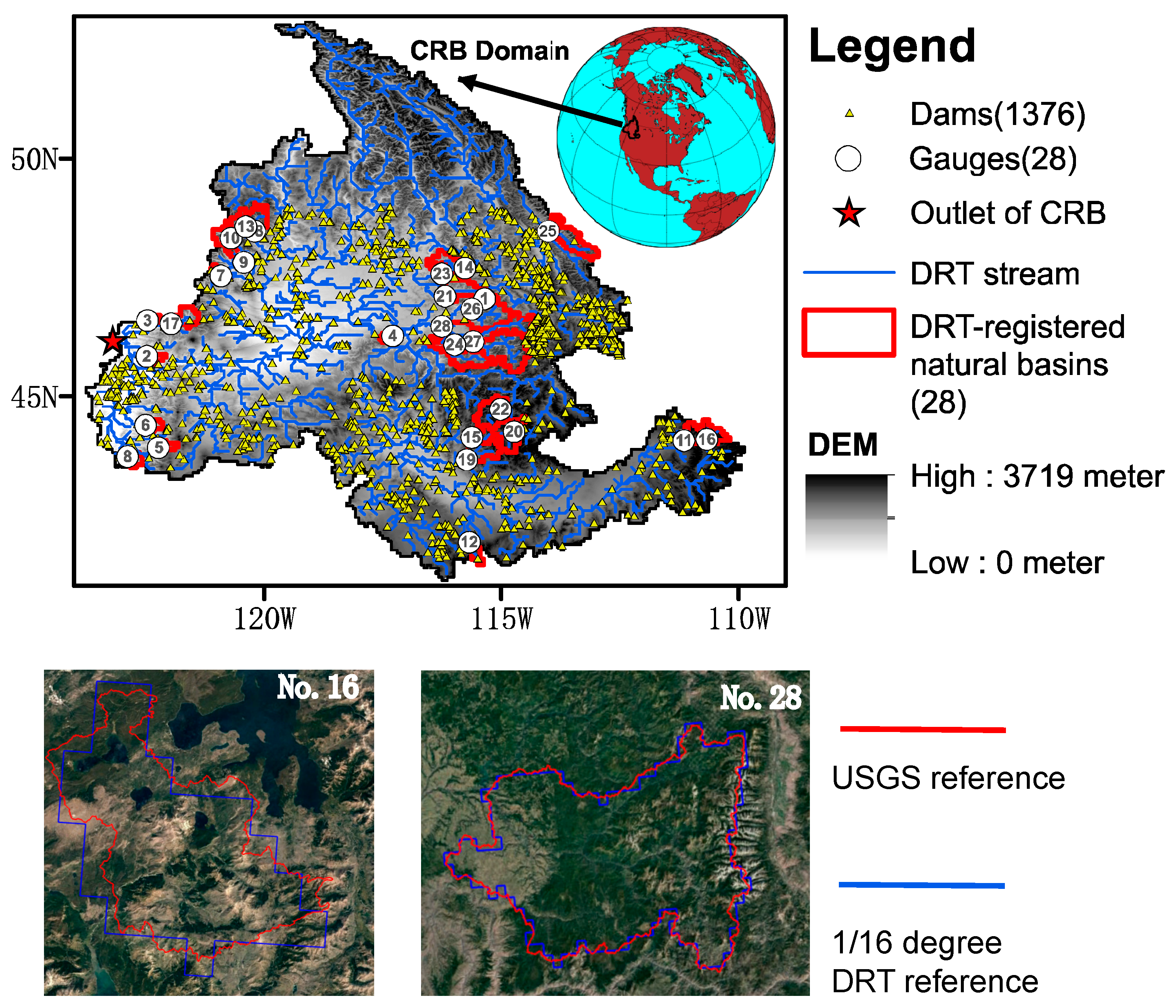
3. The Test Area and Datasets
4. Results
4.1. The Baseline Simulation
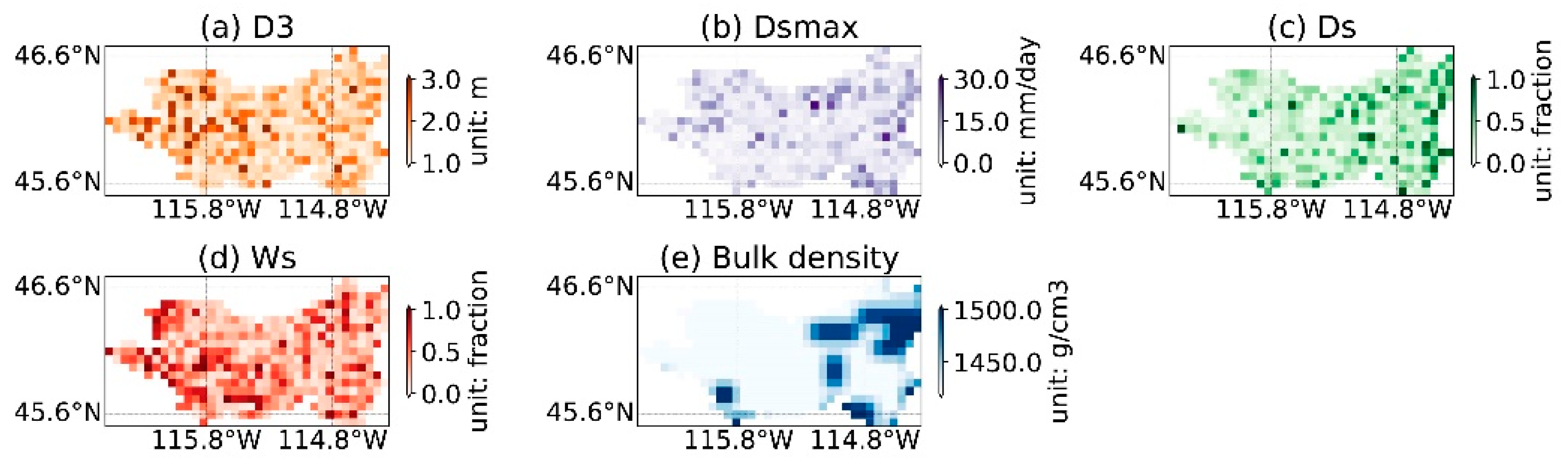
4.2. Sensitivity Analysis of Soil Parameters
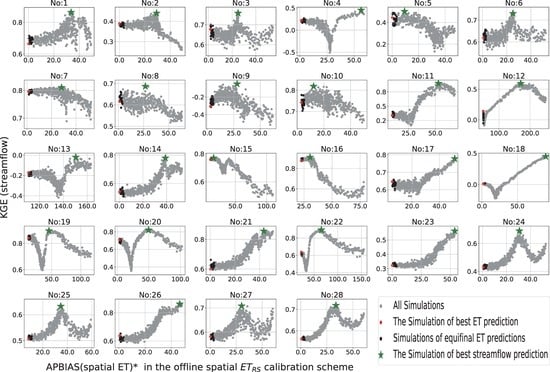
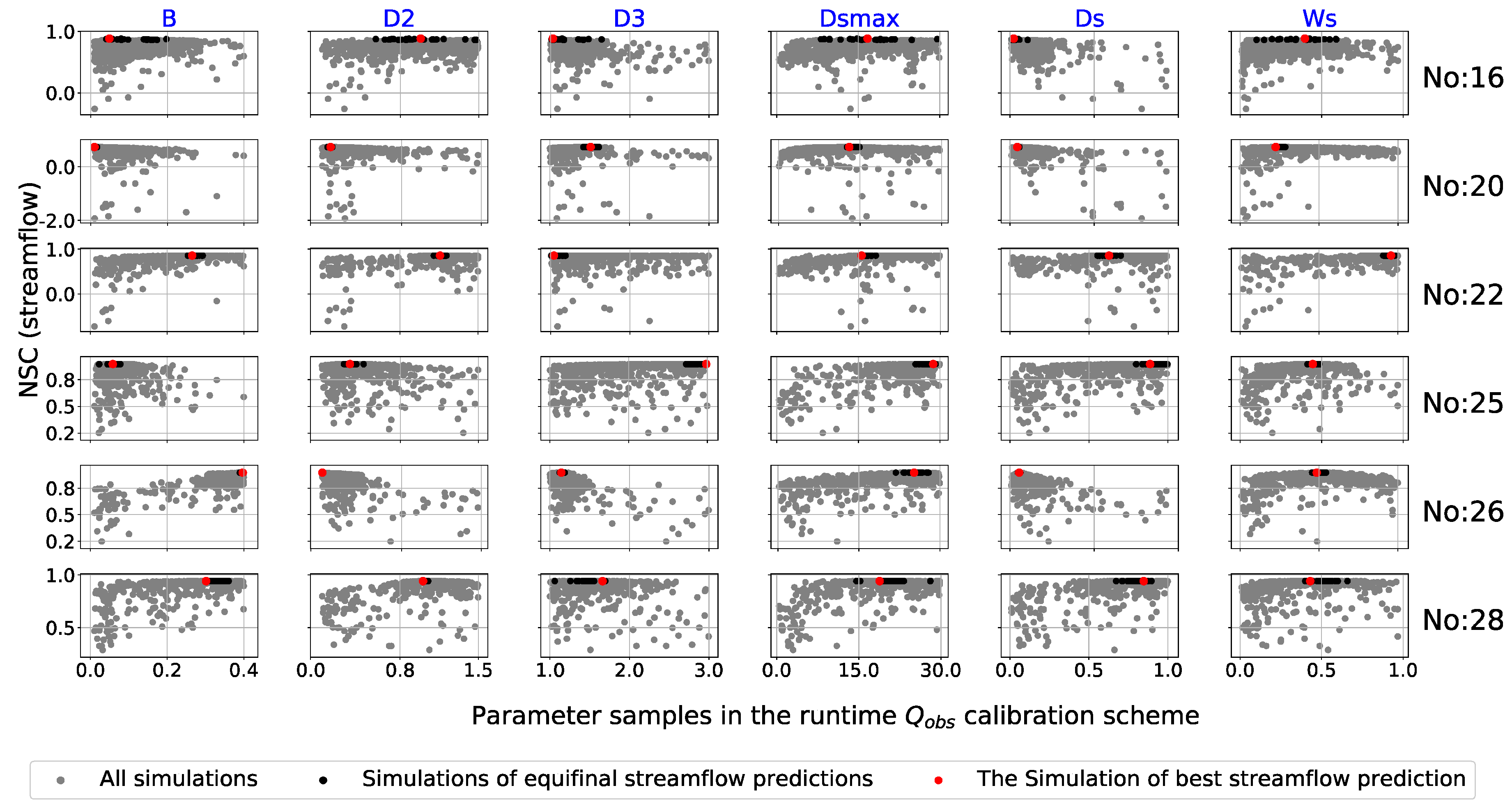
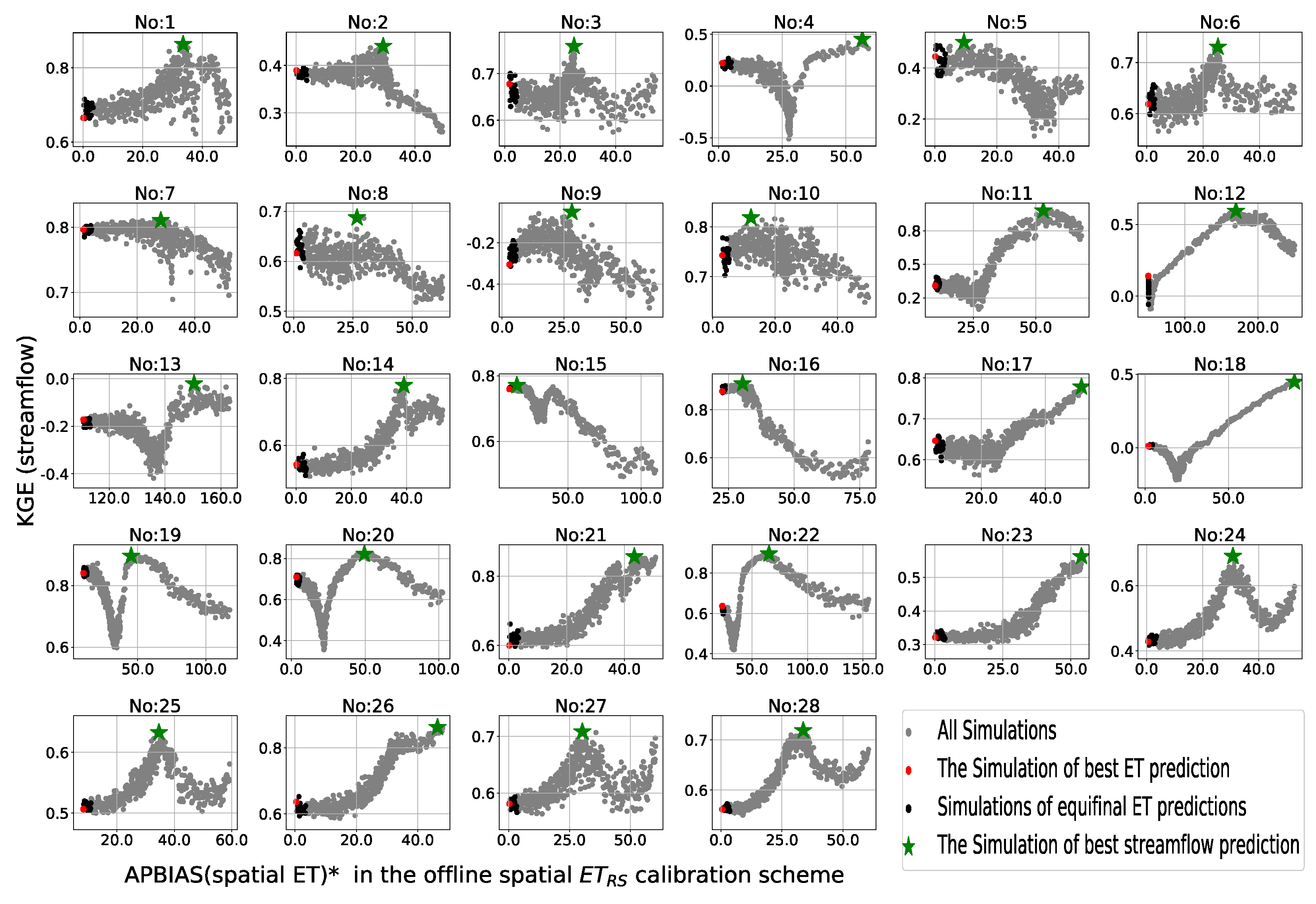
4.3. Uncertainty in the Calibrated Model Parameters
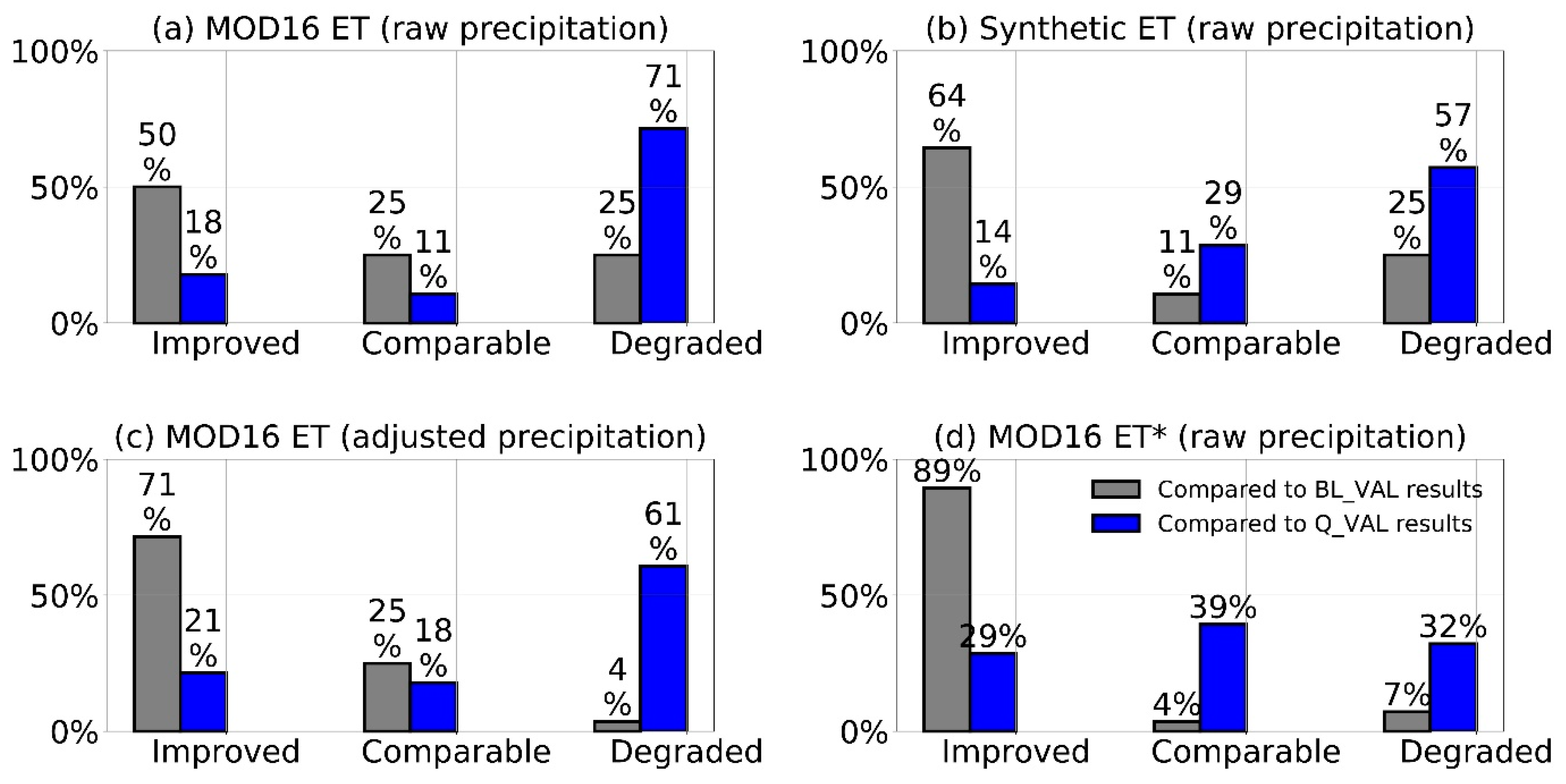
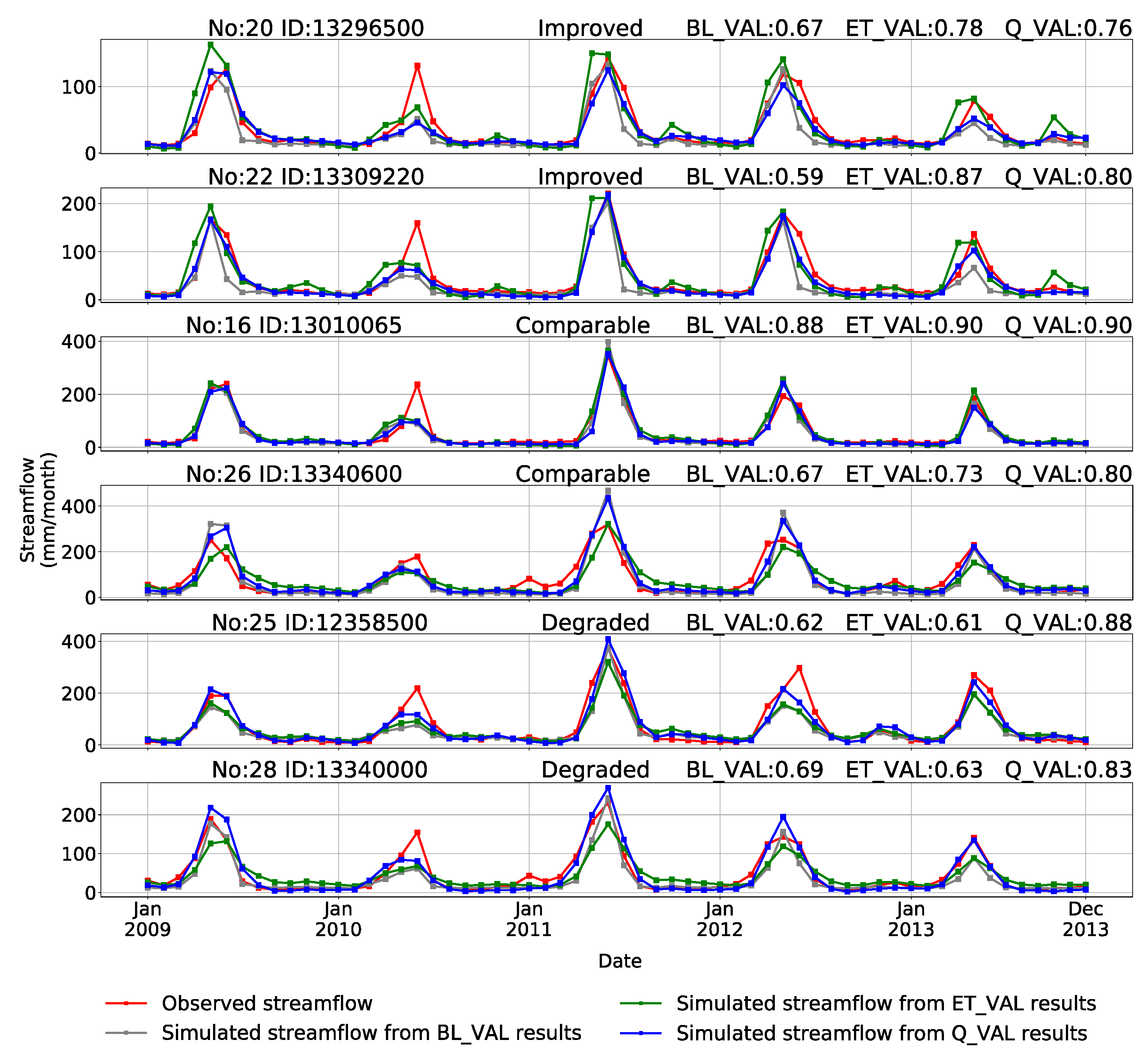
4.4. Validation and Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Arnold, J.G.; Youssef, M.A.; Yen, H.; White, M.J.; Sheshukov, A.Y.; Sadeghi, A.M.; Moriasi, D.N.; Steiner, J.L.; Amatya, D.M.; Skaggs, R.W.; et al. Hydrological processes and model representation: Impact of soft data on calibration. Trans. ASABE 2015, 58, 1637–1660. [Google Scholar] [CrossRef]
- Wu, H.; Kimball, J.S.; Elsner, M.M.; Mantua, N.; Adler, R.F.; Stanford, J. Projected climate change impacts on the hydrology and temperature of Pacific Northwest rivers. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow prediction in ungauged basins: Review of regionalization methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Mendiguren, G.; Koch, J.; Stisen, S. Spatial pattern evaluation of a calibrated national hydrological model—A remote-sensing-based diagnostic approach. Hydrol. Earth Syst. Sci. 2017, 21, 5987–6005. [Google Scholar] [CrossRef]
- Wi, S.; Yang, Y.C.E.; Steinschneider, S.; Khalil, A.; Brown, C.M. Calibration approaches for distributed hydrologic models in poorly gaged basins: Implication for streamflow projections under climate change. Hydrol. Earth Syst. Sci. 2015, 19, 857–876. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Billesbach, D.; Oechel, W.; Zhang, J.H.; Meyers, T.; Martin, T.A.; Matamala, R.; Baldocchi, D.; Bohrer, G.; et al. Global estimation of evapotranspiration using a leaf area index-based surface energy and water balance model. Remote Sens. Environ. 2012, 124, 581–595. [Google Scholar] [CrossRef]
- Yebra, M.; Van Dijk, A.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of optical remote sensing to estimate actual evapotranspiration and canopy conductance. Remote Sens. Environ. 2013, 129, 250–261. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Savenije, H.H.G.; Bastiaanssen, W.G.M. Constraining model parameters on remotely sensed evaporation: Justification for distribution in ungauged basins? Hydrol. Earth Syst. Sci. 2008, 12, 1403–1413. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Zhang, L.; Li, H. Use of remotely sensed actual evapotranspiration to improve rainfall-runoff modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Vervoort, R.W.; Miechels, S.F.; van Ogtrop, F.F.; Guillaume, J.H.A. Remotely sensed evapotranspiration to calibrate a lumped conceptual model: Pitfalls and opportunities. J. Hydrol. 2014, 519, 3223–3236. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction. J. Hydrol. 2016, 535, 509–524. [Google Scholar] [CrossRef]
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Constraining SWAT Calibration with Remotely Sensed Evapotranspiration Data. J. Am. Water Resour. Assoc. 2017, 53, 593–604. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. Remotely sensed ET for streamflow modelling in catchments with contrasting flow characteristics: An attempt to improve efficiency. Stoch. Environ. Res. Risk Assess. 2018, 32, 1973–1992. [Google Scholar] [CrossRef]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining Conceptual Hydrological Models with Multiple Information Sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef]
- Pan, S.; Liu, L.; Bai, Z.; Xu, Y.P. Integration of remote sensing evapotranspiration into multi-objective calibration of distributed hydrology-soil-vegetation model (DHSVM) in a humid region of China. Water 2018, 10. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Kumar, R. Computationally efficient multivariate calibration and validation of a grid-based hydrologic model in sparsely gauged West African river basins. Water 2018, 10. [Google Scholar] [CrossRef]
- Rajib, A.; Evenson, G.R.; Golden, H.E.; Lane, C.R. Hydrologic model predictability improves with spatially explicit calibration using remotely sensed evapotranspiration and biophysical parameters. J. Hydrol. 2018, 567, 668–683. [Google Scholar] [CrossRef] [PubMed]
- Wambura, F.J.; Dietrich, O.; Lischeid, G. Improving a distributed hydrological model using evapotranspiration-related boundary conditions as additional constraints in a data-scarce river basin. Hydrol. Process. 2018, 32, 759–775. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577. [Google Scholar] [CrossRef]
- Odusanya, A.E.; Mehdi, B.; Schürz, C.; Oke, A.O.; Awokola, O.S.; Awomeso, J.A.; Adejuwon, J.O.; Schulz, K. Multi-site calibration and validation of SWAT with satellite-based evapotranspiration in a data-sparse catchment in southwestern Nigeria. Hydrol. Earth Syst. Sci. 2019, 23, 1113–1144. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Improving alpine summertime streamflow simulations by the incorporation of evapotranspiration data. Water 2019, 11. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.; Tian, Y.; Gu, G.; Huffman, G. Evaluation of Quantitative Precipitation Estimations through Hydrological Modeling in IFloodS River Basins. J. Hydrometeorol. 2017, 18, 529–553. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. WIREs Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef]
- Prudhomme, C.; Giuntoli, I.; Robinson, E.L.; Clark, D.B.; Arnell, N.W.; Dankers, R.; Fekete, B.M.; Franssen, W.; Gerten, D.; Gosling, S.N.; et al. Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment. Proc. Natl. Acad. Sci. USA 2014, 111, 3262–3267. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J. Real-time global flood estimation using satellite-based precipitation and a coupled land surface and routing model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Salamon, P.; Beck, H.E.; Lorini, V.; Alfieri, L.; Zsoter, E.; Dadson, S.J. Calibration of the Global Flood Awareness System (GloFAS) using daily streamflow data. J. Hydrol. 2018, 566, 595–606. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Olivera, F.; Famiglietti, J.; Asante, K. Global-scale flow routing using a source-to-sink algorithm. Water Resour. Res. 2000, 36, 2197–2207. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Change 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Wiberg, D.; Leduc, S.; Riahi, K. Power-generation system vulnerability and adaptation to changes in climate and water resources. Nat. Clim. Change 2016, 6, 375–380. [Google Scholar] [CrossRef]
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining mountain snowpack in western north America. Bull. Am. Meteorol. Soc. 2005, 86, 39–49. [Google Scholar] [CrossRef]
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P.; Palmer, R.N. The effects of climate change on the hydrology and water resources of the Colorado River basin. Clim. Change 2004, 62, 337–363. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W.; Hidalgo, H.G.; Bonfils, C.; Santer, B.D.; Das, T.; Bala, G.; Wood, A.W.; Nozawa, T.; Mirin, A.A.; et al. Human-induced changes in the hydrology of the Western United States. Science 2008, 319, 1080–1083. [Google Scholar] [CrossRef]
- Tang, Q.; Vivoni, E.R.; MuñOz-Arriola, F.; Lettenmaier, D.P. Predictability of evapotranspiration patterns using remotely sensed vegetation dynamics during the North American Monsoon. J. Hydrometeorol. 2012, 13, 103–121. [Google Scholar] [CrossRef]
- Livneh, B.; Bohn, T.J.; Pierce, D.W.; Munoz-Arriola, F.; Nijssen, B.; Vose, R.; Cayan, D.R.; Brekke, L. A spatially comprehensive, hydrometeorological data set for Mexico, the U.S., and Southern Canada 1950–2013. Sci. Data 2015, 2. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Sohlberg, R.; Defries, R.S.; Townshend, J.R.G. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Miller, D.A.; White, R.A. A conterminous United States multilayer soil characteristics dataset for regional climate and hydrology modeling. Earth Interactions 1998, 2. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Mishra, A.K.; Singh, V.P. Regionalization of drought characteristics using an entropy approach. J. Hydrol. Eng. 2013, 18, 870–887. [Google Scholar] [CrossRef]
- Shukla, S.; McNally, A.; Husak, G.; Funk, C. A seasonal agricultural drought forecast system for food-insecure regions of East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 3907–3921. [Google Scholar] [CrossRef]
- Lievens, H.; Al Bitar, A.; Verhoest, N.E.C.; Cabot, F.; de Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.J.; Kerr, Y.; Tomer, S.K.; et al. Optimization of a radiative transfer forward operator for simulating SMOS brightness temperatures over the upper Mississippi basin. J. Hydrometeorol. 2015, 16, 1109–1134. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Hydrologic drought atlas for Texas. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Naz, B.S.; Kao, S.C.; Ashfaq, M.; Rastogi, D.; Mei, R.; Bowling, L.C. Regional hydrologic response to climate change in the conterminous United States using high-resolution hydroclimate simulations. Glob. Planet. Chang. 2016, 143, 100–117. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4. [Google Scholar] [CrossRef] [PubMed]
- Park, D.; Markus, M. A new method for establishing hydrologic fidelity of snow depth measurements based on snowmelt–runoff hydrographs. Hydrol. Sci. J. 2018, 63, 369–385. [Google Scholar] [CrossRef]
- Ford, T.W.; Quiring, S.M. Influence of MODIS-derived dynamic vegetation on VIC-simulated soil moisture in oklahoma. J. Hydrometeorol. 2013, 14, 1910–1921. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G.; Bjerklie, D. Integrating remote sensing data on evapotranspiration and leaf area index with hydrological modeling: Impacts on model performance and future predictions. J. Hydrometeorol. 2015, 16, 2086–2100. [Google Scholar] [CrossRef]
- Bohn, T.J.; Vivoni, E.R. Process-based characterization of evapotranspiration sources over the North American monsoon region. Water Resour. Res. 2016, 52, 358–384. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Beechie, T.; Imaki, H. Predicting natural channel patterns based on landscape and geomorphic controls in the Columbia River basin, USA. Water Resour. Res. 2014, 50, 39–57. [Google Scholar] [CrossRef]
- Rajagopalan, K.; Chinnayakanahalli, K.J.; Stockle, C.O.; Nelson, R.L.; Kruger, C.E.; Brady, M.P.; Malek, K.; Dinesh, S.T.; Barber, M.E.; Hamlet, A.F.; et al. Impacts of Near-Term Climate Change on Irrigation Demands and Crop Yields in the Columbia River Basin. Water Resour. Res. 2018, 54, 2152–2182. [Google Scholar] [CrossRef]
- Falcone, J.A. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; US Geological Survey, 2011.
- Falcone, J.A.; Carlisle, D.M.; Wolock, D.M.; Meador, M.R. GAGES: A stream gage database for evaluating natural and altered flow conditions in the conterminous United States: Ecological archives E091-045. Ecology 2010, 91, 621. [Google Scholar] [CrossRef]
- Wu, H.; Kimball, J.S.; Mantua, N.; Stanford, J. Automated upscaling of river networks for macroscale hydrological modeling. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Halldin, S.; Rodhe, A.; Xu, C.Y.; Westerberg, I.K. Disinformative data in large-scale hydrological modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2845–2857. [Google Scholar] [CrossRef]
- Bisselink, B.; Zambrano-Bigiarini, M.; Burek, P.; de Roo, A. Assessing the role of uncertain precipitation estimates on the robustness of hydrological model parameters under highly variable climate conditions. J. Hydrol. Reg. Stud. 2016, 8, 112–129. [Google Scholar] [CrossRef]
- Shepard, D.S. Computer mapping: The SYMAP interpolation algorithm. In Spatial Statistics and Models; Springer, 1984; pp. 133–145. [Google Scholar]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Kumar, S.V.; Mocko, D.M.; Tian, Y. Estimating evapotranspiration with land data assimilation systems. Hydrol. Process. 2011, 25, 3979–3992. [Google Scholar] [CrossRef]
- Kumar, S.V.; Zaitchik, B.F.; Peters-Lidard, C.D.; Rodell, M.; Reichle, R.; Li, B.; Jasinski, M.; Mocko, D.; Getirana, A.; De Lannoy, G.; et al. Assimilation of Gridded GRACE terrestrial water storage estimates in the North American land data assimilation system. J. Hydrometeorol. 2016, 17, 1951–1972. [Google Scholar] [CrossRef]
- Zou, L.; Zhan, C.; Xia, J.; Wang, T.; Gippel, C.J. Implementation of evapotranspiration data assimilation with catchment scale distributed hydrological model via an ensemble Kalman Filter. J. Hydrol. 2017, 549, 685–702. [Google Scholar] [CrossRef]
- Peng, J.; Dan, L.; Dong, W. Estimate of extended long-term LAI data set derived from AVHRR and MODIS based on the correlations between LAI and key variables of the climate system from 1982 to 2009. Int. J. Remote Sens. 2013, 34, 7761–7778. [Google Scholar] [CrossRef]
- Xu, M.; Liang, X.Z.; Samel, A.; Gao, W. MODIS consistent vegetation parameter specifications and their impacts on regional climate simulations. J. Clim. 2014, 27, 8578–8596. [Google Scholar] [CrossRef]

| Reference | River Basin | ETRS* | Model Configuration | Precipitation Input |
|---|---|---|---|---|
| Immerzeel and Droogers [16] | One regulated basin, India (45,678 km2) | SEBAL(MODIS) | Distributed SWAT model (6 to 53) | Field measurements |
| Winsemius et al. [17] | One regulated basin, Zambia (15,000 km2) | SEBAL(MODIS) | Distributed HBV model (7) | Satellite estimations |
| Zhang et al. [18] | 120 basins, Australia (50 to 2000 km2) | P–M (MODIS) | Lumped SIMHYD model (7) | Field measurements |
| Rientjes et al. [19] | Seven basins, Iran (1286 to 9873 km2) | SEBS(MODIS) | Lumped HBV model (7) | Field measurements |
| Vervoort et al. [20] | Four basins, Australia (147 to 2183 km2) | MOD16 ET | Lumped SMA model (8) | Field measurements |
| Kunnath-Poovakka et al. [21] | 11 basins, Australia (62 to 1028 km2) | CMRSET | Distributed AWRA-L model (5) | Field measurements |
| López et al. [22] | One basin, Morocco (38,025 km2) | GLEAM ET | Distributed PCR-GLOBWB model (6) | Multi-Source data |
| Tobin and Bennett [23] | One basin, the United States (610 km2) | GLEAM ET | Distributed SWAT model (16) | Multi-Source data |
| Demirel et al. [24] | One basin, Denmark (2500 km2) | TSEB(MODIS) | Distributed mHM model (26) | Field measurements |
| Herman et al. [25] | One basin, the United States (1110 km2) | ALEXI (GOES), SSEBop(MODIS) | Distributed SWAT model (3 to 15) | Field measurements |
| Kunnath-Poovakka et al. [26] | 28 basins, Australia (55 to 193 km2) | CMRSET | Distributed AWRA-L model (5) | Field measurements |
| Nijzink et al. [27] | 27 basins, Europe (144 to 1587 km2) | LSA-SAF ET, MOD16 ET | Lumped (*) models (*) | Multi-Source data |
| Pan et al. [28] | One basin, China (5996 km2) | SEBAL(MODIS) | Distributed DHSVM model (8) | Field measurements |
| Poméon et al. [29] | 36 basins, Africa (473,718 km2 in total ) | GLEAM ET, MOD16 ET | Distributed mHM model (29) | Multi-Source data |
| Rajib et al. [30] | One basin, the United States (1670 km2) | MOD16 ET | Distributed SWAT model (21 to 31) | Field measurements |
| Wambura et al. [31] | One basin, Tanzania (41,170 km2) | MOD16 ET | Distributed SWAT model (19) | Field measurements |
| Becker et al. [32] | One basin, Pakistan (15,000 km2) | SEBAL(MODIS) | Distributed SWAT model (44) | Field measurements |
| Odusanya et al. [33] | One basin, Nigeria (20,292 km2) | GLEAM ET, MOD16 ET | Distributed SWAT model (11) | Field measurements |
| Tobin and Bennett [34] | One basin, the United States (3356 km2) | GLEAM ET | Distributed SWAT model (23) | Field measurements |
| This study | 28 basins, the United States (326 to 14,332 km2) | MOD16 ET | Distributed VIC model (4 to 6) | Field measurements |
| Parameters | Unit | Description | Range |
|---|---|---|---|
| B | N/A | The variable infiltration curve parameter | 0.0–0.4 |
| Dsmax | mm/day | maximum baseflow that can occur in the third soil layer | 0.0–30.0 |
| Ds | fraction | The fraction of Dsmax where non-linear baseflow begins | 0.0–1.0 |
| Ws | fraction | The fraction of maximum soil moisture where non-linear baseflow occurs | 0.0–1.0 |
| D2 | M | Depth of second soil layer | 0.1–1.5 |
| D3 | M | Depth of third soil layer | 1.0–3.0 |
| Note: All six parameters (B, Dsmax, Ds, Ws, D2, and D3) will be used in Qobs calibration model, and four parameters (Dsmax, Ds, Ws, and D3) will be used in ETRS calibration model. | |||
| No. | Gauge Information | Basin Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ID (USGS) | Latitude (degree) | Longitude (degree) | Drainage area (km²) | Streamflow (mm/year) | Precipitation (mm/year) | Temperature (°C) | Elevation (m) | ||
| 1 | 12413875 | 47.06 | −115.35 | 325.7 | 946.1 | 1383.8 | 5.0 | 1640.3 | |
| 2 | 14222500 | 45.84 | −122.47 | 333.1 | 1785.2 | 2455.4 | 9.4 | 573.3 | |
| 3 | 14236200 | 46.60 | −122.46 | 385.8 | 1791.7 | 1772.6 | 8.6 | 672.9 | |
| 4 | 13334450 | 46.27 | −117.29 | 395.0 | 115.1 | 561.8 | 7.8 | 1271.8 | |
| 5 | 14159200 | 44.05 | −122.22 | 435.7 | 1336.5 | 1782.8 | 7.6 | 1280.8 | |
| 6 | 14185000 | 44.39 | −122.50 | 449.4 | 1573.7 | 1998.6 | 9.0 | 889.5 | |
| 7 | 12458000 | 47.54 | −120.72 | 532.9 | 973.2 | 1655.0 | 4.7 | 1547.5 | |
| 8 | 14154500 | 43.74 | −122.87 | 539.7 | 927.0 | 1561.4 | 9.9 | 857.5 | |
| 9 | 12452800 | 47.82 | −120.42 | 553.0 | 559.1 | 962.4 | 5.7 | 1519.8 | |
| 10 | 12451000 | 48.33 | −120.69 | 878.2 | 1419.1 | 1494.8 | 4.9 | 1534.0 | |
| 11 | 13046995 | 44.06 | −111.15 | 939.2 | 806.7 | 1175.2 | 2.8 | 2349.5 | |
| 12 | 13161500 | 41.93 | −115.68 | 994.2 | 96.0 | 450.4 | 6.0 | 2045.0 | |
| 13 | 12447383 | 48.57 | −120.39 | 1065.9 | 401.4 | 984.8 | 3.7 | 1685.7 | |
| 14 | 12411000 | 47.71 | −115.98 | 1078.6 | 536.3 | 1254.2 | 6.4 | 1202.5 | |
| 15 | 13235000 | 44.09 | −115.62 | 1187.7 | 570.8 | 936.6 | 4.9 | 2079.0 | |
| 16 | 13010065 | 44.10 | −110.67 | 1304.6 | 571.9 | 981.4 | 2.0 | 2508.5 | |
| 17 | 14231000 | 46.53 | −121.96 | 1492.9 | 1715.3 | 1804.6 | 6.5 | 1128.6 | |
| 18 | 12448000 | 48.48 | −120.19 | 1784.1 | 206.1 | 617.4 | 4.4 | 1613.0 | |
| 19 | 13185000 | 43.67 | −115.73 | 2144.7 | 455.1 | 883.8 | 5.9 | 1955.1 | |
| 20 | 13296500 | 44.27 | −114.73 | 2168.3 | 358.0 | 753.8 | 3.1 | 2375.2 | |
| 21 | 12414500 | 47.27 | −116.19 | 2656.6 | 724.4 | 1231.0 | 6.3 | 1381.3 | |
| 22 | 13309220 | 44.72 | −115.01 | 2666.8 | 455.6 | 897.8 | 3.8 | 2192.4 | |
| 23 | 12413000 | 47.57 | −116.25 | 2712.7 | 587.1 | 1207.0 | 6.7 | 1167.8 | |
| 24 | 13338500 | 46.09 | −115.98 | 3077.4 | 227.4 | 863.8 | 6.1 | 1384.6 | |
| 25 | 12358500 | 48.50 | −114.01 | 3239.1 | 771.9 | 1166.6 | 3.8 | 1723.7 | |
| 26 | 13340600 | 46.84 | −115.62 | 3354.2 | 846.4 | 1426.0 | 5.9 | 1442.7 | |
| 27 | 13337000 | 46.15 | −115.59 | 3962.2 | 579.0 | 1245.0 | 5.3 | 1584.1 | |
| 28 | 13340000 | 46.48 | −116.26 | 14,331.7 | 493.5 | 1021.2 | 6.0 | 1443.6 | |
| ID | Raw Precipitation | Adjusted Precipitation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NO. | (USGS) | BL_VAL | ET_VAL (MOD16 ET) | ET_VAL (MOD16 ET*) | ET_VAL (Synthetic ET) | Q_VAL | BL_VAL | ET_VAL (MOD16 ET) | Q_VAL |
| 1 | 12413875 | 0.53 | 0.63 | 0.55 | 0.69 | 0.56 | 0.71 | 0.74 | 0.62 |
| 2 | 14222500 | 0.48 | 0.47 | 0.51 | 0.47 | 0.49 | 0.57 | 0.57 | 0.55 |
| 3 | 14236200 | 0.68 | 0.66 | 0.78 | 0.93 | 0.86 | 0.84 | 0.77 | 0.87 |
| 4 | 13334450 | 0.49 | 0.31 | 0.50 | 0.63 | 0.13 | 0.16 | 0.54 | 0.57 |
| 5 | 14159200 | −0.12 | 0.23 | 0.35 | 0.20 | 0.52 | 0.06 | 0.36 | 0.48 |
| 6 | 14185000 | 0.52 | 0.56 | 0.66 | 0.56 | 0.69 | 0.48 | 0.54 | 0.66 |
| 7 | 12458000 | 0.73 | 0.85 | 0.83 | 0.90 | 0.92 | 0.78 | 0.89 | 0.91 |
| 8 | 14154500 | 0.56 | 0.60 | 0.76 | 0.57 | 0.72 | 0.57 | 0.62 | 0.58 |
| 9 | 12452800 | 0.04 | −0.11 | −0.02 | 0.03 | 0.29 | 0.56 | 0.43 | 0.66 |
| 10 | 12451000 | 0.74 | 0.80 | 0.86 | 0.85 | 0.90 | 0.58 | 0.66 | 0.86 |
| 11 | 13046995 | 0.36 | 0.43 | 0.90 | 0.73 | 0.91 | 0.17 | 0.25 | 0.95 |
| 12 | 13161500 | 0.37 | 0.26 | 0.57 | 0.34 | 0.74 | 0.26 | 0.81 | 0.72 |
| 13 | 12447383 | 0.42 | 0.26 | 0.37 | 0.43 | 0.45 | 0.49 | 0.59 | 0.83 |
| 14 | 12411000 | 0.56 | 0.60 | 0.83 | 0.62 | 0.82 | 0.38 | 0.54 | 0.89 |
| 15 | 13235000 | 0.69 | 0.89 | 0.82 | 0.73 | 0.85 | 0.54 | 0.54 | 0.90 |
| 16 | 13010065 | 0.85 | 0.91 | 0.91 | 0.55 | 0.86 | 0.88 | 0.90 | 0.90 |
| 17 | 14231000 | 0.63 | 0.70 | 0.76 | 0.74 | 0.78 | 0.51 | 0.68 | 0.68 |
| 18 | 12448000 | 0.28 | −0.02 | 0.31 | 0.47 | 0.48 | 0.32 | 0.46 | 0.79 |
| 19 | 13185000 | 0.66 | 0.95 | 0.91 | 0.68 | 0.83 | 0.77 | 0.79 | 0.92 |
| 20 | 13296500 | 0.46 | 0.44 | 0.52 | 0.68 | 0.58 | 0.67 | 0.78 | 0.76 |
| 21 | 12414500 | 0.83 | 0.72 | 0.80 | 0.73 | 0.77 | 0.77 | 0.72 | 0.85 |
| 22 | 13309220 | 0.74 | 0.76 | 0.84 | 0.51 | 0.85 | 0.59 | 0.87 | 0.80 |
| 23 | 12413000 | 0.32 | 0.40 | 0.68 | 0.45 | 0.82 | 0.26 | 0.38 | 0.81 |
| 24 | 13338500 | 0.49 | 0.48 | 0.79 | 0.48 | 0.78 | 0.27 | 0.41 | 0.88 |
| 25 | 12358500 | 0.66 | 0.61 | 0.77 | 0.88 | 0.92 | 0.62 | 0.61 | 0.88 |
| 26 | 13340600 | 0.71 | 0.62 | 0.85 | 0.61 | 0.86 | 0.67 | 0.73 | 0.80 |
| 27 | 13337000 | 0.62 | 0.56 | 0.70 | 0.51 | 0.82 | 0.60 | 0.56 | 0.87 |
| 28 | 13340000 | 0.62 | 0.59 | 0.81 | 0.52 | 0.89 | 0.69 | 0.63 | 0.83 |
| Average | 0.53 | 0.54 | 0.68 | 0.59 | 0.72 | 0.53 | 0.62 | 0.78 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Wu, H.; Tao, J.; Kimball, J.S.; Alfieri, L.; Chen, X. Satellite-Based Evapotranspiration in Hydrological Model Calibration. Remote Sens. 2020, 12, 428. https://doi.org/10.3390/rs12030428
Jiang L, Wu H, Tao J, Kimball JS, Alfieri L, Chen X. Satellite-Based Evapotranspiration in Hydrological Model Calibration. Remote Sensing. 2020; 12(3):428. https://doi.org/10.3390/rs12030428
Chicago/Turabian StyleJiang, Lulu, Huan Wu, Jing Tao, John S. Kimball, Lorenzo Alfieri, and Xiuwan Chen. 2020. "Satellite-Based Evapotranspiration in Hydrological Model Calibration" Remote Sensing 12, no. 3: 428. https://doi.org/10.3390/rs12030428
APA StyleJiang, L., Wu, H., Tao, J., Kimball, J. S., Alfieri, L., & Chen, X. (2020). Satellite-Based Evapotranspiration in Hydrological Model Calibration. Remote Sensing, 12(3), 428. https://doi.org/10.3390/rs12030428