Temperature and Humidity Profiles Retrieval in a Plain Area from Fengyun-3D/HIRAS Sensor Using a 1D-VAR Assimilation Scheme
Abstract
:1. Introduction
2. Datasets and Model
2.1. Fengyun-3D Hyperspectral Infrared Radiation Atmospheric Sounding (FY-3D/HIRAS) Data and Pre-Processing
2.2. WRF Model
2.3. RTTOV Model
3. Development of a 1D-VAR Assimilation System
3.1. Retrieval Algorithm Mathematical Background
3.2. Cloud-Screening
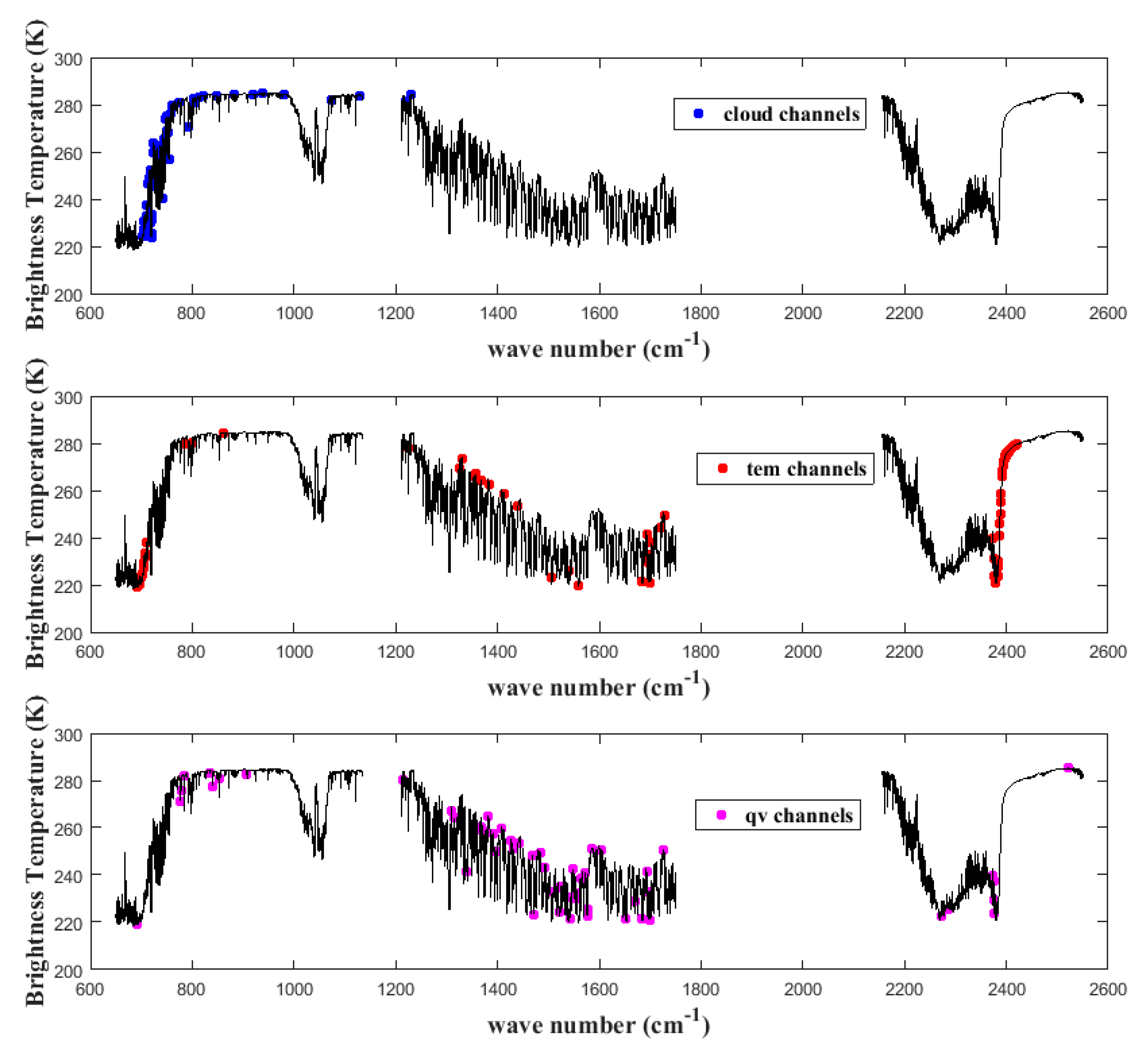
3.3. Channel Selection
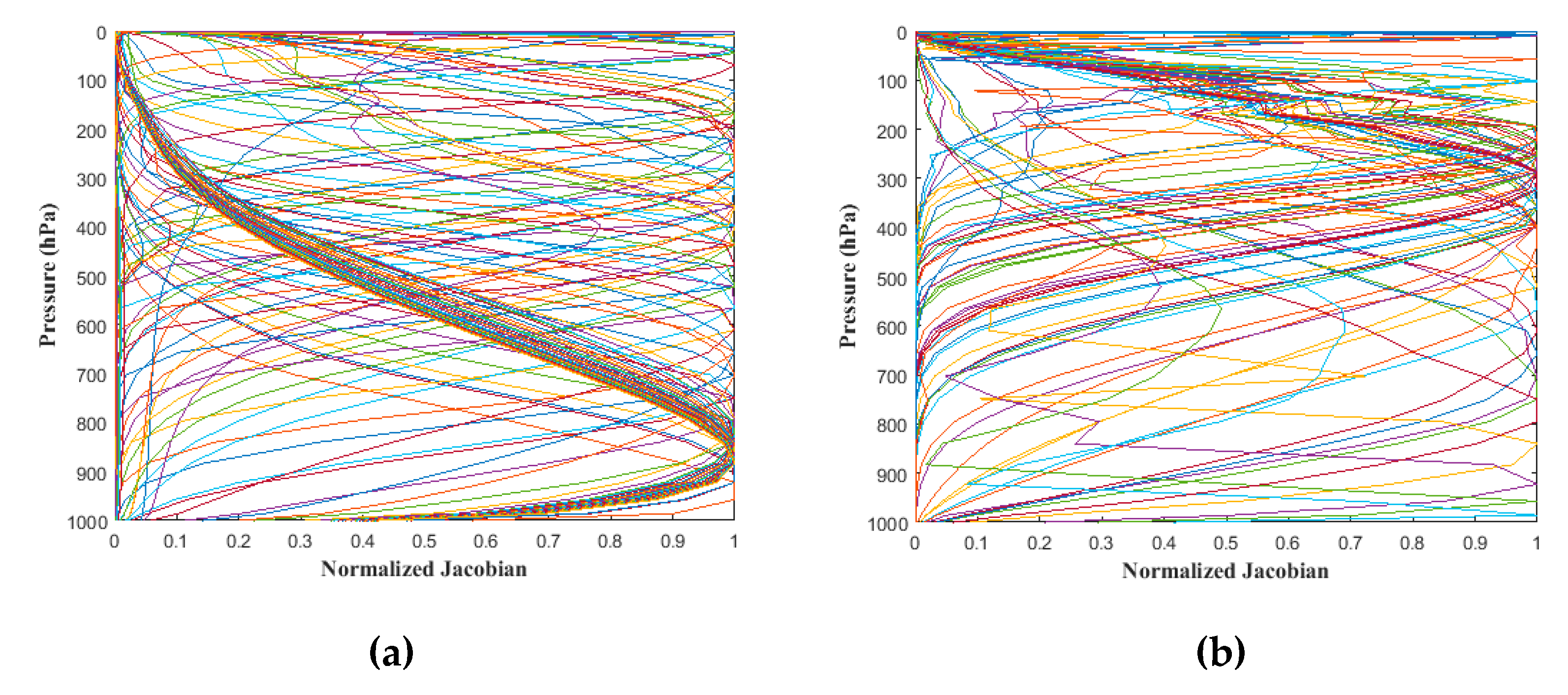
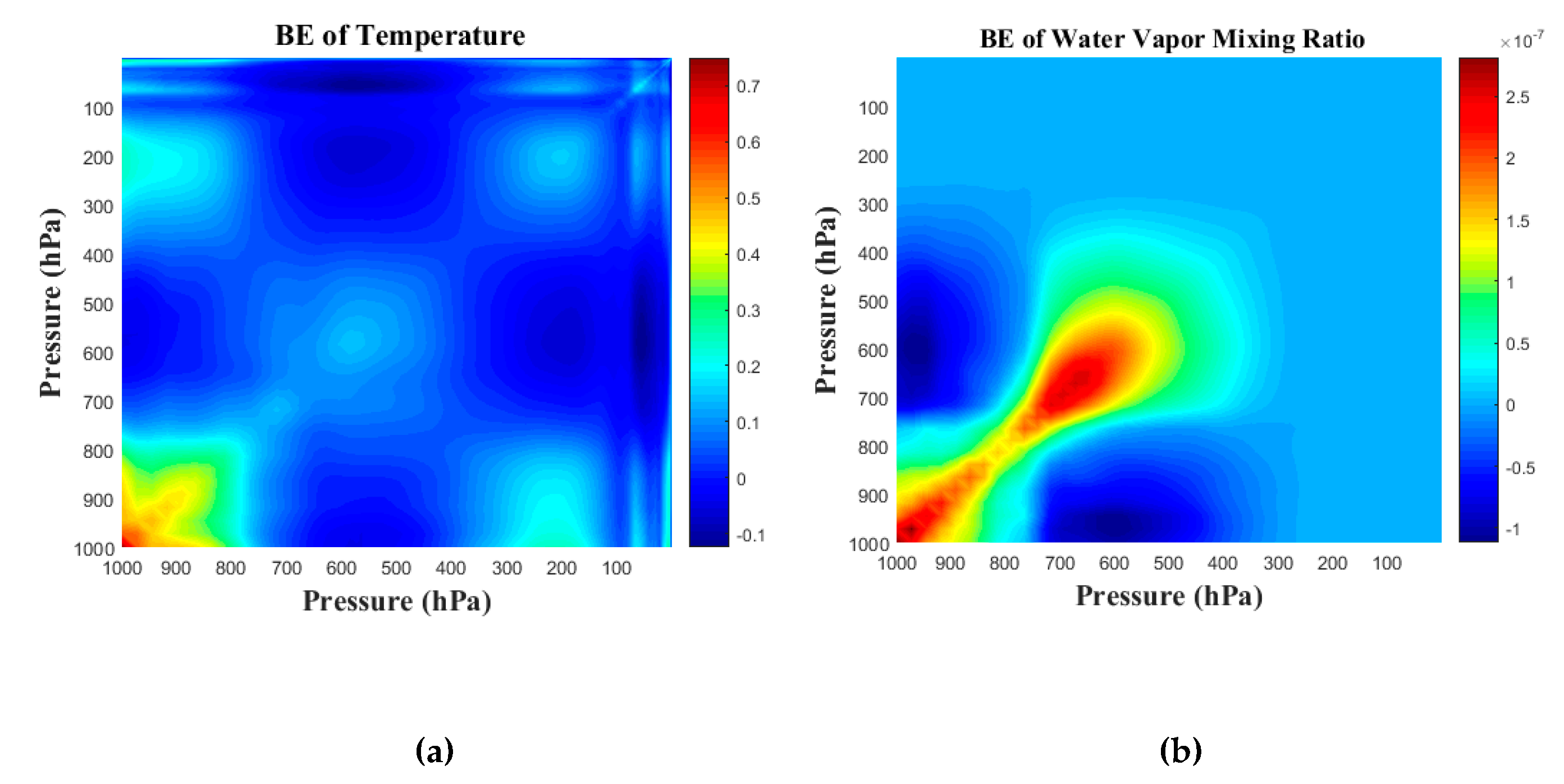
3.4. Background Error Covariance Matrix Localization
3.5. Observation Error Covariance Matrix
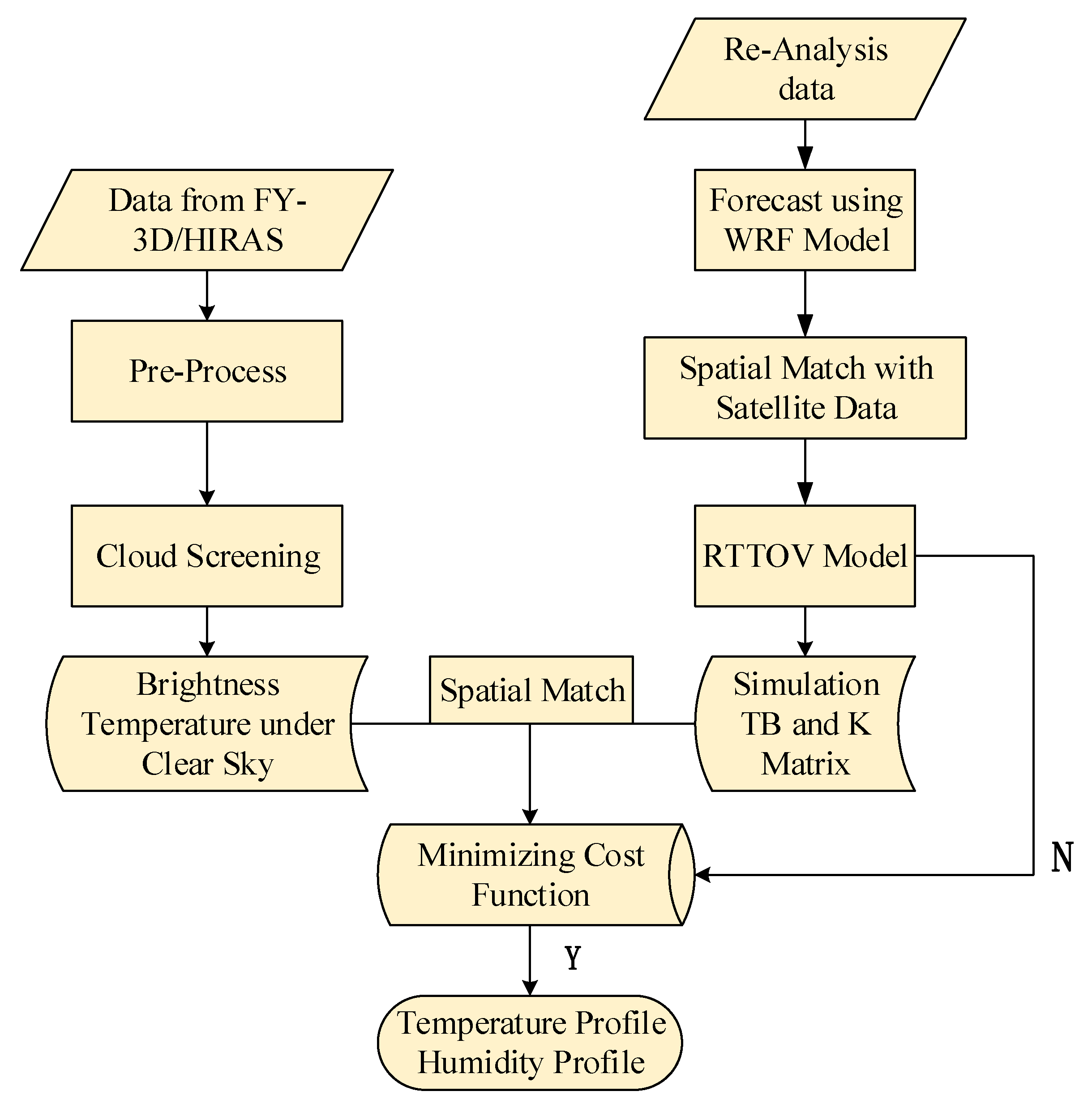
3.6. Retrieval System Framwork
4. Case Study
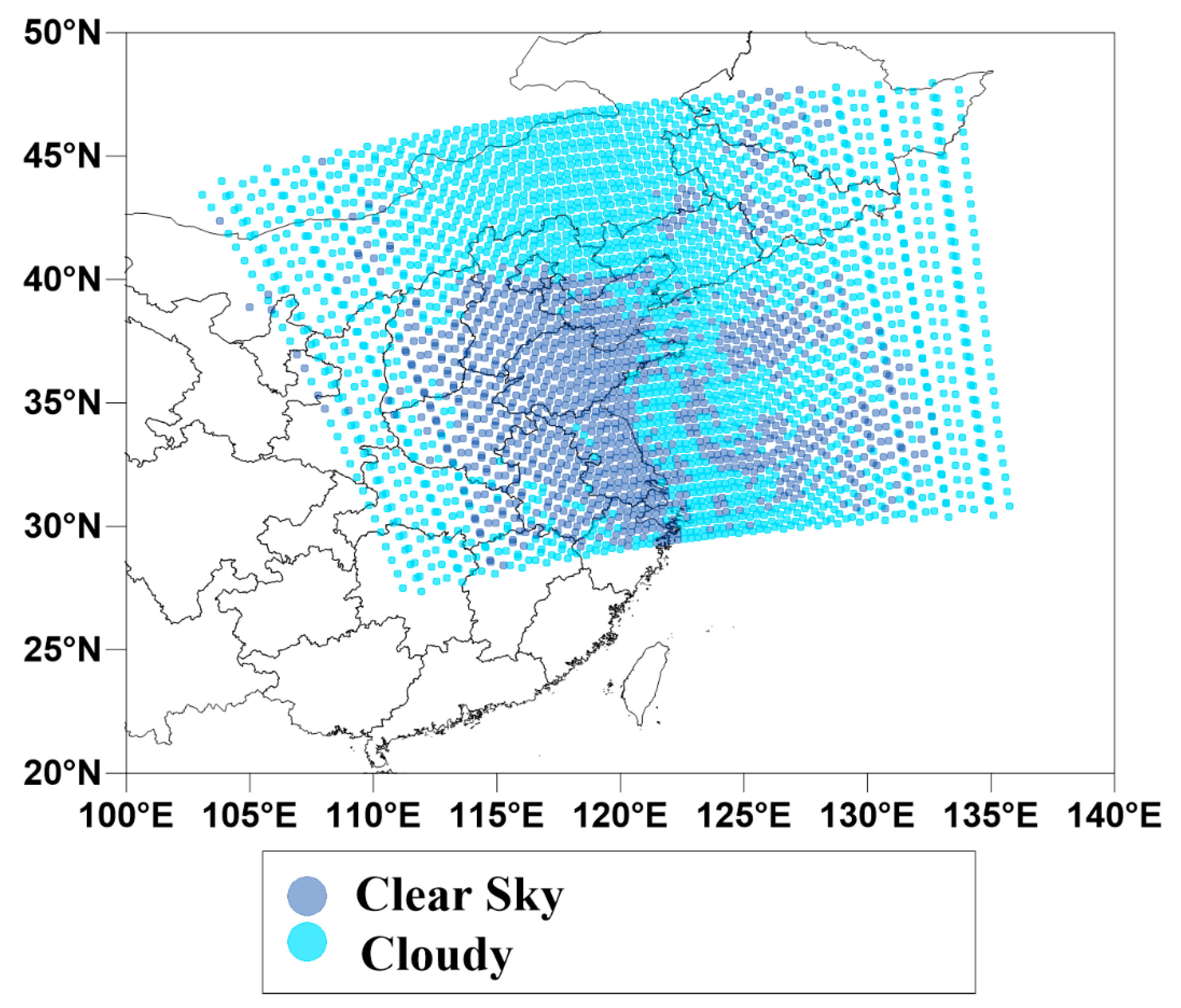
4.1. Cloud Detection
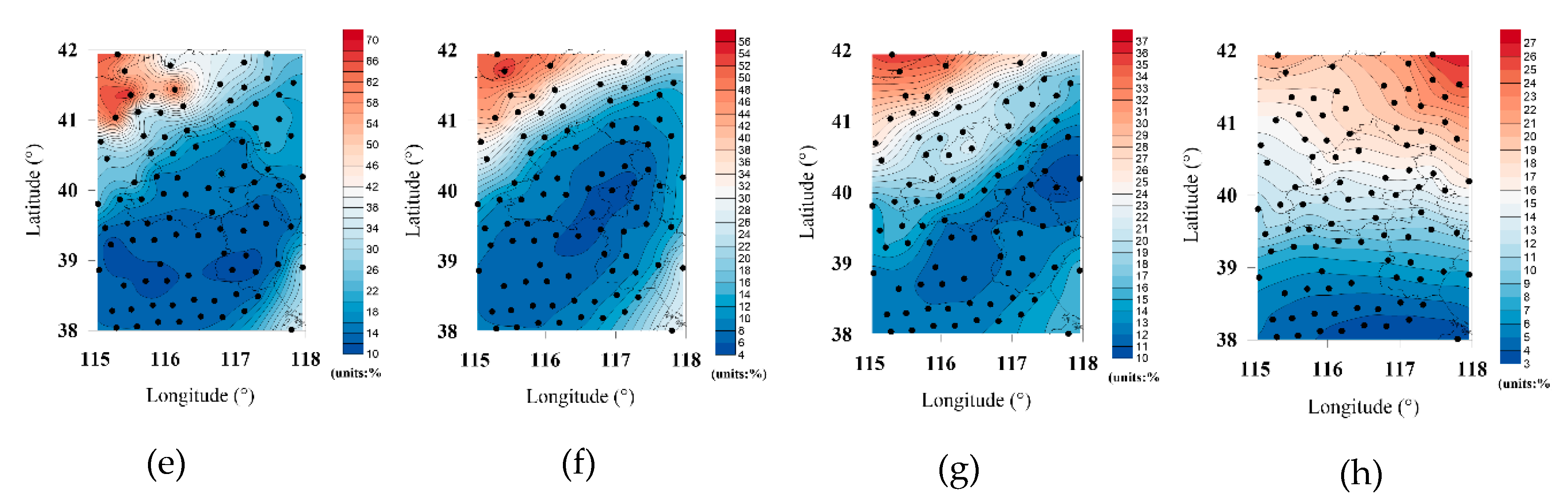
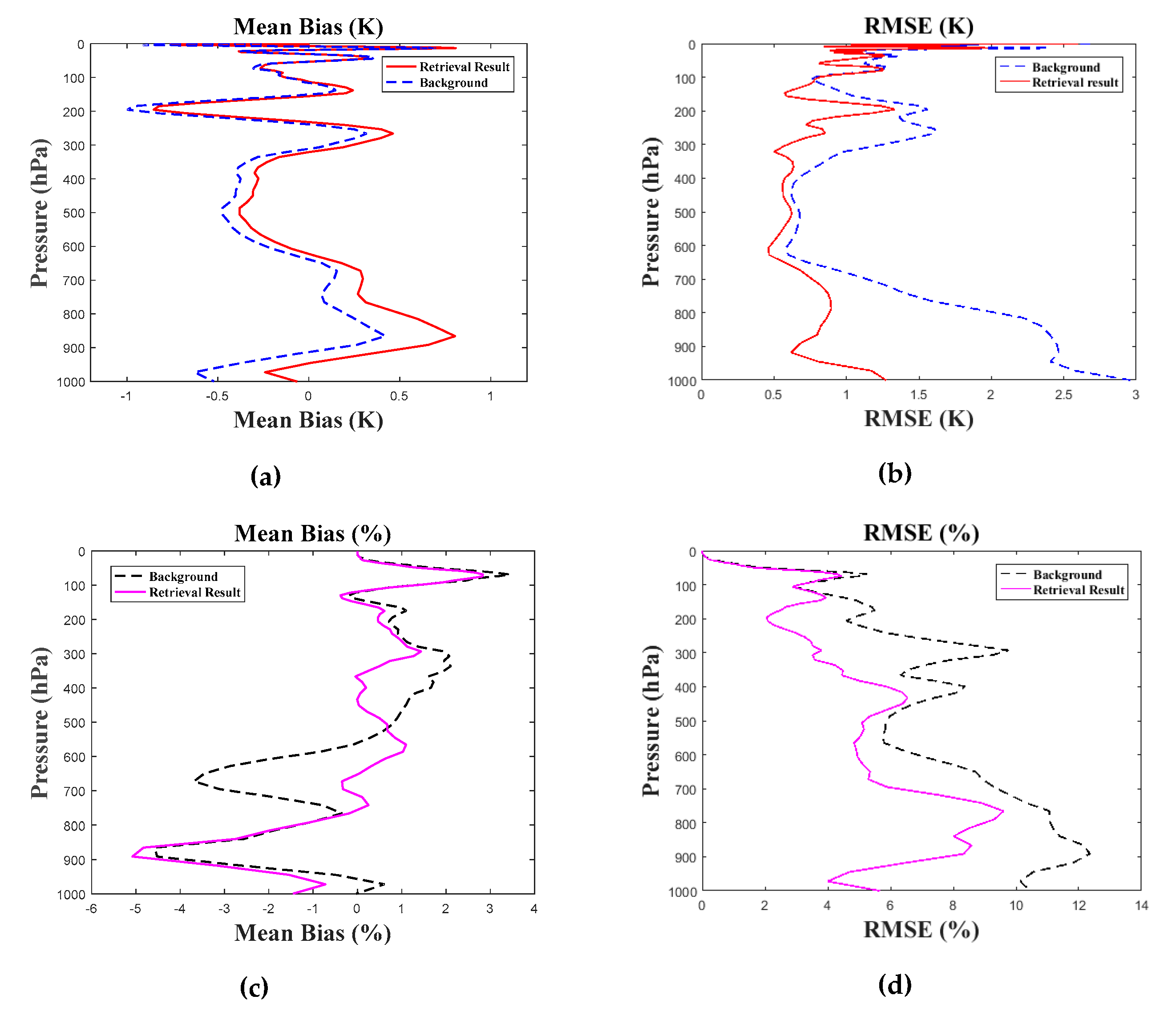
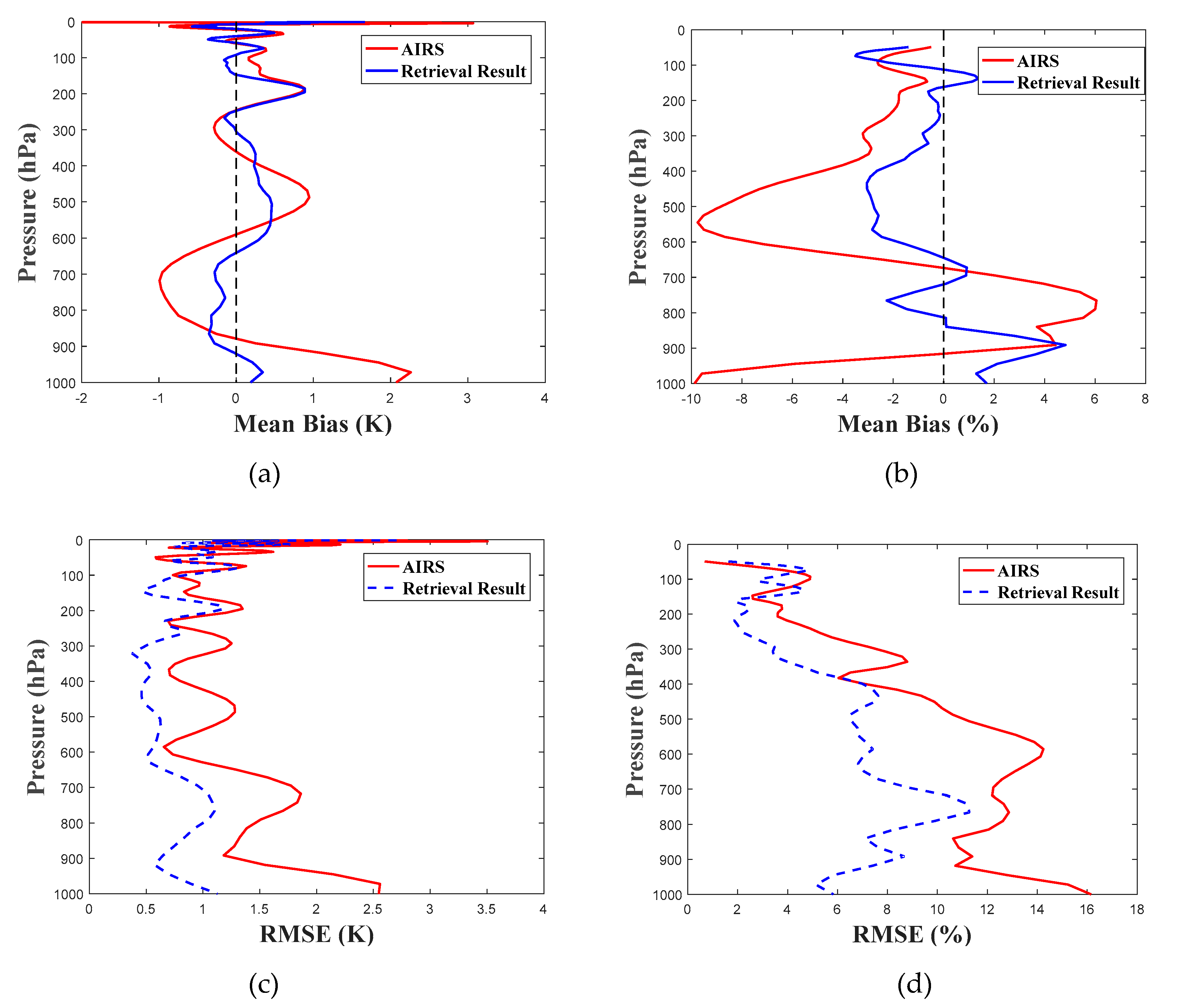
4.2. Results of 1D-VAR Retrieval
5. Conclusions
- Time matching: When establishing the observation error covariance matrix, the input of the forward operator adopted the 05:00 simulation results of the WRF, and the corresponding satellite orbit transit time had a deviation of 0–1.5 hours.
- Space matching: In the inversion algorithm, the satellite pixel and the spatial grid point of the simulated background field from the WRF were not completely spatially matched. The method of spatial matching introduced herein found the closest grid point of the background field within the range of 0.1° with the satellite pixel as the center of longitude and latitude.
- The forward operator (RTTOV) simulation was not accurate, and there were some errors in the radiation transmission mode. Although some errors were corrected to ensure the Gaussian distribution of the errors in the establishment of the inversion system, such errors could not completely eliminate the effects of simulation errors.
- The cloud detection model was not accurate. Cloud detection is the premise of temperature and humidity profile inversion. In this inversion system, the accuracy of the cloud detection model was 86.8%, and the clear-sky pixels could not be completely detected.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bao, Y.; Cai, X.; Qian, C.; Min, J.; Lu, Q.; Zuo, Q. 0-10 KM Temperature and Humidity Profiles Retrieval from Ground-based Microwave Radiometer. J. Trop. Meteorol. 2018, 24, 243–252. [Google Scholar] [CrossRef]
- Li, J.; Li, J.L.; Otkin, J.; Schmit, T.J.; Liu, C.Y. Warning Information in a Preconvection Environment from the Geostationary Advanced Infrared Sounding System—A Simulation Study Using the IHOP Case. J. Appl. Meteorol. Clim. 2011, 50, 776–783. [Google Scholar] [CrossRef]
- Menzel, W.P.; Schmit, T.J.; Zhang, P.; Li, J. Satellite-based atmospheric infrared sounder development and applications. B Am. Meteorol. Soc. 2018, 99, 583–603. [Google Scholar] [CrossRef]
- Smith, W.L.; Woolf, H.M. The Use of Eigenvectors of Statistical Covariance Matrices for Interpreting Satellite Sounding Radiometer Observations. J. Atmos. Sci. 1976, 33, 1127–1140. [Google Scholar] [CrossRef] [Green Version]
- Guan, L.; Huang, A.; Li, J. A Study on Retrieving Atmospheric Profiles from EOS/AIRS Observations. J. Meteorol. Res. Prc. 2005, 19, 112–119. [Google Scholar]
- Guan, L. Retrieving Atmospheric Profiles from MODIS/AIRS Observations. I. Eigenvector Regression Algorithms. J. Nanjing Inst. Meteorol. 2006, 6, 756–761. [Google Scholar] [CrossRef]
- Liu, H.; Dong, C.H.; Zhang, W.J.; Zhang, P. Retrieval of clear air atmospheric temperature profiles using AIRS observation. Acta Meteorol. Sin. 2006, 66, 513–519. [Google Scholar]
- Zhang, J.; Li, Z.L.; Li, J.; Li, J.L. Ensemble Retrieval of Atmospheric Temperature Profiles from AIRS. Adv. Atmos. Sci. 2014, 31, 559–569. [Google Scholar] [CrossRef]
- Cabreramercader, C.R.; Staelin, D.H. Passive microwave relative humidity retrievals using feedforward neural networks. IEEE Trans. Geosci. Remote 2002, 33, 1324–1328. [Google Scholar] [CrossRef]
- Shi, L. Retrieval of Atmospheric Temperature Profiles from AMSU-A Measurement Using a Neural Network Approach. J. Atmos. Ocean. Technol. 2000, 18, 340–347. [Google Scholar] [CrossRef]
- Churnside, J.H.; Stermitz, T.A.; Schroeder, J.A. Temperature Profiling with Neural Network Inversion of Microwave Radiometer Data. J. Atmos. Ocean. Technol. 1994, 11, 105. [Google Scholar] [CrossRef] [Green Version]
- Devendra, S.; Bhatia, R.C. Study of temperature and moisture profiles retrieved from microwave and hyperspectral infrared sounder data over Indian regions. Indian Radio Space Phys. 2006, 35, 286–292. [Google Scholar]
- Cimini, D.; Hewison, T.J.; Martin, L.; Guldner, J.; Gaffard, C.; Marzano, F.S. Temperature and humidity profile retrievals from ground-based microwave radiometers during TUC. Meteorol. Z. 2006, 15, 45–56. [Google Scholar] [CrossRef]
- Hewison, T.J. 1D-VAR Retrieval of Temperature and Humidity Profiles from a Ground-Based Microwave Radiometer. IEEE Trans. Geosci. Remote 2007, 45, 2163–2168. [Google Scholar] [CrossRef]
- Mirza, C.R.; Koike, T.; Yang, K.; Graf, T. Retrieval of Atmospheric Integrated Water Vapor and Cloud Liquid Water Content Over the Ocean from Satellite Data Using the 1-D-Var Ice Cloud Microphysics Data Assimilation System (IMDAS). IEEE Trans. Geosci. Remote 2007, 46, 119–129. [Google Scholar] [CrossRef]
- Boukabara, S.A.; Garrett, K.; Chen, W.C.; Sanchez, F.I.; Grassotti, C.; Kongoli, C.; Chen, R.Y.; Liu, Q.H.; Yan, B.H.; Weng, F.Z.; et al. MiRS: An all-weather 1DVAR satellite data assimilation and retrieval system. IEEE Trans. Geosci. Remote 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Q.C. Atmospheric infrared remote sensing and its retrieval problems in clear sky: I. Theoretical study. Chin. J. Atmos. Sci. 1997, 21, 1–9. [Google Scholar]
- Li, J.; Zeng, Q.C. Atmospheric infrared remote sensing and its retrieval problems in clear sky: II. Research on retrieval test. Chin. J. Atmos. Sci. 1997, 21, 87–95. [Google Scholar]
- Liu, Q.H.; Weng, F.Z. One-dimensional variational retrieval algorithm of temperature, water vapor, and cloud water profiles from advanced microwave sounding unit (AMSU). IEEE Trans. Geosci. Remote 2005, 43, 1087–1095. [Google Scholar] [CrossRef]
- Duncan, D.I.; Kummerow, C.D. A 1DVAR retrieval applied to GMI: Algorithm description, validation, and sensitivities. J. Geophys. Res. Atmos. 2016, 121, 7415–7429. [Google Scholar] [CrossRef] [Green Version]
- Jang, H.S.; Sohn, B.J.; Chun, H.W.; Li, J.; Weisz, E. Improved AIRS temperature and moisture soundings with local a priori information for the 1DVAR method. J. Atmos. Ocean. Technol. 2017, 34, 1083–1095. [Google Scholar] [CrossRef]
- Martinet, P.; Cimini, D.; Angelis, F.D.; Canut, G.; Unger, V.; Guillot, R.; Tzanos, D.; Paci, A. Combining ground-based microwave radiometer and the AROME convective scale model through 1DVAR retrievals in complex terrain: An Alpine valley case study. Atmos. Meas. Technol. 2017, 10, 3385–3402. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhang, P.; Lu, N.M.; Yang, Z.D.; Shi, J.M.; Dong, C.H. Improvements on global meteorological observations from the current Fengyun 3 satellites and beyond. Int. J. Digit. Earth 2012, 5, 251–265. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, Q.; Hu, X.; Gu, S.; Yang, L.; Min, M.; Chen, L.; Xu, N.; Sun, L.; Bai, W.; et al. Latest Progress of the Chinese Meteorological Satellite Program and Core Data Processing Technologies. Adv. Atmos. Sci. 2019, 36, 1027–1045. [Google Scholar] [CrossRef]
- Saunders, R.; Matricardi, M.; Brunel, P. An improved fast radiative transfer model for assimilation of satellite radiance observations. Q. J. R. Meteor. Soc. 1999, 125, 1407–1425. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef] [Green Version]
- Martinet, P.; Dabas, A.; Donier, J.M.; Doffer, T.; Garrouste, O.; Guillot, R. 1D-Var temperature retrievals from microwave radiometer and convective scale model. Tellus A 2015, 67, 27925. [Google Scholar] [CrossRef] [Green Version]
- Guan, Y.H.; Chen, H.; Ren, J.; Zheng, T.W. An Analytical Study on the Differential Equation of Mesoscale Symmetric Instability under Deep Convection. In Proceedings of the International Conference on Applied Mathematics and Mechanics (ICAMM), Bangkok, Thailand, 29–30 October 2016. [Google Scholar] [CrossRef] [Green Version]
- Mcnally, A.P.; Watts, P.D. A cloud detection algorithm for high-spectral-resolution infrared sounders. Q. J. R. Meteor. Soc. 2003, 129, 3411–3423. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Susskind, J.; Barnet, C.D.; Blaisdell, J.M. Retrieval of atmospheric and surface parameters from AIRS/AMSU/HSB data in the presence of clouds. IEEE Trans. Geosci. Remote 2003, 41, 90–409. [Google Scholar] [CrossRef]
- Cao, X.Q.; Zhang, W.M.; Song, J.Q.; Zhang, L.L. Modeling Background Error Covariance in Variational Data Assimilation with Wavelet Method. In Proceedings of the Third International Conference on Information & Computing(ICIC), Wuxi, China, 4–6 June 2010. [Google Scholar] [CrossRef]
- Deblonde, G.; Garand, L.; Gauthier, P.; Grassotti, C. Assimilation of SSM/I and GOES Humidity Retrievals with a One-Dimensional Variational Analysis Scheme. J. Appl. Meteorol. 1995, 34, 1536–1550. [Google Scholar] [CrossRef] [Green Version]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Bannister, R.N. Collection of Results on Background Error Covariance Models. DARC Internal Report 7. Reading, UK, 2006. Available online: https://scholar.google.com.tw/scholar?hl=en&as_sdt=0%2C5&q=Collection+of+Results+on+Background+Error+Covariance+Models&btnG= (accessed on 6 January 2020).
- Bouttier, F.; Courtier, P. Data assimilation concepts and methods March 1999. Meteorological training course lecture series. Available online: https://scholar.google.com.tw/scholar?hl=en&as_sdt=0%2C5&q=Data+assimilation+concepts+and+methods+March+1999&btnG= (accessed on 6 January 2020).
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteor. Soc. 2010, 133, 631–642. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S. Variational bias correction of satellite radiance data in the ERA-Interim reanalysis. Q. J. R. Meteor. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]
- Yang, J.; Min, Q. Retrieval of Atmospheric Profiles in the New York State Mesonet Using One-Dimensional Variational Algorithm. J. Geophys. Res. Atmos. 2018, 123, 7563–7575. [Google Scholar] [CrossRef]
- Che, Y.; Ma, S.; Xing, F.; Li, S.; Dai, Y. An improvement of the retrieval of temperature and relative humidity profiles from a combination of active and passive remote sensing. Meteorol. Atmos. Phys. 2019, 131, 681–695. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; He, J. Temperature and humidity profiles retrieving over land using clear sky measurements of microwave humidity-temperature sounder on Chinese FY-3C satellite. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4161–4164. [Google Scholar]
- Subrahmanyam, K.V.; Kumar, K.K. Megha-Tropiques/SAPHIR measurements of humidity profiles: Validation with AIRS and global radiosonde network. Atmos. Meas. Technol. 2013, 6, 11405–11437. [Google Scholar] [CrossRef]






| Band Name | Spectral Range (cm−1) | Spectral Resolution (cm−1) | Sensitivity (NEΔT@250 K) |
|---|---|---|---|
| Long Wave | 650–1136 (15.3 μm–8.8 μm) | 0.625 | 0.15–0.4 K |
| Medium Wave 1 | 1210–1750 (8.26 μm–5.71 μm) | 1.25 | 0.1–0.7 K |
| Medium Wave 2 | 2155–2550 (4.64 μm–3.92 μm) | 2.5 | 0.3–1.2 K |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Bao, Y.; Petropoulos, G.P.; Zhang, P.; Lu, F.; Lu, Q.; Wu, Y.; Xu, D. Temperature and Humidity Profiles Retrieval in a Plain Area from Fengyun-3D/HIRAS Sensor Using a 1D-VAR Assimilation Scheme. Remote Sens. 2020, 12, 435. https://doi.org/10.3390/rs12030435
Zhu L, Bao Y, Petropoulos GP, Zhang P, Lu F, Lu Q, Wu Y, Xu D. Temperature and Humidity Profiles Retrieval in a Plain Area from Fengyun-3D/HIRAS Sensor Using a 1D-VAR Assimilation Scheme. Remote Sensing. 2020; 12(3):435. https://doi.org/10.3390/rs12030435
Chicago/Turabian StyleZhu, Liuhua, Yansong Bao, George P. Petropoulos, Peng Zhang, Feng Lu, Qifeng Lu, Ying Wu, and Dan Xu. 2020. "Temperature and Humidity Profiles Retrieval in a Plain Area from Fengyun-3D/HIRAS Sensor Using a 1D-VAR Assimilation Scheme" Remote Sensing 12, no. 3: 435. https://doi.org/10.3390/rs12030435
APA StyleZhu, L., Bao, Y., Petropoulos, G. P., Zhang, P., Lu, F., Lu, Q., Wu, Y., & Xu, D. (2020). Temperature and Humidity Profiles Retrieval in a Plain Area from Fengyun-3D/HIRAS Sensor Using a 1D-VAR Assimilation Scheme. Remote Sensing, 12(3), 435. https://doi.org/10.3390/rs12030435








