Modelling Global Ionosphere Based on Multi-Frequency, Multi-Constellation GNSS Observations and IRI Model
Abstract
1. Introduction
2. Mathematical Model
2.1. Ionospheric Observation Equation
2.2. Initial Ionospheric Information from the International Reference Ionosphere (IRI)
2.3. Global Ionospheric Representation
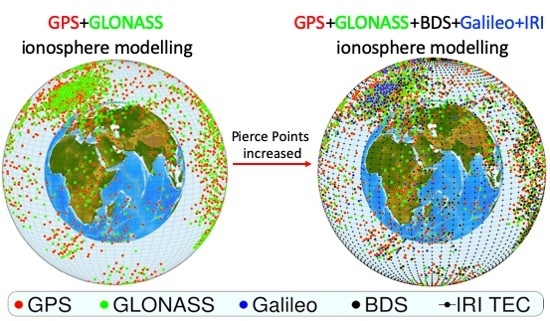
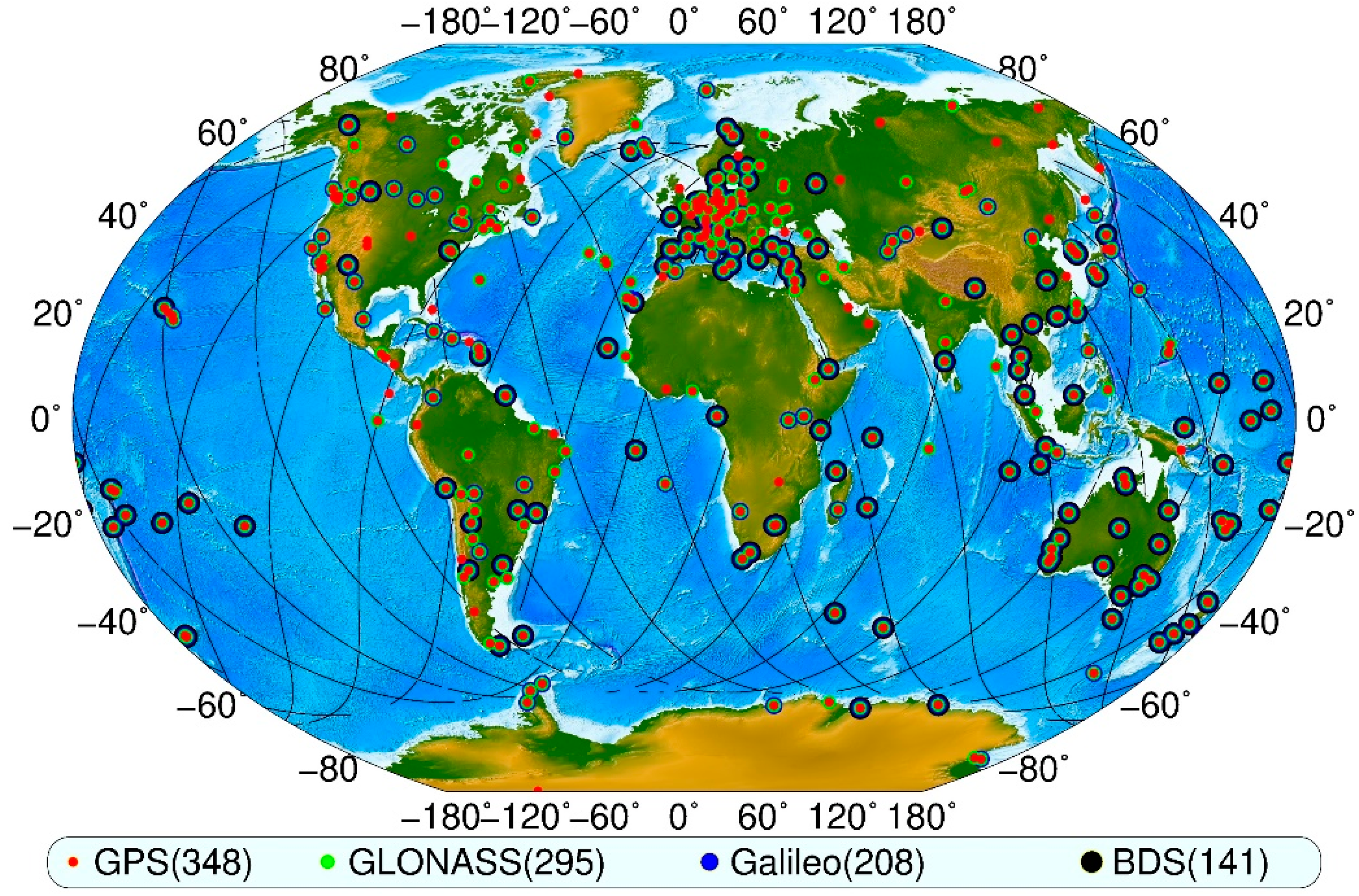
3. Data Sources
4. Results and Analysis
4.1. Comparison with IAACs’ Solutions
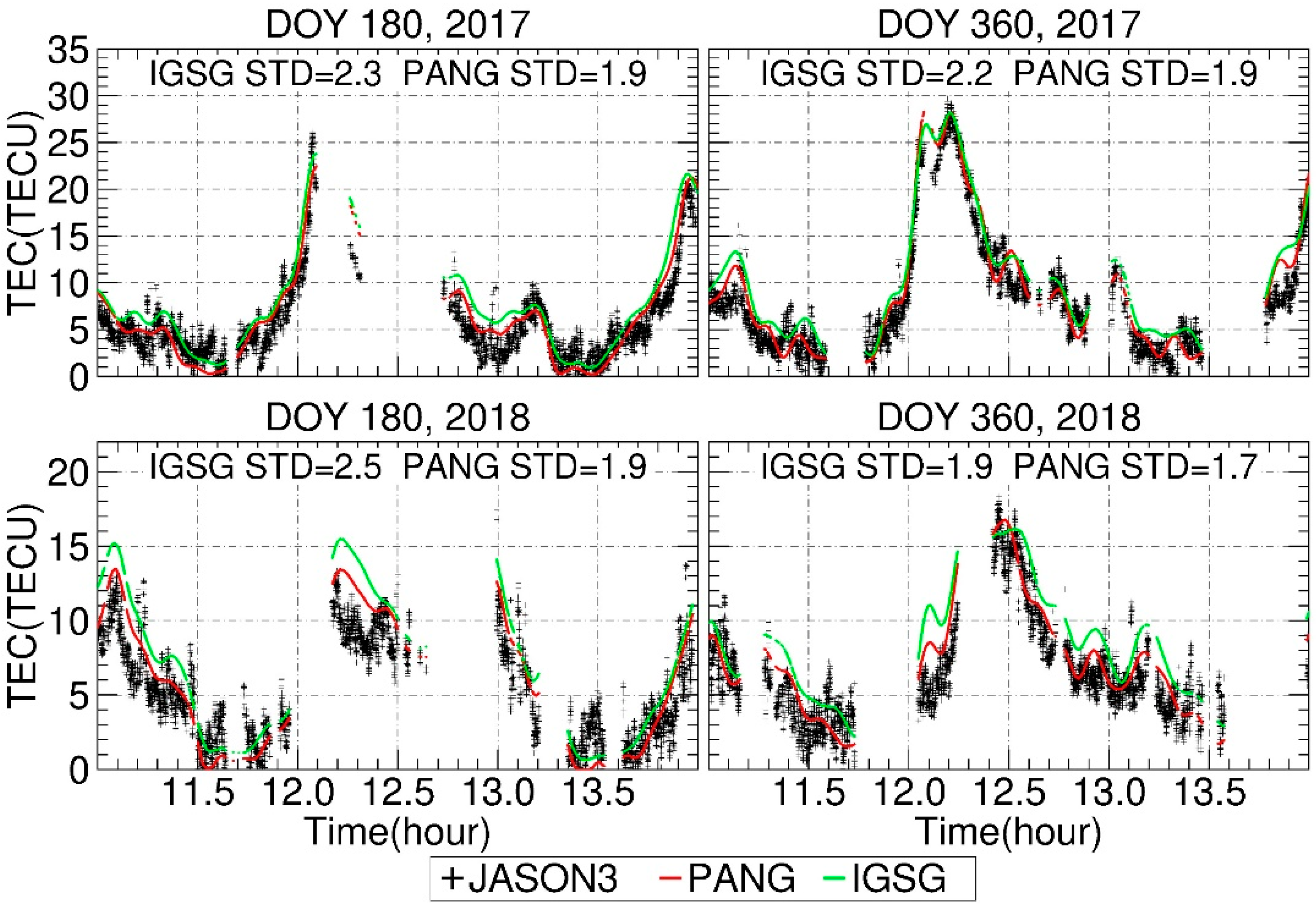
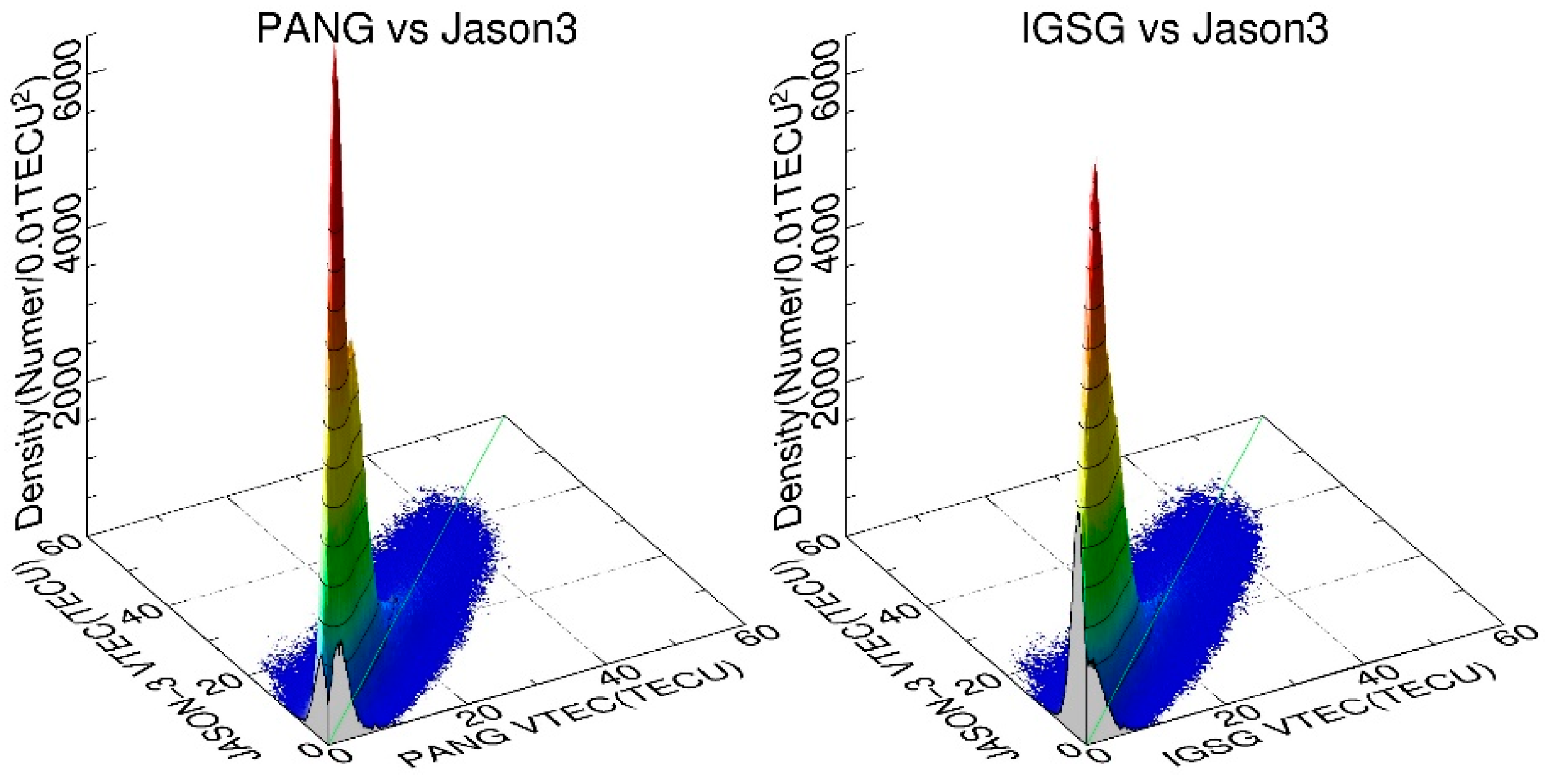
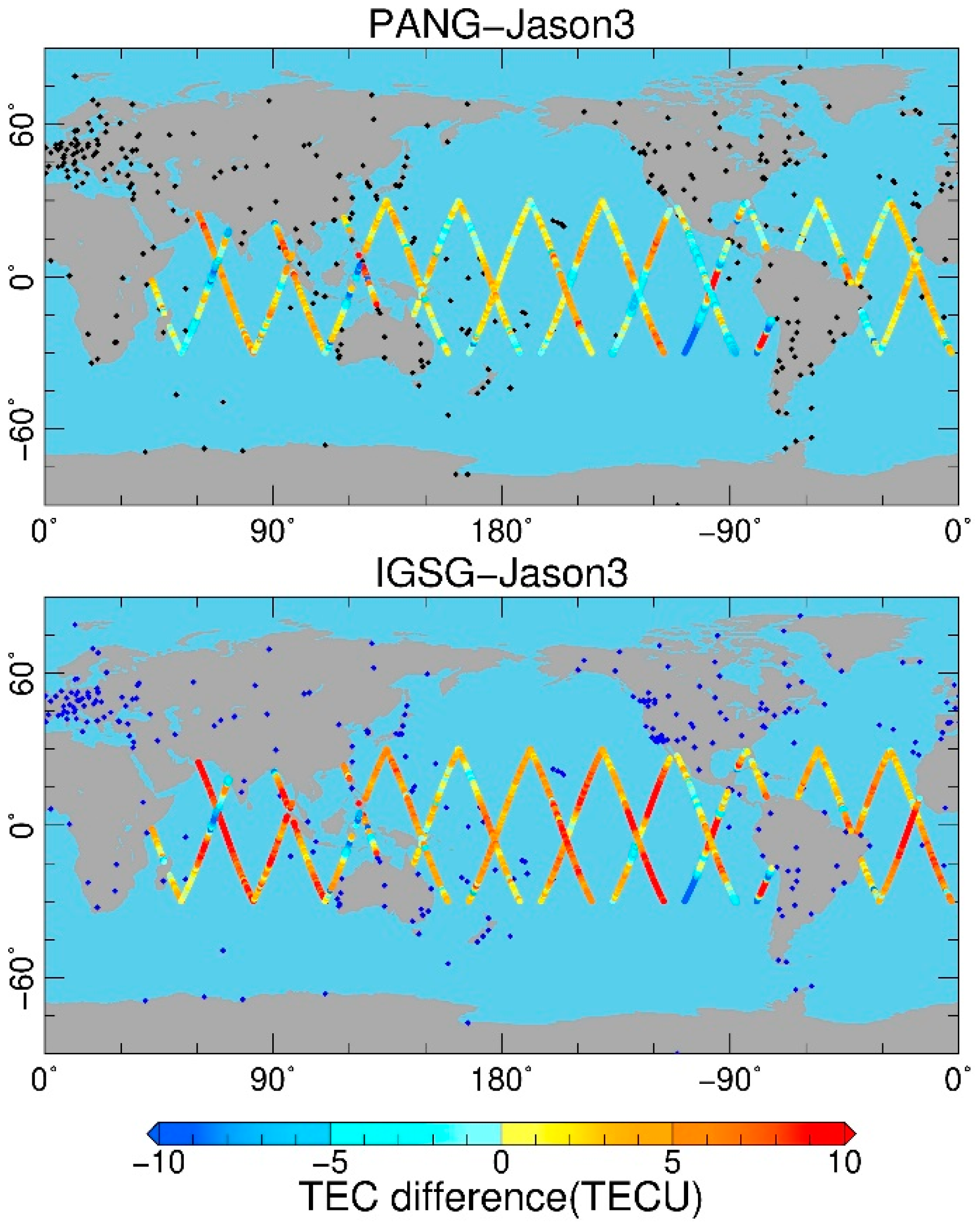
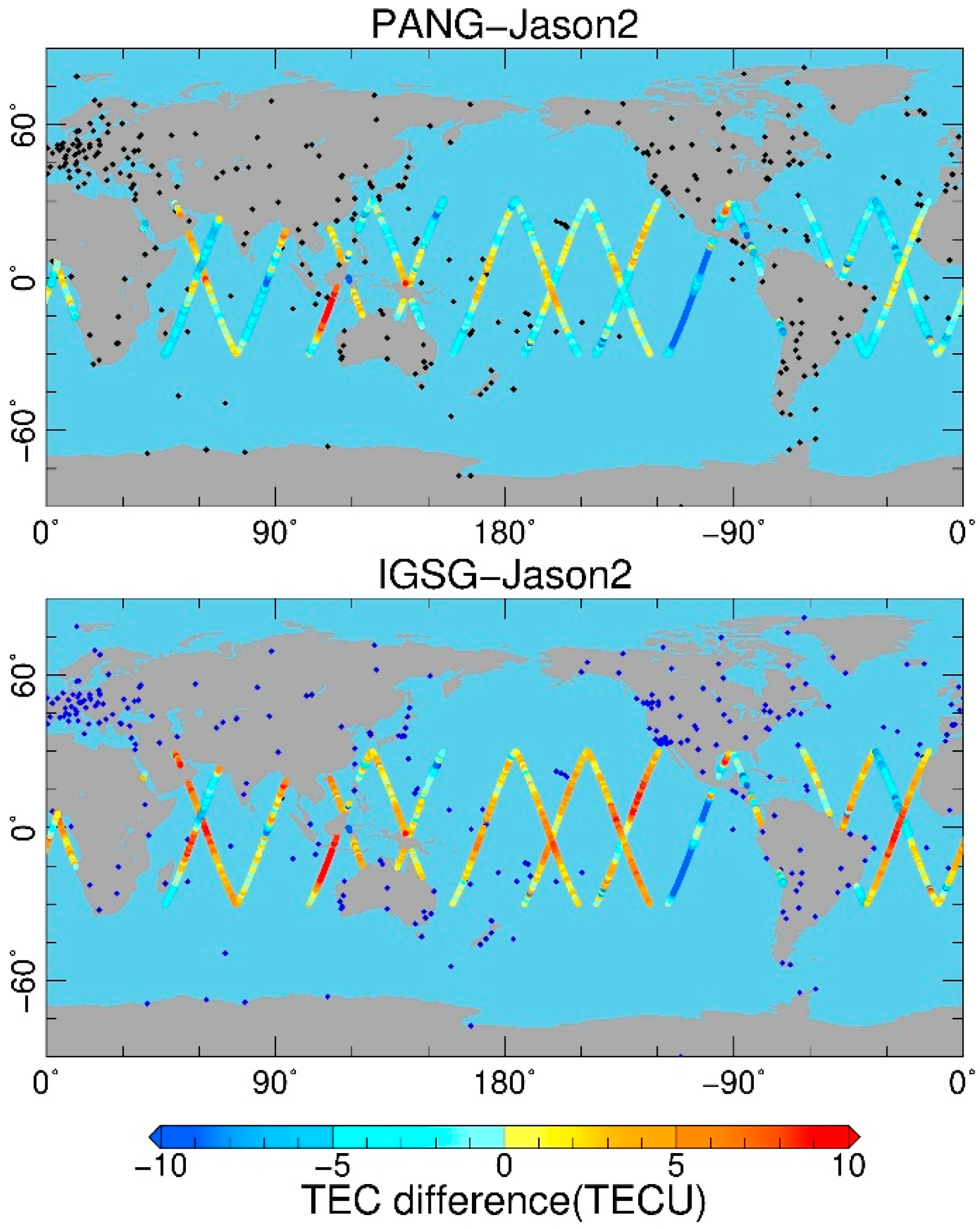
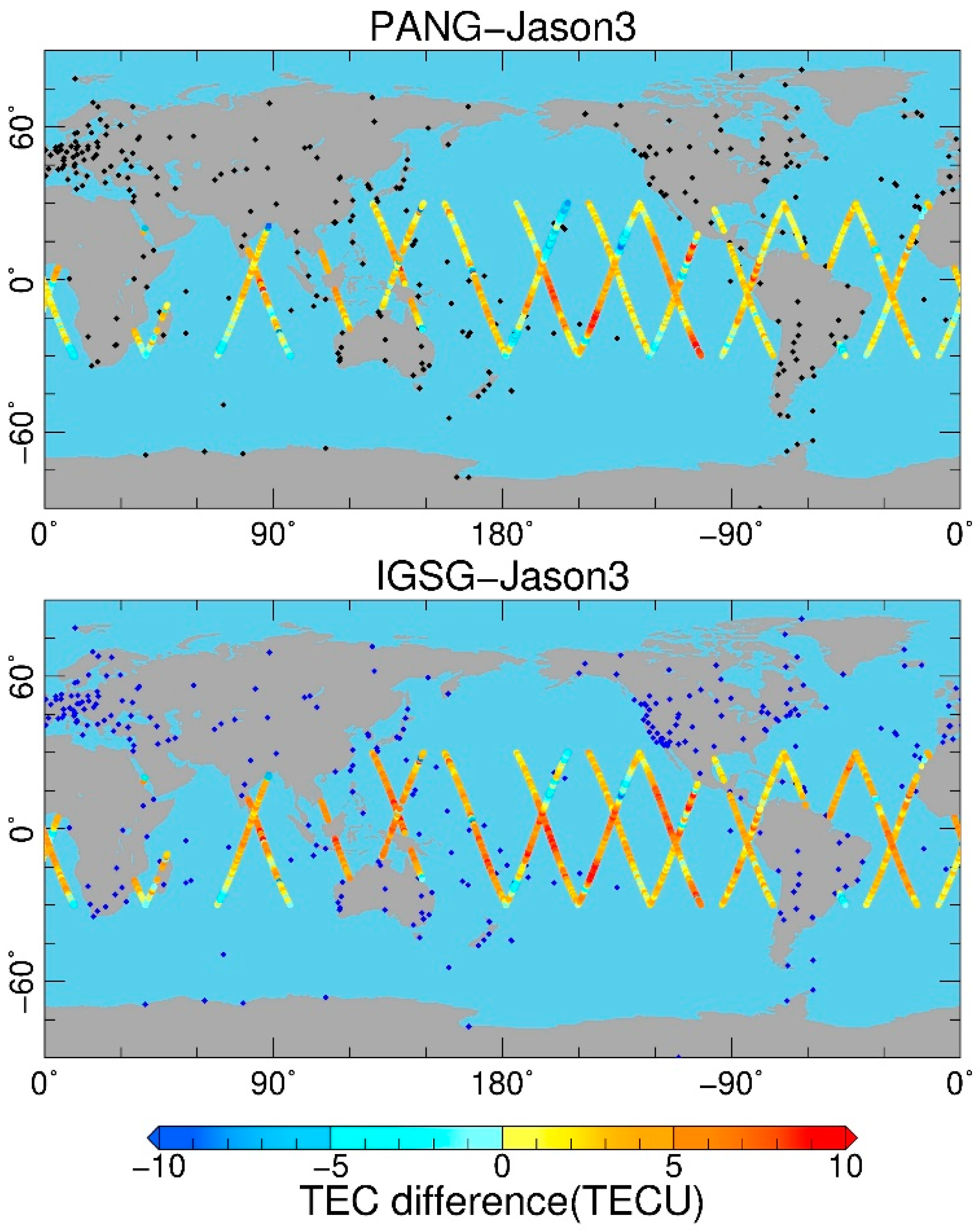
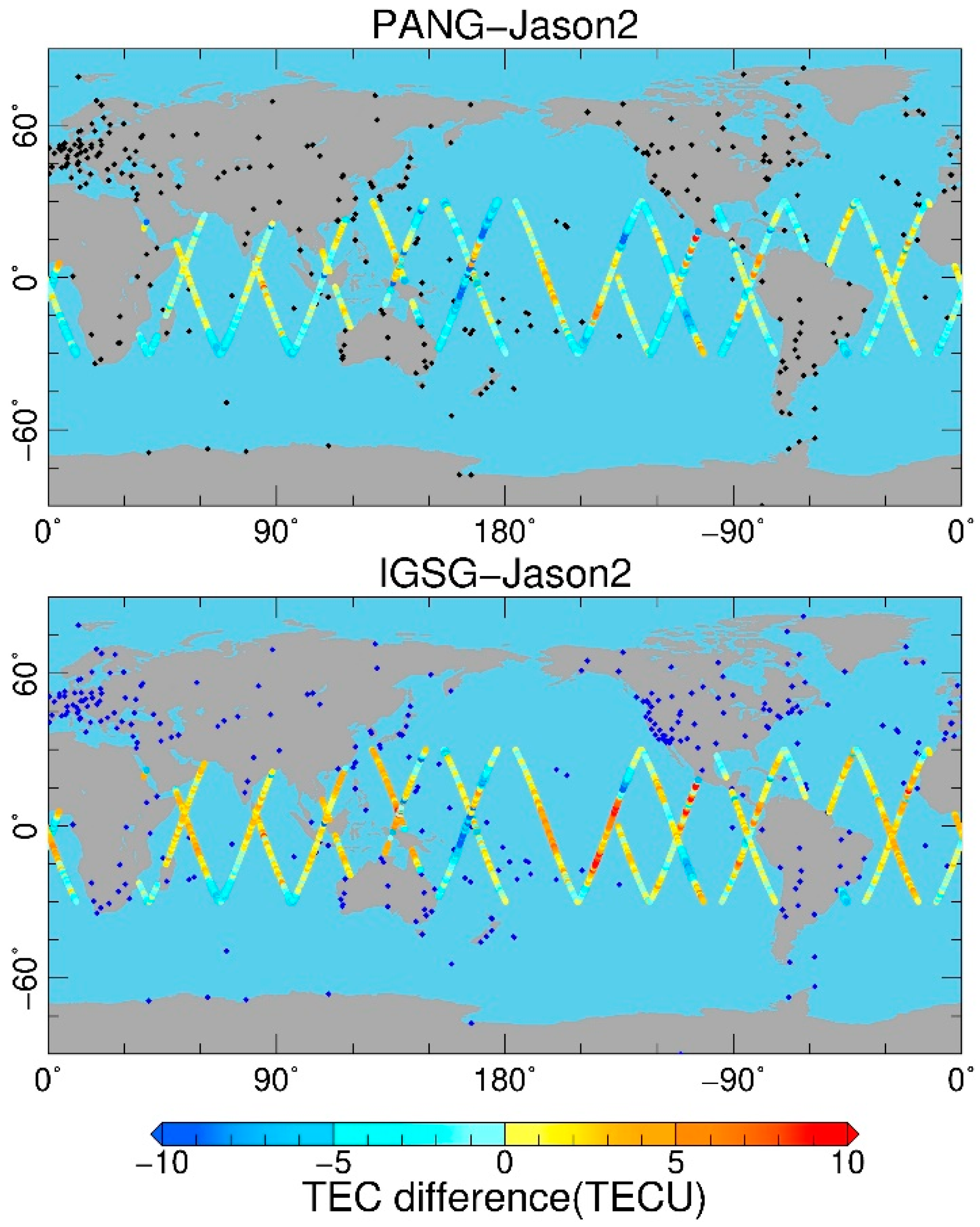
4.2. Satellite Altimetry Validation
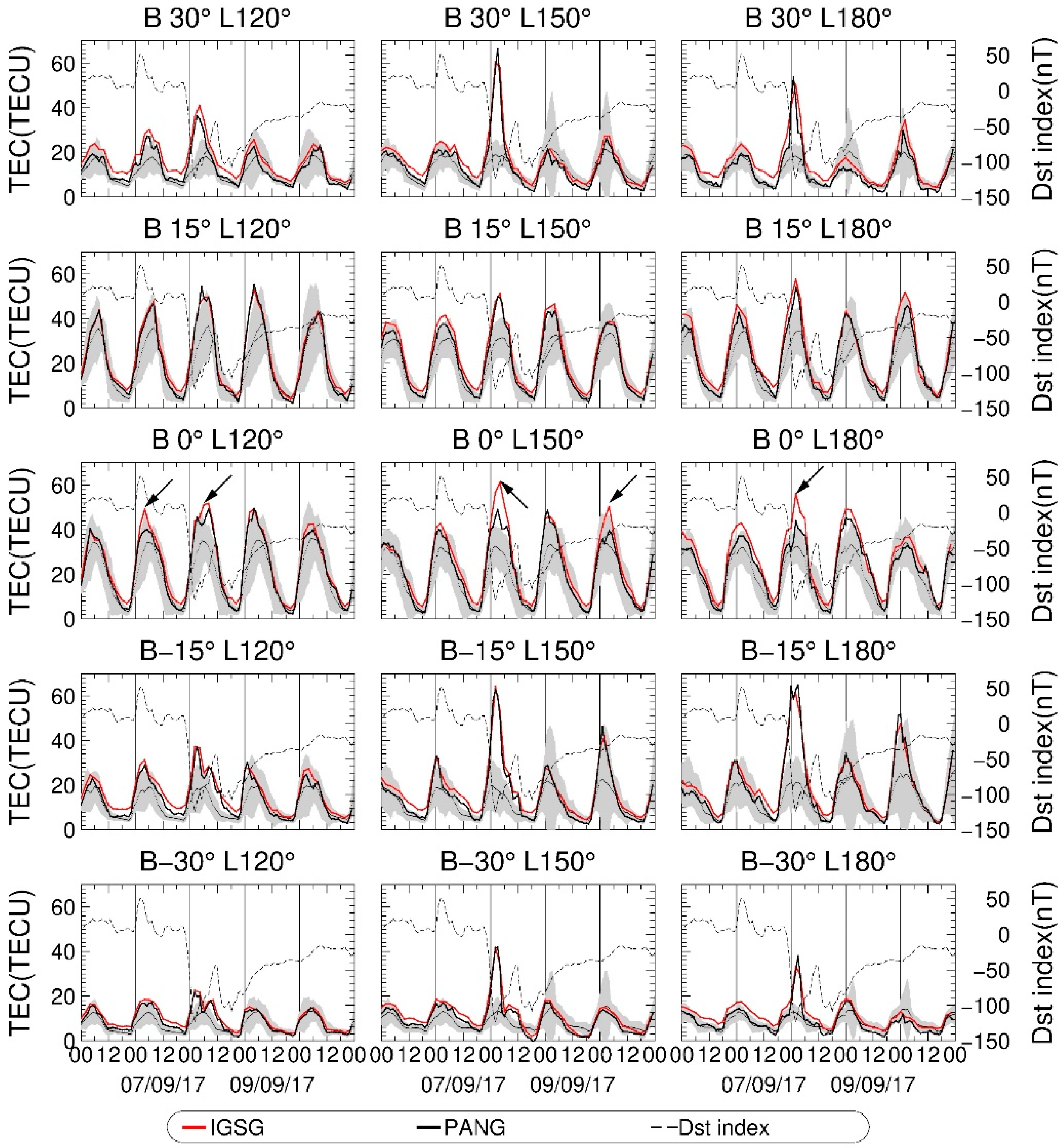
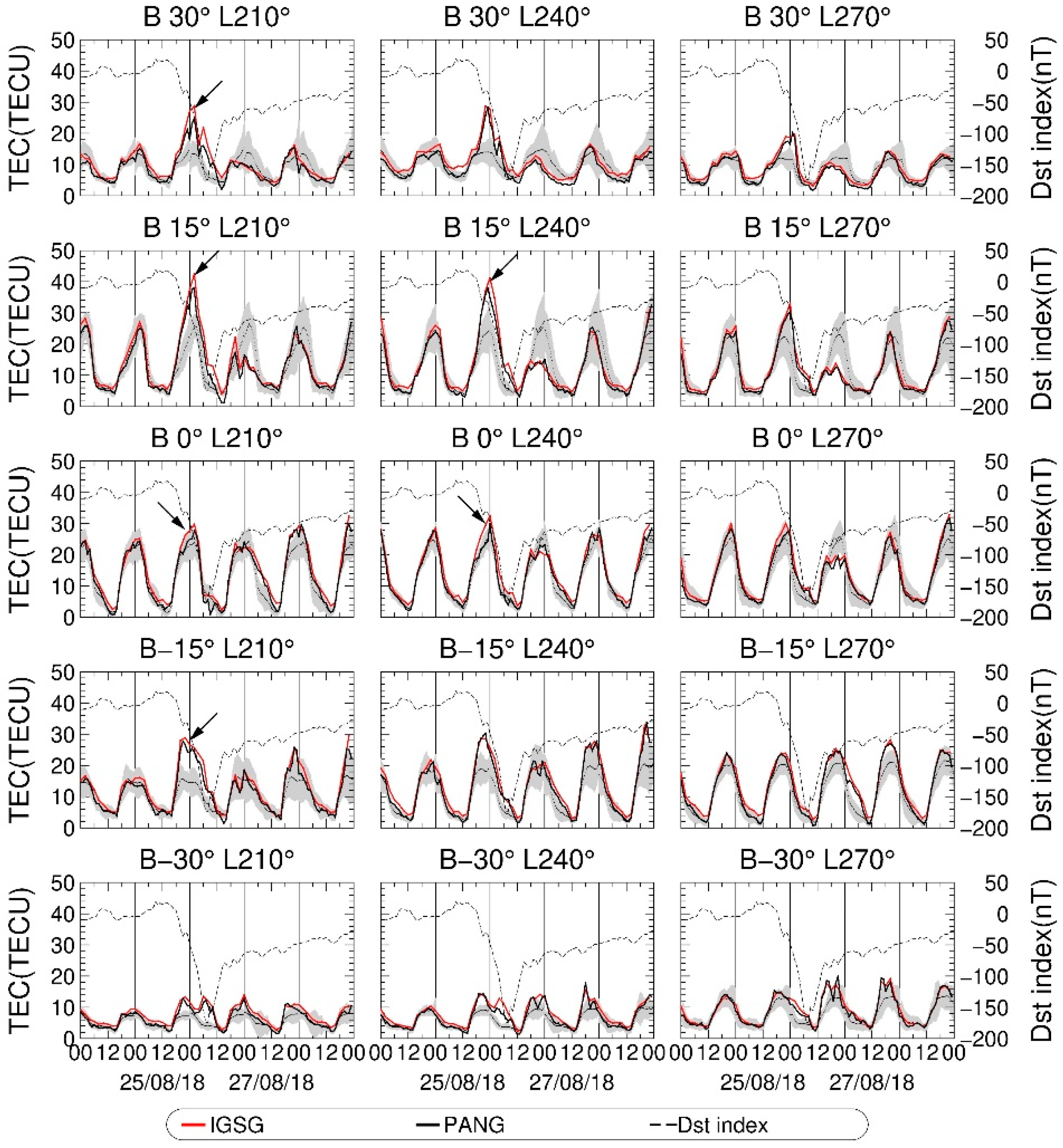
4.3. Monitor Ionospheric Disturbance
4.3.1. Ionospheric Responses for the Geomagnetic Storm that Happened on 8 September 2017
4.3.2. Ionospheric Responses for the Geomagnetic Storm Happened on 26 August 2018
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lanyi, G.E.; Roth, T. A comparison of mapped and measured total ionospheric electron content using global positioning system and beacon satellite observations. Radio Sci. 1988, 23, 483–492. [Google Scholar] [CrossRef]
- Mannucci, A.; Wilson, B.; Edwards, C. A new method for monitoring the earth’s ionospheric total electron content using the GPS global network. In Proceedings of the ION GPS-93, the 6th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 22–24 September 1993; pp. 1323–1332. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J. High resolution TEC monitoring method using permanent ground GPS receivers. Geophys. Res. Lett. 1997, 24, 1643–1646. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, University of Berne, Berne, Switzerland, 25 March 1999. [Google Scholar]
- Feltens, J. Development of a new three-dimensional mathematical ionosphere model at European Space Agency/European Space Operations Centre. Space Weather 2007, 5, S12002. [Google Scholar] [CrossRef]
- Feltens, J.; Angling, M.; Jackson-Booth, N.; Jakowski, N.; Hoque, M.; Hernández-Pajares, M.; Zandbergen, R. Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. 2011, 46, 1–11. [Google Scholar] [CrossRef]
- Hein, W.Z.; Goto, Y.; Kasahara, Y. Estimation method of ionospheric TEC distribution using single-frequency measurements of GPS signals. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 1–6. [Google Scholar]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J. Global observation of ionospheric electronic response to solar events using ground and LEO GPS data. J. Geophys. Res. 1998, 103, 20789–20796. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Zomoza, J.M.J.; Subirana, J.S.; Colombo, O.L. Feasibility of wide-area subdecimeter navigation with GALILEO and modernized GPS. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2128–2131. [Google Scholar] [CrossRef]
- Tang, W.; Jin, L.; Xu, K. Performance analysis of ionosphere monitoring with BeiDou CORS observational data. J. Navig. 2014, 67, 511–522. [Google Scholar] [CrossRef]
- Zhang, R.; Song, W.; Yao, Y.; Shi, C.; Lou, Y.; Yi, W. Modeling regional ionospheric delay with ground-based BeiDou and GPS observations in China. GPS Solut. 2015, 19, 649–658. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, X.; Xie, W.; Zhang, K.; Yuan, Y.; Li, X. Global ionospheric modelling using multi-GNSS: BeiDou, Galileo, GLONASS and GPS. Sci. Rep. 2016, 6, 33499. [Google Scholar] [CrossRef] [PubMed]
- Rawer, K.; Bilitza, D.; Ramakrishnan, S. Goals and status of the International Reference Ionosphere. Rev. Geophys. 1978, 16, 177–181. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the International Standard for the Ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.B.; Kim, Y.H.; Chung, J.K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Space Phys. 2010, 115, A10. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W.; Feltens, F. IONEX: The IONosphere map exchange format version 1. In Proceedings of the 1998 IGS analysis centers workshop, Darmstadt, Germany, 9–11 February 1998. [Google Scholar]
- Galav, P.; Dashora, N.; Sharma, S.; Pandey, R. Characterization of low latitude GPS-TEC during very low solar activity phase. J. Atmos. Sol.-Terr. Phys. 2010, 72, 1309–1317. [Google Scholar] [CrossRef]
- Mosert, M.; Gende, M.; Brunini, C.; Ezquer, R.; Altadill, D. Comparisons of IRI TEC predictions with GPS and digisonde measurements at Ebro. Adv. Space Res. 2007, 39, 841–847. [Google Scholar] [CrossRef]
- Tariku, Y.A. Patterns of GPS-TEC variation over low-latitude regions (African sector) during the deep solar minimum (2008 to 2009) and solar maximum (2012 to 2013) phases. Earth, Planets and Space 2015, 67, 35. [Google Scholar] [CrossRef]
- Schaer, S.; Beutler, G.; Mervart, L.; Rothacher, M.; Wild, U. Global and regional ionosphere models using the GPS double difference phase observable. In Proceedings of the IGS workshop on special topics and new directions, Potsdam, Germany, 15–17 May 1995; pp. 77–92. [Google Scholar]
- IERS Technical Note 21, IERS Conventions (1996). Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn21.html (accessed on 15 November 2019).
- Rao, K.D.; Dutt, V.S.I. An Assessment of Mapping Functions for VTEC Estimation using Measurements of Low Latitude Dual Frequency GPS Receiver. Int. J. Appl. Eng. Res. 2017, 12, 422–427. [Google Scholar]
- Wanninger, L. Carrier-phase inter-frequency biases of GLONASS receivers. J. Geod. 2012, 86, 139–148. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.B.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the Ground for Multi-Constellation GNSS Science. InsideGNSS 2014, 9, 42–49. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–Achievements, Prospects and Challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
- Seeber, G. Satellite Geodesy, Foundations, Methods and Application. Available online: https://books.google.com.hk/books/about/Satellite_Geodesy.html?id=qZTS6OI9NGoC&printsec=frontcover&source=kp_read_button&redir_esc=y#v=onepage&q&f=false (accessed on 15 November 2019).
- Imel, D.A. Evaluation of the TOPEX/POSEIDON dual-frequency ionosphere correction. J. Geophys. Res. 1994, 99, 24895–24906. [Google Scholar] [CrossRef]
- Alizadeh, M.M.; Schuh, H.; Todorova, S.; Schmidt, M. Global ionosphere maps of VTEC from GNSS, satellite altimetry, and Formosat-3/COSMIC data. J. Geod. 2011, 85, 975–987. [Google Scholar] [CrossRef]





| GIM | Method | Shell Model | DCB Computation | Spatial Resolution (Lon. × Lat.) | Temporal Resolution | GNSS Data Sets |
|---|---|---|---|---|---|---|
| PANG | Spherical Harmonics | Modified 2-D | Estimated with VTEC | × | 1-h | GPS, GLONASS, BDS, Galileo |
| IGSG | Weighted mean | Combined | Combined | × | 2-h | GPS, GLONASS |
| CODG | Spherical Harmonics | Modified 2-D | Estimated with VTEC | × | 1-h | GPS, GLONASS |
| ESAG | Spherical Harmonics | 2-D | Estimated with VTEC | × | 2-h | GPS, CLONASS |
| JPLG | Three-shell Mode | 3-D | Estimated with VTEC | × | 2-h | GPS |
| UPCG | Tomographic with splines | 3-D | Estimated from VTEC | × | 2-h | GPS |
| Items | Maximum (TECU) | Minimum (TECU) | Mean (TECU) |
|---|---|---|---|
| IGSG | 6.1 | 0.9 | 1.5 |
| CODG | 5.3 | 0.6 | 1.1 |
| ESAG | 5.6 | 1.0 | 1.8 |
| JPLG | 6.4 | 1.7 | 2.6 |
| UPCG | 6.6 | 1.0 | 1.9 |
| Year | PANG-Jason3 (TECU) | IGSG-Jason3 (TECU) | ||
|---|---|---|---|---|
| Offset | STD | Offset | STD | |
| 2017 | 1.1 | 2.5 | 2.4 | 2.8 |
| 2018 | 1.2 | 2.4 | 2.1 | 2.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, X.; Meng, X.; Chen, H.; Jiang, W.; Xi, R.; Chen, Q. Modelling Global Ionosphere Based on Multi-Frequency, Multi-Constellation GNSS Observations and IRI Model. Remote Sens. 2020, 12, 439. https://doi.org/10.3390/rs12030439
An X, Meng X, Chen H, Jiang W, Xi R, Chen Q. Modelling Global Ionosphere Based on Multi-Frequency, Multi-Constellation GNSS Observations and IRI Model. Remote Sensing. 2020; 12(3):439. https://doi.org/10.3390/rs12030439
Chicago/Turabian StyleAn, Xiangdong, Xiaolin Meng, Hua Chen, Weiping Jiang, Ruijie Xi, and Qusen Chen. 2020. "Modelling Global Ionosphere Based on Multi-Frequency, Multi-Constellation GNSS Observations and IRI Model" Remote Sensing 12, no. 3: 439. https://doi.org/10.3390/rs12030439
APA StyleAn, X., Meng, X., Chen, H., Jiang, W., Xi, R., & Chen, Q. (2020). Modelling Global Ionosphere Based on Multi-Frequency, Multi-Constellation GNSS Observations and IRI Model. Remote Sensing, 12(3), 439. https://doi.org/10.3390/rs12030439