Automatic Detection of Near-Surface Targets for Unmanned Aerial Vehicle (UAV) Magnetic Survey
Abstract
:1. Introduction
2. System and Workflow
2.1. UAV-Magnetometer System
2.2. Workflow for UAV-Borne Magnetic Survey
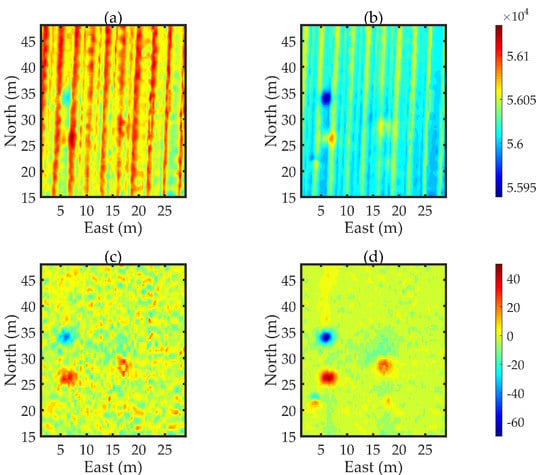
- Background field elimination: The background field consists of the local geomagnetic field and the magnetic field produced by the ambient sources, like power grid, traffic, buildings. We are concerned with the magnetic anomaly signal from the underground objects, so the background field should firstly be removed.
- UAV interference field removal: Unlike the interference field from the external environment, UAV interference field is an inherent noise signal from system, which is related to the attitude of the drone. Herein, we propose a calibration method based on the signal correlation to separate the magnetic anomaly signal from the total field signal.
- Data gridding: It is customary to perform data gridding, which is to compute the magnetic field of regular grid nodes from the irregularly distributed sampling points by interpolation. Thus, a two-dimensional contour magnetic map is produced to reflect the abnormal distribution of the entire test area.
3. Materials and Methods
3.1. Background Field Elimination
3.2. UAV Interference Field Removal
3.3. Data Gridding
3.4. YOLOv3-based Euler Deconvolution
3.4.1. Euler Deconvolution
3.4.2. YOLOv3
- A window contains at least three observation points because there are three unknown parameters in Equation (7).
- Based on the principal of Euler deconvolution, the anomaly data within the windows must be generated from an isolated object, avoiding the effects from the adjacent sources.
- For the real data, the higher SNR of magnetic data is, the more reliable the results of Euler deconvolution are. The size of window is determined by a threshold that is defined as the ratio of the maximum and minimum values of the magnetic field in a window. The anomaly field with lower SNR is removed by the setting of threshold, which is set to 50% here.
3.4.3. Summary of YOLOv3-based Euler Deconvolution
| Algorithm 1: YOLOv3-based Euler Deconvolution |
| Input: Gridded magnetic data and a 2D magnetic contour map Output: The location of underground targets 1: The magnetic contour map is inputted into the trained YOLOv3 2: A total of Nwindows anomaly windows are detected by YOLOv3, extract the magnetic field data inside each window 3: for k = 1:Nwindows do 4: Determine the Euler solution based on the data within the window 5: end for 6: Cluster, if ( and are Euler solutions obtained by Positive and Negative anomaly windows). 7: return the location of potential targets, which is same as the clustered results |
4. Field Experiment
4.1. UAV-Borne Magnetic Survey
4.2. Results
5. Discussion
5.1. Analysis on the Processing Flow
5.2. Limits of the Research and the Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nabighian, M.N.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. The historical development of the magnetic method in exploration. Geophysics 2005, 70, 33–61. [Google Scholar] [CrossRef]
- Caetano, D.M.; Rabuske, T.; Fernandes, J.; Pelkner, M.; Fermon, C.; Cardoso, S.; Ribes, B.; Franco, F.; Paul, J.; Piedade, M.; et al. High-resolution nondestructive test probes based on magnetoresistive sensors. IEEE Trans. Ind. Electron. 2019, 66, 7326–7377. [Google Scholar] [CrossRef]
- Hansen, R.O.; Racic, L.; Grauch, V.J.S. Magnetic methods in near-surface geophysics. In Near-surface Geophysics, 1st ed.; Dwain, K.B., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005; pp. 151–175. [Google Scholar]
- Meyer, U.; Siemon, B.; Becken, M.; Stolz, R.; Noell, U.; Frei, M.; Buchholz, P.; Steuer, A.; Costabel, S.; Martin, T.; et al. New airborne methods and procedures for the exploration of mineral resources—An overview of BGR activities. In Near Surface Geoscience 2016–22nd European Meeting of Environmental and Engineering Geophysics, 04 Sep 2016; Curran Associates: Turin, Italy, 2016. [Google Scholar]
- Munschy, M.; Boulanger, D.; Ulrich, P.; Bouiflane, M. Magnetic mapping for the detection and characterization of UXO: Use of multi-sensor fluxgate 3-axis magnetometers and methods of interpretation. J. Appl. Geophys. 2007, 61, 168–183. [Google Scholar] [CrossRef]
- Billings, S.D. Discrimination and classification of buried unexploded ordnance using magnetometry. IEEE Trans. Geosci. Remote Sensing 2004, 42, 1241–1251. [Google Scholar] [CrossRef]
- Fassbinder, J.W.E. Magnetometry for archaeology. In Encyclopedia of Geoarchaeology, 1st ed; Gilbert, A.S., Goldberg, P., Eds.; Springer: Dordrecht, The Netherlands, 2017; pp. 499–514. [Google Scholar]
- Ege, Y.; Nazlibilek, S.; Kakilli, A.; Citak, H.; Kalender, O.; Erturk, K.L.; Sengul, G.; Karacor, D. A magnetic measurement system and identification method for buried magnetic materials within wet and dry soils. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1803–1811. [Google Scholar] [CrossRef]
- Faley, M.I.; Dammers, J.; Maslennikov, Y.V.; Schneiderman, J.F.; Winkler, D.; Koshelets, V.P.; Shah, N.J.; Dunin-Borkowski, R.E. High-Tc SQUID biomagnetometers. Supercond. Sci. Technol. 2017, 20, 1–21. [Google Scholar]
- Oyama, D.; Kobayashi, K.; Yoshizawa, M.; Uchikawa, Y. Mobile high-Tc SQUID system for MCG measurement. IEEE Trans. Appl. Supercond. 2009, 19, 871–873. [Google Scholar] [CrossRef]
- Gavazzi, B.; Maire, P.L.; Munschy, M.; Dechamp, A. Fluxgate vector magnetometers: A multisensor device for ground, UAV, and airborne magnetic surveys. Lead. Edge 2016, 35, 795–797. [Google Scholar] [CrossRef] [Green Version]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–329. [Google Scholar] [CrossRef] [Green Version]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef] [Green Version]
- Robert, J.; Yuleika, M.; Robert, Z.; Markku, P.; Ari, S.; Björn, H.H.; Heikki, S.; Jukka-Pekka, K.; Louis, A.; Richard, G. Drone-borne hyperspectral and magnetic data integration: Otanmäki Fe-Ti-V deposit in Finland. Remote Sens. 2019, 11, 2084–2111. [Google Scholar]
- Douglas, G.M.; Héctor, I.A.; Perez, I.; Paulo, A.F.R.; Guilherme, A.P.; Luiz, C.C.B.; André, W.; Gustavo, M.F.; Luis, G.U.G.; Mario, F.M.C. Autonomous aeromagnetic surveys using a fluxgate magnetometer. Sensors 2016, 16, 2169. [Google Scholar]
- Malehmir, A.; Dynesius, L.; Paulusson, K.; Paulusson, A.; Johansson, H.; Bastani, M.; Wedmark, M.; Marsden, P. The potential of rotary-wing UAV-based magnetic surveys for mineral exploration: A case study from central Sweden. Lead. Edge 2017, 36, 552–557. [Google Scholar] [CrossRef]
- Eck, C.; Imbach, B. Aerial magnetic sensing with an UAV helicopter. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Zurich, Switzerland, 14–16 September 2011. [Google Scholar]
- Wood, A.; Cook, I.; Doyle, B.; Cunningham, M.; Samson, C. Experimental aeromagnetic survey using an unmanned air system. Lead. Edge 2016, 35, 270–273. [Google Scholar] [CrossRef]
- Walter, C.A.; Braun, A.; Fotopoulos, G. Impact of 3-D Attitude Variations of a UAV Magnetometry System on Magnetic Data Quality. Geophys. Prospect. 2018, 67, 465–479. [Google Scholar] [CrossRef]
- Tolles, W.E.; Mineola, N.Y. Compensation of Aircraft Magnetic Fields. U.S. Patent US2692970A, 26 October 1954. [Google Scholar]
- Noriega, G. Aeromagnetic compensation in gradiometry—performance, model stability, and robustness. IEEE Geosci. Remote Sens. Lett. 2015, 12, 117–121. [Google Scholar] [CrossRef]
- Oruç, B. Location and depth estimation of point-dipole and line of dipoles using analytic signals of the magnetic gradient tensor and magnitude of vector components. J. Appl. Geophys. 2010, 70, 27–37. [Google Scholar] [CrossRef]
- Billings, S.; Wright, D. Interpretation of high-resolution low-altitude helicopter magnetometer surveys over sites contaminated with unexploded ordnance. J. Appl. Geophys. 2010, 72, 225–231. [Google Scholar] [CrossRef]
- Reid, A.B.; Allsop, J.M.; Granser, H.; Millett, A.J.; Somerton, I.W. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Davis, K.; Li, Y.; Nabighian, M. Automatic detection of UXO magnetic anomalies using extended Euler deconvolution. Geophysics 2010, 75, 13–20. [Google Scholar] [CrossRef]
- Davis, K.; Li, Y.; Nabighian, M. Automatic detection of UXO magnetic anomalies using extended Euler deconvolution. In 2005 SEG Annual Meeting, Houston, TX, USA, 6-11 November 2005; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005. [Google Scholar]
- Gerovska, D.; Araúzo-Bravo, M.J. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index. Comput. Geosci. 2003, 29, 949–960. [Google Scholar] [CrossRef]
- Usman, N.; Abdullah, K.; Nawawi, M.; Khalil, A.E. New approach of solving Euler deconvolution relation for the automatic interpretation of magnetic data. Terr. Atmos. Ocean. Sci. 2018, 29, 243–259. [Google Scholar] [CrossRef] [Green Version]
- Sheinker, A.; Moldwin, M.B. Adaptive interference cancelation using a pair of magnetometers. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 307–318. [Google Scholar] [CrossRef]
- Mu, Y.X.; Zhang, X.J.; Chen, L.Z.; Zheng, Y.X.; Xie, W.P. Compensation method for multi-rotor UAV-magnetometer system, IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019). in press.
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Daya, Z.A.; Birsan, M.; Holtham, P.M.; Holtham, P.M. The magnitude and distribution of ambient fluctuations in the scalar magnetic field. In OCEANS 2005 MTS, 17–23 Sept. 2005; IEEE: Washington, DC, USA, 2005. [Google Scholar]
- Topics in Gridding. Available online: https://www.geosoft.com/media/uploads/resources/technical-papers/topicsingriddingworkshop.pdf (accessed on 16 June 2019).
- Wang, X.H.; Zhang, C.C.; Liu, F.Y.; Dong, Y.N.; Xu, X.L. Exponentially weighted particle filter for simultaneous localization and mapping based on magnetic field measurements. IEEE Trans. Instrum. Meas. 2017, 66, 1658–1667. [Google Scholar] [CrossRef]
- Pilkington, M.; Gregotski, M.E.; Todoeschuck, J.P. Using fractal crustal magnetization models in magnetic interpretation. Geophys. Prospect. 1994, 42, 677–692. [Google Scholar] [CrossRef]
- Feng, Y.; Jiang, Y.; Jiang, Y.; Li, Z.; Jiang, J.; Liu, Z.W.; Ye, M.C.; Wang, H.S.; Li, X.M. Regional magnetic anomaly fields: 3D Taylor polynomial and surface spline models. Appl. Geophys. 2016, 13, 59–68. [Google Scholar] [CrossRef]
- Briggs, I.C. Machine contouring using minimum curvature. Geophysics 1974, 39, 39–48. [Google Scholar] [CrossRef]
- Fan, Z.F.; Huang, L.; Zhang, X.J.; Fang, G.Y. An elaborately designed virtual frame to level aeromagnetic data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1153–1157. [Google Scholar] [CrossRef]
- Li, Y.G.; Krahenbuhl, R.; Meglich, T.; Oldenburg, D.; Pasion, L.; Billings, S.; Dam, R.V.; Harrison, B. Improving UXO Detection and Discrimination in Magnetic Environments; SERDP Project MM-1414; Colorado School of Mines Golden Dept of Geophysics: Boulder, CO, USA, May 2010. [Google Scholar]
- Maysam, A.; Kiomars, M.; Hamid, D.; Ahmad, M.Z. Geological noise removal in geophysical magnetic survey to detect unexploded ordnance based on image filtering. Iran. J. Geophys. 2016, 9, 11–23. [Google Scholar]














| True Location (m) | YOLOv3-based Euler Deconvolution (m) | SW-based Euler Deconvolution (m) | |
|---|---|---|---|
| 1 | (6.17, 33.96, 0.8) | (6.03, 34.19, 0.70) | (5.98, 34.20, 0.11) |
| 2 | (6.31, 26.61, 1.0) | (6.32, 26.52, 0.75) | (6.45, 26.52, 0.21) |
| 3 | (3.99, 22.15, 0.1) | (4.01, 22.24, 0.10) | (3.85, 22.22, -0.40) |
| 4 | (17.16, 29.47, 1.1) | (16.95, 29.54, 1.06) | (16.72, 29.43, 0.11) |
| 5 | (18.07, 22.21, 0.5) | (17.78, 22.18, 0.56) | (17.96, 22.18, -0.35) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Y.; Zhang, X.; Xie, W.; Zheng, Y. Automatic Detection of Near-Surface Targets for Unmanned Aerial Vehicle (UAV) Magnetic Survey. Remote Sens. 2020, 12, 452. https://doi.org/10.3390/rs12030452
Mu Y, Zhang X, Xie W, Zheng Y. Automatic Detection of Near-Surface Targets for Unmanned Aerial Vehicle (UAV) Magnetic Survey. Remote Sensing. 2020; 12(3):452. https://doi.org/10.3390/rs12030452
Chicago/Turabian StyleMu, Yaxin, Xiaojuan Zhang, Wupeng Xie, and Yaoxin Zheng. 2020. "Automatic Detection of Near-Surface Targets for Unmanned Aerial Vehicle (UAV) Magnetic Survey" Remote Sensing 12, no. 3: 452. https://doi.org/10.3390/rs12030452
APA StyleMu, Y., Zhang, X., Xie, W., & Zheng, Y. (2020). Automatic Detection of Near-Surface Targets for Unmanned Aerial Vehicle (UAV) Magnetic Survey. Remote Sensing, 12(3), 452. https://doi.org/10.3390/rs12030452