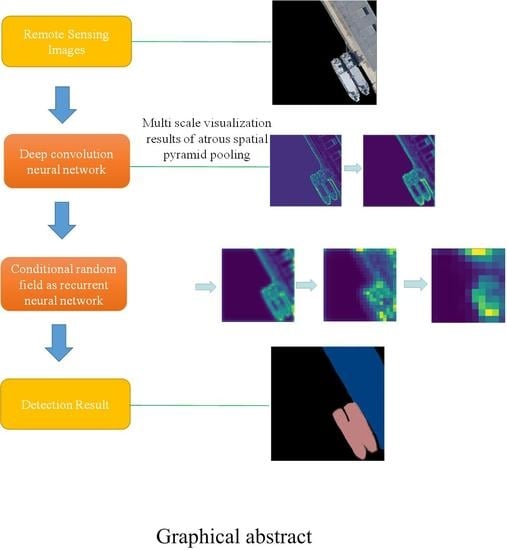
1. Introduction
With the rapid development of space remote sensing technology, ship detection using remote sensing images research [
1] has received considerable attention in the marine field. The world has rich marine resources, and ship detection using remote sensing images is necessary. For example, in the civil field, ports provide special support for the garrison to repair ships. As such, improving the detection, classification, and recognition of ship targets in the port is required. This will strengthen the monitoring and management of the port. When a ship loses contact in poor weather conditions, remote sensing images could be used to quickly and accurately detect the location of the ship in distress, which is conducive to rescue work.
Traditional ship detection methods in remote sensing images include (1) saliency detection [
2], which simulates the human visual perception mechanism but detects other significant targets when detecting port ships, such as small islands; (2) edge information detection [
3], which is combined with the shape characteristics of the ship and the edge information to obtain the proposal region; (3) detection of the fractal model [
4], which completes the automatic detection work according to whether the ship target or other backgrounds have obvious fractal features (however, Methods (3) and (4) have poor detection performance under complex sea conditions); and (4) the semantic segmentation method [
5,
6], which clusters pixels belonging to the same category in an image into one region. The ship can be clearly separated from the surrounding background. Compared with image classification or target detection, semantic segmentation can describe the image more accurately. The traditional classification methods used for semantic segmentation are (1) random decision forests [
7], which is a classification method that uses multiple trees to train and predict samples; (2) Markov random fields [
8], which is an undirected graph model that defines markers for each pixel; and (3) condition random field [
9,
10], which represents a Markov random field with a set of input random variables X and another set of output random variables Y. The test results are affected by real complex nature conditions in remote sensing images, such as thin clouds, ports, and islands. However, the classification effect of these traditional methods is still poor.
Deep learning has been widely used in computer vision, achieving breakthrough success especially in image classification. DeepLab [
11,
12] was proposed by the Google team for semantics segmentation. Solving the problem of spatial resolution degradation caused by continuous pooling and downsampling in traditional classification deep convolutional neural networks (DCNNs) [
13,
14] improved the segmentation effect. However, DeepLab still experiences some problems. It uses DCNN for coarse segmentation, then uses the fully connected conditional random field (fully connected CRF) to perform fine segmentation. As such, end-to-end training cannot be achieved, which results in low classification accuracy. In addition, DeepLab’s ability to capture fine details of ship targets is poor.
To solve the above problems, this paper proposes a new semantic segmentation model of convolutional neural networks based on DeepLab, which was applied to ship detection under complex sea conditions. This paper builds further on the work of Chen et al. (References [
11] and [
12]), with the addition of end-to-end training. Combining CRF with deep convolutional neural networks, and using Gaussian pairwise potential and mean field approximation theorem, the CRF is established as a recurrent neural network (RNN) [
15], which is used as part of the neural network [
16] to produce a deep end-to-end network with both DCNN and CRF. We call it deep semantic segmentation (DSS).
Section 2 reviews the development of semantic segmentation and describes the basic principles of DeepLab.
Section 3 is the focus of this paper, and describes the specific method used in ship detection.
Section 4 is the experimental section, which verifies the feasibility of the DSS.
2. Related Work
Deep learning [
17,
18,
19] has been widely used in the field of computer vision and has achieved breakthrough success in image classification. Several general architectures have been constructed for deep learning, such as the VGG [
20] and Resnet [
21] networks. VGG was proposed by the Computer Visual Group of the University of Oxford, which explored the relationship between the depth of the convolutional neural network and its performance. A deep neural network was successfully constructed by repeatedly stacking small convolutional layers and max pooling layers. The advantage is that although the network is deepened, the parameter explosion problem does not occur, and the learning ability is strong. However, more memory is required due to the increase in the number of layers and parameters. Resnet proposed a residual module and introduced an identity map to solve the degradation problem in the depth grid. We assume that the input of a neural network is
x and the expected output is
H(x). If the input
x is directly transmitted to the output as the initial result, the goal we need to learn is
F(x) = H(x)-x. This is a Resnet unit, which is equivalent to changing the learning goal and no longer learning a complete output. Compared with VGG, Resnet can deepen the grid as much as possible. Resnet has a lower error rate and low computational complexity.
The segmentation method based on deep learning has developed rapidly. Three semantic segmentation methods are based on deep learning. The first method is based on upsampling. CNN loses some details when sampling. This process is irreversible, leading to low image resolution. Upsampling can fill in some missing information, which results in more accurate segmentation boundaries. For example, Long proposed the fully convolutional networks (FCNs) [
22], which are applied to semantic segmentation and are highly accurate. However, FCNs are not sensitive to the details in the image and do not fully consider the relationship between pixels. This produces a lack of spatial consistency. The second method is the probability graph model. For example, the second-order CRF is used to smooth noise and couple adjacent nodes, which is beneficial for assigning similar spatial pixels to the same marker. At this stage of the DCNN, the score map is usually very smooth, and the goal is to restore the detailed local structure. In this case, the traditional conditional random field model will miss small structures. Fully connected CRFs can overcome this shortcoming and capture fine details. The third segmentation method involves improving the feature resolution, restoring the resolution due to the DCNN, and thus obtains more context information. DeepLab [
11,
12], combined with DCNN and a probability map, can adjust the resolution by atrous convolution, expand the receptive field, and reduce the calculation. The multi-scale feature extraction is performed by atrous spatial pyramid pooling (ASPP) to obtain global and local features. Then, the edge effect is optimized by the fully connected CRF. However, DeepLab cannot achieve end-to-end connectivity.
In the traditional convolution neural network, pooling is usually used to reduce the dimension. This has some side effects on image semantic segmentation. Due to the low pixel size on the feature layer after pooling, the accuracy in the feature map is lost even if upsampling is used. Therefore, the purpose of atrous convolution is to not need a pooling layer. After pooling, pixel information is reduced normally, which leads to information loss. DeepLab uses atrous convolution to enlarge the receptive field. Then, a new feature map operation with a large receptive field is used to achieve more accurate semantic segmentation, which can enlarge the receptive field exponentially without reducing the resolution and size of the feature.
DeepLab uses atrous convolution to sample feature maps, enlarging the receptive field and reducing the steps. Atrous convolution extends the standard convolution operation. By adjusting the receptive field of the convolution filter to capture multi-scale context information, characteristics of different resolutions are output. Considering one-dimensional (1D) signals, the output
y of atrous convolution of a 1D input signal
x with a filter
w(
k) of length
k is defined in Equation (1) [
11,
12]. The rate parameter
r corresponds to the stride with which we sample the input signal.
DeepLab is based on Resnet and transforms the fully connected layers of Resnet into convolutional layers. The last two pooling layers remove the downsampling and use atrous convolution [
11,
12] instead of the convolution kernel of the subsequent convolutional layer. Then, DeepLab fine-tunes the weight of Resnet, thereby improving the resolution of the output feature map and enlarging the receptive field. The next step is multi-scale extraction. The traditional method is to input a multi-scale image into the network, and then fuse the features. After trying this method in the network, the network performance improved. However, due to the feature extraction of the input for each scale, the calculation amount increased. Therefore, DeepLab introduces the ASPP operation. By inserting ASPP after the specific convolution layer of the network, the characteristic images of the original image are convoluted using the atrous convolution for different rates. Thus, different scale versions of features can be obtained. This is equivalent to the multi-scale operation of the input image.
DeepLab uses r = (6,12,18,24) 3 × 3 atrous convolution parallel sampling. The results of each atrous convolution branch sampled by ASPP are fused together, and then a final prediction result is obtained. DeepLab scales the image in different degrees through different atrous convolutions, and achieves better results. In ASPP, when the rate is larger, it will be close to the size of the feature map. The 3 × 3 convolution degenerates into a 1 × 1 convolution. So, we changed the rate to (6,12,18). Then, we added the batch normalization (BN) layer in ASPP, which can improve the generalization ability of the network and speed-up the network training.
The contribution of this study is using a deep convolutional neural network to extract object features and achieve an end-to-end connection with fully connected conditional random fields to refine object edges.
4. Experiment
In the experiment, our proposed model was used to detect a ship target from a remote sensing image under complex sea conditions and we compared the result with other state-of-the-art methods to verify the advantages of the model. For all experiments, we used the popular Caffe deep learning library. We established a high-quality remote sensing image dataset for ships, which was derived from Google Earth (
https://earth.google.com/web/) and NWPU-RESISC45 datasets (
http://www.escience.cn/people/JunweiHan/NWPU-RESISC45.html). Google Earth’s satellite images are not a single data source; multiple satellite images are integrated. Part of its satellite images are obtained from the QuickBird commercial satellite and the Earthsat company of the DigitalGlobe company in the United States. The NWPU-RESISC45 dataset is a publicly available benchmark for remote sensing image scene classification (RESISC), created by Northwestern Polytechnical University (NWPU). The total number of the images is 5260. In the experiment, we used the poly strategy in the training process, as shown in Equation (9) [
11,
12]. The number of iterations in the deep convolution neural network was set to 20,000. An epoch means that all samples in the training set are trained once. We used 80 epochs in these experiments. The initial value of learning rate was 0.001. If the learning rate is too high, it will be unstable when converging to the optimal position. So, the learning rate should decrease exponentially with the training process. We used a weight decay of 0.0005 and momentum of 0.9. The background of the dataset includes a harbor, calm sea, an island, and thin cloud, with 1660 images from offshore ships and 3600 images from nearshore ships. We used 60% of the images to train, 20% to validate, and 20% to test. Finally, we performed data enhancement, which involved rotating each image by 90°, 180°, and 270°. Finally, we obtained a dataset containing 10,520 images. We examined the experimental results including ship semantics segmentation, quantitative analysis, and time analysis.
where
power is the parameter and the value is 0.9,
iter represents the number of iterations, and
max_iter represents the maximum number of iterations.
4.1. Semantic Segmentation Result
Firstly, we compared the results of CRF-RNN (Conditional random field as recurrent neural network), DeepLab, and our method for ship detection. The experimental background was a calm sea, with sea clutter, harbor, thin cloud, and an island.
Figure 4 shows the results of ship detection with a calm sea surface. The classification effects of the two models are better than the proposed method, but our method has strong ability to capture the fine details of the target.
Figure 5 depicts a calm sea ship with Gaussian noise. The Gaussian noise coefficient was 0.4. From the results of semantic segmentation, CRF-RNN was affected by noise, resulting in missed detection. In the DeepLab result, the edge of ship target is fuzzy. The method proposed in this paper is not affected by noise; it can accurately classify ships. The ship detection results under sea clutter are shown in
Figure 6; the CRF-RNN result was the worst. DeepLab captured some details of the image due to the combination of deep learning and a fully connected CRF. However, the edge details are unclear. Our method improves the segmentation accuracy due to the improved end-to-end connection.
As shown in
Figure 7, when the ship was located in the port, the CRF-RNN misclassified one of the ships. Although the DeepLab model correctly classifies the ships and ports, the target edges are already unclear. DSS can overcome their shortcomings and improve the segmentation accuracy. As shown in
Figure 8, the background is under the thin cloud The three images all overcome the interference of thin cloud. Our method captures the fine details of the target edge.
Figure 9 depicts a semantic segmentation result with the island. The CRF-RNN classifies the ship and the sea surface into one category, resulting in misclassification. DeepLab did not completely classify the objects, but our method correctly classified the islands and ships, and the edge details are clear. The experiments showed that our method is superior to the other models under the conditions of sea clutter, harbor interior, thin clouds, and islands. In addition, the fine details are clearer.
4.2. Quantitative Result
We then quantitatively analyzed the model. Qualitative analysis is not enough, since detailed and specific conclusions cannot be generated. Therefore, quantitative methods can provide more detailed and specific data support for the argumentation process. These methods include precision, recall, F-measure analysis, receiver operating characteristic (ROC) and area under the curve (AUC) analysis, s confusion matrix, and runtime analysis.
4.2.1. Precision, Recall, and F-Measure Analysis
We used precision, recall, and F-measure [
24] as evaluation criteria to verify the advantages of the model. Precision is the ratio of the number of positive samples predicted correctly to the number of all predicted positive samples. Recall is the ratio of the number of correctly predicted positive samples to the total number of true positive samples. The F-measure is the weighted harmonic average of precision and recall, which are defined in Equations (10)–(12), respectively.
where
TP is true positive, which is a sample that is determined to be positive and is actually positive;
FP is false positive, which is a sample determined to be positive, but is actually negative;
FN is false negative, which is a sample determined to be negative but is actually positive; and
β2 is 1.
Figure 10 shows the quantitative analysis results of the four models. The figure shows that the precision of the proposed model (93.20%) is 6.28% higher than that of DeepLab (86.92%). The recall (79.31%) is 11.24% higher than that of DeepLab (68.07%). The F-measure shows that the model proposed in this paper (85.70%) is better than other models when it comes to ship detection. Because the end-to-end connection is implemented, the accuracy of the model is improved. The F-measures for DeepLab, CRF-RNN, and FCN-8s were 76.35%, 69.42%, and 65.5%, respectively.
4.2.2. ROC and AUC Analysis
We used the ROC [
25] curve to test the performance of the network structure. ROC was originally used to evaluate radar performance. The method is simple and intuitive, and the accuracy of the analysis method can be observed through the diagram. The ROC curve is based on the true positive rate (TPR) as the ordinate, with the false positive rate (FPR) as the abscissa. The ROC curve combines the true positive rate and false positive rate to accurately reflect the performance of the learner. The closer the ROC curve to the top left, the better the performance of the model. The calculation equations are
where
TN is true negative, meaning a sample is determined to be a negative and the sample is actually negative.
The experimental results are shown in
Figure 11. The models with the worst curve performance were FCN-8s and CRF-RNN. Because the network model is not deep enough, the result was poor. Both DeepLab and the proposed model are better, with the curves being close to the top left. However, our method is better than DeepLab because it realizes the end-to-end connection between the deep convolution neural network and the fully connected conditional random field, so the effect is better.
The area under the curve (AUC) [
26] is defined as the area enclosed by the coordinate axis under the ROC curve. The value of this area cannot be greater than 1. Because the ROC curve is generally above the line y = x, the value of AUC ranges between 0.5 and 1. The closer the AUC is to 1.0, the higher the accuracy of the detection method. When the AUC value is equal to 0.5, the accuracy is the lowest, so the method has no application value. The AUC values of our model and the other advanced methods are shown in
Table 2, which shows that the AUC value of our method is the highest, meaning it has the best performance.
4.2.3. Confusion Matrix
To verify the accuracy of the proposed algorithm, an experimentally measured classification confusion matrix [
27,
28,
29,
30] for ship target recognition was used. This matrix is primarily used for evaluating the classification accuracy of an image. Each column represents a prediction category, and the total number of data in each column represents the percentage of data projected for that category. Each row represents the true category of data, and the total number of data in each row is the percentage of table instances. For example, the value in the first column of the first row indicates the probability of a ship actually belonging to the first category being predicted as the first category. The value of the first row and the second column indicates the probability of a ship actually belonging to the first category being mispredicted as the second category. The other values are calculated in the same way. The confusion matrix of this algorithm is shown in
Table 3.
Table 3 shows that the classification accuracy for the port was the lowest. This occurred due to the complex background provided by the port. The methods are most likely to judge incorrectly here between ships and ports. Ships that sometimes dock in the port, connecting to the port, lead to classification errors. The classification accuracy of the proposed method is high, thereby satisfying the needs for remote sensing image ship target recognition.
4.2.4. Runtime Analysis
Table 4 compares the runtime of the proposed method with those of other state-of-the-art models. The table shows that DeepLab takes up to 1 s because the end-to-end connection between the DCNN and fully connected CRF is not realized. DSS is relatively fast and DSS and FCN-8s are in the same order of magnitude, guaranteeing the detection accuracy.