Building Shadow Detection on Ghost Images
Abstract
:1. Introduction
2. Materials and Methods
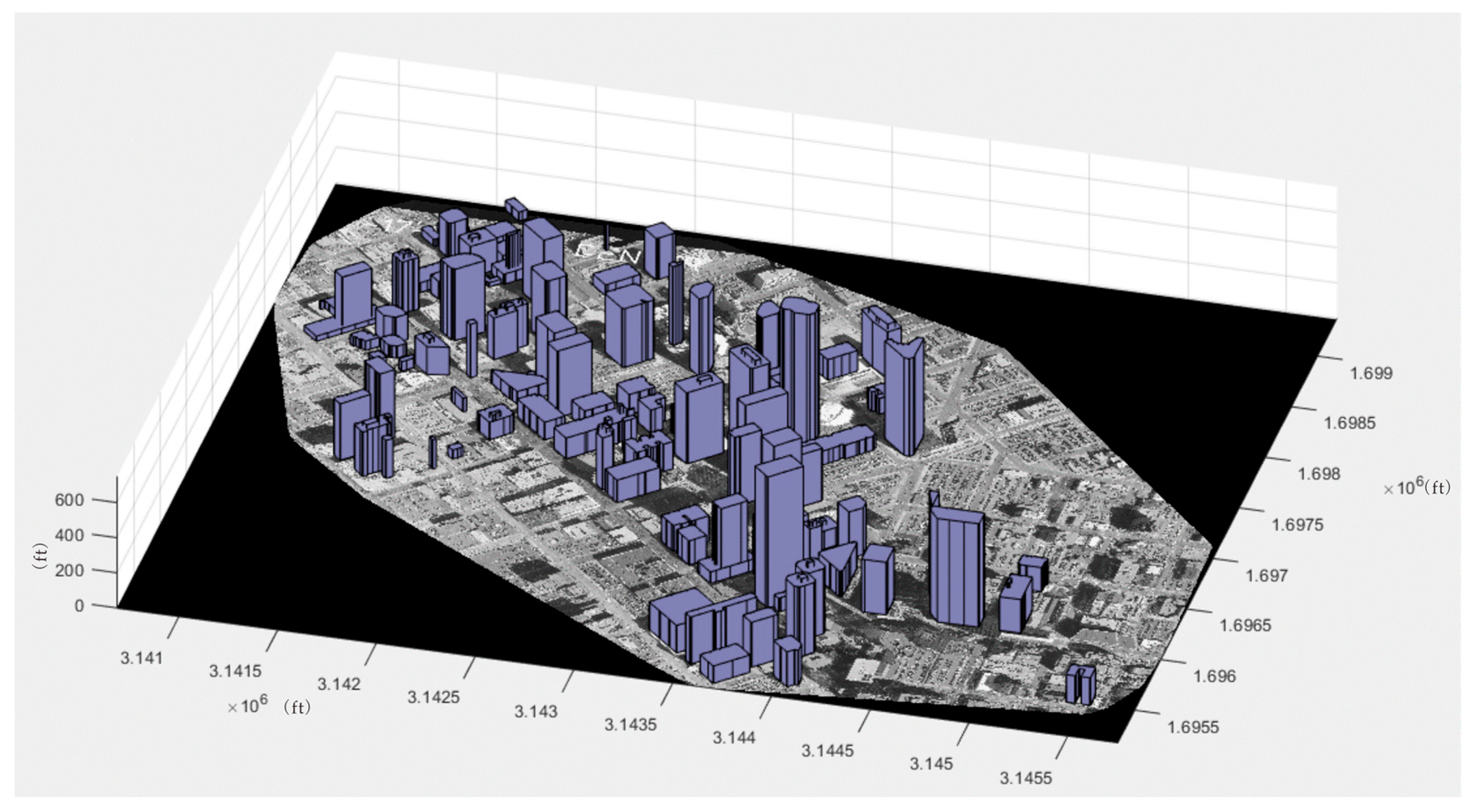
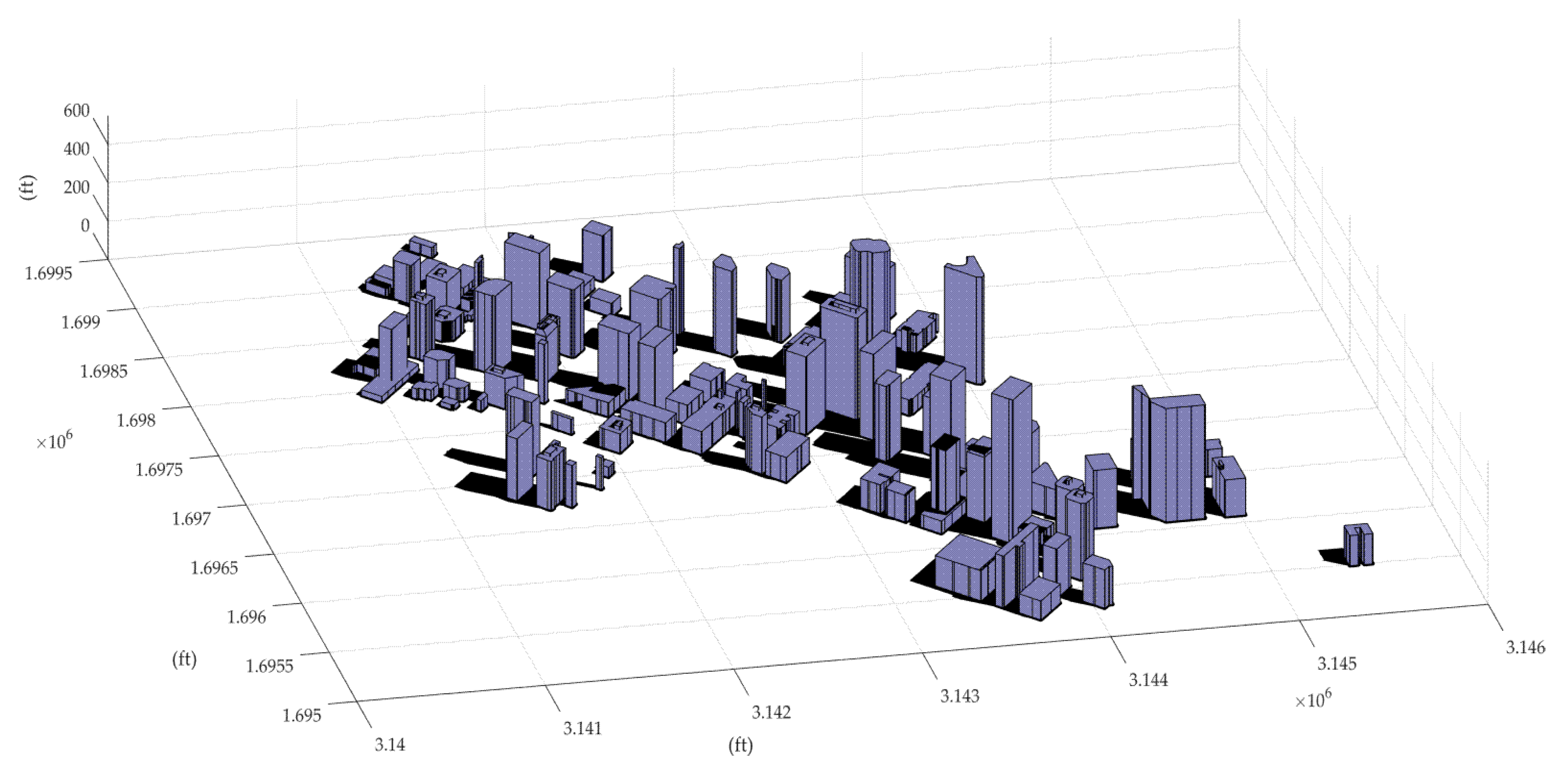
2.1. Data Set
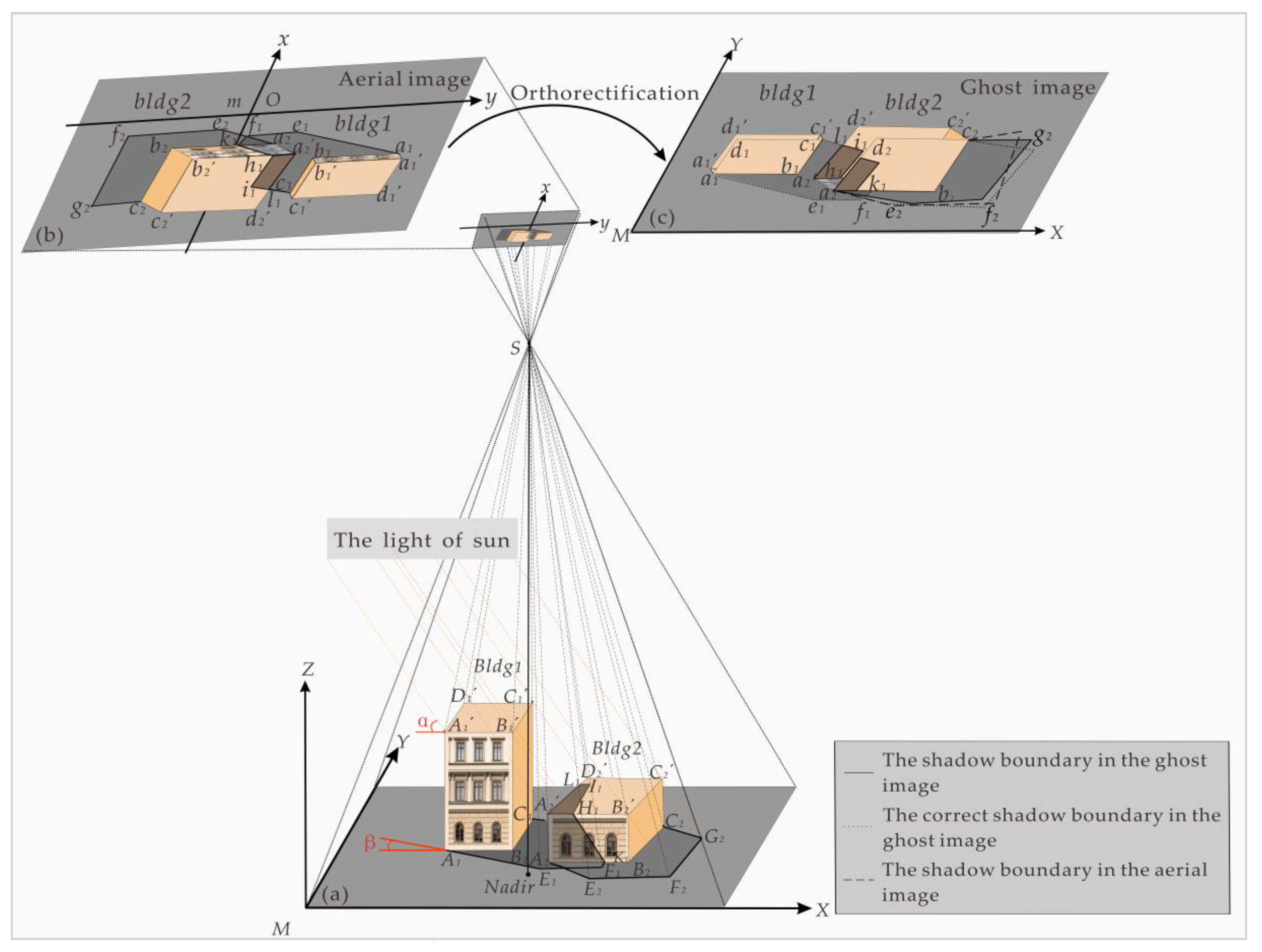
2.2. The Shadow’s Relationship between the Original Aerial Image and the Ghost Image
2.2.1. The Shadow Boundary on the Ground
2.2.2. The Shadow Boundary on the Building Roof
- If a building is shadowed on another tall building, this building shadow can consist of two parts: the first part is on the ground and the other part is on the wall of the front tall building.
- If a building is shadowed on another low building this building shadow can consist of three parts: the first part is on the ground, the second part is on the wall of the front low building and the third part is on the roof of the front low building. The corner point on the shadow boundary, noted as, I1 in the coordinate system M-XYZ is taken as an example to determine the shadow boundary on the roof. When the building Bldg1 is shadowed on another low building Bldg2, the corner point, I1, corresponding to the corner point of building roof C1′ from Bldg1 will be directly projected on the roof of Bldg2. The coordinates of point I1 can be determined by the solar zenith angle α, the solar altitude angle β, the height of buildings and point C1 (XC1, YC1, ZC1). The coordinates of C1 can be obtained directly from the DBM.
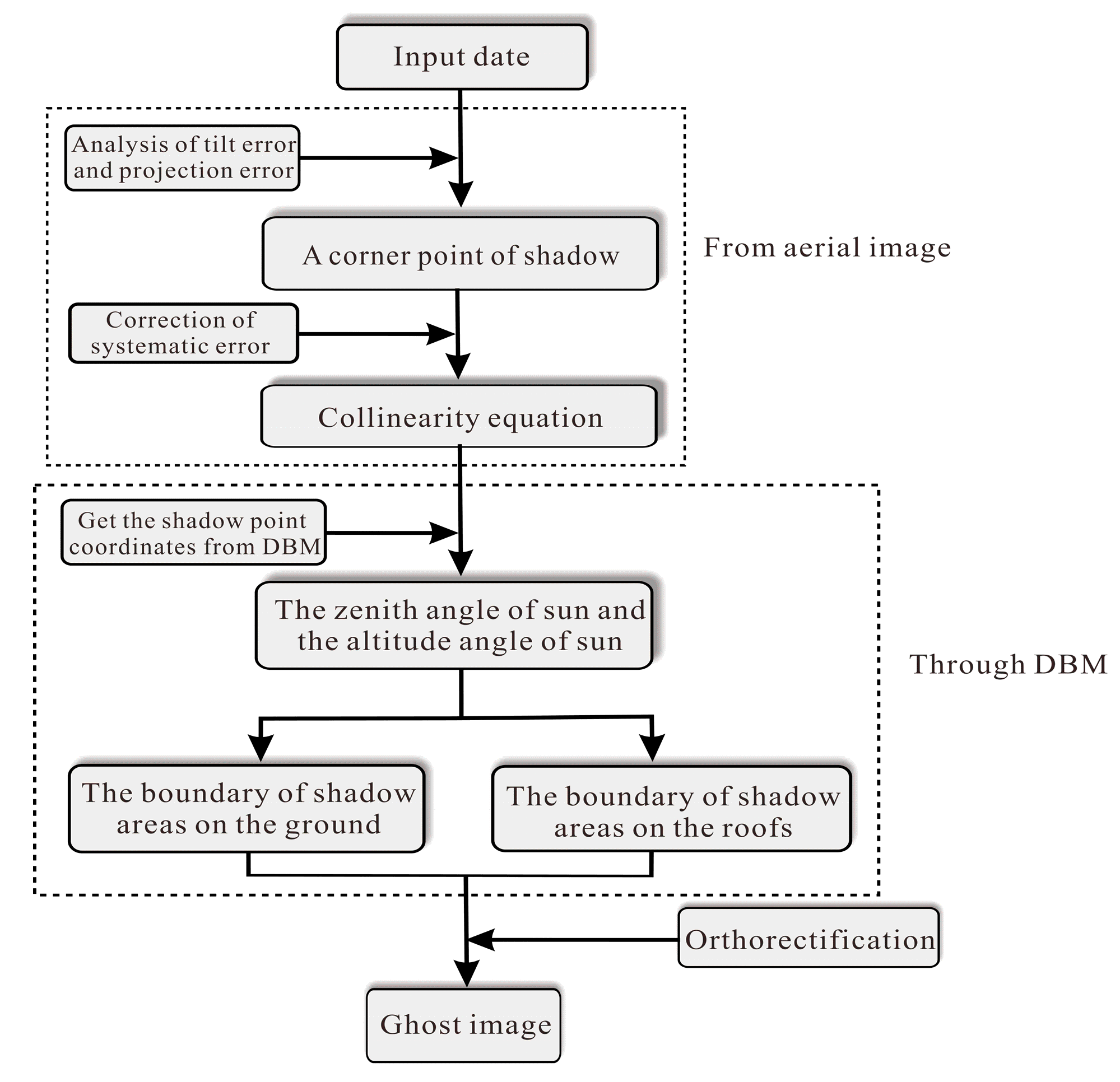
2.3. The Mathematical Model of the Proposed Method
2.3.1. Selection of a Shadow Boundary Point on Aerial Image
2.3.2. Determination of the Solar Zenith Angle and the Solar Altitude Angle
2.3.3. Shadow Detection
The Shadow Boundary Detection on the Ground
The Shadow Boundary Detection on the Roof
3. Results and Discussion
3.1. Results
3.1.1. Determination the Solar Zenith Angle and the Solar Altitude Angle
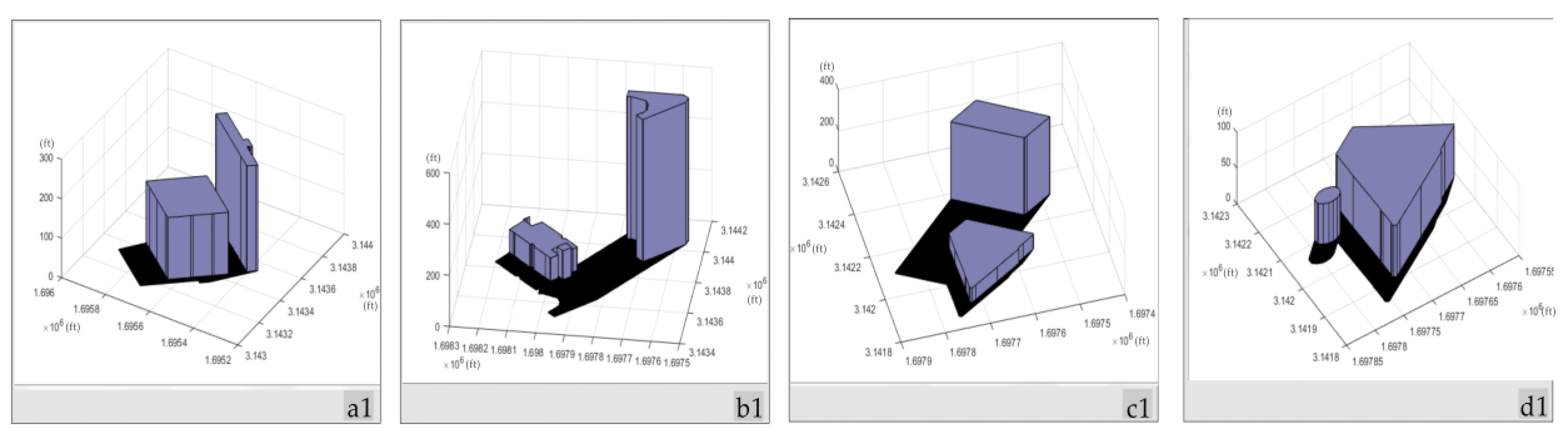
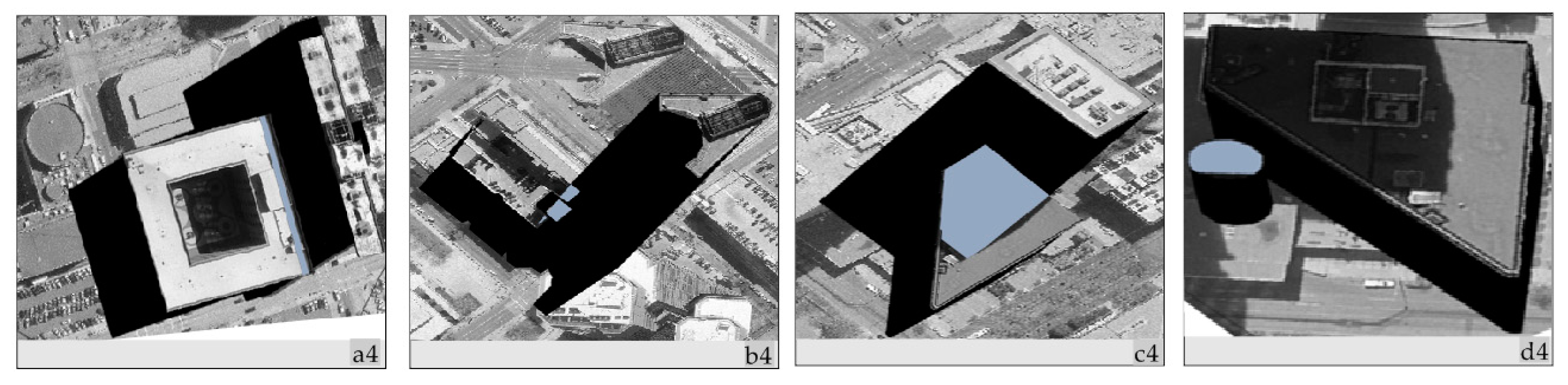
3.1.2. Shadow Detection
The Shadow Area on the Ground
The Shadow Area on the Roof
- (1)
- The shadow areas associated with all the 120 buildings in the study area are completely detected.
- (2)
- The proposed method not only detects the shadow areas on the horizontal roofs, but also detects shadow from buildings having tilts in the roofs, and buildings having some small rooms on the roofs (see a(2) and b(2)). The shadow from buildings having tilts in the roofs, and buildings having some small rooms on the roofs (see a(1), b(1), a(3) and b(3)).
- (3)
- The proposed method can simultaneously detect the shadows of buildings on the roofs and on the grounds.
3.2. Discussion
3.2.1. Accuracy Analysis
3.2.2. Accuracy Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, G.; Xie, W.; Cheng, P. Orthoimage Creation of Extremely High Buildings. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4132–4141. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, R.; Liu, N.; Huang, J.; Zhou, X. On-Board Ortho-Rectification for Images Based on an FPGA. Remote Sens. 2017, 9, 874. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Yan, L.; Yuan, Q.; Ma, Z. An Automatic Shadow Detection Method for VHR Remote Sensing Orthoimagery. Remote Sens. 2017, 9, 469. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Schickler, W.; Thorpe, A.; Song, P.; Chen, W.; Song, C. True orthoimage generation in urban areas with very tall buildings. Int. J. Remote Sens. 2004, 25, 5163–5180. [Google Scholar] [CrossRef]
- Wu, J.; Bauer, M.E. Evaluating the Effects of Shadow Detection on QuickBird Image Classification and Spectroradiometric Restoration. Remote Sens. 2013, 5, 4450–4469. [Google Scholar] [CrossRef] [Green Version]
- Türker, M.; Sümer, E. Building-based damage detection due to earthquake using the watershed segmentation of the post-event aerial images. Int. J. Remote Sens. 2008, 29, 3073–3089. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Troy, A.R.; Cadenasso, M. Object-based land cover classification of shaded areas in high spatial resolution imagery of urban areas: A comparison study. Remote Sens. Environ. 2009, 113, 1769–1777. [Google Scholar] [CrossRef]
- Liu, W.; Yamazaki, F. Object-Based Shadow Extraction and Correction of High-Resolution Optical Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1296–1302. [Google Scholar] [CrossRef]
- Chen, D.; Shang, S.; Wu, C. Shadow-based Building Detection and Segmentation in High-resolution Remote Sensing Image. J. Multimed. 2014, 9, 181–188. [Google Scholar] [CrossRef]
- Nandini, D.U.; Leni, E.S. Efficient shadow detection by using PSO segmentation and region-based boundary detection technique. J. Supercomput. 2018, 75, 3522–3533. [Google Scholar] [CrossRef]
- Ye, Q.; Xie, H.; Xu, Q. Removing Shadows from High-Resolution Urban Aerial Images Based on Color Constancy. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 21, 525–530. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Wang, L.; Shao, Z.; Li, D. Development of a multi-scale object-based shadow detection method for high spatial resolution image. Remote Sens. Lett. 2015, 6, 59–68. [Google Scholar] [CrossRef]
- Mo, N.; Zhu, R.; Yan, L.; Zhao, Z. Deshadowing of Urban Airborne Imagery Based on Object-Oriented Automatic Shadow Detection and Regional Matching Compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 585–605. [Google Scholar] [CrossRef]
- Li, Y.; Gong, P.; Sasagawa, T. Integrated shadow removal based on photogrammetry and image analysis. Int. J. Remote Sens. 2005, 26, 3911–3929. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, W.; Kelmelis, J.; Zhang, D. A comprehensive study on urban true orthorectification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2138–2147. [Google Scholar] [CrossRef]
- Tian, J.; Sun, J.; Tang, Y. Tricolor Attenuation Model for Shadow Detection. IEEE Trans. Image Process. 2009, 18, 2355–2363. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. Morphological Building/Shadow Index for Building Extraction From High-Resolution Imagery Over Urban Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 5, 161–172. [Google Scholar] [CrossRef]
- Elbakary, M.I.; Iftekharuddin, K.M. Shadow Detection of Man-Made Buildings in High-Resolution Panchromatic Satellite Images. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5374–5386. [Google Scholar] [CrossRef]
- Tong, X.; Lin, X.; Feng, T.; Xie, H.; Liu, S.; Hong, Z.; Chen, P. Use of shadows for detection of earthquake-induced collapsed buildings in high-resolution satellite imagery. ISPRS J. Photogramm. Remote Sens. 2013, 79, 53–67. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. Joint Model and Observation Cues for Single-Image Shadow Detection. Remote Sens. 2016, 8, 484. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Wang, Y.; Yue, T.; Ye, S.; Wang, W. Building Occlusion Detection from Ghost Images. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1074–1084. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry with Applications in GIS, 3rd ed.; McGraw-Hill: San Mateo, CA, USA, 2000; pp. 217–218. [Google Scholar]




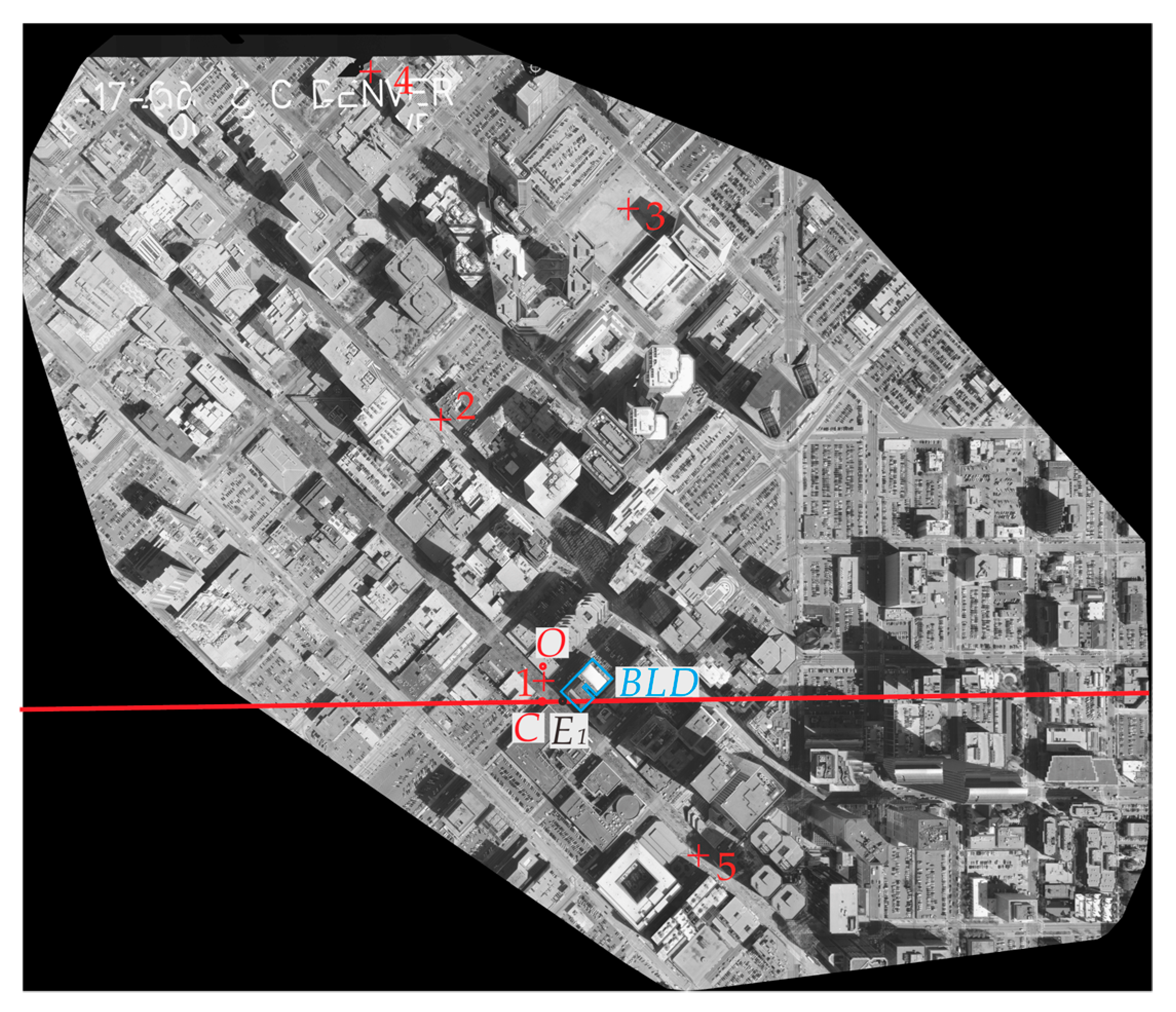





| The Corner Point of Shadow | α/° | β/° | The Height of BLD/ft | The Actual Height of BLD/ft | The Difference between the Height of BLD and the Actual Height of BLD/ft |
|---|---|---|---|---|---|
| E1 | 49.812 | 57.500 | 148.838 | 148.900 | 0.062 |
| 2 | 51.147 | 58.586 | 152.479 | 148.900 | 3.579 |
| 3 | 48.964 | 57.176 | 144.444 | 148.900 | 4.456 |
| 4 | 47.808 | 57.300 | 138.693 | 148.900 | 10.207 |
| 5 | 49.694 | 58.096 | 148.216 | 148.900 | 0.684 |
| Approach | Number of Detected Buildings | Number of the Shadow Areas on the Ground Detected | Number of the Shadow Areas on the Roofs Detected | Improved Shadow Detection Rate on the Ground | Improved Shadow Detection Rate on the Roof |
|---|---|---|---|---|---|
| The traditional shadow detection method based on features of the shadow | 120 | 113 | 10 | - | - |
| Our method | 120 | 120 | 15 | 9.42% | 33.33% |
| The Results | The Traditional Shadow Detection Method Based on Features of the Shadow (The Number of Buildings) | The Proposed Method (The Number of Buildings) |
|---|---|---|
| Ct | 120 | 120 |
| Cd | 116 | 120 |
| Ctd | 102 | 120 |
| Cfd | 7 | 0 |
| Cld | 11 | 0 |
| Ptd | 85% | 100% |
| Pfd | 6.54% | 0 |
| Pld | 9.17% | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Sha, H. Building Shadow Detection on Ghost Images. Remote Sens. 2020, 12, 679. https://doi.org/10.3390/rs12040679
Zhou G, Sha H. Building Shadow Detection on Ghost Images. Remote Sensing. 2020; 12(4):679. https://doi.org/10.3390/rs12040679
Chicago/Turabian StyleZhou, Guoqing, and Hongjun Sha. 2020. "Building Shadow Detection on Ghost Images" Remote Sensing 12, no. 4: 679. https://doi.org/10.3390/rs12040679
APA StyleZhou, G., & Sha, H. (2020). Building Shadow Detection on Ghost Images. Remote Sensing, 12(4), 679. https://doi.org/10.3390/rs12040679






