Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data
Abstract
:1. Introduction
- (1)
- Develop an ALS-based method to characterize tree spatial distribution patterns at the landscape level quantitatively;
- (2)
- Characterize the competitive effects among tree crowns using ALS-based metrics;
- (3)
- Investigate the factors impacting ALS-based tree crown segmentation algorithms and the impacts of observation window sizes on tree spatial distribution patterns.
2. Materials and Methods
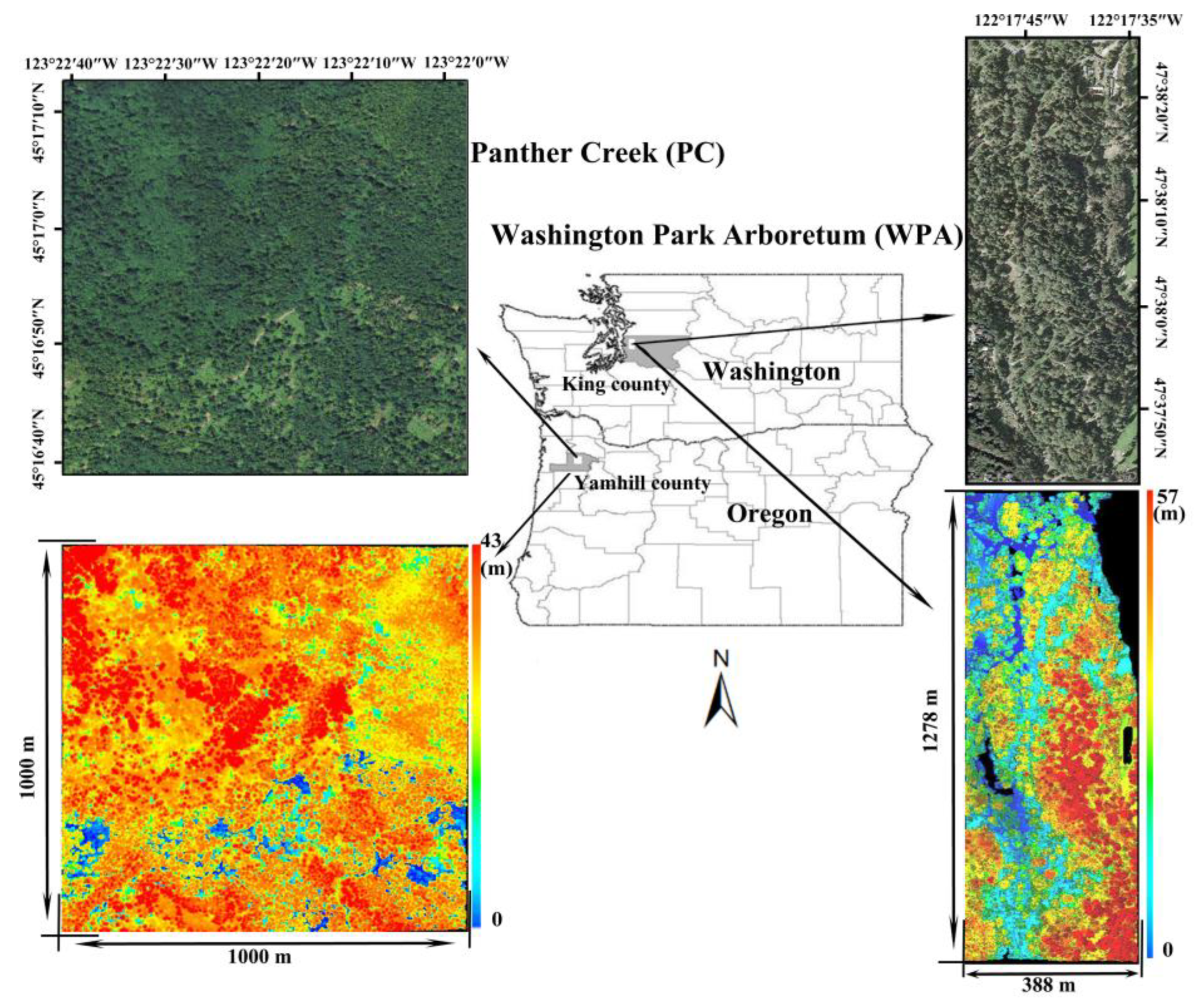
2.1. Study Sites
2.2. Datasets
2.3. ALS-Based Tree Crown Segmentation
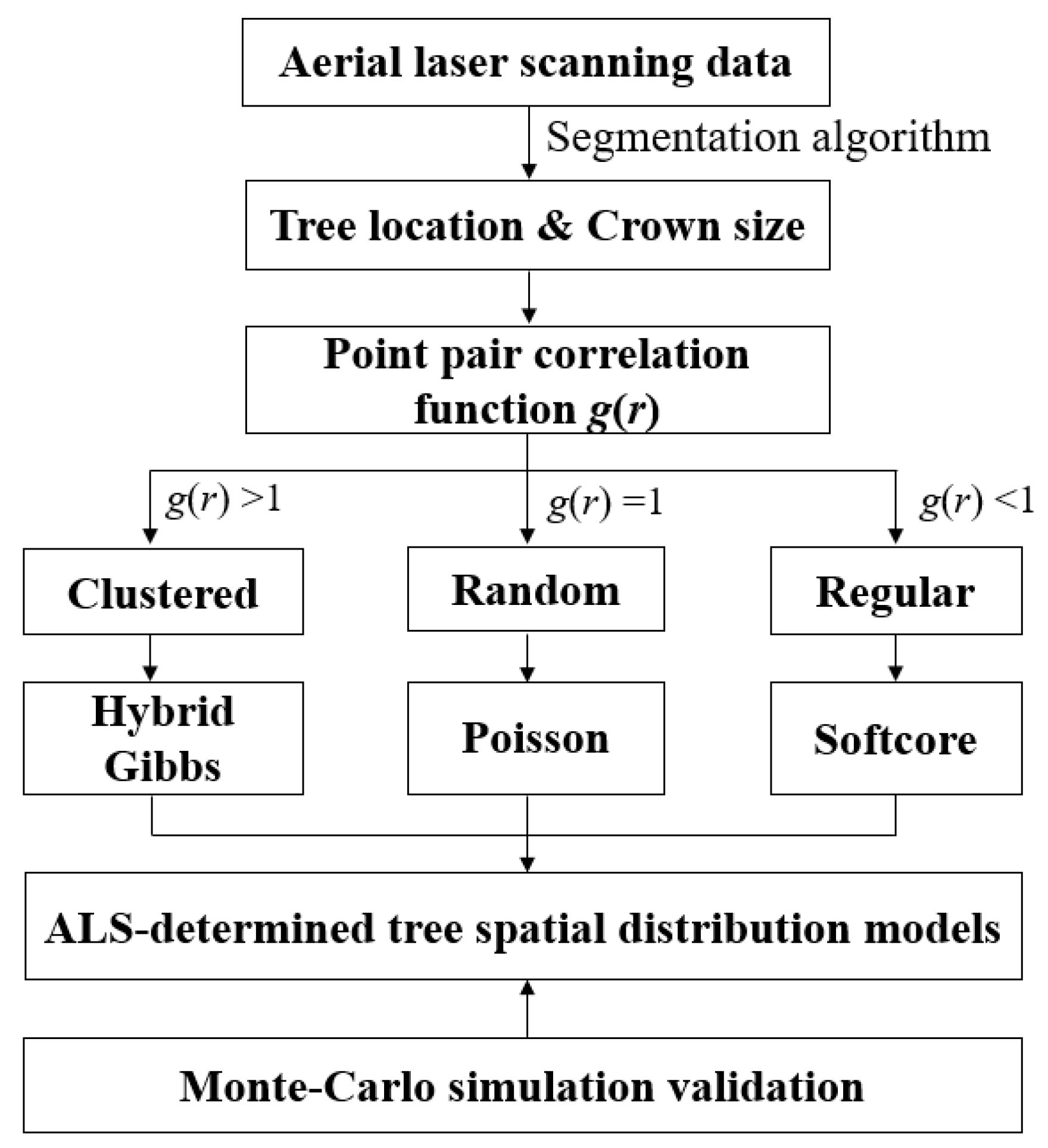
2.4. Tree Spatial Distribution Pattern Identification
2.5. ALS-Based Statistical Model Parameters Determination
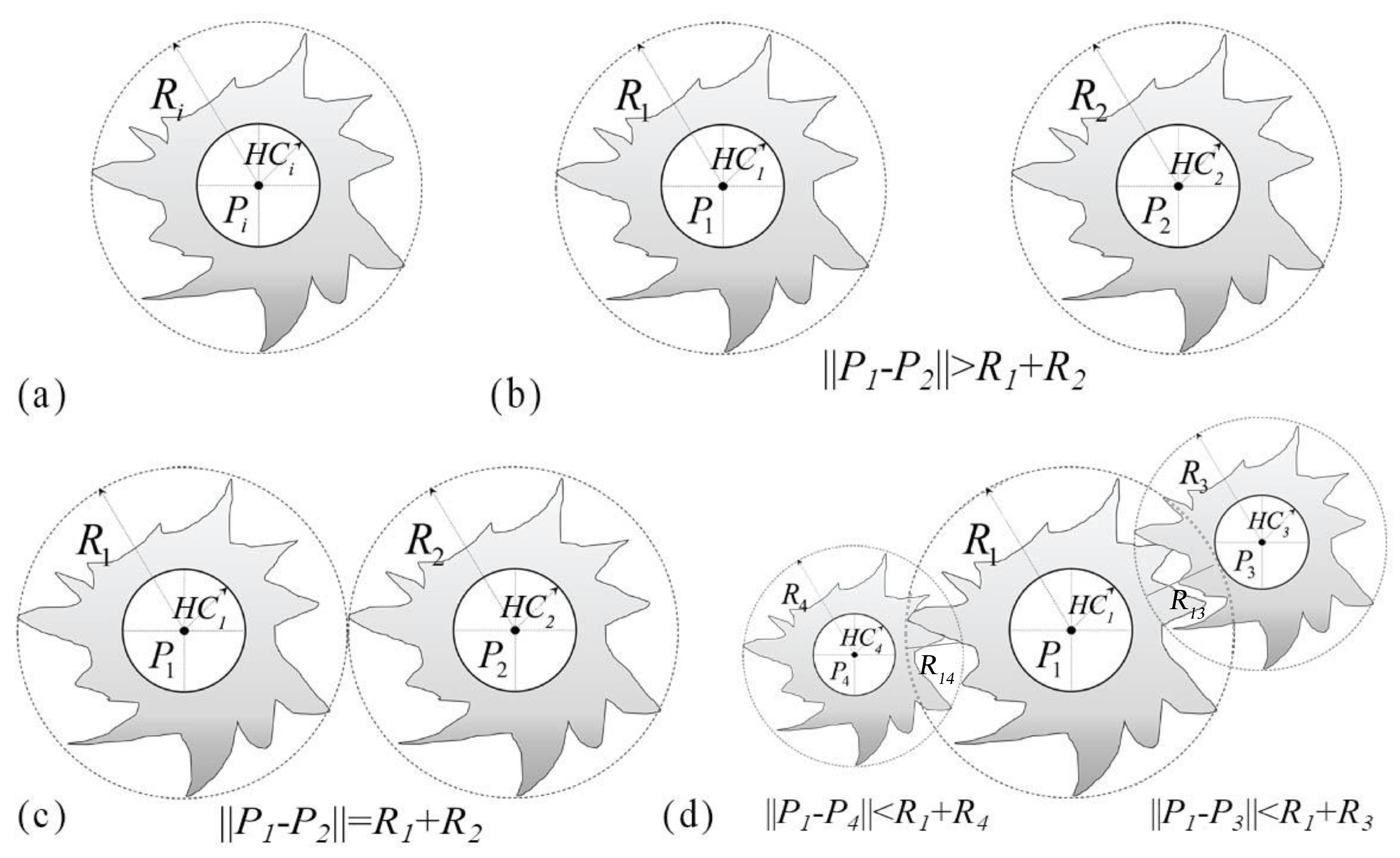
2.5.1. Tree Crown Competitive Effects Characterization
2.5.2. Three Different Tree Spatial Distribution Patterns
2.6. ALS-Determined Tree Spatial Distribution Models Validation
2.7. Sensitivity Analysis
3. Results
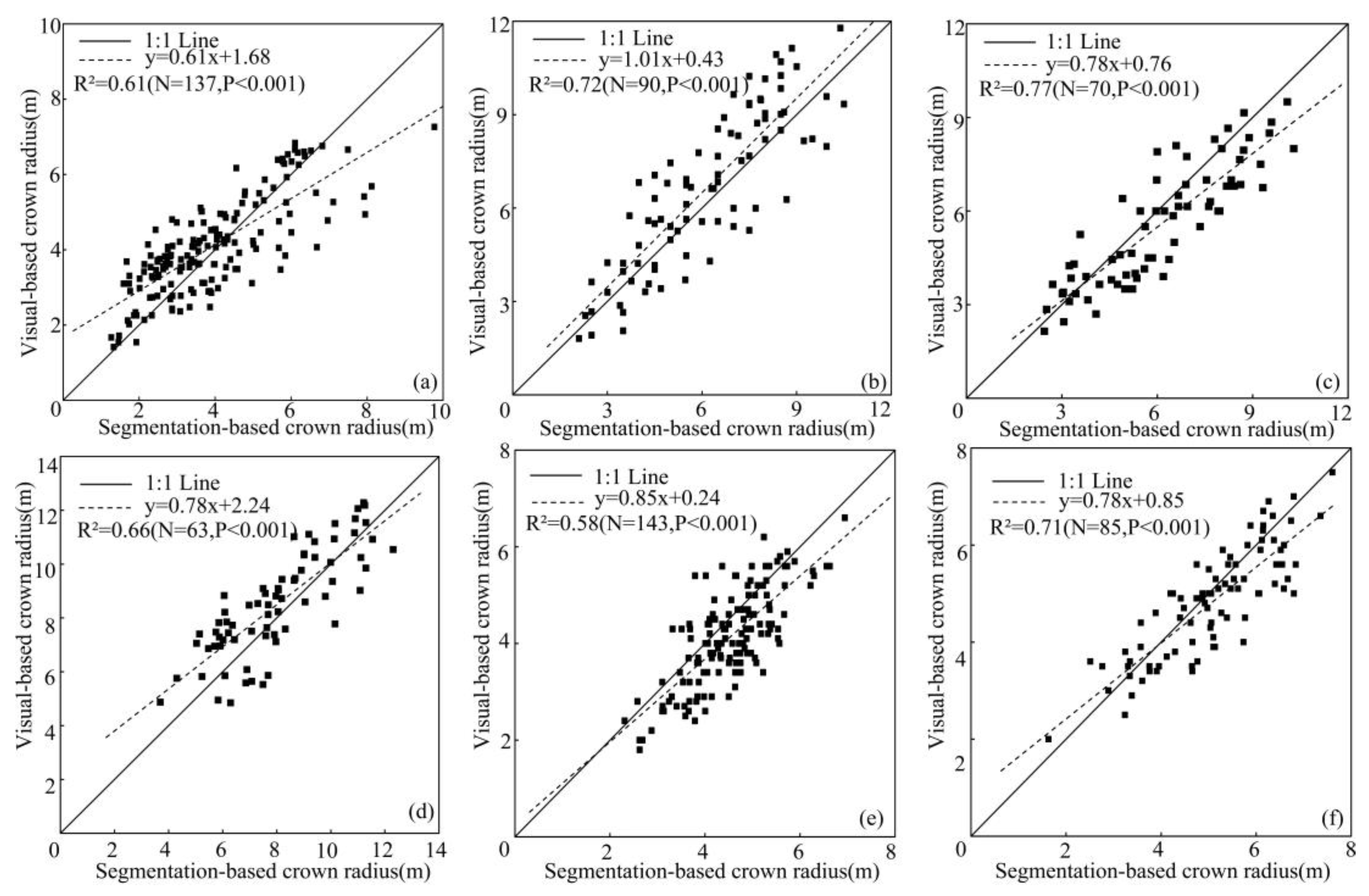
3.1. ALS-Based Tree Locations and Crown Sizes
3.2. ALS-Based Tree Spatial Distribution Patterns
3.3. ALS-Determined Parameters of Tree Spatial Distribution Models
3.4. Validation of ALS-Determined Tree Spatial Distribution Models
4. Discussion
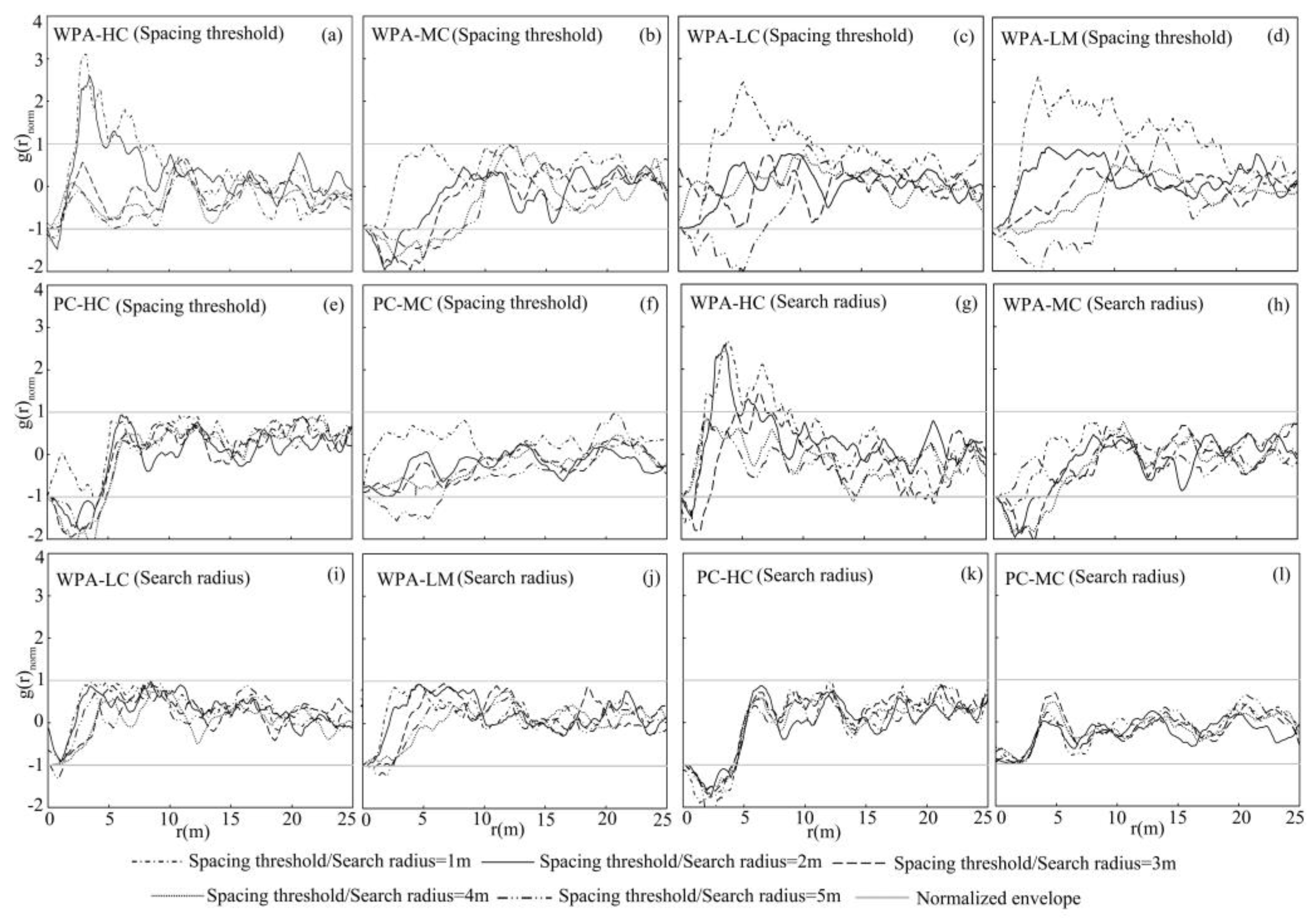
4.1. Tree Segmentation Accuracy Analysis
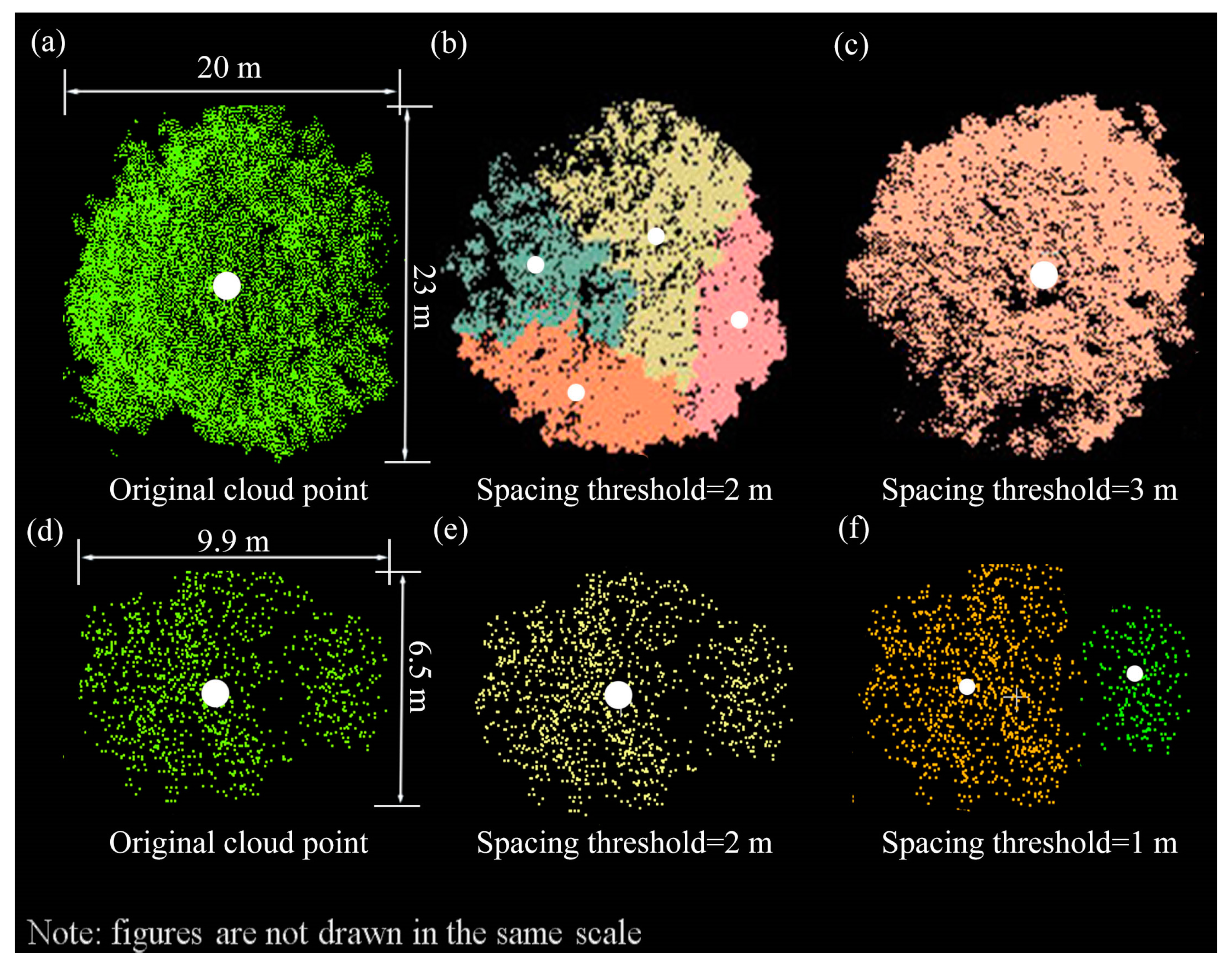
4.1.1. Spacing Threshold Effects
4.1.2. Search Radius Effects
4.1.3. Effect of Overlap on Individual Tree Segmentation
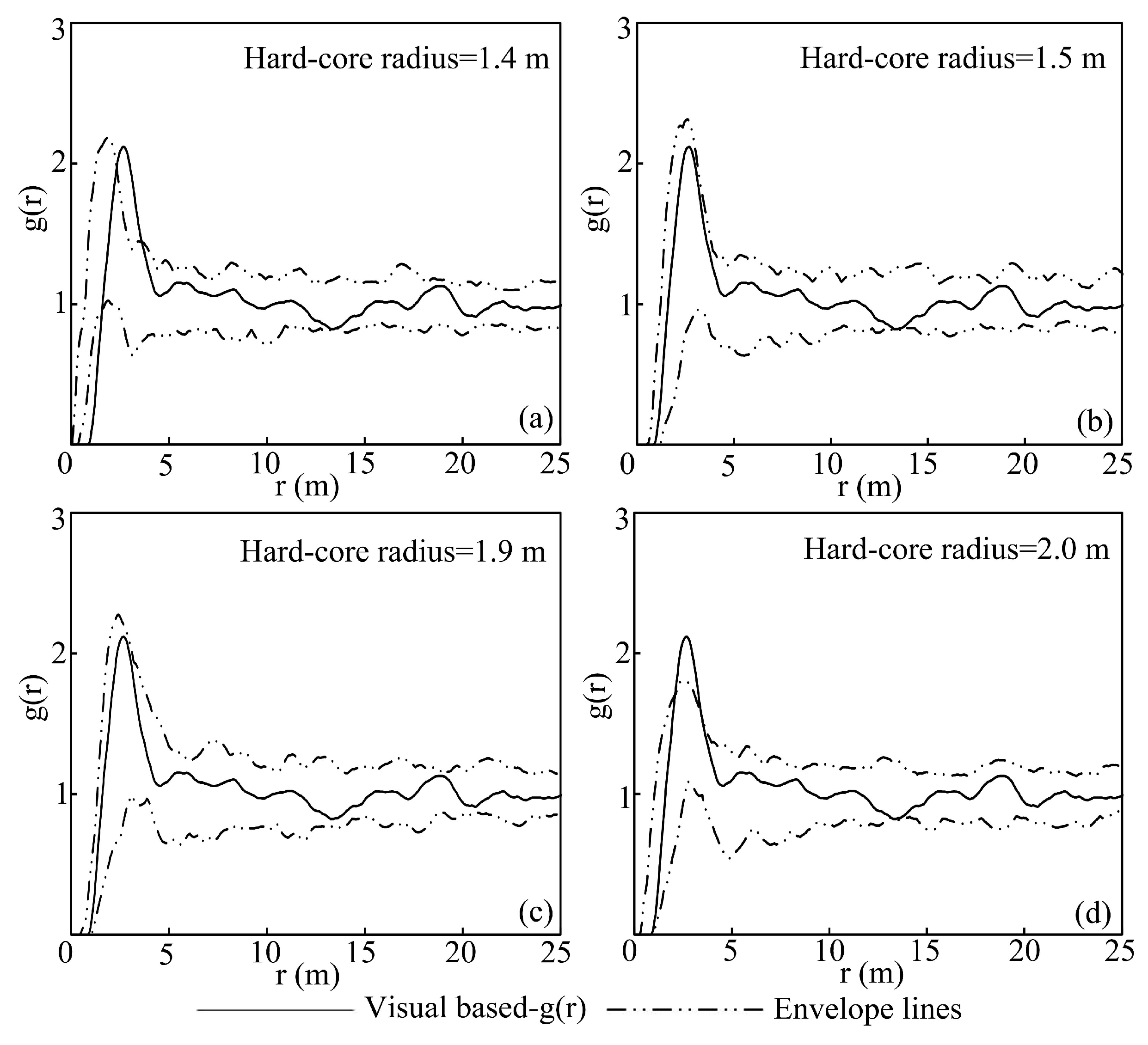
4.2. Effect of the Hard-Core Radius on Tree Spatial Distribution Pattern
4.3. Spatial Variations of Tree Spatial Distribution Patterns
4.4. Tree Spatial Pattern Effects on the Probability of Viewing Ground Area
4.5. The Effects of Tree Location Proxy Selection
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Plot ID | Observed Patterns | Observed Tree # | Spacing Threshold (m) | Segmented Tree # | Crown Radii (m) | Predicted Patterns | |
|---|---|---|---|---|---|---|---|
| Range (Min–Max.) | Average | ||||||
| WPA-HC | Clustered | 159 | 1 | 252 | 1.03–6.79 | 2.96 | Clustered |
| 2 | 137 | 1.26–8.77 | 3.38 | Clustered | |||
| 3 | 110 | 2.30–10.71 | 5.92 | Random | |||
| 4 | 89 | 2.35–11.32 | 7.72 | Random | |||
| 5 | 77 | 2.50–12.06 | 8.67 | Random | |||
| WPA-MC | Regular | 95 | 1 | 130 | 1.59–7.79 | 3.37 | Random |
| 2 | 90 | 2.10–10.50 | 6.13 | Regular | |||
| 3 | 85 | 2.98–11.06 | 6.57 | Regular | |||
| 4 | 67 | 2.69–11.17 | 7.55 | Regular | |||
| 5 | 58 | 2.94–11.5 | 9.61 | Regular | |||
| WPA-LC | Random | 75 | 1 | 156 | 1.08–7.41 | 3.09 | Clustered |
| 2 | 70 | 2.45–10.31 | 6.09 | Random | |||
| 3 | 63 | 2.52–11.32 | 6.42 | Random | |||
| 4 | 61 | 2.85–11.30 | 6.69 | Random | |||
| 5 | 57 | 2.85–11.33 | 8.23 | Regular | |||
| WPA-LM | Random | 66 | 1 | 123 | 1.47–10.94 | 5.32 | Clustered |
| 2 | 83 | 2.30–11.30 | 6.61 | Random | |||
| 3 | 63 | 2.50–12.70 | 7.13 | Random | |||
| 4 | 50 | 3.21–12.28 | 7.63 | Regular | |||
| 5 | 47 | 4.70–12.53 | 7.96 | Regular | |||
| PC-HC | Regular | 150 | 1 | 171 | 1.61–6.65 | 3.70 | Random |
| 2 | 143 | 2.32–6.94 | 4.53 | Regular | |||
| 3 | 129 | 2.42–9.66 | 5.26 | Regular | |||
| 4 | 106 | 3.11–10.05 | 5.85 | Regular | |||
| 5 | 81 | 2.61–10.47 | 6.32 | Regular | |||
| PC-MC | Random | 92 | 1 | 120 | 1.38–7.32 | 3.65 | Random |
| 2 | 85 | 1.63–7.75 | 5.08 | Random | |||
| 3 | 83 | 2.64–10.12 | 6.56 | Random | |||
| 4 | 72 | 2.98–10.47 | 7.15 | Random | |||
| 5 | 60 | 2.86–10.72 | 7.55 | Regular | |||
| Plot ID | Observed Patterns | Observed Trees # | Searching Radius (m) | Segmented Trees # | Crown Radii (m) | Predicted Patterns | |
|---|---|---|---|---|---|---|---|
| Range (Min.–Max.) | Average | ||||||
| WPA-HC | Clustered | 159 | 1 | 189 | 1.05–7.02 | 3.13 | Clustered |
| 2 | 137 | 1.26–8.77 | 3.38 | Clustered | |||
| 3 | 129 | 2.11–9.55 | 4.65 | Clustered | |||
| 4 | 113 | 2.59–10.97 | 6.10 | Random | |||
| 5 | 108 | 2.65–11.32 | 7.21 | Random | |||
| WPA-MC | Regular | 95 | 1 | 114 | 1.43–10.24 | 4.12 | Regular |
| 2 | 90 | 2.10–10.50 | 6.13 | Regular | |||
| 3 | 83 | 2.25–10.74 | 6.35 | Regular | |||
| 4 | 78 | 2.26–11.60 | 6.79 | Regular | |||
| 5 | 65 | 2.56–11.70 | 7.03 | Random | |||
| WPA-LC | Random | 75 | 1 | 115 | 1.13–9.44 | 3.85 | Random |
| 2 | 70 | 2.45–10.31 | 6.09 | Random | |||
| 3 | 62 | 2.46–11.32 | 6.31 | Random | |||
| 4 | 59 | 2.49–11.33 | 6.33 | Random | |||
| 5 | 45 | 2.59–11.33 | 6.96 | Regular | |||
| WPA-LM | Random | 66 | 1 | 113 | 1.05–11.30 | 5.79 | Random |
| 2 | 63 | 2.50–12.30 | 6.61 | Random | |||
| 3 | 59 | 2.64–11.50 | 6.65 | Random | |||
| 4 | 57 | 2.53–11.33 | 6.87 | Random | |||
| 5 | 44 | 4.70–12.53 | 7.12 | Regular | |||
| PC-HC | Regular | 150 | 1 | 160 | 1.51–8.65 | 4.54 | Regular |
| 2 | 143 | 2.32–6.94 | 4.53 | Regular | |||
| 3 | 140 | 2.22–8.65 | 4.89 | Regular | |||
| 4 | 131 | 2.22–9.66 | 5.07 | Regular | |||
| 5 | 128 | 2.32–9.87 | 5.23 | Regular | |||
| PC-MC | Random | 92 | 1 | 97 | 1.47–6.97 | 4.43 | Random |
| 2 | 85 | 1.63–7.75 | 5.08 | Random | |||
| 3 | 83 | 3.22–8.97 | 6.05 | Random | |||
| 4 | 81 | 3.20–9.37 | 6.12 | Random | |||
| 5 | 82 | 3.90–9.72 | 6.51 | Random | |||
References
- Boyden, S.; Dan, B.; Shepperd, W. Spatial and temporal patterns in structure, regeneration, and mortality of an old-growth ponderosa pine forest in the colorado front range. For. Ecol. Manag. 2005, 219, 43–55. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, J.; Song, B.; Ye, J.; Li, B. Vertical structure and spatial associations of dominant tree species in an old-growth temperate forest. For. Ecol. Manag. 2007, 252, 1–11. [Google Scholar] [CrossRef]
- Looney, C.E.; D’Amato, A.W.; Palik, B.J.; Fraver, S.; Kastendick, D.N. Size-growth relationship, tree spatial patterns, and tree-tree competition influence tree growth and stand complexity in a 160-year red pine chronosequence. For. Ecol. Manag. 2018, 424, 85–94. [Google Scholar] [CrossRef]
- Martens, S.N.; Breshears, D.D.; Meyer, C.W. Spatial distributions of understory light along the grassland/forest continuum: Effects of cover, height, and spatial pattern of tree canopies. Ecol. Model. 2000, 126, 79–93. [Google Scholar] [CrossRef]
- Okuda, T.; Kachi, N.; Yap, S.K.; Manokaran, N. Tree distribution pattern and fate of juveniles in a lowland tropical rain forest–implications for regeneration and maintenance of species diversity. Plant Ecol. 1997, 131, 155–171. [Google Scholar] [CrossRef]
- Paluch, J.G. The influence of the spatial pattern of trees on forest floor vegetation and silver fir (Abies alba Mill.) regeneration in uneven-aged forests. For. Ecol. Manag. 2005, 205, 283–298. [Google Scholar] [CrossRef]
- Petritan, I.C.; Marzano, R.; Petritan, A.M.; Lingua, E. Overstory succession in a mixed quercus petraea–fagus sylvatica old growth forest revealed through the spatial pattern of competition and mortality. For. Ecol. Manag. 2014, 326, 9–17. [Google Scholar] [CrossRef]
- Dale, M.R.T. Spatial pattern analysis in plant ecology. Weed Technol. 1999, 15, 195–196. [Google Scholar]
- Wiegand, T.; Gunatilleke, S.; Gunatilleke, N.; Okuda, T. Analyzing the spatial structure of a sri lankan tree species with multiple scales of clustering. Ecology 2007, 88, 3088–3102. [Google Scholar] [CrossRef]
- Cescatti, A. Effects of needle clumping in shoots and crowns on the radiative regime of a norway spruce canopy. Ann. Sci. 1998, 55, 89–102. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1985, 23, 705–721. [Google Scholar] [CrossRef] [Green Version]
- Tomppo, E. Models and Methods for Analysing Spatial Patterns of Trees; The Finnish Forest Research Institute: Joensuu, Finland, 1986; pp. 5–8. [Google Scholar]
- Dessard, H.; Picard, N.; Raphaël, P.; Collinet-Vaurier, F. Spatial patterns of the most abundant tree species. In Ecology an Management of Neotropical Rainforest; Gourlet-Fleury, S., Guehl, J.M., Laroussinie, O., Eds.; Elsevier Publisher: Paris, France, 2004; pp. 177–190. ISBN 2-84299-455-8. [Google Scholar]
- Forman, R.T.T.; Hahn, D.C. Spatial patterns of trees in a caribbean semievergreen forest. Ecology 1980, 61, 1267–1274. [Google Scholar] [CrossRef]
- Neeff, T.; Biging, G.S.; Dutra, L.V.; Freitas, C.C.; Santos, J.R.D. Markov point processes for modeling of spatial forest patterns in amazonia derived from interferometric height. Remote Sens. Environ. 2005, 97, 484–494. [Google Scholar] [CrossRef]
- Wiegand, T.; Moloney, K.A. Handbook of Spatial Point Pattern Analysis in Ecology; CRC Press: Boca Raton, FL, USA, 2013; pp. 15–17. [Google Scholar]
- Mateu, J.; Usó, J.L.; Montes, F. The spatial pattern of a forest ecosystem. Ecol. Model. 1998, 108, 163–174. [Google Scholar] [CrossRef]
- Stoyan, D.; Penttinen, A. Recent applications of point process methods in forestry statistics. Stat. Sci. 2000, 15, 61–78. [Google Scholar]
- Geng, J.; Chen, J.M.; Tu, L.L.; Tian, Q.J.; Wang, L.; Yang, R.R.; Yang, Y.J.; Huang, Y.; Fan, W.L.; Lv, C.G. Influence of the exclusion distance among trees on gap fraction and foliage clumping index of forest plantations. Trees 2016, 30, 1–11. [Google Scholar] [CrossRef]
- Picard, N.; BAR-HEN, A.; Mortier, F. The multi scale marked area interaction point process: A model for the spatial pattern of trees. Scand. J. Stat. 2009, 36, 23–41. [Google Scholar] [CrossRef]
- Stoyan, D.; Stoyan, H. Estimating pair correlation functions of planar cluster processes. Biom. J. 2010, 38, 259–271. [Google Scholar] [CrossRef]
- Moeur, M. Characterizing spatial patterns of trees using stem-mapped data. For. Sci. 1993, 39, 756–775. [Google Scholar]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Umeki, K. Importance of crown position and morphological plasticity in competitive interaction in a population of xanthium canadense. Ann. Bot. 1995, 75, 259–265. [Google Scholar] [CrossRef]
- Vacchiano, G.; Castagneri, D.; Meloni, F.; Lingua, E.; Motta, R. Point pattern analysis of crown-to-crown interactions in mountain forests. In Proceedings of the 1st International Conference on Spatial Statistics -Mapping Global Change, Enschede, The Netherlands, 23–25 March 2011. [Google Scholar]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Ngo Bieng, M.A.; Ginisty, C.; Goreaud, F. Point process models for mixed sessile forest stands. Ann. For. Sci. 2011, 68, 267–274. [Google Scholar] [CrossRef] [Green Version]
- Vastaranta, M.; Melkas, T.; Holopainen, M.; Kaartinen, H.; Hyyppä, J.; Hyyppä, H. Laser-based field measurements in tree-level forest data acquisition. Photogramm. J. Finl. 2009, 21, 51–61. [Google Scholar]
- Thorpe, H.C.; Astrup, R.; Trowbridge, A.; Coates, K.D. Competition and tree crowns: A neighborhood analysis of three boreal tree species. For. Ecol. Manag. 2010, 259, 1586–1596. [Google Scholar] [CrossRef]
- Baddeley, A.; Turner, R.; Mateu, J.; Bevan, A.; Grün, B.; Pebesma, E.; Zeileis, A. Hybrids of gibbs point process models and their implementation. J. Stat. Softw. 2013, 55, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Iftimi, A.; Montes, F.; Mateu, J.; Ayyad, C. Measuring spatial inhomogeneity at different spatial scales using hybrids of Gibbs point process models. Stoch. Environ. Res. Risk Assess. 2016, 31, 1–15. [Google Scholar] [CrossRef]
- Franklin, J.; Michaelsen, J.; Strahler, A.H. Spatial analysis of density dependent pattern in coniferous forest stands. Vegetatio 1985, 64, 29–36. [Google Scholar] [CrossRef]
- Nelson, T.; Boots, B.; Wulder, M.A. Techniques for accuracy assessment of tree locations extracted from remotely sensed imagery. J. Environ. Manag. 2005, 74, 265–271. [Google Scholar] [CrossRef]
- Uuttera, J.; Haara, A.; Tokola, T.; Maltamo, M. Determination of the spatial distribution of trees from digital aerial photographs. For. Ecol. Manag. 1998, 110, 275–282. [Google Scholar] [CrossRef]
- Paris, C.; Bruzzone, L. A three-dimensional model-based approach to the estimation of the treetop height by fusing low-density LiDAR data and very high resolution optical images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 467–480. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar remote sensing of the canopy structure and biophysical properties of douglas-fir western hemlock forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Dalponte, M.; Ene, L.T.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting selected forest stand characteristics with multispectral ALS data. Remote Sens. 2018, 10, 586. [Google Scholar] [CrossRef] [Green Version]
- Packalén, P.; Vauhkonen, J.; Kallio, E.; Peuhkurinen, J.; Pitkänen, J.; Pippuri, I.; Maltamo, M. Comparison of the Spatial Pattern of Trees Obtained by ALS Based Forest Inventory Techniques; SilviLaser: Tasmania, Australia, October 2011. [Google Scholar]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Li, W.K.; Guo, Q.H.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A comparative assessment of the performance of individual tree crowns delineation algorithms from ALS data in tropical forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical analysis and modelling of spatial point patterns. Technometrics 2008, 47, 516–517. [Google Scholar]
- Ripley, B.D. Modelling spatial patterns. J. R. Statist. Soc. B 1977, 39, 172–192. [Google Scholar] [CrossRef]
- Uria-Diez, J.A. Pommerening. Crown plasticity in scots pine (pinus sylvestris L.) as a strategy of adaptation to competition and environmental factors. Ecol. Model. 2017, 356, 117–126. [Google Scholar] [CrossRef]
- Wiegand, T.A.; Moloney, K. Rings, circles, and null models for point pattern analysis in ecology. Oikos 2004, 104, 209–229. [Google Scholar] [CrossRef]
- Raychaudhuri, S. Introduction to monte carlo simulation. AIP Conf. Proc. 2008, 1204, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Versace, S.; Gianelle, D.; Frizzera, L.; Tognetti, R.; Garfi, V.; Dalponte, M. Prediction of Competition Indices in a Norway Spruce and Silver Fir-Dominated Forest Using Lidar Data. Remote Sens. 2019, 11, 2734. [Google Scholar] [CrossRef] [Green Version]
- Strahler, A.H.; Jupp, D.L. Modeling bidirectional reflectance of forests and woodlands using boolean models and geometric optics. Remote Sens. Environ. 1990, 34, 153–166. [Google Scholar] [CrossRef]
- Stoyan, D. Statistical analysis of spatial point processes: A soft-core model and cross-correlations of marks. Biom. J. 1987, 29, 971–980. [Google Scholar] [CrossRef]
- Mallet, A. A maximum likelihood estimation method for random coefficient regression models. Biometrika 1986, 73, 645–656. [Google Scholar] [CrossRef]
- Baddeley, A.; Turner, R. Practical maximum pseudolikelihood for spatial point patterns. Aust. N. Z. J. Stat. 2000, 42, 283–322. [Google Scholar] [CrossRef]
- Guan, Y. A minimum contrast estimation for estimating the second-order parameters of inhomogeneous spatial point process. Stat. Interface 2009, 2, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Geyer, C. Likelihood Inference for Spatial Point Processes. Seminaire-Europeen-de-Statistique on Stochastic Geometry, Theory and Applications, 3rd ed.; University Paul Sabatier: Toulouse, France, May 1996. [Google Scholar]
- Zheng, G.; Ma, L.; Eitel, J.U.H.; He, W.; Magney, T.S.; Moskal, L.M.; Li, M. Retrieving directional gap fraction, extinction coefficient, and effective leaf area Index by incorporating scan angle information from discrete aerial lidar data. IEEE Trans. Geosci. Remote Sens. 2016, 55, 577–590. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Khosravipour, A. Imputation of Individual Longleaf Pine (Pinus palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Lidr: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. Available online: https://cran.r-project.org/web/packages/lidR/lidR.pdf (accessed on 21 January 2020).
- Gerard, F.; North, P. Analyzing the effect of structural variability and canopy gaps on forest BRDF using a geometric-optical model. Remote Sens. Environ. 1997, 62, 46–62. [Google Scholar] [CrossRef]
- Kobayashi, H.; Baldocchi, D.D.; Ryu, Y.; Chen, Q.; Ma, S.; Osuna, J.L.; Ustin, S.L. Modeling energy and carbon fluxes in a heterogeneous oak woodland: A three-dimensional approach. Agric. For. Meteorol. 2012, 152, 83–100. [Google Scholar] [CrossRef] [Green Version]
- Li, X.W.; Strahler, A.H.; Woodcock, C.E. A hybrid geometric optical-radiative transfer approach for modeling albedo and directional reflectance of discontinuous canopies. IEEE Trans. Geosci. Remote Sens. 1995, 33, 466–480. [Google Scholar] [CrossRef]
- Hu, B.; Li, J.; Jing, L.; Judah, A. Improving the efficiency and accuracy of individual tree crown delineation from high-density LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation—Evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogram. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]




| Plot Type | Plot ID | Density | Tree # | Forest Type | Crown Radii (m) | ||
|---|---|---|---|---|---|---|---|
| Max. | Min. | Average | |||||
| Natural forest plots | WPA-HC | High | 159 | Conifer | 7.26 | 1.62 | 3.72 |
| WPA-MC | Medium | 95 | Conifer | 11.78 | 2.80 | 6.28 | |
| WPA-LC | Low | 75 | Conifer | 9.50 | 2.15 | 5.41 | |
| WPA-LM | Low | 66 | Mixed | 12.27 | 2.45 | 7.23 | |
| PC-HC | High | 150 | Conifer | 6.60 | 1.80 | 4.15 | |
| PC-MC | Medium | 92 | Conifer | 7.50 | 2.00 | 4.90 | |
| Modeled forest plots | Plot-1 | Low | 79 | Conifer | 3.81 | 3.81 | 3.81 |
| Plot-2 | High | 110 | Conifer | 3.81 | 3.81 | 3.81 | |
| Plot-3 | Low | 79 | Conifer | 3.81 | 3.81 | 3.81 | |
| Plot-4 | High | 105 | Conifer | 3.81 | 3.81 | 3.81 | |
| Plot-5 | Low | 79 | Conifer | 3.81 | 3.81 | 3.81 | |
| Plot-6 | Medium | 95 | Conifer | 3.81 | 3.81 | 3.81 | |
| Plot ID | Density | Tree # | Tree Detection Rate | Tree Location RMSE (m) | Crown Radii (m) | ||
|---|---|---|---|---|---|---|---|
| Range (Max.–Min.) | Average | RMSE | |||||
| WPA-HC | High | 137 | 86% | 2.51 | 8.770–1.26 | 3.38 | 1.45 |
| WPA-MC | Medium | 90 | 95% | 2.20 | 10.50–2.10 | 6.13 | 1.39 |
| WPA-LC | Low | 70 | 93% | 1.46 | 10.31–2.45 | 6.09 | 1.16 |
| WPA-LM | Low | 63 | 95% | 1.47 | 12.28–2.50 | 6.83 | 1.50 |
| PC-HC | High | 143 | 95% | 1.72 | 6.94–2.30 | 4.53 | 1.05 |
| PC-MC | Medium | 85 | 92% | 1.67 | 7.75–1.63 | 5.08 | 0.85 |
| Statistical Models | Input Parameters | ALS-Based Values | Visual-Based Values |
|---|---|---|---|
| Hybrid Gibbs (WPA-HC) | Control factor of density (β) | 0.007 | 0.009 |
| Hard-core distance (HC) | 1.650 | 1.500 | |
| Interaction radius (rg) | 3.500 | 3.000 | |
| Saturation threshold (S) | 3.000 | 3.000 | |
| Interaction parameter gamma (γ) | 1.920 | 2.110 | |
| Neyman-A (WPA-HC) | Density of cluster centers(λN) | 0.016 | 0.018 |
| Radius of the clusters (rN) | 5.090 | 3.250 | |
| Mean number of points per cluster (mN) | 1.370 | 1.500 | |
| Poisson (WPA-LM/ WPA –LC/ PC-MC) | Density (λ) | 0.006/ 0.007/ 0.008 | 0.006/ 0.007/ 0.009 |
| Soft-core (WPA-MC/ PC-HC) | Interaction distance (σ) | 5.450/ 4.450 | 4.500/ 3.700 |
| Control factor of interaction strength (κ) | 0.500/ 0.400 | 0.390/ 0.320 | |
| Control factor of density (β) | 0.020/ 0.027 | 0.045/ 0.035 |
| Sites | Coverage | Tree # | Crown Radii (m) | Model Type | Input Parameters | |||
|---|---|---|---|---|---|---|---|---|
| Range (Min.–Max.) | Average | β | σ | κ | ||||
| WPA | 392 m × 1282 m | 2745 | 1.26–11.30 | 5.49 | soft-core | 0.10 | 4.73 | 0.60 |
| PC | 1 km × 1 km | 7669 | 2.56–10.37 | 5.03 | soft-core | 0.19 | 6.52 | 0.75 |
| Forest Type | Crown Overlap(m) | Crown Size (m) (Tree-1/Tree-2) | Point Number# (Tree-1/Tree-2) | Average Error Crown Size (m) | Average Error (Point Number) |
|---|---|---|---|---|---|
| Conifer + Conifer | 0 | 8.03/8.03 | 2931/2931 | 0 | 0 |
| 1.0 | 8.20/7.47 | 3086/2776 | 0.36 | 155 | |
| 1.5 | 8.10/7.54 | 3105/2757 | 0.28 | 174 | |
| 2.0 | 8.50/7.30 | 3306/2556 | 0.60 | 375 | |
| 2.5 | 8.96/6.85 | 3506/2356 | 1.05 | 575 | |
| 3.0 | 9.25/6.17 | 3525/2337 | 1.54 | 594 | |
| 3.5 | 9.18/5.72 | 3708/2404 | 1.73 | 652 | |
| 4.0 | 9.87/5.63 | 3757/2105 | 2.12 | 826 | |
| Conifer + Broadleaf | 0 | 7.59/10.26 | 1863/6877 | 0 | 0 |
| 1.0 | 7.07/10.62 | 1974/6766 | 0.44 | 111 | |
| 1.5 | 6.90/10.46 | 2049/6691 | 0.45 | 186 | |
| 2.0 | 7.02/10.14 | 2166/6574 | 0.35 | 303 | |
| 2.5 | 7.1/10.59 | 2319/6421 | 0.41 | 456 | |
| 3.0 | 7.49/11.86 | 2501/6239 | 0.85 | 638 | |
| 3.5 | 13.79/2.55 | 8127/613 | 6.95 | 6264 | |
| 4.0 | 12.87/0 | 8740/0 | — | — | |
| Broadleaf + Broadleaf | 0 | 10.26/10.26 | 6876/6876 | 0 | 0 |
| 1.0 | 9.58/10.09 | 6684/7068 | 0.42 | 192 | |
| 1.5 | 9.51/9.85 | 6664/7088 | 0.58 | 212 | |
| 2.0 | 9.51/9.88 | 6535/7217 | 0.57 | 341 | |
| 2.5 | 7.26/9.35 | 5217/8535 | 1.95 | 1659 | |
| 3.0 | 7.18/9.26 | 5238/8514 | 2.04 | 1638 | |
| 3.5 | 7.38/12.66 | 5079/8673 | 2.64 | 1797 | |
| 4.0 | 7.02/12.85 | 5019/8733 | 2.92 | 1857 |
| Modeled Patterns | Plot ID | Determined Parameters | Probability of Viewing Ground Surface Area (%) | ||||
|---|---|---|---|---|---|---|---|
| VZ = 0°, VA = 90° | VZ = 30°, VA = 90° | VZ = 60°, VA = 90° | VZ = 30°, VA = 270° | VZ = 60°, VA = 270° | |||
| Regular (Softcore) | Plot-1 | β - 0.013 κ - 0.1 σ - 4.64 | 55.63 | 52.87 | 31.83 | 42.43 | 26.06 |
| Plot-2 | β - 0.025 κ - 0.1 σ - 4.50 | 44.38 | 41.65 | 22.31 | 30.96 | 17.16 | |
| Random (Poisson) | Plot-3 | λ - 0.007 | 59.52 | 56.87 | 36.15 | 47.06 | 30.37 |
| Plot-4 | λ - 0.012 | 39.92 | 36.88 | 16.67 | 26.79 | 12.99 | |
| Clustered (Neyman) | Plot-5 | 𝜆N - 0.002 rN - 7.578 mN - 3.083 | 66.01 | 64.41 | 47.29 | 55.56 | 40.16 |
| Plot-6 | 𝜆N - 0.002 rN - 4.378 mN - 3.783 | 73.26 | 72.11 | 56.70 | 64.32 | 51.19 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zheng, G.; Yun, Z.; Moskal, L.M. Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data. Remote Sens. 2020, 12, 712. https://doi.org/10.3390/rs12040712
Wang X, Zheng G, Yun Z, Moskal LM. Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data. Remote Sensing. 2020; 12(4):712. https://doi.org/10.3390/rs12040712
Chicago/Turabian StyleWang, Xiaofei, Guang Zheng, Zengxin Yun, and L. Monika Moskal. 2020. "Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data" Remote Sensing 12, no. 4: 712. https://doi.org/10.3390/rs12040712
APA StyleWang, X., Zheng, G., Yun, Z., & Moskal, L. M. (2020). Characterizing Tree Spatial Distribution Patterns Using Discrete Aerial Lidar Data. Remote Sensing, 12(4), 712. https://doi.org/10.3390/rs12040712







