Drone-borne Differential SAR Interferometry
Abstract
:1. Introduction
2. Materials and Methods
- The GNSS ground station was placed close to the starting position of the drone, and the GNSS recording was initiated.
- Three flights were carried out, each consisting of the following successive steps: turning on the drone and the radar; waiting 15 min for simultaneous and stationary recording of ground station and radar GNSS data; take-off; executing the same west-east flight track; landing; waiting 15 min for simultaneous and stationary recording of ground station and radar GNSS data; turning-off the radar and the drone.
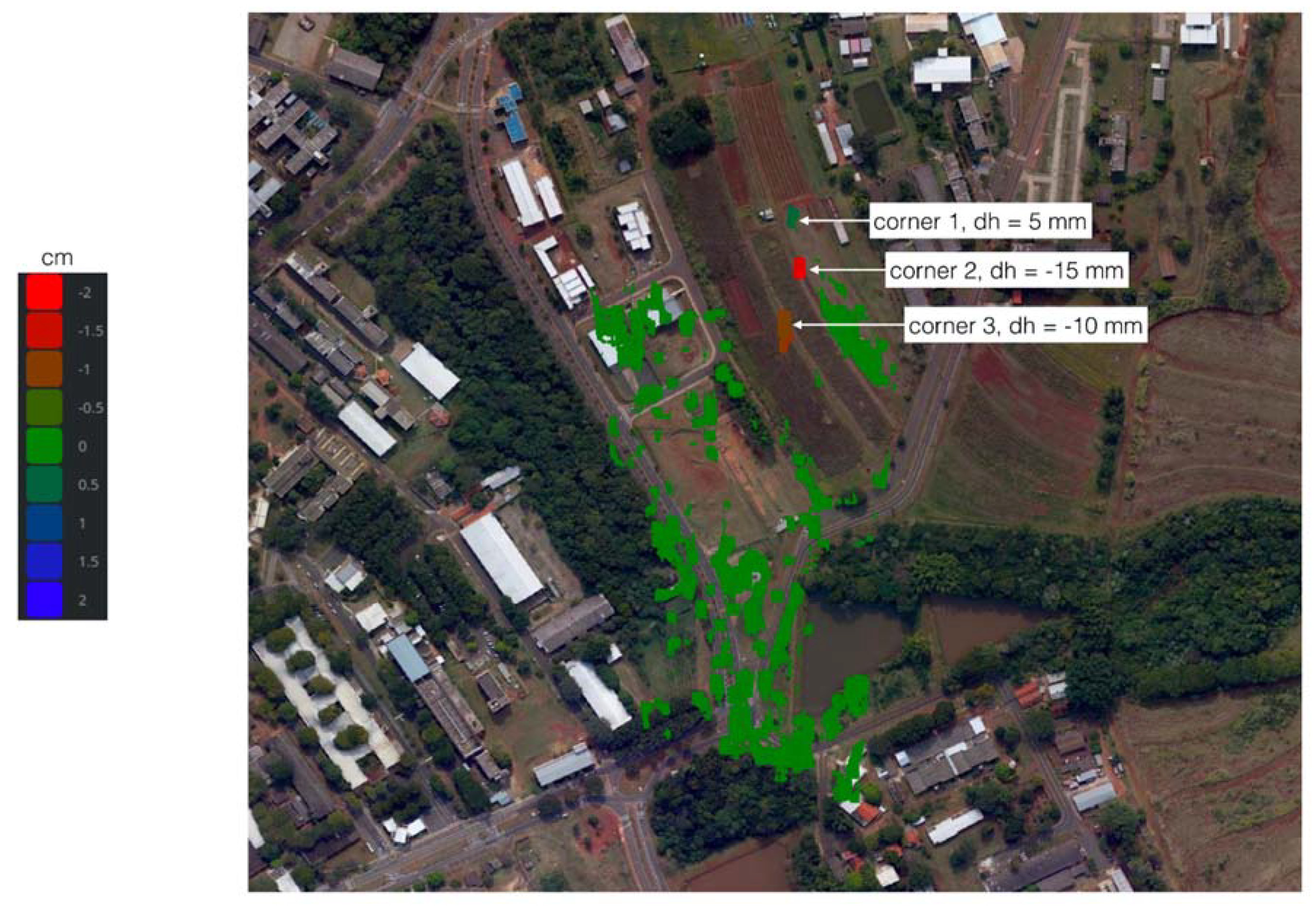
- The three corner reflectors were positioned at the UNICAMP test site at different radar incidence angles, between 36 and 60 degrees, as shown in Figure 2. Corner reflector 1, in the nearest range, had an incidence angle of 36 degrees. Corner reflector 2, in the middle range between 1 and 3, had an incidence angle of 52 degrees. Corner reflector 3, in far range, had an incidence angle of 60 degrees. Corner 2 was lifted differently during the second and third flights to validate the displacement measurement methodology.
- During the first flight, all three corner reflectors were placed horizontally on the ground, looking north.
- During the second flight, only the corner reflector number 2 was lifted 4 cm off the ground, as shown in Figure 1b. Corner reflectors 1 and 3 remained at ground level.
- During the third flight, only the corner reflector number 2 was lifted 2 cm off the ground. Corner reflectors 1 and 3 were still at ground level.
- The GNSS ground station and the drone were dismounted. The acquired data were downloaded for processing.
- Perform the differential GNSS processing of ground station and radar GNSS receivers.
- Generate position and antennae orientation history with IMU and differential GNSS data fusion.
- Process the raw radar data for each of the three flight paths mentioned above (raw data 1, 2, and 3) according to the processing chain described in [10] and shown in Figure 3: range and azimuth compression with motion compensation; recording of the three resulting single-look complex (SLC) images; interferometry (SLC 1 with SLC 2, generating the interferogram 1 and 2, and SLC 1 with SLC 3, producing the interferogram 1 and 3); topography subtraction and phase to height conversion; and complex filtering. The output consists of two deformation maps, plus the three SLCs, all in slant range geometry. Each interferogram is calculated from the SLCs with 0.1-m resolution in azimuth and 1 m resolution in the slant range. Complex filtering results on a final spatial resolution of 3 m in both slant range and azimuth directions for each deformation map.
- Check the absolute position of the corner reflectors by searching their maximum power positions on the three slant range SLC images.
- Use the azimuth and slant range coordinates found in step 4 to read the displacement for each corner reflector on the deformation maps. Compare the displacement with the expected results:
- Null differential height offsets for corner reflectors 1 and 3 on both deformation maps, since they were always at ground level;
- A 4 cm lift for corner reflector 2 on the deformation map of interferogram 1 and 2;
- A 2 cm lift for corner reflector 2 on the deformation map of interferogram 1 and 3.
- Geocode the two deformation maps.
- Generate the multi-look images from the SLCs with 1 m × 1 m resolution in slant range and geocode them, as shown in Figure 2a.
3. Results
- signal-to-noise ratio;
- time decorrelation between the revisits;
- radar and processing phase stability;
- antennae environment;
- motion data.
3.1. Signal-to-Noise Ratio
3.2. Time Decorrelation Between the Revisits
3.3. Radar and Processing Phase Stability
3.4. Antennae Environment
3.5. Motion Data
4. Discussion
5. Conclusions
- The accuracy assessment in L-band presented here is, as far as we know, novel;
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Lopez-Dekker, P.; De Zan, F.; Yagüe-Martínez, N.; Zonno, M.; Rodriguez-Cassola, M. Performance of 3-D surface deformation estimation for simultaneous squinted SAR acquisitions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2147–2158. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.; Lu, Z.; Sherhperd, A.; Wright, T. Simulation of the superSAR multi-azimuth Synthetic Aperture Radar imaging system for precise measurement of three-dimensional earth surface displacement. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6196–6206. [Google Scholar] [CrossRef]
- Kimura, H. Three-dimensional surface deformation mapping from multi-directional SAR interferograms. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1692–1695. [Google Scholar]
- Jo, M.; Jung, H.; Won, J.; Poland, M.P.; Miklius, A. Measurement of three-dimensional surface deformation of the March 2011 Kamoamoa fissure eruption, Kilauea Volcano, Hawai’i. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 437–440. [Google Scholar]
- Jung, H.; Yung, S.; Jo, M. An improvement of Multiple-Aperture SAR interferometry performance in the presence of complex and large line-of-sight deformation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1743–1752. [Google Scholar] [CrossRef]
- Reigber, A.; Scheiber, R. Airborne differential SAR interferometry: First results at L-band. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1516–1520. [Google Scholar] [CrossRef]
- Fornaro, G.; Lanari, R.; Sansosti, E.; Franceschetti, G.; Perna, S.; Gois, A.; Moreira, J. Airborne differential interferometry: X-band experiments. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 20‒24 September 2004; Volume 5, pp. 3329–3332. [Google Scholar]
- De Macedo, K.A.C.; Wimmer, C.; Barreto, T.L.M.; Lübeck, D.; Moreira, J.R.; Rabaco, L.M.L.; de Oliveira, W.J. Long-term airborne DInSAR measurements: P- and X-band cases. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24‒29 July 2011; pp. 1175–1178. [Google Scholar]
- Perna, S.; Wimmer, C. X-Band Airborne Differential Interferometry: Results of the OrbiSAR Campaign Over the Perugia Area. IEEE Trans. Geosci. Remote Sens. 2008, 46, 489–503. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.; Glennie, C.; Wang, G.; Lu, Z.; Fernandez-Diaz, J.C. Airborne DInSAR Results Using Time-Domain Backprojection Algorithm: A Case Study Over the Slumgullion Landslide in Colorado With Validation Using Spaceborne SAR, Airborne LiDAR, and Ground-Based Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4987–5000. [Google Scholar] [CrossRef]
- Moreira, L.; Castro, F.; Góes, J.A.; Bins, L.; Teruel, B.; Fracarolli, J.; Castro, V.; Alcântara, M.; Oré, G.; Luebeck, D.; et al. A Drone-borne Multiband DInSAR: Results and Applications. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22‒26 April 2019; pp. 1–6. [Google Scholar]
- Just, D.; Bamler, R. Phase statistics of interferograms with applications to synthetic aperture radar. Appl. Opt. 1994, 33, 4361. [Google Scholar] [CrossRef] [PubMed]
- Casu, F.; Manzo, M.; Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Env. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Bonano, M.; Manunta, M.; Pepe, A.; Paglia, L.; Lanari, R. From Previous C-Band to New X-Band SAR Systems: Assessment of the DInSAR Mapping Improvement for Deformation Time-Series Retrieval in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1973–1984. [Google Scholar] [CrossRef]
- Manunta, M.; De Luca, C.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS Approach for Sentinel-1 Interferometric Wide Swath Deformation Time-Series Generation: Algorithm Description and Products Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]




| Radar Parameters | Value |
|---|---|
| Carrier Wavelength | 22.84 cm |
| Bandwidth | 150 MHz |
| Polarization | HH |
| Peak Power | 100 mW |
| Mean Power | 1 mW |
| PRF | 10 kHz |
| Incidence Angle | 45 deg. |
| Mean Drone Height | 120 m |
| Mean Drone Velocity | 2 m/s |
| Motion Sensing System (MSS) | D-GNSS+IMU |
| Range Resolution | 1 m |
| Azimuth Resolution | 0.1 m |
| Processed Azimuth Bandwidth | 20 Hz |
| Processed Aperture at 45 deg. Incidence Angle | 196 m |
| SLC Range Sampling | 0.61 m |
| SLC Azimuth Sampling | 0.05 m |
| MSS Accuracy Specifications | Value |
|---|---|
| Position, Absolute | 0.015 m |
| Position, Relative | <0.01 m |
| Roll and Pitch | 0.1 deg. |
| True Heading | 2 deg. |
| IMU Run Bias Stability | 2 deg./h |
| IMU Angular Random Walk | 0.1 deg./square root hour |
| Corner Reflectors | Deformation Map of 1 and 2 [mm] | Deformation Map 1 and 3 [mm] | ||||
|---|---|---|---|---|---|---|
| Ideal | Measured | Difference | Ideal | Measured | Difference | |
| 1 | 0 | 11 | 11 | 0 | 5 | 5 |
| 2 | −40 | −45 | −5 | −20 | −15 | 5 |
| 3 | 0 | −6 | −6 | 0 | −10 | −10 |
| Targets | Standard Deviation [mm] |
|---|---|
| Corner Reflectors | 7.4 |
| Areas with Coherence Better than 0.6 | 4–6 |
| Targets | Reflectivity [dB] | SNR [dB] | Coherence [0–1] | Unfiltered Phase Noise [deg.] | Filtered Phase Noise [deg.] | Standard Deviation of the Displacement Measurement Error [mm] |
|---|---|---|---|---|---|---|
| Corner reflectors | 20 | 32 | ~1 | 4 | 0.4 | 0.13 |
| Grass | −5 | 7 | 0.8 | 52 | 5.2 | 1.6 |
| Bare soil | −9 | 3 | 0.6 | 70 | 7 | 2.2 |
| Error Sources | Standard Deviation [mm] |
|---|---|
| SNR | <2.2 |
| Time Decorrelation | ~0 |
| Radar and Processing Phase Stability | <0.4 |
| Antenna Environment | ~0 |
| Motion Data | ~5 |
| Total Measured RMS Error | 4–7.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luebeck, D.; Wimmer, C.; F. Moreira, L.; Alcântara, M.; Oré, G.; A. Góes, J.; P. Oliveira, L.; Teruel, B.; S. Bins, L.; H. Gabrielli, L.; et al. Drone-borne Differential SAR Interferometry. Remote Sens. 2020, 12, 778. https://doi.org/10.3390/rs12050778
Luebeck D, Wimmer C, F. Moreira L, Alcântara M, Oré G, A. Góes J, P. Oliveira L, Teruel B, S. Bins L, H. Gabrielli L, et al. Drone-borne Differential SAR Interferometry. Remote Sensing. 2020; 12(5):778. https://doi.org/10.3390/rs12050778
Chicago/Turabian StyleLuebeck, Dieter, Christian Wimmer, Laila F. Moreira, Marlon Alcântara, Gian Oré, Juliana A. Góes, Luciano P. Oliveira, Bárbara Teruel, Leonardo S. Bins, Lucas H. Gabrielli, and et al. 2020. "Drone-borne Differential SAR Interferometry" Remote Sensing 12, no. 5: 778. https://doi.org/10.3390/rs12050778
APA StyleLuebeck, D., Wimmer, C., F. Moreira, L., Alcântara, M., Oré, G., A. Góes, J., P. Oliveira, L., Teruel, B., S. Bins, L., H. Gabrielli, L., & Hernandez-Figueroa, H. E. (2020). Drone-borne Differential SAR Interferometry. Remote Sensing, 12(5), 778. https://doi.org/10.3390/rs12050778





