Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm
Abstract
:1. Introduction
2. Materials and Methods
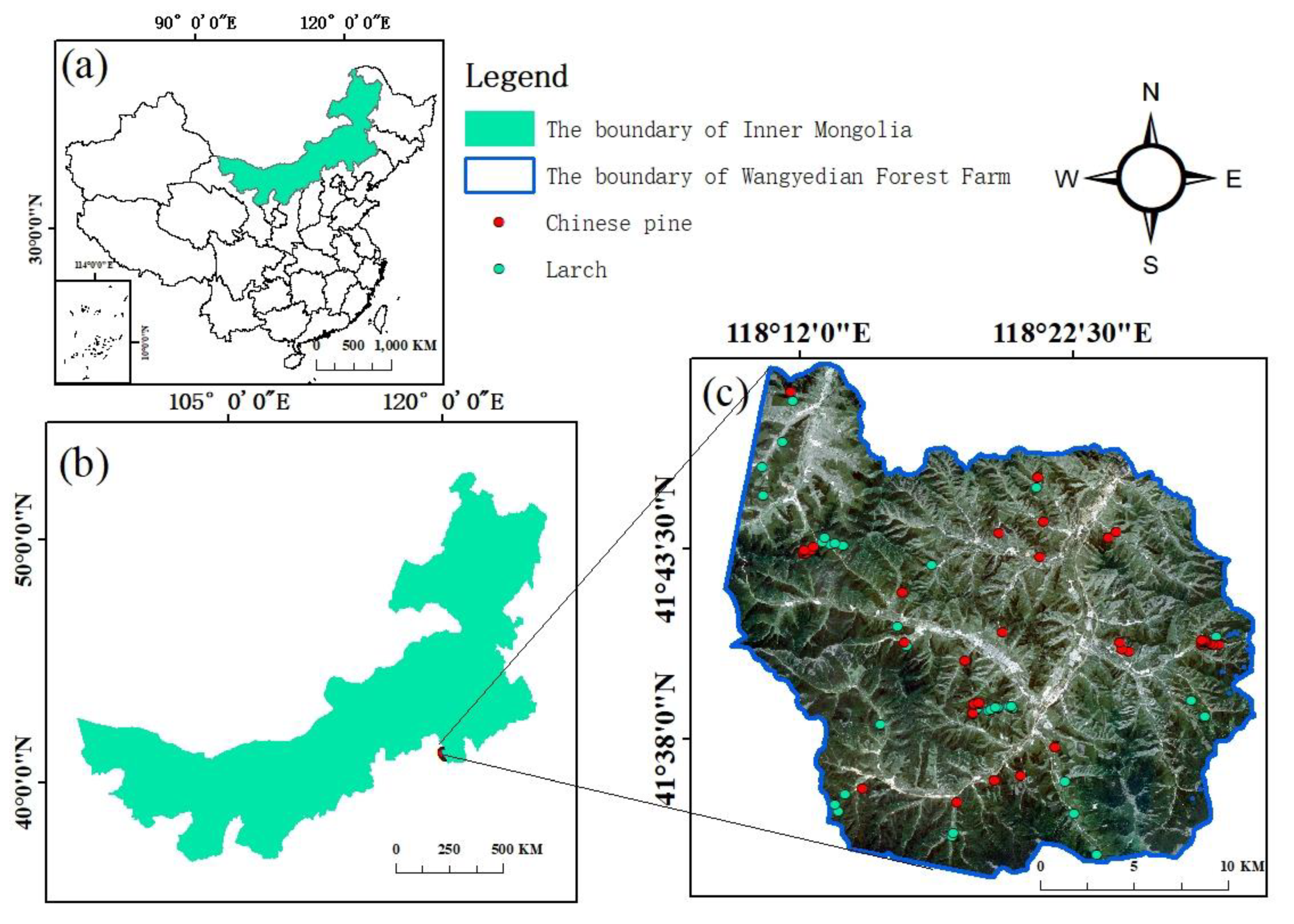
2.1. Study Area
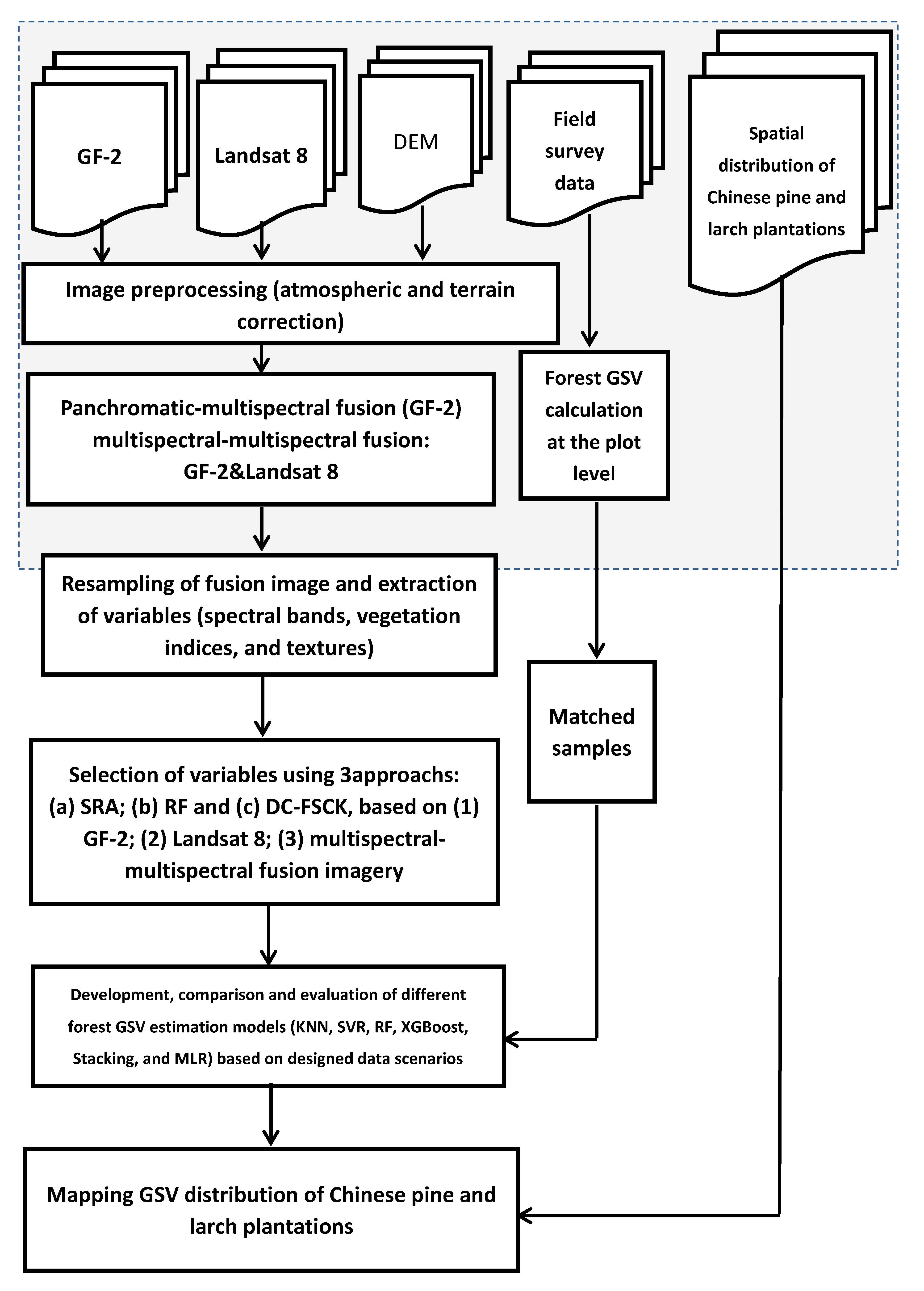
2.2. Framework of This Research
2.3. Data Collection and Processing
2.3.1. Field Plot Data Collection
2.3.2. Satellite Image Collection and Pre-Processing
2.3.3. Data Fusion and Matching
2.4. Extraction of Feature Variables
2.5. Selection of Optimal Variable Combination
2.5.1. Distance Correlation
2.5.2. Selection of Suitable Variables Using an Improved Method
2.6. Model Development, Evaluation and Application
2.6.1. GSV Estimation Models
2.6.2. Evaluation of Modeling Results
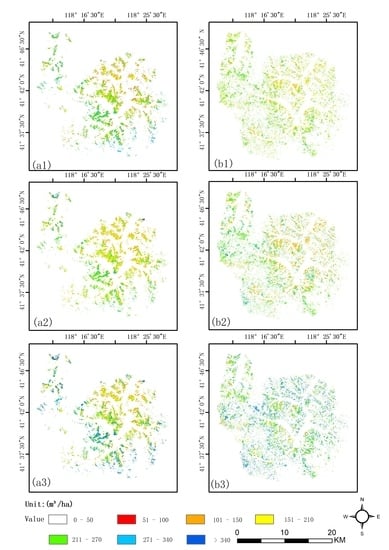
2.6.3. Mapping the GSV of Chinese Pine and Larch Plantations
3. Results
3.1. Data Fusion for Estimating Plantation GSV
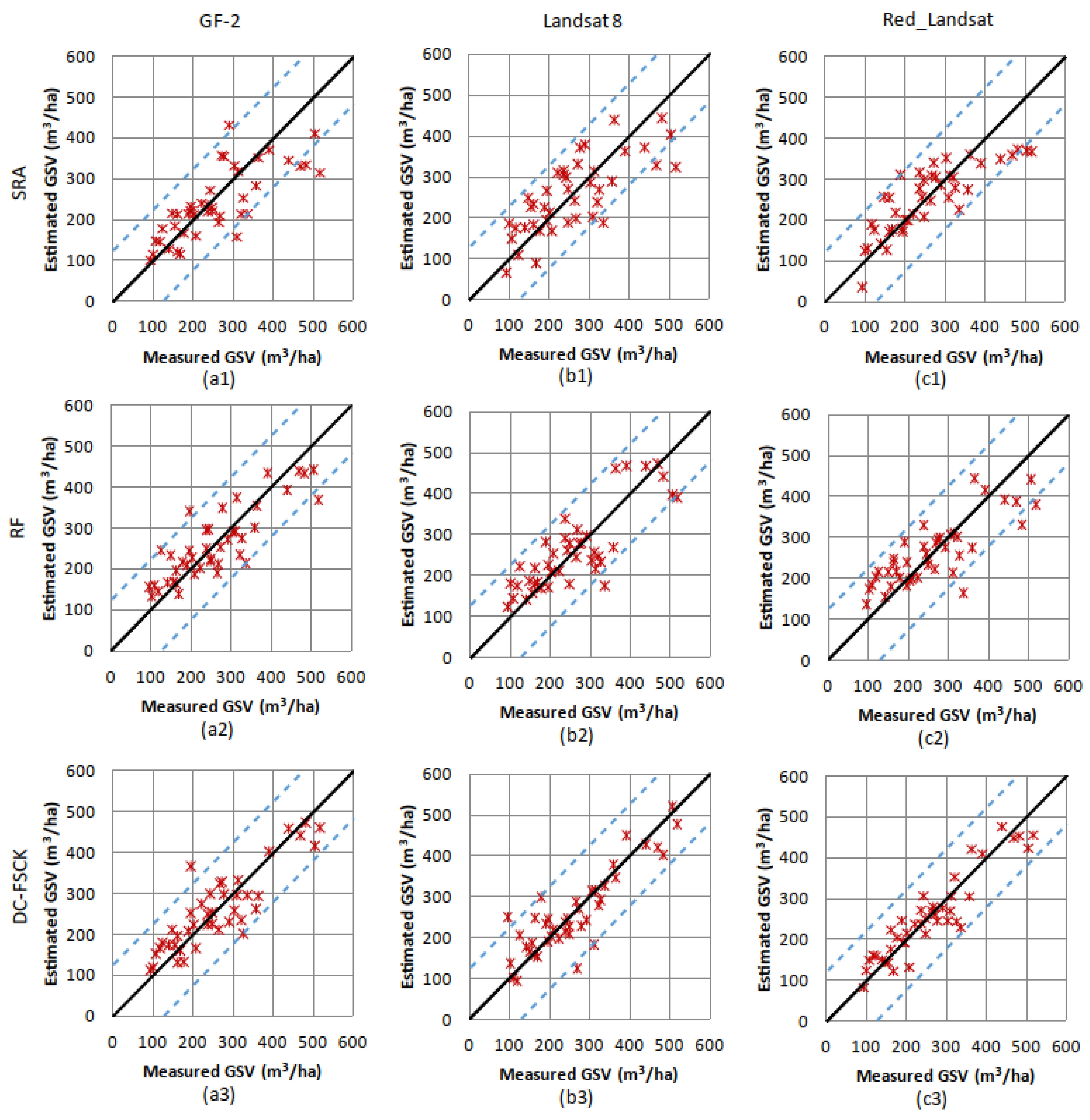
3.2. Variables Selection and Estimation Result Comparison
3.2.1. Feature Variables Selected by Three Methods
3.2.2. Estimation Results of the Chinese Pine
3.2.3. Estimation Results of Larch
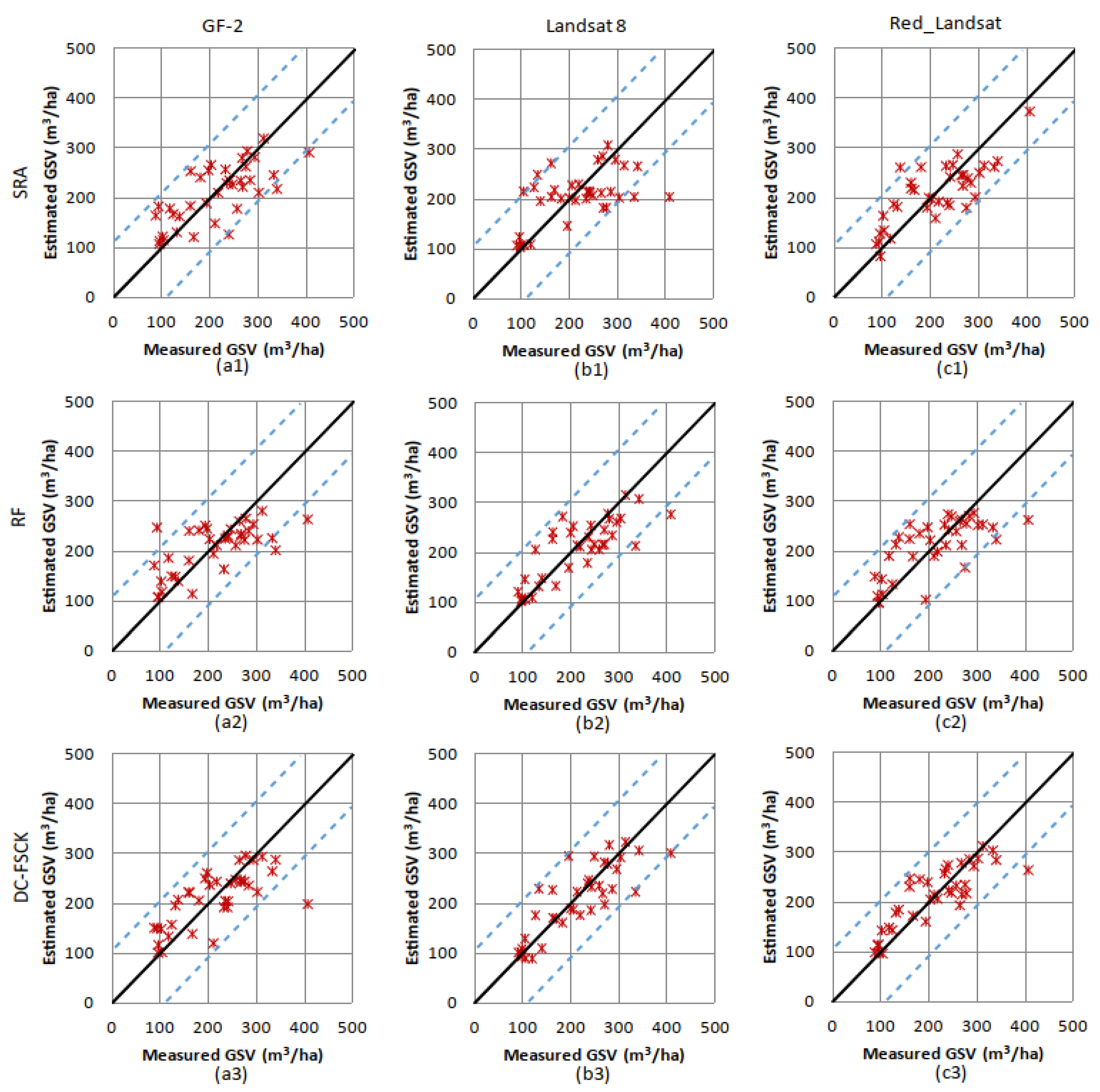
3.2.4. Residuals and Potential Saturation Levels of GSV Estimation
3.3. Mapping the GSV of Chinese Pine and Larch Plantations
4. Discussion
4.1. The Role of Data Fusion in GSV Estimation
4.2. Effective Methods for Improving Spectral Variable Selection and Data Saturation
4.3. Selection of Suitable and Stable Estimation Algorithms
4.4. Implication of Methods for Improving GSV Estimation of Chinese Pine and Larch Plantations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Brockerhoff, E.G.; Jactel, H.; Parrotta, J.A.; Ferraz, S.F.B. Role of eucalypt and other planted forests in biodiversity conservation and the provision of biodiversity-related ecosystem services. Ecol. Manag. 2013, 301, 43–50. [Google Scholar] [CrossRef]
- Carnus, J.; Parrotta, J.; Brockerhoff, E.G.; Arbez, M.; Jactel, H.; Kremer, A.; Lamb, D.; O’Hara, K.; Walters, B. Planted forests and biodiversity. J. For. 2006, 104, 65–77. [Google Scholar]
- Cormac, J.O.; Irwin, S.; Byrne, K.A.; O’Halloran, J. The role of planted forests in the provision of habitat: An Irish perspective. Biodivers. Conserv. 2016, 26, 3103–3124. [Google Scholar]
- Berger, A.; Gschwantner, T.; Mcroberts, R.E.; Schadauer, K. Effects of Measurement Errors on Individual Tree Stem Volume Estimates for the Austrian National Forest Inventory. For. Sci. 2014, 60, 14–24. [Google Scholar] [CrossRef]
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Di Cosmo, L.; Gasparini, P.; Tabacchi, G. A national-scale, stand-level model to predict total above-ground tree biomass from growing stock volume. Ecol. Manag. 2016, 361, 269–276. [Google Scholar] [CrossRef]
- Krejza, J.; Svˇetlík, J.; Bedná, P. Allometric relationship and biomass expansion factors (BEFs) for above- and below-ground biomass prediction and stem volume estimation for ash (Fraxinus excelsior L.) and oak (Quercus robur L.). Trees 2017, 31, 1303–1316. [Google Scholar] [CrossRef]
- Shvidenko, A.; Schepaschenko, D.; Nilsson, S.; Bouloui, Y. Semi-empirical models for assessing biological productivity of Northern Eurasian forests. Ecol. Model. 2007, 204, 163–179. [Google Scholar] [CrossRef]
- Wijaya, A.; Kusnadi, S.; Gloaguen, R.; Heilmeier, H. Improved strategy for estimating stem volume and forest biomass using moderate resolution remote sensing data and GIS. J. For. Res. Jpn. 2010, 21, 1–12. [Google Scholar] [CrossRef]
- Long, J.; Lin, H.; Wang, G.; Sun, H.; Yan, E. Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images. Remote Sens. 2019, 11, 1872. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhu, J.; Wang, C.; Lin, H.; Long, J.; Zhao, L.; Fu, H.; Liu, Z. Forest Growing Stock Volume Estimation in Subtropical Mountain Areas Using PALSAR-2 L-Band PolSAR Data. Forests 2019, 10, 276. [Google Scholar] [CrossRef] [Green Version]
- Santoro, M.; Beaudoin, A.; Beer, C.; Cartus, O.; Fransson, J.E.S.; Hall, R.J.; Pathe, C.; Schmullius, C.; Schepaschenko, D.; Shvidenko, A.; et al. Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR. Remote Sens. Environ. 2015, 168, 316–334. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Thiel, C.; Schmullius, C. Growing stock volume estimation from L-band ALOS PALSAR polarimetric coherence in Siberian forest. Remote Sens. Environ. 2014, 155, 129–144. [Google Scholar] [CrossRef]
- Bilous, A.; Myroniuk, A.; Holiaka, D.; Bilous, S.; See, L.; Schepaschenko, D. Mapping growing stock volume and forest live biomass: A case study of the Polissya region of Ukraine. Environ. Res. Lett. 2017, 12, 105001. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y. Estimating Basal Area and Stem Volume for Individual Trees from LIDAR Data. Photogramm. Eng. Remote Sens. 2007, 73, 1355–1365. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S.; Gao, C.; Dang, Y.; Xiang, H.; Zhao, J.; Zhang, Y.; Wang, X.; Guo, H. Retrieval of forest growing stock volume by two different methods using Landsat TM images. Int. J. Remote Sens. 2014, 35, 29–43. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Song, R.; Lin, H.; Wang, G.; Yan, E.; Ye, Z. Improving selection of spectral variables for vegetation classification of east dongting lake, China, Using a Gaofen-1 image. Remote Sens. 2018, 10, 50. [Google Scholar] [CrossRef] [Green Version]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef] [Green Version]
- Nafiseh, G.; Reza, S.; Ali, M. A review on biomass estimation methods using synthetic aperture radar data. Int. J. Geomat. Geosci. 2011, 1, 776–788. [Google Scholar]
- Saatchi, S.; Marlier, M.; Chazdon, L.R.; Clark, D.B.; Russell, A.E. Impact of Spatial Variability of Tropical Forest Structure on Radar Estimation of Aboveground Biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O. Forest Biomass Change Estimated from Height Change in Interferometric SAR Height Models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pulliainen, J.; Engdahl, M.; Hallikainen, M. Feasibility of Multi-temporal Interferometric SAR Data for Stand-level Estimation of Boreal Forest Stem Volume. Remote Sens. Environ. 2003, 85, 397–409. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of Airborne Lidar and Vegetation Types Derived from Aerial Photography for Mapping Aboveground Live Biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Fu, L.; Liu, Q.; Sun, H.; Wang, S.; Li, Z.; Chen, E.; Pang, Y.; Song, X.; Wang, G. Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Xie, Z.; Jiang, X.; Lu, D.; Chen, E. Integration of ZiYuan-3 Multispectral and Stereo Data for Modeling Aboveground Biomass of Larch Plantations in North China. Remote Sens. 2019, 11, 2328. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Li, L.; Lu, D.; Li, D. Exploring bamboo forest aboveground biomass estimation using Sentinel-2 data. Remote Sens. 2019, 11, 7. [Google Scholar] [CrossRef] [Green Version]
- Sousa, A.M.O.; Gonçalves, A.C.; Mesquita, P.; da Silva, J.R.M. Biomass estimation with high resolution satellite images: A case study of Quercus rotundifolia. ISPRS J. Photogramm. Remote Sens. 2015, 101, 69–79. [Google Scholar] [CrossRef] [Green Version]
- Macedo, F.; Adélia, M.; Ana, C.; José, R.; Marques, D.; Paulo, A.; Ricardo, A. Above-ground biomass estimation for Quercus rotundifolia using vegetation indices derived from high spatial resolution satellite images. Eur. J. Remote Sens. 2018, 51, 932–944. [Google Scholar] [CrossRef] [Green Version]
- Ni, W.; Zhang, Z.; Sun, G.; Liu, Q. Modeling the stereoscopic features of mountainous forest landscapes for the extraction of forest heights from stereo imagery. Remote Sens. 2019, 11, 1222. [Google Scholar] [CrossRef] [Green Version]
- Chopping, M.; Schaaf, C.B.; Zhao, F.; Wang, Z.; Nolin, A.W.; Moisen, G.G.; Martonchik, J.V.; Bull, M. Forest Structure and Aboveground Biomass in the Southwestern United States from MODIS and MISR. Remote Sens. Environ. 2011, 115, 2943–2953. [Google Scholar] [CrossRef] [Green Version]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor Data Fusion: A Review of the State-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Zhang, J. Multi-source Remote Sensing Data Fusion: Status and Trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef] [Green Version]
- Karathanassi, V.; Kolokousis, P.; Ioannidou, S. A comparison study on fusion methods using evaluation indicators. Int. J. Remote Sens. 2007, 28, 2309–2341. [Google Scholar] [CrossRef]
- Ehlers, M.; Klonus, S.; Åstrand, P.J.; Rosso, P. Multi-sensor Image Fusion for Pansharpening in Remote Sensing. Int. J. Image Data Fusion 2010, 1, 25–45. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M.E.; de Miranda, E.; Moran, E. A Comparative Study of Landsat TM and SPOT HRG Images for Vegetation Classification in the Brazilian Amazon. Photogram Metr. Eng. Remote Sens. 2008, 74, 311–321. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Wang, C.; Wu, H. Using GF-2 Imagery and the Conditional Random Field Model for Urban Forest Cover Mapping. Remote Sens. Lett. 2016, 7, 378–387. [Google Scholar] [CrossRef]
- Peng, L.; Liu, K.; Cao, J.; Zhu, Y.; Li, F.; Liu, L. Combining GF-2 and RapidEye satellite data for mapping mangrove species using ensemble machine-learning methods. Int. J. Remote Sens. 2019, 41, 813–838. [Google Scholar] [CrossRef]
- Ge, S.; Bin, X.; Yunxiang, J.; Shi, C.; Wenbo, Z.; Jian, G.; Hang, L.; Yujing, Z.; Xiuchun, Y. Monitoring wind farms occupying grasslands based on remote-sensing data from China’s GF-2 HD satellite—A case study of Jiuquan city, Gansu province, China. Resour. Conserv. Recycl. 2017, 121, 128–136. [Google Scholar]
- Lu, D. The Potential and Challenge of Remote Sensing-based Biomass Estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, Y.; Lu, D.; Li, G.; Chen, E. Classification of Land Cover, Forest, and Tree Species Classes with ZiYuan-3 Multispectral and Stereo Data. Remote Sens. 2019, 11, 164. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space (with discussion). J. R. Stat. Soc. Ser. B 2008, 70, 849–911. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zhong, W.; Zhu, L. Feature Screening via Distance Correlation Learning. J. Am. Stat. Assoc. 2012, 107, 1129–1139. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.; Jiang, H.; Wang, W.; Li, Z.; Chen, E.; Yan, M.; Tian, X. Forest Above-Ground Biomass Estimation Using KNN-FIFS Method Based on Multi-Source Remote Sensing Data. Sci. Silvae Sincae 2018, 54, 73–82. [Google Scholar]
- Zhang, C.; Xie, Z. Object-Based Vegetation Mapping in the Kissimmee River Watershed Using HyMAP Data and Machine Learning Techniques. Wetlands 2013, 33, 233–244. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Combining Object-Based Texture Measures with a Neural Network for Vegetation Mapping in the Everglades from Hyperspectral Imagery. Remote Sens. Environ. 2012, 124, 310–320. [Google Scholar] [CrossRef]
- Zhang, C.; Denkaa, S.; Coopera, H.; Deepak, R.M. Quantification of sawgrass marsh aboveground biomass in the coastal Everglades using object-based ensemble analysis and Landsat data. Remote Sens. Environ. 2018, 204, 366–379. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Peng, Y.; Wang, H.; Shen, J. Prediction of forest unit volume based on hybrid feature selection and ensemble learning. Evol. Intell. 2019, 4, 21–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Wang, J.; Gribskov, M. IRESpy: An XGBoost model for prediction of internal ribosome entry sites. BMC Bioinform. 2019, 20, 409. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Lin, C.; Huang, J.; Zeng, Z. On the Functional Equivalence of TSK Fuzzy Systems to Neural Networks, Mixture of Experts, CART, and Stacking Ensemble Regression. IEEE Trans. Fuzzy Syst. 2019, 10, 1109. [Google Scholar] [CrossRef] [Green Version]
- Wan, S.; Yang, H. Comparison among Methods of Ensemble Learning. In Proceedings of the 2013 International Symposium on Biometrics and Security Technologies, Chengdu, China, 2–5 July 2013. [Google Scholar]
- Tao, Y.; Peng, Y.; Jiang, Q.; Li, Y.; Fang, S.; Gong, Y. Remote Detection of Critical Growth Stages in Rapeseed Using Vegetation Spectral and Stacking Combination Method. J. Geomat. 2019, 44, 20–23. [Google Scholar]
- Li, W.; Ma, C.; Jin, D.; Hui, J. Sustainable Forest Management Model of Wangyedian Experimental Forest Farm in Karaqin Banner. Inn. Mong. For. Investig. Des. 2016, 6, 47–50. [Google Scholar]
- Wu, C.; Ma, C. Struggle for sixty years, dream and flourishing industry—Record of development of Wangye Dian Experimental Forest Farm in Chifeng. Land Green. 2015, 7, 16–19. [Google Scholar]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A modified Sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Li, G.; Peng, H.; Zhang, J.; Zhu, L. Robust rank correlation based screening. Ann. Stat. 2012, 40, 1846–1877. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Zhang, J. Martingale difference correlation and its use in high dimensional variable screening. J. Am. Stat. Assoc. 2014, 109, 1302–1318. [Google Scholar] [CrossRef]
- Sz’ekely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Q.; Wang, G.; Lin, H.; Luo, P.; Li, J.; Zeng, S.; Xu, X.; Ren, L. Optimizing kNN for Mapping Vegetation Cover of Arid and Semi-Arid Areas Using Landsat images. Remote Sens. 2018, 10, 1248. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Oyana, T.; Zhang, M.; Adu-Prah, S.; Zeng, S.; Lin, H.; Se, J. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. For. Ecol. Manag. 2009, 258, 1275–1283. [Google Scholar] [CrossRef]
| Tree Species | GSV Equations | Remarks |
|---|---|---|
| Larch | V = −0.001498 + 0.00007 × D^2 + 0.000901 × H + 0.000032 × H × D^2 | V: GSV D: DBH H: Tree Height |
| Chinese pine | V = 0.013464 − 0.001967 × D + 0.000089 × D^2 + 0.000628 × D × H + 0.000032 × H × D^2 − 0.003173 × H |
| Year of Field Measurements | Number of Plots | GSV Range (M3/ha) | Mean (M3/ha) | Standard Deviation | |
|---|---|---|---|---|---|
| Chinese pine | 2017 | 42 | 91.97~514.96 | 257.15 | 112.63 |
| Larch | 2017 | 37 | 87.44~405.56 | 211.69 | 81.51 |
| Vegetation Indices | Definitions |
|---|---|
| Simple two-band ratios | RVIi = Bandi/Bandj, i, j = 2, …, 7, i ≠ j |
| Difference vegetation indices | DVIij = Bandi − Bandj, i, j = 2, …, 7, i ≠ j |
| Normalized difference vegetation index | NDVI = (Nir − Red)/(Nir + Red) NDVI563 = (Nir + SWIR1 − Green)/(Nir + SWIR1 + Green) |
| Similar normalized difference vegetation indices | NDVI ij = (Bandi − Bandj)/(Bandi + Bandj), i, j = 2, …, 7, i ≠ j, Not including NDVI. |
| Soil adjusted vegetation indices | SAVI i = (Nir − Red)(1 + i)/(Nir + Red + i), i = 0.1, 0.25, 0.35, 0.5 |
| Atmospherically resistant vegetation index | ARVI = (Nir − (2 × Red − Blue))/(Nir + (2 × Red − Blue)) |
| Enhanced vegetation index | EVI = 2.5 × (Nir − Red)/(Nir + 6 × Red − 7.5 × Blue + 1) |
| Triangular vegetation index | TVI = 0.5 × (120×(Nir − Green) − 200 × (Red − Green)) |
| Modified simple ratio | MSR = (Nir/Red − 1)/SQRT(Nir/Red + 1) |
| Modified Soil adjusted vegetation index | MSAVI = ((2× Nir + 0.25) − SQRT((2× Nir + 0.25)^2 − 8×(Nir − Red)))/2 |
| Perpendicular vegetation index | PVI = 0.939× Nir − 0.344 × Red + 0.09 |
| Blue_Landsat | Green_Landsat | Red_Landsat | Nir_Landsat | Pan_Landsat | |
|---|---|---|---|---|---|
| Chinese pine | |||||
| RMSE(m3/ha) | 64.86 | 68.05 | 63.34 | 76.72 | 74.85 |
| R2 | 0.7010 | 0.6620 | 0.7070 | 0.5590 | 0.5695 |
| Adjusted R2 | 0.6680 | 0.6350 | 0.6840 | 0.5360 | 0.5476 |
| larch | |||||
| RMSE(m3/ha) | 57.31 | 61.98 | 56.44 | 59.72 | 61.76 |
| R2 | 0.5330 | 0.4380 | 0.7360 | 0.4930 | 0.4392 |
| Adjusted R2 | 0.5060 | 0.4220 | 0.7160 | 0.4630 | 0.4231 |
| Tree Species | Datasets | Methods | Spectral Variables |
|---|---|---|---|
| Chinese pine | GF-2 | SRA | Red_S, Blue, Blue_ Cor |
| RF | Blue, Blue_M, Green_Cor, Green_D, Nir_Con, Blue _Con, NDVI23 | ||
| DC-FSCK | Blue_M, NDVI13, NDVI12, NDVI24, RVI24 | ||
| Landsat 8 | SRA | Nir_E, RVI24, ND47 | |
| RF | Blue, NDVI57, SWIR2_Cor, RVI35, NDVI56, NDVI35, RVI24 | ||
| DC-FSCK | Green, Red_Con, RVI57, NDVI24 | ||
| Red_Landsat | SRA | Blue_M, Blue_H, Coastal _Cor | |
| RF | Blue_M, Coastal _M, SWIR2_E, Green_S, DVI34, Blue_S, SWIR2_M, NDVI34 | ||
| DC-FSCK | Blue_M, Green_Dis, Green_S, SWIR2_H, Red_H, SAVI0.25, Coastal _S | ||
| Larch | GF-2 | SRA | ND13, ARVI, RVI34 |
| RF | Blue, ARVI, RVI14, Blue_M, Green, RVI24, NDVI14 | ||
| DC-FSCK | Blue, Nir_M, Nir_E, Nir_D, Green_Cor, Red_H, ARVI | ||
| Landsat 8 | SRA | DVI34, Red_E, Blue_H | |
| RF | NDVI67, RVI67, DVI46, DVI24, DVI26, SWIR1_M | ||
| DC-FSCK | MSR, RVI23, RVI34, Blue_H, RVI27, SAVI0.35 | ||
| Red_Landsat | SRA | RVI27, EVI, Green_V | |
| RF | DVI34, RVI67, SWIR2_M, NDVI57, Blue_M, RVI45, Red_M, NDVI35 | ||
| DC-FSCK | MSR, Blue_M, Coastal _M, Nir_Cor, Nir_V, Green_Dis, MSAVI, SAVI0.1, NDVI46 |
| Tree Species | Data Scenarios | Variable Selection Methods | Performance Evaluation of Six Models | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR | kNN | SVR | RF | XGBoost | Stacking | |||||||||
| Adjusted R2 | RMSEr (%) | Adjusted R2 | RMSEr (%) | Adjusted R2 | RMSEr (%) | Adjusted R2 | RMSEr (%) | Adjusted R2 | RMSEr (%) | Adjusted R2 | RMSEr (%) | |||
| Chinses pine | GF-2 | SRA | 0.4756 | 30.17 | 0.4237 | 31.62 | 0.3591 | 33.35 | 0.4593 | 30.63 | 0.5393 | 28.28 | 0.5307 | 28.74 |
| RF | 0.3351 | 32.13 | 0.2401 | 34.35 | 0.3948 | 30.66 | 0.5999 | 24.93 | 0.5744 | 25.71 | 0.5825 | 25.17 | ||
| DC-FSCK | 0.3222 | 33.38 | 0.6687 | 23.34 | 0.6005 | 25.63 | 0.5266 | 27.90 | 0.5811 | 26.24 | 0.7226 | 21.35 | ||
| Landsat 8 | SRA | 0.5257 | 28.69 | 0.2247 | 36.68 | 0.3837 | 32.70 | 0.4631 | 30.53 | 0.5192 | 28.89 | 0.5244 | 28.83 | |
| RF | 0.3780 | 31.08 | 0.2335 | 34.50 | 0.2783 | 33.48 | 0.6112 | 24.57 | 0.5380 | 26.79 | 0.6066 | 24.74 | ||
| DC-FSCK | 0.3821 | 32.31 | 0.7209 | 21.72 | 0.7315 | 21.30 | 0.6978 | 22.60 | 0.7172 | 21.86 | 0.7234 | 21.56 | ||
| Fusion imagery: Red_Landsat | SRA | 0.6189 | 25.72 | 0.5964 | 26.47 | 0.6443 | 24.85 | 0.6383 | 25.05 | 0.6255 | 25.49 | 0.6356 | 25.19 | |
| RF | 0.4833 | 27.91 | 0.0676 | 37.49 | 0.2754 | 33.05 | 0.5480 | 26.10 | 0.5327 | 26.54 | 0.5458 | 26.17 | ||
| DC-FSCK | 0.4956 | 27.99 | 0.7963 | 17.78 | 0.5740 | 25.72 | 0.4568 | 29.05 | 0.4757 | 28.54 | 0.8127 | 17.05 | ||
| Larch | GF-2 | SRA | 0.1937 | 32.66 | 0.3857 | 28.50 | 0.1881 | 32.77 | 0.3590 | 29.12 | 0.4668 | 26.56 | 0.4583 | 27.33 |
| RF | −0.0078 | 34.22 | 0.0785 | 32.73 | 0.0635 | 32.99 | 0.3652 | 27.01 | 0.1768 | 30.93 | 0.3613 | 27.25 | ||
| DC-FSCK | −0.0578 | 36.08 | 0.3971 | 26.47 | 0.0328 | 33.53 | 0.3486 | 27.51 | 0.1533 | 31.37 | 0.4062 | 25.72 | ||
| Landsat 8 | SRA | 0.2401 | 31.70 | 0.2467 | 31.56 | 0.2054 | 32.42 | 0.0340 | 36.14 | 0.0045 | 37.26 | 0.2457 | 31.85 | |
| RF | 0.2802 | 29.42 | −0.0415 | 35.38 | 0.2657 | 29.71 | 0.5638 | 23.21 | 0.5543 | 24.31 | 0.5612 | 23.37 | ||
| DC-FSCK | 0.0869 | 33.13 | 0.5700 | 23.13 | 0.2114 | 30.79 | 0.3774 | 27.36 | 0.2867 | 29.28 | 0.5602 | 23.52 | ||
| Fusion imagery: Red_Landsat | SRA | 0.5606 | 24.11 | 0.3175 | 30.04 | 0.5028 | 25.64 | 0.3039 | 30.34 | 0.3781 | 28.68 | 0.5116 | 25.32 | |
| RF | 0.1572 | 30.75 | 0.2239 | 29.51 | 0.2092 | 29.79 | 0.3622 | 26.75 | 0.2747 | 28.53 | 0.3550 | 26.96 | ||
| DC-FSCK | 0.0240 | 32.50 | 0.5649 | 21.70 | 0.4665 | 24.02 | 0.3984 | 25.51 | 0.4209 | 25.03 | 0.6047 | 20.68 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm. Remote Sens. 2020, 12, 871. https://doi.org/10.3390/rs12050871
Li X, Liu Z, Lin H, Wang G, Sun H, Long J, Zhang M. Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm. Remote Sensing. 2020; 12(5):871. https://doi.org/10.3390/rs12050871
Chicago/Turabian StyleLi, Xinyu, Zhaohua Liu, Hui Lin, Guangxing Wang, Hua Sun, Jiangping Long, and Meng Zhang. 2020. "Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm" Remote Sensing 12, no. 5: 871. https://doi.org/10.3390/rs12050871
APA StyleLi, X., Liu, Z., Lin, H., Wang, G., Sun, H., Long, J., & Zhang, M. (2020). Estimating the Growing Stem Volume of Chinese Pine and Larch Plantations based on Fused Optical Data Using an Improved Variable Screening Method and Stacking Algorithm. Remote Sensing, 12(5), 871. https://doi.org/10.3390/rs12050871