Point Cloud Semantic Segmentation Using a Deep Learning Framework for Cultural Heritage

Abstract

In the Digital Cultural Heritage (DCH) domain, the semantic segmentation of 3D Point Clouds with Deep Learning (DL) techniques can help to recognize historical architectural elements, at an adequate level of detail, and thus speed up the process of modeling of historical buildings for developing BIM models from survey data, referred to as HBIM (Historical Building Information Modeling). In this paper, we propose a DL framework for Point Cloud segmentation, which employs an improved DGCNN (Dynamic Graph Convolutional Neural Network) by adding meaningful features such as normal and colour. The approach has been applied to a newly collected DCH Dataset which is publicy available: ArCH (Architectural Cultural Heritage) Dataset. This dataset comprises 11 labeled points clouds, derived from the union of several single scans or from the integration of the latter with photogrammetric surveys. The involved scenes are both indoor and outdoor, with churches, chapels, cloisters, porticoes and loggias covered by a variety of vaults and beared by many different types of columns. They belong to different historical periods and different styles, in order to make the dataset the least possible uniform and homogeneous (in the repetition of the architectural elements) and the results as general as possible. The experiments yield high accuracy, demonstrating the effectiveness and suitability of the proposed approach.

1. Introduction

In the Digital Cultural Heritage (DCH) domain, the generation of 3D Point Clouds is, nowadays, the more efficient way to manage CH assets. Being a well-established methodology, the representation of CH artifacts through 3D data is a state of art technology to perform several tasks: morphological analysis, map degradation or data enrichment are just some examples of possible ways to exploit such rich informative virtual representation. Management of DCH information is fundamental for better understanding heritage data and for the development of appropriate conservation strategies. An efficient information management strategy should take into consideration three main concepts: segmentation, organization of the hierarchical relationships and semantic enrichment [1]. Terrestrial Laser Scanning (TLS) and digital photogrammetry allow to generate large amounts of detailed 3D scenes, with geometric information attributes depending on the method used. As well, the development in the last years of technologies such as Mobile Mapping System (MMS) is contributing the massive 3D metric documentation of the built heritage [2,3]. Therefore, Point Clouds management, processing and interpretation is gaining importance in the field of geomatics and digital representation. These geometrical structures are becoming progressively mandatory not only for creating multimedia experiences [4,5], but also (and mainly) for supporting the 3D modeling process [6,7,8,9], where even neural networks are lately starting to be employed [10,11].

Simultaneously, the recent research trends in HBIM (Historical Building Information Modeling) are aimed at managing multiple and various architectural heritage data [12,13,14], facing the issue of transforming 3D models from a geometrical representation to an enriched and informative data collector [15]. Achieving such result is not trivial, since HBIM is generally based on scan-to-BIM processes that allow to generate a parametric 3D model from Point Cloud [16]; these processes, although very reliable since they are made manually by domain experts, have two drawbacks that are noteworthy: first, it is very time consuming and, secondly, it wastes an uncountable amount of data, given that a 3D scanning (both TLS or Close Range Photogrammetry based), contains much more information than the ones required for describing a parametric object. The literature demonstrates that, up to now, traditional methods applied to DCH field still make extensive use of manual operations to capture the real estate from Point Clouds [17,18,19,20]. Lately, towards this end, a very promising research field is the development of Deep Learning (DL) frameworks for Point Cloud such as Point- Net/Pointnet++ [21,22] open up more powerful and efficient ways to handle 3D data [23]. These methods are designed to recognize Point Clouds. The tasks performed by these frameworks are: Point Cloud classification and segmentation. The Point Cloud classification takes the whole Point Cloud as input and output the category of the input Point Cloud. The segmentation aims at classifying each point to a specific part of the Point Cloud [24]. Albeit the literature for 3D instance segmentation is limited, if compared to its 2D counterpart (mainly due to the high memory and computational cost required by Convolutional Neural Network (CNN) for scene understanding [25,26,27]), these frameworks may facilitate the recognition of historical architectural elements, at an appropriate level of detail, and thus speeding up the process of reconstruction of geometries in the HBIM environment or in object-oriented software [28,29,30,31]. To the best of our knowledge, these methods are not applied for the automatic recognition of DCH elements yet. In fact, even if they revealed to be suitable for handling Point Cloud of regular shapes, DCH goods are characterised by complex geometries, highly variable between them and defined only with a high level of detail. In [19], the authors study the potential offered by DL approaches for the supervised classification of 3D heritage obtaining promising results. However, the work does not cope with the irregular nature of CH data.

To address these drawbacks, we propose a DL framework for Point Cloud segmentation, inspired by the work presented in [32]. Instead of employing individual points like PointNet [21], the approach proposed in [32] exploits local geometric structures by constructing a local neighborhood graph and applying convolution-like operations on the edges connecting neighboring pairs of points. This network has been improved by adding relevant features such as normal and HSV encoded color. The experiments has been performed to a completely new DCH dataset. This dataset comprises 11 labeled points clouds, derived from the union of several single scans or from the integration of the latter with photogrammetric surveys. The involved scenes are both indoor and outdoor, with churches, chapels, cloisters, porticoes and archades covered by a variety of vaults and beared by many different types of columns. They belong to different historical periods and different styles, in order to make the dataset the least possible uniform and homogeneous (in the repetition of the architectural elements) and the results as general as possible. In contrast to many existing datasets, it has been manually labelled by domain experts, thus providing a more precise dataset. We show that the resulting network achieves promising performance in recognizing elements. A comprehensive overall picture of the developed framework is reported in Figure 1. Moreover, the research community dealing with Point Cloud segmentation can benefit from this work, as it makes available a labelled dataset of DCH elements. As well, the pipeline of work might represent a baseline for further experiments from other researchers dealing with Semantic Segmentation of Point Clouds with DL approaches.

The main contributions of this paper with respect to the state-of-the-art approaches are: (i) a DL framework for DCH semantic segmentation of Point Cloud, useful for the 3D documentation of monuments and sites; (ii) an improved DL approach based on DGCNN with additional Point Cloud features; (iii) a new DCH dataset that is publicly available to the scientific community for testing and comparing different approaches and iv) the definition of a consistent set of architectural element classes, based on the analysis of existing standard classifications.

The paper is organized as follows. Section 2 provides a description of the approaches that were adopted for Point Clouds semantic segmentation. Section 3 describes our approach to present a novel DL network operation for learning from Point Clouds, to better capture local geometric features of Point Clouds and a new challenging dataset for the DCH domain. Section 4 offers an extensive comparative evaluation and a detailed analysis of our approach. Finally, Section 6 draws conclusions and discuss future directions for this field of research.

2. State of the Art

In this section we review the relevant literature concerning the classification and semantic segmentation for digital representation of cultural heritage. We then focus on the semantic segmentation of Point Cloud data, discussing different existing approaches.

2.1. Classification and Semantic Segmentation in the Field of Dch

In the field of CH, the classification and semantic segmentation associated with DL techniques, can help to recognize historical architectural elements, at an adequate level of detail, and thus speed up the process of reconstructing geometries in the BIM environment. To date, there are many studies in which Point Clouds are used for the recognition and reconstruction of geometries related to BIM models [29,30,31], however these methods have not been applied to DCH yet and do not fully exploit DL strategies. Cultural assets are in fact characterized by more complex geometries, very variable even within the same class and describable only with a high level of detail, making therefore much more complicated to apply DL strategies to this domain.

Despite some works that attempt at classifying DCH images by employing different kinds of techniques [33,34,35,36] already exist, there are still few researches who seek to directly exploit the Point Clouds of CH for semantic classification or segmentation through ML [37] or DL techniques. One of them is [38], where a segmentation of 3D models of historical buildings is proposed for FEA analysis, starting from Point Clouds and meshes. Barsanti et al. tested some algorithms such as the region growing, directly on the Point Clouds, proving its effectiveness for the segmentation of flat and well-defined structures, nevertheless more complex geometries such as curves or gaps have not been correctly segmented and the computational times increased considerably. Some software were then tested for the direct segmentation of the meshes, but in this case the results show that the process is still completely manual and, in the only case in which the segmentation is semi-automatic, the software is not able to manage large models, thus it is necessary to split the file and proceed to the analysis of single portions. Finally, it should be emphasized that the case study used for mesh segmentation (The Neptune Temple in Paestum) is a rather regular and symmetrical architecture, hence relatively easy to segment on the basis of some horizontal planes.

As Point Clouds are geometric structures of irregular nature, characterized by the lack of a grid, with a high variability of density, unordered and invariant to transformation and permutation [39], their exploitation with DL approaches is still not straightforward and it is even more challenging when dealing with DCH oriented dataset.

At the best of our knowledge, the only recent attempt to use DL for the semantic classification of Point Clouds of DCH is [19]. The method described consists of a workflow composed of feature extraction, feature selection and classification, as proposed in [40], for the subdivision into a high level of detailed architectural elements, using and comparing both ML and DL strategies. For the ML, among all the classifiers, the authors use the Random Forest (RF) and One-vs.-One, optimizing the parameters for the RF by choosing those with the value of the higher F1-score in Scikit-learn. In this way, they achieve excellent performances in most of the classes identified, however no feature correlation has been carried out and, most of all, the different geometric features are selected depending on the peculiarities of the case study to be analyzed. On the other side, for the DL approaches, they use a 1D and a 2D CNN, in addition to Bi-LSTM RNN which is usually used for the prediction of sequences or texts. The choice of this type of neural networks is due to the interpretation of the Point Cloud as a sequence of points, nevertheless the results of the ML outperfom those of DL. This could be due to the choice of not using any of the recent networks designed specifically for taking into account the third dimension of the Point Cloud data. Furthermore, the test phase of the DL is carried out on the remaining part of the Point Cloud, very similar to the data presented in the training phase, so this setting does not generalize adequately the methodology proposed.

Based on the above considerations, in this work some of the latest state-of-art NNs for 3D data have been selected and compared. Moreover, we intend to set up a method that generalizes as much as possible, with case studies one different from the other and with a parameter setting equal for all the scenes, so as to diminish human involvement.

2.2. Semantic Segmentation of Point Clouds

As well stated in the literature, thanks to their third dimension, Point Clouds can be exploited not only for the 3D reconstruction and modeling of buildings or architectural elements, but also for object detection in many other areas such as, for example, robotics [41], indoor navigation or autonomous navigation [42,43], urban environments [44,45,46], and it is just in these fields that the exploitation of Point Clouds has been mainly developed. Currently, Point Cloud semantic segmentation approaches in the DL framework can be divided in three categories [47]:

• Multiview-based: creation of a set of images from Point Clouds, on which ConvNets can be applied, having shown to achieve very high accuracy both in terms of classification and segmentation;
• Voxel-based: rasterization of Point Clouds in voxels, which allow to have an ordered grid of Point Clouds, while maintaining the continous properties and the third dimension, thus permitting the application of CNNs;
• Point-based: the classification and semantic segmentation are performed by applying features-based approaches; the DL has shown good results in numerous fields, but has not been applied to DCH oriented dataset yet.

A natural choice for the 3D reconstruction in the BIM software is to explore Point Cloud segmentation methods directly on the raw data. Over recent years, several DL approaches are emerging. In contrast to multiview-based [48,49,50,51,52] and voxel-based approaches [41,43,53,54], such approaches do not need specific pre-processing steps, and have been proved to provide state-of-the-art performances in semantic segmentation and classification task on standard benchmarks. Since the main objective of this work is to directly exploit the three-dimensionality of Point Clouds, a comprehensive overview of the multiview and voxel based methods is out of the scope, therefore only the point-based methods will be detailed.

One of the pioneer and best known DL architectures that works directly on Point Clouds is PointNet [21], an end-to-end deep neural network able to learn itself the features for classification, part segmentation and semantic segmentation. It is composed by a sequence of MLPs that first explore the point features and then identify the global features, through the approximation of a symmetric function, the max pooling layer, that also allows to obtain the input permutation invariance. Finally, fully connected layers aggregate the values for labels prediction and classification. However, as stated by the authors, since PointNet does not capture the local geometries, a development has been proposed, PointNet++ [22]. In this research, a hierarchical grouping is introduced to learn local features thanks to the exploitation of the metric space distances, a good robustness and detail capture has been ensured by the consideration of local neighbourhoods and improved results if compared with their state-of-art have been obtained. Inspiring from PointNet and PointNet++, the works on 3D DL aim at putting attention on feature augmentation, principally to local features and relationships among points. This is done by utilising knowledge from other fields to improve the performance of the basic PointNet and PointNet++ algorithms.

Several researchers have preferred a substitute to PointNet, applying the convolution as an essential and compelling component, with their deeper understanding on point-based learning. PointCNN adopted a X- transformation instead of symmetric functions to canonicalize the order, which is a generalization of CNNs to feature learning from unorderd and unstructured Point Clouds [55]. SParse LATtice Networks (SPLATNet) has been proposed as a Point Cloud segmentation framework that could join 2D images with 3D Point Clouds [56].

As regards to convolution kernels as nonlinear functions of the local coordinates of 3D points comprised of weight and density functions, in [57], it has been presented PointConv, an extension to the Monte Carlo approximation of the 3D continuous convolution operator.

Alternative development of PointNet and PointNet++ are [58,59,60] where the features are learnt in a hierarchical manner, in particular [58], uses the Kd-trees to subdivide the space and try to take local info into account by also applying a hierarchical grouping. As stated in [61], in the Klokov’s work the Kd-trees are used as underlying graphs to simulate CNNs and the idea to use graphs for neural networks has been carried out by various researches as [24,32,62,63]. Their use, in recent years, has grown above all thanks to the fact that they have many elements in common with CNNs [43], in fact the main elements of the latter such as local connections, the presence of weights and the use of multi-layers, are also characteristic of graphs. Wang et al. [64] have introduced a Graph Attention Convolution (GAC), in which kernels could be dynamically adapted to the structure of an object. GAC can capture the structural features of Point Clouds while avoiding feature contamination between objects. In [62], Landrieu and Simonovsk have proposed SuperPoint Graph (SPG) for achieving richer edge features, offering a representation of the relationships among object parts rather than points. In the partition of the superpoint there is a kind of nonsemantic presegmentation and a downsampling step. After SPG construction, each superpoint is embedded in a basic PointNet network and then refined in Gated Recurrent Units (GRUs) for Point Cloud seantic segmentation. In the DGCNN [32] the authors reason on the neighborhood, rather than on the single points, building a neighborhood graph that allows to exploit the local geometric structures. With the use of an edge convolutional operator, eventually interleaved with pooling, the process relies on the identification of edge features able to define the relationship between the center point chosen and the edge vector connecting its neighbors to itself. The application of a further K-nn of a point, changing from layer to layer, renders the graph dynamic and allows to calculate the proximity both in the feature space and in the Euclidean one. The advantage of using Dynamic graphs is that they allow to dynamically vary the input signals and, in the case of the DGCNN, they have shown excellent results for classification, part segmentation and indoor scene segmentation respectively tested on the ModelNet40, ShapeNet and S3DIS datasets.

Another example is [24], a recent development of [32], in which the authors try to reshape the dimensions of the DGCNN by eliminating the transformation network, used to solve the transformation invariance problem, using MLP to extract the transformation invariant features. It has been noticed that the DGCNN is able to work properly even with very different Point Clouds of considerable size (>10 M points), see

Table 1. Number of points per class and overall for the whole scene. The point cloud of the Trompone church has been split into right (r) and left (l) part according to the tests conducted in Section 4.

Scene/Class	Arc	Column	Decoration	Floor	Door	Wall	Window	Stairs	Vault	Roof	TOTAL
	0	1	2	3	4	5	6	7	8	9
TR_cloister	900,403	955,791	765,864	1,948,029	779,019	10,962,235	863,792	2806	2,759,284	1,223,300	21,160,523
TR_church_r	466,472	658,100	1,967,398	1,221,331	85,001	3,387,149	145,177	84,118	2,366,115	0	10,380,861
TR_church_l	439,269	554,673	1,999,991	1,329,265	44,241	3,148,777	128,433	38,141	2,339,801	0	10,022,591
VAL	300,923	409,123	204,355	1,011,034	69,830	920,418	406,895	0	869,535	0	4,192,113
CA	17,299	172,044	0	0	30,208	3,068,802	33,780	11,181	0	1,559,138	4,892,452
SMG	309,496	1,131,090	915,282	1,609,202	18,736	7,187,003	137,954	478,627	2,085,185	7,671,775	21,544,350
SMV_1	46,632	314,723	409,441	457,462	0	1,598,516	2011	274,163	122,522	620,550	3,846,020
SMV_naz	472,004	80,471	847,281	1,401,120	42,362	2,846,324	16,559	232,748	4,378,069	527,490	10,844,428
SMV_24	146,104	406,065	154,634	20,085	469	366,2361	6742	131,137	305,086	159,480	4,992,163
SMV_28	36,991	495,794	18,826	192,331		1,965,782	4481	13,734	184,261	197,679	3,109,879
SMV_pil	584,981	595,117	1,025,534	1,146,079	26,081	7,358,536	313,925	811,724	2,081,080	3,059,959	17,003,016
SMV_10	0	16,621	0	125,731	0	1,360,738	106,186	113,287	0	499,159	2,221,722
TOTAL	3,720,574	5,789,612	8,308,606	10,461,669	1,095,947	47,466,641	2,165,935	2,191,666	17,490,938	15,518,530	114,210,118

, while PointNet++ is less generalizable, it seems to have good performances mainly with small datasets and simple classes as the case of ScanNet.

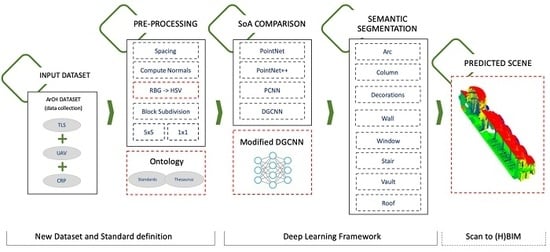
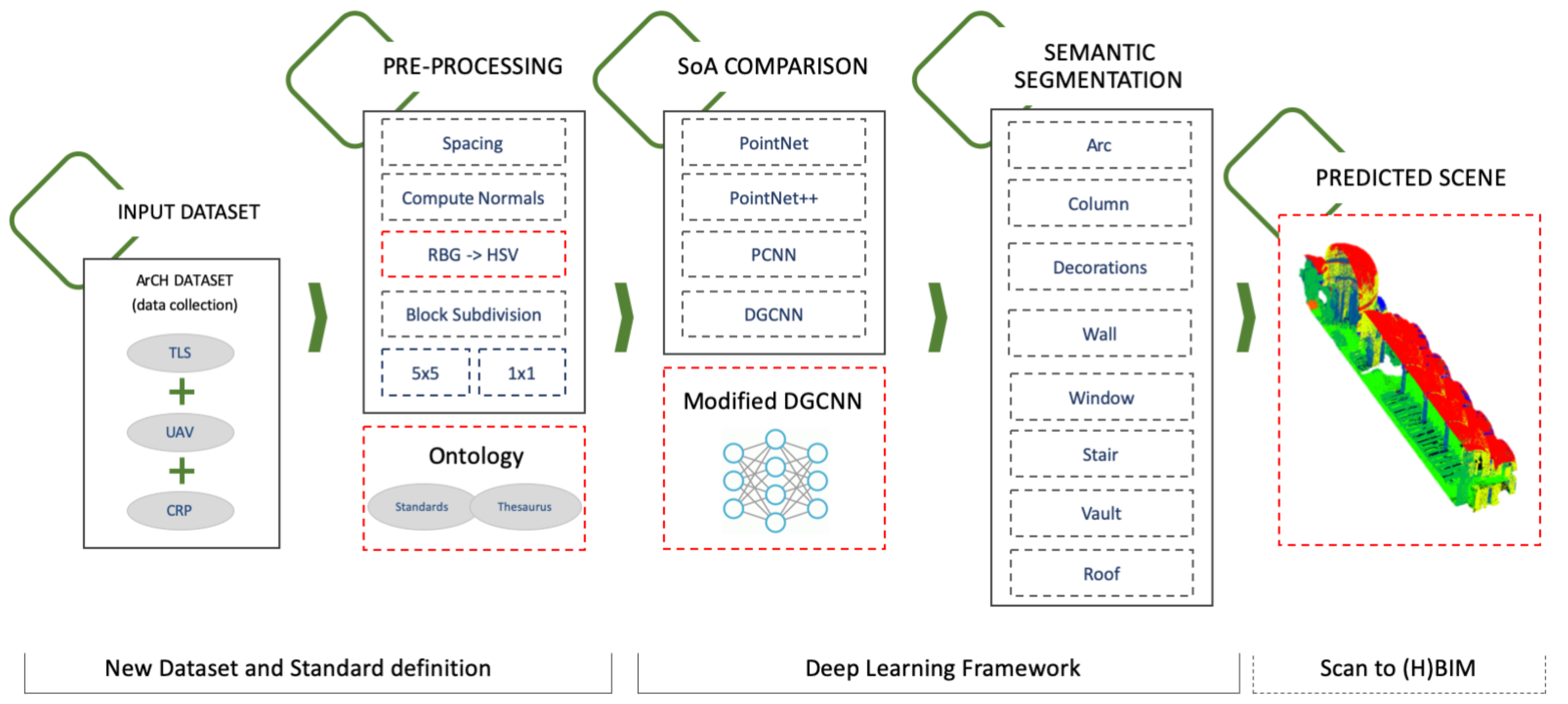
3. Materials and Methods

In this section, we introduce the DL framework as well as the dataset used for evaluation. The framework, as said in the introduction section, is depicted in Figure 1. We use a novel modified DGCNN for Point Cloud semantic segmentation. Further details are given in the following subsections. The framework is comprehensively evaluated on the ArCH Dataset, a publicly available dataset collected for this work.

3.1. ArCH Dataset for Point Cloud Semantic Segmentation

In the state of the art, the most used datasets to train neural networks are: ModelNet 40 [53] with more than 100k CAD models of objects, mainly furnitures, from 40 different categories; KITTI [65] that includes camera images and laser scans for autonomous navigation; Sydney Urban Objects [66] dataset acquired with Velodyne HDL-64E LiDAR in urban environments with 26 classes and 631 individual scans; Semantic3D [67] with urban scenes as churches, streets, railroad tracks, squares and so on; S3DIS [68] that includes mainly office areas and it has been collected with the Matterport scanner with 3D structured light sensors and the Oakland 3-D Point Cloud dataset [69] consisting of labeled laser scanner 3D Point Clouds, collected from a moving platform in a urban environment. Most of the current datasets collect data from urban environments, with scans composed of around 100 K points, and to date there are still no published datasets focusing on immovable cultural assets with an adequate level of detail.

Our proposed dataset, named ArCH (Architectural Cultural Heritage) is composed of 11 labeled scenes (Figure 2), derived from the union of several single scans or from the integration of the latter with photogrammetric surveys. There are also as many Point Clouds which, however, have not been labeled yet, so they have not been used for the tests presented in this work.

The involved scenes are both indoor and outdoor, with churches, chapels, cloisters, porticoes and archades covered by a variety of vaults and beared by many different types of columns. They belong to different historical periods and different styles, in order to make the dataset the least possible uniform and homogeneous (in the repetition of the architectural elements) and the results as general as possible.

Different case studies are taken into exam and are described as follows: The Sacri Monti (Sacred Mounts) of Ghiffa (SMG) and Varallo (SMV); The Sanctuary of Trompone (TR); The Church of Santo Stefano (CA); The indoor scene of the Castello del Valentino (VA). The ArCH Dataset is publicly available(http://vrai.dii.univpm.it/content/arch-dataset-point-cloud-semantic-segmentation) for research purposes.

• The Sacri Monti (Sacred Mounts) of Ghiffa and Varallo. These two devotional complexes in northern Italy have been included in the UNESCO World Heritage List (WHL) in 2003. In the case of the Sacro Monte di Ghiffa, a 30 m loggia with tuscanic stone columns and half pilasters has been chosen; while for the Sacro Monte of Varallo 6 buildings have been included in the dataset, containing a total of 16 chapels, some of which very complex from an architectural point of view: barrel vaults, sometimes with lunettes, cross vaults, arcades, balustrades and so on.
• The Sanctuary of Trompone (TR). This is a wide complex dating back to the 16th century and it consists of a church (about 40 × 10 m) and a cloister (about 25 × 25 m), both included in the dataset. The internal structure of the church is composed of 3 naves covered by cross vaults supported in turn by stone columns. There is also a wide dome at the apse and a series of half-pilasters covering the sidewalls.
• The Church of Santo Stefano (CA) has a completely different compositional structure if compared with the previous one, being a small rural church from the 11th century. There is a stone masonry, not plastered, brick arches above the small windows and a series of Lombard band defining a decorated moulding under the tiled roof.
• The indoor scene of the Castello del Valentino (VA) is a courtly room part of an historical building recast from the 17th century. This hall is covered by cross vaults leaning on six sturdy breccia columns. Wide French windows illuminate the room and oval niches surrounded by decorative stuccoes are placed on the sidewalls. This case study is part of a serial site inserted in the WHL. of UNESCO in 1997.

In the majority of cases, the final scene was obtained through the integration of different Point Clouds, those acquired with the terrestrial laser scanner (TLS), and those deriving from photogrammetry (mainly aerial for surveying the roofs), after appropriate evaluation of the accuracy. This integration results in a complete Point Cloud, with different density according to the sensors used, however leading to increasing the overall Point Cloud size and requiring a pre-processing phase for the NN.

The common structure of the Point Clouds is therefore based on the sequence of the coordinates x, y, z and the R, G, B values.

In the future, other point clouds will be added to the ArCH dataset, to improve the representation of complex CH objects with the potential contribution of all the other researchers involved in this field.

3.2. Data Pre-Processing

To prepare the dataset for the network, pre-processing operations have been carried out in order to make the cloud structures more homogeneous. The pre-processing methods, for this dataset, have followed 3 steps: translation, subsampling and choice of features.

The spatial translation of the Point Clouds is necessary because of the georeferencing of the scenes, the coordinate values are in fact too large to be processed by the deep network, so the coordinates are truncated and each single scene is spatially moved close to the point cardinal (0,0,0). This operation on the one hand has led to the loss of georeferencing, on the other hand, however, it has made possible to reduce the size of the files and the space to be analyzed, thus also leading to a decrease in the required computational power.

The subsampling operation, which became necessary due to the high number of points (mostly redundant) present in each scene (>20 M points), was instead more complex. It was in fact necessary to establish which of the three different subsampling options was the most adequate to provide the best typology of input data to the neural network. The option of random subsampling was discarded because it would limit the test repeatability, then both the other two methods have been tested: octree and space. The first is efficient for nearest neighbor extraction, while the second provides, in the output Point Cloud, points not closer than the distance specified. As far as space is concerned, it has been set a minimum space between points of 0.01 m, in this way a high level of detail is ensured, but at the same time it is possible to considerably reduce the number of points and the size of the file, in addition to regularize the geometric structure of the Point Cloud

As for the octree, applied only in the first tests on half of the Trompone Church scene, level 20 was set, so that the number of final points was more or less similar to that of the scene subsampled with the space method. The software used for this operation is CloudCompare. An analysis of the number of points for each scene is detailed in Table 1, where it is possible to see the lack of points for some classes and the highest total value for the ‘Wall’ class.

The extraction of features directly from the Point Clouds is instead an open and constantly evolving field of research. Most of the features are handcrafted for specific tasks and can be subdivided and classified into intrinsic and extrinsic, or also used for local and global descriptors [40,70]. The local features define statistical properties of the local neighborhood geometric information, while the global features describe the whole geometry of the Point Cloud. Those mostly used are the local ones, such as eigenvalues based descriptors, 3D Shape context and so on, however in our case, since the last networks developed [22,32] tend to let the network itself learn the features and since our main goal is to generalize as much as possible, in addition to reduce the human involvement in the pre-proccessing phases, the only features calculated are the normals and the curvature. The normals are calculated on Cloud Compare and have been computed and orientated with different settings depending on the surface model and 3D data acquisition. Specifically a plane or quadric ‘local surface model’ as surface approximation for the normals computation has been used and a ‘minimum spanning tree’ with Knn = 10 has been set for their orientation. The latter has been further checked on MATLAB^®.

3.3. Deep Learning for Point Cloud Semantic Segmentation

State-of-the-art deep neural networks are specifically designed to deal with the irregularity of Point Clouds, directly managing raw Point Cloud data rather than using an intermediate regular representation. In this contribution, the performances obtained with the ArCH dataset of some state-of-art architectures are therefore compared and then evaluated with regards to the DGCNN we have modified. The NNs selected are:

• PointNet [21], as it was the pioneer of this approach, obtaining permutation invariance of points by operating on each point independently and applying a symmetric function to accumulate features.
• its extensions PointNet++ [22] that analyzes neighborhoods of points in preference of acting on each separately, allowing the exploitation of local features even if with still some important limitations.
• PCNN [71], a DL framework for applying CNN to Point Clouds generalizing image CNNs. The extension and restriction operators are involved, permitting the use of volumetric functions associated to the Point Cloud.
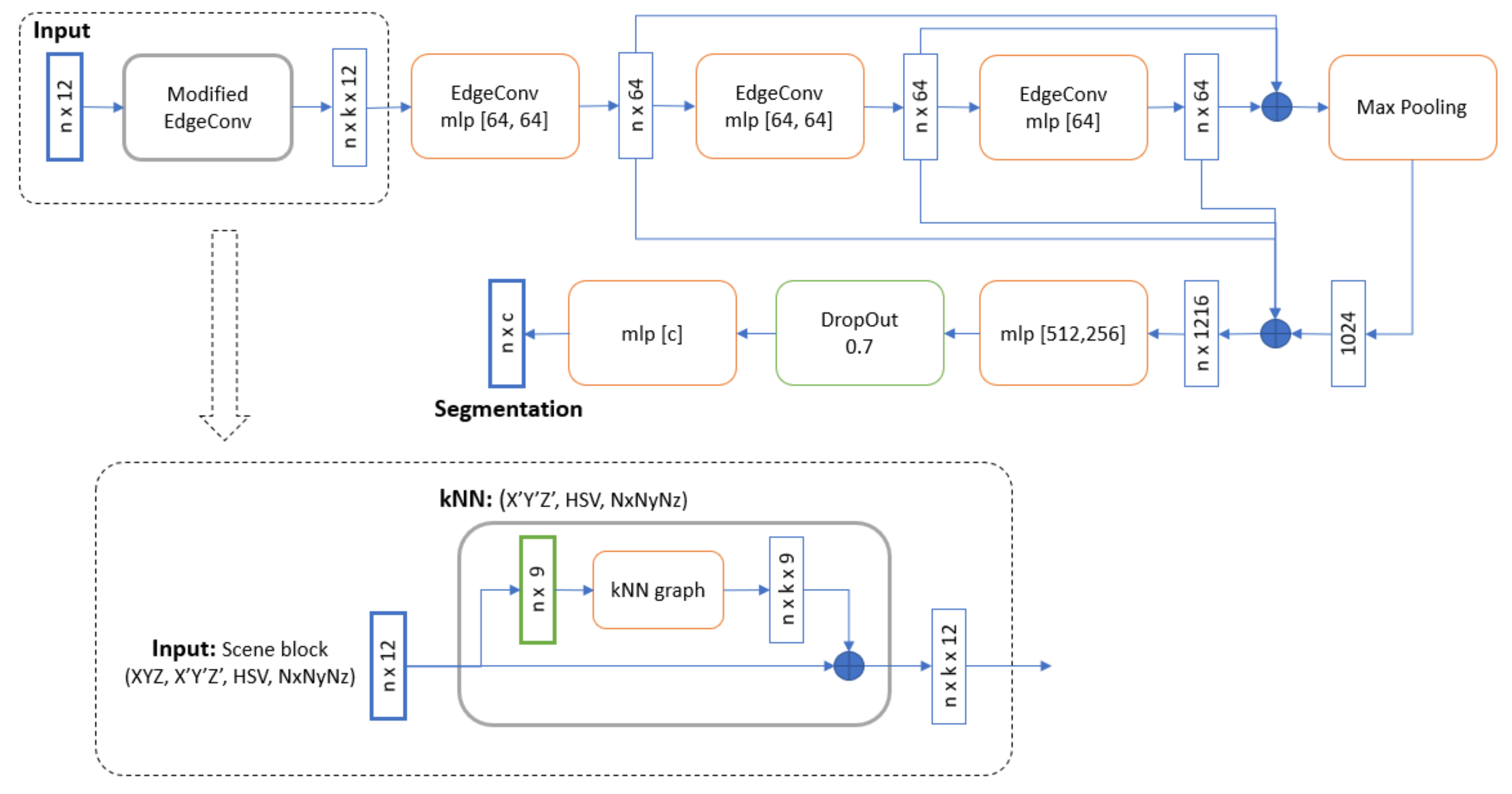
• DGCNN [32] that addresses these shortcomings by adding the EdgeConv operation. EdgeConv is a module that creates edge features describing the relationships between a point and its neighbors rather than generating point features directly from their embeddings. This module is permutation invariant and it is able to group points thanks to local graph, learning from the edges that link points.

3.4. DGCNN for DCH Point Cloud Dataset

In our experiments, we build upon the DGCNN implementation provided by [32]. Such an implementation of DGCNN uses k-nearest neighbors (kNN) to individuate the k points closest to the point to be classified, thus defining the neighboring region of the point. The edge features are then calculated from such a neighboring region and provided as input to the following layer of the network. Such a edge convolution operation is performed on the output of each layer of the network. In the original implementation, at the input layer kNN is fed with normalized points coordinates only, while in our implementation we use all the available features. Specifically, we added color features, expressed as RGB or HSV, and normal vectors.

Figure 3 shows the overall structure of the network. We give in input a scene block, composed of 12 features for each point: XYZ coords, X’Y’Z’ normalized coords, color features (HSV channels), normals features. These blocks pass through 4 EdgeConv layers and a max-pooling layer to extract global features of the block. The original XYZ coordinates are kept to take into account the positioning of the points in the whole scene, while the normalized coordinates represent the positioning within each block. The KNN module is fed with normalized coordinates only and both original and normalized coordinates are used as input features for the neural network. RGB channels have been converted to HSV channels in two steps: first they are normalized to values between 0 and 1, then they are converted to HSV channels using the rgb2hsv() function of the scikit-image library implemented in python. This conversion is useful because the individual channels H, S and V are independent one from the other, each of them has a different typology information, making them independent features. Channels R, G and B are conversely somehow related to each other, they share a part of the same data type, so they should not be used separately.

The choice of using normals and HSV is based on different reasons. On one side the RGB component, based on the sensors used in data acquisition, is most of the time present as a property of the point cloud and therefore it has been decided to fully exploit this kind of data; on the other the RGB components define the radiometric properties of the point cloud, while the normals define some geometric properties. In this way we are using as input for the NN different kinds of information. Moreover, the decision to convert the RGB into HSV is borrowed from other research works [72] that, even if developed for different tasks, show the effectiveness of this operation.

We have therefore tried to support the NN, in order to increase the accuracy, with few common features that could be easily obtained by any user.

These features are then concatenated with the local features of each EdgeConv. We have modified the first EdgeConv layer so that the kNN could also use color and normal features to be able to select k neighbors for each point. Finally, through 3 convolutional layers and a dropout layer, we will output the same block of points but with segmentation scores (one for each class to be recognized). The output of the segmentation will be given by the class with the largest score.

4. Results

In this section, the results of the experiments conducted on “ArCH Dataset” are reported. In addition to the performance of our modified DGCNN, we also present the performance of PointNet [21], PointNet++ [22], PCNN [71] and DGCNN [32] which form the basis of the improvement of our network.

Our experiments are separated in two phases. In the first one, we attempt at tuning the networks, choosing the best parameters for the task of semantically segmenting our ArCH dataset. To this end we have considered a single scene and used an annotated portion of it for training the network, evaluating the performances on the remaining portion of the scene. We have chosen to perform such first experiments on the TR_church (Trompone) as it presents a relatively high symmetry, allowing us to subdivide it in parts with similar characteristics, and it includes almost all the considered classes (9 out of the 10). Such an experimental setting addresses the problem of automatically annotating a scene that has been only partially annotated manually. While this has in fact practical applications, and could speed up the process of annotating an entire scene, our goal is to evaluate the automatic annotation of an scene that was never seen before. We address this more challenging problem, in the second experimental phase, where we train the networks with 10 different scenes and then attempt at automatically segmenting the remaining one. Segmentation of the entire Point Cloud into sub-parts (blocks) is a needed pre-processing step for all the analysed neural architectures. For each block a fixed number of points have to be sampled. This is due to the fact that neural networks need a constant number of points as input and that it would be computationally unfeasible to provide all the points at once to the networks.

4.1. Segmentation of Partially Annotated Scene

Two different settings have been evaluated in this phase: a k-fold cross-validation and a single splitting of the labeled dataset into a training set and a test set. In the first case the overall number of test samples is small and the network is trained on more samples. In the second case, an equal number of samples is used to train and to evaluate the network, possibly leading to very different results. This, for completeness, we experimented with both settings.

In the first setting, the TR_church scene was divided into 6 parts and we have performed a cross-validation with 6 Fold, as shown in Figure 4. We have tested different combinations of hyperparameters of the various networks to be able to verify which was the best, as we can see in

Table 2. 6-Fold Cross-Validation on the Trompone scene. We can see different combinations of hyperparameters for the various state-of-the-art networks.

Network	Features	Mean Acc.
DGCNN	XYZ + RGB	0.897
PointNet++	XYZ	0.543
PointNet	XYZ	0.459
PCNN	XYZ	0.742
DGCNN-Mod	XYZ + Norm	0.781
Ours	XYZ + HSV + Norm	0.918

, where the mean accuracy is derived from calculating the accuracy of each test (fold), then averaging them.

Regarding the pointcloud preprocessing steps, which consists in segmenting the whole scene into blocks and, for each block, sampling a number of points, we used, for each evaluated model, the settings used in the corresponding original paper. PointNet and PointNet++ use blocks are of size $2\times 2$ meters and 4096 points for cloud sampling. In the case of the DGCNN, we have used blocks of size $1\times 1$ and 4096 points per block. Finally, the PCNN network was tested using the same sampling as the DGCNN ($1\times 1$), but using 2048 points, as this is the default setting used in the PCNN paper. We also tested PCNN providing 4096 points per block, but results were slightly worse. We also notice that the performances improve slightly using the color features represented as HSV color-map. The HSV (hue, saturation, value) representation is known for more closely aligning with the human perception of colors and, by representing colors as three independent variables, allows, for example, to take into account variations, e.g., due to shadows and different light conditions.

In the second setting, we have split the TR-cloister scene in half, choosing the left side for the training and the right side for the test. Furthermore, we split the left side into a training set (80%) and a validation set (20%). We used the validation set to test overall accuracy at the end of each training epoch and we performed evaluation on the test set (right side). In

Table 3. The scene was divided into 3 parts: Train, Validation, Test. In this table, we can see the average of the metrics calculated on the different parts: accuracy for Train, Validation and Test; precision, recall, F1-score and support for the Test.

Network	Train Acc.	Valid Acc.	Test Acc.	Prec.	Rec.	F1-Score	Supp.
DGCNN	0.993	0.799	0.733	0.721	0.733	0.707	1,437,696
PointNet++	0.887	0.387	0.441	0.480	0.487	0.448	1,384,448
PointNet	0.890	0.320	0.307	0.405	0.306	0.287	1,335,622
PCNN	0.961	0.687	0.623	0.642	0.608	0.636	1,254,631
Ours	0.992	0.745	0.743	0.748	0.742	0.722	1,437,696

, the performance of state-of-the-art networks are reported. We report results obtained with the hyperparameters combinations that best performed in the cross-validation experiment.

Table 4. The scene was divided into 3 parts: Train, Validation, Test. In this table we can see the metrics for every class, calculated on the Test set.

Network	Metrics	Arc	Col	Dec	Floor	Door	Wall	Wind	Stair	Vault
DGCNN	Precision	0.484	0.258	0.635	0.983	0.000	0.531	0.222	0.988	0.819
	Recall	0.389	0.564	0.920	0.943	0.000	0.262	0.013	0.211	0.918
	F1-Score	0.431	0.354	0.751	0.963	0.000	0.351	0.024	0.348	0.865
	Support	69,611	36,802	240,806	287,064	8562	285,128	20,619	14,703	474,401
	IoU	0.275	0.215	0.602	0.929	0.000	0.213	0.012	0.210	0.764
PointNet++	Precision	0.000	0.000	0.301	0.717	0.000	0.531	0.000	0.000	0.654
	Recall	0.000	0.000	0.792	0.430	0.000	0.284	0.000	0.000	0.765
	F1-Score	0.000	0.000	0.437	0.538	0.000	0.370	0.000	0.000	0.705
	Support	74,427	59,611	235,615	230,033	12,327	334,080	40,475	13,743	384,137
	IoU	0.000	0.000	0.311	0.409	0.000	0.215	0.000	0.000	0.681
PointNet	Precision	0.000	0.000	0.155	0.588	0.000	0.424	0.175	0.000	0.600
	Recall	0.000	0.000	0.916	0.422	0.000	0.078	0.004	0.000	0.387
	F1-Score	0.000	0.000	0.265	0.492	0.000	0.132	0.008	0.000	0.470
	Support	30,646	11,020	29,962	43,947	1851	69,174	3212	1057	87,659
	IoU	0.000	0.000	0.213	0.406	0.000	0.051	0.003	0.000	0.311
PCNN	Precision	0.426	0.214	0.546	0.816	0.000	0.478	0.193	0.178	0.704
	Recall	0.338	0.474	0.782	0.754	0.000	0.231	0.012	0.188	0.744
	F1-Score	0.349	0.294	0.608	0.809	0.000	0.281	0.021	0.306	0.779
	Support	65,231	32,138	220,776	212,554	8276	253,122	18,688	12,670	431,176
	IoU	0.298	0.273	0.592	0.722	0.000	0.210	0.010	0.172	0.703
Ours	Precision	0.574	0.317	0.621	0.991	0.952	0.571	0.722	0.872	0.825
	Recall	0.424	0.606	0.932	0.920	0.002	0.324	0.006	0.284	0.907
	F1-Score	0.488	0.417	0.746	0.954	0.005	0.413	0.011	0.428	0.865
	Support	69,460	36,766	240,331	286,456	8420	285,485	20,542	14,790	475,446
	IoU	0.322	0.263	0.594	0.913	0.002	0.260	0.005	0.272	0.761

shows the metrics in the test phase for each class of the Trompone’s right side. In this table we report, for each class, precision, recall, F-1 score and Intersection over Union (IoU). This table allows us to understand which are the classes that are best discriminated by the various approaches, to understand which are their weak points and their strengths (as broadly discussed in Section 5).

Finally, Figure 5 depicts the manually annotated test scene (ground truth) and the automatic segmentation results obtained with our approach.

4.2. Segmentation of an Unseen Scene

In the second experimental phase, we used all the scenes of ArCH Dataset: 9 scenes were used for the Training, 1 scene as Validation (Ghiffa scene), 1 scene for the Final Test (SMV). State-of-the-art networks were evaluated, comparing the results with our DGCNN-based approach. In

Table 5. Results of the tests performed on an unknown scene, training the network on the others.

Network	Valid Acc.	Test Acc.	Prec.	Rec.	F1-Score	Supp.
DGCNN	0.756	0.740	0.768	0.740	0.738	2,613,248
PointNet++	0.669	0.528	0.532	0.528	0.479	2,433,024
PointNet	0.453	0.351	0.536	0.351	0.269	2,318,440
PCNN	0.635	0.629	0.653	0.622	0.635	2,482,581
Ours	0.831	0.825	0.809	0.825	0.814	2,613,248

, the overall performances are reported for each tested model, while in

Table 6. Tests performed on all scenes of the dataset in terms of Precision, Recall, F1-Score and Support of each class for the Test scene.

Network	Metrics	Arc	Col	Dec	Floor	Door	Wall	Wind	Stair	Vault	Roof
DGCNN	Precision	0.135	0.206	0.179	0.496	0.000	0.745	0.046	0.727	0.667	0.954
	Recall	0.098	0.086	0.407	0.900	0.000	0.760	0.007	0.205	0.703	0.880
	F1-Score	0.114	0.121	0.249	0.640	0.000	0.752	0.012	0.319	0.684	0.916
	Support	54,746	37,460	71,184	182,912	2642	642,188	18,280	172,270	288,389	1,143,177
	IoU	0.060	0.064	0.142	0.470	0.000	0.603	0.006	0.190	0.520	0.845
PointNet++	Precision	0.000	0.000	0.124	0.635	0.000	0.387	0.000	0.000	0.110	0.738
	Recall	0.000	0.000	0.002	0.012	0.000	0.842	0.000	0.000	0.091	0.639
	F1-Score	0.000	0.000	0.004	0.023	0.000	0.530	0.000	0.000	0.099	0.685
	Support	52,866	49,826	88,578	161,741	3032	756,905	26,682	165,169	245,929	882,296
	IoU	0.000	0.000	0.002	0.009	0.000	0.514	0.000	0.000	0.074	0.608
PointNet	Precision	0.000	0.000	0.240	0.763	0.000	0.299	0.000	0.000	0.298	0.738
	Recall	0.000	0.000	0.001	0.354	0.000	0.984	0.000	0.000	0.566	0.106
	F1-Score	0.000	0.000	0.001	0.484	0.000	0.458	0.000	0.000	0.391	0.186
	Support	51,280	46,836	85,920	155,271	2880	726,628	25,614	158,562	236,091	829,358
	IoU	0.000	0.000	0.001	0.294	0.000	0.411	0.000	0.000	0.337	0.094
PCNN	Precision	0.119	0.181	0.143	0.441	0.000	0.633	0.041	0.582	0.580	0.801
	Recall	0.086	0.070	0.330	0.783	0.000	0.608	0.006	0.164	0.605	0.783
	F1-Score	0.103	0.108	0.217	0.544	0.000	0.654	0.010	0.268	0.616	0.824
	Support	52,008	35,587	67,624	173,766	2509	610,078	17,366	163,656	273,969	1,086,018
	IoU	0.072	0.062	0.198	0.482	0.000	0.581	0.004	0.082	0.468	0.658
Ours	Precision	0.288	0.391	0.270	0.798	0.000	0.729	0.035	0.707	0.806	0.959
	Recall	0.107	0.157	0.173	0.806	0.000	0.868	0.010	0.692	0.810	0.940
	F1-Score	0.156	0.224	0.211	0.802	0.000	0.791	0.015	0.699	0.808	0.950
	Support	54,746	37,460	71,184	182,912	2642	642,188	18,280	172,270	288,389	1,143,177
	IoU	0.085	0.126	0.118	0.669	0.000	0.655	0.008	0.538	0.678	0.905

reports detailed results on the individual classes of the test scene. Figure 6 and Figure 7 depict the confusion matrix and the segmentation results of the last experiment: 9 scenes for Training, 1 scene for validation and 1 scene for test.

The performance gain provided by our approach is more evident than in previous experiments, leading to an improvement of around 0.8 in overall accuracy as well as in F1-score. The IoU also increases. In Table 6, one can see that our approach outperforms the others in the segmentation of almost all classes. For some classes values of Precision and Recall are lower than the original DGCNN. However, our modified DGCNN generally improves performance in terms of F1-score. This metric is a combination of Precision and Recall, thus it allows to better understand how the network is learning.

5. Discussion

This research rises remarkable research directions (and challenges) that is worth to deepen. First of all, looking at the first experimental setting, performances are worse than those obtained in the K-fold experiment (referring to Table 3). This is probably do to the fact that the network has less points to learn on. As in the previous experiment, the results on the test set is obtained with our approach, confirming that HSV and Normals does in fact help the network to learn higher level features of the different classes. Besides, as reported in Table 4 and confirmed in Figure 5, we can notice that using our setting helps in detecting vaults, increasing precision, recall and IoU, as well as columns and stairs, by sensibly increasing recall and IoU.

Dealing with the second experimental setting (see Section 4.2), it is worth to notice that all evaluated approaches fail in recognizing classes with low support, as doors, windows and arcs. Beside, for these classes we observe a high variability in shapes across the dataset, this probably contributes to the bad accuracy obtained by the networks.

More insights can be drawn from the confusion matrix, shown in Figure 6. It reveals, for example, that arcs are often confused with vaults, as they clearly share geometrical features, while columns are often confused with walls. The latter behaviour can be possibly due to the presence of half-pilasters, which are labeled as columns but have a shape similar to walls. The unbalanced nature of the number of points per class is clearly highlighted in Figure 8.

Furthermore, if we consider the classes individually, we can see that the lowest values are in Arc, Dec, Door and Window. More in detail:

• Arc: the geometry of the elements of this class is very similar to that of the vaults and, although the dimensions of the arcs are not similar to the latter, most of the time they are really close to the vaults, almost a continuation of these elements. For these reasons the result is partly justifiable and could lead to the merging of these two classes.
• Dec: in this class, which can also be defined as “Others” or “Unassigned”, all the elements that are not part of the other classes (such as benches, paintings, confessionals…) are included. Therefore it is not fully considered among the results.
• Door: the null result is almost certainly due to the very low number of points present in this class (Figure 8). This is due to the fact that, in the proposed case studies of CH, it is more common to find large arches that mark the passage from one space to another and the doors are barely present. In addition, many times, the doors were open or with occlusions, generating a partial view and acquisition of these elements.
• Window: in this case the result is not due to the low number of windows present in the case study, but to the high heterogeneity between them. In fact, although the number of points in this class is greater, the shapes of the openings are very different from each other (three-foiled, circular, elliptical, square and rectangular) (Figure 9). Moreover, being mostly composed of glazed surfaces, these surfaces are not detected by the sensors involved such as the TLS, therefore, unlike the use of images, in this case the number of points useful to describe these elements is reduced.

6. Conclusions

The semantic segmentation of Point Clouds is a relevant task in DCH as it allows to automatically recognise different types of historical architectural elements, thus possibly saving time and speeding up the process of analysing Point Clouds acquired on-site and building parametric 3D representations. In the context of historical buildings, Point Cloud semantic segmentation is made particularly challenging by the complexity and high variability of the objects to be detected. In this paper, we provide a first assessment of state-of-the-art DL based Point Cloud segmentation techniques in the Historical Building context. Beside comparing the performances of existing approaches on ArCH (Architectural Cultural Heritage), created on purpose and released to the research community, we propose an improvement which increase the segmentation accuracy, demonstrating the effectiveness and suitability of our approach. Our DL framweork is based on a modified version of DGCNN and it has been applied to a newly puclic collected dataset: ArCH (Architectural Cultural Heritage). Results prove that the proposed methodology is suitable for Point Cloud semantic segmentation with relevant applications. The proposed research starts from the idea of collecting relevant DCH dataset which is shared together with the framework source codes to ensure comparisons with the proposed method and future improvements and collaborations over this challenging problems. The paper describes one of the more extensive test based on DCH data, and it has huge potential in the field of HBIM, in order to make the scan-to-BIM process affordable.

However, the developed framework highlighted some shortcomings and open challenges that is fair to mention. First of all, the framework is not able to assess the accuracy performances with respect to the acquisition techniques. In other words, we seek to uncover, in future experiments, if the adoption of Point Clouds acquired with other methods changes the DL framework performances. Moreover, as stated in the results section, the dimensions of points per classes is unbalanced and not homogeneous, with the consequent biases in the confusion matrix. This bottleneck could be solved by labelling a more detailed dataset or creating synthetic Point Clouds. The research group is focusing his efforts even in this direction [73]. In future works, we plan to improve and better integrate the framework with more effective architectures, in order to improve performances and test also different kind of input features [19,74].