Next Article in Journal
Modeling and Prediction of Regular Ionospheric Variations and Deterministic Anomalies
Previous Article in Journal
A Mapping Review on Urban Landscape Factors of Dengue Retrieved from Earth Observation Data, GIS Techniques, and Survey Questionnaires
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 6
10.3390/rs12060934
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Impact of Pan-Sharpening and Spectral Resolution on Vineyard Segmentation through Machine Learning

by
Eriita G. Jones
1,2,3,*,
Sebastien Wong
2,
Anthony Milton
2,
Joseph Sclauzero
2,
Holly Whittenbury
2,3 and
Mark D. McDonnell
1,2,*
1
Computational Learning Systems Laboratory, School of Information Technology and Mathematical Sciences, University of South Australia, Adealide, SA 5095, Australia
2
Consilium Technology, Adelaide, SA 5000, Australia
3
School of Natural and Built Environments, University of South Australia, Adelaide, SA 5095, Australia
*
Authors to whom correspondence should be addressed.
Remote Sens. 2020, 12(6), 934; https://doi.org/10.3390/rs12060934
Submission received: 2 March 2020 / Accepted: 4 March 2020 / Published: 13 March 2020
(This article belongs to the Section Remote Sensing Image Processing)
Browse Figures
Versions Notes

Abstract

:
Precision viticulture benefits from the accurate detection of vineyard vegetation from remote sensing, without a priori knowledge of vine locations. Vineyard detection enables efficient, and potentially automated, derivation of spatial measures such as length and area of crop, and hence required volumes of water, fertilizer, and other resources. Machine learning techniques have provided significant advancements in recent years in the areas of image segmentation, classification, and object detection, with neural networks shown to perform well in the detection of vineyards and other crops. However, what has not been extensively quantitatively examined is the extent to which the initial choice of input imagery impacts detection/segmentation accuracy. Here, we use a standard deep convolutional neural network (CNN) to detect and segment vineyards across Australia using DigitalGlobe Worldview-2 images at ∼50 cm (panchromatic) and ∼2 m (multispectral) spatial resolution. A quantitative assessment of the variation in model performance with input parameters during model training is presented from a remote sensing perspective, with combinations of panchromatic, multispectral, pan-sharpened multispectral, and the spectral Normalised Difference Vegetation Index (NDVI) considered. The impact of image acquisition parameters—namely, the off-nadir angle and solar elevation angle—on the quality of pan-sharpening is also assessed. The results are synthesised into a ‘recipe’ for optimising the accuracy of vineyard segmentation, which can provide a guide to others aiming to implement or improve automated crop detection and classification.

1. Introduction

Viticultural practices worldwide have been transformed over the last two decades by the application of precision viticulture (PV). PV is the implementation of high precision spatial information for adoption of site-specific vineyard management plans, optimisation of vineyard production potential, and reduction of environmental impact [1]. Spatial information is essential for determining planting locations and automating crop harvesting. When companion spectral information is also available, products such as vine health, vigor, forecasted estimates of wine grade/quality and yield, and continual health and infection monitoring can also be derived. PV enables growers to be responsive to the spatial variability of the crop environment and vine performance within a vineyard block [2]. Remote sensing provides a valuable tool for precision viticulture and is a key complement to, and in some cases improvement of, ground based observations [3]. However, before the full capabilities of remotely sensed data and PV can be realised, accurate identification and classification of vineyard boundaries (planting blocks) are frequently required. Depending on the nature of the data users (e.g., government statutory bodies, growers associations, individual vineyard managers), vineyard block identification may be required across a large spatial area. This problem can be successfully addressed using remotely sensed imagery and advanced modern computational techniques, such as artificial neural networks and other methods (e.g., [4,5,6,7,8]).
One challenge in the detection of vineyards, and the discrimination of vine vegetation from other row crops, is the ratio of vineyard vegetation to inter-vinerow materials. At spatial scales coarser than 1 m, most vineyard pixels will contain mixtures of materials [9] (e.g., vine, shadow, soil, subcanopy) and, at the vineyard block scale, the spectral signature will be dominated by the interrow materials. In Australia, the ratio of interrow width (typically ∼3 m) to vinerow width (at maximum canopy extent vegetation width is typically ∼1 m) is generally at least 3:1. The use of high spatial resolution data are therefore crucial for accurate detection of grapevine vegetation, differentiation of row from interrow, and discrimination of vine vegetation from orchards and other similarly planted crops. The question remains, however, what spatial resolution is necessary, or sufficient, for accurate automated grapevine detection? At sub-metre pixel sizes, the presence of interrow materials [10], young vine plants with less extensive or sparse canopy, or other factors (e.g., crop disease) reducing the vine vegetation reflectance in the VNIR (visible and near-infrared wavelengths), present a challenge to accurate vineyard identification [4]. In the face of these challenges, vineyard detection may be further enhanced by the incorporation of multispectral data allowing for a more detail characterisation of the unique signature of grapevine vegetation, and spectral indices which enhance the differences between vineyard vegetation and other materials. For example, Karakizi et al. [4] identified a number of parameters for optimising vineyard detection, including the mean and standard deviations of reflectance in single wavelength bands, or simple ratio indices of reflectance values, at visible and near-infrared wavelengths (VNIR). Although the inclusion of multispectral VNIR data would be expected to improve vine block delineation, for some applications, the use of only a single unsharpened red wavelength band has been shown to be sufficient. This is due to the high contrast between vegetation (low reflectance) and interrow soil (high reflectance) at these wavelengths [11,12], even when interrow vegetation, such as grasses, are present. Furthermore, satellite based multispectral data may not achieve sub-1 m resolution needed to visually delineate vinerows without applying pan-sharpening methods.
Many modern sensors acquire data in both a higher resolution panchromatic band spanning the VNIR, and spatially coarser multispectral bands (e.g., Worldview-2 & 3, SPOT 5-7, Landsat 7 and 8). This allows for pansharpening techniques to increase the spatial resolution of the multispectral bands in the VNIR. Pansharpening refers to a broad suite of image fusion methods that blend the high resolution spatial information stored in a panchromatic band, with spatially coarser multispectral image—thereby resulting in high spatial and spectral resolution (at some information cost) [13]. This process, however, typically comes at the expense of introducing spectral or spatial (e.g., ringing or aliasing effects) distortions to the multispectral information [14,15,16,17]. Analogous to this work, a number of other viticultural remote sensing studies have undertaken vine block detection using high resolution sub-metre pansharpened satellite imagery ([4] using high pass filter (HPF) sharpening, and [18] with pan-sharpening method unknown). Other studies utilized higher resolution UAV or aerial imagery that does not require pansharpening for vinerow detection [6,12,19,20,21,22,23] (other works using significantly coarser spatial resolutions will not be discussed in detail here, e.g., [8]). Detection completeness from these studies ranged from 72–90% of real vine blocks detected, with the main type of classification error being real vineyards that were missed/unclassified. The likely sources of this error were: low visibility of vinerows, due to very young vines with small canopy coverage; low visibility of interrows, due to rows being poorly maintained, small plots with fewer rows, or smaller interrow spacing; and low contrast between interrows and vinerow vegetation, due to the growth stage of vegetation, soil colour, surface conditions (e.g., soil wetness), and image acquisition conditions (e.g., solar angle and shadowing) [24,25]. Darker (due to mineralogy) or wetter soils will have lower red reflectance, and hence will be more similar to photosynthetic vegetation (p.s.v.) at red wavelengths. Similarly, shadowing of interrow materials will reduce their red reflectance [19], and this effect will be more significant at certain sun and vinerow angles [26]. The incorporation of multiple wavelength information can compensate for many of these similarities encountered when using a single visible wavelength band. For example, the incorporation of NIR (760–900 nm) information [27], or ratio indices such as the Normalised Difference Vegetation Index (NDVI) and Ratio Vegetation Index (RVI) [28], can discriminate shadowed vines from dark soil and other surfaces that are dark at visible wavelengths. Soil line vegetation indices, such as the perpendicular vegetation index (PVI) amongst others, can also be utilised to derive vegetation properties. Their utility, however, is contingent on the accuracy of the derived soil-line gradient, and they may be less strongly correlated with grapevine biophysical variables (e.g., leaf-area index) than ratio indices [29]. The inclusion of ratio indices and multiple NIR wavelength channels, can assist in the differentiation of vineyards from other agricultural crops planted in similar patterns, such as orchards and olive gardens [5]. Misclassification of non-vineyard areas can occur for crops with a similar planting pattern (e.g., comparable interrow spacing), or true vineyards with a different planting pattern that is less common in the region (e.g., gridwise or distributed [5]) may be missed. Classification accuracy is improved by image acquisition in summer so that both vine and soil are visible [30]. This discussion highlights that there are many factors which impact the resulting accuracy of vineyard block detection in satellite imagery. These factors translate into non-trivial decisions in the initial selection of that imagery, including: which wavelengths and/or spectral indices should be incorporated, whether sharpening should be employed, in which season should imagery be acquired, in order to optimise detection success. Despite the aforementioned studies mentioning the utility of multispectral information in vineyard detection, a systematic evaluation of the separate and combined impacts of pan-sharpening of multiple wavelength bands, the inclusion of spectral indices, and the role of viewing and solar angles has not been undertaken.
This paper quantitatively investigates how the initial choices in remote sensing imagery for vine block detection impact on the resulting detection accuracy of a deep convolutional neural network (see Section 2.2 for more detail), in order to identify what combination of imagery parameters optimises the resulting vine block segmentation. In particular, the following issues are evaluated using Worldview-2 imagery: (i) whether the incorporation of multispectral information enhances vineyard detection capabilities; (ii) the sensitivity of Gram–Schmidt (GS) pan-sharpening to image acquisition parameters; and (ii) whether the inclusion of GS pan-sharpened VNIR multispectral data and derived vegetation indices, rather than the off-sensor resolution of the VNIR bands, improves detection accuracy.

2. Methodology

This work targeted vineyards in wine regions across multiple states in Australia. The locations of wine regions were identified from Wine Australia’s Geographical Indicators (GIs) [31], which provide the geographic boundaries of official wine zones, regions, or subregions. Nine images were utilised in the analysis, originating from Tasmania [32], and the GIs Wrattonbully (South Australia), Riverland (South Australia), Barossa (South Australia), Riverina (New South Wales), Geographe (Western Australia), South Burnett (Queensland) and Goulburn Valley (Victoria) [31].

2.1. Satellite Imagery

Multispectral visible to near-infrared (VNIR) imagery from DigitalGlobe’s Worldview-2 satellite was utilised in this work. Details of the platform and the resolutions of the imagery are provided in Table 1, and image metadata in Appendix Table A1. The dates of image acquisition were chosen from within the period of maximum correlation between image data and grape properties, which has been shown to be during veraison [33], i.e., the onset of ripening and changing berry colour [34]. The timing of veraison varies with both broad climate zone and local climate factors such as temperatures, rainfall and soil moisture [35], but in the southern hemisphere typically falls within late summer. The accuracy of vineyard vegetation classification via satellite imagery is highest in summer when the vines are experiencing a growth period and the vegetation canopy reaches its greatest extent [30,33,36]. Ideally, imagery is obtained when the visibility of the vinerows is high, the interrows are clear, and the soil is dry; these factors increase the vinerow and interrow contrast. Additional potential selection criteria for imagery include cloud coverage, observation angle (off-nadir angle compared to a vertical downwards view), sun elevation angle (compared to directly overhead) and sun azimuthal angle (compared to compass directions). Given limitations in the availability of recent imagery within the pre-defined timeframe and GIs of interest, the secondary criteria considered were a restriction of cloud coverage (to <10% of the scene) and minimisation of the off-nadir angle.
Raw data were processed, orthorectified, radiometrically calibrated and atmospherically corrected through DigitalGlobe’s GBDX platform, utilising the Advanced Image Preprocessor algorithms [37]. Orthorectification involved correcting the imagery for geometric distortions due to the curvature of the Earth, surface relief (terrain) and the sensor geometry (such as orientation/tilt of the image, and movement of the sensor relative to the terrain). The orthorectified imagery provided had been was registered to the SRTM + USGS NED digital elevation model (DEM) with accuracy derived through comparison to ground control points. The horizontal accuracy for WorldView-2 orthorectified products is 3.5 m CE90 (i.e., 90 percent of all products will achieve this accuracy) [38]. The 4.2 m CE90 map-scale ortho products achieve a point RMSE of 2.0 m or better, hence we estimate the RMSE of the product to used here to be similar. The vertical accuracy of orthorectified images is 3.6 m CE90. Additional post-processing was undertaken by the imagery provider, including adaptive smoothing to reduce noise. Radiometric calibration and atmospheric corrections converted the pixel values from digital numbers into true reflectance values (percent of solar flux reflected by surface), and corrected for atmospheric and solar illumination effects. Although data processing into true reflectance values is not required for accurate vineyard detection from single band data (e.g., calibrated digital numbers [12]), it is important when using multispectral data or comparing multiple images from different sensors and viewing conditions.
Where used in our experiments, pan-sharpening was undertaken to fuse the high spatial resolution information of the panchromatic band with the lower spatial resolution multispectral bands, obtaining both high spatial and high spectral sensitivity. A number of broad families of pan-sharping methodologies exist, differing in the way in which spatial details are generated and blended [13]: component substitution (CS) methods, which includes techniques such as intensity–hue–saturation (IHS) [39], Gram–Schmidt (GS) [40] and adaptive Gram–Schmidt (GSA) [14], and principal component analysis (PCA) [41]; multi-resolution analysis (MRA) methods, which includes wavelet-based methods [42], high-pass filtering (HPF) [43], generalized Laplacian pyramids (GLP) [44]; and hybrid techniques, such as generalized band-dependent spatial detail (BDSD) [45]). In this work, spectral pansharpening was undertaken through the ENVI software package using the Gram–Schmidt routine [40,46] with Worldview-2 parameters. Gram–Schmidt was chosen as it is able to sharpen more than three spectral bands, performs well in preserving the quality of the multispectral information (minimsing spectral distortions) compared to other methods [47], is less computationally complex than some other methods (e.g., Intensity-Hue Saturation) and is still widely utilized for satellite imagery (e.g., [48]). Gram–Schmidt is also appropriate as it is from the CS family of methods, which have been shown to have higher tolerance to aliasing, shift, and other visual artefacts, due to, for example, spatial misalignment between the multispectral and panchromatic bands [49]. This was considered particularly important due to the narrow width of the vinerows requiring detection—similar in width to the pan-sharpened pixel size. Although recent work in comparing fusion algorithms for landcover segmentation (the particular application of relevance in this work) demonstrated that the GS fusion method had strong performance, other members of the CS family such as PCS and GSA surpassed it [14,47]. Therefore, although GS is appropriate in the context of this work (vine row segmentation), future work will focus on implementing a range of CS and other pansharpening family methods to assess whether any significant gains in machine learning segmentation are achieved.
The Gram–Schmidt (GS) algorithm is based on Gram–Schmidt vector orthogonalization. A simulated panchromatic band is constructed and all bands (including multispectral) are decorrelated, then back-transformed in high resolution [40]. Best pansharpening results—determined from minimal visible distortion of RGB ‘natural look’ imagery and minimal creation of null or negative pixels—were obtained using cubic convolution resampling. Spectral distortions, however, likely differ for each wavelength band [47], and spectral indices derived from band ratios may have a multiplicative effect on spectral distortions (thereby reducing their quality) [50,51,52], so these distortions were assessed prior to vine block segmentation.

2.2. Machine Learning

A computer vision technique known as semantic segmentation was used to detect and delineate the boundaries of vineyard blocks [53]. The objective in this method is to segment image regions by classifying every pixel in the image as belonging to exactly one of a number of designated categories. In this paper, we consider only binary classification, namely that each pixel should be classified as belonging to a vineyard (e.g., pixels could contain grapevine vegetation or inter-vinerow materials), or not belonging to a vineyard.
In the last five years, deep convolutional neural networks trained by supervised learning have been empirically shown to nearly always outperform alternative machine learning methods in computer vision problems (e.g., [54]), and semantic segmentation is no exception [55]. Hence, we also used deep convolutional neural networks (specifically a U-net semantic segmenter—see Section 2.2.2). Human-labelled ‘ground truth’ labels that segment each training image are required for such supervised learning—see Section 2.3. Following training, the weights in the neural network are assumed to predict segmented regions in these training annotations with very high accuracy, and ideally to also generalise to correctly segment unlabelled data not used in training.

2.2.1. Data Models

As shown in Table 2, five different input data models were investigated (labelled as M1, M2, M3, M4, and M5), with the aim of determining if multispectral information was important for identifying vineyard pixels, and whether derived information, such as pan-sharpened spectral bands, or a vegetation index (NDVI), might enable better performance than raw PAN and MS channels. A vegetation index is included to test the whether the spectral properties of grapevines can be sufficiently summarised (in order to differentiate them from other row crops) by the information captured in only two additional bands (in this case, red and near-infrared wavelengths). Although many other vegetation indices are available, NDVI is widely applied in viticulture (e.g., [56]).
Note also that we undertook preliminary investigations into models that included all eight multispectral bands pan sharpened to higher resolution. These were difficult to pursue, due to the need for extra computational resources (i.e., RAM because pan-sharpened bands require 16 times more RAM per image per channel than the corresponding MS band) that was not readily available to us. For this reason, and because we found the performance of such models to be worse than that of M3 baselines, we did not pursue further as primary Data Models in this paper.

2.2.2. Neural Network Architecture

Several alternative designs for deep convolutional neural network semantic segmenters were investigated: SegNet [57], U-net [58] and DeepLab-v3 [59]. Both U-net and DeepLab-v3 provided better results than SegNet, but U-net was selected due to being being relatively small in its model size (as measured by the number of learned parameters), while there was no significant difference in performance. We hypothesise that while DeepLab-v3 is known to be better than U-net for multi-class semantic segmentation [59] that this is due to the greater diversity of imagery it tends to be applied to in such cases, such as that obtained from self-driving cars. In contrast here, and more broadly in crop detection in satellite imagery, we have a relatively simple segmentation task (binary in this case), with relatively little viewpoint and object-scale diversity, which may explain why we found no benefits from DeepLab-v3.

2.2.3. Neural Network Training

We found it useful to use transfer learning [60]. It has recently been shown that the “fine-tuning” method of transfer learning, where all weights in a network previously trained on one dataset are updated during training on a new dataset, tends to provide better results than the more well-known approach where a pre-trained neural network is used only to convert input data into a feature set for training a new model [60]. The fine-tuning method can therefore be thought of as an alternative to randomly initialisating the weights in a deep network. Empirically, fine-tuning tends to work best by training for a relatively small number of epochs and a very low learning rate [60].
For the purposes of this paper, we made use of a U-net model (which we label as M0) that was originally trained on many more images than used in this paper (nine of these are listed in Table A1). We used the weights of model M0 for transfer-learning using fine-tuning, and hence the architecture of our models in this paper were all identical, and identical to that of M0, except for the very first layer of weights, which differed in the number of input channels, due to differing numbers of channels in the data models investigated. We therefore used random random weights for the first weights layer only.
We created a dataset for training by tiling each image (and corresponding label masks) into patches of size 256 × 256 from Images 1, 2 and 3 (Table A1). The other six images were not accessible for training models for this paper. The total percentage of pixels in the vineyard class in the three training images was very small (0.1%, 0.2% and 5% in Images 1, 2 and 3 respectively). This means that there are many times more pixels in the ‘not vineyard’ class than within the ‘vineyard’ class, resulting in a classic example of the ‘class imbalance’ problem from machine learning [61]. To enable our models to learn effectively despite class imbalance, a form of compensation known as minority class oversampling [62] was used. The version we devised followed from the need to subdivide each image into small tiles, as is typical in semantic segmentation, in order to benefit from speeding up training on GPUs with 12 GB of RAM. Each such patch was assigned as an ‘oversample’ patch, if any pixel in it was labelled as within a vineyard. Access to labelling of ‘edge cases’ was available, that is, examples of images that resembled vineyards but were verified to be other areas such as strawberry fields, or ploughed paddocks. Patches in this category were also assigned as ‘oversampling patches’, since the total area of these cases was very low. During training using stochastic gradient descent [63], sequences of batches of patches were randomly selected such that all ‘oversample’ patches were selected exactly once during one epoch of training. For each epoch, an equal number of patches not in the ‘oversample’ list were randomly chosen, and then not used again until all such patches had been used once, which took about 10 epochs. The downside of oversampling in this way is that the neural network may well overfit to outliers in the oversample patches. This was the main reason we used transfer learning, which is known to be a good way to help avoid overfitting.
We used the standard fine-tuning approach of stochastic gradient descent with momentum and weight decay, with a very low learning rate (0.0001). We found 20 epochs of training to suffice for convergence on validation data. When we report validation results below, the patches used for training were excluded from use in calculation of performance measures.

2.3. Measuring Vineyard Detection Performance

The performance of the automated vineyard detection was measured through comparison to an independent manually labeled dataset of vine block boundaries. This ground-truth boundary shapefile was generated through reference to the Worldview-2 imagery (particularly, a pan-sharpened ‘natural colour’ image composite, pan-sharpened colour infrared composites, and pan-sharpened NDVI), as well as online mapping datasets Google Earth and Google Street View [64]. The Google Street View dataset typically pre-dated the satellite images, and, in some circumstances, was inaccurate due to land-use change. A number of quantitative metrics for measuring the validity of vineyard detections were considered, chosen for their widespread usage in either the geospatial and remote sensing, or machine learning and semantic segmentation fields. The metrics utilized all correspond to the case where one of the binary categories is designated as a “positive” class (in this case, ‘vineyard’): “precision” (also known as “map user’s accuracy”), “recall” (also known as “map producer’s accuracy”), “area ratio” and “Jaccard Index” (JI). For completeness, we also consider metrics that treat both classes (in this case, ‘vineyard’ and ‘not vineyard’) equally: “overall accuracy” with associated kappa statistic (which requires calculation of the expected accuracy of a random classifier).
Through comparison to the ground-truth data, the following categories of pixel classification can be defined: true positives (TP), i.e., vineyard pixels correctly classified; false positives (FP), non-vineyard pixels incorrectly classified as vineyards; true negatives (TN), non-vineyard pixels correctly classified; and false negatives (FN), vineyard pixels incorrectly classified as non-vineyard.
The aforementioned performance metrics which are referenced to a designated positive-class are:
  • Precision = TP/(FP + TP). This provides a measure of the total fraction of predictions that really are vineyard.
  • Recall = TP/(TP + FN). This provides a measure of the total fraction of actual vineyard correctly predicted as vineyard.
  • Jaccard Index = TP / (TP + FP + FN). In addition, expressed as “intersection over union” (IOU), this is a measure of the spatial overlap between pixels predicted to be in vineyards, and pixels labelled as being in vineyards.
  • Area ratio = (TP + FP)/(TP + FN). This is the ratio of the spatial area (in number of pixels) of predicted vineyards over real vineyards. It is also the ratio of recall over precision. However, even when a high agreement between predicted and actual vineyard area is achieved, the predicted vineyard block boundaries could potentially be non-overlapping with the real boundaries. Penalising such a case is ignored by area ratio but not by Jaccard Index.
Those performance metrics that consider each class equally are:
  • Overall Accuracy = (TP + TN)/(TP + TN + FP + FN). This is the fraction of all pixels that were correctly classified.
  • Expected Accuracy = ((TN + FP) × (TN + FN) + (FN + TP) × (FP + TP))/(TP + TN + FP + FN) 2 . The expected accuracy estimates the overall accuracy value that could be obtained from a random system. The denominator equals the square of the total number of observations.
  • Kappa statistic = (Overall Accuracy − Expected Accuracy)/( 1 − Expected Accuracy) [65,66]. This provides a measure of the level of agreement between classification and ground-truth that could originate through chance. A large and positive Kappa (near one) indicates that the overall accuracy is high and exceeds the accuracy that could be expected to arise from random chance. This can be interpreted as the classifier providing a statistically significant improvement in the classification of ‘vineyard’ and ‘not vineyard’ than could be obtained through random assignment of pixels to the binary classes.
A number of implicit relationships exist between the above metrics, such as area accuracy, is the ratio of precision to recall.
For vineyard identification, we consider the metrics referenced to a positive class as of more value than those that are not, since the total number of pixels in the vineyard class are far fewer than those in the non-vineyard class.

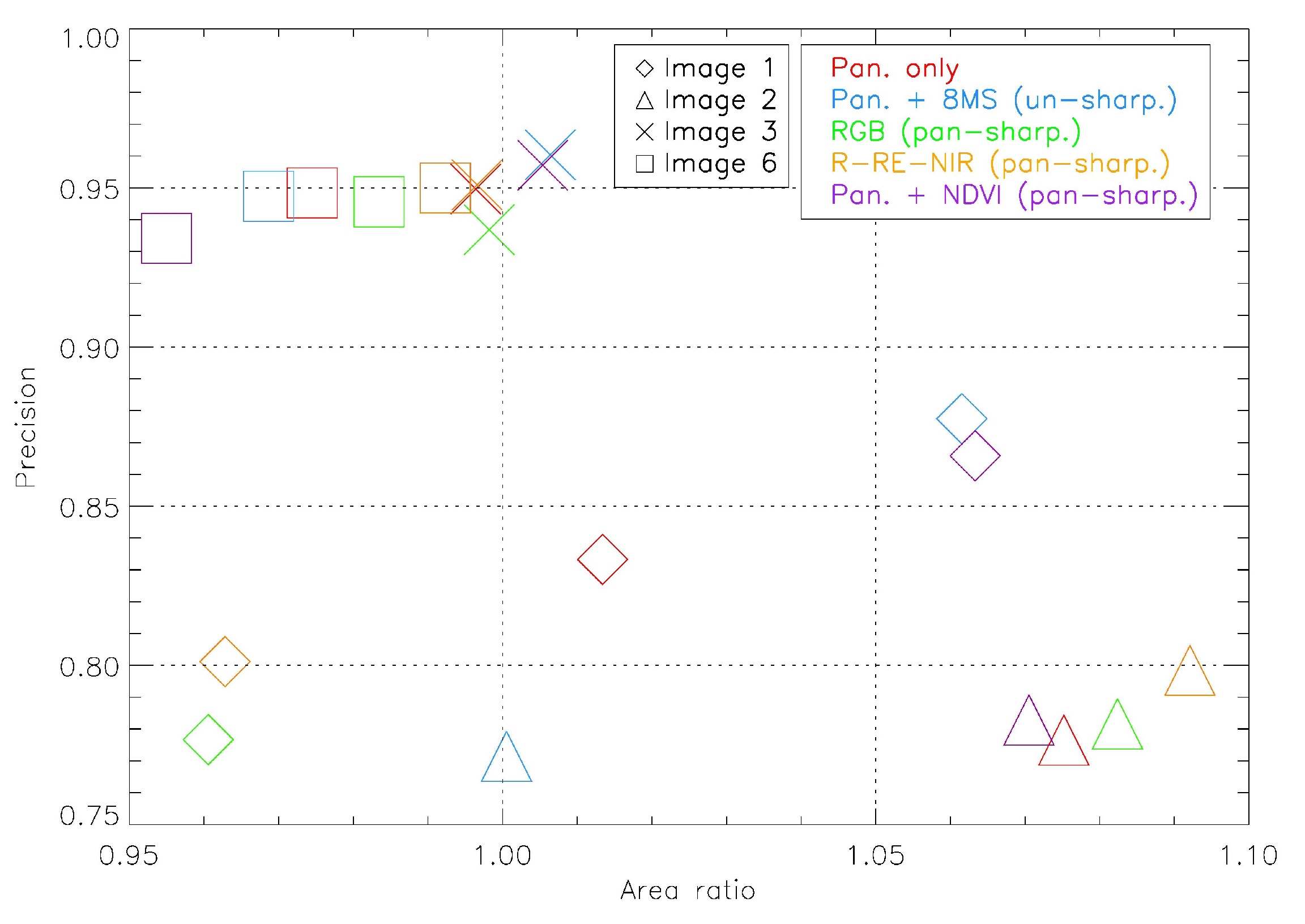
3. Results

3.1. Pan-Sharpening

The impact of pan-sharpening on the spectral values of grapevine vegetation (along vinerows) was examined, considering wavelength, the NDVI spectral index, and the viewing conditions under which the imagery was acquired (vinerow statistics are provided in Table A2) Although the Gram–Schmidt algorithm used for pan-sharpening (PS) is considered to obtain good spatial results whilst minimizing spectral distortions, the potential for some spectral distortion is known (see Section 2.1) and was observed here. Here, we compare the pansharpened pixel values with the original multispectral values, for vinerow vegetation (not on a whole image basis). Figure 1 illustrates that the magnitude of spectral distortion varied with wavelength but was typically within 50% of un-sharpened reflectance values. The Gram–Schmidt algorithm generally reduced mean reflectance values locally within the vinerows. Statistically, spectral differences between the two profiles were more significant at visible wavelengths (where the PS profile was more than 1 σ below the mean un-sharpened profile); however, this result is likely to be highly dependent on the characteristics (e.g., homogeneity) of the vineyard vegetation selected. Spectral shape was generally preserved, and the difference in spectral slopes was less significant than the differences in mean pixel values. Spectral distortions were expected to be largest in the two wavelength bands (coastal 400–450 nm and NIR2 860–1040 nm), which are non-overlapping with the panchromatic band (450–800 nm). In the spectral profiles shown in Figure 1 and Figure 2, the differences across the longer wavelengths >700 nm remained generally small, while the largest differences were observed at visible wavelengths, particularly at blue and red wavelengths.
Image acquisition parameters appear to have a significant impact on the magnitude of distortion of the reflectance values through PS. Ideally, imagery would be acquired at nadir (0 ° off-nadir angle) and with the sun at zenith (90 ° solar elevation). From Figure 2, imagery obtained under near-ideal conditions (green and black profiles) certainly led to better performance of Gram–Schmidt pan-sharpening, incurring minimal spectral distortions across all wavelengths (i.e., spectral profile ratio near 1.0). The improvement was observed most significantly in the blue and red wavelength bands, where the spectral distortions from images obtained under poorer viewing conditions were typically substantial. For example, the blue (Image 7) and magenta (Image 9) profiles both have a factor of 2 distortion in the spectral reflectance at blue and red wavelengths, and have off-nadir angles greater than 26.7 ° and solar elevation less than 49.1 ° . In general, pan-sharpening reduced the reflectance from the un-sharpened values, by a factor of <2. These results indicate that, under non-ideal viewing conditions, the pan-sharpening process is likely to substantially change the visual appearance and ‘colours’ of the scene captured through R, G, B composite imagery (‘natural look’) as the relationship between the R, G, B bands is altered. More significantly, PS may distort the interpretation of vegetation characteristics derived from the relationship between red wavelength reflectance and other bands (examined below). It is unclear whether either of the image viewing conditions examined had a greater impact on sharpening spectral quality (Figure 3). The off-nadir angle was more strongly correlated with the ‘spectral profile ratio’, having a Pearson’s correlation coefficient of 0.66 between the angle and the mean spectral profile ratio across visible wavelengths. This is compared to a correlation coefficient of −0.39 with the solar elevation angle. This result indicates that minimising the off-nadir view may be more important to image quality than optimising the solar elevation angle (which is likely to cause significant interrow shadowing for most vinerow orientations); however, neither of these correlations is statistically significant given the number of images available for examination.
Figure 4 illustrates the impact of pan-sharpening on the vegetation index NDVI, which is derived from the normalised difference in reflectance of red and near-infrared wavelengths. In a general vinerow, mean NDVI values are increased through the pan-sharpening process, and are within a factor of 1.3 of the un-sharpened values. The distribution of NDVI per pixel values may also be skewed, as indicated by the non-circular mean-centred one standard deviation envelopes, as the algorithm increased the variance in NDVI values across each vinerow. No significant correlation between NDVI change and image acquisition parameters was observed; however the least skewed mean values originated from the images taken under near-ideal conditions (black and green profiles). Similar trends were also observed when comparing un-sharpened and pan-sharpened NDVI values of generally homogeneous (at the panchromatic spatial resolution) vegetation regions, namely irrigated ovals/sports fields. As observed for vinerows, in all cases, the mean sharpened NDVI of ovals/sports fields was on the order of 10% greater than the un-sharpened mean, and the variance generally greater. This illustrates that the change in the mean and distribution of NDVI values observed for vinerows is not related to the periodic variation in vinerow–interrow signatures being separated in the pan-sharpened imagery, but encompassed within the vinerow ROIs in the un-sharpened imagery.

3.2. Quantitative Data Model Comparisons

The impact of spatial resolution, spectral resolution, and pan-sharpening (and, implicitly, image acquisition parameters) on model performance are quantified in Table 3 (with additional metrics in Table A3). Four key metrics (defined in Section 2.3) are utilised to compare the vineyard block predictions with ground-truth labels of vineyard boundaries, and thereby assess the accuracy of the resulting segmentation. Several visual examples of vineyard segmentations from models M1–M5 are provided in Figure 5, Figure 6 and Figure 7. The results for recall and precision are visualised in Figure 8, and for precision and area ratio in Figure 9. Although strongly correlated in this case (Table A4), it is conventional within machine learning fields to visually compare the output of precision and recall. The accuracy and JI results are not visualised as they were also both highly correlated with recall. In contrast, precision and area ratio were only weakly correlated (Table A4). In general, the best predictive performance was achieved by the M2 model trained and run on the panchromatic band and all eight multispectral channels in un-sharpened (coarse) resolution. This model typically achieved higher recall, higher Jaccard Index, and an area ratio close to 1.0 (also better Kappa statistic, Table A3). Precision on one image was slightly poorer than was achieved by using M4 (pan-sharpened R-RE-NIR bands), and on another the area ratio was slightly poorer than achieved with M4. In general, the results for the M1, M3 (pan-sharpened RGB bands) and M4 models included more false detections compared to M2, while M3 obtained poorer area prediction and spatial overlap with more misses of true vineyards. The performance of M5 was generally very similar to M2, being the most dissimilar in the recall for Image 2. The variance in performance across the models was observed to be image dependent, likely due to variations in vineyard vegetation and image acquisition/quality parameters (i.e., the off-nadir angle and solar elevation angles) that were not adequately captured in the model training dataset. From Figure 8, all models for Images 3 and 6 obtained relatively similar precision, recall, and area ratio measures (each varied by <2%), while for Images 1 and 2 the improved performance of M2 in precision and recall was more substantial. When comparing precision and area ratio in Figure 9, M2 for Image 2 provided a significant improvement in the estimation of vineyard area, although for Image 1 the area ratio of M1 was the most accurate, albeit with lowered precision compared to M2. In general, the precision, recall, and JI metrics were more sensitive to the choice of model (Table 4), while variation in area ratio between models was smaller. In contrast, the area ratio and Jaccard Index (spatial area overlap) were more sensitive to variations between imagery.
Although the measures of accuracy reported here represent differing sources of included error, they generally agreed on the relative ranking of the model results. M2 was generally the highest performing, with M5 the most similar, and M1 and M3 typically only slightly poorer (with the exception of Image 1). For all images, the best performing model had a Kappa statistic indicating >77% better agreement between predictions and ground-truth than would be likely to be obtained through chance (Table A3).
Figure 8 and Figure 9 also provide some insights into the generalizability of the results to different images. A model whose performance is robust to imagery obtained at different locations and times (assuming the choice of input bands to the model is fixed) would result in symbols with the same colour in Figure 8 being clustered together. This was generally not the case. This result is also seen in the range of the coefficient of variation between models in Table 4.

4. Discussion

4.1. Interplay between Spatial Resolution and Spectral Values (Image Fusion)

Spectral analysis with pan-sharpened multispectral values should typically be undertaken with caution. Pan-sharpening algorithms typically introduce distortions to the spectral reflectances that vary in magnitude with wavelength, image characteristics, and choice of algorithm. Pan-sharpened satellite imagery was necessary for vinerow delineation and vine canopy extraction, due to the spatial resolution required to visually differentiate vegetation from interrows. This work, however, has assessed the costs and benefits associated with utilizing pan-sharpened multispectral data for automated segmentation of vine block boundaries through a CNN. Although vineyard detection can be achieved using a single high-resolution spatial but broad spectral panchromatic band (e.g., [4,12,19,30] and results from our model M1), there are many factors that can reduce contrast between vines and interrow materials and reduce the overall accuracy of grapevine vegetation classification. These factors include the visibility of the vines and interrows, grapevine growth state, interrow spacing, surface conditions (e.g., soil wetness), and image acquisition conditions. The incorporation of other wavelengths, particularly the near-infrared, can compensate for these similarities and increase detection accuracy [27]. The Shannon–Nyquist theorem—which regards the discrete sampling frequency needed for the reconstruction of a continuous signal [67]–can be utilised to estimate the spatial resolution required for vinerow detection. Through application of the theorem, periodic patterns can be reliably detected in imagery with a spatial resolution >2× smaller (finer) than the pattern period [30]. Given interrow widths in Australia are typically 3 m to 3.3 m wide, while vinerows typically have <1 m width, the relevant vine planting period would be expected to be less than 4.3 m, requiring imagery with a pixel size no larger than 2.15 m for detection of vineyard rows. In order to precisely delineate the vinerow vegetation and reliably separate the canopy edges from the interrows, greater spatial sensitivity is required. For this task, at least three pixels overlapping each interrow are desired (two pixels of vinerow vegetation and interrow, and one pure interrow pixel), and hence resolutions of finer than 1.1 m. From Table 1, this necessitates pan-sharpening of Worldview-2 multispectral imagery.
Figure 1 and Figure 2 examine the impact of pan-sharpening on grapevine vegetation values, revealing that PS introduced a non-trivial distortion (typically a reduction) of reflectance values but generally preserved the shape of the vegetation spectral profile and the spectral slopes. The magnitude of spectral distortion was less when comparing image slopes rather than mean pixel values, implying that spectral slope classification methods [68] may be more robust than pixel based classifiers such as K-Means and Maximum Likelihood (e.g., [69]). Spectral distortions increased with poorer image acquisition conditions (larger off-nadir angle and smaller solar elevation angle). The distortions were generally largest at visible wavelengths, particularly the blue and red bands. Significant changes to coastal and NIR2 band reflectance values were expected as these bands do not spectrally overlap with the panchromatic band. Hence, the fusion of spatial information from the simulated low resolution Pan band (computed as a weighted linear combination of the multispectral bands with weight 0 for bands 1 and 8, see Table 1) into the coastal and NIR2 band will be dependent on the spatial-spectral relationships between the other multispectral bands and the PAN band. However, significant spectral distortions to the coastal band was not observed, nor to the NIR2 band (likely due to the spectral redundancy i.e., partial overlap with the NIR1 band [70]). Although ideally all non-overlapping multispectral bands would be excluded from the pan-sharpening, the implementation of Gram–Schmidt sharpening through ENVI software outputs a high-spatial resolution transformation of all bands. The distortions at red wavelengths may be attributed to sun-angle differences. Changes in sun angle are known to strongly affect red wavelength vegetation reflectance, and are largely dependent on the foliar distribution and leaf-area-index [71]. The most severe spectral distortions in Figure 2 originated from images taken under the lowest sun elevation angles and largest off-nadir angles. This suggests that the initial radiometric corrections for sun elevation and differences in atmospheric path length across the image were insufficient. Another plausible explanation is that the manual delineation of vinerows was confused by the presence of interrow shadow and displaced from the centre of the vinerow, and hence did not constitute a pure grapevine vegetation signal. The latter explanation is unlikely, as multiple image products (false-colour composites and vegetation indices) were utilised in the selection of grapevine ROIs.
The results demonstrate the sensitivity of pan-sharpening quality to solar and sensor viewing angles, which in turn directly impacts the accuracy of vine block detection using sharpened multispectral data (see Section 4.2 below). It is difficult to assess the generalizability of these conclusions to other vine detection studies (at the same scale). One key uncontrolled variables that may impact the robustness of the spectral results is the intra-image differences in the vegetation ROIs used for spectral profiles, due to differences in vigor, canopy structure, or even cultivars/grape varieties. These differences in vegetation account for an unknown fraction of the variance between images. This could only be further mitigated by aiming to capture as much variance in grapevine vegetation within each image as possible. A potential avenue for future work is to extend this study by incorporating shortwave infrared (SWIR) reflectance from the Worldview-3 satellite. The response of vegetation at these wavelengths is strongly related to their water content, and has been shown in viticultural studies to be highly sensitive to water stress [72], and can be used to infer other biophysical parameters and forecast plant production/yield. The incorporation of SWIR reflectance may also provide benefit in the discrimination of grapevine vegetation from other types of row crops, thereby increasing the accuracy of the automated grapevine detection and image segmentation. However, similarly to reflectance at shorter wavelengths (VIS-NIR), SWIR reflectance is also sensitive to variation in the bidirectional reflectance distribution, and the pan-sharpened bands would be expected to vary in quality with solar and sensor viewing angles, as demonstrated in this work. Previous works have shown that vegetation indices derived from SWIR bands can likewise be strongly impacted by sun-target-sensor geometry (e.g., [73]). An additional caveat is that the Worldview-3 SWIR bands are ~three times coarser than the spatial resolution of the multispectral sensor, and hence more significant distortion of spectral values as a result of the pan-sharpening would be expected.

4.2. Performance Validation

The spectral and spatial resolution of input imagery had a significant impact on the accuracy of predicted vineyard block boundaries. Despite a mean coefficient of variation in precision, recall, and JI on the order of 10% across images and 3% across models (Table 4), the validity of the predictions remained high. Classification mistakes (i.e., false detections) typically constituted <12% of the predictions, and the predicted vineyard area was generally within 5% of actual. Missed vineyard pixels were a slight larger source of error, constituting <23% of the predictions. This was likely due to the variation in vineyard vegetation being insufficiently captured in the labelled data used in training. The mean Jaccard Index for the highest performing model (M2) was 0.8, outperforming the current state-of-the-art from a CNN architecture achieved by the top ranked participants in recent image segmentation competitions (e.g., [74,75]). Ref. [4] utilised an object-based classifier to undertake a similar vineyard detection task. The input imagery consisted of pan-sharpened Worldview-2 multispectral reflectance, spectral ratios, and derived textural features. They reported correctness (analogous to precision) and completeness (analogous to recall) over 89%, averaging 92% correctness and 93% completeness, respectively. Ref. [5] utilised similar methods and input imagery to [4], and reported user’s (analogous to precision) and producer’s (analogous to recall) accuracy’s for vineyards ranging from 92.5–97.5% and 94.87–100%, respectively, depending on image region. These results are comparable to the highest-performing model discussed here (M2), which achieved mean correctness/precision of 89% and mean completeness/recall of 88% across all images (also mean area ratio of 1.01 and mean accuracy of 99.8%, calculated from Table 3), without the incorporation of pan-sharpening, spectral indices or textural features.
The results clearly illustrate the importance of incorporating multispectral data rather than simply using a high resolution panchromatic band. The sensitivity to chlorophyll absorption and plant tissue structure from red and infrared wavelength absorption, and hence the ability to differentiate vegetation based on attributes such as vigour, canopy density and structure, translated into improved vineyard detection and more accurate prediction of vineyard area. However, the incorporation of a high-resolution subset of the multispectral data—pan-sharpened visible red, green and blue bands—resulted in generally similar or poorer performance across all performance measures, compared to the use of the panchromatic band only. This can be attributed both to the spectral distortions introduced by the pan-sharpening process (quantified in Section 3.1), particularly at blue and red wavelengths, and the insufficient sensitivity to vegetation when only visible wavelengths are used. When the red, red edge and near-infrared wavelengths were incorporated to capture the unique spectral response of green vegetation, at pan-sharpened resolution, the model performance slightly improved on two images compared to panchromatic only, but still did not exceed the use of coarse un-sharpened multispectral. When the spectral response of vegetation was summarised through a high resolution spectral index (NDVI), a greater improvement was observed with the performance then approaching the un-sharpened multispectral model. This improvement in performance can be explained by the enhanced sensitivity to vegetation, while minimizing the spectral distortions introduced through pan-sharpening by using a normalised difference product of the sharpened spectral bands rather than bands themselves (see Section 3.1).
The machine learning model we used was trained to perform binary image segmentation, i.e., to classify each pixel as either part of a vineyward, or not part of a vineyward. In future work, it would be interesting to extend to more than two classes, and enable classification of vineyard by grape variety. Similar multi-class problems have been tackled using semantic segmentation applied to high resolution satellite imagery, for example where the pixel categories include forest, water, urban, and several others [76].

5. Conclusions

This work quantified the impact of initial choices in Worldview-2 remote sensing imagery–namely the wavelengths used, their spatial resolution, and, implicitly, the image acquisition parameters– on the accuracy of vineyard boundary detection via a machine learning methodology. The incorporation of multispectral information at its native off-sensor resolution was found to enhance vineyard detection capability and spatial area prediction, when compared to the performance of the algorithm on a single panchromatic band. However, pan-sharpening—a frequently used technique in remote sensing for precision viticulture—was found to cause significant spectral distortions that were dependent on both wavelength and image acquisition parameters. These distortions led to poorer vineyard detection performance when the model was run on high-spatial resolution visible wavelength bands, and on high-spatial resolution red, red edge, and near-infrared bands (chosen to enhance sensitivity to green vegetation). The use of the high-resolution NDVI index resulted in similar (but slightly poorer) performance to the coarse multispectral model, as the spectral distortions introduced by pan-sharpening were reduced through taking the normalised difference ratio of the spectral bands. In summary, the imagery parameter choices which optimized the automated vineyard segmentation were input bands: panchromatic and un-sharpened multispectral. If pan-sharpening is necessitated, then results may be optimised by minimization of the off-nadir angle, and maximization of the solar elevation angle. These results provide valuable information for others working more broadly on crop detection, and the derivation of grapevines or other vegetation characteristics at fine spatial scales from space.

Author Contributions

E.G.J. conceived the model experiment types and conceived and performed the pan-sharpening experiments, analyzed the data, produced figures and wrote the paper. S.W. conceived, designed, and coded the machine learning architecture. A.M. conceived, designed, and coded the machine learning architecture, and contributed substantial edits to the paper. J.S. conceived, designed, and coded the machine learning architecture. M.D.M. conceived, designed, and coded the machine learning architecture, performed the machine learning model experiments, analyzed the data, wrote sections of the methodology, and contributed substantial edits to the paper. H.W. contributed hand-labelled data and interpretation, used for model training and validation. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

Innovation Connections grants ICG000351 and ICG000357 from the Australian Federal Government’s Department of Industry, Innovation, and Science are gratefully acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PVPrecision Viticulture
PANPanchromatic
p.s.v.Photosynthetic vegetation
MSMultispectral
NIRNear-infrared
VNIRVisible and Near-Infrared wavelengths
SWIRShort-Wave Infrared Wavelengths
NDVINormalized Difference Vegetation Index
GSGram–Schmidt pan-sharpening algorithm.

Appendix A

Table
Table A1. Metadata of imagery.
Table A1. Metadata of imagery.
FieldValue
LabelImage 1
Catalog ID1030010065A6AD00
Acquisition date14th February 2017
Acquisition time (ACST # )9:53:02 AM
Pixel size GSD (meters)0.509 (PAN); 2.036 (MS)
Mean view-angle16.4 °
Mean solar elevation51.4 °
LabelImage 2
Catalog ID1030010066252A00
Acquisition date28th February 2017
Acquisition time (ACST)9:36:41 AM
Pixel size GSD (meters)0.509 (PAN); 1.986 (MS)
Mean view-angle13.4 °
Mean solar elevation44.1 °
Catalog ID10300100737F4D00
Acquisition date22th November 2017
Acquisition time (ACST)10:32:29 AM
Pixel size GSD (meters)0.550 (PAN); 2.200 (MS)
Mean view-angle23.5 °
Mean solar elevation65.8 °
LabelImage 4
Catalog ID103001002DA07900
Acquisition date15th January 2014
Acquisition time (ACST)10:32:35 AM
Pixel size GSD (meters)0.475 (PAN); 1.895 (MS)
Mean view-angle5.4 °
Mean solar elevation63.4 °
LabelImage 5
Catalog ID1030010078903800
Acquisition date7th February 2018
Acquisition time (ACST)10:01:20 AM
Pixel size GSD (meters)0.488 (PAN); 1.945 (MS)
Mean view-angle11.4 °
Mean solar elevation57.5 °
LabelImage 6
Catalog ID1030010063A7F700
Acquisition date10th February 2017
Acquisition time (ACST)10:38:36 AM
Pixel size GSD (meters)0.549 (PAN); 2.187 (MS)
Mean view-angle23.1 °
Mean solar elevation58.0 °
LabelImage 7
Catalog ID1030010052802F00
Acquisition date9th March 2016
Acquisition time (ACST)12:52:15 PM
Pixel size GSD (meters)0.576 (PAN); 2.303 (MS)
Mean view-angle26.7 °
Mean solar elevation49.1 °
LabelImage 8
Catalog ID1030010088661E00
Acquisition date12th November 2018
Acquisition time (ACST)10:39:46 AM
Pixel size GSD (meters)0.476 (PAN); 1.900 (MS)
Mean view-angle7.6 °
Mean solar elevation68.1 °
LabelImage 9
Catalog ID103001007C181200
Acquisition date2nd April 2018
Acquisition time (ACST)11:18:09 AM
Pixel size GSD (meters)0.589 (PAN); 2.362 (MS)
Mean view-angle28.0 °
Mean solar elevation42.8 °
# Australian Central Standard Time.
Table
Table A2. Vinerow ROI counts.
Table A2. Vinerow ROI counts.
ImageNumber of PixelsNumber (km Length) of Vinerows
Image 5387085698 (190.3)
Image 6214789493 (108.5)
Image 7167487389 (86.1)
Image 4100159267 (42.8)
Image 2107230375 (54.3)
Image 162057327 (30.3)
Image 8102583187 (55.6)
Image 9128171284 (75.6)
* Number of image pixels relates to the resolution of the panchromatic band image; geodetic vinerow length calculated in the GDA 1994 Australia Albers projection (EPSG 3577).
Table
Table A3. Machine learning model results: metrics where both vineyard and background are weighted equally.
Table A3. Machine learning model results: metrics where both vineyard and background are weighted equally.
ModelPerformance Measures
KappaAccuracy
Image 1M10.831.00
M20.851.00
M30.791.00
M40.821.00
M50.841.00
Image 2M10.751.00
M20.771.00
M30.751.00
M40.761.00
M50.761.00
Image 3M10.950.99
M20.961.00
M30.930.99
M40.951.00
M50.951.00
Image 6M10.961.00
M20.961.00
M30.951.00
M40.951.00
M50.951.00
* Shading indicates best values of performance measure for each image.
Table
Table A4. Pearson correlation coefficients between performance measures, across all images and models (higher values indicate parameters are strongly correlated).
Table A4. Pearson correlation coefficients between performance measures, across all images and models (higher values indicate parameters are strongly correlated).
PrecisionRecallAccuracyKappaArea RatioJI
Precision1.000.95−0.790.98−0.490.98
Recall 1.00−0.750.99−0.740.99
Accuracy 1.00−0.770.36−0.79
Kappa 1.00−0.601.00
Area Ratio 1.00−0.63
JI 1.00

References

  1. Bramley, R.G.V.; Pearse, B.; Chamberlain, P. Being Profitable Precisely—A Case Study of Precision Viticulture from Margaret River. Aust. N. Z. Grapegrow. Winemak. 2003, 473, 84–87. [Google Scholar]
  2. Arno, J.; Martinez Casasnovas, J.A.; Dasi, M.R.; Rosell, J.R. Precision Viticulture. Research Topics, Challenges and Opportunities in Site-Specific Vineyard Management. Span. J. Agric. Res. 2009, 7, 779. [Google Scholar] [CrossRef] [Green Version]
  3. Matese, A.; Di Gennaro, S.F. Technology in Precision Viticulture: A State of the Art Review. Int. J. Wine Res. 2015, 7, 69–81. [Google Scholar] [CrossRef] [Green Version]
  4. Karakizi, C.; Oikonomou, M.; Karantzalos, K. Vineyard Detection and Vine Variety Discrimination from Very High Resolution Satellite Data. Remote Sens. 2016, 8, 235. [Google Scholar] [CrossRef] [Green Version]
  5. Sertel, E.; Yay, I. Vineyard parcel identification from Worldview-2 images using object- based classification model. J. Appl. Remote Sens. 2014, 8, 1–17. [Google Scholar] [CrossRef]
  6. Poblete-Echeverria, C.; Olmedo, G.F.; Ingram, B.; Bardeen, M. Detection and segmentation of vine canopy in ultra-high spatial resolution RGB imagery obtained from Unmanned Aerial Vehicle (UAV): A case study in a commercial vineyard. Remote Sens. 2017, 9, 268. [Google Scholar] [CrossRef] [Green Version]
  7. Shanmuganathan, S.; Sallis, P.; Pavesi, L.; Munoz, M.C.J. Computational intelligence and geo-informatics in viticulture. In Proceedings of the Second Asia International Conference on Modelling & Simulation (AMS), Kuala Lumpur, Malaysia, 13–15 May 2008; 2008; Volume 2, pp. 480–485. [Google Scholar]
  8. Rodriguez-Perez, J.R.; Alvarez-Lopez, C.J.; Miranda, D.; Alvarez, M.F. Vineyard Area Estimation Using Medium Spatial Resolution. Span. J. Agric. Res. 2006, 6, 441–452. [Google Scholar] [CrossRef] [Green Version]
  9. Hall, A.; Lamb, D.W.; Holzapfel, B.; Louis, J. Optical Remote Sensing Applications in Viticulture- a Review. Aust. J. Grape Wine Res. 2002, 8, 36–47. [Google Scholar] [CrossRef]
  10. Khaliq, A.; Comba, L.; Biglia, A.; Aimonino, D.; Chiaberge, M.; Gay, P. Comparison of Satellite and UAV-Based Multispectral Imagery for Vineyard Variability Assessment. Remote Sens. 2019, 11, 436. [Google Scholar] [CrossRef] [Green Version]
  11. Delenne, C.; Rabatel, G.; Agurto, V.; Deshayes, M. Vine Plot Detection in Aerial Images Using Fourier Analysis. In Proceedings of the 1st International Conference on Object-Based Image Analysis, Salzburg, Austria, 4–5 July 2006; Volume 1, pp. 1–6. [Google Scholar]
  12. Delenne, C.; Durrieu, S.; Rabatel, G.; Deshayes, M. From Pixel to Vine Parcel: A Complete Methodology for Vineyard Delineation and Characterization Using Remote-Sensing Data. Comput. Electron. Agric. 2010, 70, 78–83. [Google Scholar] [CrossRef] [Green Version]
  13. Kaplan, G.; Avdan, U. Sentinel-2 Pan Sharpening—Comparative Analysis. Proceedings 2018, 2, 345. [Google Scholar] [CrossRef] [Green Version]
  14. Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Giorgio, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
  15. Du, Q.; King, R. On the Performance Evaluation of Pan-Sharpening Techniques. IEEE Geosci. Remote Sens. 2007, 4, 518–522. [Google Scholar] [CrossRef]
  16. Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of Pansharpening Algorithms: Outcome of the 2006 GRS-S Data-Fusion Contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef] [Green Version]
  17. Amro, I.; Mateos, J.; Vega, M.; Molina, R.; Katsaggelos, A. A survey of classical methods and new trends in pansharpening of multispectral images. EURASIP J. Adv. Signal Process. 2011, 79, 1–22. [Google Scholar] [CrossRef] [Green Version]
  18. Sertel, E.; Seker, D.; Yay, I.; Ozelkan, E.; Saglan, M.; Boz, Y.; Gunduz, A. Vineyard mapping using remote sensing technologies. In Proceedings of the FIG Working Week 2012: Knowing to Manage the Territory, Protect the Environment, Evaluate the Cultural Heritage, Rome, Italy, 6–10 May 2012; pp. 1–8. [Google Scholar]
  19. Smit, J.L.; Sithole, G.; Strever, A.E. Vine Signal Extraction–an Application of Remote Sensing in Precision Viticulture. S. Afr. J. Enol. Vitic. 2010, 31, 65–73. [Google Scholar] [CrossRef] [Green Version]
  20. Comba, L.; Gay, P.; Primicerio, J.; Aimonino, D. Vineyard detection from unmanned aerial systems images. Comput. Electron. Agric. 2015, 114, 78–87. [Google Scholar] [CrossRef]
  21. Cinat, P.; Di Gennaro, S.; Berton, A.; Matese, A. Comparison of Unsupervised Algorithms for Vineyard Canopy Segmentation from UAV Multispectral Images. Remote Sens. 2019, 11, 1023. [Google Scholar] [CrossRef] [Green Version]
  22. Pádua, L.; Marques, P.; Hruška, J.; Adão, T.; Bessa, J.; Sousa, A.; Peres, E.; Morais, R.; Sousa, J. Vineyard properties extraction combining UAS-based RGB imagery with elevation data. Int. J. Remote Sens. 2018, 39, 5377–5401. [Google Scholar] [CrossRef]
  23. Delenne, C.; Rabatel, G.; Deshayes, M. An automatized frequency analysis for vine plot detection and delineation in remote sensing. IEEE Geosci. Remote Sens. Lett. 2008, 5, 341–345. [Google Scholar] [CrossRef] [Green Version]
  24. Rabatel, G.; Delenne, C.; Deshayes, M. A Non-Supervised Approach Using Gabor Filters for Vine-Plot Detection in Aerial Images. Comput. Electron. Agric. 2008, 62, 159–168. [Google Scholar] [CrossRef]
  25. Ranchin, T.; Naert, B.; Albuisson, M.; Boyer, G.; Astrand, P. An Automatic Method for Vine Detection in Airborne Imagery Using Wavelet Transform and Multiresolution Analysis. Photogramm. Eng. Remote Sens. 2001, 67, 91–98. [Google Scholar]
  26. Gao, F.; He, T.; Masek, J.G.; Shuai, Y.; Schaaf, C.B.; Wang, Z. Angular effects and correction for medium resolution sensors to support crop monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4480–4489. [Google Scholar] [CrossRef]
  27. Poblete, T.; Ortega-Farías, S.; Ryu, D. Automatic Coregistration Algorithm to Remove Canopy Shaded Pixels in UAV-Borne Thermal Images to Improve the Estimation of Crop Water Stress Index of a Drip-Irrigated Cabernet Sauvignon Vineyard. Sensors 2018, 18, 397. [Google Scholar] [CrossRef] [Green Version]
  28. Hall, A.; Louis, J.; Lamb, D.A. Method For Extracting Detailed Information From High Resolution Multispectral Images Of Vineyards. In Proceedings of the 6th International Conference on Geocomputation, Brisbane, Australia, 24–26 September 2001; Volume 6, pp. 1–9. [Google Scholar]
  29. Towers, P.; Strever, A.; Poblete-Echeverría, C. Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies With and Without Grenbiule Hail-Protection Netting. Remote Sens. 2019, 11, 16. [Google Scholar] [CrossRef] [Green Version]
  30. Delenne, C.; Durrieu, S.; Rabatel, G.; Deshayes, M.; Bailly, J.S.; Lelong, C.; Couteron, P. Textural Approaches for Vineyard Detection and Characterization Using Very High Spatial Resolution Remote Sensing Data. Int. J. Remote Sens. 2008, 29, 1153–1167. [Google Scholar] [CrossRef]
  31. WineAustralia. Geographical Indications. Available online: https://www.wineaustralia.com/labelling/register-of-protected-gis-and-other-terms/geographical-indications (accessed on 22 May 2018).
  32. Halliday, J. Wine Atlas of Australia, 3rd ed.; Hardie Grant Books: Richmond, VA, USA, 2014. [Google Scholar]
  33. Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.A.; et al. Daily mapping of 30 m LAI and NDVI for grape yield prediction in California vineyards. Remote Sens. 2017, 9, 317. [Google Scholar] [CrossRef] [Green Version]
  34. Lamb, D.W.; Weedon, M.M.; Bramley, R.G.V. Using remote sensing to predict grape phenolics and colour at harvest in a Cabernet Sauvignon vineyard: Timing observations against vine phenology and optimising image resolution. Aust. J. Grape Wine Res. 2008, 10, 46–54. [Google Scholar] [CrossRef] [Green Version]
  35. Webb, L.B.; Whetton, P.H.; Bhend, J.; Darbyshire, R.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.A.; et al. Earlier wine-grape ripening driven by climatic warming and drying and management practices. Nat. Clim. Chang. 2012, 2, 259–264. [Google Scholar] [CrossRef]
  36. Jackson, R.S. Vineyard Practice, 4th ed.; Wine Science—Principles and Applications; Academic Press: San Diego, CA, USA, 2015; pp. 143–306. [Google Scholar]
  37. Globe, D. Advanced Image Preprocessor with AComp. Available online: https://gbdxdocs.digitalglobe.com/docs/advanced-image-preprocessor (accessed on 22 May 2018).
  38. DigitalGlobe. Accuracy of Worldview Products. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/38/DG_ACCURACY_WP_V3.pdf (accessed on 22 May 2019).
  39. Carper, W.; Lillesand, T.; Kiefer, R. The use of intensity-hue- saturation transformations for merging SPOT panchromatic and multi- spectral image data. Photogramm. Eng. Remote Sens. 1990, 56, 459–467. [Google Scholar]
  40. Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
  41. Chavez, P., Jr.; Kwarteng, A. Extracting spectral contrast in Landsat thematic mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 338–348. [Google Scholar]
  42. Lui, W.; Wang, Z. A practical pan-sharpening method with wavelet transform and sparse representation. In Proceedings of the 2013 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 22–23 October 2013; pp. 288–293. [Google Scholar]
  43. Palubinskas, G. Fast, simple, and good pan-sharpening method. J. Appl. Rem. Sens. 2013, 7, 073526. [Google Scholar] [CrossRef]
  44. Aiazzi, B.; Alparone, L.; Baronti, S.; Lotti, F. Lossless image compression by quantization feedback in a content-driven enhanced Laplacian pyramid. IEEE Trans. Image Process. 1997, 6, 831–843. [Google Scholar] [CrossRef] [PubMed]
  45. Imani, M. Band Dependent Spatial Details Injection Based on Collaborative Representation for Pansharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4994–5004. [Google Scholar] [CrossRef]
  46. HarrisGeospatialSolutions. Gram-Schmidt Pan Sharpening. Available online: http://www.harrisgeospatial.com/docs/GramSchmidtSpectralSharpening.html (accessed on 22 May 2018).
  47. Song, S.; Liu, J.; Pu, H.; Liu, Y.; Luo, J. The comparison of fusion methods for HSRRSI considering the effectiveness of land cover (Features) object recognition based on deep learning. Remote Sens. 2019, 11, 1435. [Google Scholar] [CrossRef] [Green Version]
  48. Zhou, C.; Liang, D.; Yang, X.; Xu, B.; Yang, G. Recognition of wheat spike from field based phenotype platform using multi-sensor fusion and improved maximum entropy segmentation algorithms. Remote Sens. 2018, 10, 246. [Google Scholar] [CrossRef] [Green Version]
  49. Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A Theoretical Analysis of the Effects of Aliasing and Misregistration on Pansharpened Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
  50. Li, H.; Jing, L.; Tang, Y. Assessment of pan-sharpening methods applied to WorldView-2 imagery fusion. Sensors 2017, 17, 89. [Google Scholar] [CrossRef]
  51. Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simões, M.; et al. Hyperspectral Pansharpening: A Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 1–15. [Google Scholar] [CrossRef] [Green Version]
  52. Basaeed, E.; Bhaskar, H.; Al-mualla, M. Comparative Analysis of Pan-sharpening Techniques on DubaiSat-1 images. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; Volume 16, pp. 227–234. [Google Scholar]
  53. Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Martinez-Gonzalez, P.; Garcia-Rodriguez, J. A survey on deep learning techniques for image and video semantic segmentation. Appl. Soft Comput. 2018, 70, 41–65. [Google Scholar] [CrossRef]
  54. Huang, B.; Zhao, B.; Song, T. Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
  55. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
  56. Sozzi, M.; Kayad, A.; Tomasi, D.; Lovat, L.; Marinello, F.; Sartori, L. Assessment of grapevine yield and quality using a canopy spectral index in white grape variety. In Proceedings of the Precision Agriculture ’19, Montpellier, France, 8–11 July 2019. [Google Scholar]
  57. Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
  58. Olaf Ronneberger, P.F.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015. [Google Scholar]
  59. Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:1802.02611. [Google Scholar]
  60. Kornblith, S.; Shlens, J.; Le, Q.V. Do Better ImageNet Models Transfer Better? arXiv 2018, arXiv:1805.08974. [Google Scholar]
  61. Wong, S.C.; Gatt, A.; Stamatescu, V.; McDonnell, M.D. Understanding Data Augmentation for Classification: When to Warp? In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, QLD, Australia, 30 November–2 December 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
  62. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [CrossRef] [Green Version]
  63. Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
  64. Google. Google Maps. Available online: http://maps.google.com/ (accessed on 22 January 2019).
  65. Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
  66. Congalton, R.G. Accuracy assessment and validation of remotely sensed and other spatial information. Int. J. Wildland Fire 2001, 10, 321–328. [Google Scholar] [CrossRef] [Green Version]
  67. Jerri, A.J. The Shannon Sampling Theorem—Its Various Extensions and Applications: A Tutorial Review. Proc. IEEE 1977, 65, 1565–1596. [Google Scholar] [CrossRef]
  68. Aswatha, S.M.; Mukhopadhyay, J.; Biswas, P.K. Spectral Slopes for Automated Classification of Land Cover in Landsat Images. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 4354–4358. [Google Scholar]
  69. Jones, E.G.; Caprarelli, G.; Mills, F.P.; Doran, B.; Clarke, J. An Alternative Approach to Mapping Thermophysical Units from Martian Thermal Inertia and Albedo Data Using a Combination of Unsupervised Classification Techniques. Remote Sens. 2014, 6, 5184–5237. [Google Scholar] [CrossRef] [Green Version]
  70. Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef] [Green Version]
  71. Lord, D.; Desjardins, R.L.; Dube, P.A. Sun-angle effects on the red and near infrared reflectances of five different crop canopies. Can. J. Remote Sens. 1988, 14, 46–55. [Google Scholar] [CrossRef] [Green Version]
  72. Rodríguez-Pérez, J.; Ordóñez, C.; González-Fernández, A.; Sanz-Ablanedo, E.; Valenciano, J.; Marcelo, V. Leaf Water Content Estimation By Functional Linear Regression of Field Spectroscopy Data. Biosyst. Eng. 2018, 165, 36–46. [Google Scholar] [CrossRef]
  73. Huber, S.; Tagesson, T.; Fensholt, R. An Automated Field Spectrometer System For Studying VIS, NIR and SWIR Anisotropy For Semi-Arid Savanna. Remote Sens. Environ. 2014, 152, 547–556. [Google Scholar] [CrossRef] [Green Version]
  74. Codella, N.C.F.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin lesion analysis toward melanoma detection: A challenge at the 2017 International symposium on biomedical imaging (ISBI), hosted by the international skin imaging collaboration (ISIC). arXiv 2018, arXiv:1710.05006. [Google Scholar]
  75. Iglovikov, V.; Mushinskiy, S.; Osin, V. Satellite Imagery Feature Detection using Deep Convolutional Neural Network: A Kaggle Competition. arXiv 2017, arXiv:1706.06169. [Google Scholar]
  76. Tian, C.; Li, C.; Shi, J. Dense Fusion Classmate Network for Land Cover Classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
Remotesensing 12 00934 g001 550
Figure 1. Comparison between the spectral profile (top) and spectral slopes (bottom) of a vinerow in both native resolution and pan-sharpened multispectral data. The green shaded region in the top plot gives the one standard deviation envelope around the mean un-sharpened reflectance values. The pan-sharpened spectral profile was calculated from 895 pixels within Image 4 (ideal viewing conditions).
Figure 1. Comparison between the spectral profile (top) and spectral slopes (bottom) of a vinerow in both native resolution and pan-sharpened multispectral data. The green shaded region in the top plot gives the one standard deviation envelope around the mean un-sharpened reflectance values. The pan-sharpened spectral profile was calculated from 895 pixels within Image 4 (ideal viewing conditions).
Remotesensing 12 00934 g001
Remotesensing 12 00934 g002 550
Figure 2. Comparison between the spectral profile ratio (un-sharpened over pan-sharpened) of vinerows imaged under different conditions. Off-nadir angles and solar elevation angles, respectively, are given for each image profile in brackets. All profiles showed a strong vegetation signature in both pan-sharpened and un-sharpened images (pixel counts are provided in Table A2). The dashed line at a spectral ratio of 1.0 indicates no spectral distortions introduced through the pan-sharpening process.
Figure 2. Comparison between the spectral profile ratio (un-sharpened over pan-sharpened) of vinerows imaged under different conditions. Off-nadir angles and solar elevation angles, respectively, are given for each image profile in brackets. All profiles showed a strong vegetation signature in both pan-sharpened and un-sharpened images (pixel counts are provided in Table A2). The dashed line at a spectral ratio of 1.0 indicates no spectral distortions introduced through the pan-sharpening process.
Remotesensing 12 00934 g002
Remotesensing 12 00934 g003 550
Figure 3. The solar elevation angles and off-nadir angles for the nine images listed in Table A1. Symbol colours provide the mean un-sharpened to pan-sharpened spectral ratio (plotted in Figure 2) across bands 1 to 5 (visible wavelengths). A weak positive correlation is observed between the magnitude of the spectral distortions and the degrees off-nadir (Pearson correlation coefficient 0.66).
Figure 3. The solar elevation angles and off-nadir angles for the nine images listed in Table A1. Symbol colours provide the mean un-sharpened to pan-sharpened spectral ratio (plotted in Figure 2) across bands 1 to 5 (visible wavelengths). A weak positive correlation is observed between the magnitude of the spectral distortions and the degrees off-nadir (Pearson correlation coefficient 0.66).
Remotesensing 12 00934 g003
Remotesensing 12 00934 g004 550
Figure 4. Comparison between the vinerow NDVI values derived from un-sharpened and pan-sharpened images. The mean values within each image are plotted as symbols (pixel counts provided in Table A2), while the dashed lines indicate the mean centered 1 standard deviation ellipses. The aspect ratio of the ellipses (semi-minor over semi-major axis length) is provided in brackets (a circle would have an aspect ratio of 1) to highlight whether the distribution of pixel values was significantly skewed by the pan-sharpening process.
Figure 4. Comparison between the vinerow NDVI values derived from un-sharpened and pan-sharpened images. The mean values within each image are plotted as symbols (pixel counts provided in Table A2), while the dashed lines indicate the mean centered 1 standard deviation ellipses. The aspect ratio of the ellipses (semi-minor over semi-major axis length) is provided in brackets (a circle would have an aspect ratio of 1) to highlight whether the distribution of pixel values was significantly skewed by the pan-sharpening process.
Remotesensing 12 00934 g004
Remotesensing 12 00934 g005 550
Figure 5. An example patch of size 512 × 512 pixels for M2 with good results, JI = 98.7%, Precision = 99.1%, Recall = 99.6%.
Figure 5. An example patch of size 512 × 512 pixels for M2 with good results, JI = 98.7%, Precision = 99.1%, Recall = 99.6%.
Remotesensing 12 00934 g005
Remotesensing 12 00934 g006 550
Figure 6. An example patch of size 512 × 512 pixels for M2 with missed detections, JI = 73%, Precision = 99%, Recall = 73%.
Figure 6. An example patch of size 512 × 512 pixels for M2 with missed detections, JI = 73%, Precision = 99%, Recall = 73%.
Remotesensing 12 00934 g006
Remotesensing 12 00934 g007 550
Figure 7. An example patch of size 512 × 512 pixels for M2 with false detections, JI = 0%, Precision = 0%, Recall = undefined.
Figure 7. An example patch of size 512 × 512 pixels for M2 with false detections, JI = 0%, Precision = 0%, Recall = undefined.
Remotesensing 12 00934 g007
Remotesensing 12 00934 g008 550
Figure 8. Comparison of precision and recall for different images (symbol type) and models (symbol color). The incorporation of un-sharpened multispectral data generally enhances recall but reduces precision. The worst recall and precision results were generally obtained from the use of pan-sharpened RGB multispectral.
Figure 8. Comparison of precision and recall for different images (symbol type) and models (symbol color). The incorporation of un-sharpened multispectral data generally enhances recall but reduces precision. The worst recall and precision results were generally obtained from the use of pan-sharpened RGB multispectral.
Remotesensing 12 00934 g008
Remotesensing 12 00934 g009 550
Figure 9. Comparison of precision and area ratio for different images (symbol type) and models (symbol color). There is no clear relationship between model parameters and area ratio, suggesting it is more strongly related to the image characteristics. Image 1 shows the largest variation in area ratio performance between models.
Figure 9. Comparison of precision and area ratio for different images (symbol type) and models (symbol color). There is no clear relationship between model parameters and area ratio, suggesting it is more strongly related to the image characteristics. Image 1 shows the largest variation in area ratio performance between models.
Remotesensing 12 00934 g009
Table
Table 1. Nominal characteristics of the Worldview-2 platform.
Table 1. Nominal characteristics of the Worldview-2 platform.
ParameterSensor
PANMS
Spatial resolution (m)0.461.85
Radiometric resolution (bits/pixel)1111
Spectral resolution (nm)450–800 (VNIR)400–450 (coastal)
450–510 (blue)
510–580 (green)
585–625 (yellow)
630–690 (red)
705–745 (red edge)
770–895 (NIR1)
860–1040 (NIR2)
Temporal resolution<2 days; 3.7 days at 20 ° off-nadir or less
Field of view16.4 × 112 km (single strip)
OrbitGeocentric sun-synchronous; altitude 770 km
Table
Table 2. Data Models. A different U-net semantic segmenter was trained for each of M1 to M5.
Table 2. Data Models. A different U-net semantic segmenter was trained for each of M1 to M5.
ModelDescription
M1Panchromatic band only.
M2Panchromatic band, 8 multispectral bands (native resolution).
M3R-G-B (3 pan-sharpened bands).
M4R-RE-NIR1 (3 pan-sharpened bands).
M5Panchromatic band and NDVI (derived from pan-sharpened).
Table
Table 3. Machine learning model results. Shading indicates best values of performance measure for each image. Green shading indicates the primary metric, JI.
Table 3. Machine learning model results. Shading indicates best values of performance measure for each image. Green shading indicates the primary metric, JI.
ModelPerformance Measures
PrecisionRecallJIArea Ratio
Image 1M10.830.820.711.01
M20.880.830.741.06
M30.780.810.660.96
M40.800.830.690.96
M50.870.810.721.06
Image 2M10.780.720.601.08
M20.770.770.631.00
M30.780.720.601.08
M40.800.730.621.09
M50.780.730.611.07
Image 3M10.950.950.911.00
M20.960.950.921.01
M30.940.940.881.00
M40.950.950.911.00
M50.960.950.911.01
Image 6M10.950.980.930.98
M20.950.980.930.97
M30.950.960.910.98
M40.950.960.910.99
M50.930.980.920.95
Table
Table 4. Results sensitivity.
Table 4. Results sensitivity.
CV # across ModelsPerformance Measure
PrecisionRecallArea RatioJI
Image 15155
Image 21443
Image 31112
Image 61121
CV across Images
Model 11014420
Model 21011418
Model 31113521
Model 4913721
Model 5913619
# Coefficient of Variation calculated as the ratio of the standard deviation to the mean, expressed as a percentage.

Share and Cite

MDPI and ACS Style

Jones, E.G.; Wong, S.; Milton, A.; Sclauzero, J.; Whittenbury, H.; McDonnell, M.D. The Impact of Pan-Sharpening and Spectral Resolution on Vineyard Segmentation through Machine Learning. Remote Sens. 2020, 12, 934. https://doi.org/10.3390/rs12060934

AMA Style

Jones EG, Wong S, Milton A, Sclauzero J, Whittenbury H, McDonnell MD. The Impact of Pan-Sharpening and Spectral Resolution on Vineyard Segmentation through Machine Learning. Remote Sensing. 2020; 12(6):934. https://doi.org/10.3390/rs12060934

Chicago/Turabian Style

Jones, Eriita G., Sebastien Wong, Anthony Milton, Joseph Sclauzero, Holly Whittenbury, and Mark D. McDonnell. 2020. "The Impact of Pan-Sharpening and Spectral Resolution on Vineyard Segmentation through Machine Learning" Remote Sensing 12, no. 6: 934. https://doi.org/10.3390/rs12060934

APA Style

Jones, E. G., Wong, S., Milton, A., Sclauzero, J., Whittenbury, H., & McDonnell, M. D. (2020). The Impact of Pan-Sharpening and Spectral Resolution on Vineyard Segmentation through Machine Learning. Remote Sensing, 12(6), 934. https://doi.org/10.3390/rs12060934

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop