Synergistic Use of Single-Pass Interferometry and Radar Altimetry to Measure Mass Loss of NEGIS Outlet Glaciers between 2011 and 2014
Abstract
1. Introduction
2. Data and Methods
2.1. TanDEM-X Surface Elevation Change Rate
2.2. CryoSat-2 Surface Elevation Change Rate
2.3. Combination of Surface Elevation Change Rates
2.4. Volume to Mass Conversion
3. Uncertainty of the Mass Balance
3.1. Uncertainty of TDM Mass Change Rate
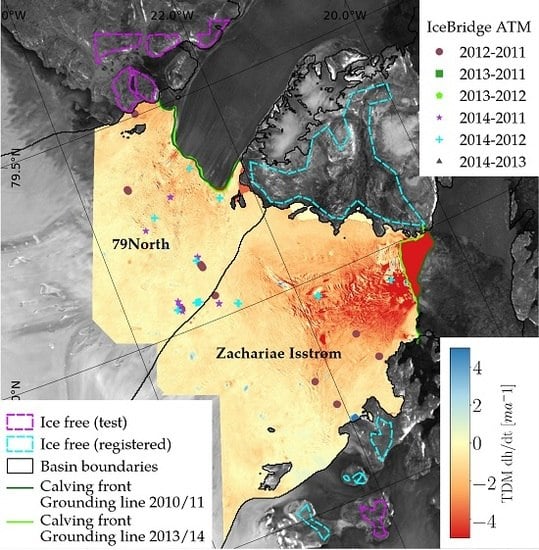
- The vertical bias between two differenced RawDEMs has been removed during vertical co-registration of all TDM RawDEMs. To estimate the uncertainty of this correction, we further analysed the SECR over flat, ice free areas that were not used during vertical co-registration (magenta areas in Figure 1) where no elevation change is expected. We measured remaining biases between and . Combined with the resulting differences to the CS-2 SECR in overlapping regions above 600 shown in Figure 5a, we assumed a value of as uncertainty in vertical co-registration for each pixel which is captured in the mass change uncertainty .
- Interferometric phase jumps and the resulting biases in the surface elevation change map can occur due to phase unwrapping errors during DEM generation. They appear as constant offsets in the DEM difference measurements. Areas possibly affected by phase unwrapping errors, radar shadow and layover are provided in a layer by ITP [30]. The resulting DEMs have been checked for such cases and no occurrences have been found in the observed area.
- Errors stemming from signal penetration into ice and snow could not be measured directly but are discussed in detail below. Because only the differences in signal penetration affect the measured SEC we assumed no uncertainties for areas with dB in both backscattering mosaics or where the absolute difference between the values is <1 dB. In all other areas, the uncertainty due to signal penetration was set to . Note that elevation biases due to a difference in signal penetration would manifest themselves in Figure 5a. Therefore, part of this error has already been accounted for in the error budget of the vertical co-registration and larger biases due to signal penetration have been ruled out in this comparison. The mass change error due to signal penetration is termed .
3.2. Uncertainty of CS-2 Mass Change Rate
4. Comparison to IceBridge ATM Elevation Changes
5. Results and Discussion
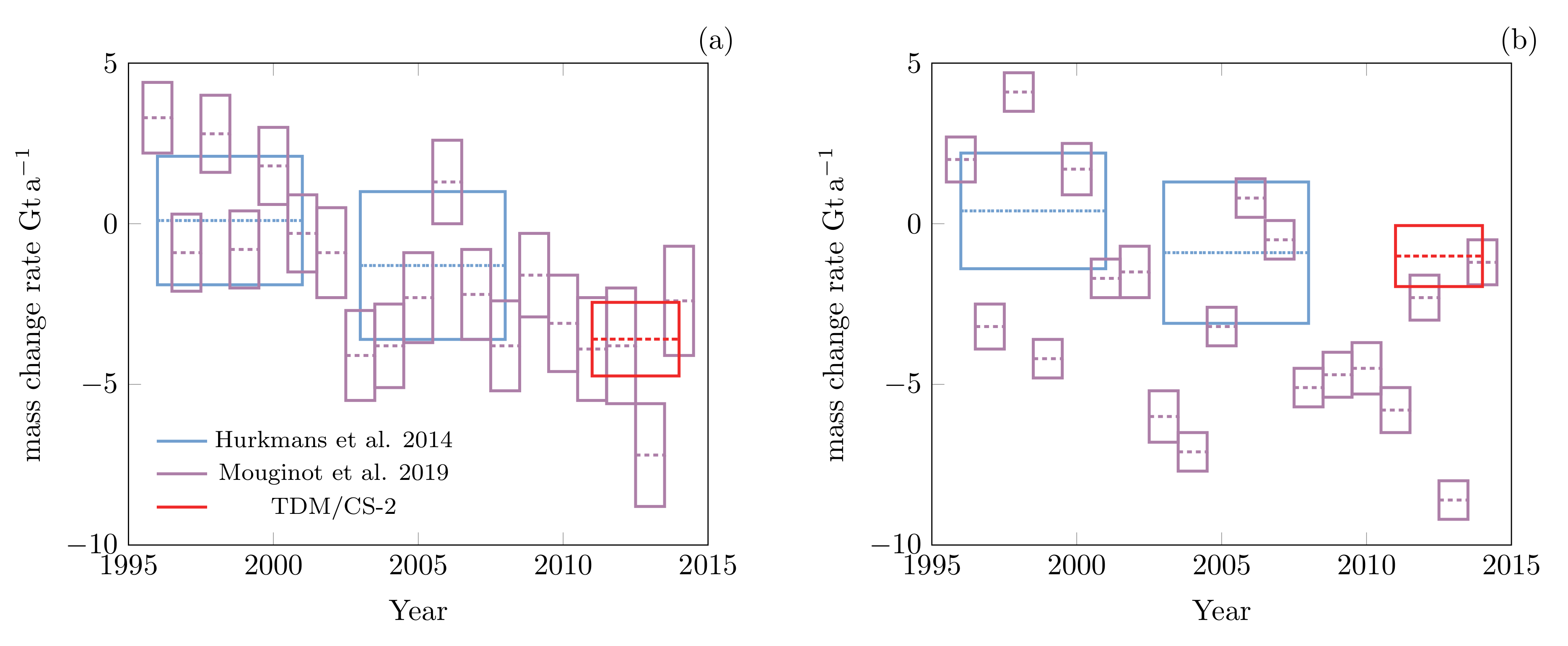
5.1. Comparison with Previous Mass Balance Estimates
5.2. Comparison of Different CS-2 Processing Strategies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GrIS | Greenland Ice Sheet |
| NEGIS | Northeast Greenland Ice Stream |
| 79North | Nioghalvfjerdsfjorden |
| ZI | Zachariæ Isstrøm |
| SMB | Surface Mass Balance |
| DEM | Digital Elevation Model |
| TDM | TanDEM-X |
| CS-2 | CryoSat-2 |
| SECR | Surface Elevation Change Rate |
| ITP | Integrated TDM Processor |
| NESZ | Noise Equivalent Sigma Zero |
| RAA | Repeat Altimetry Analysis |
| ESA | European Space Agency |
| LRM | Low-Resolution Mode |
| SARIn | Interferometric Synthetic Aperture Radar |
| GIMP | Greenland Ice Mapping Project |
| OCOG | Offset Center Of Gravity |
| TFMRA | Threshold First-Maximum Retracker |
| POCA | Point Of Closest Approach |
| HFK | Heterogeneous measurement-error Filtered Kriging |
| LeW | Leading edge Width |
| VCR | Volume Change Rate |
| FC | Firn Compaction |
| GIA | Glacial Isostatic Adjustment |
| EBU | Elastic Bed Uplift |
| HEM | Height Error Map |
References
- Vaughan, D.G.; Comiso, J.C.; Allison, I.; Carrasco, J.; Kaser, G.; Kwok, R.; Mote, P.; Murray, T.; Paul, F.; Ren, J.; et al. Observations: Cryosphere. Clim. Chang. 2013, 2103, 317–382. [Google Scholar]
- Van den Broeke, M.R.; Bamber, J.L.; Ettema, J.; Rignot, E.; Schrama, E.J.O.; van de Berg, W.J.; van Meijgaard, E.; Velicogna, I.; Wouters, B. Partitioning Recent Greenland Mass Loss. Science 2009, 326, 984–986. [Google Scholar] [CrossRef] [PubMed]
- Hanna, E.; Navarro, F.J.; Pattyn, F.; Domingues, C.M.; Fettweis, X.; Ivins, E.R.; Nicholls, R.J.; Ritz, C.; Smith, B.; Tulaczyk, S.; et al. Ice-Sheet Mass Balance and Climate Change. Nature 2013, 498, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, A.; Ivins, E.R.; Geruo, A.; Barletta, V.R.; Bentley, M.J.; Bettadpur, S.; Briggs, K.H.; Bromwich, D.H.; Forsberg, R.; Galin, N.; et al. A Reconciled Estimate of Ice-Sheet Mass Balance. Science 2012, 338, 1183–1189. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.A.; Aschwanden, A.; Bjørk, A.A.; Wahr, J.; Kjeldsen, K.K.; Kjær, K.H. Greenland Ice Sheet Mass Balance: A Review. Rep. Prog. Phys. 2015, 78, 046801. [Google Scholar] [CrossRef] [PubMed]
- Moon, T.; Joughin, I.R.; Smith, B.; Howat, I.M. 21st-Century Evolution of Greenland Outlet Glacier Velocities. Science 2012, 336, 576–578. [Google Scholar] [CrossRef]
- Kehrl, L.M.; Joughin, I.R.; Shean, D.E.; Floricioiu, D.; Krieger, L. Seasonal and Interannual Variabilities in Terminus Position, Glacier Velocity, and Surface Elevation at Helheim and Kangerlussuaq Glaciers from 2008 to 2016. J. Geophys. Res. Earth Surf. 2017, 122, 1635–1652. [Google Scholar] [CrossRef]
- Khan, S.A.; Kjær, K.H.; Bevis, M.; Bamber, J.L.; Wahr, J.; Kjeldsen, K.K.; Bjørk, A.A.; Korsgaard, N.J.; Stearns, L.A.; van den Broeke, M.R.; et al. Sustained Mass Loss of the Northeast Greenland Ice Sheet Triggered by Regional Warming. Nat. Clim. Chang. 2014, 4, 292–299. [Google Scholar] [CrossRef]
- Krieger, L.; Floricioiu, D.; Neckel, N. Drainage Basin Delineation for Outlet Glaciers of Northeast Greenland Based on Sentinel-1 Ice Velocities and TanDEM-X Elevations. Remote Sens. Environ. 2020, 237, 111483. [Google Scholar] [CrossRef]
- Hurkmans, R.T.W.L.; Bamber, J.L.; Davis, C.H.; Joughin, I.R.; Khvorostovsky, K.S.; Smith, B.S.; Schoen, N. Time-Evolving Mass Loss of the Greenland Ice Sheet from Satellite Altimetry. Cryosphere 2014, 8, 1725–1740. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Sundal, A.V.; Briggs, K.H.; Muir, A.; Ridout, A.J.; Hogg, A.E.; Wingham, D.J. Increased Ice Losses from Antarctica Detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- McMillan, M.; Leeson, A.; Shepherd, A.; Briggs, K.H.; Armitage, T.W.K.; Hogg, A.E.; Munneke, P.K.; van den Broeke, M.R.; Noël, B.P.Y.; van de Berg, W.J.; et al. A High-Resolution Record of Greenland Mass Balance. Geophys. Res. Lett. 2016, 43, 7002–7010. [Google Scholar] [CrossRef]
- Enderlin, E.M.; Howat, I.M.; Jeong, S.; Noh, M.J.; van Angelen, J.H.; van den Broeke, M.R. An Improved Mass Budget for the Greenland Ice Sheet. Geophys. Res. Lett. 2014, 41, 866–872. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Bjørk, A.A.; van den Broeke, M.R.; Millan, R.; Morlighem, M.; Noël, B.P.Y.; Scheuchl, B.; Wood, M. Forty-Six Years of Greenland Ice Sheet Mass Balance from 1972 to 2018. Proc. Natl. Acad. Sci. USA 2019, 116, 9239–9244. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zwally, H.J.; Abdalati, W.; Rowlands, D.D.; Ray, R.D.; Nerem, R.S.; Lemoine, F.G.; McCarthy, J.J.; Chinn, D.S. Recent Greenland Ice Mass Loss by Drainage System from Satellite Gravity Observations. Science 2006, 314, 1286–1289. [Google Scholar] [CrossRef]
- Sasgen, I.; van den Broeke, M.; Bamber, J.L.; Rignot, E.; Sørensen, L.S.; Wouters, B.; Martinec, Z.; Velicogna, I.; Simonsen, S.B. Timing and Origin of Recent Regional Ice-Mass Loss in Greenland. Earth Planet. Sci. Lett. 2012, 333-334, 293–303. [Google Scholar] [CrossRef]
- Howat, I.M.; Ahn, Y.; Joughin, I.; van den Broeke, M.R.; Lenaerts, J.T.M.; Smith, B. Mass Balance of Greenland’s Three Largest Outlet Glaciers, 2000–2010. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Scheuchl, B.; Fenty, I.; Khazendar, A.; Morlighem, M.; Buzzi, A.; Paden, J. Fast Retreat of Zachariæ Isstrøm, Northeast Greenland. Science 2015, 350, 1357–1361. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E. Glacier Catchments/Basins for the Greenland Ice Sheet; UC Irvine Dash: Irvine, CA, USA, 2019. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and Elevation Change of Greenland and Antarctica Derived from CryoSat-2. Cryosphere 2014, 8, 1539–1559. [Google Scholar] [CrossRef]
- Abdel Jaber, W.; Rott, H.; Floricioiu, D.; Wuite, J.; Miranda, N. Heterogeneous Spatial and Temporal Pattern of Surface Elevation Change and Mass Balance of the Patagonian Ice Fields between 2000 and 2016. Cryosphere 2019, 13, 2511–2535. [Google Scholar] [CrossRef]
- Rott, H.; Abdel Jaber, W.; Wuite, J.; Scheiblauer, S.; Floricioiu, D.; van Wessem, J.M.; Nagler, T.; Miranda, N.; van den Broeke, M.R. Changing Pattern of Ice Flow and Mass Balance for Glaciers Discharging into the Larsen A and B Embayments, Antarctic Peninsula, 2011 to 2016. Cryosphere 2018, 12, 1273–1291. [Google Scholar] [CrossRef]
- Braun, M.H.; Malz, P.; Sommer, C.; Farías-Barahona, D.; Sauter, T.; Casassa, G.; Soruco, A.; Skvarca, P.; Seehaus, T.C. Constraining Glacier Elevation and Mass Changes in South America. Nat. Clim. Chang. 2019, 9, 130–136. [Google Scholar] [CrossRef]
- Dussaillant, I.; Berthier, E.; Brun, F.; Masiokas, M.; Hugonnet, R.; Favier, V.; Rabatel, A.; Pitte, P.; Ruiz, L. Two Decades of Glacier Mass Loss along the Andes. Nat. Geosci. 2019, 12, 802–808. [Google Scholar] [CrossRef]
- Joughin, I.R.; Shean, D.E.; Smith, B.E.; Floricioiu, D. A Decade of Variability on Jakobshavn Isbrae: Ocean Temperatures Pace Speed Through Influence on Mélange Rigidity. Cryosphere Discuss. 2019, 1–27. [Google Scholar] [CrossRef]
- Milillo, P.; Rignot, E.; Rizzoli, P.; Scheuchl, B.; Mouginot, J.; Bueso-Bello, J.; Prats-Iraola, P. Heterogeneous Retreat and Ice Melt of Thwaites Glacier, West Antarctica. Sci. Adv. 2019, 5, eaau3433. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Wessel, B.; Bertram, A.; Gruber, A.; Bemm, S.; Dech, S. A new high-resolution elevation model of Greenland derived from TanDEM-X. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 7, 9–16. [Google Scholar] [CrossRef]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New Techniques in Satellite Altimeter Tracking Systems. In Proceedings of the 1986 International Geoscience and Remote Sensing Symposium (IGARSS’86) on Remote Sensing: Today’s Solutions for Tomorrow’s Information Needs; ESA SP-254:1339–1344; ESA: Zürich, Switzerland, 1986. [Google Scholar]
- Rossi, C.; Eineder, M.; Fritz, T.; Breit, H. TanDEM-X Mission: Raw DEM Generation. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Borla Tridon, D.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and Performance Assessment of the Global TanDEM-X Digital Elevation Model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR Processing and Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Morlighem, M.; Williams, C.N.; Rignot, E.; An, L.; Arndt, J.E.; Bamber, J.L.; Catania, G.A.; Chauché, N.; Dowdeswell, J.A.; Dorschel, B.; et al. BedMachine v3: Complete Bed Topography and Ocean Bathymetry Mapping of Greenland From Multibeam Echo Sounding Combined with Mass Conservation. Geophys. Res. Lett. 2017, 44, 11051–11061. [Google Scholar] [CrossRef]
- Legrésy, B.; Rémy, F.; Blarel, F. Along Track Repeat Altimetry for Ice Sheets and Continental Surface Studies. In Proceedings Symposium on 15 Years of Progress in Radar Altimetry; ESA-SP No. 614, Paper No. 181; European Space Agency Publication Division: Noordwijk, The Netherlands, 2006. [Google Scholar]
- Flament, T.; Rémy, F. Dynamic Thinning of Antarctic Glaciers from Along-Track Repeat Radar Altimetry. J. Glaciol. 2012, 58, 830–840. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Forsberg, R.; Khvorostovsky, K.; Meister, R.; Engdahl, M.E. 25 Years of Elevation Changes of the Greenland Ice Sheet from ERS, Envisat, and CryoSat-2 Radar Altimetry. Earth Planet. Sci. Lett. 2018, 495, 234–241. [Google Scholar] [CrossRef]
- Schröder, L.; Horwath, M.; Dietrich, R.; Helm, V.; van den Broeke, M.R.; Ligtenberg, S.R.M. Four Decades of Antarctic Surface Elevation Changes from Multi-Mission Satellite Altimetry. Cryosphere 2019, 13, 427–449. [Google Scholar] [CrossRef]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A Mission to Determine the Fluctuations in Earth’s Land and Marine Ice Fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Roemer, S.; Legrésy, B.; Horwath, M.; Dietrich, R. Refined Analysis of Radar Altimetry Data Applied to the Region of the Subglacial Lake Vostok/Antarctica. Remote Sens. Environ. 2007, 106, 269–284. [Google Scholar] [CrossRef]
- Howat, I.M.; Negrete, A.; Smith, B.E. The Greenland Ice Mapping Project (GIMP) Land Classification and Surface Elevation Data Sets. Cryosphere 2014, 8, 1509–1518. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Nielsen, K.; Lucas-Picher, P.; Spada, G.; Adalgeirsdottir, G.; Forsberg, R.; Hvidberg, C.S. Mass Balance of the Greenland Ice Sheet (2003–2008) from ICESat Data—The Impact of Interpolation, Sampling and Firn Density. Cryosphere 2011, 5, 173–186. [Google Scholar] [CrossRef]
- Ewert, H.; Groh, A.; Dietrich, R. Volume and Mass Changes of the Greenland Ice Sheet Inferred from ICESat and GRACE. J. Geodyn. 2012, 59-60, 111–123. [Google Scholar] [CrossRef]
- Nilsson, J.; Vallelonga, P.; Simonsen, S.B.; Sørensen, L.S.; Forsberg, R.; Dahl-Jensen, D.; Hirabayashi, M.; Goto-Azuma, K.; Hvidberg, C.S.; Kjær, H.A.; et al. Greenland 2012 Melt Event Effects on CryoSat-2 Radar Altimetry. Geophys. Res. Lett. 2015, 42, 3919–3926. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Sørensen, L.S. Implications of Changing Scattering Properties on Greenland Ice Sheet Volume Change from Cryosat-2 Altimetry. Remote Sens. Environ. 2017, 190, 207–216. [Google Scholar] [CrossRef]
- Legrésy, B.; Rémy, F. Altimetric Observations of Surface Characteristics of the Antarctic Ice Sheet. J. Glaciol. 1997, 43, 265–275. [Google Scholar] [CrossRef]
- Burgess, E.W.; Forster, R.R.; Box, J.E.; Mosley-Thompson, E.; Bromwich, D.H.; Bales, R.C.; Smith, L.C. A Spatially Calibrated Model of Annual Accumulation Rate on the Greenland Ice Sheet (1958–2007). J. Geophys. Res.: Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Christensen, W.F. Filtered Kriging for Spatial Data with Heterogeneous Measurement Error Variances. Biometrics 2011, 67, 947–957. [Google Scholar] [CrossRef] [PubMed]
- Wake, L.M.; Lecavalier, B.S.; Bevis, M. Glacial Isostatic Adjustment (GIA) in Greenland: A Review. Curr. Clim. Chang. Rep. 2016, 2, 101–111. [Google Scholar] [CrossRef]
- Peltier, W.R. Global Glacial Isostasy and the Surface of the Ice-Age Earth: The ice-5G (VM2) Model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Kuipers Munneke, P.; Ligtenberg, S.R.M.; Noël, B.P.Y.; Howat, I.M.; Box, J.E.; Mosley-Thompson, E.; McConnell, J.R.; Steffen, K.; Harper, J.T.; Das, S.B.; et al. Elevation Change of the Greenland Ice Sheet Due to Surface Mass Balance and Firn Processes, 1960–2014. Cryosphere 2015, 9, 2009–2025. [Google Scholar] [CrossRef]
- Ligtenberg, S.R.M.; Kuipers Munneke, P.; Noël, B.P.Y.; van den Broeke, M.R. Brief Communication: Improved Simulation of the Present-Day Greenland Firn Layer (1960–2016). Cryosphere 2018, 12, 1643–1649. [Google Scholar]
- Porter, C.; Morin, P.; Howat, I.; Noh, M.J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. ArcticDEM Harvard Dataverse V1; visited on 06/12/2019; Polar Geospatial Center: St. Paul, MN, USA, 2018. [Google Scholar] [CrossRef]
- Mätzler, C. Applications of the Interaction of Microwaves with the Natural Snow Cover. Remote Sens. Rev. 1987, 2, 259–387. [Google Scholar] [CrossRef]
- Stiles, W.; Ulaby, F. Dielectric Properties of Snow, RSL Technical Report 527-1, 1981. Available online: https://pdfs.semanticscholar.org/929e/a3c9076ec2b65defb9f5974f1b0180da41d5.pdf (accessed on 1 March 2020).
- Fischer, G.; Jäger, M.; Papathanassiou, K.; Hajnsek, I. Modeling the Vertical Backscattering Distribution in the Percolation Zone of the Greenland Ice Sheet with SAR Tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4389–4405. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Rott, H.; Moreira, A. Characterization of Snow Facies on the Greenland Ice Sheet Observed by TanDEM-X Interferometric SAR Data. Remote Sens. 2017, 9, 315. [Google Scholar] [CrossRef]
- Strößenreuther, U.; Horwath, M.; Schröder, L. How Different Analysis and Interpolation Methods Affect the Accuracy of Ice Surface Elevation Changes Inferred from Satellite Altimetry. Math. Geosci. 2020. [Google Scholar] [CrossRef]
- Rignot, E.; Bamber, J.L.; van den Broeke, M.R.; Davis, C.; Li, Y.; van de Berg, W.J.; van Meijgaard, E. Recent Antarctic Ice Mass Loss from Radar Interferometry and Regional Climate Modelling. Nat. Geosci. 2008, 1, 106–110. [Google Scholar] [CrossRef]
- Davis, C. A Robust Threshold Retracking Algorithm for Measuring Ice-Sheet Surface Elevation Change from Satellite Radar Altimeters. IEEE Trans. Geosci. Remote Sens. 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Nilsson, J.; Gardner, A.; Sandberg Sørensen, L.; Forsberg, R. Improved Retrieval of Land Ice Topography from CryoSat-2 Data and Its Impact for Volume-Change Estimation of the Greenland Ice Sheet. Cryosphere 2016, 10, 2953–2969. [Google Scholar] [CrossRef]
- Studinger, M. IceBridge ATM L4 Surface Elevation Rate of Change, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014; updated 2018. [Google Scholar]
- Noël, B.P.Y.; van de Berg, W.J.; van Wessem, J.M.; van Meijgaard, E.; van As, D.; Lenaerts, J.T.M.; Lhermitte, S.; Kuipers Munneke, P.; Smeets, C.J.P.P.; van Ulft, L.H.; et al. Modelling the Climate and Surface Mass Balance of Polar Ice Sheets Using RACMO2—Part 1: Greenland (1958–2016). Cryosphere 2018, 12, 811–831. [Google Scholar] [CrossRef]
- Mayer, C.; Schaffer, J.; Hattermann, T.; Floricioiu, D.; Krieger, L.; Dodd, P.A.; Kanzow, T.; Licciulli, C.; Schannwell, C. Large Ice Loss Variability at Nioghalvfjerdsfjorden Glacier, Northeast-Greenland. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Rott, H.; Rack, W.; Skvarca, P.; Angelis, H.D. Northern Larsen Ice Shelf, Antarctica: Further Retreat after Collapse. Ann. Glaciol. 2002, 34, 277–282. [Google Scholar] [CrossRef]






| Acquisition Date | Acquisition Item Id | Scene Ids | Rel. Orbit/ Direction | Baseline | HoA | Inc. Angle | ||
|---|---|---|---|---|---|---|---|---|
| Zachariæ Isstrøm & 79North | Master | 16 December 2010 | 1009366 | 8 | 71/A | 134.05 | 50.69 | 40.70 |
| 17 December 2010 | 1009396 | 3,4,5 | 86/A | 135.21 | 50.20 | 40.62 | ||
| 22 December 2010 | 1009542 | 6,7,8 | 162/A | 132.25 | 51.34 | 40.65 | ||
| 23 December 2010 | 1009578 | 2,3,4 | 10/A | 124.13 | 50.81 | 38.43 | ||
| 2 January 2011 | 1009916 | 7,8,9 | 162/A | 124.78 | 50.55 | 38.53 | ||
| 8 January 2011 | 1010081 | 3,4,5 | 86/A | 122.65 | 51.40 | 38.47 | ||
| Slave | 9 December 2013 | 1169543 | 6,7 | 65/D | 78.24 | 87.12 | 40.62 | |
| 10 December 2013 | 1169593 | 2,3 | 80/D | 80.32 | 84.99 | 40.68 | ||
| 15 December 2013 | 1169873 | 4,5,6 | 156/D | 80.19 | 84.82 | 40.60 | ||
| 20 December 2013 | 1170205 | 6,7 | 65/D | 86.95 | 75.07 | 39.37 | ||
| 21 December 2013 | 1170271 | 2,3 | 80/D | 86.79 | 75.19 | 39.37 | ||
| 26 December 2013 | 1170601 | 4,5,6 | 156/D | 88.33 | 73.90 | 39.36 | ||
| 12 January 2014 | 1171828 | 1,2,3 | 80/D | 93.34 | 75.21 | 41.47 | ||
| 17 January 2014 | 1172172 | 1,2,3,4 | 156/D | 93.84 | 74.78 | 41.44 |
| Sensor | Test Year | Ref. Year | [] | [] | Median [] | # |
|---|---|---|---|---|---|---|
| TDM | 2012 | 2011 | -0.213803 | 0.240390 | -0.173089 | 70 |
| 2014 | 2011 | 0.093840 | 0.210953 | 0.164076 | 63 | |
| 2014 | 2012 | -0.456726 | 1.123732 | -0.187544 | 104 | |
| - | - | -0.238624 | 0.793954 | -0.098592 | 237 | |
| CS-2 | 2012 | 2011 | 0.029139 | 0.115690 | 0.056126 | 392 |
| 2013 | 2011 | 0.069246 | 0.070397 | 0.067729 | 6504 | |
| 2013 | 2012 | 0.219659 | 0.119956 | 0.183430 | 62 | |
| 2014 | 2011 | 0.031706 | 0.065367 | 0.038373 | 443 | |
| 2014 | 2012 | 0.090216 | 0.057170 | 0.085921 | 3920 | |
| 2014 | 2013 | -0.055979 | 0.106620 | -0.041550 | 11,814 | |
| - | - | 0.007857 | 0.111920 | 0.028002 | 23,135 |
| Glacier Name | TDM | CS-2 (contrib.) | TDM+CS-2 | CS-2 (total) | Subaqua. | SMB | D |
|---|---|---|---|---|---|---|---|
| Including firn compaction: | |||||||
| ZI | -5.37 ± 0.62 | 1.78 ± 0.96 | -3.59 ± 1.15 | -1.25± 1.00 | -11.15 ± 0.03 | 8.95 | −12.54 |
| 79North | -1.31 ± 0.34 | 0.30 ± 0.88 | -1.01 ± 0.95 | -0.62 ± 0.91 | -0.05 ± 0.01 | 9.79 | −10.80 |
| Combined | -6.67 ± 0.71 | 2.08 ± 1.31 | -4.60 ± 1.49 | -1.87 ± 1.35 | -11.20 ± 0.03 | 18.74 | −23.34 |
| No correction for firn compaction: | |||||||
| ZI | -5.37 ± 0.62 | 1.11 ± 0.96 | -4.27 ± 1.14 | -1.92 ± 0.99 | -11.15 ± 0.03 | 8.95 | −13.21 |
| 79North | -1.31 ± 0.34 | -0.39 ± 0.88 | -1.70 ± 0.94 | -1.32 ± 0.90 | -0.05 ± 0.01 | 9.79 | −11.50 |
| Combined | -6.68 ± 0.71 | 0.71 ± 1.30 | -5.97 ± 1.48 | -3.24 ± 1.34 | -11.20 ± 0.03 | 18.74 | −24.71 |
| Glacier Name | A [] | [%] | [] | [] | [] |
|---|---|---|---|---|---|
| ZI | 3221 | 3.8 | -1.82 ± 0.55 | -5.86 ± 0.67 | -5.37 ± 0.62 |
| 79North | 1784 | 1.6 | -0.80 ± 0.55 | -1.43 ± 0.37 | -1.31 ± 0.34 |
| Combined | 5005 | 2.6 | -2.62 ± 0.77 | -7.29 ± 0.77 | -6.67 ± 0.71 |
| LRM Retracking | SARIn Retracking | LeW in LRM Regression | in SARIn Regression | |
|---|---|---|---|---|
| TU Dresden | 10% OCOG | TFMRA | ✓ | ✓ |
| AWI swath | TFMRA | swath | - | - |
| AWI TFMRA | TFMRA | TFMRA | - | - |
| AWI TFMRA + LeW | TFMRA | TFMRA | ✓ | - |
| CS-2 Processing | TDM Processing | Zachariæ Isstrøm | 79North | Total Mass Loss |
|---|---|---|---|---|
| TU Dresden | ✓ | -3.59 ± 1.15 | -1.01 ± 0.95 | -4.60 ± 1.49 |
| TU Dresden | - | -1.25 ± 1.00 | -0.62 ± 0.91 | -1.87 ± 1.35 |
| AWI swath | ✓ | -4.07 ± 3.86 | -1.85 ± 3.48 | -5.92 ± 5.19 |
| AWI swath | - | -3.33 ± 3.88 | -1.73 ± 3.53 | -5.05 ± 5.24 |
| AWI TFMRA | ✓ | -3.30 ± 1.53 | -0.54 ± 1.29 | -3.84 ± 2.00 |
| AWI TFMRA | - | -1.15 ± 1.45 | -0.18 ± 1.29 | -1.33 ± 1.94 |
| AWI TFMRA + LeW | ✓ | -3.95 ± 1.60 | -1.05 ± 1.36 | -5.00 ± 2.10 |
| AWI TFMRA + LeW | - | -1.81 ± 1.53 | -0.67 ± 1.35 | -2.48 ± 2.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krieger, L.; Strößenreuther, U.; Helm, V.; Floricioiu, D.; Horwath, M. Synergistic Use of Single-Pass Interferometry and Radar Altimetry to Measure Mass Loss of NEGIS Outlet Glaciers between 2011 and 2014. Remote Sens. 2020, 12, 996. https://doi.org/10.3390/rs12060996
Krieger L, Strößenreuther U, Helm V, Floricioiu D, Horwath M. Synergistic Use of Single-Pass Interferometry and Radar Altimetry to Measure Mass Loss of NEGIS Outlet Glaciers between 2011 and 2014. Remote Sensing. 2020; 12(6):996. https://doi.org/10.3390/rs12060996
Chicago/Turabian StyleKrieger, Lukas, Undine Strößenreuther, Veit Helm, Dana Floricioiu, and Martin Horwath. 2020. "Synergistic Use of Single-Pass Interferometry and Radar Altimetry to Measure Mass Loss of NEGIS Outlet Glaciers between 2011 and 2014" Remote Sensing 12, no. 6: 996. https://doi.org/10.3390/rs12060996
APA StyleKrieger, L., Strößenreuther, U., Helm, V., Floricioiu, D., & Horwath, M. (2020). Synergistic Use of Single-Pass Interferometry and Radar Altimetry to Measure Mass Loss of NEGIS Outlet Glaciers between 2011 and 2014. Remote Sensing, 12(6), 996. https://doi.org/10.3390/rs12060996