Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software
Abstract
1. Introduction
2. Methodology
2.1. The Filtering Parameters
2.2. Description of Functions Included in HyOF
2.2.1. Selection of Seed Points: OWM Function
2.2.2. Calculation of Penetrability: PNT Function
2.2.3. Decimation of the Point Cloud: DecHPoints Function
2.3. Integration of Functions in HyOF
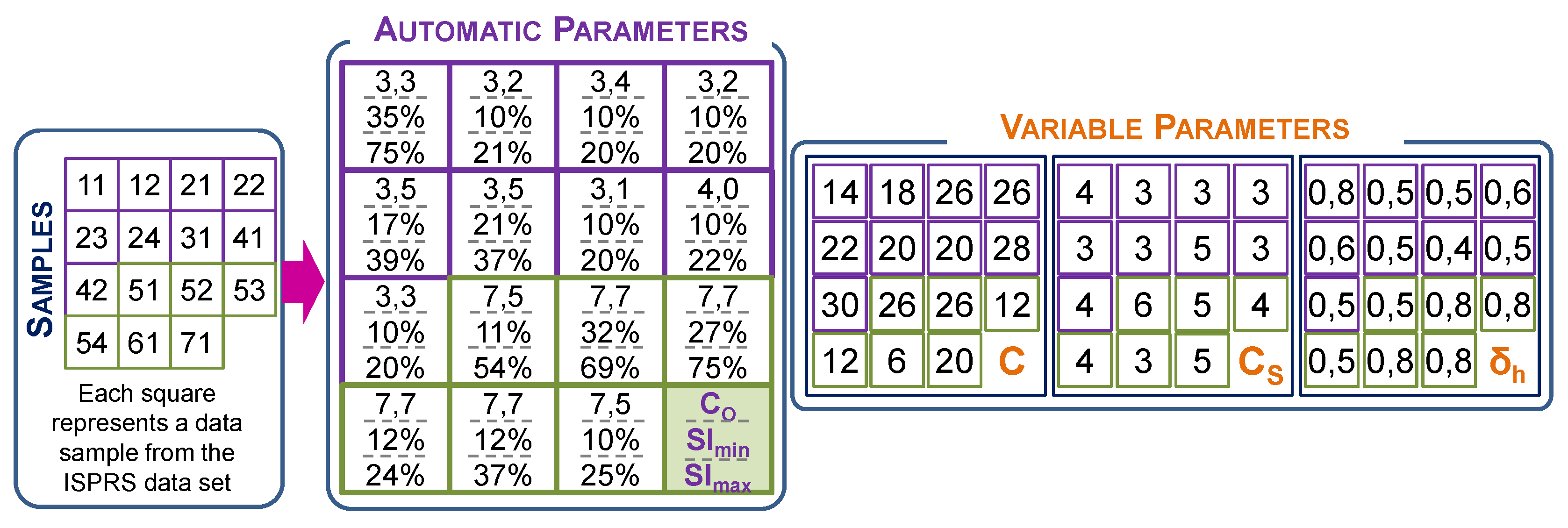
- Block 1. Automatic calculation of variables. The aim of this block of operations is to extract additional information from the LiDAR data (point density and penetrability) in order to assign values to the automatic parameters (C, Sl, and Sl). First, the mean weighted density (D) of the LiDAR point cloud is calculated. Then, the minimum and maximum slope thresholds are calculated from the 65% and 90% quantiles of the cell values of slope surface () and are assigned to the parameters Sl and Sl, respectively. To obtain the slope surface, a set of local lowest points (P) is first identified by using the OWM function (description in Section 2.2.1), where the values of the parameters are as follows: point cloud = point LiDAR cloud, w = W = C, OF = FO = 0.8, and OL = LO = 0.8 (description in Section 2.2.1). A statistical filtering technique is then applied to this point cloud to detect and remove points with abnormally high elevations that could lead to overestimation of the values of the parameters Sl and Sl. After this process, the selected points (P) are interpolated using the functions Tps (the field package in R software v.8.2-1) and interpolate (the raster package v.2.4-20), thus producing . This surface and the ground function (raster package v.2.4-20) are then used to calculate . Then, the automatic parameter C is obtained as . Finally, the penetrability raster () is calculated using the PNT function (description in Section 2.2.2). The values of the parameters of the PNT function are as follows: point cloud = point LiDAR cloud, = , W = C, and = .
- Block 2. Selection of ground seed points. The aim of this block is to identify the ground seed points (P) from a decimated cloud of non-ground points (P). Before selecting the ground seed points, the greatest possible number of non-ground points in the LiDAR point cloud are first identified and removed using the DecHPoints function (description in Section 2.2.3). The values of the parameters of this function are as follows: point cloud = point LiDAR cloud; W = C; = ; S = Sl; S = Sl; and = . The result of this function is a decimated point cloud (P). The OWM function is then applied to P to select the ground seed points. This method of selecting the local lowest points is one of the main differences between our hybrid filter and other algorithms that include seed point selection in the filtering process. As a novel feature, the OWM function includes the use of a moving window to select the points, by displacement with a longitudinal overlap between consecutive windows and transverse overlap between passes. In this case, the values of the parameters of the OWM function are as follows: point cloud = P, w = C, W = C, OF = FO = 0.8, OL = LO = 0.8. This process yields the ground seed points (P). Finally, the first reference surface () is created from the ground seed points. The choice of the interpolation method is one of the factors to be considered in the filtering process. On the basis of the findings reported by [31] and the experience of other authors in similar studies [4,29], we used the Tps function to interpolate the points classified as ground points in each iteration. The default values of the parameters are used so that the smoothing parameter lambda is automatically calculated by the Tps function. Finally, the interpolate function is used to transform the model generated with the Tps function to raster format with a resolution of C (C = 1 m).
- Block 3. Densification. The densification is carried out with the aim of identifying new ground points amongst unclassified points in order to reduce the number of omission errors. For this purpose, the difference in elevation between each point of original point cloud and a reference surface ( in the first iteration, iteratively up-dating with the inclusion of new points: ) is calculated. Although in other studies, the residuals have been calculated by considering the central cell and the eight neighboring cells [29], in this study, only the value of the central cell is taken into account (using the extract function, method option = “simple”, field package v.8.2-1) to prevent overestimation of the value of the residuals in heterogeneous or steep slope areas. All points with residuals lower than or equal to are considered ground points and are added to the ground point cloud (P). Finally, the ground point cloud is interpolated to calculate a new reference surface (). Many studies have used the residuals for classifying new points as ground points. On the basis of the findings of [23], the work in [8] demonstrated the need to assign different values to the parameter controlling the densification process according to the ground characteristics. Although this approach could have been used in the present study, it was found that it increased the number commission errors originating from the selection of the ground seed points, as well as the omission errors in a steep slope such as banks and gullies. Taking the above into account and the high level of detail of , we opted to assign a single threshold to the entire area (). The residuals obtained and the posterior densification of the point cloud are repeated either until no new ground points are added or until the maximum number of iterations defined by I is reached.
3. Experiments, Results, and Discussion
3.1. LiDAR Data
3.2. Accuracy Assessment
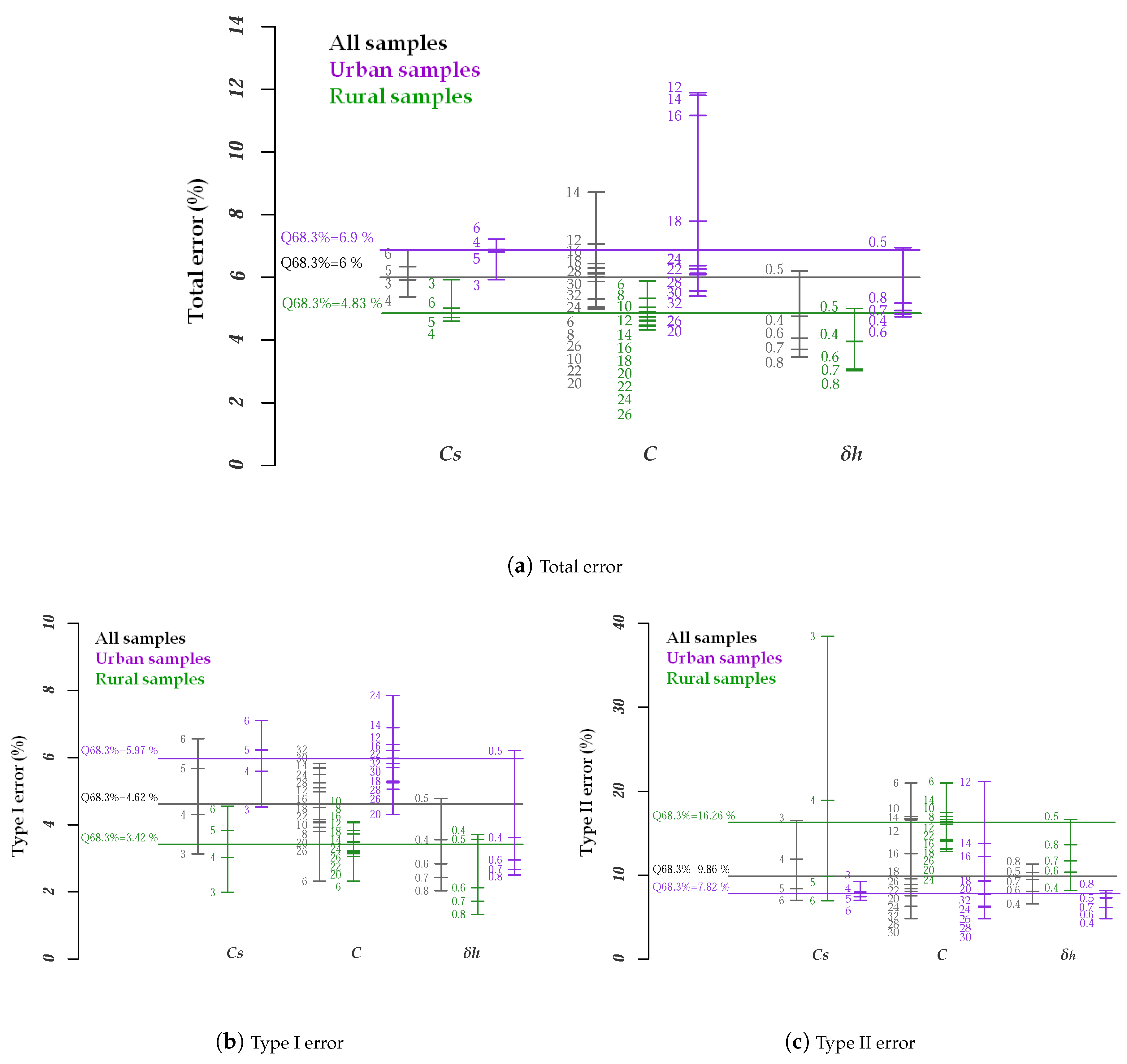
3.3. Parameter Tuning Results
3.4. Evaluation of HyOF Performance
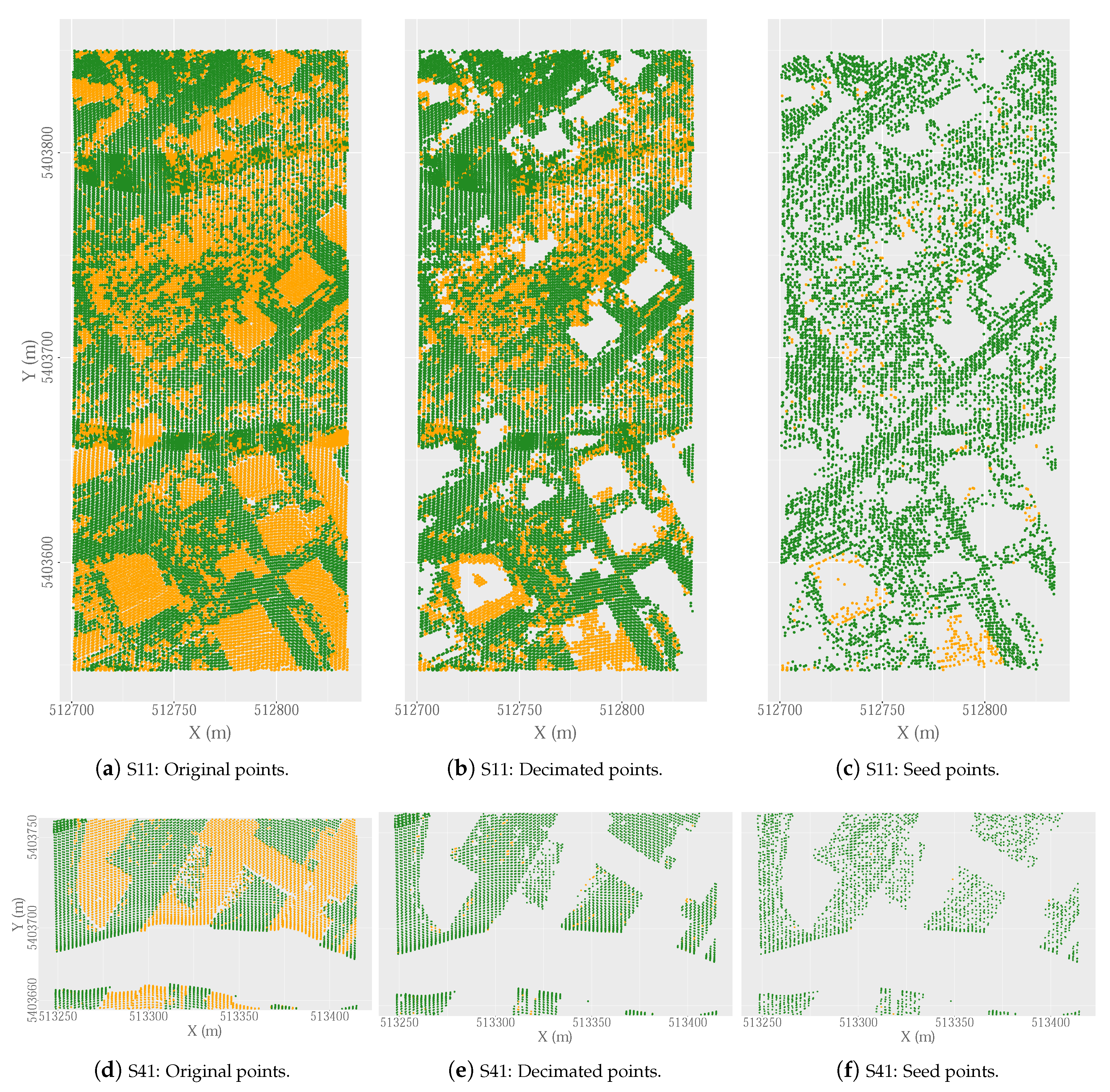
3.4.1. Efficacy of the Penetrability during the Decimation Process
3.4.2. Efficacy of the Decimation Process
3.4.3. Influence of the OWM Method on the Selection of Ground Seed Points
3.4.4. Influence of the Variable Parameters on the Filtering Accuracy
3.5. Assessment of Filtering Accuracy
3.5.1. Quantitative and Qualitative Results of HyOF
3.5.2. Comparison with Other Filtering Algorithms
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DecHPoints | Decimation of Highest Points |
| FO | Forward Overlap |
| HyOF | Hybrid Overlap Filter |
| LLP | Local Lowest Point |
| LMM | Local Minimum Method |
| LO | Lateral Overlap |
| OWM | Overlap Window Method |
References
- Moreira, J. La cartografía hoy: Evolución o revolución?. Las nuevas tecnologías y los cambios en la representación del territorio. In Actas del Congreso Año mil, año dos mil. Dos milenios en la Historia de España; Sociedad Estatal España Nuevo Milenio: Madrid, Spain, 2001; Volume 2, pp. 433–451. [Google Scholar]
- Li, Z.; Zhu, C.; Gold, C. Digital Terrain Modeling: Principles and Methodology; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ullrich, A.; Hollaus, M.; Briese, C.; Doneus, W.W.; Mücke, W. Improvements in DTM generation by using full-waveform Airborne Laser Scanning data. In Proceedings of the 7th International Conference on “Laser Scanning and Digital Aerial Photography. Today and Tomorrow”, Moscow, Russia, 6–7 December 2007; Volume 6, pp. 1–9. [Google Scholar]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Flood, M. LiDAR activities and research priorities in the commercial sector. Int. Arch. Photogramm. Remote Sens. 2001, 34, 3–8. [Google Scholar]
- Renslow, M. Manual of Airborne Topographic Lidar; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2012; p. 884. [Google Scholar]
- Chen, H.; Cheng, M.; Li, J.; Liu, Y. An iterative terrain recovery approach to automated DTM generation from airborne LIDAR point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 363–368. [Google Scholar] [CrossRef]
- Hu, H.; Ding, Y.; Zhu, Q.; Wu, B.; Lin, H.; Du, Z.; Zhang, Y.; Zhang, Y. An adaptative surface filter for airborne laser scanning point clouds by means of regularization and bending energy. ISPRS J. Photogramm. Remote Sens. 2014, 92, 98–111. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-step adaptive extraction method for ground points and breaklines from lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Maguya, A.S.; Junttila, V.; Kauranne, T. Adaptive algorithm for large scale dtm interpolation from lidar data for forestry applications in steep forested terrain. ISPRS J. Photogramm. Remote Sens. 2013, 85, 74–83. [Google Scholar] [CrossRef]
- Silván-Cárdenas, J.; Wang, L. A multi-resolution approach for filtering LiDAR altimetry data. ISPRS J. Photogramm. Remote Sens. 2006, 61, 11–22. [Google Scholar] [CrossRef]
- Shao, Y.C.; Chen, L.C. Automated Searching of Ground Points from Airborne Lidar Data Using a Climbing and Sliding Method. Photogramm. Eng. Remote Sens. 2008, 74, 625–635. [Google Scholar] [CrossRef]
- Hui, Z.; Hu, Y.; Yevenyo, Y.Z.; Yu, X. An Improved Morphological Algorithm for Filtering Airborne LiDAR Point Cloud Based on Multi-Level Kriging Interpolation. Remote Sens. 2016, 8, 35. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, J.-X.; Zhang, L.; Gao, J.-X. Urban DEM generation from airborne Lidar data. In 2009 Urban Remote Sensing Joint Event; IEEE: Shanghai, China, 2009; pp. 1–5. [Google Scholar]
- Yuan, F.; Zhang, J.; Zhang, L.; Gao, J. DEM generation from airborne LIDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 308–312. [Google Scholar]
- Lin, X.; Zhang, J. Segmentation-Based Filtering of Airborne LiDAR Point Clouds by Progressive Densification of Terrain Segments. Remote Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X. Filtering airborne LiDAR data by embedding smoothness-constrained segmentation in progressive TIN densification. ISPRS J. Photogramm. Remote Sens. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 111–118. [Google Scholar]
- Tóvári, D.; Pfeifer, N. Segmentation based robust interpoation—A new approach to laser data filtering. In Proceedings of the ISPRS WG III/3, III/4, V/3 Workshop “Laser scanning 2005”, Enschede, The Netherlands, 12–14 September 2005; pp. 79–84. [Google Scholar]
- Buján, S.; Sellers, C.A.; Cordero, M.; Miranda, D. DecHPoints: A new tool for improving LiDAR data filtering in urban areas. J. Photogramm. Remote Sens. Geoinf. Sci. 2020. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-art: DTM generation using airborne LIDAR data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Véga, C.; Durrieu, S.; Morel, J.; Allouis, T. A sequential iterative dual-filter for Lidar terrain modeling optimized for complex forested environments. Comput. Geosci. 2012, 44, 31–41. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Chang, L.D. Bare-Earth Extraction and Vehicle Detection in Forested Terrain from Airborne Lidar Point Clouds. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2010. [Google Scholar]
- Lu, W.L.; Little, J.J.; Sheffer, A.; Fu, H. Deforestation: Extracting 3D Bare-Earth Surface from Airborne LiDAR Data. In Proceedings of the Canadian Conference on Computer and Robot Vision, 2008. CRV ’08, Windsor, ON, Canada, 28–30 May 2008; pp. 203–210. [Google Scholar]
- ISO 9241-11. Ergonomic Requirements for Office Work with Visual Display Terminals (VDT)s—Part 11 Guidance on Usability; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- Hassan, Y.; Fernández, F.J.M.; Iazza, G. Diseño Web Centrado en el Usuario: Usabilidad y Arquitectura de la Información. Hipertext.net 2004. No 2. Available online: http://hdl.handle.net/10760/8998 (accessed on 10 April 2019).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Development Core Team: Vienna, Austria, 2010. [Google Scholar]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A multiresolution hierarchical classification algorithm for filtering airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A robust method of thin plate spline and its application to DEM construction. Comput. Geosci. 2012, 48, 9–16. [Google Scholar] [CrossRef]
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Report: ISPRS Comparison of Filters; Technical Report, ISPRS, Commission III, Working Group 3; Delft University of Technology: Delft, The Netherlands, 2003. [Google Scholar]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Susaki, J. Adaptive slope filtering of airborne LiDAR data in urban areas for Digital Terrain Model (DTM) generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef]
- Jahromi, A.B.; Zoej, M.J.V.; Mohammadzadeh, A.; Sadeghian, S. A novel filtering algorithm for bare-earth extraction from airborne laser scanning data using an artificial neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 836–843. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, W.; Liang, X.; Wan, P.; Qi, J.; Yu, S.; Yan, G.; Shao, J. Filtering Airborne LiDAR Data Through Complementary Cloth Simulation and Progressive TIN Densification Filters. Remote Sens. 2019, 11, 1037. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An improved simple morphological filter for the terrain classification of airborne LIDAR data. ISPRS J. Photogramm. Remote Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Zhao, N.; Guo, J.; Liu, G. A fast and robust interpolation filter for airborne lidar point clouds. PLoS ONE 2017, 12, e0176954. [Google Scholar] [CrossRef]
- Pfeifer, N.; Kostli, A.; Kraus, K. Interpolation and filtering of laser scanner data—Implementation and first results. Int. Arch. Photogramm. Remote Sens. 1998, 32 Pt 3/1, 31–36. [Google Scholar]
- Axelsson, P. Processing of laser scanner data—Algorithms and applications. ISPRS J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Elmqvist, M.; Jungert, E.; Lantz, F.; Persson, A.; Soderman, U. Terrain modelling and analysis using laser scanner data. Int. Arch. Photogramm. Remote Sens. 2001, 34, 219–226. [Google Scholar]
- Roggero, M. Airborne laser scanning: Clustering in raw data. Int. Arch. Photogramm. Remote Sens. 2001, 34, 227–232. [Google Scholar]
- Sithole, G. Filtering of laser altimetry data using a slope adaptive filter. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 203–210. [Google Scholar]
- Brovelli, M.A.; Cannata, M.; Longoni, U.M. Managing and processing LIDAR data within GRASS. In Proceedings of the GRASS Users Conference, Trento, Italy, 11–13 September 2002; Volume 29, pp. 1–29. [Google Scholar]
- Sohn, G.; Dowman, I. Terrain surface reconstruction by the use of tetrahedron model with the MDL criterion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34 Pt 3/A, 336–344. [Google Scholar]
- Wack, R.; Wimmer, A. Digital terrain models from airborne laserscanner data-a grid based approach. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34 Pt 3/B, 293–296. [Google Scholar]
- Yan, M.; Blaschke, T.; Liu, Y.; Wu, L. An object-based analysis filtering algorithm for airborne laser scanning. Int. J. Remote Sens. 2012, 33, 7099–7116. [Google Scholar] [CrossRef]
- Li, Y. Filtering Airborne LiDAR Data by an Improved Morphological Method Based on Multi-Gradient Analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40 Pt 1/W1, 191–194. [Google Scholar] [CrossRef]
- Li, Y.; Yong, B.; Wu, H.; An, R.; Xu, H. An Improved Top-Hat Filter with Sloped Brim for Extracting Ground Points from Airborne Lidar Point Clouds. Remote Sens. 2014, 6, 12885–12908. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Computationally Efficient Method for the Generation of a Digital Terrain Model From Airborne LiDAR Data Using Connected Operators. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 340–351. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Li, Y.; Yong, B.; Van Oosterom, P.; Lemmens, M.; Wu, H.; Ren, L.; Zheng, M.; Zhou, J. Airborne LiDAR Data Filtering Based on Geodesic Transformations of Mathematical Morphology. Remote Sens. 2017, 9, 1104. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X.; Luo, S.; Qin, H. A revised progressive TIN densification for filtering airborne LiDAR data. Measurement 2017, 104, 70–77. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Li, Y. Aerial Lidar Point Cloud Voxelization with its 3D Ground Filtering Application. Photogramm. Eng. Remote Sens. 2017, 83, 95–107. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Zhang, J.; Chen, D.; Peethambaran, J. Joint Clusters and Iterative Graph Cuts for ALS Point Cloud Filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 990–1004. [Google Scholar] [CrossRef]
- Hui, Z.; Li, D.; Jin, S.; Ziggah, Y.Y.; Wang, L.; Hu, Y. Automatic DTM extraction from airborne LiDAR based on expectation-maximization. Opt. Laser Technol. 2019, 112, 43–55. [Google Scholar] [CrossRef]
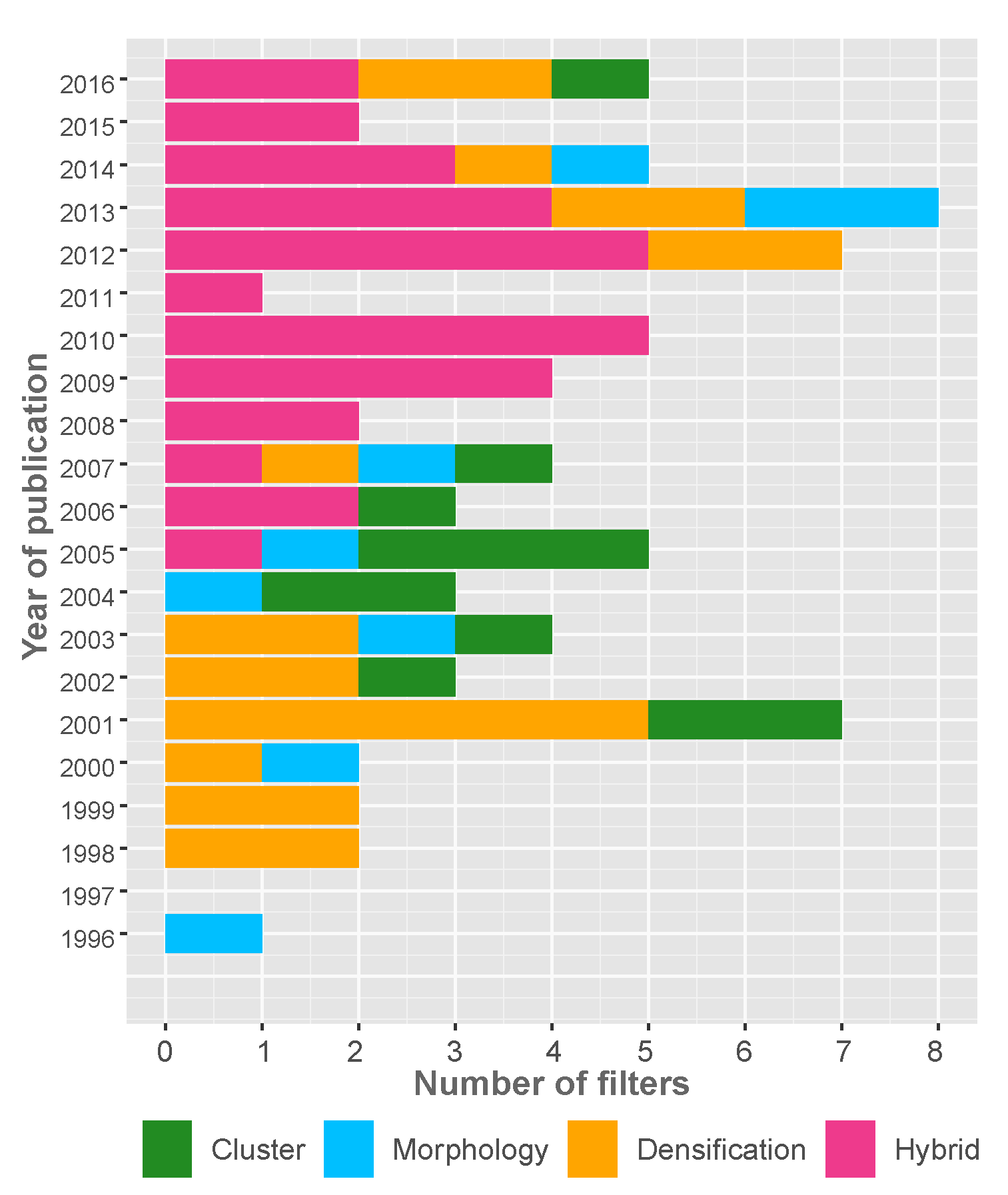








| Main Classic Categories of Filtering Methods | Suitable for | Limitations | Computational Efficiency |
|---|---|---|---|
| Morphology. These methods, based on mathematical morphology, retain terrain details by comparing the elevation of neighboring points. | Terrains with small objects. | • The size and shape of the structuring element. • Forest areas. • Low-density point cloud. • Rough and steep terrains. • Commission errors due to buildings of different heights and complex-shapes. | High |
| Cluster. These methods employ segmentation and clustering techniques to separate terrain points using the point attributes (position, elevation, intensity, etc.). | Urban areas, terrains with various objects. | • Segmentation errors due to the vegetation and complex buildings. • The filtering accuracy depends on the segmentation quality. • Overlapping surfaces (e.g., bridges). • Low-density point clouds make it difficult to find the segment borders. • High-density point cloud ⟶ too many small segments. | – |
| Densification. These methods compare the elevation of points with the estimated values through various interpolation methods (TIN, spline, etc.). In these cases, it is necessary to apply an iterative processing strategy. | Forest areas and steep terrains. | • Dense vegetation or buildings on hillside areas. • Succession of flat and steep areas. • Ramps. • Difficulty in identifying the ground points on breaklines. • Small objects. • Discontinuous terrains. | Middle |
| Fixed | Optimal number of points.np is the mean number of points per cell considered necessary to calculate the penetrability. Default value = 10. |
| Longitudinal and transverse overlap.FO (Forward Overlap) and LO (Lateral Overlap) represent the percentage longitudinal and transverse overlap (expressed as a decimal) between the windows used for selecting the seed points. Default value = 0.8. | |
| Resolution of intermediate raster models.C is the pixel size of the intermediate raster models generated in the densification phase from the points identified as ground points. Default value = 1 m. | |
| Maximum number of iterations.I is the maximum number of repetitions of the densification process. The process will end at the moment at which no new points are classified as ground points or I iterations have been carried out. Default value = 6. | |
| Variable | Maximum size of the area without ground points. C is set on the basis of the length of the shortest side of the largest building in the study area. In forest areas with dense vegetation, where the laser beam does not reach the soil, it is considered to be the maximum distance between any ground point and its nearest neighboring ground point. |
| Size of the window used for selecting the seed points. CS is the size of the moving window used to select the ground seed points. | |
| Residual. is the maximum distance permitted between a point and the reference surface to be considered the ground point. | |
| Automatic | Optimal cell size. CO is the size of the square cell that contains a mean number of np points. It is obtained from the square root of the ratio between np and the weighted mean of point density (D). |
| Minimum and maximum slope threshold. Slmin and Slmax. Some authors [17] use specific percentiles to assign a value automatically to specific parameters during the filtering process, which enables the parameter to be adjusted to the specific characteristics of each study area. In this case, the 65% percentile of the values of the cells of a slope raster () is used to set the value of the parameter Slmin and the 90% percentile to set the parameter Slmax. is calculated from an initial surface () obtained after interpolating a combination of local lowest points. These points are selected with a window size of C by using the OWM function. |
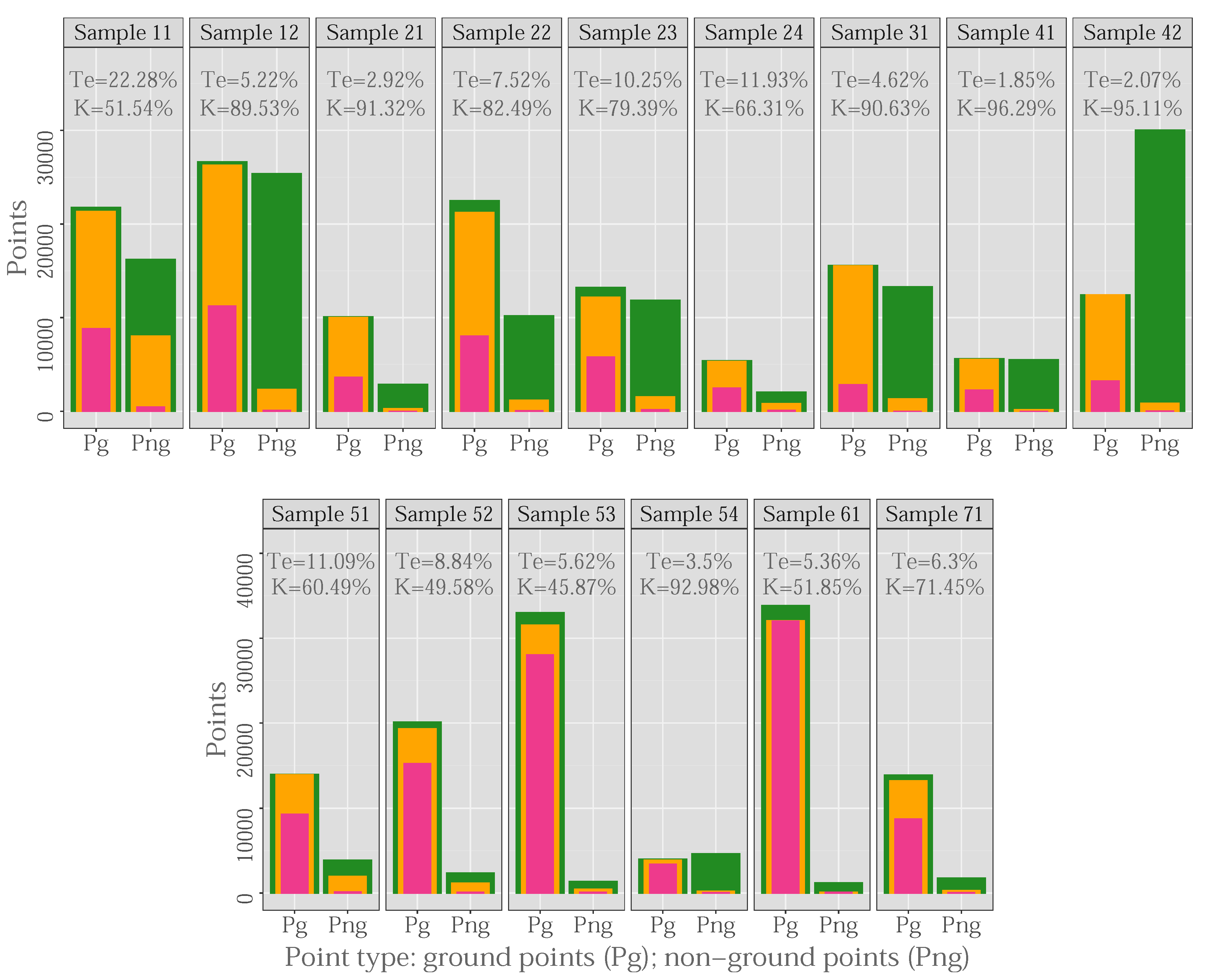
| Samples | Points | Density | Slope (%) | |||
|---|---|---|---|---|---|---|
| Pg(outliers) | Png(outliers) | pts/m | Mean | Q90 | ||
| S11-Urb.Vegetation and buildings on hillside. | 21,786(9) | 16,224 (13) | 1.3 | 0.93 | 53.8 | 100.0 |
| S12-Urb. Buildings and cars. | 26,691 (37) | 25,428 (35) | 1.0 | 0.95 | 11.9 | 26.8 |
| S21-Urb. Narrow bridge. | 10,085 (0) | 2875 (0) | 3.5 | 0.89 | 7.5 | 17.2 |
| S22-Urb. Bridge and gangway. | 22,504 (6) | 10,202 (17) | 2.2 | 0.96 | 16.4 | 43.9 |
| S23-Urb. Large buildings and data gaps. | 13,223 (0) | 11,872 (1) | 1.1 | 0.82 | 24.2 | 60.4 |
| S24-Urb. Ramp. | 5434 (30) | 2059 (1) | 2.6 | 0.83 | 24.1 | 57.0 |
| S31-Urb. Large buildings. | 15,556 (2) | 13,306 (14) | 1.2 | 1.01 | 4.6 | 9.2 |
| S41-Urb. Outliers (multi-path error). | 5602 (0) | 5629 (116) | 1.0 | 0.63 | 12.8 | 28.2 |
| S42-Urb. Railway station. | 12,443 (0) | 30,027 (2) | 0.4 | 0.91 | 6.8 | 15.5 |
| S51-Rur.Vegetation on moderate slopes. | 13,950 (0) | 3895 (0) | 3.6 | 0.18 | 18.9 | 56.2 |
| S52-Rur. Vegetation on river bank. | 20,112 (0) | 2362 (0) | 8.5 | 0.17 | 33.3 | 78.2 |
| S53-Rur. Terrain discontinuities. | 32,989 (0) | 1389 (0) | 23.8 | 0.17 | 39.2 | 78.3 |
| S54-Rur. Low resolution buildings. | 3983 (0) | 4625 (5) | 0.9 | 0.17 | 11.7 | 23.8 |
| S61-Rur. Sharp ridge and embankments. | 33,854 (0) | 1206 (0) | 28.1 | 0.17 | 16.3 | 40.2 |
| S71-Rur. Ramp, bridge, and underpass. | 13,875 (0) | 1770 (0) | 7.8 | 0.18 | 15.0 | 45.4 |
| Sample | Optimal Results | Unique Combination Results | ||||||
|---|---|---|---|---|---|---|---|---|
| TIe (%) | TIIe (%) | Te (%) | K (%) | TIe (%) | TIIe (%) | Te (%) | K (%) | |
| S11. Vegetation and buildings on hillside. | 9.59 | 12.06 | 10.64 | 78.27 | 11.76 | 16.90 | 13.95 | 71.44 |
| S12. Buildings and cars. | 2.33 | 2.65 | 2.49 | 95.02 | 3.06 | 3.16 | 3.11 | 93.78 |
| S21. Narrow bridge. | 0.22 | 3.76 | 1.00 | 97.06 | 0.21 | 3.90 | 1.03 | 96.99 |
| S22. Bridge and gangway. | 3.80 | 7.84 | 5.06 | 88.23 | 5.86 | 6.90 | 6.19 | 85.82 |
| S23. Large buildings and data gaps. | 5.49 | 5.86 | 5.67 | 88.64 | 11.16 | 4.30 | 7.91 | 84.19 |
| S24. Ramp. | 2.74 | 9.18 | 4.51 | 88.61 | 5.43 | 7.82 | 6.09 | 85.03 |
| S31. Large buildings. | 0.80 | 1.72 | 1.22 | 97.54 | 0.53 | 2.41 | 1.40 | 97.19 |
| S41. Outliers (multi-path error). | 2.12 | 1.23 | 1.67 | 96.65 | 2.71 | 1.05 | 1.88 | 96.24 |
| S42. Railway station. | 1.10 | 0.69 | 0.81 | 98.05 | 1.10 | 0.69 | 0.81 | 98.05 |
| S51. Vegetation on moderate slope. | 0.47 | 6.42 | 1.77 | 94.72 | 0.18 | 18.95 | 4.28 | 86.59 |
| S52. Vegetation on river bank. | 1.89 | 16.26 | 3.40 | 81.91 | 2.01 | 21.30 | 4.04 | 78.14 |
| S53. Terrain discontinuities. | 2.89 | 20.59 | 3.60 | 62.21 | 4.17 | 17.64 | 4.72 | 56.25 |
| S54. Low resolution buildings. | 1.93 | 2.79 | 2.39 | 95.19 | 1.73 | 4.58 | 3.26 | 93.45 |
| S61. Sharp ridge and embankments. | 0.62 | 11.77 | 1.00 | 85.29 | 3.03 | 2.90 | 3.03 | 67.37 |
| S71. Ramp, bridge, and underpass. | 0.59 | 7.18 | 1.34 | 93.27 | 1.23 | 6.84 | 1.87 | 90.81 |
| All samples | 2.62 | 4.70 | 3.34 | 92.62 | 3.94 | 5.63 | 4.52 | 90.04 |
| Author | S11 | S12 | S21 | S22 | S23 | S24 | S31 | S41 | S42 | S51 | S52 | S53 | S54 | S61 | S71 | K | K | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pfeifer (1998) [40] | 66.3 | 91.1 | 92.8 | 85.2 | 83.7 | 79.2 | 96.4 | 78.6 | 93.8 | 89.6 | 41.2 | 31.1 | 90.1 | 47.1 | 66.8 | 83.2 | 86.6 | 62.4 |
| Axelsson (1999) [41] | 78.6 | 93.6 | 86.2 | 91.4 | 92.0 | 88.8 | 90.5 | 72.4 | 96.2 | 91.7 | 83.7 | 39.4 | 70.7 | 74.5 | 91.5 | 89.3 | 90.1 | 78.3 |
| Elmqvist (2001) [42] | 58.9 | 84.2 | 54.9 | 69.3 | 76.6 | 52.1 | 88.7 | 84.8 | 93.6 | 30.1 | 3.3 | 0.6 | 88.9 | 0.7 | 6.9 | 40.9 | 77.8 | 4.8 |
| Roggero (2001) [43] | 59.9 | 86.9 | 75.7 | 54.7 | 54.9 | 54.5 | 95.7 | 75.8 | 89.7 | 91.2 | 60.8 | 25.8 | 50.1 | 21.8 | 78.3 | 73.7 | 75.3 | 54.5 |
| Sithole (2001) [44] | 55.5 | 79.9 | 80.2 | 59.4 | 55.8 | 50.7 | 93.7 | 51.3 | 90.8 | 80.7 | 31.1 | 10.6 | 84.5 | 19.2 | 40.8 | 65.7 | 72.9 | 37.5 |
| Brovelli (2002) [45] | 32.2 | 67.9 | 76.6 | 56.6 | 46.1 | 35.8 | 74.6 | 67.2 | 84.2 | 50.4 | 15.9 | 6.0 | 87.2 | 19.2 | 25.5 | 53.2 | 62.1 | 25.8 |
| Sohn (2002) [46] | 59.5 | 83.2 | 76.1 | 82.3 | 80.2 | 68.6 | 87.1 | 77.6 | 95.7 | 75.5 | 55.0 | 20.3 | 93.5 | 67.5 | 89.1 | 79.8 | 81.6 | 63.3 |
| Wack (2002) [47] | 54.1 | 86.9 | 87.6 | 83.5 | 78.3 | 74.3 | 95.6 | 81.9 | 91.6 | 71.4 | 36.4 | 16.8 | 88.5 | 29.7 | 48.3 | 75.0 | 82.4 | 45.8 |
| Lu (2008) [25] | 43.2 | 80.5 | 69.1 | 72.9 | 78.7 | 64.6 | 89.8 | 73.9 | 88.3 | 82.8 | 57.2 | 17.9 | 86.9 | 46.2 | 62.9 | 75.5 | 75.4 | 58.9 |
| Shao (2008) [12] | 76.0 | 92.0 | 87.2 | 88.6 | 90.4 | 87.7 | 97.6 | 90.1 | 94.8 | 88.9 | 85.6 | 55.0 | 94.5 | 80.7 | 84.7 | 90.5 | 90.1 | 84.7 |
| Shao (2008) [12] | 75.9 | 92.0 | 87.2 | 85.9 | 90.4 | 87.7 | 97.5 | 90.1 | 94.8 | 88.4 | 85.6 | 55.0 | 93.8 | 80.7 | 82.6 | 90.3 | 89.9 | 84.2 |
| Chang (2010) (SMSM) [24] | 72.2 | 93.0 | 96.4 | 93.9 | 91.9 | 84.3 | 97.5 | 85.9 | 96.8 | 90.5 | 79.6 | 60.8 | 94.4 | 82.9 | 89.3 | 91.6 | 91.1 | 87.0 |
| Chang (2010) (SMSM) [24] | 68.9 | 91.2 | 95.3 | 90.9 | 91.9 | 83.9 | 93.4 | 85.0 | 95.0 | 88.2 | 77.5 | 52.2 | 93.5 | 72.4 | 87.7 | 89.2 | 89.1 | 82.1 |
| Chang (2010) (SSA) [24] | 78.1 | 94.3 | 95.0 | 92.2 | 90.6 | 86.7 | 97.9 | 93.9 | 96.6 | 89.3 | 84.9 | 69.5 | 91.4 | 81.0 | 88.2 | 92.6 | 92.2 | 87.8 |
| Mongus (2012) [4] | 77.3 | 89.7 | 94.1 | 84.7 | 88.3 | 80.0 | 93.3 | 92.6 | 87.0 | 92.2 | 68.4 | 42.1 | 86.6 | 65.1 | 85.0 | 87.1 | 87.8 | 76.7 |
| TerraScan | 68.4 | 77.0 | 71.4 | 76.8 | 84.0 | 71.0 | 82.6 | 74.2 | 91.9 | 98.9 | 78.4 | 62.8 | 83.1 | 78.4 | 90.9 | 83.6 | 79.8 | 85.7 |
| Yan (2012) [48] | 62.8 | 86.7 | 82.0 | 75.4 | 68.8 | 55.7 | 92.3 | 71.9 | 87.8 | 81.6 | 57.5 | 24.4 | 84.1 | 33.9 | 52.7 | 76.9 | 79.6 | 56.6 |
| Chen (2013) [29] | 74.1 | 93.2 | 96.1 | 89.0 | 89.5 | 84.5 | 97.8 | 88.8 | 95.8 | 95.2 | 78.9 | 46.7 | 93.8 | 77.4 | 93.2 | 90.5 | 90.5 | 83.4 |
| Li (2013) [49] | 74.3 | 92.5 | 92.8 | 90.6 | 87.7 | 86.1 | 95.0 | 86.6 | 92.8 | 88.5 | 47.1 | 33.1 | 92.1 | 50.0 | 79.2 | 86.2 | 89.4 | 66.6 |
| Pingel (2013) [38] | 83.1 | 94.1 | 96.8 | 92.2 | 90.7 | 91.1 | 98.2 | 88.2 | 96.5 | 95.8 | 81.0 | 68.2 | 95.4 | 87.3 | 91.8 | 93.3 | 92.9 | 90.1 |
| Zhang (2013) [17] | 63.4 | 88.2 | 84.9 | 70.1 | 76.0 | 55.6 | 95.3 | 59.1 | 90.3 | 83.9 | 50.6 | 44.8 | 87.2 | 25.0 | 59.5 | 78.9 | 80.5 | 60.0 |
| Hu (2014) [8] | 83.0 | 94.8 | 97.2 | 92.4 | 91.2 | 90.4 | 98.2 | 88.2 | 98.3 | 93.9 | 86.2 | 66.4 | 95.3 | 86.8 | 92.6 | 93.6 | 93.3 | 89.74 |
| Hu (2014) [8] | 82.8 | 94.0 | 94.3 | 91.8 | 90.5 | 89.5 | 93.4 | 87.5 | 97.1 | 91.5 | 83.7 | 53.1 | 94.6 | 71.1 | 90.5 | 91.7 | 92.1 | 84.1 |
| Li (2014) [50] | 71.8 | 93.5 | 92.7 | 89.7 | 85.3 | 86.6 | 94.9 | 78.5 | 93.6 | 88.6 | 43.6 | 33.7 | 90.7 | 55.6 | 81.3 | 85.8 | 88.7 | 66.6 |
| Lin (2014) [16] | 61.4 | 90.1 | 80.9 | 78.4 | 71.4 | 86.8 | 97.0 | 35.9 | 84.8 | 87.9 | 65.6 | 36.7 | 78.7 | 48.0 | 73.4 | 81.0 | 80.6 | 68.4 |
| Mongus (2014) [51] | 79.0 | 93.4 | 96.0 | 90.1 | 87.6 | 88.8 | 92.9 | 91.9 | 93.2 | 80.1 | 75.6 | 55.6 | 90.8 | 60.1 | 82.5 | 90.0 | 90.6 | 78.8 |
| Hui (2016) [13] | 72.9 | 93.0 | 93.4 | 87.6 | 89.7 | 81.9 | 97.3 | 78.8 | 95.4 | 85.1 | 69.5 | 41.8 | 91.6 | 67.8 | 79.9 | 88.7 | 89.5 | 76.7 |
| Yang (2016) [9] | 78.7 | 94.6 | 91.7 | 89.2 | 91.0 | 91.3 | 96.8 | 95.0 | 97.0 | 88.9 | 84.1 | 66.6 | 93.7 | 81.6 | 70.9 | 92.1 | 92.1 | 85.4 |
| Zhang (2016) [52] | 75.2 | 94.0 | 90.5 | 77.7 | 90.4 | 92.7 | 96.8 | 89.7 | 96.2 | 91.1 | 77.1 | 46.9 | 93.6 | 78.1 | 68.0 | 89.8 | 89.9 | 81.9 |
| Chen (2017) [39] | 80.6 | 94.3 | 96.7 | 91.0 | 91.0 | 90.8 | 97.4 | 92.4 | 98.0 | 94.5 | 83.1 | 62.0 | 94.4 | 85.3 | 90.0 | 93.0 | 92.8 | 88.6 |
| Li (2017) [53] | 74.2 | 92.9 | 94.7 | 91.0 | 89.3 | 85.2 | 91.5 | 75.1 | 85.4 | 86.7 | 67.8 | 38.8 | 89.2 | 73.1 | 86.5 | 87.2 | 87.8 | 75.9 |
| Nie (2017) [54] | 57.8 | 86.9 | 84.1 | 65.5 | 61.6 | 42.7 | 95.6 | 47.7 | 93.1 | 91.8 | 50.8 | 24.0 | 91.8 | 42.8 | 79.9 | 76.3 | 76.6 | 61.8 |
| Wang (2017) [55] | 60.5 | 92.0 | 94.0 | 88.3 | 88.1 | 93.2 | 96.8 | 95.7 | 97.4 | 74.6 | 70.2 | 48.4 | 88.8 | 63.2 | 72.2 | 88.4 | 88.6 | 76.9 |
| Ni (2018) [56] | 63.1 | 82.3 | 79.1 | 69.5 | 79.6 | 58.6 | 85.7 | 88.5 | 87.2 | 93.0 | 54.3 | 31.1 | 89.4 | 61.9 | 73.5 | 79.6 | 79.2 | 69.2 |
| Cai (2019) [37] | 66.0 | 82.3 | 65.2 | 90.0 | 82.8 | 55.3 | 85.5 | 74.1 | 88.4 | 89.1 | 71.9 | 55.8 | 94.8 | 86.9 | 89.3 | 84.5 | 81.7 | 85.2 |
| Hui (2019) [57] | 65.6 | 85.7 | 92.6 | 71.3 | 82.1 | 64.8 | 86.1 | 77.1 | 89.7 | 83.4 | 56.1 | 13.7 | 88.8 | 14.4 | 72.8 | 74.5 | 81.8 | 46.2 |
| HyOF | 78.3 | 95.0 | 97.1 | 88.2 | 88.6 | 88.6 | 97.5 | 96.7 | 98.1 | 94.7 | 81.9 | 62.2 | 95.2 | 85.3 | 93.3 | 92.6 | 92.2 | 88.7 |
| HyOF | 71.4 | 93.8 | 97.0 | 85.8 | 84.2 | 85.0 | 97.2 | 96.2 | 98.1 | 86.6 | 78.1 | 56.3 | 93.5 | 67.4 | 90.8 | 90.1 | 90.0 | 82.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buján, S.; Cordero, M.; Miranda, D. Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software. Remote Sens. 2020, 12, 1051. https://doi.org/10.3390/rs12071051
Buján S, Cordero M, Miranda D. Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software. Remote Sensing. 2020; 12(7):1051. https://doi.org/10.3390/rs12071051
Chicago/Turabian StyleBuján, Sandra, Miguel Cordero, and David Miranda. 2020. "Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software" Remote Sensing 12, no. 7: 1051. https://doi.org/10.3390/rs12071051
APA StyleBuján, S., Cordero, M., & Miranda, D. (2020). Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software. Remote Sensing, 12(7), 1051. https://doi.org/10.3390/rs12071051







