Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model
Abstract
:1. Introduction
- What machine learning algorithm should be selected? The back-propagation (BP) neural network model is a commonly chosen model. The input of the BP model is the data at a time point. As is known, the change of water level caused by precipitation is not an instant process and it always has a time delay. Therefore, a neural network model considering the time delay effect, such as the nonlinear autoregressive exogenous model (NARX), may achieve better results than the BP neural network model [21,22].
- What is the effect of different grid precipitation products for modeling the relationship? There are several types of grid precipitation products. Many studies have discussed the accuracy of precipitation products and their applicability in different regions and used them as data sources for data-driven methods [21,23], but the effect on using different data sources for modeling the relationship of precipitation and water level has not been discussed [24,25,26].
- What is the effect of different spatial resolution data from the same precipitation products in modeling the relationship?
2. Materials and Methods
2.1. Study Area and Data Used
2.2. Methodology
- (I) Selection of input parameters: This part determined the inputs of the used models. Considering the physical model, the input variables of the neural network were selected by referring to the physical process of the hydrological model in part I.
- (II) Train data preprocessing: This part prepared training data for the neural network models. To improve the performance of the neural network model and avoid the over-fitting of models, the unnecessary information and some noise were removed by the principal component analysis (PCA) dimensionality reduction in order to speed up the convergence of the model in part II.
- (III) Precipitation–water level modeling: This part compared the modeling methods. As for model fitting, we chose a BP neural network to build the relationship between precipitation and water level; meanwhile, a NARX time series network was also chosen to build the relationship between precipitation and water level in part III.
- (IV) Evaluation of precipitation–water level modeling: This part chose correlation coefficients (R), percentage bias (PBias), root-mean-square error (RMSE), Nash–Sutcliffe efficiency (NSE), and mean absolute error (MAE) as the criteria for the evaluation of precipitation–water level modeling.
2.2.1. Selection of Input Parameters
2.2.2. Train Data Preprocessing
- Here is a sample set D:
- Decentralize all samples:
- Compute the covariance matrix of samples: XXT;
- Eigenvalue decomposition of covariance matrix XXT;
- Extract the largest characteristic value eigenvalues:
- Output the projection matrix after dimension reduction:
2.2.3. Precipitation–Water Level Modeling
Back Propagation Neural Network Model
Nonlinear Autoregressive Exogenous Model
2.2.4. Evaluation of Precipitation–Water Level Modeling
3. Results and Discussion
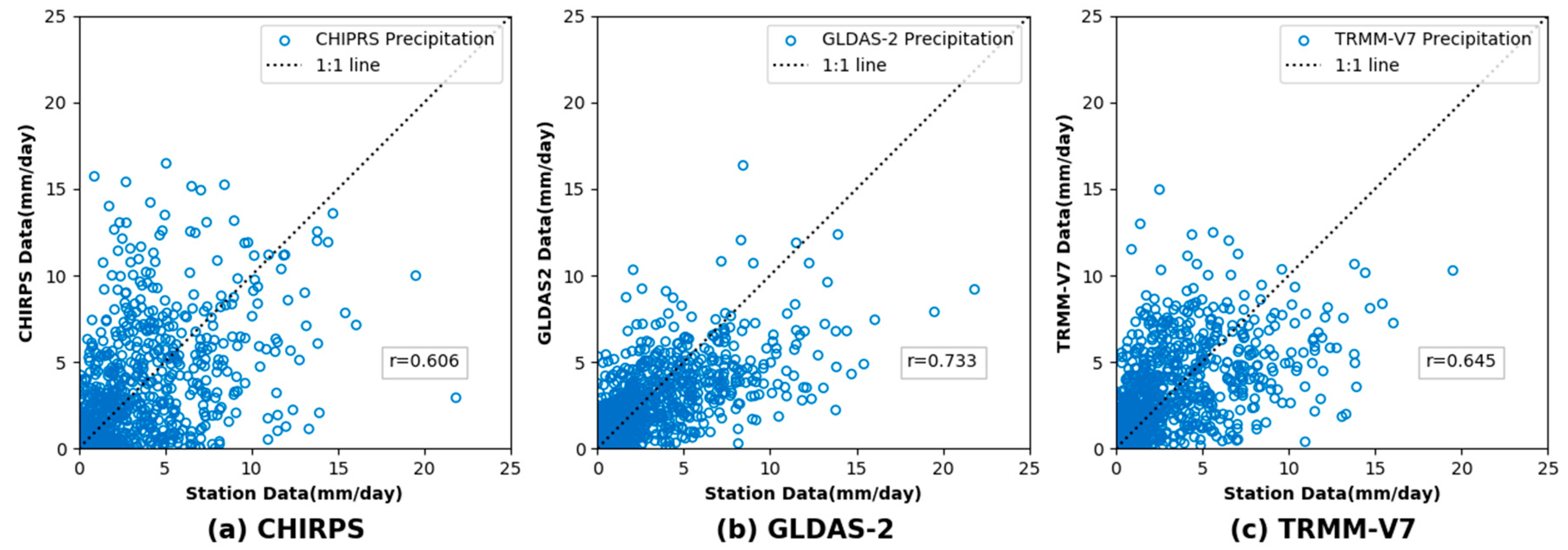
3.1. Comparison of Different Grid Precipitation Products with Respect to the Observed Data
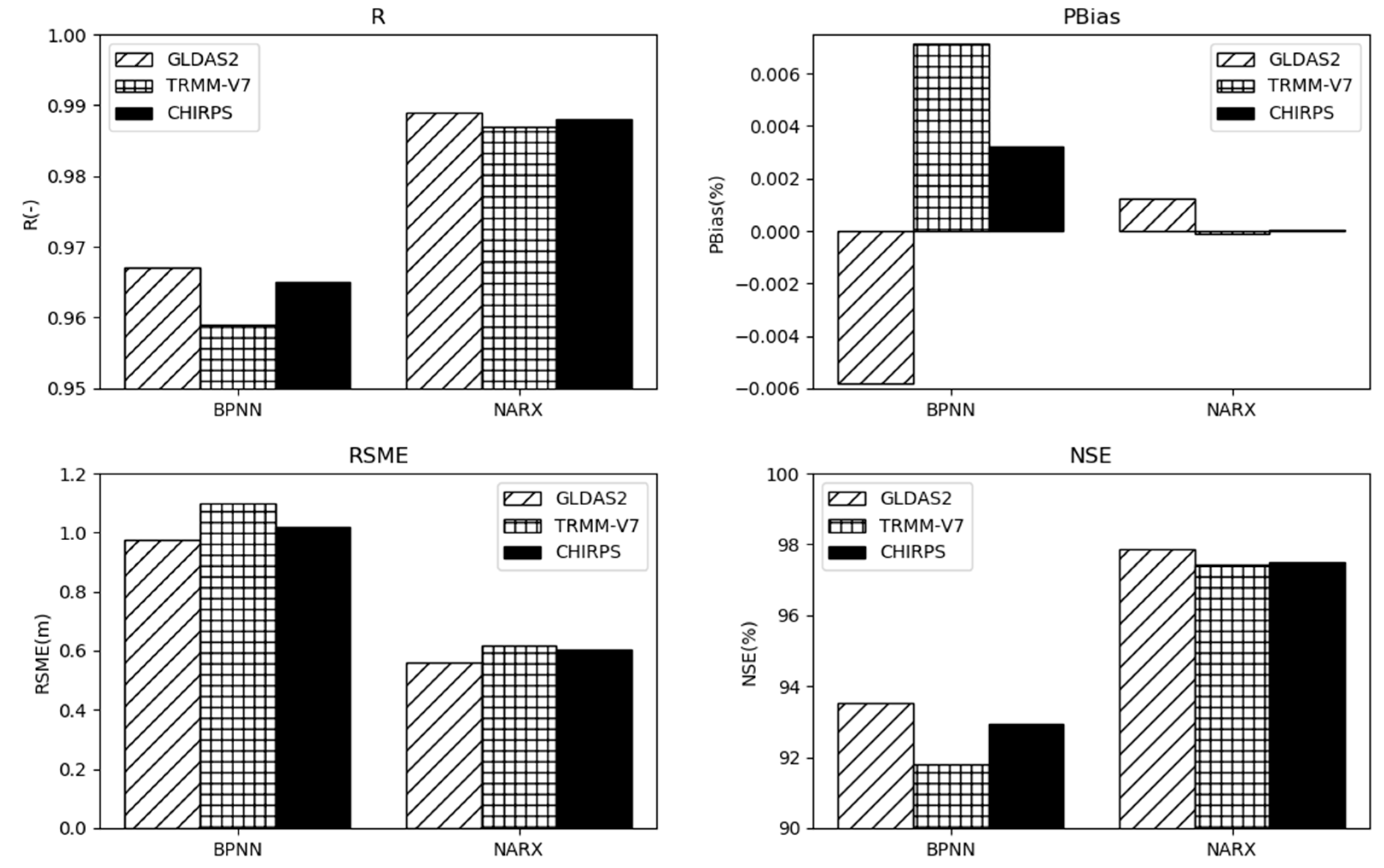
3.2. Performance of the BP Neural Network Model and NARX Network Model for Water Level Modeling
3.2.1. Parameter Optimization of Neural Network
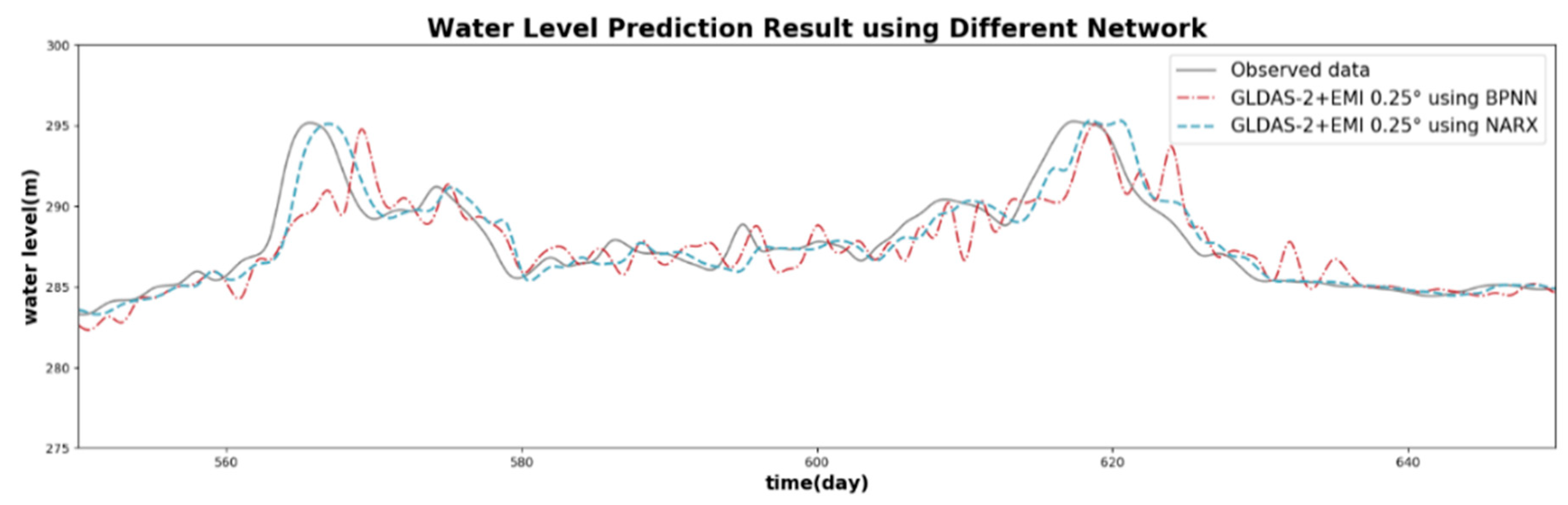
3.2.2. Modeling Results of BP Neural Network Model and NARX Network
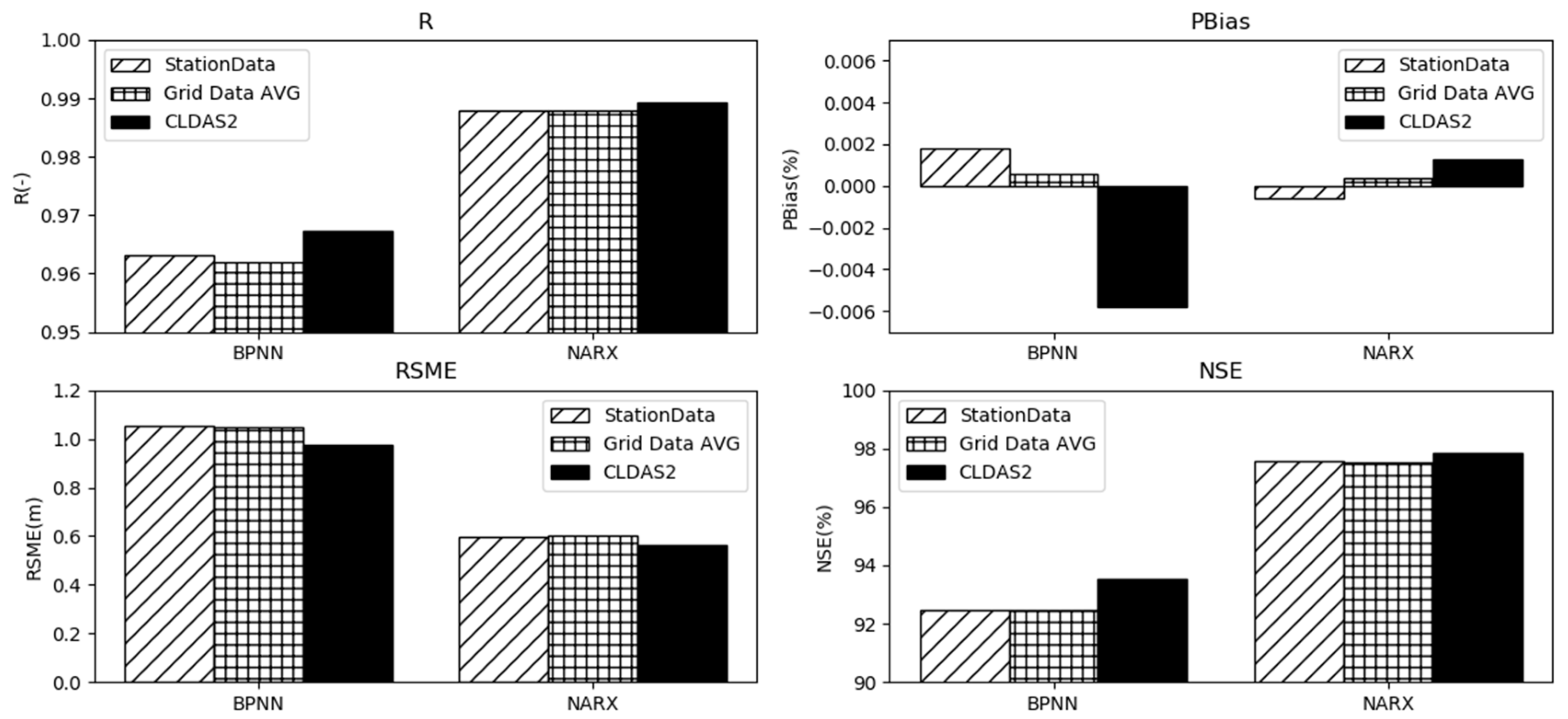
3.3. Comparison of Modeling Results using Grid Products and Station Data
3.3.1. Influence of using Different Precipitation Products
3.3.2. Influence of using Different Resolution Products
4. Conclusions
- Compared with the BP neural network, the NARX time series network can significantly improve the accuracy of water level modeling, which is related to the NARX network, considering the time lag effect.
- Compared with the ground station, the grid data can get similar results in general. The GLDAS 2 data are better than the ground station in water level modeling. Therefore, in an area where the water level station is missing, the surface rainfall data can be used as an available alternative of ground battle points for water level modeling experiments.
- Under the same resolution, the water level modeling results with different data sources are similar, although the GLDAS 2 results are slightly better. Using the same data source, the experimental results of water level modeling with different resolutions of surface rainfall data have little difference, so it is of little significance to pursue high-resolution surface rainfall products in the construction of a precipitation–water level model.
- In this paper, by putting forward a method for building a precipitation–water level model, the influencing factors of each part of the water level model are discussed, which has certain guiding significance for future research into water level modeling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, N.; Xiong, C.; Du, W.; Wang, C.; Lin, X.; Chen, Z. An Improved Genetic Algorithm Coupling a Back-Propagation Neural Network Model (IGA-BPNN) for Water-Level Predictions. Water 2019, 11, 1795. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Hao, Z.-C.; Tong, K.; Liu, X.-L.; Zhang, L.-L. Capability of TMPA products to simulate streamflow in upper Yellow and Yangtze River basins on Tibetan Plateau. Water Sci. Eng. 2014, 7, 237–249. [Google Scholar]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. (Online) 2017, 21. [Google Scholar] [CrossRef] [Green Version]
- Dhar, V. Data science and prediction. Commun. ACM 2013, 56, 64–73. [Google Scholar] [CrossRef]
- Khan, M.; Hasan, F.; Panwar, S.; Chakrapani, G. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga Basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef] [Green Version]
- Leahy, P.; Kiely, G.; Corcoran, G. Structural optimisation and input selection of an artificial neural network for river level prediction. J. Hydrol. 2008, 355, 192–201. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Piasecki, A.; Jurasz, J.; Skowron, R. Forecasting surface water level fluctuations of lake Serwy (Northeastern Poland) by artificial neural networks and multiple linear regression. J. Environ. Eng. Landsc. Manag. 2017, 25, 379–388. [Google Scholar] [CrossRef] [Green Version]
- Zhong, C.; Jiang, Z.; Chu, X.; Guo, T.; Wen, Q. Water level forecasting using a hybrid algorithm of artificial neural networks and local Kalman filtering. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 174–185. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A Data-Driven Approach for Accurate Rainfall Prediction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9323–9331. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, A.; Samantaray, S.; Bankuru, S.; Ghose, D.K. Prediction of Flood Using Adaptive Neuro-Fuzzy Inference Systems: A Case Study. In Smart Intelligent Computing and Applications; Springer: Singapore, 2020; pp. 733–739. [Google Scholar]
- Samantaray, S.; Sahoo, A. Appraisal of runoff through BPNN, RNN, and RBFN in Tentulikhunti Watershed: A case study. In Frontiers in Intelligent Computing: Theory and Applications; Springer: Singapore, 2020; pp. 258–267. [Google Scholar]
- Samantaray, S.; Sahoo, A. Estimation of runoff through BPNN and SVM in Agalpur Watershed. In Frontiers in Intelligent Computing: Theory and Applications; Springer: Singapore, 2020; pp. 268–275. [Google Scholar]
- Garcia, F.C.C.; Retamar, A.E.; Javier, J.C. Development of a predictive model for on-demand remote river level nowcasting: Case study in Cagayan River Basin, Philippines. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 3275–3279. [Google Scholar]
- Adnan, R.; Ruslan, F.A.; Samad, A.M.; Zain, Z.M. Flood water level modelling and prediction using artificial neural network: Case study of Sungai Batu Pahat in Johor. In Proceedings of the 2012 IEEE Control and System Graduate Research Colloquium, Shah Alam, Selangor, Malaysia, 16–17 July 2012; pp. 22–25. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Nanda, T.; Sahoo, B.; Beria, H.; Chatterjee, C. A wavelet-based non-linear autoregressive with exogenous inputs (WNARX) dynamic neural network model for real-time flood forecasting using satellite-based rainfall products. J. Hydrol. 2016, 539, 57–73. [Google Scholar] [CrossRef]
- Chen, P.-A.; Chang, L.-C.; Chang, F.-J. Reinforced recurrent neural networks for multi-step-ahead flood forecasts. J. Hydrol. 2013, 497, 71–79. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network based rainfall–runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Huang, Y. Application of TRMM Precipitation in VIC Hydrological Model for Streamflow Simulations in the Upstream of Yangtze River. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2017. [Google Scholar]
- Guo, D.; Wang, H.; Zhang, X.; Liu, G. Evaluation and Analysis of Grid Precipitation Fusion Products in Jinsha River Basin Based on China Meteorological Assimilation Datasets for the SWAT Model. Water 2019, 11, 253. [Google Scholar] [CrossRef] [Green Version]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Xu, C.-Y.; Becker, S.; Jiang, T. Sediment and runoff changes in the Yangtze River basin during past 50 years. J. Hydrol. 2006, 331, 511–523. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS satellite-rainfall products over mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Cui, W.; Wang, X.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of versions 6 and 7 3-hourly TRMM multi-satellite precipitation analysis (TMPA) research products. Atmos. Res. 2015, 163, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Shi, C.-X. Modeling and analysis of effects of precipitation and vegetation coverage on runoff and sediment yield in Jinsha River Basin. Water Sci. Eng. 2013, 6, 44–58. [Google Scholar]
- Hamman, J.J.; Nijssen, B.; Bohn, T.J.; Gergel, D.R.; Mao, Y. The Variable Infiltration Capacity model version 5 (VIC-5): Infrastructure improvements for new applications and reproducibility. Geosci. Model Dev. 2018, 11, 3481–3496. [Google Scholar] [CrossRef] [Green Version]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. In Neurocomputing: Foundations of Research; James, A.A., Edward, R., Eds.; MIT Press: Cambridge, MA, USA, 1988; pp. 696–699. [Google Scholar]
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar]
- Thomas, A.J.; Petridis, M.; Walters, S.D.; Gheytassi, S.M.; Morgan, R.E. Two hidden layers are usually better than one. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Athens, Greece, 25–27 August 2017; pp. 279–290. [Google Scholar]
- Paredes-Trejo, F.J.; Barbosa, H.; Kumar, T.L. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
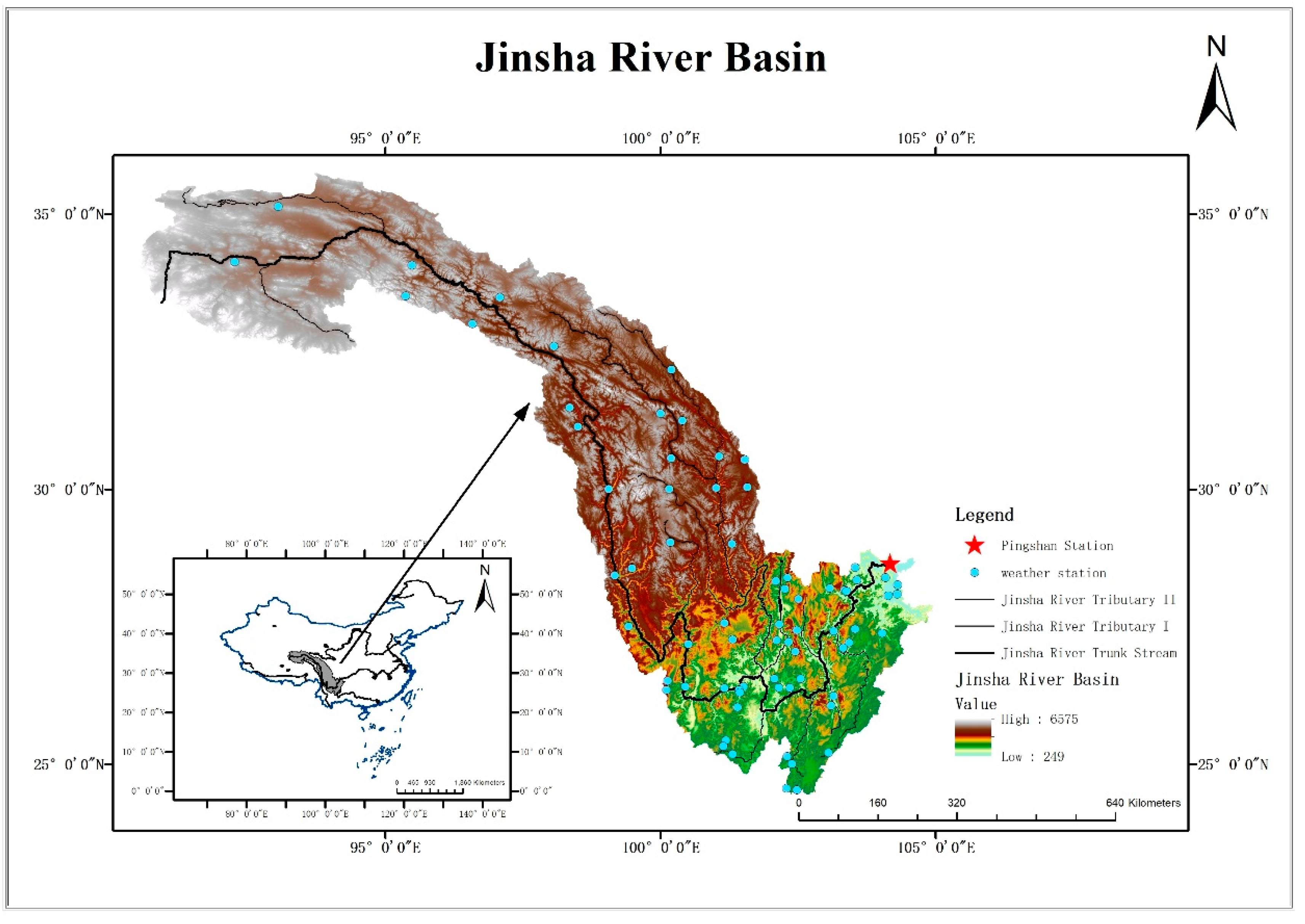


| Data Name | Data Type | Temporal/Spatial Resolution | Time Range |
|---|---|---|---|
| Pingshan Water Level | Hydrological station data | 1 day/- | 2006/01/01~2009/12/30 |
| CHIRPS | Grid data | 1 day/0.05° × 0.05° | |
| GLDAS-2 | Grid data | 1 day/0.25° × 0.25° | |
| TRMM-V7 | Grid data | 1 day/0.25° × 0.25° | |
| In situ data | Gauge-based data | 1 day/- |
| Network Type | BPNN | NARX | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Name | SR | R | Pbias | RSME | NSE | MAE | R | Pbias | RSME | NSE | MAE |
| GLDAS-2+ EMI | 0.25° | 0.967 | –0.00581 | 0.976 | 93.520 | 0.543 | 0.989 | 0.00126 | 0.561 | 97.858 | 0.336 |
| 0.5° | 0.966 | 0.00249 | 1.006 | 93.109 | 0.560 | 0.987 | −0.00013 | 0.625 | 97.339 | 0.358 | |
| TRMM-V7+ EMI | 0.25° | 0.959 | 0.00714 | 1.098 | 91.787 | 0.584 | 0.987 | −0.00009 | 0.616 | 97.419 | 0.349 |
| 0.5° | 0.961 | 0.00250 | 1.065 | 92.276 | 0.564 | 0.988 | 0.00118 | 0.584 | 97.677 | 0.342 | |
| CHIRPS+ EMI | 0.05° | 0.954 | −0.00792 | 1.159 | 90.857 | 0.632 | 0.987 | −0.00247 | 0.612 | 97.447 | 0.353 |
| 0.5° | 0.965 | 0.00325 | 1.019 | 92.933 | 0.564 | 0.988 | 0.00007 | 0.605 | 97.505 | 0.342 | |
| 0.25° | 0.964 | 0.00405 | 1.033 | 92.727 | 0.566 | 0.986 | 0.00053 | 0.632 | 97.277 | 0.357 | |
| Station rainfall data + EMI | 0.963 | 0.00180 | 1.053 | 92.450 | 0.562 | 0.988 | −0.00060 | 0.599 | 97.560 | 0.335 | |
| Use station rainfall input only | 0.948 | –0.00382 | 1.243 | 89.482 | 0.697 | 0.987 | 0.00317 | 0.619 | 97.393 | 0.359 | |
| Accuracy Criteria | Rainfall Station | CHIRPS | GLDAS-2 | TRMM-V7 |
|---|---|---|---|---|
| R | 1 | 0.606 | 0.7326 | 0.645 |
| Pbias (%) | 0 | −3.40 | −17.40 | 4.23 |
| Parameter Type | Parameters of Neural Networks |
|---|---|
| Study parameter | Learning rate = 0.01 |
| momentum factor = 0.9 | |
| transfer function = | |
| Structure parameter | Number of input nodes : determined by the spatial resolution of input remote sensing data and the result of principal component analysis |
| Number of the first hidden layer of nodes: = | |
| Number of the second hidden layer of nodes: | |
| Number of hidden layers = 2 | |
| Number of output nodes = 1 |
| Time Lag | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| CCF | 0.6914 | 0.7057 | 0.7246 | 0.7396 | 0.7514 | 0.7559 | 0.7557 | 0.751 |
| R | PBias | RSME | NSE | MAE | |
|---|---|---|---|---|---|
| BPNN | 0.961 | 0.00041 | 1.072 | 92.127 | 0.586 |
| NARX | 0.987 | 0.00032 | 0.606 | 97.497 | 0.348 |
| Data Name | BPNN | NARX | ||||||
|---|---|---|---|---|---|---|---|---|
| R | Pbias | RSME | NSE | R | Pbias | RSME | NSE | |
| GLDAS-2+EMI 0.25° | 0.967 | −0.00581 | 0.976 | 93.520 | 0.989 | 0.00126 | 0.561 | 97.858 |
| average resultsof grid data | 0.962 | 0.000574 | 1.049 | 92.485 | 0.988 | 0.00034 | 0.600 | 97.544 |
| Station Data | 0.963 | 0.00180 | 1.053 | 92.450 | 0.988 | −0.00060 | 0.599 | 97.560 |
| Data Name | BPNN | NARX | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SR | R | Pbias | RSME | NSE | R | Pbias | RSME | NSE | |
| GLDAS-2 | 0.25° | 0.967 | −0.00581 | 0.976 | 93.520 | 0.989 | 0.00126 | 0.561 | 97.858 |
| TRMM-V7 | 0.25° | 0.959 | 0.00714 | 1.098 | 91.787 | 0.987 | −0.00009 | 0.616 | 97.419 |
| CHIRPS | 0.25° | 0.965 | 0.00325 | 1.019 | 92.933 | 0.988 | 0.00007 | 0.605 | 97.505 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Lin, X.; Xiong, C.; Chen, N. Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model. Remote Sens. 2020, 12, 1096. https://doi.org/10.3390/rs12071096
Chen Z, Lin X, Xiong C, Chen N. Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model. Remote Sensing. 2020; 12(7):1096. https://doi.org/10.3390/rs12071096
Chicago/Turabian StyleChen, Zeqiang, Xin Lin, Chang Xiong, and Nengcheng Chen. 2020. "Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model" Remote Sensing 12, no. 7: 1096. https://doi.org/10.3390/rs12071096
APA StyleChen, Z., Lin, X., Xiong, C., & Chen, N. (2020). Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model. Remote Sensing, 12(7), 1096. https://doi.org/10.3390/rs12071096






