Abstract
Rapid and uncontrolled population growth along with economic and industrial development, especially in developing countries during the late twentieth and early twenty-first centuries, have increased the rate of land-use/land-cover (LULC) change many times. Since quantitative assessment of changes in LULC is one of the most efficient means to understand and manage the land transformation, there is a need to examine the accuracy of different algorithms for LULC mapping in order to identify the best classifier for further applications of earth observations. In this article, six machine-learning algorithms, namely random forest (RF), support vector machine (SVM), artificial neural network (ANN), fuzzy adaptive resonance theory-supervised predictive mapping (Fuzzy ARTMAP), spectral angle mapper (SAM) and Mahalanobis distance (MD) were examined. Accuracy assessment was performed by using Kappa coefficient, receiver operational curve (RoC), index-based validation and root mean square error (RMSE). Results of Kappa coefficient show that all the classifiers have a similar accuracy level with minor variation, but the RF algorithm has the highest accuracy of 0.89 and the MD algorithm (parametric classifier) has the least accuracy of 0.82. In addition, the index-based LULC and visual cross-validation show that the RF algorithm (correlations between RF and normalised differentiation water index, normalised differentiation vegetation index and normalised differentiation built-up index are 0.96, 0.99 and 1, respectively, at 0.05 level of significance) has the highest accuracy level in comparison to the other classifiers adopted. Findings from the literature also proved that ANN and RF algorithms are the best LULC classifiers, although a non-parametric classifier like SAM (Kappa coefficient 0.84; area under curve (AUC) 0.85) has a better and consistent accuracy level than the other machine-learning algorithms. Finally, this review concludes that the RF algorithm is the best machine-learning LULC classifier, among the six examined algorithms although it is necessary to further test the RF algorithm in different morphoclimatic conditions in the future.
1. Introduction
Knowledge of land-use/land-cover (LULC) change is essential in a number of fields based on the use of Earth observations, such as urban and regional planning [1,2], environmental vulnerability and impact assessment [3,4,5,6,7], natural disasters and hazards monitoring [8,9,10,11,12,13] and estimation of soil erosion and salinity, etc. [14,15,16,17]. Quantitative assessment and prediction of LULC dynamics are the most efficient means to manage and understand the landscape transformation [18]. Mapping LULC change has been identified as an essential aspect of a wide range of activities and applications, such as in planning for land use or global warming mitigation [19,20]. Consequently, assessment in LULC change is inevitably required for a variety of purposes for the welfare of human beings in the context of rapid and uncontrolled population growth along with economic and industrial development, especially in developing countries with intensified LULC changes [20,21,22,23]. These changes have a series of impacts on both human society and environment in many ways like increasing flood and drought vulnerability, environmental degradation, loss of ecosystem services, groundwater depletion, landslide hazards, soil erosion and others [14,15,24,25,26,27].
Several techniques have been developed to map LULC patterns and dynamics from the satellite observations, including traditional terrestrial mapping, as well as satellite-based mapping. Terrestrial mapping, known as a field survey, is a direct way of mapping in which the map can be produced at various scales incorporating information with different levels of precision, although it is a manpower-based, time- and money-consuming way to map large areas [28]. Moreover, there is a chance of subjectivity in mapping. On the other hand, the satellite- and aerial photograph-based mapping of LULC are cost-effective, spatially extensive, multi-temporal, and time-saving [29]. Earlier, the spatial resolution of satellite data was comparatively less than that of the maps prepared through terrestrial surveys. With the advancement of remote-sensing (RS) techniques and microwave sensors, satellites provide data at various spatial and temporal scales [30,31,32]. RS provides the opportunity for rapid acquisition of information on LULC at a much reduced price compared to the other methods like ground surveys [33,34]. The satellite images have the advantages of multi-temporal availability as well as large spatial coverage for the LULC mapping [35,36]. In the past few decades, studies on mapping, monitoring and forecasting of LULC dynamics have been carried out using medium- and low-resolution observations from satellites, such as Landsat, Satellite Pour l’Observation de la Terre, or Satellite for observation of Earth (SPOT), Indian Remote Sensing (IRS) Satellite Resourcesat, Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), Moderate Resolution Imaging Spectroradiomete (MODIS) and others [18,31,37,38,39,40]. With the advancement of hyperspectral satellite sensors, the importance of RS has increased many times in the research field and for planning purposes.
Recently, the application of machine-learning algorithms on remotely-sensed imageries for LULC mapping has been attracting considerable attention [41,42]. The machine-learning techniques have been categorized into two sub-types; supervised and unsupervised techniques [43,44]. The supervised classification techniques include support vector machine (SVM), random forest (RF), spectral angle mapper (SAM), fuzzy adaptive resonance theory-supervised predictive mapping (Fuzzy ARTMAP), Mahalanobis distance (MD), radial basis function (RBF), decision tree (DT), multilayer perception (MLP), naive Bayes (NB), maximum likelihood classifier (MLC), and fuzzy logic [45,46], while the unsupervised classification techniques include Affinity Propagation (AP) cluster algorithm, fuzzy c-means algorithms, K-means algorithm, ISODATA (iterative self-organizing data) etc. [41,47].
Over the last decade, more advanced methods, such as artificial neural networks (ANN), SVM, RF, decision tree, and other models, have gained exceptional attention in remote sensing-based applications, such as LULC classification. Thus, numerous studies on the LULC modelling have been carried out using different machine-learning algorithms [14,48,49,50,51] as well as comparing the machine-learning algorithms [52,53,54]. Furthermore, a few studies have been carried out to identify the best suited and accurate algorithm among used machine-learning classifiers for LULC mapping [52,53,54,55]. Each machine-learning technique has different types of accuracy levels. It has been found that ANN, SVM, and RF generally provide better accuracy as compared with the other traditional classifier techniques [56], while SVM and RF are the best techniques for the LULC classification compared to all other machine-learning techniques [57,58]. However, the sensor characteristics and image data-related factors, such as spatial and temporal resolution, processing software and hardware, etc. determine the accuracy of LULC classification [59].
Several studies found that the LULC classification using medium- and low-resolution observations from satellites has several spectral and spatial limitations that affect its accuracy [24,60,61,62]. Therefore, researchers have been applying machine-learning algorithms to reduce the aforementioned limitations and obtain high-precision LULC images. Furthermore, all machine-learning techniques do not always produce a high-precision LULC map because good results depend on the machine-learning model set-up, training samples and input parameters. Up to the present, numerous studies have been conducted on land-use classification using machine-learning algorithms [20,63], but the performance of models is not well examined. In this article, we utilized six machine-learning techniques to understand which method can produce a high-precision LULC map based on accuracy statistics.
2. Materials and Methods
2.1. Study Area
We selected a stretch of riparian landscape of the river Ganga from Rajmahal to Farakka barrage in India emphasizing three major dynamic river islands (locally, charland) dominated by patches. LULC classification in relatively stable areas is easier than highly dynamic landscape like charland and such work is undertaken by many scholars. How far the advanced methods are useful for delineating LULC units in such a dynamic area was given emphasis with different approaches of accuracy assessment. Successful application of one method in different similar sites proves its usability. Hence, to test the precision of the applied methods three such patches from the study stretch were used. The study area covers parts of Jharkhand and the West Bengal states of India. More precisely, it covers some parts of Sahibganj District of Jharkhand and Malda and the Murshidabad districts of West Bengal (Figure 1). The topography of the study area is dominated by alluvial plain, which is formed by the sediments deposited by Ganga, Mahananda and Kalindi rivers. The elevation of the region varies between approximately 12 meters to 90 meters. The regular flooding makes the region suitable for agriculture with seasonal water scarcity. The climate of the region is of sub-humid monsoon type (Koppen-Cwg) with average annual rainfall more than 1500 mm and temperature ranges from 10 and 38 °C. The rapidly increasing population causes large-scale landscape transformation by the expansion of agricultural land and human settlement along with well-defined riverbank erosion and flood hazards. Riverbank erosion has caused significant changes in the LULC pattern in the area for a long time. The frequent flooding and riverbank erosion have caused large-scale displacement of the human settlements in the region during the first decade of the 21st century [64].
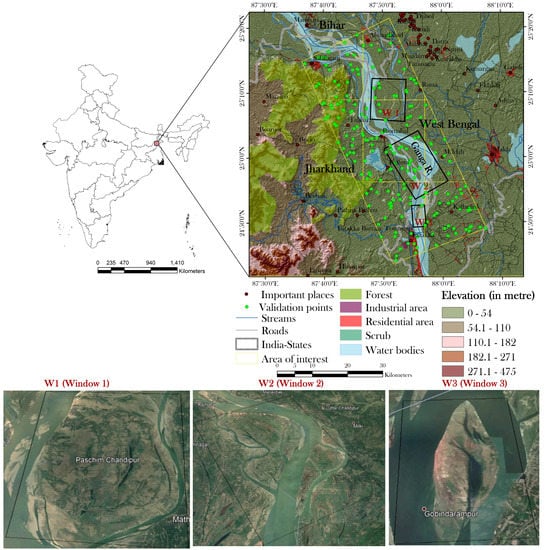
Figure 1.
Location map and details of the study area.
2.2. Materials
In this work, the Landsat 8 Operational Land Imager (OLI) image (path/row 139/43) downloaded from the United States Geological Survey (USGS) website (https://earthexplorer.usgs.gov) ) has been used to map the LULC using different machine-learning algorithms (Figure 2). Six first-order LULC classes have been identified based on a comprehensive literature survey and expert-based knowledge about the study area (Table 1). The acquisition date of the Landsat data downloaded was 03 October 2019. Furthermore, the Google Earth image and field-based observations have been used for the accuracy assessment of the LULC maps prepared.
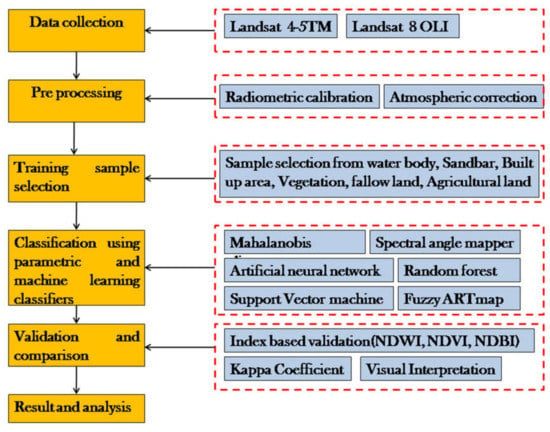
Figure 2.
Flowchart of the methodology.

Table 1.
Description of the land-use/land-cover (LULC) classes identified.
2.3. Methods for Land-Use/Land-Cover (LULC) Modelling
The LULC classification was performed using the six most popular machine-learning classifiers. The descriptions of the parameters for optimizing the models and software used to perform the LULC classification are given in Table 2.

Table 2.
Optimized parameters for different classifiers used for the LULC modelling.
2.3.1. Methods for Machine-Learning Classifiers
1. Artificial Neural Network (ANN)
The ANN is the most widely applied machine-learning technique, which can be efficiently used in non-linear phenomena such as parameter retrieval [65,66,67], LULC changes with the ability to work on big data analysis. It is currently one of the most used non-parametric classification techniques [68]. It does not depend on any assumption of generally distributed data [69].
The ANN is a forward structure black-box model, which is trained by back propagation algorithm (supervised training algorithm). The ANN is functioned like a human brain or nervous system containing nerve fibres with many interconnections through other axons [70]. It can learn and produce meaningful results from examples, even when the input data having error or complexity and incomplete. Therefore, it can simulate exactly like the human nervous system. However, the ANN has one input layer, at least one hidden layer and one output layer. Each layer is formed by neurons (like brain nerves) (Figure 3). These neurons are non-linear processing units. However, all the neurons in a layer are interconnected to all other neurons in the adjacent layers and formed networks. In addition, the connection between neurons in successive layers are weighted. This process (transferring information from one neuron to another or one layer to other layer) is called forward connection. This automatic learning is accomplished through a dynamic adjustment of network inter-connection associated with each neuron [66].
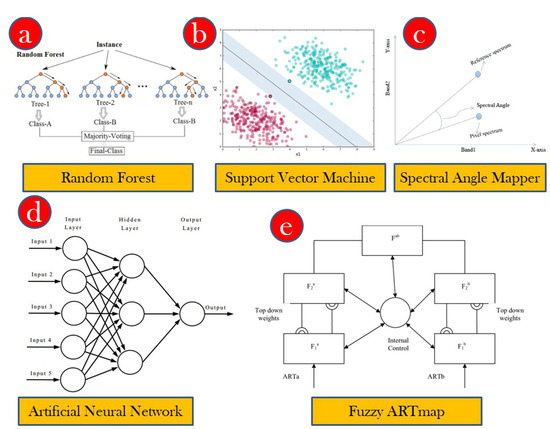
Figure 3.
Schematic architecture of land use land cover classifiers (a) random forest, (b) support vector machine, (c) spectral angle mapper, (d) artificial neural network, and (e) fuzzy ARTMAP.
One of most important algorithms that ANN usually uses is the back propagation algorithm, which is a gradient-decent algorithm. The main function of it is to minimize the error between the actual network outputs and the outputs of training input/output pairs [71]. The network repeatedly receives the numbers of input/output pairs and the error is propagated from the output back to the input layer. The learning rate and update rule renew the weights of the backward paths [72,73]. In addition, the default processing unit, training and learning rate cannot uniquely specify the ANN. Therefore, the trial and error process of changes of model parameters can only be the best way to obtain better result. In this review article, the multilayer perceptron (MLP) ANN architecture used in the LULC classification is modelled using a layered feed-forwarded model in the TerrSet Geospatial Modelling Software.
The MLP architecture can be explained mathematically. In MLP architecture, the input layer comprises the n0 neurons, which collect a normalized set of input variables of xi (i = 1, 2……n0). The second layer is also known as the hidden layer that contains the n1 neurons and receives a set of variables of yj(j = 1, 2……...n1), which are the output of the first layer. Each of the layers receive a bias value of 1 in each of the neurons that rectify their outputs. The third or output layer consists of the n2 neurons with number equal to output variables of zk(K = 1, 2…., n2). A continuous non-linear mapping is performed in the n0 neurons of xi variables in the output layer to the yi variables in the hidden layer after summing them up using an activation function. The parameter of this function is also defined as weights of neurons in each hidden layer for each result of neurons of the input layer [74]. One of the most common methods for ANN training is the back-propagation algorithm defined by minimizing the cost function as presented in Equation (1).
where n represents the number of classes, denotes the expected output, and is the response of designed ANN from the i neuron of the total n neurons in the output layer.
2. Support Vector Machine (SVM)
SVM is a non-parametric supervised machine learning technique and initially aimed to solve the binary classification problems [41,75]. It is based on the concept of structural risk minimization (SRM), which maximizes and separates the hyper-plane and data points nearest the spectral angle mapper (SAM) of the hyper-plane. It separates data points into various classes using a hyper-spectral plane. In this process, the vectors ensure that the width of the margin will be maximized [76]. SVM can support multiple continuous and categorical variables as well as linear and non-linear samples in different class membership. The training samples or bordering samples that delineate the margin or hyper-plane of SVM are known as support vectors [46]. In remote sensing, the polynomial and radial basis function (RBF) kernel has been used most commonly [41], but for LULC classification RBF is the most popular technique and gives better accuracy than the other traditional methods.
The original SVM method has been launched with a set of data, and its objective is to find the hyper-plane that can separate the datasets into a number of classes, as the aim of SVM is to find the optimal separating hyper-plane from the available hyper-planes [77]. Furthermore, the SVM algorithm needs a proper kernel function to establish the hyper-planes accurately and minimize the classification errors [78]. The essential part of the SVM technique is the kernel type used. The functionality of the SVM mainly depends on the kernel size, and the similarity of a smooth surface depends on the more significant kernel density. For simulated and real-world hyperspectral satellite data, the genetically optimized SVM using the support vectors shows the best performance [79]. The primary function of SVM is to find the optimal boundary, which will increase the separation between the entire support vectors. The RBF and polynomial function kernel were performed on ENVI software version 5.3 for LULC mapping.
3. Fuzzy ARTMAP (FA)
The fuzzy ARTMAP technique is based on the similarity of the fuzzy subset calculation as well as the adaptive and vibrant category selection through the feature space search. The structure of fuzzy ARTMAP includes two modules, i.e., ARTa and ARTb. These two modules can be further sub-divided into two sub-modules in the function (attention and orientation subsystem). The attention subsystem has several functions. For example, it deals with the modules, establishes the exact internal illustration, and creates fine-tuning for the modules. In contrast, the orientation subsystem is used for dealing with the newly appeared module [80]. Each module of the fuzzy ARTMAP consists of three layers, namely F0 as input layer, F1 as comparison layer and F2 as recognition layer. These characteristics of fuzzy ARTMAP are identical to the artificial neural network. Furthermore, each layer has its respective neuron units M, M, N as well as the control connections associated with the layers. F1 is used for the detection of features and it has adequate nodes for the mode coding, while the nodes of F2 show the categories concerning the input.
Based on the comprehensive investigation of fuzzy ARTMAP as well as the characteristics of remote-sensing data, a simplified fuzzy ARTMAP algorithm has been applied using the Terrset software. It comprises two layers in which the first is used for the feature data input and the second for the classification of remote-sensing data. In the first layer, the numbers of neurons are equal to the feature dimensions of the data, while in the second layer, the numbers of neurons are decided by the user as per the trial and process results [81]. The fuzzy ARTMAP firstly calculates the comparison between the new pattern and the existing active pattern. Then all active values are arranged in ascending order to degree of matching and compared with warning values. If the warning values are exceeded by the matching degree, the pattern of the training sample will be the same as the output layer. The fuzzy ARTMAP combines the pattern of output layer neurons and uses the weight between the output-input layers and the radius. If all the output layer neurons do not meet the matching requirements, a new output layer neuron will be built to store the new pattern and, thus, the results of classification become more accurate with more output layers.
4. Random Forest
RF is a new non-parametric ensemble machine-learning algorithm developed by Breiman [82]. The RF algorithm has been widely applied for solving the environmental problems, like water resource management and natural hazard management. It can handle a variety of data, like satellite imageries, and numerical data [83]. It is an ensemble learning method based on a decision tree, which combines with massive ensemble regression and classification trees. For setting up the RF model, two parameters are needed and called the base of the method. These parameters are (1) the number of trees, which can be explained by ‘n-tree’ and (2) many features in each split, which can be explained by ‘m-try.’ Classification trees provide an individual choosing power or vote and accurate classification in regulating the majority vote from trees in the entire forest.
In recent times, several studies have shown a satisfactory performance for LULC classification using RF in the field of remote-sensing applications [42,52,57]. A vast number of trees of this method provide better accuracy in the field of image classification [84] and land-use modelling. Breiman [82] stated that using more trees compared to required trees is an unnecessary and time-consuming process, but it does not hamper the entire model. Furthermore, Feng et al. [85] selected 200 decision trees in their study and noted that the performance of RF was accurate. The RF technique has been benefited with the two more powerful algorithms: bagging and random, which are called the powerhouse of this method. In our study, the ‘randomForest’ package in R has been used to produce the LULC map. As suggested by Feng et al. [85], 200 decision trees have been used with 3 input features (m-try) in our study.
2.3.2. Method for Parametric Classifier
1. Mahalanobis Distance (MD)
Supervised image classification is performed to detect the quantitative approach in the remote-sensing image. The prime goals of supervised classification are to segment the spectral domain into the areas that match the ground cover interest classes for a particular purpose. The Mahalanobis distance (MD) supervised image classification algorithm was developed by an Indian applied statistician Mahalanobis in the 1930s [86]. In MD classification, training data are given to specify the spectral classes of the pixel based on the user-defined classes. MD classification is same as maximum likelihood classification where statistics have been used for each class and it considers only equal class coefficients. The MD method measures the distance between two or more than two correlated variables. In mathematical term, MD distance is equal to Euclidean distance (ED) when the covariance matrix is the unit matrix. The small value of MD increases the chance of an observation being closer to the group’s centre. For each feature vector, the MD () towards class means is calculated as in the following equation:
where is the vector showing the pixel of image data, is the sample mean vector of the kth class, V is the variance/covariance matrix for class i; and T represents transpose of the matrix.
2.3.3. Method for Non-Parametric Classifier
1. Spectral Angle Mapper (SAM)
SAM is an auto-generated supervised spectral classifier machine learning technique that is used to determine the spectral similarity between the given image spectra and reference spectra in an n (here n denotes the spectral band number) dimensional space using the calculation of the angle between the spectra [87]. In recent times, a large number of bands have been used in hyper-spectral remote sensing to identify the different objects accurately and the SAM is able to analyse all bands together. Reference spectra refer to the spectra that can be taken either by field investigation or directly from satellite images. For LULC classification, reference spectra can be taken as a signature from the satellite image [88].
In SAM, only angular information can be used to identify the pixel spectra. Thus, SAM uses only angular information to identify the pixel spectra, which assumes that an observed reflectance spectrum in a vector format is a multidimensional space with the number of dimensions equal to the number of bands. The difference between image spectra and reference spectra is shown as the level of angle where a small angle indicates high similarity and a high angle indicates low similarity. The maximum threshold limits of tolerance of angle are not classified. Hence, it is better to define a threshold angle limit (in radians) under which a pixel cannot be classified. In our study, SAM has been applied using the ENVI 5.3 image processing environment for LULC classification. This technique is comparatively intensive for illumination and albedo conditions while calibrating reflectance information. The SAM is auto-generated supervised classification.
2.4. Similarity Test among the Classifiers
For representing the difference of performance of the algorithms for delineating LULC, similarity ratio (SR) is computed. It is simply the ratio between proportions of area of a given LULC computed by two algorithms. SR = 1 signifies the absolute similarity of the areal proportion of LULC computed by two algorithms. A value >1 or <1 means growing dissimilarity.
2.5. Accuracy Assessment and Correlation among the Classifiers
The post-classification accuracy assessment has been considered as the most vital part of validating the LULC maps produced by the models [61,89]. The high-precision LULC map can generate fundamental grounds for successful planning and management. The statistics only can tell about the accuracy assessment and the Kappa coefficient is a statistical technique that has been applied in the present study for assessing the accuracy. Monserud and Leemans [90] suggested five levels of agreement, poor or very poor, fair, good, very good, and excellent corresponding to the values lower than 0.4, from 0.4 to 0.55, from 0.55 to 0.70, from 0.70 to 0.85, and higher than 0.85, respectively, between images and ground reality. Thus, the Kappa coefficient has been calculated using 200 randomly selected sample ground control points in order to evaluate the accuracy of LULC maps produced by using different algorithms (the random points are shown in Figure 1). The sample points have been selected from the field observation and using Google Earth Pro for the remote and inaccessible areas.
The receiver operating characteristics (RoC) curve graph was plotted to validate the performance of LULC classifiers for detecting the different features of LULC. The graph was plotted between sensitivity and specificity being on y and x axes, respectively. The sensitivity of a model represents the proportion of correctly predicted positive pixels (i.e., the pixels belonging to a particular LULC class were correctly predicted or identified), while the specificity refers to the proportion of correctly predicted negative pixels (i.e., the pixels not belonging to a particular LULC class was correctly predicted or identified). The sensitivity and specificity were calculated following Equations (3) and (4):
where represents true positive, d refers to true negative, b means false positive, and c represents false negative.
The area under curve (AUC) of the RoC curve depict the performance of classifiers for predicting the LULC. The value of AUC ranges from 0–1, while the AUC close to 1 represents the high degree of model performances.
The root mean square error (RMSE) was computed to evaluating the performance of machine learning classifiers using the observed and prediction sample points. The RMSE was calculated by using Equation (5). The lower the RMSE, the higher the accuracy of LULC prediction:
where n represents the number of sample points.
The “index-based technique” has been introduced to evaluate and select the best machine-learning technique for LULC mapping. Thus, three satellite data-derived indices; normalized differential vegetation index (NDVI), normalized differential water index (NDWI) and normalized differential built-up index (NDBI), have been calculated for this purpose. Each index has been classified based on a manual threshold. For better visualization, LULC classes (water, vegetation-agricultural land, built-up area) and threshold-based NDWI, NDVI, NDBI have been masked out from the study area using the selected three windows. The closeness of the area between the index-derived area and classifier-derived LULC area could be considered as a good result and vice versa. Then, we used correlation matrix among the area of land use classes of six LULC models and satellite data-derived indices to statistically validate the index-based methods:
We also used a visual interpretation procedure to evaluate the accuracy assessment of LULC models. Furthermore, Karl Pearson’s coefficient of correlation technique was applied to understand the association among the results of area coverage of land use classes obtained from the six LULC models. Higher correlation coefficient values indicate conformity of the models.
3. Results
3.1. LULC Classification
The spatial analysis of the LULC map shows that the built-up area, and rivers and wetland are more prominent and clearer in the outputs of SVM and random forest classifiers, while they are least prominent in the output of SAM. On the other hand, the fallow land and agricultural land are more prominent in the output of ANN, followed by fuzzy ARTMAP and Mahalanobis distance classifiers. The vegetation cover and sand bar are fairly classified in all classifiers. In RF and SVM, they are excellently classified (Figure 4). Overall, maximum coverage of built-up land was classified by the SVM and fuzzy ARTMAP methods, whereas least coverage of built-up land was classified by SAM and random forest. On the other hand, the highest coverage of vegetation is found by the SAM classifier, followed by RF and SVM classifiers, while the least coverage is found by ANN. The coverage of fallow land is completely reciprocal to the vegetation cover and the ANN classifier has the highest coverage, followed by fuzzy ARTMAP and MD classifiers, while SAM has the least coverage (Table 3). The coverage of rivers and wetland and sand bar are almost equally classified in all classifiers.
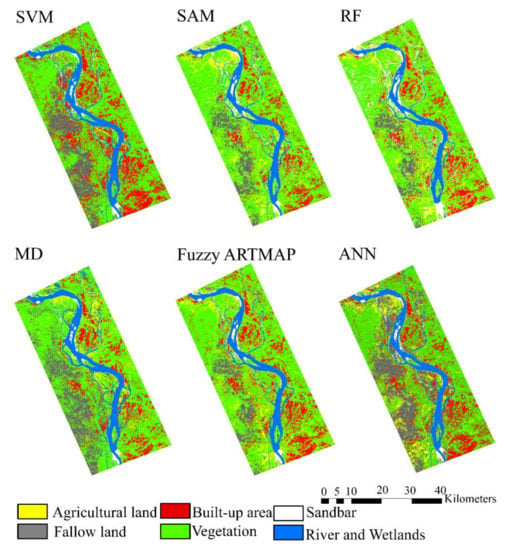
Figure 4.
LULC map with different machine-learning techniques.

Table 3.
Percentage of areal coverage of different LULC classes.
Table 3 shows the percentage share of each LULC class with respect to the total land coverage in the study area for each classifier. Vegetation cover is the most dominant land-use class in the region classified by all classifiers. It covers about half of the total land surface, while the sand bar has the least share in the total land surface area. The percentage share of vegetation cover in total area varies from 44.07% by ANN to 58.62% by SAM. The built-up area (from 9.99% by SAM to 19.59% by fuzzy ARTMAP) and fallow land (from 5.37% by RF to 18.29% by ANN) and agricultural land (from 6.72% by fuzzy ARTMAP to 18.20% by RF) are at the second, third and fourth positions in terms of areal share, while sand bar has the least percentage share with respect to the total surface area by all the classifiers used (from 0.94% by RF to 1.84% by SAM).
Computed standard deviation (SD) and coefficient of variation (CV) among the percentage share of area in a single LULC class by different classifiers are also displayed in Table 3. This vividly exhibits that vegetation, river and water bodies are classified more accurately as all the classifiers accounted for quite uniform areas with very low coefficient of variation. In contrast, fallow land and agricultural land are less well classified as all the classifiers accounted areal extent with considerable differences. Based on the result of similarity test, it can be stated that fuzzy ARTmap and MD, fuzzy ARTmap and SVM methods are quite similar in their performance. The difference is found to be maximum between ANN and SAM algorithms (Table 4).

Table 4.
Similarity ratio matrix of the proportion of LULC between two algorithms.
3.2. Validation of the LULC Classification
The overall accuracy (in percentage) using Kappa coefficient (K) for all the classifiers is shown in Table 5. The RF classifier has been detected as the highly accurate LULC model with Kappa coefficient of 0.89 among all the classifiers followed by ANN (K = 0.87), SVM (K = 0.86), fuzzy ARTMAP (K = 0.85), SAM (K = 0.84) and MD (K = 0.82). RF, ANN and SVM models exhibit excellent agreement and the other models show very good agreement between classified LULC map and ground reality. All the models can be treated as useful but the RF algorithm can be recommended as the best suited classifier of LULC. However, the agricultural land and river and wetland were classified better by using the RF and ANN algorithms (user’s accuracy of RF and ANN: 94%, 92%) in comparison to the other algorithms. Similarly, most of the LULC classes were well classified by using RF, fuzzy ARTmap and ANN (See details in supplementary Table S1). The computed area under curve (AUC) of ROC and RMSE stated in Table 5 also yield the same result as identified when using the Kappa coefficient.

Table 5.
Overall accuracy level of the classifiers used in this study.
The areas of the three spectral indices; normalized differential water index (NDWI), normalized differential vegetation index (NDVI), and normalized differential built-up index (NDBI) have been computed and compared with the areas of water body, vegetation-agricultural land and built-up of LULC maps by using the six classifiers. Results show that the RF classifier performs better than the other classifiers because the total area of three spectral indices is strongly correlated with the area of three LULC classes (Table 6). It is thus considered as the best-fit classifier for preparing LULC in the present study area. Table 6 shows the departure of the area between spectral indices (NDWI, NDVI, and NDBI) and maximum likelihood (ML) algorithms of three LULC units (Figure 5). The total area of NDVI-based vegetation and agricultural land in the three windows is 155.87 km2 and the departure of the area is −0.68 km2. It is very close to the area detected by the RF classifier (156.55 km2). The NDWI-based water body area is 79.57 km2 and departure of area is 0.78km2 in the selected window. It is the most similar with the water body area computed by the RF classifier (78.79 km2) (Table 6). A similar result is found in the case of NDBI-based built-up area.

Table 6.
Area of different LULC computed by the spectral indices and departure of area from the computed areas of the LULC by the Machine Learning (ML) algorithms.
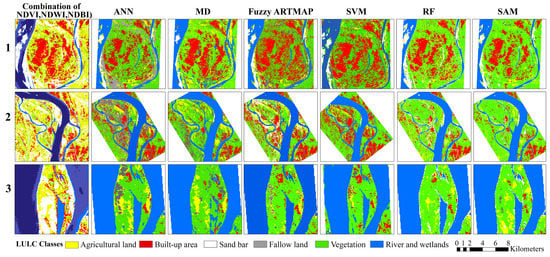
Figure 5.
Validation of LULC of different classifiers with satellite data-derived indices (normalized differential vegetation index (NDVI), normalized differential water index (NDWI), and normalized differential built-up index (NDBI)).
The earlier analysis of closeness between the LULC models and satellite data-derived indices is based on the comparison of the absolute values, but it does not assure robustness. Similarity in area coverage does not always refer to the identical geographical location of any feature. Therefore, we conducted correlation matrix analysis between all LULC models and satellite data-derived indices. Figure 6a presents the correlation between the vegetation and agricultural land by the six classifiers and NDVI in window 1, where the maximum correlation (0.99) can be found by the RF classifier and NDVI at 0.001% significance level, followed by ANN (0.98), Fuzzy ARTMAP (0.97) and SVM (0.97), while the least correlation can be found by the Mahalanobis distance (0.87) with NDVI. The highest correlation (0.96) between water body by RF and NDWI can be found in window 2 at a significance level of 0.001% (Figure 6b), followed by Fuzzy ARTMAP (0.95), SVM (0.94) and ANN (0.93), while the least correlation (0.88) can be detected between SAM and NDWI (Figure 6b). The highest correlation (1) is found between built-up area by RF classifier and NDBI at a significant level of 0.001% followed by Fuzzy ARTMAP (1) at 0.01% of significance level, SVM (0.99) and ANN (0.93) in window 3 (Figure 6c). The lowest correlation (0.91) between SAM and NDBI has been detected (Figure 6c).
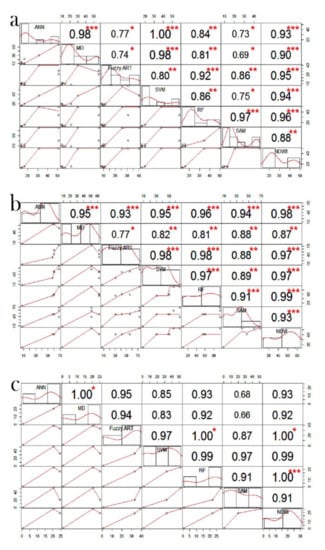
Figure 6.
The correlation among the six LULC classifiers and satellite data-derived indices (NDWI, NDVI and NDBI) for (a) window 1, (b) window 2, and (c) window 3. (*, ** and *** are the significant levels at 0.001, 0.01, and 0.05, respectively).
We validated the LULC modelling using six classifiers by comparing the high-resolution images provided by Google Earth. The aforementioned three sites were selected for comparison (Figure 5). The water bodies and wetlands have been classified very well and they can be matched with the Google Earth images in three sites, whereas both vegetation and agricultural land have been prominently visualized by all classifiers. In the cases of RF, fuzzy ARTMAP and SVM, the land-use features were classified very well as proved by comparing with the Google Earth images. Although it is very difficult to model a built-up area with 30-meter resolution images, machine-learning algorithms with good training sites can perform predictions very well. Therefore, in the present study, some classifiers like MD and fuzzy ARTMAP generated more built-up area than the other classifiers and even the reality. However, the ANN, RF and SAM have classified built-up area as found in Google Earth images and even similar to what we have found in the field survey.
4. Discussion
4.1. Variation in LULC in the Output of Classifiers Used
Several studies reported that the areas of LULC classes are not equal in all the classification techniques, whether machine-learning algorithms or traditional classification techniques are adopted [54,91,92]. In this study, the variation is also found in the results of six classifiers (Figure 5). The area under any land-use class of a classifier does not exactly match with the area under the same land-use class of another different classifier. The area under each land-use class for the same region also varied in the different satellite data due to the atmospheric, illumination and geometric variations [92]. However, the differences in area under LULC classes of different classifiers occur due to the differences in the parameter optimization of the models, techniques and the accuracy differences in the algorithms used [42,92]. Furthermore, a few studies reported that the machine-learning techniques do not have significant difference in the results [42,52]. In our study, we also found similar kinds of result with small variation in a few land-use classes but not in every case. The coefficient of variation showed significant difference of area computed under various LULC classes. The chi square value clearly exhibited that as the difference in result produced in applied classifiers is significantly high, it is not due to random chance. Hence, we need to justify the suitability of any one or two model(s) adopted here.
4.2. Comparison of Accuracy Assessment of Different Classifiers with the Literature
The accuracy of a classification varied with methods, techniques, time and space [41,52,93,94]. Several studies reported minor to moderate fluctuation in the accuracy of the LULC classification using different classifiers [95,96,97,98]. The accuracy assessment in this study shows a small variation among the outputs of the classifiers used in the present case. The accuracy of a LULC classification does not only vary with classifier but also with space and time. This is possibly due to the influence of atmospheric, surface and illumination variations [53,61]. The Kappa coefficient is the most popular technique used to analyse the accuracy. The result shows that the maximum accuracy has been observed in the case of the RF classifier (0.89). Previous studies like Adam et al. [42] and Ma et al. [57] noted that the accuracy levels were 0.93 and 0.90, respectively, for the RF classifier. On the other hand, the minimum accuracy has been found in the case of MD (0.82). The previous studies on LULC classification using MD classifier reported the accuracy level of 0.89 [99], which is higher than the result of the present study. A small difference is found between the previous study and the present study on the accuracy levels of ANN, SAM, fuzzy ARTMAP and SVM [75,100,101]. In this study, the validation of LULC models using satellite image-derived indices is novel and the findings show that RF has modelled LULC in a very good manner, followed by Fuzzy ARTMA, SVM and ANN. However, on the basis of Kappa coefficient, index-based accuracy assessment and empirical observations, it can be concluded that RF is the best classifier for LULC classification. A number of studies from literature also noted that SVM and RF have the highest accuracy in LULC classification (Table 7), while SAM and MD have the lowest accuracy levels. Furthermore, Li et al. [53] noted that the accuracy of SVM and RF has very little difference, but the difference increases between either SVM and ANN or RF and ANN. The result shows that the difference between accuracies of RF and SVM is more than that between RF and ANN.

Table 7.
Suitability of classifier in LULC modelling as per the previous works.
5. Conclusions
This study was conducted to examine the accuracy of different machine-learning classifiers for LULC mapping for satellite observations. The aim was to suggest the best classifier. Six machine-learning algorithms were applied on the Landsat 8 (OLI) data for the LULC classification. Accuracy assessments were undertaken by using the Kappa coefficient, an index-based technique and empirical observations. Results suggest that the area under each LULC class varies under different classifiers. The maximum variation is observed for the agricultural and fallow lands, while the minimum for the water bodies and wetlands. Such variation requires a need to prove the best suited classifier.
Furthermore, the Kappa coefficient and index-based analysis also show variation in the accuracy of each LULC classifier. The variation in the accuracy of the classifiers used is found to be minor, but this minor variation has very important significance in the area of LULC mapping and planning. Both the Kappa coefficient and index-based analysis show that the RF has the highest accuracy of all classifiers applied in this study. To justify the result, previous literature on this was taken into consideration and most of the studies concluded that either RF or ANN is the best classifier. Although the previous studies found a higher accuracy for RF and ANN than this study, this study concludes that RF is the best machine-learning classifier for LULC modelling in the highly dynamic charland-dominated areas. Furthermore, numerous studies suggested that the accuracy of LULC mapping varies with time and location. Thus, for future research, it is suggested to analyse the accuracy of the classifiers for different morphoclimatic and geomorphic conditions.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/12/7/1135/s1, Table S1: The accuracy assessment of LULC mapping of six classifiers using Kappa coefficient.
Author Contributions
Conceptualization, S.T.; methodology, S.T., S.P.; software, S.T.; validation, S.T., S.P. and S.M.; formal analysis, S.T., S.P. and Y.-A.L.; investigation, S.T., P.S.; resources, S.T., S.; data curation, S.T., P.S; writing—original draft preparation, S., S.M., S.P., S.T. and A.R.; writing—review and editing, Y.-A.L., S.P., S.M., S.T. and A.R.; visualization, S.T., P.S. and S.M.; supervision, Y.-A.L., S.P., A.R. and S.T.; project administration, S.T., S.M., S.P., Y.-A.L. and P.S.; funding acquisition, Y.-A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Ministry of Science and Technology under Grant MOST 108-2111-M-008 -036 -MY2, and Grant number 108-2923-M-008 -002 -MY3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hashem, N.; Balakrishnan, P. Change analysis of land use/land cover and modelling urban growth in Greater Doha, Qatar. Ann. Gis 2015, 21, 233–247. [Google Scholar] [CrossRef]
- Rahman, A.; Kumar, S.; Fazal, S.; Siddiqui, M.A. Assessment of land use/land cover change in the North-West District of Delhi using remote sensing and GIS techniques. J. Indian Soc. Remote Sens. 2012, 40, 689–697. [Google Scholar] [CrossRef]
- Liou, Y.A.; Nguyen, A.K.; Li, M.H. Assessing spatiotemporal eco-environmental vulnerability by Landsat data. Ecol. Indic. 2017, 80, 52–65. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Liou, Y.A. Mapping global eco-environment vulnerability due to human and nature disturbances. MethodsX 2019, 6, 862–875. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Liou, Y.A. Global mapping of eco-environmental vulnerability from human and nature disturbances. Sci. Total Environ. 2019, 664, 995–1004. [Google Scholar] [CrossRef] [PubMed]
- Talukdar, S.; Pal, S. Wetland habitat vulnerability of lower Punarbhaba river basin of the uplifted Barind region of Indo-Bangladesh. Geocarto Int. 2018, 1–30. [Google Scholar] [CrossRef]
- Nguyen, A.K.; Liou, Y.A.; Li, M.H.; Tran, T.A. Zoning eco-environmental vulnerability for environmental management and protection. Ecol. Indic. 2016, 69, 100–117. [Google Scholar] [CrossRef]
- Che, T.; Xiao, L.; Liou, Y.A. Changes in glaciers and glacial lakes and the identification of dangerous glacial lakes in the Pumqu River Basin, Xizang (Tibet). Adv. Meteorol. 2014, 2014, 903709. [Google Scholar] [CrossRef]
- Dao, P.D.; Liou, Y.A. Object-based flood mapping and affected rice field estimation with Landsat 8 OLI and MODIS data. Remote Sens. 2015, 7, 5077–5097. [Google Scholar] [CrossRef]
- Liou, Y.A.; Kar, S.K.; Chang, L. Use of high-resolution FORMOSAT-2 satellite images for post-earthquake disaster assessment: A study following the 12 May 2008 Wenchuan Earthquake. Int. J. Remote Sens. 2010, 31, 3355–3368. [Google Scholar] [CrossRef]
- Liou, Y.A.; Sha, H.C.; Chen, T.M.; Wang, T.S.; Li, Y.T.; Lai, Y.C.; Lu, L.T. Assessment of disaster losses in rice paddy field and yield after Tsunami induced by the 2011 great east Japan earthquake. J. Mar. Sci. Technol. 2012, 20, 618–623. [Google Scholar]
- Zhang, Y.; Ge, T.; Tian, W.; Liou, Y.A. Debris Flow Susceptibility Mapping Using Machine-Learning Techniques in Shigatse Area, China. Remote Sens. 2019, 11, 2801. [Google Scholar] [CrossRef]
- Talukdar, S.; Pal, S. Effects of damming on the hydrological regime of Punarbhaba river basin wetlands. Ecol. Eng. 2019, 135, 61–74. [Google Scholar] [CrossRef]
- Talukdar, S.; Singha, P.; Mahato, S.; Praveen, B.; Rahman, A. Dynamics of ecosystem services (ESs) in response to land use land cover (LU/LC) changes in the lower Gangetic plain of India. Ecol. Indic. 2020, 112, 106121. [Google Scholar]
- Chen, Z.; Wang, L.; Wei, A.; Gao, J.; Lu, Y.; Zhou, J. Land-use change from arable lands to orchards reduced soil erosion and increased nutrient loss in a small catchment. Sci. Total Environ. 2019, 648, 1097–1104. [Google Scholar] [CrossRef] [PubMed]
- Braun, A.; Hochschild, V. A SAR-Based Index for Landscape Changes in African Savannas. Remote Sens. 2017, 9, 359. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Liou, Y.A.; Tran, H.P.; Hoang, P.P.; Nguyen, T.H. Soil salinity assessment by using near-infrared channel and Vegetation Soil Salinity Index derived from Landsat 8 OLI data: A case study in the Tra Vinh Province, Mekong Delta, Vietnam. Prog. Earth Planet. Sci. 2020, 7, 1–16. [Google Scholar] [CrossRef]
- Mas, J.F.; Lemoine-Rodríguez, R.; González-López, R.; López-Sánchez, J.; Piña-Garduño, A.; Herrera-Flores, E. Land use/land cover change detection combining automatic processing and visual interpretation. Eur. J. Remote Sens. 2017, 50, 626–635. [Google Scholar] [CrossRef]
- Reis, S. Analyzing Land Use/Land Cover Changes Using Remote Sensing and GIS in Rize, North-East Turkey. Sensors 2008, 8, 6188–6202. [Google Scholar] [CrossRef]
- Dutta, D.; Rahman, A.; Paul, S.K.; Kundu, A. Changing pattern of urban landscape and its effect on land surface temperature in and around Delhi. Environ. Monit. Assess. 2019, 191, 551. [Google Scholar] [CrossRef]
- Hoan, N.T.; Liou, Y.A.; Nguyen, K.A.; Sharma, R.C.; Tran, D.P.; Liou, C.L.; Cham, D.D. Assessing the Effects of Land-Use Types in Surface Urban Heat Islands for Developing Comfortable Living in Hanoi City. Remote Sens. 2018, 10, 1965. [Google Scholar] [CrossRef]
- Rahman, A.; Aggarwal, S.P.; Netzband, M.; Fazal, S. Monitoring Urban Sprawl Using Remote Sensing and GIS Techniques of a Fast Growing Urban Centre, India. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2011, 4, 56–64. [Google Scholar] [CrossRef]
- Kumari, B.; Tayyab, M.; Hang, H.T.; Khan, M.F.; Rahman, A. Assessment of public open spaces (POS) and landscape quality based on per capita POS index in Delhi, India. SN Appl. Sci. 2019, 1, 368. [Google Scholar]
- Pal, S.; Talukdar, S. Assessing the role of hydrological modifications on land use/land cover dynamics in Punarbhaba river basin of Indo-Bangladesh. Environ. Dev. Sustain. 2018, 22, 363–382. [Google Scholar] [CrossRef]
- Cerovski-Darriau, C.; Roering, J.J. Influence of anthropogenic land-use change on hillslope erosion in the Waipaoa River Basin, New Zealand. Earth Surf. Process. Landf. 2016, 41, 2167–2176. [Google Scholar] [CrossRef]
- Pal, S.; Kundu, S.; Mahato, S. Groundwater potential zones for sustainable management plans in a river basin of India and Bangladesh. J. Clean. Prod. 2020, 257, 120311. [Google Scholar] [CrossRef]
- Mahato, S.; Pal, S. Groundwater potential mapping in a rural river basin by union (OR) and intersection (AND) of four multi-criteria decision-making models. Nat. Resour. Res. 2019, 28, 523–545. [Google Scholar] [CrossRef]
- Langat, P.K.; Kumar, L.; Koech, R.; Ghosh, M.K. Monitoring of land use/land-cover dynamics using remote sensing: A case of Tana River Basin, Kenya. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Hoffmann, J. The future of satellite remote sensing in hydrogeology. Hydrogeol. J. 2005, 13, 247–250. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Wu, A.-M.; Lin, H.-Y. FORMOSAT-2 Quick Imaging. In Optical Payloads for Space Missions; Qian, S.-E., Ed.; Wiley: Oxford, UK, 2016; 1008p, ISBN 9781118945148. [Google Scholar]
- Wentz, E.A.; Nelson, D.; Rahman, A.; Stefanov, W.L.; Roy, S.S. Expert system classification of urban land use/cover for Delhi, India. Int. J. Remote Sens. 2008, 29, 4405–4427. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote Sensing for Landslide Investigations: An Overview of Recent Achievements and Perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J. Land use and land cover change detection using satellite remote sensing techniques in the mountainous Three Gorges Area, China. Int. J. Remote Sens. 2010, 31, 1519–1542. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Assessment of the effectiveness of support vector machines for hyperspectral data. Future Gener. Comput. Syst. 2004, 20, 1215–1225. [Google Scholar] [CrossRef]
- Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of two dimensional multitemporal Sentinel-2 data with three-dimensional remote sensing data sources for forest inventory parameter estimation over a boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Viana, C.M.; Girão, I.; Rocha, J. Long-Term Satellite Image Time-Series for Land Use/Land Cover Change Detection Using Refined Open Source Data in a Rural Region. Remote Sens. 2019, 11, 1104. [Google Scholar] [CrossRef]
- Gurjar, S.K.; Tare, V. Estimating long-term LULC changes in an agriculture-dominated basin using CORONA (1970) and LISS IV (2013–14) satellite images: A case study of Ramganga River, India. Environ. Monitor. Assess. 2019, 191, 217. [Google Scholar] [CrossRef] [PubMed]
- Toure, S.I.; Stow, D.A.; Shih, H.C.; Weeks, J.; Lopez-Carr, D. Land cover and land use change analysis using multi-spatial resolution data and object-based image analysis. Remote Sens. Environ. 2018, 210, 259–268. [Google Scholar] [CrossRef]
- Usman, M.; Liedl, R.; Shahid, M.A.; Abbas, A. Land use/land cover classification and its change detection using multi-temporal MODIS NDVI data. J. Geogr. Sci. 2015, 25, 1479–1506. [Google Scholar] [CrossRef]
- Stefanov, W.L.; Netzband, M. Assessment of ASTER Land Cover and MODIS NDVI Data at Multiple Scales for Ecological Characterization of an Arid Urban Center. Remote Sens. Environ. 2005, 99, 31–43. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using Rapid Eye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, X.; Lawes, R.; Dunkerley, D.; Zhang, H. Comparison of machine learning algorithms for classification of LiDAR points for characterization of canola canopy structure. Int. J. Remote Sens. 2019, 40, 5973–5991. [Google Scholar] [CrossRef]
- Halder, A.; Ghosh, A.; Ghosh, S. Supervised and unsupervised landuse map generation from remotely sensed images using ant based systems. Appl. Soft Comput. 2011, 11, 5770–5781. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Shih, H.C.; Stow, D.A.; Tsai, Y.H. Guidance on and comparison of machine learning classifiers for Landsat-based land cover and land use mapping. Int. J. Remote Sens. 2019, 40, 1248–1274. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Benediktsson, J.A.; Bruzzone, L.; Chanussot, J. Introduction to the issue on advances in remote sensing image processing. IEEE J. Sel. Top. Signal Process. 2011, 5, 365–369. [Google Scholar] [CrossRef]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. Joint Deep Learning for land cover and land use classification. Remote Sens. Environ. 2019, 221, 173–187. [Google Scholar] [CrossRef]
- Teluguntla, P.; Thenkabail, P.S.; Oliphant, A.; Xiong, J.; Gumma, M.K.; Congalton, R.G.; Huete, A. A 30-m Landsat-derived cropland extent product of Australia and China using random forest machine learning algorithm on Google Earth Engine cloud computing platform. ISPRS J. Photogramm. Remote Sens. 2018, 144, 325–340. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Civco, D.L. Artificial neural networks for land-cover classification and mapping. Int. J. Geogr. Inf. Sci. 1993, 7, 173–186. [Google Scholar] [CrossRef]
- Camargo, F.F.; Sano, E.E.; Almeida, C.M.; Mura, J.C.; Almeida, T. A comparative assessment of machine-learning techniques for land use and land cover classification of the Brazilian tropical savanna using ALOS-2/PALSAR-2 polarimetric images. Remote Sens. 2019, 11, 1600. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Cheng, X.; Wang, L. A comparison of machine learning algorithms for mapping of complex surface-mined and agricultural landscapes using ZiYuan-3 stereo satellite imagery. Remote Sens. 2016, 8, 514. [Google Scholar] [CrossRef]
- Rogan, J.; Franklin, J.; Stow, D.; Miller, J.; Woodcock, C.; Roberts, D. Mapping land-cover modifications over large areas: A comparison of machine learning algorithms. Remote Sens. Environ. 2008, 112, 2272–2283. [Google Scholar] [CrossRef]
- Jamali, A. Evaluation and comparison of eight machine learning models in land use/land cover mapping using Landsat 8 OLI: A case study of the northern region of Iran. SN Appl. Sci. 2019, 1, 1448. [Google Scholar] [CrossRef]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A framework for evaluating land use and land cover classification using convolutional neural networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Yang, C.; Wu, G.; Ding, K.; Shi, T.; Li, Q.; Wang, J. Improving land use/land cover classification by integrating pixel unmixing and decision tree methods. Remote Sens. 2017, 9, 1222. [Google Scholar] [CrossRef]
- Manandhar, R.; Odeh, I.O.; Ancev, T. Improving the accuracy of land use and land cover classification of Landsat data using post-classification enhancement. Remote Sens. 2009, 1, 330–344. [Google Scholar] [CrossRef]
- Latifovic, R.; Olthof, I. Accuracy assessment using sub-pixel fractional error matrices of global land cover products derived from satellite data. Remote Sens. Environ. 2004, 90, 153–165. [Google Scholar] [CrossRef]
- Pal, S.; Ziaul, S.K. Detection of land use and land cover change and land surface temperature in English Bazar urban centre. Egypt. J. Remote Sens. Space Sci. 2017, 20, 125–145. [Google Scholar] [CrossRef]
- Iqbal, S. Flood and Erosion Induced Population Displacements: A Socio-economic Case Study in the Gangetic Riverine Tract at Malda District, West Bengal, India. J. Human Ecol. 2010, 30, 201–211. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Schuman, C.D.; Birdwell, J.D. Dynamic artificial neural networks with affective systems. PLoS ONE 2013, 8, e80455. [Google Scholar] [CrossRef] [PubMed]
- Liou, Y.-A.; Tzeng, Y.C.; Chen, K.S. A neural network approach to radiometric sensing of land surface parameters. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2718–2724. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Liu, S.-F.; Wang, W.-J. Retrieving soil moisture from simulated brightness temperatures by a neural network. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1662–1673. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Dixon, B.; Candade, N. Multispectral landuse classification using neural networks and support vector machines: One or the other, or both? Int. J. Remote Sens. 2008, 29, 1185–1206. [Google Scholar] [CrossRef]
- Yilmaz, I.; Kaynar, O. Multiple regression, ANN (RBF, MLP) and ANFIS models for prediction of swell potential of clayey soils. Expert Syst. Appl. 2011, 38, 5958–5966. [Google Scholar] [CrossRef]
- Moody, J.; Darken, C.J. Fast learning in networks of locally-tuned processing units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Hagenauer, J.; Farajzadeh, M.; Helbich, M. Performance analysis of radial basis function networks and multi-layer perceptron networks in modelling urban change: A case study. Int. J. Geogr. Inf. Sci. 2015, 29, 606–623. [Google Scholar] [CrossRef]
- Ghassemieh, M.; Nasseri, M. Evaluation of stiffened end-plate moment connection through optimized artificial neural network. J. Softw. Eng. Appl. 2012, 5, 156–167. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Bouaziz, M.; Eisold, S.; Guermazi, E. Semiautomatic approach for land cover classification: A remote sensing study for arid climate in Southeastern Tunisia. Euro Mediterr. J. Environ. Integr. 2017, 2, 24. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Rico-Ramirez, M.A.; Bray, M.; Islam, T. Selection of classification techniques for land use/land cover change investigation. Adv. Space Res. 2012, 50, 1250–1265. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector machines for classification. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 39–66. [Google Scholar]
- Mathur, A.; Foody, G.M. Multiclass and binary SVM classification: Implications for training and classification users. IEEE Geosci. Remote Sens. Lett. 2008, 5, 241–245. [Google Scholar] [CrossRef]
- Mannan, B.; Roy, J.; Ray, A.K. Fuzzy ARTMAP supervised classification of multi-spectral remotely-sensed images. Int. J. Remote Sens. 1998, 19, 767–774. [Google Scholar] [CrossRef]
- Gopal, S. Fuzzy ARTMAP—A neural classifier for multispectral image classification. In Spatial Analysis and GeoComputation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 209–237. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Abdullah, A.Y.M.; Masrur, A.; Adnan, M.S.G.; Baky, M.; Al, A.; Hassan, Q.K.; Dewan, A. Spatio-temporal patterns of land use/land cover change in the heterogeneous coastal region of Bangladesh between 1990 and 2017. Remote Sens. 2019, 11, 790. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Feng, Q.; Gong, J.; Liu, J.; Li, Y. Flood mapping based on multiple endmember spectral mixture analysis and random forest classifier—The case of Yuyao, China. Remote Sens. 2015, 7, 12539–12562. [Google Scholar] [CrossRef]
- Mohan, B.S.S.; Sekhar, C.C. Class-Specific Mahalanobis Distance Metric Learning for Biological Image Classification. In Image Analysis and Recognition—9th International Conference, ICIAR 2012, Aveiro, Portugal, 25–27 June 2012; Campilho, A., Kamel, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7325, pp. 240–248. [Google Scholar]
- Petropoulos, G.P.; Vadrevu, K.P.; Xanthopoulos, G.; Karantounias, G.; Scholze, M. A Comparison of Spectral Angle Mapper and Artificial Neural Network Classifiers Combined with Landsat TM Imagery Analysis for Obtaining Burnt Area Mapping. Sensors 2010, 10, 1967–1985. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Ke, Y.; Gong, H.; Li, X. Object-Based Urban Tree Species Classification Using Bi-Temporal WorldView-2 and WorldView-3 Images. Remote Sens. 2015, 7, 16917–16937. [Google Scholar] [CrossRef]
- Hurskainen, P.; Adhikari, H.; Siljander, M.; Pellikka, P.K.E.; Hemp, A. Auxiliary datasets improve accuracy of object-based land use/land cover classification in heterogeneous savanna landscapes. Remote Sens. Environ. 2019, 233, 111354. [Google Scholar] [CrossRef]
- Monserud, R.A.; Leemans, R. Comparing global vegetation maps with the Kappa statistic. Ecol. Model. 1992, 62, 275–293. [Google Scholar] [CrossRef]
- Abdi, A.M. Land cover and land use classification performance of machine learning algorithms in a boreal landscape using Sentinel-2 data. GISci. Remote Sens. 2019, 1–20. [Google Scholar] [CrossRef]
- Erbek, F.S.; Özkan, C.; Taberner, M. Comparison of maximum likelihood classification method with supervised artificial neural network algorithms for land use activities. Int. J. Remote Sens. 2004, 25, 1733–1748. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2018, 18, 18. [Google Scholar]
- Rodriguez-Galiano, V.F.; Chica-Rivas, M. Evaluation of different machine learning methods for land cover mapping of a Mediterranean area using multi-seasonal Landsat images and Digital Terrain Models. Int. J. Digit. Earth 2014, 7, 492–509. [Google Scholar] [CrossRef]
- Foody, G.M. Harshness in image classification accuracy assessment. Int. J. Remote Sens. 2008, 29, 3137–3158. [Google Scholar] [CrossRef]
- Rwanga, S.S.; Ndambuki, J.M. Accuracy assessment of land use/land cover classification using remote sensing and GIS. Int. J. Geosci. 2017, 8, 611. [Google Scholar] [CrossRef]
- Islam, K.; Jashimuddin, M.; Nath, B.; Nath, T.K. Land use classification and change detection by using multi-temporal remotely sensed imagery: The case of Chunati wildlife sanctuary, Bangladesh. Egypt. J. Remote Sens. Space Sci. 2018, 21, 37–47. [Google Scholar] [CrossRef]
- Leyk, S.; Uhl, J.H.; Balk, D.; Jones, B. Assessing the accuracy of multi-temporal built-up land layers across rural-urban trajectories in the United States. Remote Sens. Environ. 2018, 204, 898–917. [Google Scholar] [CrossRef] [PubMed]
- Carvalho Júnior, O.A.; Guimarães, R.F.; Gillespie, A.R.; Silva, N.C.; Gomes, R.A. A new approach to change vector analysis using distance and similarity measures. Remote Sens. 2011, 3, 2473–2493. [Google Scholar] [CrossRef]
- Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing machine learning classifiers for object-based land cover classification using very high-resolution imagery. Remote Sens. 2015, 7, 153–168. [Google Scholar] [CrossRef]
- Szuster, B.W.; Chen, Q.; Borger, M. A comparison of classification techniques to support land cover and land use analysis in tropical coastal zones. Appl. Geogr. 2011, 31, 525–532. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GIScience Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Shiraishi, T.; Motohka, T.; Thapa, R.B.; Watanabe, M.; Shimada, M. Comparative Assessment of Supervised Classifiers for Land Use–Land Cover Classification in a Tropical Region Using Time-Series PALSAR Mosaic Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 1186–1199. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef]
- Deilmai, B.R.; Ahmad, B.B.; Zabihi, H. Comparison of two Classification methods (MLC and SVM) to extract land use and land cover in Johor Malaysia.7th IGRSM International Remote Sensing & GIS Conference and Exhibition, 22–23 April 2014, Kuala Lumpur, Malaysia. IOP Conf. Ser. Earth Environ. Sci. 2014, 20, 012052. [Google Scholar]
- Ahmad, M.; Protasov, S.; Khan, A.M.; Hussain, R.; Khattak, A.M.; Khan, W.A. Fuzziness-based active learning framework to enhance hyperspectral image classification performance for discriminative and generative classifiers. PLoS ONE 2018, 13, e0188996. [Google Scholar] [CrossRef]
- Lee, R.Y.; Ou, D.Y.; Shiu, Y.S.; Lei, T.C. Comparisons of using Random Forest and Maximum Likelihood Classifiers with Worldview-2 imagery for classifying Crop Types. In Proceedings of the 36th Asian Conference Remote Sensing Foster ACRS, Quezon City, Philippines, 24–28 October 2015. [Google Scholar]
- Abbas, A.W.; Ahmad, A.; Shah, S.; Saeed, K. Parameter investigation of Artificial Neural Network and Support Vector Machine for image classification. In Proceedings of the 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 10–14 January 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 795–798. [Google Scholar]
- Nijhawan, R.; Joshi, D.; Narang, N.; Mittal, A. A Futuristic Deep Learning Framework Approach for Land Use-Land Cover Classification Using Remote Sensing. In Advanced Computing and Communication Technologies: Proceedings of the 11th ICACCT 2018; Springer: Singapore, Singapore, 2018; Volume 702, p. 87. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





