Abstract
Forests reduce snow accumulation on the ground through canopy interception and subsequent evaporative losses. To understand snow interception and associated hydrological processes, studies have typically relied on resource-intensive point scale measurements derived from weighed trees or indirect measurements that compared snow accumulation between forested sites and nearby clearings. Weighed trees are limited to small or medium-sized trees, and indirect comparisons can be confounded by wind redistribution of snow, branch unloading, and clearing size. A potential alternative method could use terrestrial lidar (light detection and ranging) because three-dimensional lidar point clouds can be generated for any size tree and can be utilized to calculate volume of the intercepted snow. The primary objective of this study was to provide a feasibility assessment for estimating snow interception volume with terrestrial laser scanning (TLS), providing information on challenges and opportunities for future research. During the winters of 2017 and 2018, intercepted snow masses were continuously measured for two model trees suspended from load-cells. Simultaneously, autonomous terrestrial lidar scanning (ATLS) was used to develop volumetric estimates of intercepted snow. Multiplying ATLS volume estimates by snow density estimates (derived from empirical models based on air temperature) enabled the comparison of predicted vs. measured snow mass. Results indicate agreement between predicted and measured values (R2 ≥ 0.69, RMSE ≥ 0.91 kg, slope ≥ 0.97, intercept ≥ −1.39) when multiplying TLS snow interception volume with a constant snow density estimate. These results suggest that TLS might be a viable alternative to traditional approaches for mapping snow interception, potentially useful for estimating snow loads on large trees, collecting data in difficult to access terrain, and calibrating snow interception models to new forest types around the globe.
1. Introduction
The hydrology of snow-dominated forests is controlled by interactions of mass and energy fluxes between snow and forest structural elements. As forest cover increases, snow accumulation on the ground is typically reduced because of canopy snowfall interception and subsequent sublimation, which can account for as much as 60% of the cumulative snowfall depending on forest type, duration of snow storage in the canopy, and seasonal hydrometeorological conditions [1,2]. The sensitive connection between forest structure and snow interception therefore has important implications for the hydrology in any region around the globe where the major proportion of total water input comes from snow. Understanding this relationship is increasingly important with widespread observed and projected shifts from snow to rain [3], changes in the frequency of winter rain-on-snow events [4,5], and changes in forest vegetation due to fire [6], drought [7], insects [8,9], and other disturbance processes that might be altered by a changing climate and/or forest management.
While the importance of snow interception has long been acknowledged, it is also difficult to measure, map, and model. Direct measurement has typically been limited to resource-intensive point measurements derived from weighed trees, which are generally limited to small or medium trees [1,10,11,12] or tree branches [13,14]. Indirect measurements have compared snow accumulation between forested sites and nearby clearings. Although indirect measurements have advantages (e.g., estimating spatial variance), the accuracy has long been questioned [15], and the measurements can be confounded by wind redistribution of snow, branch unloading, and reference site size [16].
A potential novel method could use terrestrial lidar (TLS) because three-dimensional lidar point clouds, based on the laser return-time/distance relationship, can be generated for any size tree. The point clouds can be transformed into a convex hull with a polyhedral surface approximating the shape of the tree, from which volumes can be calculated [17,18,19]. Intercepted snow volume can be estimated by subtracting snow-free tree volume from snow-on tree volume. This volume can be converted to snow mass by multiplying by fresh snow density, an important variable in snow interception processes [1,20,21,22]. Furthermore, novel autonomous terrestrial laser scanning (ATLS) systems [23] could enable time-series characterization of seasonal dynamics associated with snow interception with minimal fieldwork and maintenance, as well as the flexibility to relocate the experiment to different forest types, thereby overcoming some of the limitations of previous studies. Ultimately, TLS-based snow interception may have a number of advantages over traditional methods, including: spatially explicit estimation of snow interception for different aspects or portions of tree canopies, data collection in difficult to access terrain [24] known to be important contributors to water budgets [25,26] and providing time-efficient data for calibration of emerging aerial lidar (ALS)-based snow interception models to specific forest types [16,27,28].
The objective of this study was to test the feasibility of using ATLS to estimate intercepted snow volume. In doing so, this study provides a preliminary feasibility assessment for estimating snow interception volume solely using terrestrial laser scanning, providing information on challenges and opportunities for future research.
2. Materials and Methods
2.1. Study Site
Two artificial model hanging trees measuring 1.83 meters (m) in height and weighing 1.65 kg each (hereafter referred to “left tree” and “right tree”—see Figure 1) were installed prior to winter 2017 following established approaches outlined in Hedstrom and Pomeroy, 1998 [1]. The trees were off-the-shelf, bilaterally symmetrical Christmas trees. The trees had 25 flexible limbs, multiple needle-types, and did not represent a specific species. The trees had an approximate leaf area index (LAI) of 5.15. LAI was estimated from ATLS point clouds using the LeafR R package [29]. Artificial trees were utilized to avoid desiccation and interception estimates that may be affected by progressive needle drop, in addition to minimizing field work and maintenance. The limbs (metal and plastic) were not analyzed for comparability to live wood elasticity. The trees were installed at the University of Idaho McCall Field Campus (44.9353472°, −116.0820167°) in the mountains of west-central Idaho, which receives an average of 3.4 m total snow fall (maximum 1.9 m snowpack depth) and 0.7 m total precipitation per year at 1528 m elevation [30].

Figure 1.
(a). Study site showing duplicate model trees hanging from load cells, datalogger, and automated terrestrial laser scanner (ATLS; see Eitel et al., 2013). “Left tree” to left of image with snow removed for illustration; “right tree” to right of image. (b). Scan of the trees on the same day.
2.2. Field Measurements
Load cells measured strain gauge output (mV/V), an electrical signal that is proportional to the applied excitation voltage, from the hanging trees in one-minute intervals. The load cells were designed to maintain accuracy (within 0.03 mV/V) with temperatures as cold as −18 °C and were shielded to prevent accumulation of snow and ice. Mean temperature during an ATLS scan was only below −18 °C on one occasion (−20.6 °C), which would have affected the maximum deviation of the calibration curve (a straight line drawn between minimum and maximum output) by no more than 0.0054% according to product specifications. Known masses were hung from the load cells to verify measurement accuracy and to develop a calibration equation (mass = 30.18 * mV/V – 4.6917), which converted strain gauge output to kg. The originating mass of a snow-free tree at the beginning of each winter was subtracted from subsequent measurements to calculate snow masses for each scan.
An ATLS scanned one side of the trees at a distance of 6.2 m and produced two high resolution point clouds per day (1.12 cm spot size and 0.20 cm point spacing at 10 m) (Figure 1b). The ATLS employs a rugged time-of-flight laser rangefinder (optoNCDT ILR 1191 with 905 nm near infrared laser and 1.7 mrad beam divergence; Micro-Epsilon Messtechnik GmbH & Co. KG, Ortenburg, Germany) designed for harsh environments (see Eitel et al., 2013 [23] for more detail). The ATLS completed one scan in 13 h.
Assuming each tree canopy to be bilaterally symmetrical and circular in shape, and given a known canopy diameter, distance from scanner to canopy perimeter, and location of the ATLS, trigonometric calculations yielded 47.7% of the tree canopy perimeter viewable by the ATLS. Rounded to 50% for the analyses, snow masses obtained from the load cells were therefore divided by two and averaged across each ATLS scan duration to allow for comparison with ATLS data.
2.3. Lidar Volume Estimates
The ATLS point clouds were transformed into convex hull structures approximating the shape and volume of the scanned trees using the “ashape3d” function in the alphashape3d R package [18]. The convex hull is fitted with Delauney Triangulation (drawing triangles between points so that there is no overlap between triangles). The convexity parameter (α) is selected by the user, corresponding to data resolution and units of the input data [17,18]. A convexity parameter of 1 corresponds to the convex hull; as α approaches zero, triangle borders are deleted to yield a better fitting, flexible, and concave hull that captures more structural detail. In this case, the TLS data resolution (2.44 cm) is the sum of the spot size (1.12 cm × 2 points) and the point spacing (0.2 cm). This value was rounded to 2.5 cm (i.e., α = 0.025 m) for construction of all “snow-on” convex hulls. The “volume_ashape3d” function was then used to calculate volumes (m3) of the convex hulls. The originating volume of a snow-free tree at the beginning of each winter (α = 0.010 m to capture fine-scale detail of branch structures) was subtracted from subsequent snow-on measurements to calculate snow volumes for each scan in the time series.
2.4. Snow Density Estimates
Hourly fresh snow density (kg/m3) was estimated using hourly air temperatures (Ta; 0.1 °C resolution) from a meteorological monitoring sensor equipped with a radiation shield (VP-4, METER, Pullman, WA, USA) positioned on a pole directly above the ATLS. Ta ranged from −20.6–6.9 °C during the entire study period, with a mean of −2.3 °C and standard deviation of 4.9 °C. Several methods [1,31,32] of estimating fresh snow density from air temperature were tested, including:
ρ (constant) = constant density of 100 kg/m3
ρ (Diamond-Lowry) = 119 + (6.48 × Ta)
ρ (LaChapelle) = 50 + 1.7 (Ta + 15)1.5
ρ (Hedstrom-Pomeroy) = 67.92 + 51.25e(Ta/2.59)
Mean fresh snow density was calculated for each ATLS scan time interval (13 h). Estimates of intercepted snow mass were calculated by multiplying the ATLS derived snow volumes (m3) by fresh snow densities derived from Equations (1)–(4) (kg/m3).
2.5. Statistical Analysis
The precision and accuracy of ATLS-derived estimates of intercepted snow mass was determined by fitting a simple linear regression model in R [33] between ATLS-derived intercepted snow mass in kg (independent variable) and load cell–derived intercepted snow mass in kg (dependent variable) [34]. Estimates of R2 (goodness-of-fit), root mean square error (RMSE) in kg, and regression intercept and slope (indicative of model bias) were determined for models utilizing each density estimation method (see Section 2.4). The optimal model was determined by selecting the best performing snow density estimation method that yielded the least under/over estimation in ATLS derived mass predictions (i.e., closest to 1:1 line) and lowest RMSE.
3. Results
Discounting days without snow, a total of 115 complete ATLS scans were recorded for the left tree in the first winter between January and April; a total of 69 complete ATLS scans were recorded for the left tree in the second winter between November and March. A total of 83 and 69 scans, respectively, were recorded for the right tree over the same time periods. Discrepancies in sample size between the left and right tree were related to incomplete ATLS scans in which scanner malfunction truncated a portion of the scene (e.g., see Figure 1b).
Data exploration using results from the left tree revealed that measured snow interception (averaged across multiple complete scans) in the first winter averaged 3.19 kg (1.0% of season total), with a standard deviation of 4.59 kg and a maximum of 16.95 kg (4.8% of season total). During the second winter, measured snow interception for the left tree averaged 3.31 kg (2.3% of season total), with a standard deviation of 2.76 kg and a maximum of 10.19 kg (4.5% of season total). Estimated mean fresh snow densities using Equations (1)–(4) for the left tree in both winters are summarized in Table 1. Density values are similar to Mair et al., 2016 [35] in which estimates produced by Equation (2) approximated the 100 kg/m3 constant, estimates produced by Equation (3) were higher than the constant, and estimates produced by Equation (4) displayed a wider range.

Table 1.
Mean snow density estimates for the left tree in both winter sampling periods utilizing each of the density estimation Equations (1)–(4) [1,31,32].
Analyses (Table 2) using data spanning both winters for both trees demonstrated that the fresh snow density constant consistently produced higher R2 (model fit) and lower RMSE (unexplained variance) than empirical variable-density Equations (2) [31], (3) [32], and (4) [1], in that order. Simple linear regression utilizing the density constant yielded R2 = 0.71/RMSE = 1.06 kg for the left tree and R2 = 0.69/RMSE = 0.91 kg for the right tree. Simple linear regression using the density constant also produced slopes closest to a 1:1 calibration between ATLS and load cell masses (slope = 0.97 for the left tree and slope = 1.07 for the right tree) (see Table 2 and Figure 2). Intercepts of −1.39 for the left tree and −1.34 for the right tree further illustrate model bias and overestimation in TLS-based mass estimates.

Table 2.
Simple linear regression results comparing predicted and measured snow interception mass for each of the density estimation Equations (1)–(4) [1,31,32]. Data spans winters 2017–2018. The snow density constant produced the best model fit and lowest error for both trees.
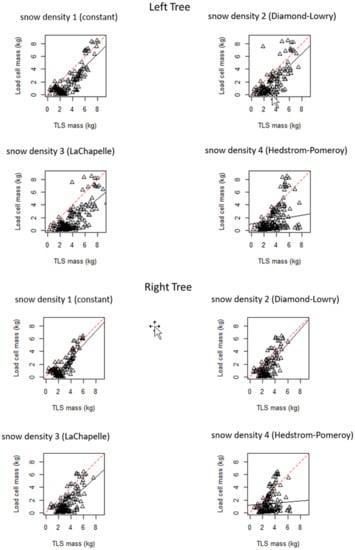
Figure 2.
Simple linear regression results comparing predicted (TLS) and measured (load cell) snow interception mass for density estimation Equations (1)–(4) [1,31,32]. Data spans winters 2017–2018. Black lines = regression lines; red lines = 1:1 lines.
4. Discussion
4.1. The Effect of Snow Density and Scan Duration on Model Performance
To our knowledge, this is the first study that explores the suitability of high resolution, automated terrestrial lidar to estimate canopy snow interception, with direct comparison to the established hanging tree method [1]. The most precise proxies for measured snow interception mass (R2 ≥ 0.69), with the least variation in unexplained variance (RMSE ≥ 0.91 kg), were obtained by multiplying the ATLS derived snow interception volume estimates by a fresh snow density constant of 100 kg/m3.
In contrast, ATLS-derived snow interception volume estimates in conjunction with dynamic fresh snow density estimation equations based on air temperature reduced R2 and increased RMSE model estimates. It may be that because Equations (2)–(4) are empirical, they represent relationships between fresh snow density and air temperature specific to their respective experimental locales: Sierra Nevada Mountains in California [31]; mid-continental Canadian boreal forest [1]; and, a variety of avalanche monitoring sites across the western United States [32]. In addition, each snow density estimation method (2–4) was derived from ground-based samples and may not represent micro-climate conditions unique to tree canopies. Finally, it should be noted that Equation (4) was derived from two sources of data [14,31] with different collection methods and air temperature values mainly limited to −10 °C and warmer [36]. This may have contributed to poor model performance when incorporating Equation (4) (Table 2). Experimental development of adjustment factors for these equations was not in the scope of this study.
Unexplained model variance in ATLS derived mass predictions may also be partially explained by the long ATLS scan duration (13 h). Increases in air temperature and subsequent changes to the density of freshly intercepted snow (i.e., metamorphism) during the course of one scan, or retention of metamorphosed snow between snow events, may have resulted in unexplained model variance. Furthermore, this study was not designed to account for losses of intercepted snow due to wind-driven sublimation and/or unloading, or asymmetrical accumulation of snow on trees during periods of high wind and wet snow [15], processes that also may have resulted in unexplained model variance. Recent advances in lidar technology might help to address the slow scan duration time with the relatively new availability of rugged, relatively low-cost (<$10,000 USD), fast scanning lidar instruments [37]. Future experiments with faster scanning terrestrial lidar that more closely matches single-load cell readings might allow for estimating snow density (kg/m3) from the division of load cell-derived masses (kg) by ATLS-derived volumes (m3). This approach may offer a path to developing a new empirical snow density equation. Further, laser return intensity data obtainable from TLS might provide valuable insights on snow properties that affect density, such as changes in grain size/shape and overall wetness [38,39]. Although this study emphasized automated data collection, model performance could also have been improved with in situ density measurements of canopy intercepted snow; fresh snow density estimate Equations (2)–(4) were derived from ground-based samples [1,31,32]. Further research is needed to devise a practical means of sampling snow density on trees.
4.2. The Effect of Weather and Snow Properties on Model Performance
TLS has been used to monitor changes in snowpack depth, but several factors were shown to decrease the number and intensity of received signals [27,40]. Atmospheric occlusion from heavy snow or fog can interfere with lidar returns, and wet snow surfaces can lead to adsorption of lidar pulses on the target itself [27,39,40]. Snow is also strongly forward-scattering; the proportion of forward scattering of lidar pulses increases with scan angle [27], potentially leading to missed returns on the edges of targets. Despite these issues, the short distance to target (6.2 m) and low scan angle (4.22°) should have minimized the variance between measured and ATLS-derived snow mass due to atmospheric occlusion or forward scattering. Likewise, sampling during the coldest months should have minimized unexplained model variance due to lidar pulse adsorption by snow with high water content.
4.3. The Effect of Changing Tree Geometry on Model Performance
It may be that occlusions due to heavy snow loading, or reductions in occupied space resulting from branch deflection, affected ATLS-derived volume estimates and led to unexplained model variance. On the other hand, the process of snow bridging may fill interstitial spaces between branches and accumulate in new space beyond the original canopy profile, thereby counteracting underestimation due to canopy occlusion or branch deflection. This study was not designed to specifically examine the relationship between branch deflection and changes to tree geometry, or to examine how plastic limb strength might compare with natural wood in its interaction with air temperature. A faster scanning ATLS could, in the future, be utilized in a similar experiment to assess variability in branch deflection, and physical laboratory testing could evaluate material elasticity. In addition, future research could explore the sensitivity of TLS to variable snow volumes within live trees of variable height, canopy density, and needle structure, as well as different air temperature conditions that affect tree geometry through branch deflection. Alternative approaches that minimize occlusion could include reducing beam divergence with more accurate TLS equipment, scanning from different scan positions [41], using full-waveform lidar [27], or exploring emerging ray tracing approaches [42] to reconstruct occluded canopy components.
5. Conclusions
This study provides valuable insights into the use of TLS for estimating intercepted snow volume. Initial results indicate agreement between predicted and measured values of intercepted snow mass (R2 ≥ 0.69 and RMSE ≥ 0.91 kg) when utilizing a constant snow density estimate (100 kg/m3). To further improve TLS derived snow interception estimates, future research is needed to develop improved approaches to estimate density of canopy intercepted snow in situ, explore the sensitivity of TLS snow volume estimates to changing snow conditions and quantities within the canopies of a variety of live trees of different sizes and for a range of temperatures that affect branch flexibility, and/or reduce beam divergence and reconstruct occluded structural elements. Snow interception is challenging to measure and model, but our findings highlight the potential of lidar technology to efficiently and accurately estimate intercepted snow mass. This is a potentially useful development for the collection of interception data in difficult to access terrain, as well as the calibration of aerial lidar–based snow interception models to distinct forest types around the globe.
Author Contributions
Conceptualization, M.R., J.U.H.E., and T.E.L.; methodology, M.R., J.U.H.E., and A.J.M.; software, M.R. and J.U.H.E.; validation, M.R., J.U.H.E., and T.E.L.; formal analysis, M.R. and J.U.H.E.; investigation, M.R., J.U.H.E., and A.J.M.; resources, M.R., J.U.H.E., and T.E.L.; data curation, M.R.; writing—original draft preparation, M.R.; writing—review and editing, M.R., J.U.H.E., A.J.M., and T.E.L.; visualization, M.R. and J.U.H.E.; supervision, J.U.H.E.; project administration, J.U.H.E.; funding acquisition, M.R. and J.U.H.E. All authors have read and agreed to the published version of the manuscript.
Funding
M.R. was supported by National Aeronautics and Space Administration Earth & Space Science Fellowship Program (18-EARTH18F-0208), the National Science Foundation Integrative Graduate Education and Research Traineeship Program, and the Curt Berklund Graduate Research Scholar Fund. J.U.H.E. and A.J.M. were supported by the NASA ABoVE grant NNX15AT86A. J.U.H.E. was further supported by the National Institute of Food and Agriculture, U.S. Department of Agriculture, McIntire Stennis project under 1018044.
Conflicts of Interest
The authors declare no conflict of interest.
Data Availability
Data and code are available through the Northwest Knowledge Network: https://www.northwestknowledge.net/ [43].
References
- Hedstrom, N.R.; Pomeroy, J.W. Measurements and modelling of snow interception in the boreal forest. Hydrol. Process. 1998, 12, 1611–1625. [Google Scholar] [CrossRef]
- Molotch, N.P.; Blanken, P.D.; Williams, M.W.; Turnipseed, A.A.; Monson, R.K.; Margulis, S.A. Estimating sublimation of intercepted and sub-canopy snow using eddy covariance systems. Hydrol. Process. 2007, 21, 1567–1575. [Google Scholar] [CrossRef]
- Klos, P.Z.; Link, T.E.; Abatzoglou, J.T. Extent of the rain-snow transition zone in the western US under historic and projected climate. Geophys. Res. Lett. 2014, 41, 4560–4568. [Google Scholar] [CrossRef]
- Floyd, W.; Weiler, M. Measuring snow accumulation and ablation dynamics during rain-on-snow events: Innovative measurement techniques. Hydrol. Process. 2008, 22, 4805–4812. [Google Scholar] [CrossRef]
- Musselman, K.N.; Lehner, F.; Ikeda, K.; Clark, M.P.; Prein, A.F.; Liu, C.; Barlage, M.; Rasmussen, R. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Chang. 2018, 8, 808. [Google Scholar] [CrossRef]
- Westerling, A.L. Increasing western US forest wildfire activity: Sensitivity to changes in the timing of spring. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2016, 371. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Cobb, N. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Bentz, B.J.; Régnière, J.; Fettig, C.J.; Hansen, E.M.; Hayes, J.L.; Hicke, J.A.; Seybold, S.J. Climate change and bark beetles of the western United States and Canada: Direct and indirect effects. BioScience 2010, 60, 602–613. [Google Scholar] [CrossRef]
- Frank, J.M.; Massman, W.J.; Ewers, B.E.; Williams, D.G. Bayesian Analyses of 17 Winters of Water Vapor Fluxes Show Bark Beetles Reduce Sublimation. Water Resour. Res. 2019, 55, 1598–1623. [Google Scholar] [CrossRef]
- Knowles, N.; Dettinger, M.D.; Cayan, D.R. Trends in snowfall versus rainfall in the western United States. J. Clim. 2006, 19, 4545–4559. [Google Scholar] [CrossRef]
- Storck, P.; Lettenmaier, D.P.; Bolton, S.M. Measurement of snow interception and canopy effects on snow accumulation and melt in a mountainous maritime climate, Oregon, United States. Water Resour. Res. 2002, 38, 1–5. [Google Scholar] [CrossRef]
- Suzuki, K.; Nakai, Y. Canopy snow influence on water and energy balances in a coniferous forest plantation in northern Japan. J. Hydrol. 2008, 352, 126–138. [Google Scholar] [CrossRef]
- Brundl, M.; Bartelt, P.; Schneebeli, M.; Fluhler, H. Measuring branch defection of spruce branches caused by intercepted snow load. Hydrol. Process. 1999, 13, 2357–2369. [Google Scholar] [CrossRef]
- Schmidt, R.A.; Gluns, D.R. Snowfall interception on branches of three conifer species. Can. J. For. Res. 1991, 21, 1262–1269. [Google Scholar] [CrossRef]
- Miller, D.H. Res. Paper PSW-RP-18. In Interception Processes During Snowstorms; Pacific Southwest Forest & Range Experiment Station, Forest Service, US Department of Agriculture: Berkeley, CA, USA, 1964; Volume 18, pp. 18–43. [Google Scholar]
- Moeser, D.; Stähli, M.; Jonas, T. Improved snow interception modeling using canopy parameters derived from airborne LiDAR data. Water Resour. Res. 2015, 51, 5041–5059. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mucke, E.P. Three-Dimensional Alpha Shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Lafarge, T.; Pateiro-López, B.; Possolo, A.; Dunkers, J.R. Implementation of a polyhedral approximation to a 3d set of points using the alpha-shape. J. Stat. Softw. 2014, 56, 1–19. [Google Scholar] [CrossRef]
- Pateiro-López, B.; Rodríguez-Casal, A. Generalizing the convex hull of a sample: The R package alphahull. J. Stat. Softw. 2010, 34, 1–28. [Google Scholar] [CrossRef]
- Judson, A.; Doesken, N. Density of freshly fallen snow in the Central Rocky Mountains. Bull. Am. Meteorol. Soc. 2000, 81, 1577–1587. [Google Scholar] [CrossRef]
- Ryan, W.A.; Doesken, N.J.; Fassnacht, S.R. Preliminary results of ultrasonic snow depth sensor testing for National Weather Service (NWS) snow measurements in the US. Hydrological Processes. Int. J. 2008, 22, 2748–2757. [Google Scholar] [CrossRef]
- Ryan, W.A.; Doesken, N.J.; Fassnacht, S.R. Evaluation of ultrasonic snow depth sensors for U.S. Snow measurements. J. Atmos. Ocean. Technol. 2008, 25, 667–684. [Google Scholar] [CrossRef]
- Eitel, J.U.; Vierling, L.A.; Magney, T.S. A lightweight, low cost autonomously operating terrestrial laser scanner for quantifying and monitoring ecosystem structural dynamics. Agric. For. Meteorol. 2013, 180, 86–96. [Google Scholar] [CrossRef]
- Adams, M.S.; Bauer, A.; Paar, G. Monitoring snow avalanche terrain with automated terrestrial laser scanning. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4006–4009. [Google Scholar]
- Buhler, Y.; Adams, M.S.; Bosch, R.; Stoffel, A. Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): Potential and limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef]
- Hood, J.; Hayashi, M. Assessing the application of a laser rangefinder for determining snow depth in inaccessible alpine terrain. Hydrol. Earth Syst. Sci. 2010, 14, 901. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef]
- Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.S.; Gehrke, F.; Winstral, A. The airborne snow observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Stark, S.C.; Silva, C.A.; Hamamura, C.; Valbuena, R. Package ‘leafR’. 2019. Available online: https://cran.r-project.org/web/packages/leafR/leafR.pdf (accessed on 23 March 2020).
- Western Regional Climate Center. 2016. Available online: https://wrcc.dri.edu/ (accessed on 1 February 2019).
- Diamond, M.; Lowry, W.P. Correlation of the Density of New Snow with 700 Mb Temperature; Snow, Ice and Permafrost Research Establishment, Corps of Engineers, US Army: Hanover, NH, USA, 1953; Volume 1. [Google Scholar]
- LaChapelle, E.R. The Density Distribution of New Snow; Alta Avalanche Study Center: Richmond, UT, USA, 1962. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Mair, E.; Leitinger, G.; Della Chiesa, S.; Niedrist, G.; Tappeiner, U.; Bertoldi, G. A simple method to combine snow height and meteorological observations to estimate winter precipitation at sub-daily resolution. Hydrol. Sci. J. 2016, 61, 2050–2060. [Google Scholar] [CrossRef][Green Version]
- Fassnacht, S.R.; Soulis, E.D. Implications during transitional periods of improvements to the snow processes in the land surface scheme-hydrological model WATCLASS. Atmos. Ocean. 2002, 40, 389–403. [Google Scholar] [CrossRef]
- Condliffe, J. This new lidar sensor could equip every autonomous car in the world by the end of 2018. MIT Technology Review. 12 April 2018. Available online: https://www.technologyreview.com/s/610858/this-new-lidar-sensor-could-equip-every-autonomous-car-in-the-world-by-the-end-of-2018/ (accessed on 15 January 2019).
- Eitel, J.U.H.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.; Glennie, C.L.; Joerg, P.C.; Lewinter, A.L.; Magney, T.S.; et al. Beyond 3-D: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Kaartinen, H.; Kukko, A. Snow cover change detection with laser scanning range and brightness measurements. EARSeL eProc. 2008, 7, 133–141. [Google Scholar]
- Prokop, A. Assessing the applicability of terrestrial laser scanning for spatial snow depth measurements. Cold Reg. Sci. Technol. 2008, 54, 155–163. [Google Scholar] [CrossRef]
- Zande, D.V.D.; Jonckheere, I.; Stuckens, J.; Verstraeten, W.W.; Coppin, P. Sampling design of ground-based lidar measurements of forest canopy structure and its effect on shadowing. Can. J. Remote Sens. 2008, 34, 526–538. [Google Scholar] [CrossRef]
- Xie, D.; Wang, X.; Qi, J.; Chen, Y.; Mu, X.; Zhang, W.; Yan, G. Reconstruction of single tree with leaves based on terrestrial lidar point cloud data. Remote Sens. 2018, 10, 686. [Google Scholar] [CrossRef]
- Russell, M.T.; Eitel, J.H.; Maguire, A.J.; Link, T.E. Dataset: Toward a Novel Laser-Based Approach for Estimating Snow Interception; Northwest Knowledge Network: Moscow, ID, USA, 2020. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).