A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification
Abstract
1. Introduction
2. Design of the Proposed AP-TAN System
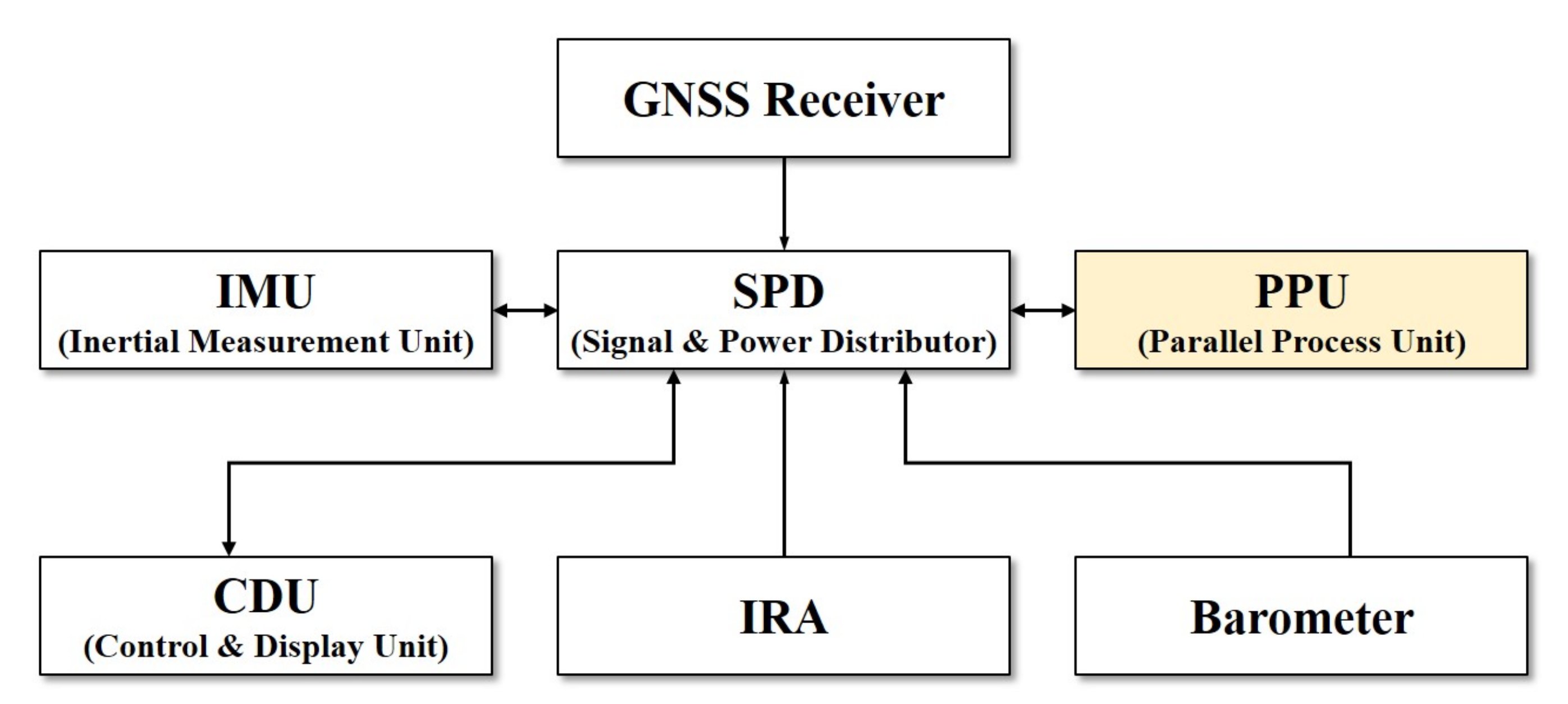
2.1. Overall Design of the AP-TAN System
- A inertial measurement unit (IMU) consists of three ring laser gyros (RLGs) and three silicon pendulum accelerometers to measure the motion of the vehicle without external helps.
- A parallel process unit (PPU) processes the outputs of a IMU and auxiliary sensors. It also performs navigation algorithms including pure navigation, INS/GNSS-aided navigation, TRN, INS/TRN-aided navigation, and INS/GNSS/TRN integrated navigation.
- A GNSS receiver provides the navigation information of the vehicle using GNSS outputs
- A barometer provide the altitude information of the vehicle by measuring the air pressure from the average sea level.
- A IRA provides 3D terrain elevation information for the nearest point.
- A control and display unit (CDU) gives control commands to the PPU and monitors the navigation results in real time.
- A signal and power distributor (SPD) delivers the commands from the CDU and the outputs of the auxiliary sensors to the PPU. It also delivers the navigation results from the PPU to the CDU. In addition, it provides adequate power for the entire system components.
2.2. Design of an INS/GNSS/TRN Integrated Navigation System
2.2.1. Design of the Master Filter Based on the Federated Filter
- Case 1.
- The state variables and covariances when GNSS is not available.
- Case 2.
- The state variables and covariances when TRN is not available.
- Case 3.
- The state variables and covariances when both GNSS and TRN are available.
- Case 4.
- The state variables and covariance when both GNSS and TRN are not available.
2.2.2. Design of the Local Filters Based on the EKF
3. Hybrid TRN Algorithm Based on an Interferometric Radar Altimeter
3.1. Error Compensation Method of IRA Measurements
3.2. Acquisition Mode Based on Batch Processing
3.3. Tracking Mode Based on a Particle Filter
3.4. Real-Time Processing of a High-Resolution Terrain Database
4. Verification of a Three-Dimensional Terrain Based System
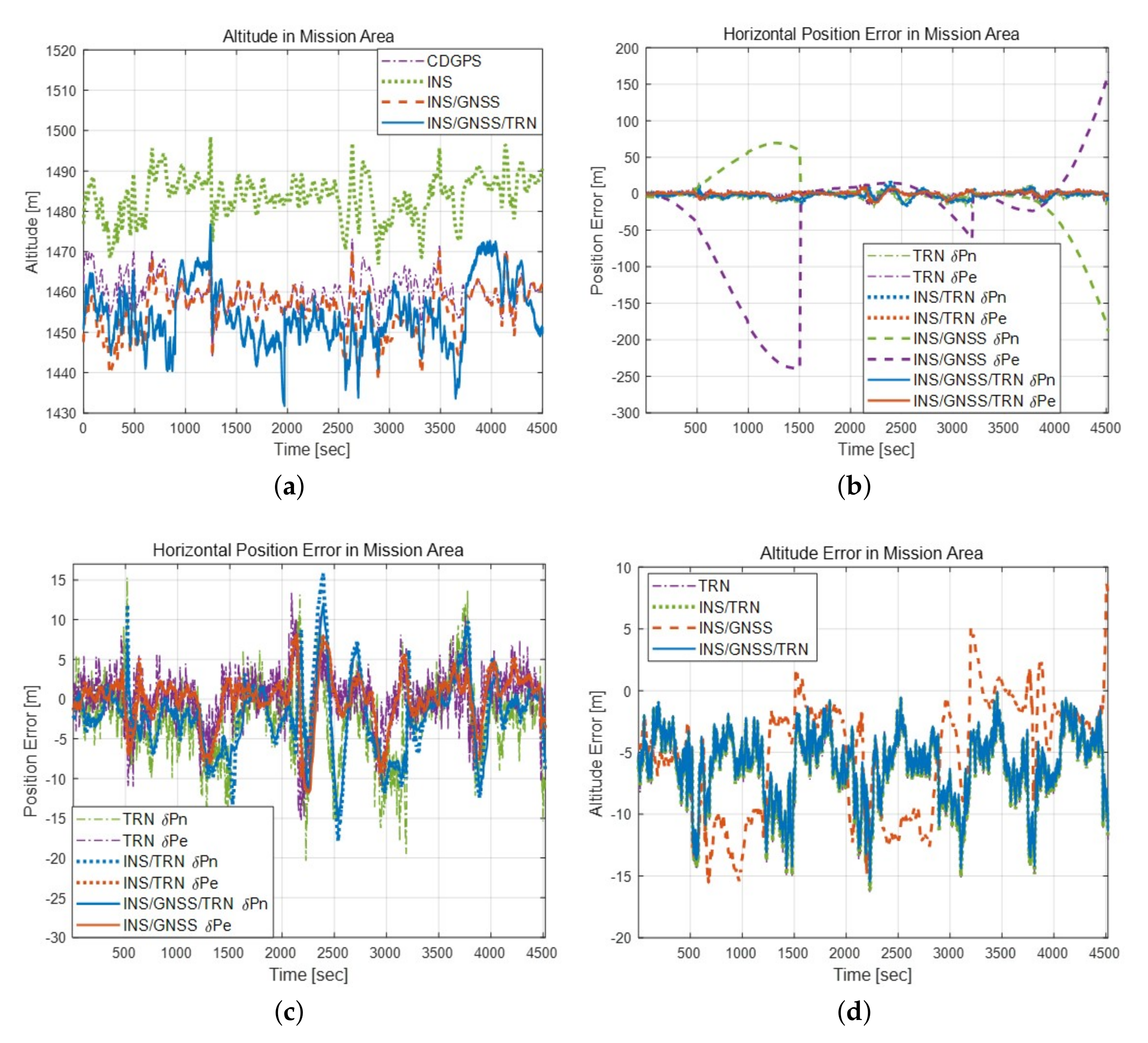
4.1. Experiment Results in a SIL Environment
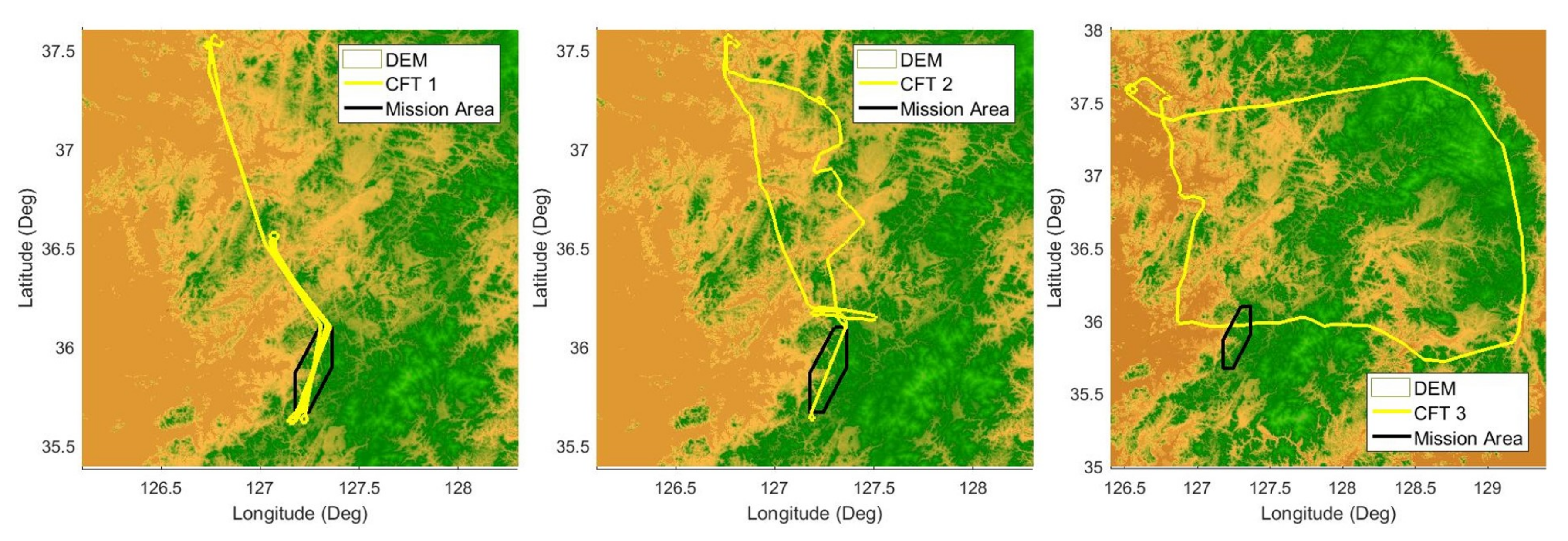
4.2. Verification Using Captive Flight Tests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhang, G.; Hsu, L.T. Intelligent GNSS/INS integrated navigation system for a commercial UAV flight control system. Aerosp. Sci. Technol. 2018, 80, 368–380. [Google Scholar] [CrossRef]
- Courbon, J.; Mezouar, Y.; Guénard, N.; Martinet, P. Vision-based navigation of unmanned aerial vehicles. Control Eng. Pract. 2010, 18, 789–799. [Google Scholar] [CrossRef]
- Belmonte, L.M.; Morales, R.; Fernández-Caballero, A. Computer Vision in Autonomous Unmanned Aerial Vehicles—A Systematic Mapping Study. Appl. Sci. 2019, 9, 3196. [Google Scholar] [CrossRef]
- Konovalenko, I.; Kuznetsova, E.; Miller, A.; Miller, B.; Popov, A.; Shepelev, D.; Stepanyan, K. New approaches to the integration of navigation systems for autonomous unmanned vehicles (UAV). Sensors 2018, 18, 3010. [Google Scholar] [CrossRef]
- Popp, M.; Scholz, G.; Prophet, S.; Trommer, G. A laser and image based navigation and guidance system for autonomous outdoor-indoor transition flights of MAVs. In Proceedings of the 2015 DGON Inertial Sensors and Systems Symposium (ISS), Karlsruhe, Germany, 22–23 September 2015; IEEE: Hoboken, NJ, USA, 2015; pp. 1–18. [Google Scholar]
- Thoma, J.; Paudel, D.P.; Chhatkuli, A.; Probst, T.; Gool, L.V. Mapping, localization and path planning for image-based navigation using visual features and map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7383–7391. [Google Scholar]
- Melo, J.; Matos, A. Survey on advances on terrain based navigation for autonomous underwater vehicles. Ocean Eng. 2017, 139, 250–264. [Google Scholar] [CrossRef]
- Jeon, H.C.; Park, W.J.; Park, C.G. Grid design for efficient and accurate point mass filter-based terrain referenced navigation. IEEE Sensors J. 2017, 18, 1731–1738. [Google Scholar] [CrossRef]
- ZELENKA, R. Integration of radar altimeter, precision navigation, and digital terrain data for low-altitude flight. In Proceedings of the Guidance, Navigation and Control Conference, Hilton Head Island, SC, USA, 10–12 August 1992; p. 4420. [Google Scholar]
- Oh, J.; Sung, C.K.; Lee, J.; Lee, S.W.; Lee, S.J.; Yu, M.J. Accurate Measurement Calculation Method for Interferometric Radar Altimeter-Based Terrain Referenced Navigation. Sensors 2019, 19, 1688. [Google Scholar] [CrossRef]
- Hager, J.R.; Almsted, L.D. Methods and Systems for Enhancing Accuracy of Terrain Aided Navigation Systems. U.S. Patent 7,409,293, 5 August 2008. [Google Scholar]
- Turan, B.; Kutay, A.T. Particle filter studies on terrain referenced navigation. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; IEEE: Hoboken, NJ, USA, 2016; pp. 949–954. [Google Scholar]
- Lee, J.; Bang, H. A robust terrain aided navigation using the Rao-Blackwellized particle filter trained by long short-term memory networks. Sensors 2018, 18, 2886. [Google Scholar] [CrossRef]
- Groves, P.D.; Handley, R.J.; Runnalls, A.R. Optimising the integration of terrain referenced navigation with INS and GPS. J. Navig. 2006, 59, 71–89. [Google Scholar] [CrossRef]
- Peters, M.A. Development of a TRN/INS/GPS integrated navigation system. In Proceedings of the IEEE/AIAA 10th Digital Avionics Systems Conference, Los Angeles, CA, USA, 14–17 October 1991; IEEE: Hoboken, NJ, USA, 1991; pp. 6–11. [Google Scholar]
- Salavasidis, G.; Munafò, A.; Harris, C.A.; Prampart, T.; Templeton, R.; Smart, M.; Roper, D.T.; Pebody, M.; McPhail, S.D.; Rogers, E.; et al. Terrain-aided navigation for long-endurance and deep-rated autonomous underwater vehicles. J. Field Robot. 2019, 36, 447–474. [Google Scholar] [CrossRef]
- Yang, L. Reliability Analysis of Multi-Sensors Integrated Navigation Systems. Ph.D. Thesis, University of New South Wales, Sydney, Australia, August 2014. [Google Scholar]
- Luyang, T.; Xiaomei, T.; Huaming, C.; Xiaohui, L. An Adaptive Federated Filter in Multi-source Fusion Information Navigation System. IOP Conf. Ser. Mater. Sci. Eng. 2018, 392, 062195. [Google Scholar] [CrossRef]
- Carlson, N.A. Federated square root filter for decentralized parallel processors. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 517–525. [Google Scholar] [CrossRef]
- Carlson, N.A.; Berarducci, M.P. Federated Kalman filter simulation results. Navigation 1994, 41, 297–322. [Google Scholar] [CrossRef]
- Seo, J.; Lee, J.G.; Park, C.G. A New error compensation scheme for INS vertical channel. IFAC Proc. Vol. 2004, 37, 1119–1124. [Google Scholar] [CrossRef]
- Lee, J.; Sung, C.; Park, B.; Lee, H. Design of INS/GNSS/TRN Integrated Navigation Considering Compensation of Barometer Error. J. Korea Inst. Mil. Sci. Technol. 2019, 22, 197–206. [Google Scholar]
- Jeong, S.H.; Yoon, J.H.; Park, M.G.; Kim, D.Y.; Sung, C.K.; Kim, H.S.; Kim, Y.H.; Kwak, H.J.; Sun, W.; Yoon, K.J. A performance analysis of terrain-aided navigation (TAN) algorithms using interferometric radar altimeter. J. Korean Soc. Aeronaut. Space Sci. 2012, 40, 285–291. [Google Scholar]
- Lee, J.; Bang, H. Radial basis function network-based available measurement classification of interferometric radar altimeter for terrain-aided navigation. IET Radar Sonar Navig. 2018, 12, 920–930. [Google Scholar] [CrossRef]
- Yoo, Y.M.; Lee, S.M.; Kwon, J.H.; Yu, M.J.; Park, C.G. Profile-based TRN/INS integration algorithm considering terrain roughness. J. Inst. Control. Robot. Syst. 2013, 19, 131–139. [Google Scholar] [CrossRef]
- Candy, J.V. Bayesian Signal Processing: Classical, Modern, and Particle Filtering Methods; John Wiley & Sons: Hoboken, NJ, USA, 2016; Volume 54. [Google Scholar]
- Pitt, M.K.; Shephard, N. Filtering via simulation: Auxiliary particle filters. J. Am. Stat. Assoc. 1999, 94, 590–599. [Google Scholar] [CrossRef]
- Teixeira, F.C.; Quintas, J.; Pascoal, A. AUV terrain-aided navigation using a Doppler velocity logger. Annu. Rev. Control 2016, 42, 166–176. [Google Scholar] [CrossRef]
- Teixeira, F.C.; Quintas, J.; Maurya, P.; Pascoal, A. Robust particle filter formulations with application to terrain-aided navigation. Int. J. Adapt. Control Signal Process. 2017, 31, 608–651. [Google Scholar] [CrossRef]
- Han, K.J.; Sung, C.K.; Yu, M.J.; Park, C.G. Performance improvement of laser TRN using particle filter incorporating gaussian mixture noise model and novel fault detection algorithm. In Proceedings of the ION/GNSS+ 2018 the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 24–28 September 2018; ION: Washington, DC, USA, 2018; pp. 3317–3326. [Google Scholar]
- Munshi, A.; Gaster, B.; Mattson, T.G.; Ginsburg, D. OpenCL Programming Guide; Pearson Education: London, UK, 2011. [Google Scholar]
- Yigit, H.; Yilmaz, G. Development of a GPU accelerated terrain referenced UAV localization and navigation algorithm. J. Intell. Robot. Syst. 2013, 70, 477–489. [Google Scholar] [CrossRef]
- Lee, J.; Sung, C.; Oh, J. Terrain Referenced Navigation Using a Multilayer Radial Basis Function-Based Extreme Learning Machine. Int. J. Aerosp. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Chen, X.; Wang, C.; Wang, X.; Ming, M.; Wang, D. Research of Terrain Aided navigation system. In Proceedings of the International Conference on Automation, Mechanical Control and Computational Engineering, Changsha, China, 24–26 April 2015; Atlantis Press: Paris, France, 2015. [Google Scholar]












| No. of Test | Total Flight Time | Mission Time | Flight Altitude | GNSS Unavailable Area |
|---|---|---|---|---|
| SIL Test 1 | 1 h. 20 min. | 13 min. | 1.3 km | Mission Area |
| SIL Test 2 | 42 min. | 23 min. | 5.3 km | Mission Area |
| SIL Test 3 | 1 h. 50 min. | 1 hr. 40 min. | 2.3 km | Whole Area |
| Hor. Pos. Error [m CEP] | SIL Test 1 | SIL Test 2 | SIL Test 3 |
|---|---|---|---|
| TRN | 4.89 m | 6.74 m | 9.13 m |
| INS/TRN | 3.54 m | 5.62 m | 7.23 m |
| INS/GNSS | 20.06 m | 39.52 m | 2242.68 m |
| INS/GNSS/TRN | 3.50 m | 5.43 m | 6.73 m |
| Altitude Error [m PE] | SIL Test 1 | SIL Test 2 | SIL Test 3 |
| TRN | 2.29 m | 1.35 m | 1.49 m |
| INS/TRN | 1.91 m | 1.13 m | 1.35 m |
| INS/GNSS | 0.14 m | 1.86 m | 0.26 m |
| INS/GNSS/TRN | 1.53 m | 0.90 m | 1.18 m |
| No. of Test | Total Flight Time | Mission Time | Flight Altitude | GNSS Unavailable Area |
|---|---|---|---|---|
| CFT 1 | 3 hr. 33 min. | 1 hr. 58 min. | 1.5 km | Mission Area |
| CFT 2 | 2 hr. 33 min. | 23 min. | 5.1 km | Mission Area |
| CFT 3 | 3 hr. 40 min. | 1 hr. 42 min. | 1.3 km∼3.3 km | Whole Area |
| No. of Test | Acquisition Time | Latitude Error | Longitude Error |
|---|---|---|---|
| CFT 1 | 47 sec | 5 m | 3.5 m |
| CFT 2 | 30 sec | −10 m | −10 m |
| CFT 3 | 24 sec | −16 m | −1 m |
| Hor. Pos. Error [m CEP] | CFT 1 | CFT 2 | CFT 3 |
|---|---|---|---|
| TRN | 3.97 m | 6.45 m | 9.85 m |
| INS/TRN | 3.07 m | 5.90 m | 8.87 m |
| INS/GNSS | 78.92 m | 164.85 m | 1212.85 m |
| INS/GNSS/TRN | 3.75 m | 6.28 m | 8.39 m |
| Altitude Error [m PE] | CFT 1 | CFT 2 | CFT 3 |
| TRN | 4.62 m | 3.33 m | 6.79 m |
| INS/TRN | 4.60 m | 3.29 m | 6.74 m |
| INS/GNSS | 4.76 m | 3.62 m | 6.47 m |
| INS/GNSS/TRN | 4.46 m | 3.16 m | 6.48 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Sung, C.-K.; Oh, J.; Han, K.; Lee, S.; Yu, M.-J. A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification. Remote Sens. 2020, 12, 1396. https://doi.org/10.3390/rs12091396
Lee J, Sung C-K, Oh J, Han K, Lee S, Yu M-J. A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification. Remote Sensing. 2020; 12(9):1396. https://doi.org/10.3390/rs12091396
Chicago/Turabian StyleLee, Jungshin, Chang-Ky Sung, Juhyun Oh, Kyungjun Han, Sangwoo Lee, and Myeong-Jong Yu. 2020. "A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification" Remote Sensing 12, no. 9: 1396. https://doi.org/10.3390/rs12091396
APA StyleLee, J., Sung, C.-K., Oh, J., Han, K., Lee, S., & Yu, M.-J. (2020). A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification. Remote Sensing, 12(9), 1396. https://doi.org/10.3390/rs12091396






