Estimation of All-Weather 1 km MODIS Land Surface Temperature for Humid Summer Days
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Saetellite Data
2.3. In Situ LST Data
3. Methods
3.1. LST Pre-Processing
3.2. Pre-Processing of Input Variables
3.3. Random Forest (RF)
3.4. Schemes for Estimating All-Weather LSTs
3.5. A Series of Validations
4. Results and Discussion
4.1. Analysis of Clear and Cloudy Sky in Situ LSTs in Summer
4.2. Evaluation of Two Schemes Using Clear Sky LSTs
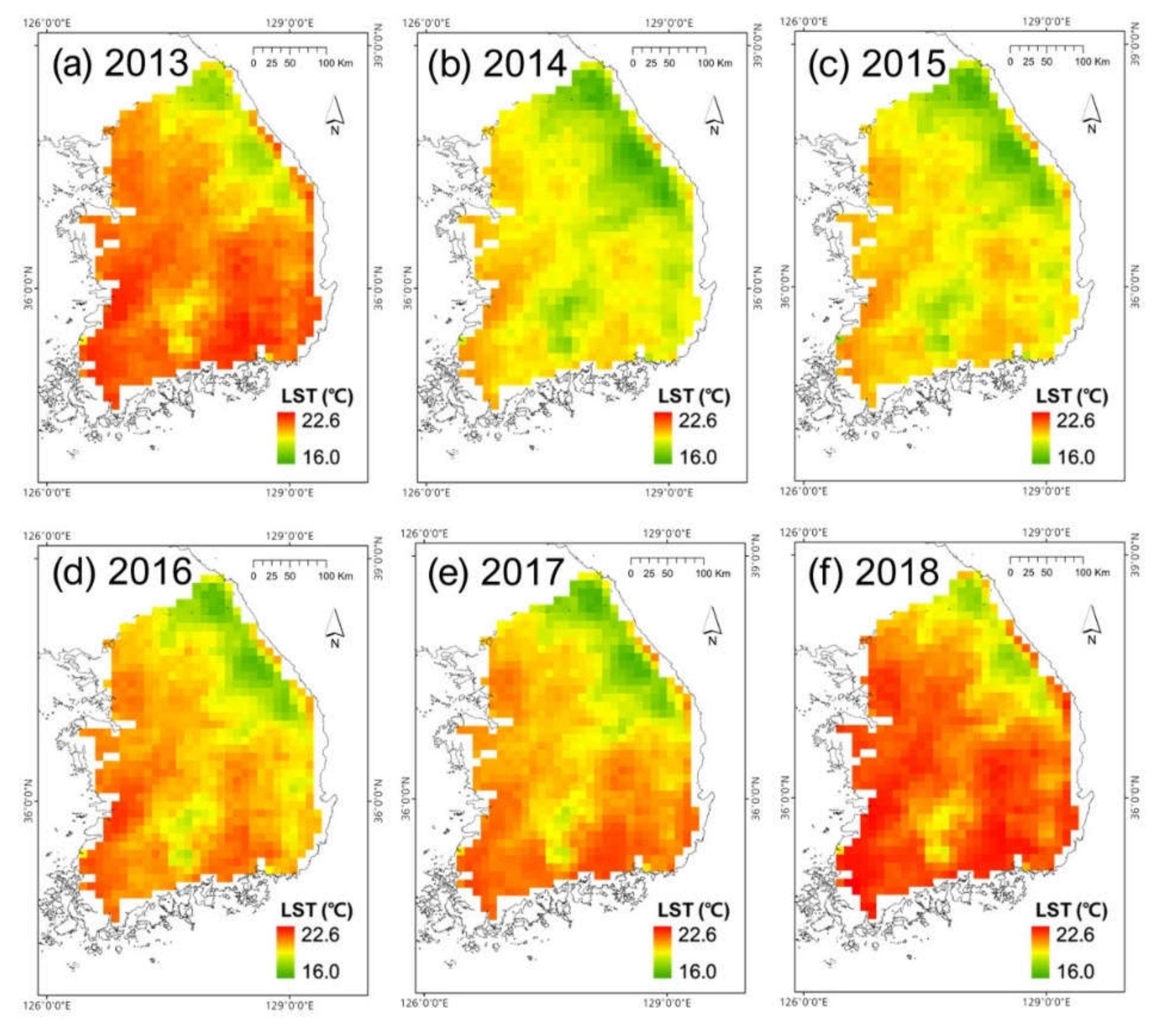
4.3. Spatial Distribution Analysis of All-weather LSTs from Two Schemes
4.4. Comparison of Two Schemes Using in Situ LSTs
4.5. Two Scheme Combinations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
A.1. Before-and after 1 km Bias-corrected in situ LSTs
| Station Number | Before Bias-correction | After Bias-correction | Sample Size | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C) | Bias (°C) | R2 | RMSE (°C) | Bias (°C) | ||
| 1 | 0.62 | 10.50 | 8.89 | 0.64 | 1.88 | −0.06 | 15 |
| 2 | 0.75 | 9.01 | 7.29 | 0.74 | 2.00 | −1.05 | 16 |
| 3 | 0.64 | 18.49 | 17.71 | 0.64 | 2.20 | −0.12 | 26 |
| 4 | 0.65 | 14.23 | 13.43 | 0.66 | 1.97 | −0.20 | 30 |
| 5 | 0.56 | 11.41 | 10.31 | 0.67 | 2.38 | −0.09 | 15 |
| 6 | 0.61 | 17.45 | 16.92 | 0.60 | 2.12 | −0.51 | 16 |
| 7 | 0.57 | 9.55 | 8.15 | 0.59 | 2.06 | 0.15 | 21 |
| 8 | 0.46 | 11.37 | 10.30 | 0.46 | 2.39 | −1.19 | 27 |
| 9 | 0.76 | 11.22 | 10.38 | 0.77 | 1.99 | −0.74 | 15 |
| 10 | 0.54 | 16.43 | 15.20 | 0.53 | 2.15 | −0.43 | 23 |
| Station Number | Before Bias-correction | After Bias-correction | Sample Size | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C) | Bias (°C) | R2 | RMSE (°C) | Bias (°C) | ||
| 1 | 0.77 | 3.34 | 3.02 | 0.78 | 1.38 | 0.01 | 58 |
| 2 | 0.72 | 2.60 | 2.27 | 0.72 | 1.28 | 0.02 | 34 |
| 3 | 0.78 | 2.99 | 2.64 | 0.79 | 1.14 | −0.05 | 55 |
| 4 | 0.85 | 2.37 | 2.10 | 0.86 | 1.01 | 0.01 | 48 |
| 5 | 0.84 | 2.54 | 2.24 | 0.84 | 1.11 | 0.02 | 46 |
| 6 | 0.83 | 2.30 | 1.88 | 0.83 | 1.21 | 0.03 | 67 |
| 7 | 0.66 | 3.96 | 3.74 | 0.66 | 1.30 | 0.06 | 59 |
| 8 | 0.52 | 3.37 | 3.00 | 0.52 | 1.46 | 0.10 | 62 |
| 9 | 0.69 | 2.42 | 1.91 | 0.70 | 1.47 | 0.10 | 49 |
| 10 | 0.70 | 2.96 | 2.55 | 0.70 | 1.29 | 0.00 | 71 |
A.2. Variable Importance Calculated from the RF Models

A.3. Two Scheme Combination (SC) Methods of Daytime
| Station | AMSR2 BTs | |||||||
|---|---|---|---|---|---|---|---|---|
| 10H | 10V | 18H | 18V | 23H | 23V | 36H | 36V | |
| 1 | 0.86 | 0.90 | 0.84 | 0.88 | 0.81 | 0.86 | 0.73 | 0.77 |
| 2 | 0.85 | 0.89 | 0.79 | 0.87 | 0.74 | 0.82 | 0.61 | 0.73 |
| 3 | 0.88 | 0.90 | 0.82 | 0.83 | 0.73 | 0.74 | 0.55 | 0.57 |
| 4 | 0.89 | 0.90 | 0.86 | 0.86 | 0.80 | 0.81 | 0.70 | 0.72 |
| 5 | 0.89 | 0.91 | 0.89 | 0.90 | 0.87 | 0.88 | 0.82 | 0.83 |
| 6 | 0.85 | 0.90 | 0.87 | 0.89 | 0.86 | 0.87 | 0.74 | 0.76 |
| 7 | 0.80 | 0.89 | 0.86 | 0.87 | 0.85 | 0.86 | 0.75 | 0.77 |
| 8 | 0.89 | 0.90 | 0.88 | 0.89 | 0.86 | 0.87 | 0.81 | 0.82 |
| 9 | 0.91 | 0.93 | 0.88 | 0.91 | 0.88 | 0.90 | 0.77 | 0.79 |
| 10 | 0.71 | 0.84 | 0.85 | 0.89 | 0.84 | 0.87 | 0.79 | 0.82 |
| Average | 0.85 | 0.90 | 0.85 | 0.88 | 0.82 | 0.85 | 0.73 | 0.76 |
References
- Bayissa, Y.A.; Tadesse, T.; Svoboda, M.; Wardlow, B.; Poulsen, C.; Swigart, J.; Van Andel, S.J. Developing a satellite-based combined drought indicator to monitor agricultural drought: A case study for Ethiopia. Gisci. Remote Sens. 2019, 56, 718–748. [Google Scholar] [CrossRef]
- Bechtel, B.; Demuzere, M.; Mills, G.; Zhan, W.; Sismanidis, P.; Small, C.; Voogt, J. SUHI analysis using Local Climate Zones—A comparison of 50 cities. Urban Clim. 2019, 28, 100451. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Weng, Q.; Liu, H.; Valavi, R. Modeling the spatial variation of urban land surface temperature in relation to environmental and anthropogenic factors: A case study of Tehran, Iran. Gisci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Song, Y.; Wu, C. Examining human heat stress with remote sensing technology. Gisci. Remote Sens. 2018, 55, 19–37. [Google Scholar] [CrossRef]
- Weng, Q.; Firozjaei, M.K.; Sedighi, A.; Kiavarz, M.; Alavipanah, S.K. Statistical analysis of surface urban heat island intensity variations: A case study of Babol city, Iran. Gisci. Remote Sens. 2019, 56, 576–604. [Google Scholar] [CrossRef]
- Ziaul, S.; Pal, S. Analyzing control of respiratory particulate matter on Land Surface Temperature in local climatic zones of English Bazar Municipality and Surroundings. Urban Clim. 2018, 24, 34–50. [Google Scholar] [CrossRef]
- Park, S.; Kang, D.; Yoo, C.; Im, J.; Lee, M.-I. Recent ENSO influence on East African drought during rainy seasons through the synergistic use of satellite and reanalysis data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 17–26. [Google Scholar] [CrossRef]
- Neinavaz, E.; Skidmore, A.K.; Darvishzadeh, R. Effects of prediction accuracy of the proportion of vegetation cover on land surface emissivity and temperature using the NDVI threshold method. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101984. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Wang, L.; Koike, T.; Yang, K.; Yeh, P.J.-F. Assessment of a distributed biosphere hydrological model against streamflow and MODIS land surface temperature in the upper Tone River Basin. J. Hydrol. 2009, 377, 21–34. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Fu, P.; Weng, Q. Consistent land surface temperature data generation from irregularly spaced Landsat imagery. Remote Sens. Environ. 2016, 184, 175–187. [Google Scholar] [CrossRef]
- Huang, C.; Duan, S.-B.; Jiang, X.-G.; Han, X.-J.; Leng, P.; Gao, M.-F.; Li, Z.-L. A physically based algorithm for retrieving land surface temperature under cloudy conditions from AMSR2 passive microwave measurements. Int. J. Remote Sens. 2019, 40, 1828–1843. [Google Scholar] [CrossRef]
- Jin, M. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle: 2. Cloudy-pixel treatment. J. Geophys. Res. Atmos. 2000, 105, 4061–4076. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 206, 84–97. [Google Scholar] [CrossRef]
- Lu, L.; Venus, V.; Skidmore, A.; Wang, T.; Luo, G. Estimating land-surface temperature under clouds using MSG/SEVIRI observations. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 265–276. [Google Scholar] [CrossRef]
- Shuai, T.; Zhang, X.; Wang, S.; Zhang, L.; Shang, K.; Chen, X.; Wang, J. A spectral angle distance-weighting reconstruction method for filled pixels of the MODIS land surface temperature product. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1514–1518. [Google Scholar] [CrossRef]
- Shwetha, H.; Kumar, D.N. Prediction of high spatio-temporal resolution land surface temperature under cloudy conditions using microwave vegetation index and ANN. ISPRS J. Photogramm. Remote Sens. 2016, 117, 40–55. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Zhan, X.; Houser, P.; Yang, C.; Chiu, L.; Yang, R. Land Surface Temperature Derivation under All Sky Conditions through Integrating AMSR-E/AMSR-2 and MODIS/GOES Observations. Remote Sens. 2019, 11, 1704. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Chen, Z.; Gao, F.; Anderson, M.; Song, L.; Wang, L.; Hu, B.; Yang, Y. Reconstructing daily clear-sky land surface temperature for cloudy regions from MODIS data. Comput. Geosci. 2017, 105, 10–20. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y.; Wu, Z. Spatial and temporal variations of land surface temperature over the Tibetan Plateau based on harmonic analysis. Mt. Res. Dev. 2013, 33, 85–94. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M.; Wang, X.; Tan, J. Estimating the land-surface temperature of pixels covered by clouds in MODIS products. J. Appl. Remote Sens. 2014, 8, 083525. [Google Scholar] [CrossRef]
- Zeng, C.; Long, D.; Shen, H.; Wu, P.; Cui, Y.; Hong, Y. A two-step framework for reconstructing remotely sensed land surface temperatures contaminated by cloud. ISPRS J. Photogramm. Remote Sens. 2018, 141, 30–45. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhong, M.; Zhang, L.; Wu, P. Reconstructing MODIS LST based on multitemporal classification and robust regression. IEEE Geosci. Remote Sens. Lett. 2014, 12, 512–516. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J. Reconstructing spatial–temporal continuous MODIS land surface temperature using the DINEOF method. J. Appl. Remote Sens. 2017, 11, 046016. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Effects of clouds, soil moisture, precipitation, and water vapor on diurnal temperature range. J. Clim. 1999, 12, 2451–2473. [Google Scholar] [CrossRef]
- Lim, Y.-K.; Kim, K.-Y.; Lee, H.-S. Temporal and spatial evolution of the Asian summer monsoon in the seasonal cycle of synoptic fields. J. Clim. 2002, 15, 3630–3644. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.; Xie, Y.; Weng, Q.; Myint, S.; Meacham-Hensold, K.; Bernacchi, C. A physical model-based method for retrieving urban land surface temperatures under cloudy conditions. Remote Sens. Environ. 2019, 230, 111191. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Göttsche, F.-M.; Zhan, W.; Liu, S.; Cao, R. A method based on temporal component decomposition for estimating 1-km all-weather land surface temperature by merging satellite thermal infrared and passive microwave observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4670–4691. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J. Estimating high spatial resolution air temperature for regions with limited in situ data using MODIS products. Remote Sens. 2014, 6, 7360–7378. [Google Scholar] [CrossRef] [Green Version]
- Yoo, C.; Im, J.; Park, S.; Quackenbush, L.J. Estimation of daily maximum and minimum air temperatures in urban landscapes using MODIS time series satellite data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 149–162. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Brown de Colstoun, E.C.; Huang, C.; Wang, P.; Tilton, J.C.; Tan, B.; Phillips, J.; Niemczura, S.; Ling, P.-Y.; Wolfe, R.E. Global Man-made Impervious Surface (GMIS) Dataset From Landsat; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2017. [Google Scholar]
- Christensen, J.H.; Boberg, F.; Christensen, O.B.; Lucas-Picher, P. On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Bechtel, B. Robustness of annual cycle parameters to characterize the urban thermal landscapes. IEEE Geosci. Remote Sens. Lett. 2012, 9, 876–880. [Google Scholar] [CrossRef]
- Stolwijk, A.; Straatman, H.; Zielhuis, G. Studying seasonality by using sine and cosine functions in regression analysis. J. Epidemiol. Community Health 1999, 53, 235–238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.; Im, J.; Park, S.; Yoo, C.; Han, H.; Rhee, J. Classification and mapping of paddy rice by combining Landsat and SAR time series data. Remote Sens. 2018, 10, 447. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Park, H.; Im, J.; Yoo, C.; Rhee, J.; Lee, B.; Kwon, C. Delineation of high resolution climate regions over the Korean Peninsula using machine learning approaches. PLoS ONE 2019, 14, e0223362. [Google Scholar] [CrossRef]
- Yoo, C.; Han, D.; Im, J.; Bechtel, B. Comparison between convolutional neural networks and random forest for local climate zone classification in mega urban areas using Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 157, 155–170. [Google Scholar] [CrossRef]
- Cho, D.; Yoo, C.; Im, J.; Cha, D.H. Comparative assessment of various machine learning-based bias correction methods for numerical weather prediction model forecasts of extreme air temperatures in urban areas. Earth Space Sci. 2020, 7, e2019EA000740. [Google Scholar] [CrossRef] [Green Version]
- McLaren, K.; McIntyre, K.; Prospere, K. Using the random forest algorithm to integrate hydroacoustic data with satellite images to improve the mapping of shallow nearshore benthic features in a marine protected area in Jamaica. Gisci. Remote Sens. 2019, 56, 1065–1092. [Google Scholar] [CrossRef]
- Mutowo, G.; Mutanga, O.; Masocha, M. Including shaded leaves in a sample affects the accuracy of remotely estimating foliar nitrogen. Gisci. Remote Sens. 2019, 56, 1114–1127. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Strobl, C.; Boulesteix, A.-L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Wei, P.; Lu, Z.; Song, J. Variable importance analysis: A comprehensive review. Reliab. Eng. Syst. Saf. 2015, 142, 399–432. [Google Scholar] [CrossRef]
- Yoo, S.; Im, J.; Wagner, J.E. Variable selection for hedonic model using machine learning approaches: A case study in Onondaga County, NY. Landsc. Urban Plan. 2012, 107, 293–306. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. arXiv 2015, arXiv:1508.04409. [Google Scholar] [CrossRef] [Green Version]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Minder, J.R.; Mote, P.W.; Lundquist, J.D. Surface temperature lapse rates over complex terrain: Lessons from the Cascade Mountains. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Lo, M.H.; Famiglietti, J.S. Precipitation response to land subsurface hydrologic processes in atmospheric general circulation model simulations. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Li, Z.-L. MODIS land surface temperature and emissivity. In Land Remote Sensing and Global Environmental Change; Springer: New York, NY, USA, 2010; pp. 563–577. [Google Scholar]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Haginoya, S. Evaluation and improvement of the MODIS land surface temperature/emissivity products using ground-based measurements at a semi-desert site on the western Tibetan Plateau. Int. J. Remote Sens. 2007, 28, 2549–2565. [Google Scholar] [CrossRef]
- Fan, X.; Tang, B.-H.; Wu, H.; Yan, G.; Li, Z.-L. Daytime land surface temperature extraction from MODIS thermal infrared data under cirrus clouds. Sensors 2015, 15, 9942–9961. [Google Scholar] [CrossRef] [Green Version]
- Guillevic, P.; Göttsche, F.; Nickeson, J.; Hulley, G.; Ghent, D.; Yu, Y.; Trigo, I.; Hook, S.; Sobrino, J.; Remedios, J. Land surface temperature product validation best practice protocol. Version 1.0. In Best Practice for Satellite-Derived Land Product Validation; Land Product Validation Subgroup (WGCV/CEOS): Washington, DC, USA, 2017; p. 31. [Google Scholar]
- Zheng, Y.; Ren, H.; Guo, J.; Ghent, D.; Tansey, K.; Hu, X.; Nie, J.; Chen, S. Land Surface Temperature Retrieval from Sentinel-3A Sea and Land Surface Temperature Radiometer, Using a Split-Window Algorithm. Remote Sens. 2019, 11, 650. [Google Scholar] [CrossRef] [Green Version]
- Stroppiana, D.; Antoninetti, M.; Brivio, P.A. Seasonality of MODIS LST over Southern Italy and correlation with land cover, topography and solar radiation. Eur. J. Remote Sens. 2014, 47, 133–152. [Google Scholar] [CrossRef]
- Bertoldi, G.; Notarnicola, C.; Leitinger, G.; Endrizzi, S.; Zebisch, M.; Della Chiesa, S.; Tappeiner, U. Topographical and ecohydrological controls on land surface temperature in an alpine catchment. Ecohydrology 2010, 3, 189–204. [Google Scholar] [CrossRef]
- Lee, X.; Goulden, M.L.; Hollinger, D.Y.; Barr, A.; Black, T.A.; Bohrer, G.; Bracho, R.; Drake, B.; Goldstein, A.; Gu, L. Observed increase in local cooling effect of deforestation at higher latitudes. Nature 2011, 479, 384–387. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, L.; Sun, Z.; Meng, F.; Wang, L.; Sun, Y. Characterizing spatial and temporal trends of surface urban heat island effect in an urban main built-up area: A 12-year case study in Beijing, China. Remote Sens. Environ. 2018, 204, 826–837. [Google Scholar] [CrossRef]
- Im, E.-S.; Thanh, N.-X.; Kim, Y.-H.; Ahn, J.-B. 2018 summer extreme temperatures in South Korea and their intensification under 3° C global warming. Environ. Res. Lett. 2019, 14, 094020. [Google Scholar] [CrossRef]
- Choi, N.; Lee, M.-I. Spatial variability and long-term trend in the occurrence frequency of heatwave and tropical night in Korea. Asia Pac. J. Atmos. Sci. 2019, 55, 101–114. [Google Scholar] [CrossRef]
- Xu, S.; Cheng, J.; Zhang, Q. Reconstructing All-Weather Land Surface Temperature Using the Bayesian Maximum Entropy Method Over the Tibetan Plateau and Heihe River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3307–3316. [Google Scholar] [CrossRef]
- Delle Monache, L.; Stull, R. An ensemble air-quality forecast over western Europe during an ozone episode. Atmos. Environ. 2003, 37, 3469–3474. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Hulley, G.; Malakar, N.; Freepartner, R. Moderate Resolution Imaging Spectroradiometer (MODIS) Land Surface Temperature and Emissivity Product (MxD21) Algorithm Theoretical Basis Document Collection-6; JPL Publication: Pasadena, CA, USA, 2016; pp. 12–17. [Google Scholar]
- Simó, G.; García-Santos, V.; Jiménez, M.A.; Martínez-Villagrasa, D.; Picos, R.; Caselles, V.; Cuxart, J. Landsat and local land surface temperatures in a heterogeneous terrain compared to modis values. Remote Sens. 2016, 8, 849. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.-l. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Meyers, T. Validating MODIS land surface temperature products using long-term nighttime ground measurements. Remote Sens. Environ. 2008, 112, 623–635. [Google Scholar] [CrossRef]









| Type | Variables | Acronym |
|---|---|---|
| AMSR2 BT | 36.5 GHz horizontal polarization | 36H |
| 36.5 GHz vertical polarization | 36V | |
| 23.8 GHz horizontal polarization | 23H | |
| 23.8 GHz vertical polarization | 23V | |
| 18.7 GHz horizontal polarization | 18H | |
| 18.7 GHz vertical polarization | 18V | |
| 10.7 GHz horizontal polarization | 10H | |
| 10.7 GHz vertical polarization | 10V | |
| Annual cycle parameters | Mean annual LST (K) | MAST |
| Mean annual amplitude of LST (K) | YAST | |
| Phase shift relative to spring equinox on the Northern hemisphere | theta | |
| Auxiliary variables | Elevation (m) | Elev |
| Impervious surface fraction (%) | Imp | |
| Latitude (°) | Lat | |
| Longitude (°) | Lon | |
| Converted day of year | DOY | |
| Year as a discrete value | Year |
| Daytime | R2 | RMSE (°C) | nRMSE (%) | Bias (°C) | Sample Size |
|---|---|---|---|---|---|
| Validation1 | 0.93 | 0.97 | 3.2 | 0.00 | 139,876 |
| Validation2 | 0.79 | 1.62 | 5.9 | 0.16 | 138,307 |
| Nighttime | R2 | RMSE (°C) | nRMSE (%) | Bias (°C) | Sample Size |
| Validation1 | 0.96 | 0.53 | 2.7 | 0.02 | 353,114 |
| Validation2 | 0.79 | 1.07 | 6.5 | 0.03 | 298,575 |
| Station | Clear Skies | Cloudy Skies | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C) | Bias (°C) | R2 | RMSE (°C) | Bias (°C) | |||||||
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | |
| 1 | 0.54 | 0.58 | 2.6 | 1.9 | −1.7 | 0.3 | 0.77 | 0.76 | 2.2 | 2.7 | −1.2 | 1.9 |
| 2 | 0.63 | 0.72 | 2.5 | 1.7 | −1.6 | 0.4 | 0.73 | 0.67 | 2.6 | 2.4 | −1.5 | 1.1 |
| 3 | 0.71 | 0.73 | 3.9 | 2.8 | −3.0 | 1.1 | 0.74 | 0.65 | 2.9 | 5.6 | −0.1 | 4.6 |
| 4 | 0.73 | 0.76 | 1.7 | 1.7 | −0.6 | 0.9 | 0.73 | 0.67 | 2.1 | 3.3 | 0.0 | 2.4 |
| 5 | 0.65 | 0.64 | 4.9 | 1.8 | −4.5 | 0.1 | 0.81 | 0.77 | 3.9 | 3.2 | −3.2 | 2.1 |
| 6 | 0.76 | 0.64 | 2.8 | 4.0 | −0.1 | 2.5 | 0.81 | 0.80 | 2.9 | 5.8 | 1.6 | 5.2 |
| 7 | 0.63 | 0.65 | 2.2 | 1.5 | −1.8 | 0.7 | 0.82 | 0.79 | 2.2 | 1.7 | −1.8 | 0.9 |
| 8 | 0.56 | 0.64 | 2.2 | 2.3 | 0.1 | 1.2 | 0.81 | 0.77 | 2.1 | 3.5 | 1.2 | 2.9 |
| 9 | 0.74 | 0.71 | 3.8 | 2.3 | −3.3 | 1.1 | 0.81 | 0.80 | 2.4 | 5.1 | −0.2 | 4.4 |
| 10 | 0.44 | 0.48 | 1.9 | 2.1 | −0.4 | 1.1 | 0.80 | 0.75 | 2.5 | 4.7 | 1.0 | 4.0 |
| Station | Clear Skies | Cloudy Skies | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C) | Bias (°C) | R2 | RMSE (°C) | Bias (°C) | |||||||
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | |
| 1 | 0.92 | 0.89 | 0.7 | 0.9 | 0.1 | 0.2 | 0.70 | 0.68 | 1.3 | 1.3 | −0.7 | −0.8 |
| 2 | 0.89 | 0.87 | 1.3 | 1.0 | −1.0 | −0.5 | 0.68 | 0.64 | 2.2 | 2.0 | −1.9 | −1.7 |
| 3 | 0.87 | 0.82 | 1.0 | 1.2 | −0.4 | −0.2 | 0.71 | 0.70 | 1.9 | 1.9 | −1.5 | −1.5 |
| 4 | 0.87 | 0.87 | 0.9 | 0.8 | 0.1 | 0.0 | 0.74 | 0.73 | 1.3 | 1.4 | −0.8 | −0.9 |
| 5 | 0.90 | 0.88 | 1.2 | 1.0 | −0.7 | −0.3 | 0.63 | 0.69 | 2.1 | 1.8 | −1.6 | −1.4 |
| 6 | 0.87 | 0.85 | 1.0 | 1.0 | 0.3 | 0.1 | 0.60 | 0.60 | 1.5 | 1.6 | −0.8 | −0.9 |
| 7 | 0.83 | 0.81 | 0.9 | 0.9 | 0.5 | 0.2 | 0.69 | 0.69 | 1.0 | 1.1 | −0.1 | −0.3 |
| 8 | 0.76 | 0.71 | 1.0 | 1.1 | 0.2 | 0.1 | 0.70 | 0.71 | 1.1 | 1.2 | −0.4 | −0.5 |
| 9 | 0.84 | 0.84 | 1.0 | 1.0 | −0.3 | 0.0 | 0.68 | 0.68 | 1.7 | 1.7 | −1.2 | −1.1 |
| 10 | 0.87 | 0.82 | 0.7 | 1.0 | 0.1 | 0.1 | 0.70 | 0.72 | 1.4 | 1.4 | −0.7 | −0.7 |
| Station | Daytime (All-weather) | Nighttime (All-weather) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C) | R2 | RMSE (°C) | |||||||||
| S1 | S2 | SC | S1 | S2 | SC | S1 | S2 | SC | S1 | S2 | SC | |
| 1 | 0.78 | 0.77 | 0.82 | 2.2 | 2.5 | 1.9 | 0.76 | 0.73 | 0.75 | 1.1 | 1.2 | 1.2 |
| 2 | 0.75 | 0.72 | 0.79 | 2.5 | 2.3 | 2.3 | 0.73 | 0.68 | 0.72 | 2.0 | 1.8 | 1.9 |
| 3 | 0.80 | 0.73 | 0.82 | 3.2 | 5.0 | 2.6 | 0.73 | 0.71 | 0.73 | 1.7 | 1.7 | 1.7 |
| 4 | 0.78 | 0.74 | 0.79 | 2.0 | 3.0 | 2.1 | 0.76 | 0.76 | 0.77 | 1.2 | 1.3 | 1.2 |
| 5 | 0.83 | 0.79 | 0.81 | 4.1 | 3.0 | 3.3 | 0.70 | 0.73 | 0.73 | 1.9 | 1.7 | 1.7 |
| 6 | 0.83 | 0.80 | 0.85 | 2.9 | 5.5 | 3.0 | 0.66 | 0.67 | 0.68 | 1.4 | 1.5 | 1.4 |
| 7 | 0.83 | 0.81 | 0.82 | 2.2 | 1.7 | 2.1 | 0.74 | 0.74 | 0.75 | 1.0 | 1.0 | 1.0 |
| 8 | 0.82 | 0.81 | 0.83 | 2.1 | 3.2 | 2.2 | 0.71 | 0.71 | 0.73 | 1.1 | 1.2 | 1.1 |
| 9 | 0.84 | 0.83 | 0.82 | 2.8 | 4.5 | 2.5 | 0.73 | 0.73 | 0.74 | 1.5 | 1.5 | 1.5 |
| 10 | 0.82 | 0.76 | 0.80 | 2.3 | 4.3 | 2.6 | 0.74 | 0.76 | 0.76 | 1.3 | 1.3 | 1.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, C.; Im, J.; Cho, D.; Yokoya, N.; Xia, J.; Bechtel, B. Estimation of All-Weather 1 km MODIS Land Surface Temperature for Humid Summer Days. Remote Sens. 2020, 12, 1398. https://doi.org/10.3390/rs12091398
Yoo C, Im J, Cho D, Yokoya N, Xia J, Bechtel B. Estimation of All-Weather 1 km MODIS Land Surface Temperature for Humid Summer Days. Remote Sensing. 2020; 12(9):1398. https://doi.org/10.3390/rs12091398
Chicago/Turabian StyleYoo, Cheolhee, Jungho Im, Dongjin Cho, Naoto Yokoya, Junshi Xia, and Benjamin Bechtel. 2020. "Estimation of All-Weather 1 km MODIS Land Surface Temperature for Humid Summer Days" Remote Sensing 12, no. 9: 1398. https://doi.org/10.3390/rs12091398
APA StyleYoo, C., Im, J., Cho, D., Yokoya, N., Xia, J., & Bechtel, B. (2020). Estimation of All-Weather 1 km MODIS Land Surface Temperature for Humid Summer Days. Remote Sensing, 12(9), 1398. https://doi.org/10.3390/rs12091398








