Remote Sensing Retrieval of Total Phosphorus in the Pearl River Channels Based on the GF-1 Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
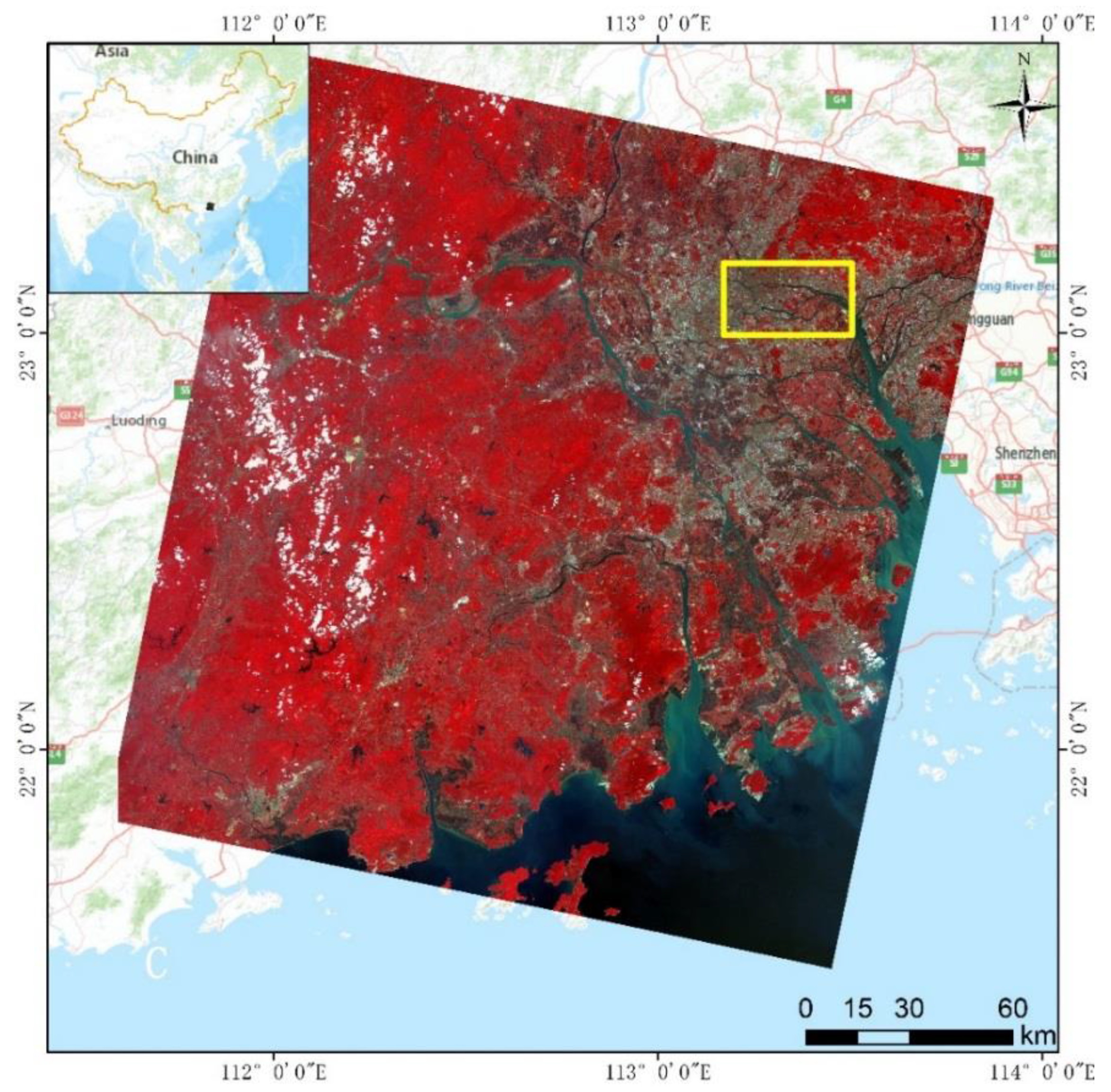
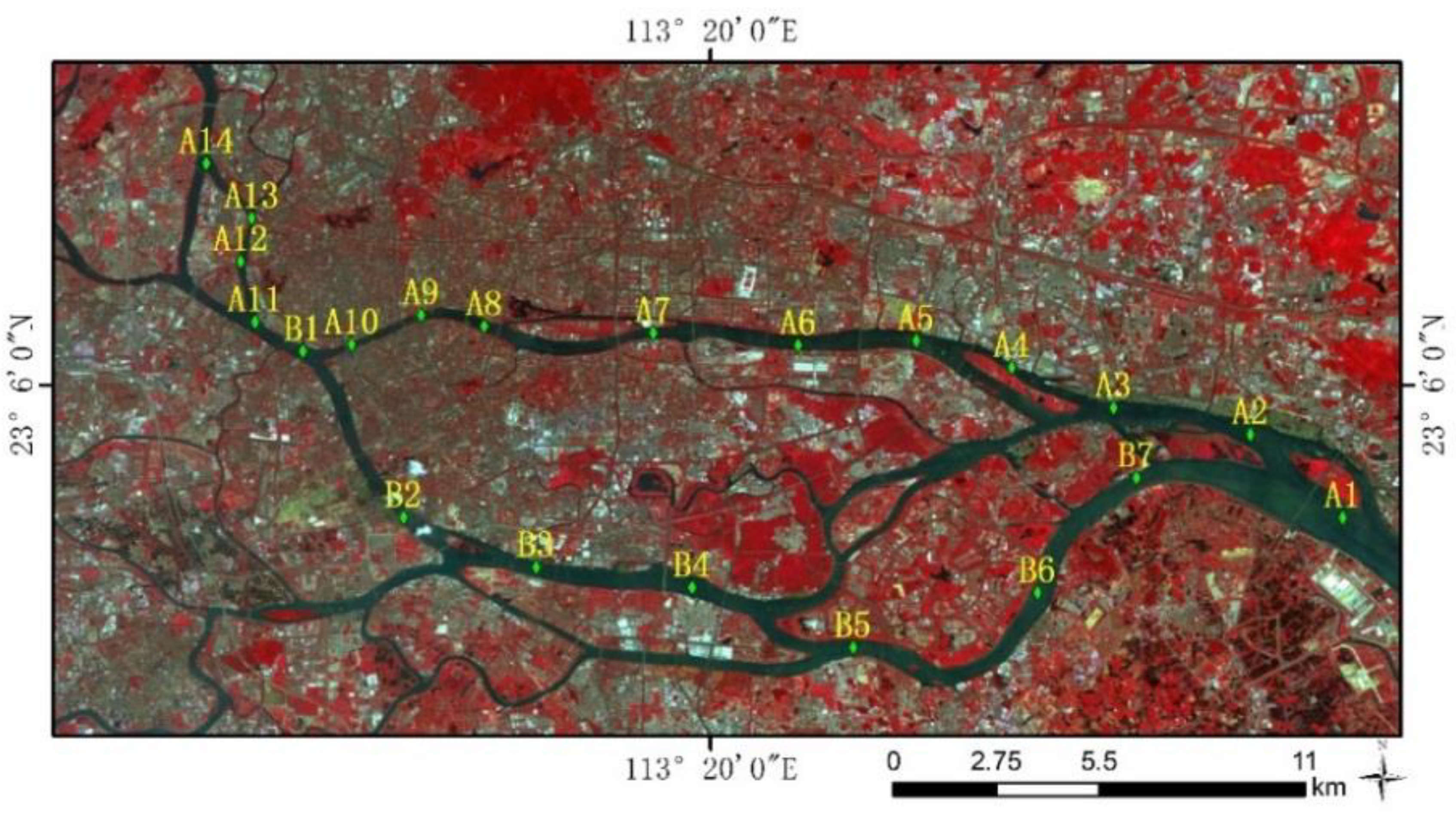
2.1. Study Area
2.2. Data
2.2.1. Measured Water Leaving Reflectance Data
2.2.2. GF-1 Remote Sensing Data
2.2.3. Water Quality Analysis Data
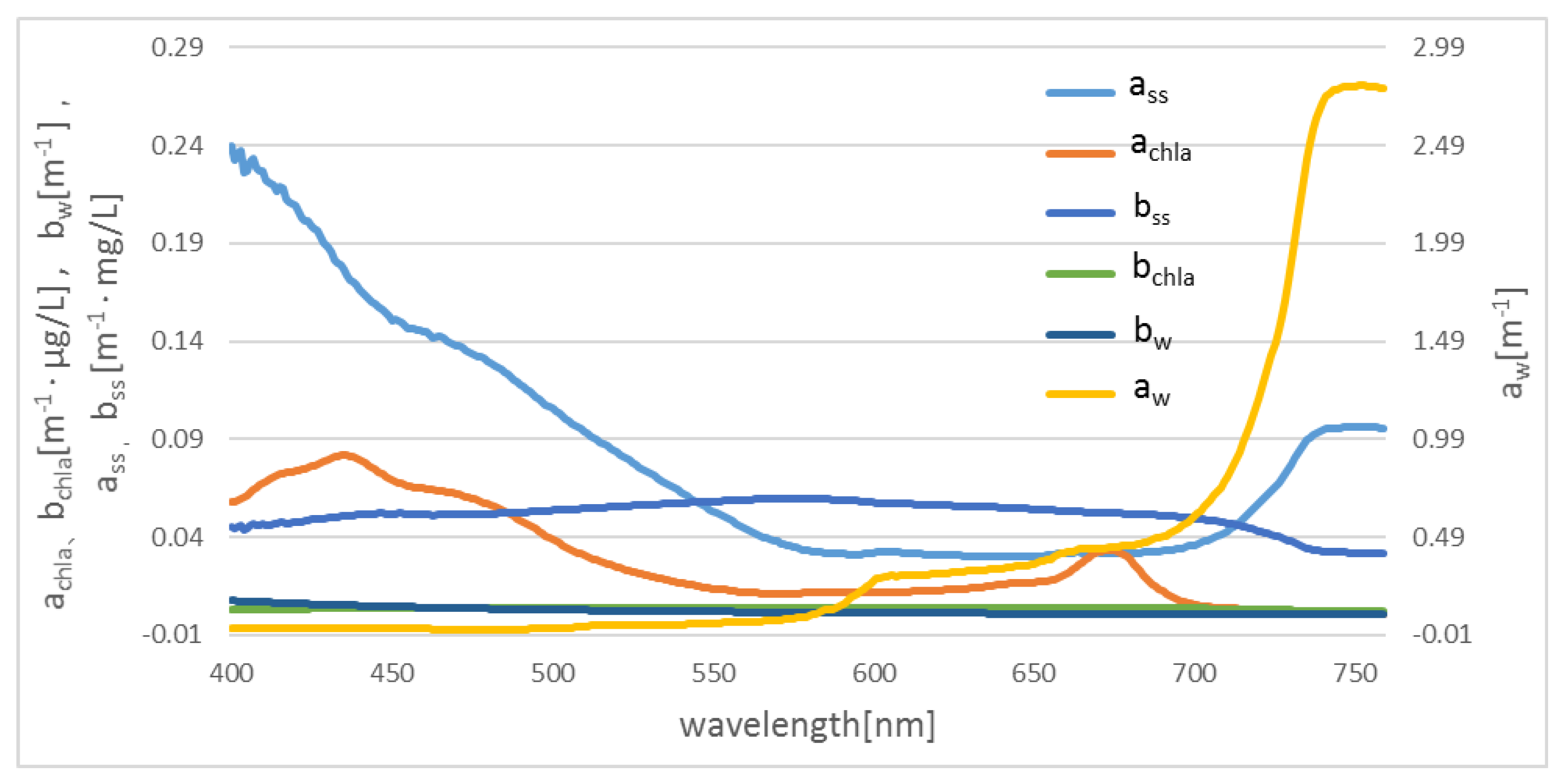
2.2.4. Optical Parameters of Water Components
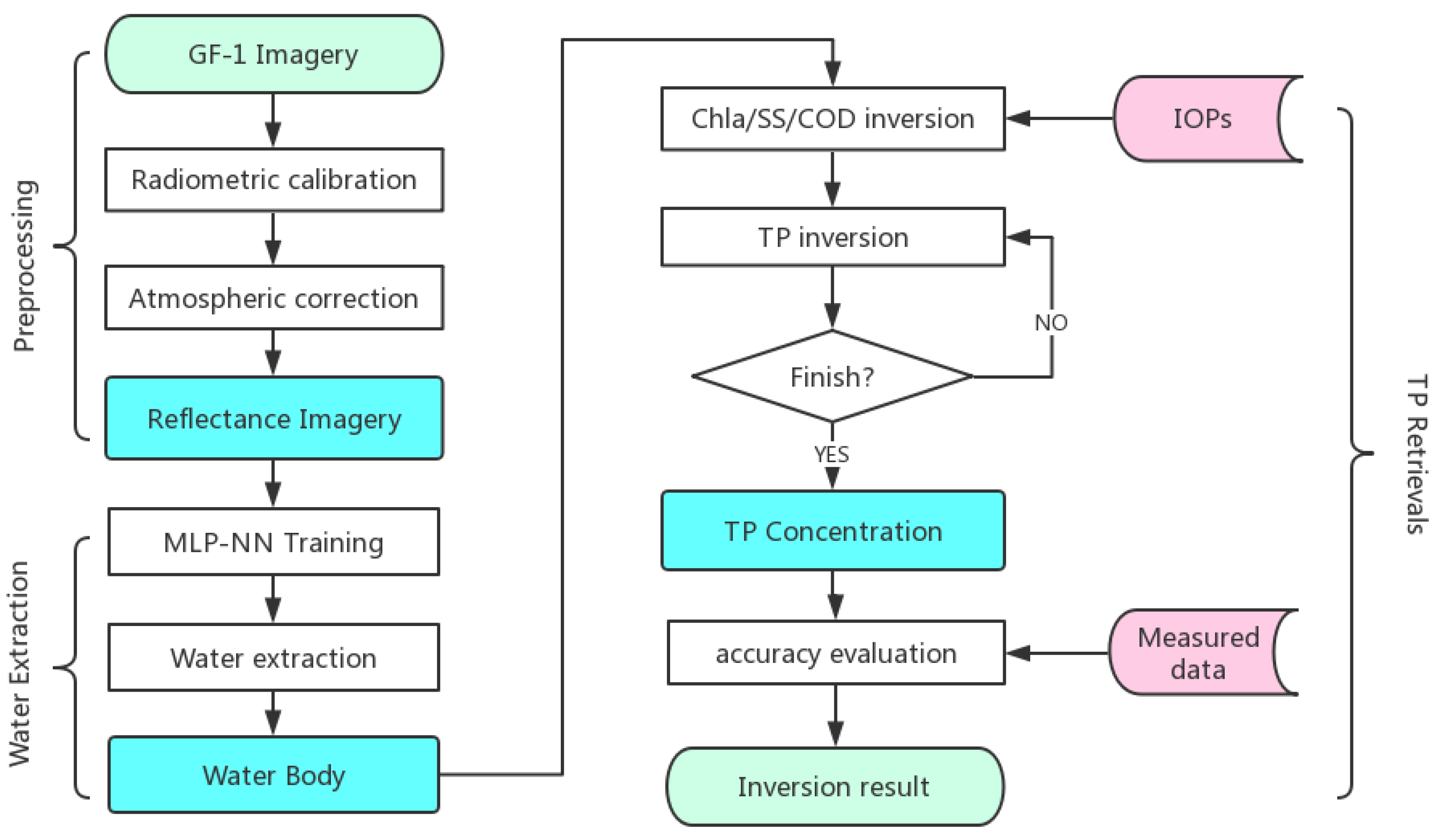
2.3. Methods
2.3.1. TP Regression Analysis
2.3.2. Semi-Analytical Model for Water Quality Retrieval
2.3.3. TP Retrieval Model
2.3.4. Optical Parameters Measurement of Organic Matter
2.3.5. Model Verification and Error Analysis
3. Results
3.1. Water Quality Analysis Results and Measured Spectrum
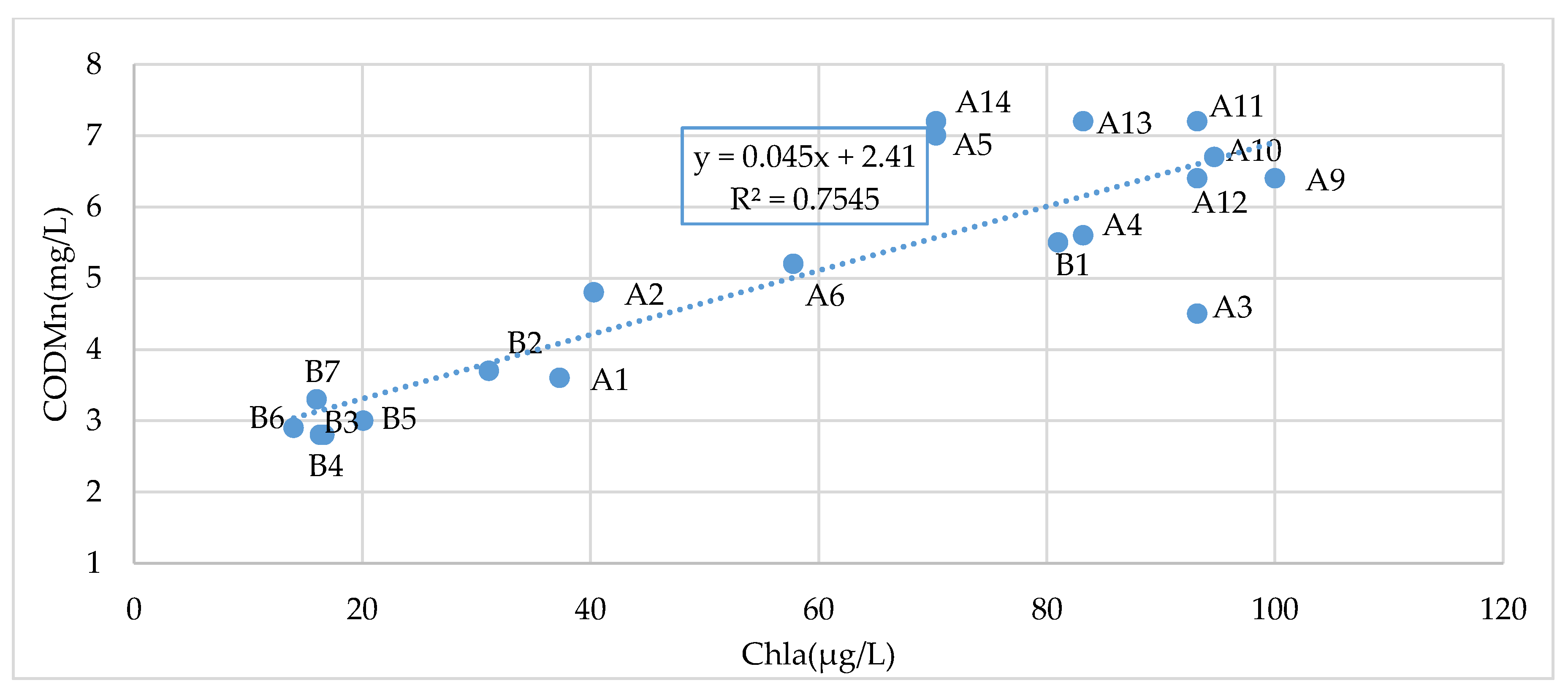
3.1.1. Water Quality Analysis Results
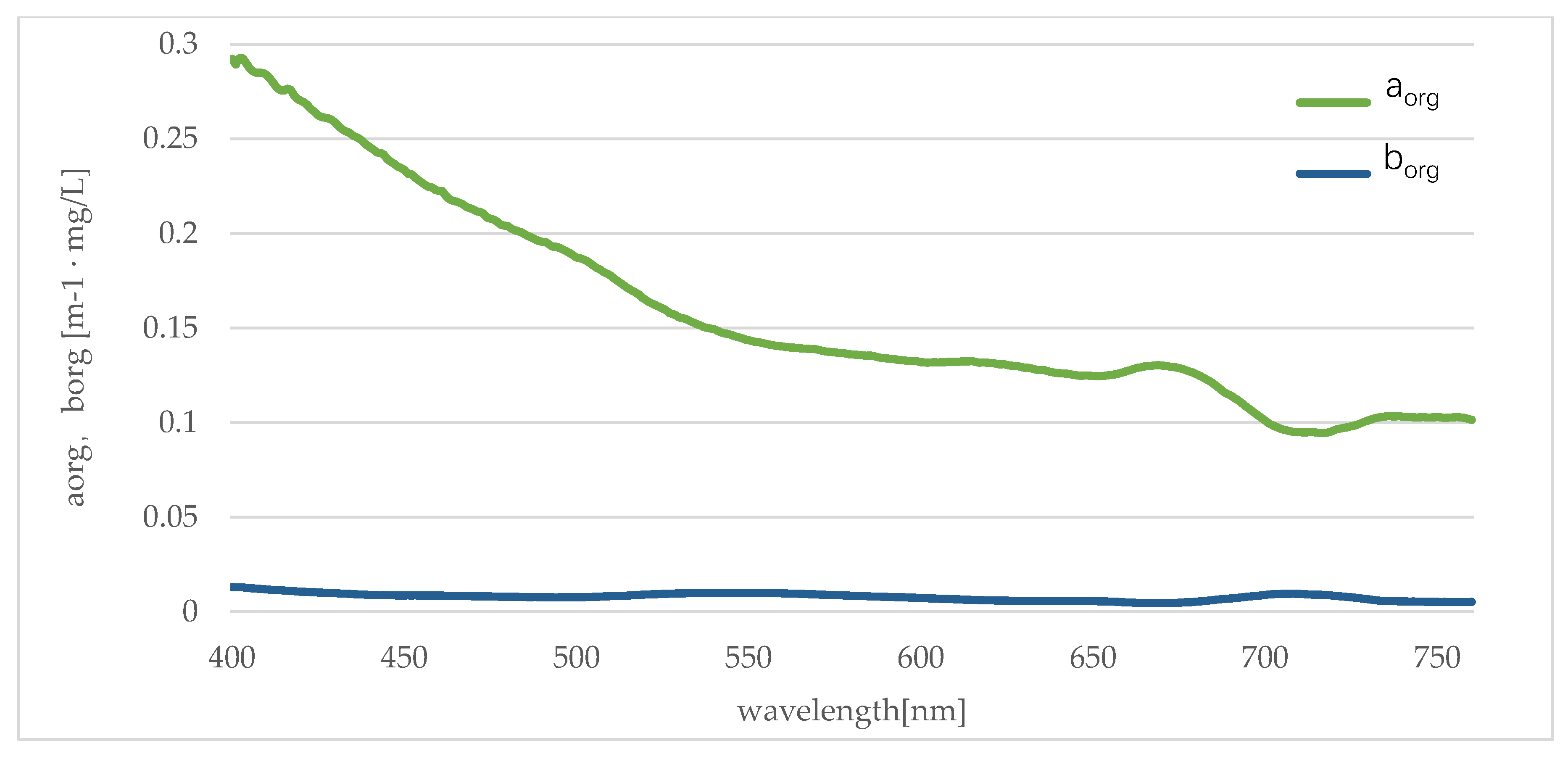
3.1.2. IOPs of Organic Matter in the Pearl River Channels in Guangzhou
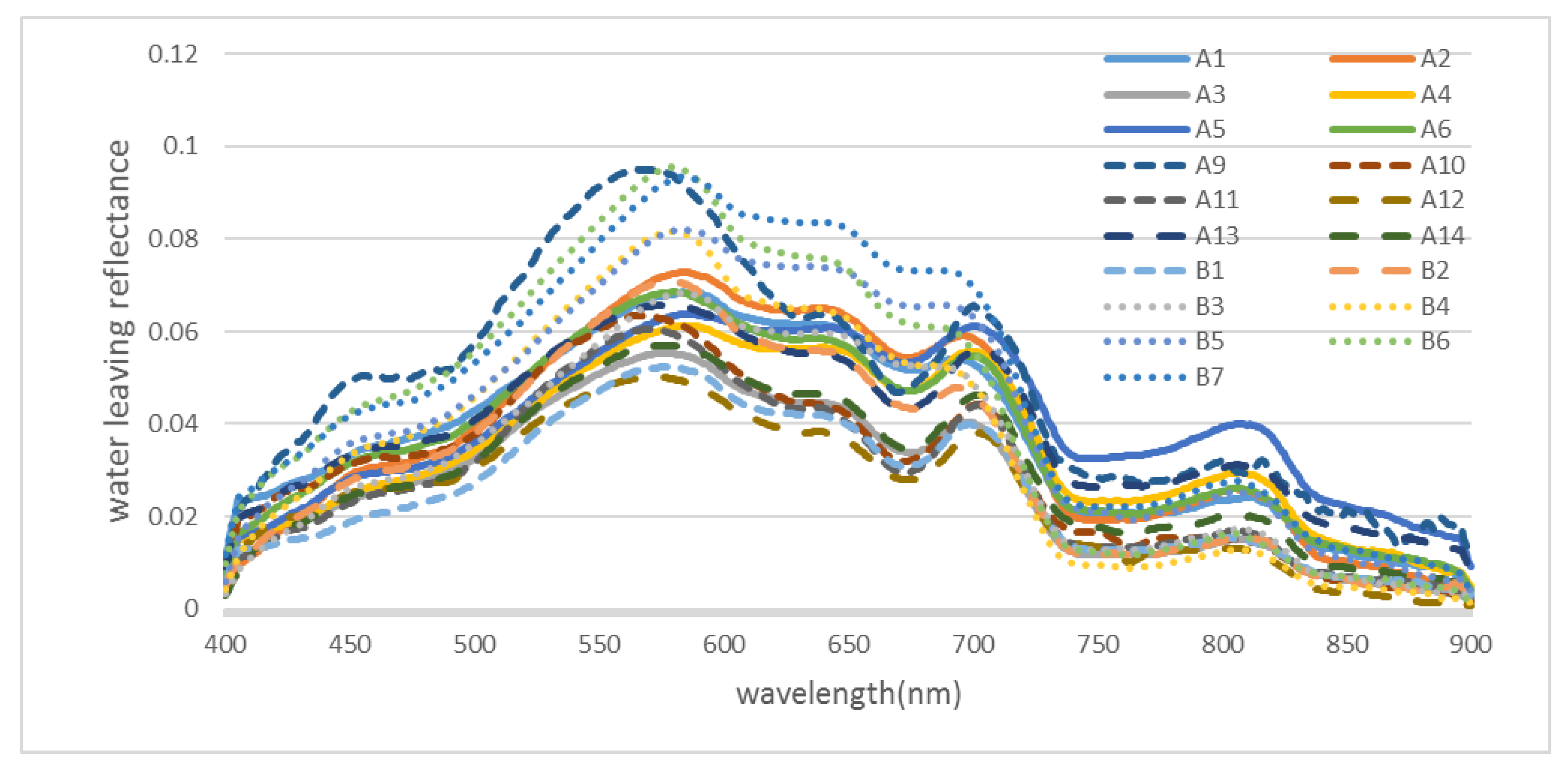
3.1.3. Measured Water Leaving Reflectance
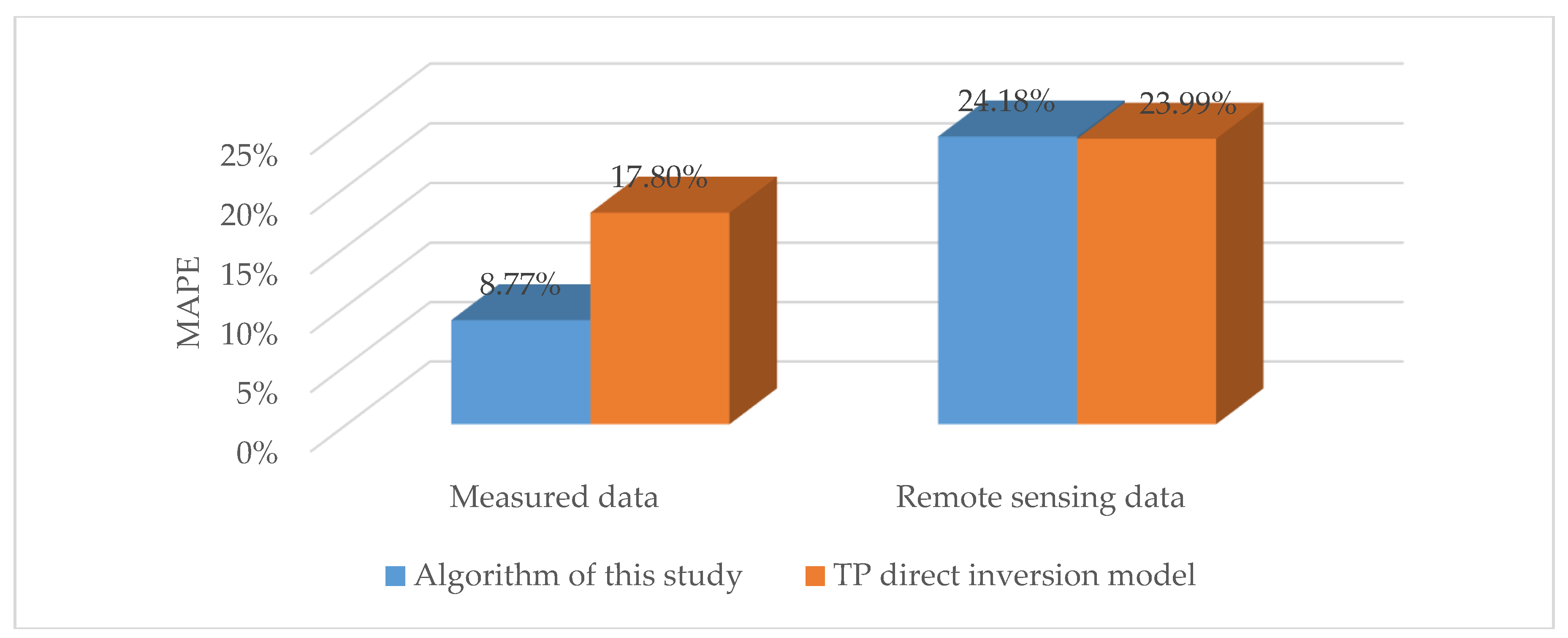
3.2. Verification of the TP Inversion Model
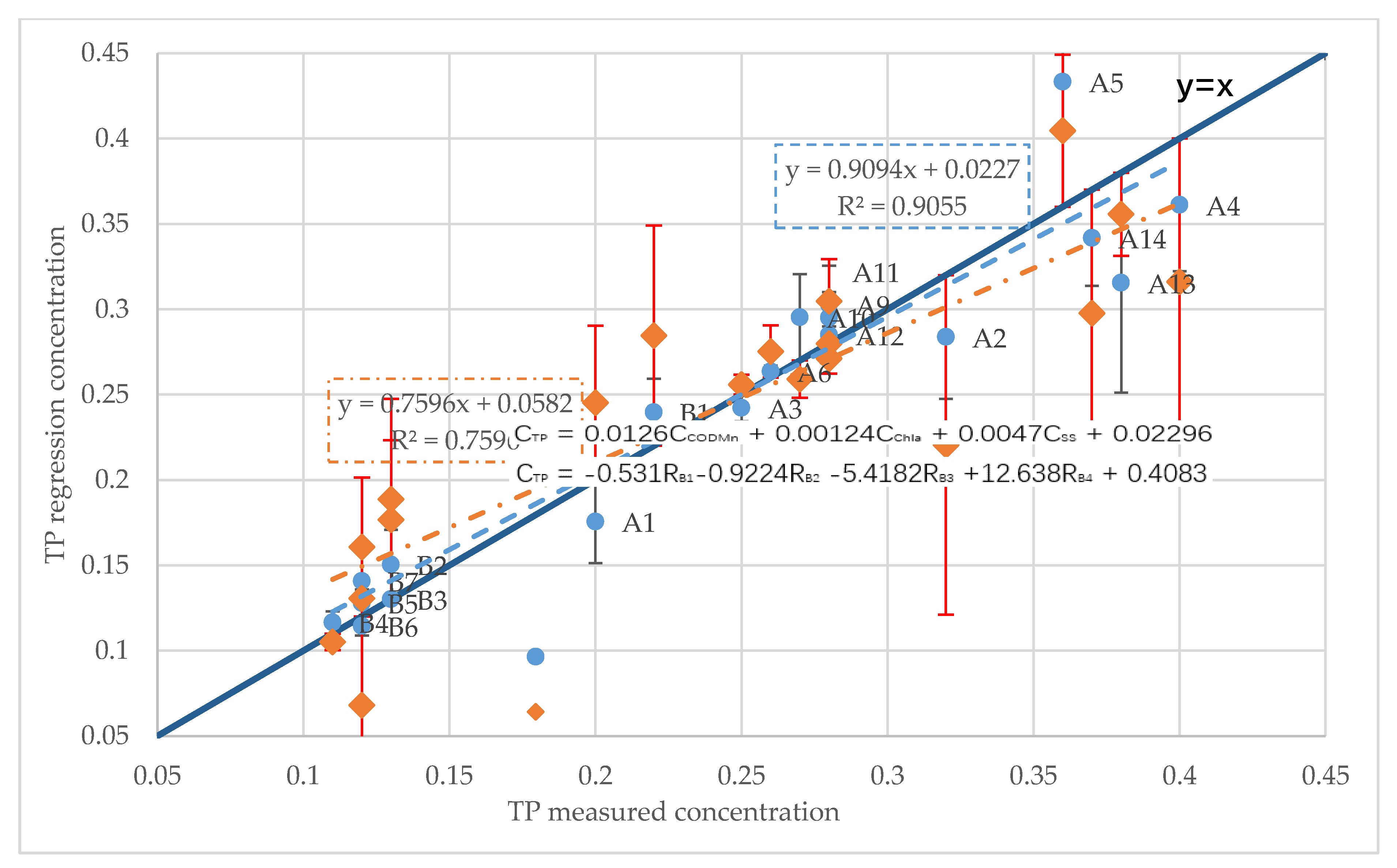
3.2.1. TP Inversion Model
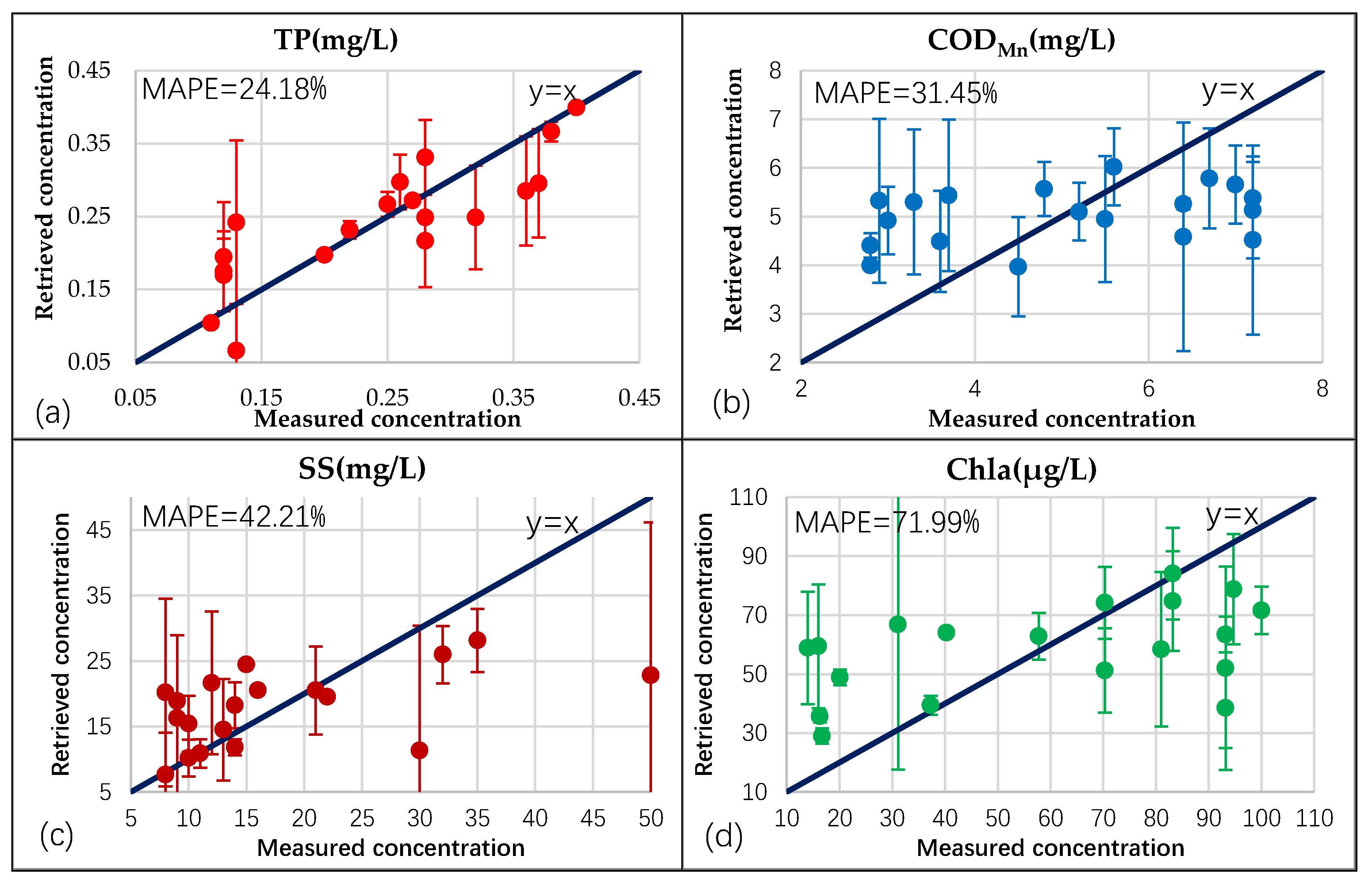
3.2.2. Inversion Results Based on Measured Data
3.3. Remote Sensing Retrieval of Water Quality Parameters in the Pearl River Channels
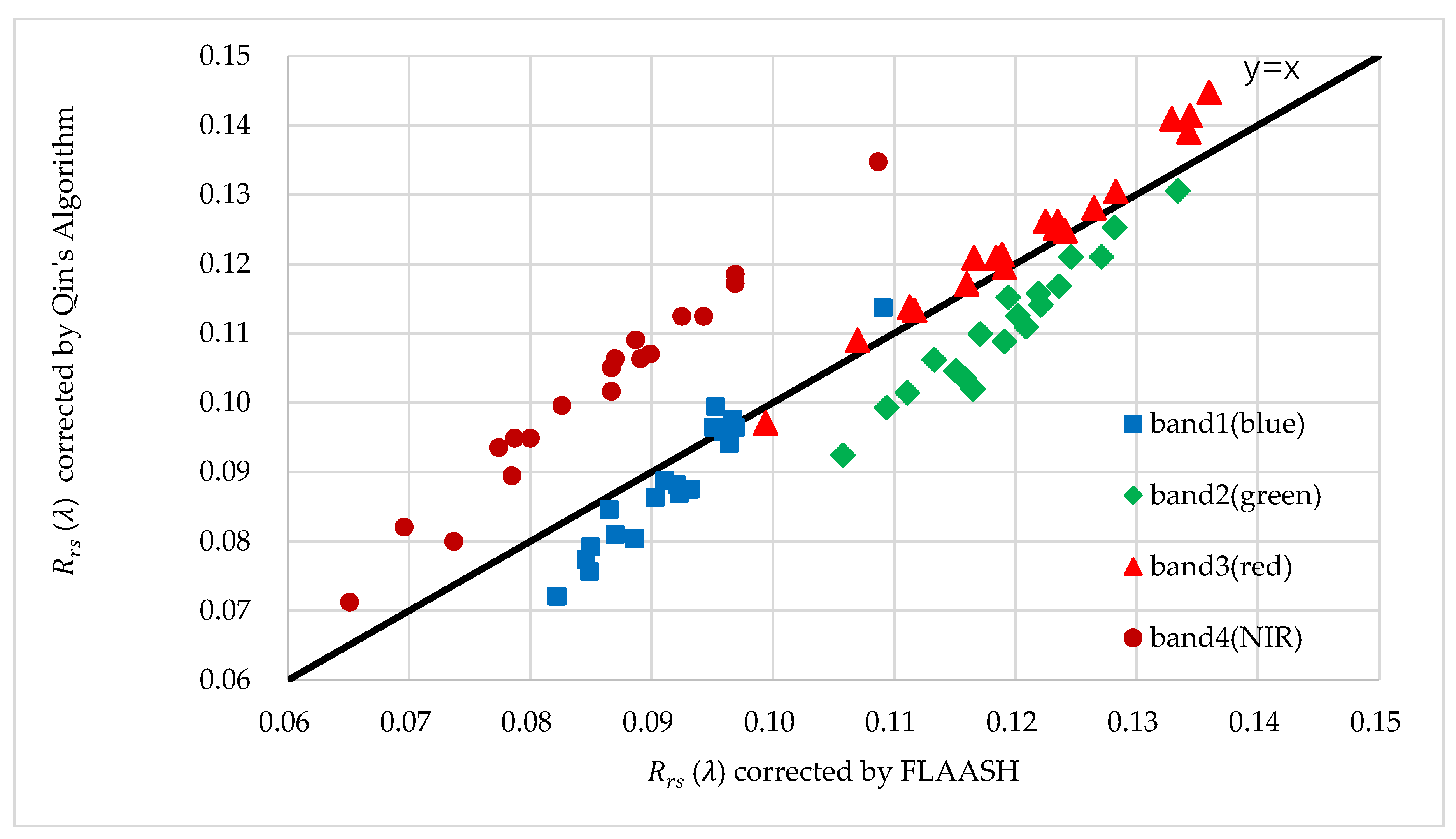
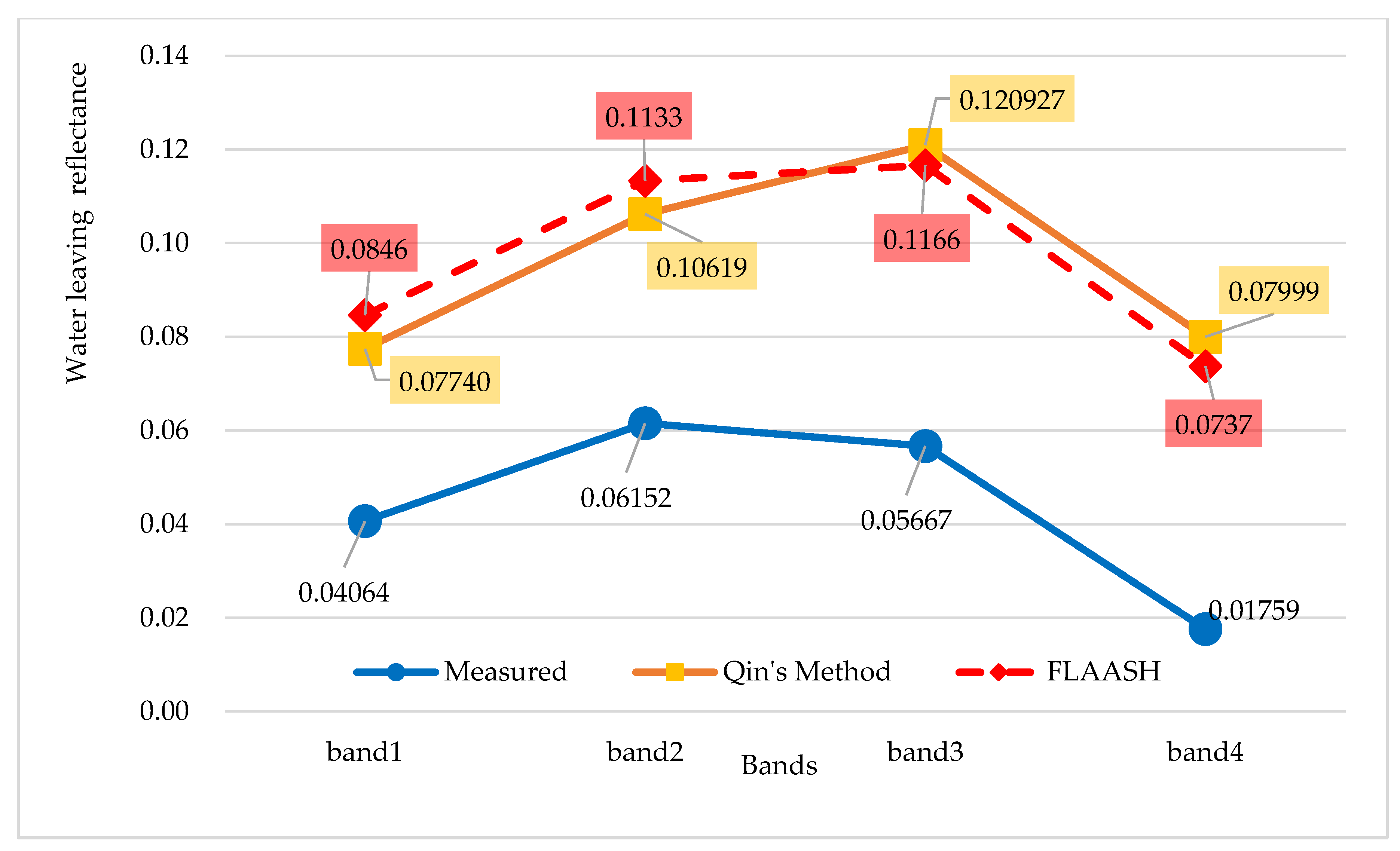
3.3.1. Water Leaving Reflectance of Remote Sensing Data
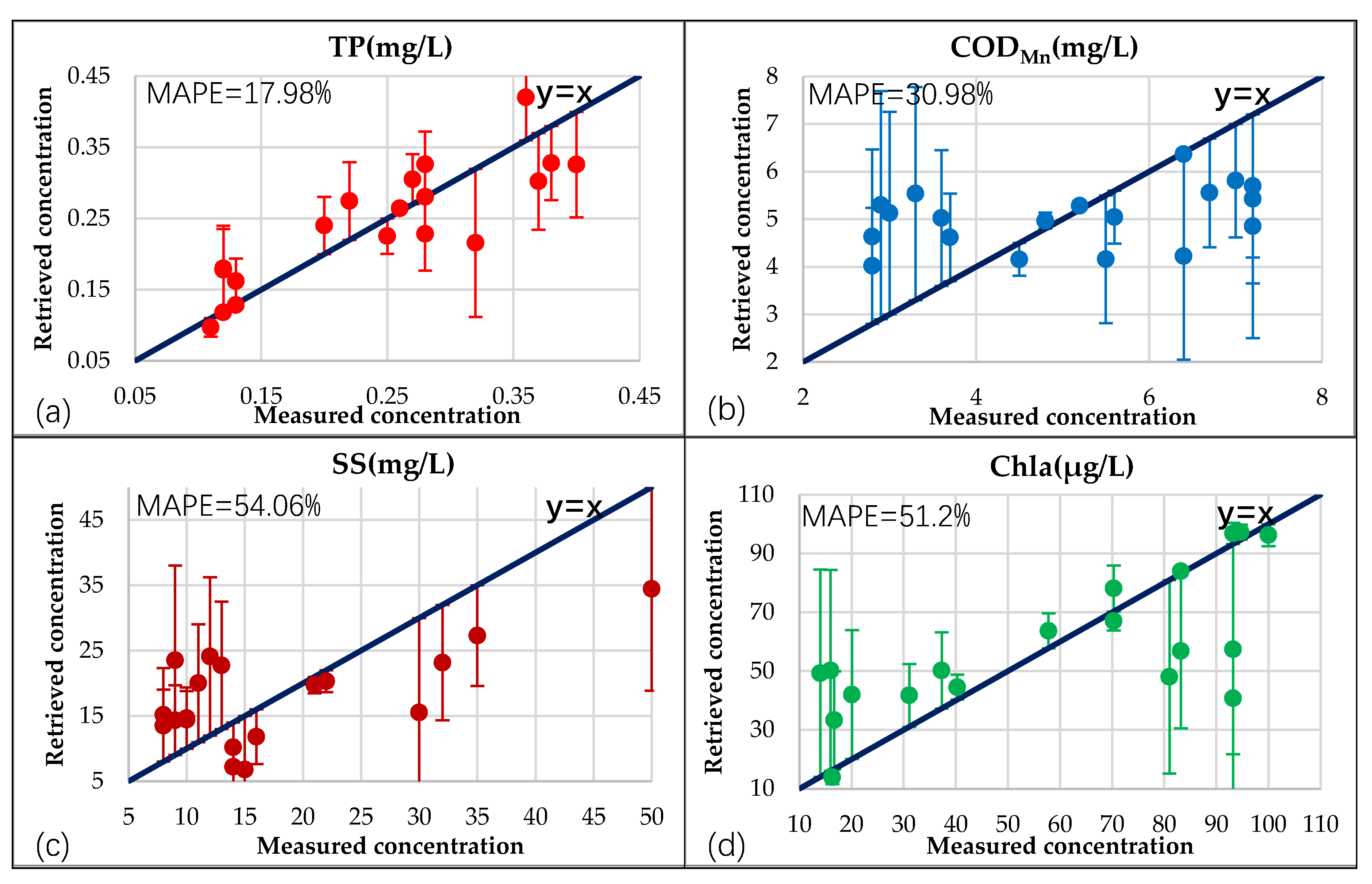
3.3.2. Remote Sensing Retrieval Result of TP in the Pearl River Channels
4. Discussion
4.1. Error Analysis of the Retrieval Results
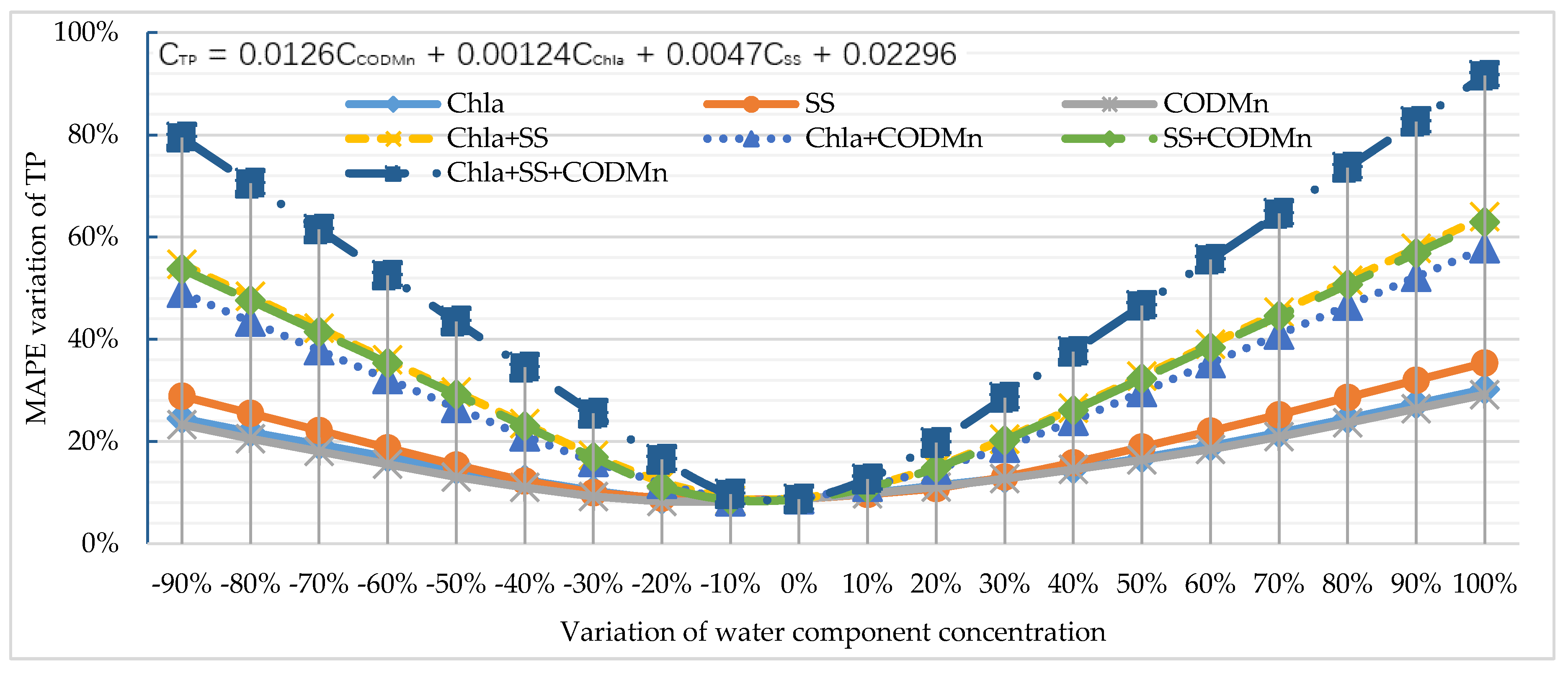
4.2. Applicability of the Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Sampling Sites | Integral Value of Measured Water Leaving Reflectance | |||
|---|---|---|---|---|
| band1 | band2 | band3 | band4 | |
| A1 | 0.04064 | 0.06152 | 0.05667 | 0.01759 |
| A2 | 0.03656 | 0.06358 | 0.05995 | 0.01702 |
| A3 | 0.03079 | 0.05039 | 0.03994 | 0.01003 |
| A4 | 0.03220 | 0.05427 | 0.05264 | 0.02059 |
| A5 | 0.03412 | 0.05628 | 0.05765 | 0.02996 |
| A6 | 0.03873 | 0.06205 | 0.05350 | 0.01857 |
| A9 | 0.05585 | 0.08819 | 0.05753 | 0.02525 |
| A10 | 0.03671 | 0.05863 | 0.03938 | 0.01090 |
| A11 | 0.03018 | 0.05501 | 0.03781 | 0.01133 |
| A12 | 0.02930 | 0.04644 | 0.03401 | 0.00835 |
| A13 | 0.03937 | 0.06086 | 0.05056 | 0.02361 |
| A14 | 0.03048 | 0.05200 | 0.04170 | 0.01420 |
| B1 | 0.02568 | 0.04692 | 0.03729 | 0.01070 |
| B2 | 0.03566 | 0.06258 | 0.05010 | 0.01017 |
| B3 | 0.03319 | 0.05866 | 0.05566 | 0.01121 |
| B4 | 0.04270 | 0.07186 | 0.05841 | 0.00809 |
| B5 | 0.04354 | 0.07140 | 0.06928 | 0.01715 |
| B6 | 0.05271 | 0.08434 | 0.06819 | 0.01068 |
| B7 | 0.05030 | 0.08101 | 0.07788 | 0.01944 |
| Sampling Sites | Remote Sensing Reflectance of GF-1 Image | |||
|---|---|---|---|---|
| band1 | band2 | band3 | band4 | |
| A1 | 0.07740 | 0.10619 | 0.120927 | 0.07999 |
| A2 | 0.0756208 | 0.101952 | 0.12474 | 0.0894474 |
| A3 | 0.07205 | 0.09242 | 0.09709 | 0.0711984 |
| A4 | 0.080971 | 0.103542 | 0.121404 | 0.109048 |
| A5 | 0.0881046 | 0.115195 | 0.130462 | 0.118511 |
| A6 | 0.0791876 | 0.101423 | 0.11330 | 0.0948545 |
| A9 | 0.0845378 | 0.09930 | 0.109008 | 0.101613 |
| A10 | 0.09762 | 0.11096 | 0.12617 | 0.11716 |
| A11 | 0.0940492 | 0.109898 | 0.120927 | 0.106345 |
| A12 | 0.0993994 | 0.114135 | 0.119497 | 0.107021 |
| A13 | 0.088699 | 0.104601 | 0.11378 | 0.112428 |
| A14 | 0.0964271 | 0.112546 | 0.11711 | 0.104993 |
| B1 | 0.0964271 | 0.116784 | 0.12617 | 0.112428 |
| B2 | 0.113666 | 0.13056 | 0.14476 | 0.134732 |
| B3 | 0.0958326 | 0.12526 | 0.14095 | 0.09350 |
| B4 | 0.0863212 | 0.115725 | 0.12522 | 0.0820126 |
| B5 | 0.08692 | 0.121022 | 0.139043 | 0.0995858 |
| B6 | 0.0875101 | 0.121022 | 0.141427 | 0.106345 |
| B7 | 0.08038 | 0.10884 | 0.12808 | 0.09485 |
References
- Gulati, R.D.; Van Donk, E. Lakes in the Netherlands, their origin, eutrophication and restoration: State-of-the-art review. Hydrobiologia 2002, 478, 73–106. [Google Scholar] [CrossRef]
- Sileika, A.S.; Wallin, M.; Gaigalis, K. Assessment of nitrogen pollution reduction options in the river Nemunas (Lithuania) using FyrisNP model. J. Environ. Eng. Landsc. Manag. 2012, 21, 141–151. [Google Scholar] [CrossRef]
- Zafar, M.; Tiecher, T.; de Castro Lima, J.A.M.; Schaefer, G.L.; Santanna, M.A.; Dos Santos, D.R. Phosphorus seasonal sorption-desorption kinetics in suspended sediment in response to land use and management in the Guaporé Catchment, Southern Brazil. Environ. Monit. Assess. 2016, 188, 643. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Shi, K.; Zhu, G.; Zhou, Y.; Zhang, Y.; Guo, Y. Monitoring spatiotemporal variations in nutrients in a large drinking water reservoir and their relationships with hydrological and meteorological conditions based on Landsat 8 imagery. Sci. Total Environ. 2017, 599–600, 1705–1717. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Qi, J.; Zhang, L.; Huang, H.; Lou, L.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, J.; Yin, H.; Liu, C.; Xia, T.; Wang, J.; Huang, Q. Remote sensing estimation of the total phosphorus concentration in a large lake using band combinations and regional multivariate statistical modeling techniques. J. Environ. Manag. 2015, 151, 33–43. [Google Scholar] [CrossRef]
- Hui, J.; Yao, L. Analysis and inversion of the nutritional status of China’s Poyang lake using MODIS data. J. Indian Soc. Remote. Sens. 2016, 44, 837–842. [Google Scholar] [CrossRef]
- Huang, C.; Guo, Y.; Yang, H.; Li, Y.; Zou, J.; Zhang, M.; Lyu, H.; Zhu, A.; Huang, T. Using remote sensing to track variation in phosphorus and its interaction with chlorophyll-a and suspended sediment. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 4171–4180. [Google Scholar] [CrossRef]
- Moses, S.A.; Janaki, L.; Joseph, S.; Kandathil, R.K. Determining the spatial variation of phosphorus in a lake system using remote sensing techniques. Lakes Reserv. Res. Manag. 2014, 19, 24–36. [Google Scholar] [CrossRef]
- Goes, J.I.; Saino, T.; Oaku, H.; Jiang, D.L. A method for estimating sea surface nitrate concentrations from remotely sensed SST and chlorophyll a-a case study for the north Pacific Ocean using OCTS/ADEOS data. IEEE Trans. Geosci. Electron. 1999, 37, 1633–1644. [Google Scholar] [CrossRef]
- Silió-Calzada, A.; Bricaud, A.; Gentili, B. Estimates of sea surface nitrate concentrations from sea surface temperature and chlorophyll concentration in upwelling areas: A case study for the Benguela system. Remote Sens. Environ. 2008, 112, 3173–3180. [Google Scholar] [CrossRef]
- Baustian, J.J.; Kowalski, K.P.; Alex, C. Using turbidity measurements to estimate total phosphorus and sediment flux in a great lakes coastal wetland. Wetlands 2018, 38, 1059–1065. [Google Scholar] [CrossRef]
- Guildford, S.J.; Hecky, R.E. Total nitrogen, total phosphorus, and nutrient limitation in lakes and oceans: Is there a common relationship? Limnol. Oceanogr. 2000, 45, 1213–1223. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Tian, G.; Wang, X.Y.; Wang, X.M.; Song, Q. The Methods of Water Spectra Measurement and Analysis Ⅰ: Above-Water Method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in GF-1 WFV imagery. Remote Sens. Environ. 2016, 191, 342–358. [Google Scholar] [CrossRef] [Green Version]
- China Centre for Resources Satellite Data and Application. Available online: http://218.247.138.119/CN/Satellite/3076.shtml (accessed on 15 October 2014).
- China Centre for Resources Satellite Data and Application. Available online: http://218.247.138.119/CN/Downloads/dbcs/6709.shtml (accessed on 14 October 2015).
- Qin, Y.; Deng, R.; He, Y.; Liu, X.; Liang, Y. Automatic retrieval of aerosol optical depth over Hong Kong using ZY-3 MUX. Acta Sci. Circum. 2015, 35, 1512–1519. [Google Scholar] [CrossRef]
- Jiang, W.; He, G.; Long, T.; Ni, Y.; Liu, H.; Peng, Y.; Lu, K.; Wang, G. Multilayer Perceptron Neural Network for Surface Water Extraction in Landsat 8 OLI Satellite Images. Remote Sens. 2018, 10, 755. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Wang, P.; Boss, E.S.; Roesler, C. Uncertainties of inherent optical properties obtained from semianalytical inversions of ocean color. Appl. Opt. 2005, 44, 4074–4085. [Google Scholar] [CrossRef]
- Pegau, W.S.; Gray, D.; Zaneveld, J.R.V. Absorption and attenuation of visible and near-infrared light in water: Dependence on temperature and salinity. Appl. Opt. 1997, 36, 6035–6046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. Ⅱ. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Volpe, V.; Silvestri, S.; Marani, M. Remote sensing retrieval of suspended sediment concentration in shallow waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Electron. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Gons, H.J.; Burger-Wiersma, T.; Otten, J.H.; Rijkeboer, M. Coupling of phytoplankton and detritus in a shallow, eutrophic lake (Lake Loosdrecht, the Netherlands). Hydrobiologia 1992, 233, 51–59. [Google Scholar] [CrossRef]
- Deng, R.; He, Y.; Qin, Y.; Cheng, Q.; Cheng, L. Pure water absorption coefficient measurement after eliminating the impact of suspended substance in spectrum from 400 nm to 900 nm. J. Remote Sens. 2012, 16, 174–191. [Google Scholar]
- He, Y.; Deng, R.; Cheng, Q.; Cheng, L.; Qin, Y. Diffuse Attenuation Coefficient of Suspended Sediment based on ASD Spectrometer. Acta Sci. Nat. Univ. Sunyatseni Nat. Sci. 2011, 50, 134–140. [Google Scholar]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the uv and visible domains. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Kheireddine, M.; Ouhssain, M.; Calleja, M.L.; Morán, X.A.G.; Sarma, Y.; Tiwari, S.P.; Jones, B.H. Characterization of light absorption by chromophoric dissolved organic matter (CDOM) in the upper layer of the red sea. Deep Sea Res. Part. I Oceanogr. Res. Pap. 2018, 133, 72–84. [Google Scholar] [CrossRef] [Green Version]
- Siegel, D.A.; Behrenfeld, M.J.; Maritorena, S.; Mcclain, C.R.; Antoine, D.; Bailey, S.W.; Bontempi, P.S.; Boss, E.S.; Dierssen, H.M.; Doney, S.C.; et al. Regional to global assessments of phytoplankton dynamics from the SeaWiFS mission. Remote Sens. Environ. 2013, 135, 77–91. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Wu, H.; Huang, F.; Lin, X. Determination of Organic Compounds in Pear River Water by Gas Chromatography- Mass Spectrometry. J. Instrum. Anal. 2002, 21, 86–88. [Google Scholar]
- Zheng, L.; Song, Z.; Meng, P.; Fang, Z. Seasonal characterization and identification of dissolved organic matter (DOM) in the pearl river, China. Environ. Sci. Pollut. Res. 2016, 23, 7462–7469. [Google Scholar] [CrossRef] [PubMed]
- Rochelle-Newall, E.J.; Fisher, T.R. Chromophoric dissolved organic matter and dissolved organic carbon in Chesapeake Bay. Mar. Chem. 2002, 77, 23–41. [Google Scholar] [CrossRef]
- Kowalczuk, P.; Cooper, W.J.; Whitehead, R.F.; Durako, M.J.; Sheldon, W. Characterization of CDOM in an organic-rich river and surrounding coastal ocean in the South Atlantic bight. Aquat. Sci. 2003, 65, 384–401. [Google Scholar] [CrossRef]
- Shong, Z.; Fang, Z. Characteristics of dissolved organic matter in Guangzhou reach of the Pearl River. Light Ind. Sci. Technol. 2013, 118–120, 156. [Google Scholar]
- André, Y.M.; Gordon, H.R. Report of the working group on water color. Bound. Layer Meteor. 1980, 18, 343–355. [Google Scholar] [CrossRef]
- Yang, W.; Chen, J.; Matsushita, B.; Fukushima, T. A relaxed matrix inversion method for retrieving water constituent concentrations in case II waters: The case of Lake Kasumigaura, Japan. IEEE Trans. Geosci. Electron. 2011, 49, 3381–3392. [Google Scholar] [CrossRef]
- Ali, K.; Witter, D.; Ortiz, J. Application of empirical and semi-analytical algorithms to MERIS data for estimating chlorophylla in Case 2 waters of Lake Erie. Environ. Earth Sci. 2014, 71, 4209–4220. [Google Scholar] [CrossRef]
- Alberotanza, L.; Braga, F.; Cavalli, R.M.; Pignatti, S.; Santini, F. Hyperspectral techniques for water quality monitoring: Application to the “Sacca di Goro”—Italy. In Proceedings of the Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), 2010 2nd Workshop on IEEE, Reykjavik, Iceland, 14–16 June 2010. [Google Scholar] [CrossRef]
- Vadakke-Chanat, S.; Shanmugam, P.; Ahn, Y.H. A model for deriving the spectral backscattering properties of particles in Inland and marine waters from in situ and remote sensing data. IEEE Trans. Geosci. Electron. 2017, 55, 1–16. [Google Scholar] [CrossRef]
- Hoge, F.E.; Lyon, P.E. Satellite retrieval of inherent optical properties by linear matrix inversion of oceanic radiance models: An analysis of model and radiance measurement errors. J. Geophys. Res. 1996, 101, 16631–16648. [Google Scholar] [CrossRef]
- Hoogenboom, H.; Dekker, A.; De Haan, J. Retrieval of chlorophyll and suspended matter in inland waters from CASI data by matrix inversion. Can. J. Remote Sens. 1998, 24, 144–152. [Google Scholar] [CrossRef]
- Campbell, G.; Phinn, S.R.; Dekker, A.G.; Brando, V.E. Remote sensing of water quality in an Australian tropical freshwater impoundment using matrix inversion and MERIS images. Remote Sens. Environ. 2012, 115, 2402–2414. [Google Scholar] [CrossRef] [Green Version]
- Yepez, S.; Laraque, A.; Martinez, J.-M.; De Sá, J.; Carrera, J.M.; Castellanos, B.; Gallay, M.; Lopez, J.L. Retrieval of suspended sediment concentrations using Landsat-8 OLI satellite images in the Orinoco River (Venezuela). C. R. Geosci. 2018, 350, 20–30. [Google Scholar] [CrossRef]
- China Centre for Resources Satellite Data and Application. Available online: http://218.247.138.119/CN/Downloads/gpxyhs/5836.shtml (accessed on 12 August 2005).
- Gilabert, M.A.; Conese, C.; Maselli, F. An atmospheric correction method for the automatic retrieval of surface reflectances from TM images. Int. J. Remote Sens. 1994, 15, 2065–2086. [Google Scholar] [CrossRef]
- Guangzhou Environmental Protection Geographic Information System. Available online: http://210.72.1.33:8022/index.html#M2.gismodel:{title:%22%E5%9C%B0%E7%90%86%E4%BF%A1%E6%81%AF%E7%B3%BB%E7%BB%9F%22} (accessed on 1 November 2014).




| Orbit Parameters | 16-m Multispectral Data Parameters | ||||
|---|---|---|---|---|---|
| Items | Parameters | Bands | Spectral Range (μm) | Swath Width (km) | Temporal Resolution |
| Orbit type | Sun Synchronous orbit | Band1 | 0.45–0.52 | 800 (four cameras combined) | 2 (day) |
| Orbit height | 645 km | Band2 | 0.52–0.59 | ||
| Orbit inclination | 98.0506° | Band3 | 0.63–0.69 | ||
| Descending node | 10:30 AM at local time | Band4 | 0.77–0.89 | ||
| Return period | 41 (day) | ||||
| Items | Measurement Units | Detection Limits | Detection Methods |
|---|---|---|---|
| CODMn | mg/L | 0.5 | Volumetric method, Water quality--Determination of permanganate index (GB/T 11892-1989) [This standard refers to the international standard ISO 8467:1986 (revised to ISO 8467:1993): Water quality--Determination of permanganate index] |
| Chla | μg/L | 0.025 | Photometry method, water and waste water monitoring and analysis method, 4th Edition (compiled by State Environmental Protection Administration, published by China Environmental Science Press, 2002), Chapter I, Section V (I), Part V |
| SS | mg/L | 4 | Gravimetric method |
| TP | mg/L | 0.01 | Ammonium molybdate spectrophotometric method, Water quality--Determination of total phosphorus--Ammonium molybdate spectrophotometric method (GB/T 11893-1989) |
| Sampling Sites | Longitude | Latitude | CODMn (mg/L) | Chla (μg/L) | SS (mg/L) | TP (mg/L) |
|---|---|---|---|---|---|---|
| A1 | 113.48527E | 23.06805N | 3.6 | 37.3 | 13 | 0.2 |
| A2 | 113.46309E | 23.08804N | 4.8 | 40.3 | 32 | 0.32 |
| A3 | 113.43014E | 23.09443N | 4.5 | 93.2 | 10 | 0.25 |
| A4 | 113.40438E | 23.10433N | 5.6 | 83.2 | 35 | 0.4 |
| A5 | 113.38273E | 23.11063N | 7 | 70.3 | 50 | 0.36 |
| A6 | 113.35436E | 23.10951N | 5.2 | 57.8 | 22 | 0.26 |
| A7 | 113.31902E | 23.11102N | 4.7 | 55.9 | 22 | 0.23 |
| A8 | 113.27800E | 23.11368N | 5.7 | 95.5 | 11 | 0.25 |
| A9 | 113.26353E | 23.11598N | 6.4 | 100 | 16 | 0.28 |
| A10 | 113.24763E | 23.10958N | 6.7 | 94.7 | 15 | 0.27 |
| A11 | 113.23928E | 23.10695N | 7.2 | 93.2 | 14 | 0.28 |
| A12 | 113.22384E | 23.11511N | 6.4 | 93.2 | 14 | 0.28 |
| A13 | 113.22289E | 23.13993N | 7.2 | 83.2 | 21 | 0.38 |
| A14 | 113.21097E | 23.15210N | 7.2 | 70.3 | 30 | 0.37 |
| B1 | 113.23506E | 23.10697N | 5.5 | 81 | 10 | 0.22 |
| B2 | 113.25994E | 23.06813N | 3.7 | 31.1 | 9 | 0.13 |
| B3 | 113.29135E | 23.05522N | 2.8 | 16.3 | 11 | 0.13 |
| B4 | 113.32910E | 23.04997N | 2.8 | 16.7 | 8 | 0.11 |
| B5 | 113.36762E | 23.03687N | 3 | 20.1 | 9 | 0.12 |
| B6 | 113.41188E | 23.05005N | 2.9 | 14 | 8 | 0.12 |
| B7 | 113.43564E | 23.07768N | 3.3 | 16 | 12 | 0.12 |
| Water Quality Parameters | Regression Equations | R2 | F |
|---|---|---|---|
| CODMn | CTP= 0.05063X − 0.0132 | 0.7437 | 49.333 |
| Chla | CTP = 0.00228X + 0.10855 | 0.5636 | 21.953 |
| SS | CTP = 0.00672X + 0.12229 | 0.5974 | 25.225 |
| CODMn + Chla | CTP = 0.05029X1 + 0.000002X2 − 0.01264 | 0.7437 | 23.217 |
| CODMn + SS | CTP = 0.03682X1 + 0.00373X2 − 0.01009 | 0.8727 | 54.828 |
| Chla + SS | CTP = 0.00174X1 + 0.005258X2 + 0.0462 | 0.8985 | 70.823 |
| CODMn + Chla + SS | CTP = 0.0126X1 + 0.00124X2 + 0.0047X3 + 0.02296 | 0.9055 | 47.886 |
| GF-1 Wavebands | Regression Equations | R2 | F |
|---|---|---|---|
| B1, B4 | CTP = −7.4893RB1 + 10.90179RB4 + 0.35623 | 0.5877 | 11.405 |
| B2, B4 | CTP = −5.27644RB2 + 10.34687RB4 + 0.4109 | 0.6215 | 13.135 |
| B3, B4 | CTP = −6.46467RB3 + 12.76875RB4 + 0.38358 | 0.7507 | 24.084 |
| B1, B2, B3 | CTP = 15.1327RB1 − 12.7831RB2 − 1.57399RB3 + 0.5503 | 0.3121 | 2.2681 |
| B1, B2, B4 | CTP = 3.9819RB1 − 7.8961RB2 + 9.5857RB4 + 0.42982 | 0.6259 | 8.3647 |
| B1, B3, B4 | CTP = −1.7354RB1 − 5.5486RB3 + 12.7926RB4 + 0.40073 | 0.7592 | 15.764 |
| B2, B3, B4 | CTP = −1.2906RB2 − 5.3924RB3 + 12.5756RB4 + 0.4108 | 0.7595 | 15.794 |
| B1, B2, B3, B4 | CTP = −0.531RB1 − 0.9224RB2 − 5.4182RB3 + 12.638RB4 + 0.4083 | 0.7596 | 11.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Deng, R.; Liang, Y.; Xiong, L.; Ai, X.; Qin, Y. Remote Sensing Retrieval of Total Phosphorus in the Pearl River Channels Based on the GF-1 Remote Sensing Data. Remote Sens. 2020, 12, 1420. https://doi.org/10.3390/rs12091420
Lu S, Deng R, Liang Y, Xiong L, Ai X, Qin Y. Remote Sensing Retrieval of Total Phosphorus in the Pearl River Channels Based on the GF-1 Remote Sensing Data. Remote Sensing. 2020; 12(9):1420. https://doi.org/10.3390/rs12091420
Chicago/Turabian StyleLu, Shijun, Ruru Deng, Yeheng Liang, Longhai Xiong, Xianjun Ai, and Yan Qin. 2020. "Remote Sensing Retrieval of Total Phosphorus in the Pearl River Channels Based on the GF-1 Remote Sensing Data" Remote Sensing 12, no. 9: 1420. https://doi.org/10.3390/rs12091420
APA StyleLu, S., Deng, R., Liang, Y., Xiong, L., Ai, X., & Qin, Y. (2020). Remote Sensing Retrieval of Total Phosphorus in the Pearl River Channels Based on the GF-1 Remote Sensing Data. Remote Sensing, 12(9), 1420. https://doi.org/10.3390/rs12091420






