Geostatistical Based Models for the Spatial Adjustment of Radar Rainfall Data in Typhoon Events at a High-Elevation River Watershed
Abstract
:1. Introduction
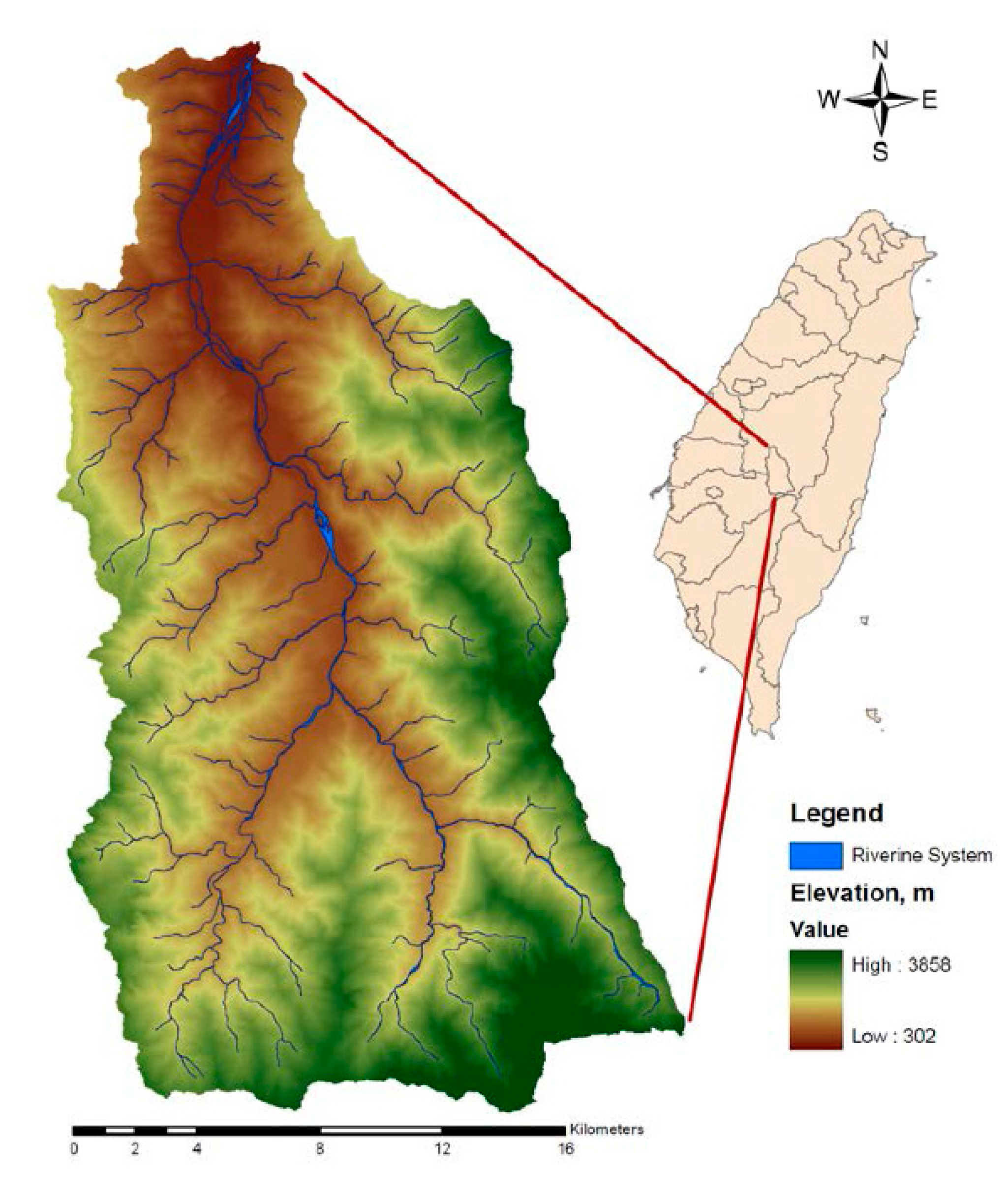
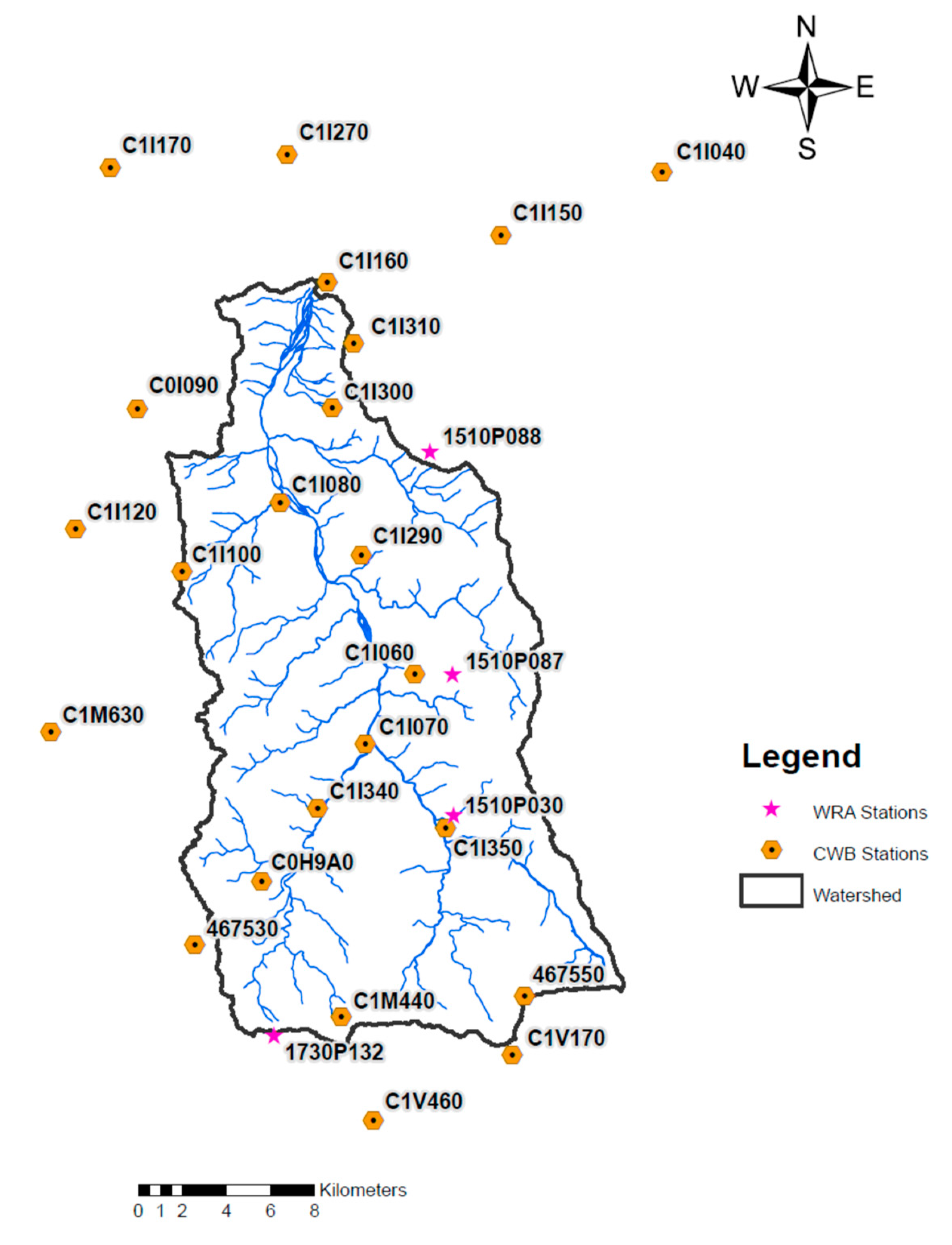
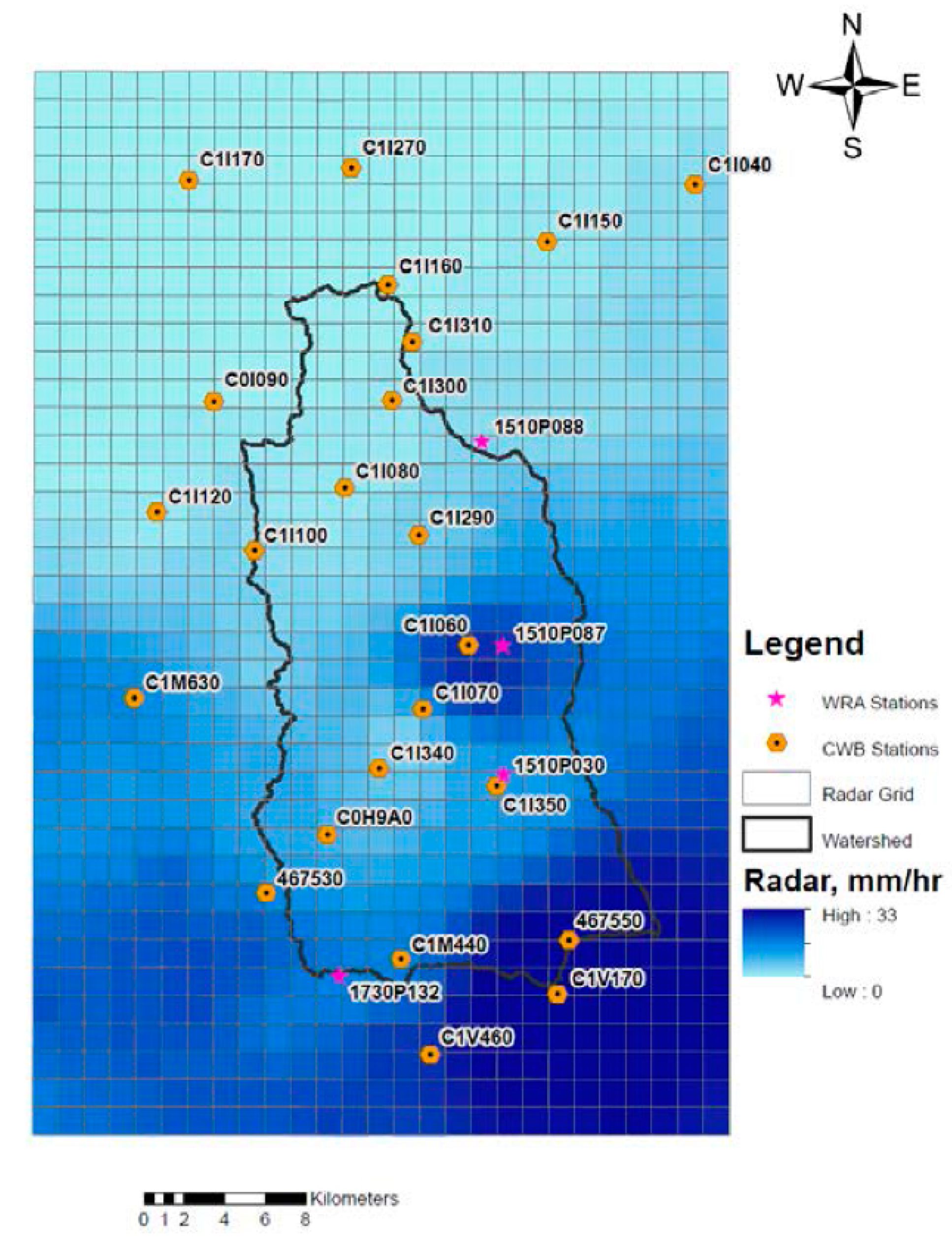
2. Study Area and Rainfall Data
3. Methodologies for Radar Rainfall Adjustment
3.1. Regression Kriging
3.2. Merging Method
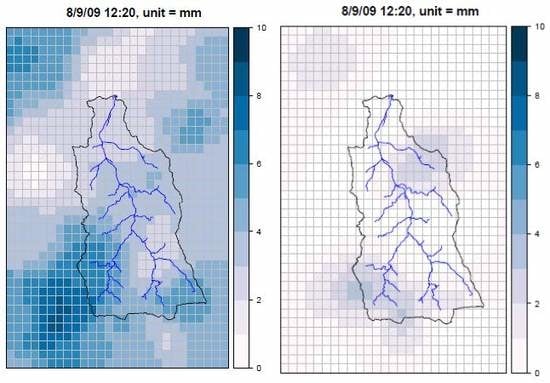
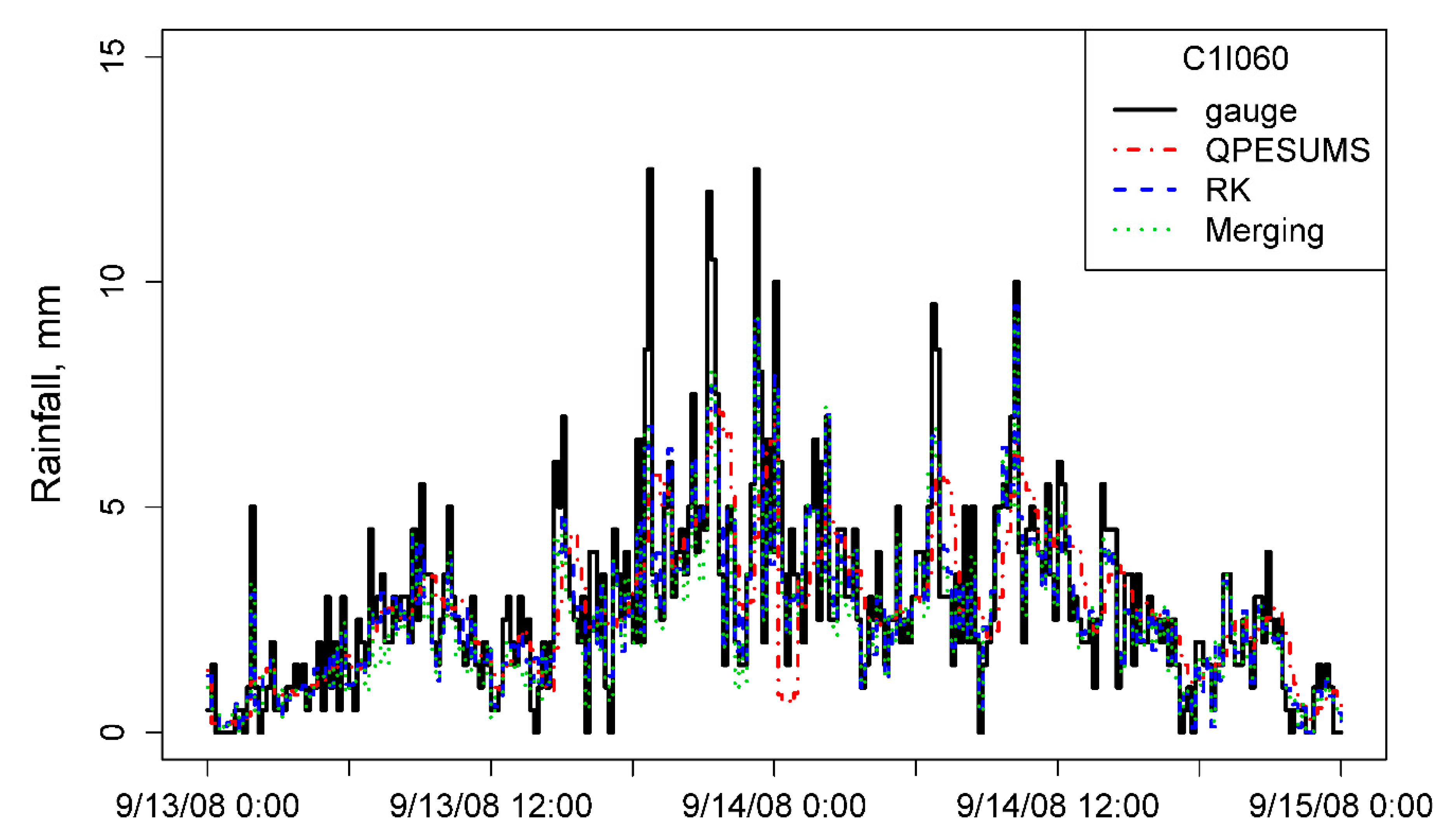
4. Results
4.1. Typhoon Kalmaegi
4.2. Typhoon Morakot
4.3. Typhoons Fungwong, Sinlaku, and Fanapi
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cole, S.J.; Moore, R.J. Distributed hydrological modeling using weather radar in gauges and ungauged basins. Adv. Water Resour. 2009, 32, 1107–1120. [Google Scholar] [CrossRef] [Green Version]
- Khakbaz, B.; Imam, B.; Hsu, K.; Sorooshian, S. From Lumped to Distributed via Semi-distributed: Calibration Strategies for Semi-distributed Hydrologic Models. J. Hydrol. 2012, 418–419, 61–77. [Google Scholar] [CrossRef] [Green Version]
- Paudel, M.; Nelson, E.J.; Downer, C.W.; Hotchkiss, R. Comparing the capability of distributed and lumped hydrologic models for analyzing the effects of land use change. J. Hydroinform. 2011, 13, 461–473. [Google Scholar] [CrossRef]
- Lin, Y.T.; Yang, M.D.; Han, J.Y.; Su, Y.F.; Jang, J.H. Quantifying Flood Water Levels Using Image-Based Volunteered Geographic Information. Remote Sens. 2020, 12, 706. [Google Scholar] [CrossRef] [Green Version]
- Jorgeson, J.; Julien, P. Peak flow forecasting with radar precipitation and the distributed model CASC2D. Water Int. 2005, 30, 40–49. [Google Scholar] [CrossRef]
- Sharif, H.O.; Yates, D.; Roberts, R.; Mueller, C. The use of an automated nowcasting system to forecast flash floods in an urban watershed. J. Hydrometeorol. 2006, 7, 190–202. [Google Scholar] [CrossRef] [Green Version]
- Vischel, T.; Pegram, G.G.S.; Sinclair, S.; Wagner, W.; Bartsch, A. Comparison of soil moisture fields estimated by catchment modelling and remote sensing: A case study in South Africa. Hydrol. Earth Syst. Sci. 2008, 12, 751–767. [Google Scholar] [CrossRef] [Green Version]
- Dutta, D.; Nakayama, K. Effects of spatial grid resolution on river flow and surface inundation simulation by physically based distributed modelling approach. Hydrol. Process. 2009, 23, 534–545. [Google Scholar] [CrossRef]
- Chu, H.-J.; Lin, Y.-P.; Huang, C.-W.; Hsu, C.-Y.; Chen, H.-Y. Modelling the hydrologic effects of dynamic land-use change using a distributed hydrologic model and a spatial land-use allocation model. Hydrol. Process. 2010, 24, 2538–2554. [Google Scholar] [CrossRef]
- Looper, J.P.; Vieux, B.E.; Moreno, M.A. Assessing the impacts of precipitation bias on distributed hydrologic model calibration and prediction accuracy. J. Hydrol. 2012, 418–419, 110–122. [Google Scholar] [CrossRef]
- Andrieu, H.; Creutin, J.D.; Delrieu, G.; Faure, D. Use of a weather radar for the hydrology of a mountainous area. Part I: Radar measurement interpretation. J. Hydrol. 1997, 193, 1–25. [Google Scholar] [CrossRef]
- Krajewski, W.F. Cokriging radar-rainfall and rain gage data. J. Geophys. Res. 1987, 92, 9571–9580. [Google Scholar] [CrossRef]
- Duncan, M.R.; Austin, B.; Fabry, F.; Austin, G.L. The effect of gauge sampling density on the accuracy of streamflow prediction for rural catchments. J. Hydrol. 1993, 142, 445–476. [Google Scholar] [CrossRef]
- Huff, F.A. Sampling errors in measurement of mean precipitation. J. Appl. Meteorol. 1970, 9, 35–44. [Google Scholar] [CrossRef]
- Silverman, B.A.; Rogers, L.K.; Dahl, D. On the sampling variance of raingage networks. J. Appl. Meteorol. 1981, 20, 1468–1478. [Google Scholar] [CrossRef] [Green Version]
- Russo, F.; Napolitano, F.; Gorgucci, E. Rainfall monitoring systems over an urban area: The City of Rome. Hydrol. Process. 2005, 19, 1007–1019. [Google Scholar] [CrossRef]
- Yang, M.D.; Yang, Y.F.; Hsu, S.C. Application of remotely sensed data to the assessment of terrain factors affecting Tsao-Ling landside. Can. J. Remote Sens. 2004, 30, 593–603. [Google Scholar] [CrossRef]
- Yang, M.D.; Su, T.C.; Hsu, C.H.; Chang, K.C.; Wu, A.M. Mapping of the 26 December 2004 tsunami disaster by using FORMOSAT-2 images. Int. J. Remote Sens. 2007, 28, 3071–3091. [Google Scholar] [CrossRef]
- Yang, M.D. A genetic algorithm (GA) based automated classifier for remote sensing imagery. Can. J. Remote Sens. 2007, 33, 593–603. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and intercomparison of hgh-resolution satellite precipitation estimates - GPM, TRMM, and CMORPH in the Tianshan Mountain area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Ricciardelli, E.; Di Paola, F.; Gentile, S.; Cersosimo, A.; Cimini, D.; Gallucci, D.; Geraldi, E.; Larosa, S.; Teodosio Nilo, S.; Ripepi, E.; et al. Analysis of Livorno heavy rainfall event: Examples of satellite-based observation techniques in support of numerical weather prediction. Remote Sens. 2018, 10, 1549. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Hu, J.; Chen, S.; Zhang, A.; Liang, Z.; Tong, X.; Xiao, L.; Min, C.; Zhang, Z. How well can IMERG products capture typhoon extreme precipitation events over southern China? Remote Sens. 2019, 11, 70. [Google Scholar] [CrossRef] [Green Version]
- Dolciné, L.; Andrieu, H.; French, M.N. Rainfall forecasting in a mountainous region using a weather radar and ground meteorological observations. Phys. Chem. Earth 1997, 22, 247–252. [Google Scholar] [CrossRef]
- Borga, M. Accuracy of radar rainfall estimates for streamflow simulation. J. Hydrol. 2002, 267, 26–39. [Google Scholar] [CrossRef]
- Creutin, J.D.; Andrieu, H.; Faure, D. Use of a weather radar for the hydrology of a mountainous area. Part II: Radar measurement validation. J. Hydrol. 1997, 193, 26–44. [Google Scholar] [CrossRef]
- Fulton, R.A.; Breidenbach, J.P.; Seo, D.-J.; Miller, D.A.; O’Bannon, T. The WSR-88D rainfall algorithm. Weather Forecast. 1998, 13, 377–395. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N.; Dinku, T.; Borga, M. Hydrological model sensitivity to parameter and radar rainfall estimation uncertainty. Hydrol. Process. 2004, 18, 3277–3291. [Google Scholar] [CrossRef]
- Stellman, K.M.; Fuelberg, H.E.; Garza, R.; Mullusky, M. An examination of radar and rain gauge-derived mean areal precipitation over Georgia watersheds. Weather Forecast. 2001, 16, 133–144. [Google Scholar] [CrossRef]
- Fang, Z.; Bedient, P.B.; Benavides, J.; Zimmer, A.L. Enhanced radar-based flood alert system and floodplain map library. J. Hydrol. Eng. 2008, 13, 926–938. [Google Scholar] [CrossRef]
- Vieux, B.E.; Park, J.-H.; Kang, B. Distributed hydrologic prediction: Sensitivity to accuracy of initial soil moisture conditions and radar rainfall input. J. Hydrol. Eng. 2009, 14, 671–689. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Z. Assessment on the function of reservoirs for flood control during typhoon seasons based on a distributed hydrological model. Hydrol. Process. 2011, 25, 2506–2517. [Google Scholar] [CrossRef]
- Austin, P.M. Relation between measured radar reflectivity and surface rainfall. Mon. Weather Rev. 1987, 115, 1053–1070. [Google Scholar] [CrossRef] [Green Version]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Doviak, R.J. A survey of radar rain measurement techniques. J. Appl. Meteorol. 1983, 22, 832–849. [Google Scholar] [CrossRef] [Green Version]
- Mandapaka, P.V.; Villarini, G.; Seo, B.-C.; Krajewski, W.F. Effect of radarrainfall uncertainties on the spatial characterization of rainfall events. J. Geophys. Res. 2010, 115, D17110. [Google Scholar] [CrossRef]
- Wilson, J.W.; Brandes, E.A. Radar measurement of rainfall—A summary. Bull. Am. Meteorol. Soc. 1979, 60, 1048–1058. [Google Scholar] [CrossRef] [Green Version]
- Cánovas-García, F.; García-Galiano, S.; Alonso-Sarría, F. Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula. Remote Sens. 2018, 10, 1023. [Google Scholar] [CrossRef] [Green Version]
- Ehrat, U. Rainfall and Flood Nowcasting in Small Catchments Using Weather Radar. Ph.D. Dissertation, Institut für Wasserbau, Universität Stuttgart, Stuttgart, Germany, 2003. [Google Scholar]
- Kim, B.S.; Hong, J.B.; Kim, H.S.; Yoon, S.Y. Combining radar and rain gauge rainfall estimates for flood forecasting using conditional merging method. In Proceedings of the 2007 World Environmental and Water Resources Congress, Tampa, FL, USA, 15–19 May 2007; Kabbes, K.C., Ed.; ASCE: Reston, VA, USA, 2007; pp. 1–16. [Google Scholar]
- Gourley, J.J.; Vieux, B.E. A method for evaluating the accuracy of quantitative precipitation estimates from a hydrologic modeling perspective. J. Hydrometeorol. 2005, 6, 115–133. [Google Scholar] [CrossRef]
- Morin, J.; Rosenfield, D.; Amitai, E. Radar rain field evaluation and possible use of its high temporal and spatial resolution for hydrological purposes. J. Hydrol. 1995, 172, 275–292. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Wolff, D.B.; Amitai, E. The window probability matching method for rainfall measurements with radar. J. Appl. Meteorol. 1994, 33, 682–693. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Read, S.M.; Zhangt, Z.; Duan, Q.; Moreda, F.; Cong, S. The distributed model intercomparison project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Steiner, M.; Smith, J.A.; Burges, S.J.; Alonso, C.V.; Darden, R.W. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 1999, 35, 2487–2503. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R. GIS-based spatial precipitation estimation using next generation radar and raingauge data. Environ. Model. Softw. 2010, 25, 1781–1788. [Google Scholar] [CrossRef]
- Ahnert, P.R.; Krajewski, W.F.; Johnson, E.R. Kalman filter estimation of radar-rainfall field bias. In Proceedings of the 23rd Conference on Radar Meteorology and the Conference on Cloud Physics, Snowmass, CO, USA, 22–26 September 1986. [Google Scholar]
- Wood, S.J.; Jones, D.A.; Moore, R.J. Static and dynamic calibration of radar data for hydrological use. Hydrol. Earth Syst. Sci. 2000, 4, 545–554. [Google Scholar] [CrossRef]
- Christensen, R. Linear Models for Multivariate, Time Series, and Spatial Data; Springer: New York, NY, USA, 1990. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Spatial prediction of soil properties from landform attributes derived from a digital elevation model. Geoderma 1994, 63, 197–214. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar] [CrossRef]
- Haberlandt, U. Geostatistical interpolation of hourly precipitation from rain gauges and radar for a large-scale extreme rainfall event. J. Hydrol. 2007, 332, 144–157. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. Comparison of Kriging with External Drift and Regression-Kriging; Technical note; International Institute for Geo-information Science and Earth Observation: Enschede, The Netherlands, 2003. [Google Scholar]
- Schuurmans, J.M.; Bierkens, M.F.P.; Pebesma, E.J.; Uijlenhoet, R. Automatic prediction of high-resolution daily rainfall fields for multiple extents: The potential of operational radar. J. Hydrometeorol. 2007, 8, 1204–1224. [Google Scholar] [CrossRef]
- Severino, E.; Alpuim, T. Spatiotemporal models in the estimation of area precipitation. Environmetrics 2005, 16, 773–802. [Google Scholar] [CrossRef]
- Krämer, S.; Verworn, H.R. Improved radar data processing algorithms for quantitative rainfall estimation in real time. Water Sci. Technol. 2009, 60, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Orasi, A.; Lasinio, G.J.; Ferrari, C. Comparison of calibration methods for the reconstruction of space-time rainfall fields during a rain enhancement experiment in Southern Italy. Environmetrics 2009, 20, 812–834. [Google Scholar] [CrossRef]
- Biggs, E.M.; Atkinson, P.M. A comparison of gauge and radar precipitation data for simulating an extreme hydrological event in the Severn Uplands, UK. Hydrol. Process. 2011, 25, 795–810. [Google Scholar] [CrossRef]
- Lin, J.Y.; Yang, M.D.; Lin, P.R.; Lin, P.S. Risk Assessment of Debris flows in Songhe, Taiwan. Eng. Geol. 2011, 123, 100–112. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Yang, M.D.; Lin, J.Y.; Yao, C.Y.; Chen, J.Y.; Su, T.C.; Jan, C.D. Landslide-induced levee failure by high concentrated sediment flow—A case of Shan-An levee at Chenyulan River, Taiwan. Eng. Geol. 2011, 123, 91–99. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping; EUR 22904 EN Scientific and Technical Research series report; European Communities: Luxembourg, 2009. [Google Scholar]
- Yang, M.D.; Tseng, H.H.; Hsu, Y.C.; Tsai, H.P. Semantic Segmentation Using Deep Learning with Vegetation Indices for Rice Lodging Identification in Multi-date UAV Visible Images. Remote Sens. 2020, 12, 633. [Google Scholar] [CrossRef] [Green Version]
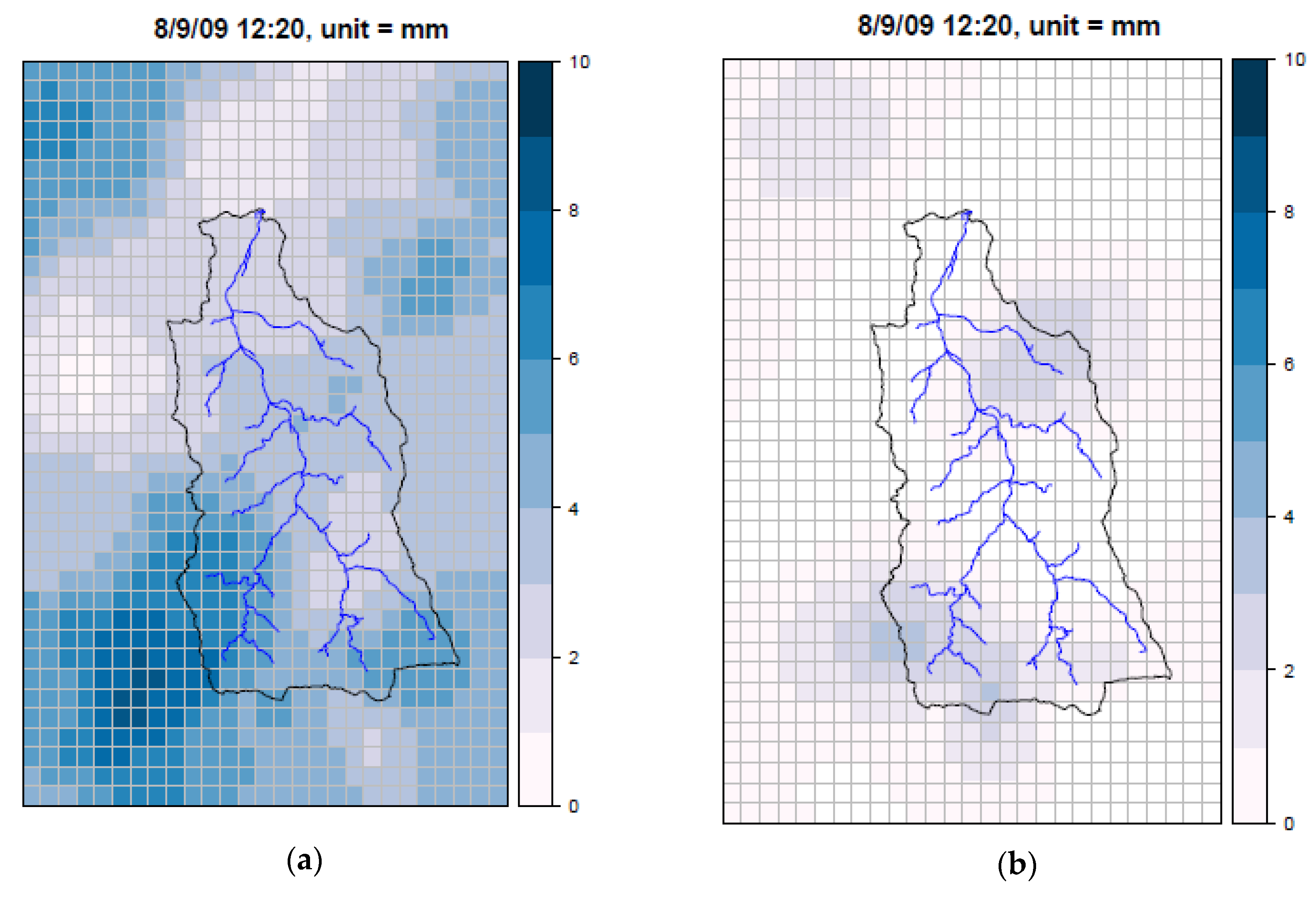
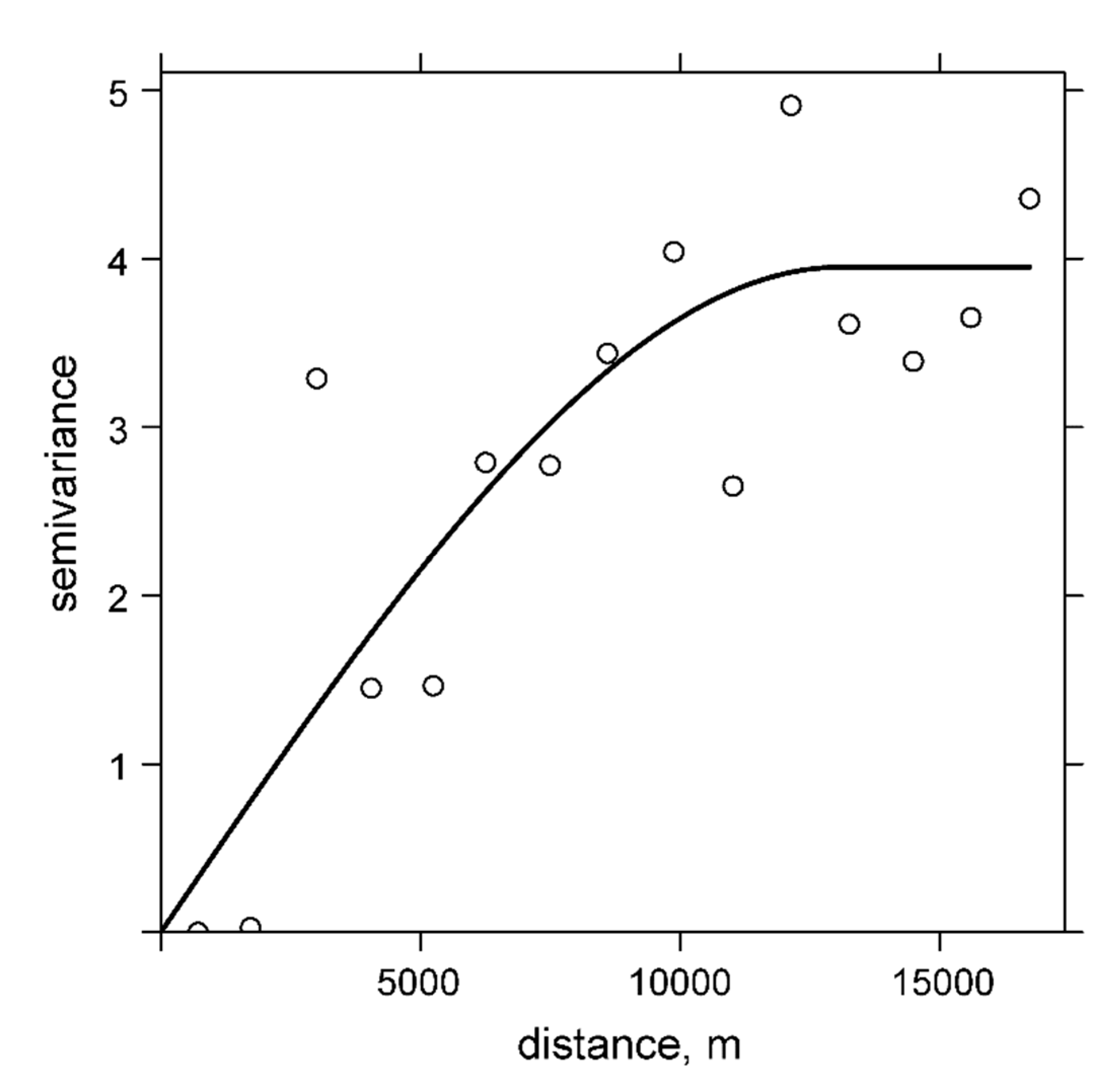
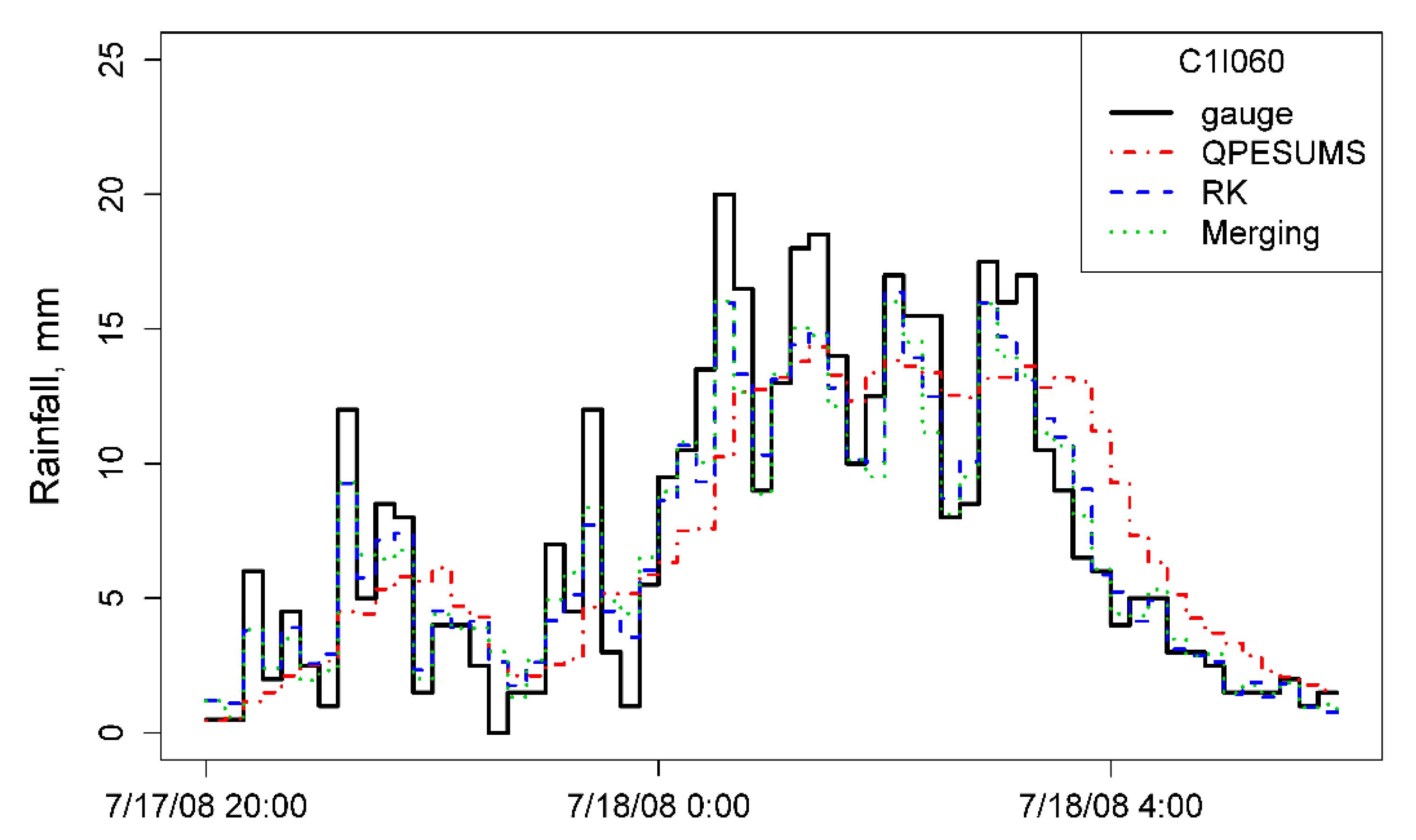


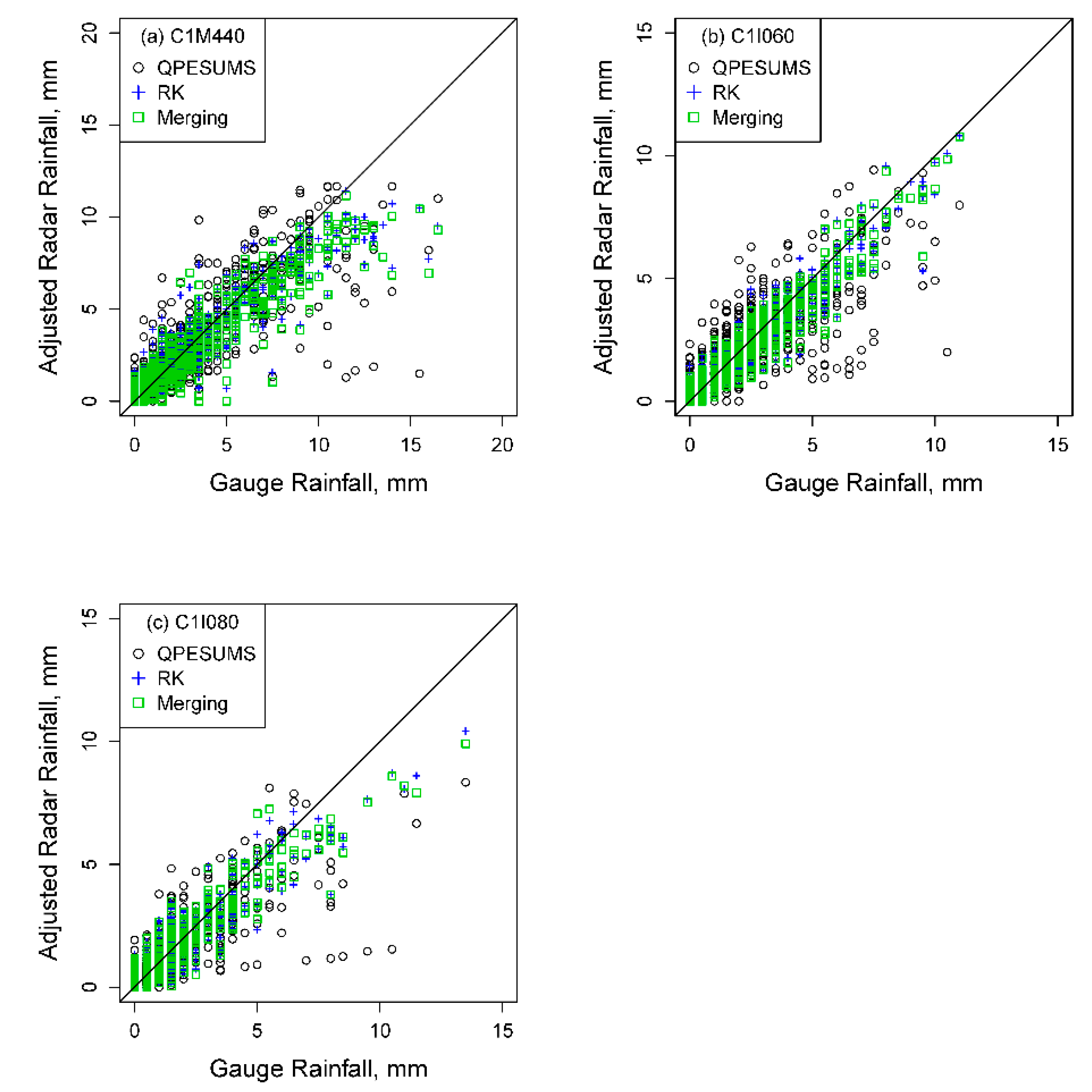

| Stations Inside the Watershed Boundary | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | Elev. (m) | QPESUMS | Rainfall Data Adjusted by RK | Rainfall Data Adjusted by Merging | |||||||
| RMSE (mm) | CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | ||
| 1510P030 | 1135 | 2.79 | 0.48 | 2.56 | 8.24 | 0.56 | 16.67 | 2.66 | 4.66 | 0.53 | 10.42 |
| 1510P087 | 2200 | 1.95 | 0.78 | 0.98 | 49.74 | 0.95 | 21.79 | 0.97 | 50.26 | 0.95 | 21.79 |
| C0H9A0 | 1595 | 2.00 | 0.81 | 1.55 | 22.50 | 0.88 | 8.64 | 1.62 | 19.00 | 0.87 | 7.41 |
| C1I060 | 2403 | 2.23 | 0.80 | 1.20 | 46.19 | 0.94 | 17.50 | 1.21 | 45.74 | 0.94 | 17.50 |
| C1I070 | 825 | 1.93 | 0.81 | 1.36 | 29.53 | 0.91 | 12.35 | 1.39 | 27.98 | 0.90 | 11.11 |
| C1I080 | 536 | 2.26 | 0.67 | 1.59 | 29.65 | 0.84 | 25.37 | 1.51 | 33.19 | 0.85 | 26.87 |
| C1I160 | 399 | 2.02 | 0.69 | 1.53 | 24.26 | 0.82 | 18.84 | 1.49 | 26.24 | 0.83 | 20.29 |
| C1I290 | 1151 | 2.20 | 0.68 | 1.59 | 27.73 | 0.83 | 22.06 | 1.63 | 25.91 | 0.83 | 22.06 |
| C1I300 | 781 | 1.89 | 0.66 | 1.33 | 29.63 | 0.83 | 25.76 | 1.35 | 28.57 | 0.83 | 25.76 |
| C1I340 | 897 | 2.05 | 0.78 | 1.58 | 22.93 | 0.87 | 11.54 | 1.61 | 21.46 | 0.87 | 11.54 |
| C1I350 | 887 | 1.94 | 0.76 | 1.72 | 11.34 | 0.81 | 6.58 | 1.72 | 11.34 | 0.81 | 6.58 |
| C1M440 | 2540 | 2.01 | 0.74 | 1.58 | 21.39 | 0.84 | 13.51 | 1.56 | 22.39 | 0.85 | 14.86 |
| Average | 2.11 | 0.72 | 1.55 | 26.93 | 0.84 | 16.72 | 1.56 | 26.39 | 0.84 | 16.35 | |
| Stations Outside or on the Watershed Boundary | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | Elev. (m) | QPESUMS | Rainfall Data Adjusted by RK | Rainfall Data Adjusted by Merging | |||||||
| RMSE (mm) | CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | ||
| C1M630 | 1052 | 2.15 | 0.85 | 2.17 | −0.93 | 0.84 | −1.18 | 2.14 | 0.47 | 0.85 | 0.00 |
| C1V170 | 3690 | 1.47 | 0.64 | 1.27 | 13.61 | 0.73 | 14.06 | 1.30 | 11.56 | 0.72 | 12.50 |
| C1V460 | 1949 | 2.06 | 0.75 | 1.93 | 6.31 | 0.78 | 4.00 | 1.81 | 12.14 | 0.80 | 6.67 |
| 1510P088 | 1666 | 2.16 | 0.71 | 1.78 | 17.59 | 0.81 | 14.08 | 1.78 | 17.59 | 0.81 | 14.08 |
| 1730P132 | 2540 | 2.74 | 0.65 | 2.25 | 17.88 | 0.77 | 18.46 | 2.21 | 19.34 | 0.78 | 20.00 |
| 467530 | 2413 | 2.47 | 0.75 | 2.18 | 11.74 | 0.81 | 8.00 | 2.35 | 4.86 | 0.77 | 2.67 |
| 467550 | 3845 | 1.90 | 0.70 | 1.83 | 3.68 | 0.72 | 2.86 | 1.83 | 3.68 | 0.72 | 2.86 |
| C0I090 | 878 | 2.18 | 0.72 | 1.86 | 14.68 | 0.79 | 9.72 | 1.96 | 10.09 | 0.77 | 6.94 |
| C1I040 | 1693 | 2.01 | 0.83 | 1.99 | 1.00 | 0.83 | 0.00 | 2.04 | −1.49 | 0.82 | −1.20 |
| C1I100 | 1771 | 1.09 | 0.25 | 1.4 | −28.44 | −0.24 | −196.0 | 1.35 | −23.85 | −0.15 | −160.0 |
| C1I120 | 1528 | 2.28 | 0.69 | 2.09 | 8.33 | 0.74 | 7.25 | 2.13 | 6.58 | 0.73 | 5.80 |
| C1I150 | 393 | 1.92 | 0.81 | 1.66 | 13.54 | 0.86 | 6.17 | 1.72 | 10.42 | 0.85 | 4.94 |
| C1I170 | 235 | 1.60 | 0.53 | 1.70 | −6.25 | 0.47 | −11.32 | 1.70 | −6.25 | 0.47 | −11.32 |
| C1I270 | 593 | 1.61 | 0.84 | 1.30 | 19.25 | 0.90 | 7.14 | 1.49 | 7.45 | 0.87 | 3.57 |
| C1I310 | 1001 | 2.00 | 0.75 | 1.30 | 35.00 | 0.89 | 18.67 | 1.32 | 34.00 | 0.89 | 18.67 |
| Average | 2.04 | 0.73 | 1.81 | 11.10 | 0.78 | 6.99 | 1.84 | 9.32 | 0.78 | 6.15 | |
| Stations Inside the Watershed Boundary | ||||||||
|---|---|---|---|---|---|---|---|---|
| Rainfall Data Adjusted by Ordinary Kriging (OK) | ||||||||
| Station ID | Typhoon Kalmaegi | Typhoon Morakot | ||||||
| RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | |
| 1510P030 | 2.72 | 2.51 | 0.51 | 6.25 | 0.86 | 39.01 | 0.85 | 44.07 |
| 1510P087 | 0.95 | 51.28 | 0.95 | 21.79 | 0.71 | 47.79 | 0.89 | 50.85 |
| C0H9A0 | 1.61 | 19.50 | 0.87 | 7.41 | 1.32 | 25.84 | 0.86 | 16.22 |
| C1I060 | 1.46 | 34.53 | 0.91 | 13.75 | 0.77 | 42.11 | 0.87 | 38.10 |
| C1I070 | 1.48 | 23.32 | 0.89 | 9.88 | 0.96 | 31.91 | 0.82 | 32.26 |
| C1I080 | 1.80 | 20.35 | 0.79 | 17.91 | 0.78 | 32.17 | 0.84 | 29.23 |
| C1I160 | 1.52 | 24.75 | 0.83 | 20.29 | 0.69 | 36.70 | 0.86 | 32.31 |
| C1I290 | 1.79 | 18.64 | 0.79 | 16.18 | 0.97 | 28.68 | 0.78 | 36.84 |
| C1I300 | 1.47 | 22.22 | 0.80 | 21.21 | 0.82 | 12.77 | 0.73 | 14.06 |
| C1I340 | 1.61 | 21.46 | 0.87 | 11.54 | 1.17 | 34.64 | 0.87 | 24.29 |
| C1I350 | 1.71 | 11.86 | 0.81 | 6.58 | 0.76 | 42.42 | 0.88 | 41.94 |
| C1M440 | 1.68 | 16.42 | 0.82 | 10.81 | 1.50 | 18.03 | 0.80 | 14.29 |
| Average | 1.65 | 22.24 | 0.82 | 13.63 | 0.94 | 32.67 | 0.84 | 31.20 |
| Stations Outside or on the Watershed Boundary | ||||||||
|---|---|---|---|---|---|---|---|---|
| Rainfall Data Adjusted by Ordinary Kriging (OK) | ||||||||
| Station ID | Typhoon Kalmaegi | Typhoon Morakot | ||||||
| RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | |
| C1M630 | 3.67 | −70.70 | 0.55 | −35.29 | 2.56 | −34.03 | 0.48 | −32.39 |
| C1V170 | 1.64 | −11.56 | 0.56 | −12.50 | 2.08 | −18.18 | −0.06 | −124.00 |
| C1V460 | 1.92 | 6.80 | 0.78 | 4.00 | 2.04 | 3.77 | 0.60 | 7.14 |
| 1510P088 | 1.79 | 17.13 | 0.80 | 12.68 | 1.00 | 28.06 | 0.71 | 61.36 |
| 1730P132 | 2.14 | 21.90 | 0.79 | 21.54 | 1.88 | 10.48 | 0.57 | 23.91 |
| 467530 | 2.38 | 3.64 | 0.77 | 2.67 | 2.76 | −9.96 | 0.62 | −10.14 |
| 467550 | 1.89 | 0.53 | 0.70 | 0.00 | 2.05 | −24.24 | 0.43 | −31.75 |
| C0I090 | 2.56 | −17.43 | 0.61 | −15.28 | 1.81 | −28.37 | 0.52 | −25.71 |
| C1I040 | 2.38 | −18.41 | 0.76 | −8.43 | 1.53 | −14.18 | 0.58 | −14.71 |
| C1I100 | 3.72 | −241.28 | −7.77 | −3208.00 | 1.34 | −55.81 | −0.25 | −151.02 |
| C1I120 | 2.66 | −16.67 | 0.57 | −17.39 | 1.65 | −103.70 | −1.17 | −343.75 |
| C1I150 | 1.92 | 0.00 | 0.81 | 0.00 | 1.13 | −5.61 | 0.46 | −9.80 |
| C1I170 | 2.59 | −61.88 | −0.23 | −143.40 | 1.33 | −41.49 | 0.22 | −63.93 |
| C1I270 | 1.90 | −18.01 | 0.78 | −7.14 | 0.99 | −5.32 | 0.51 | −10.53 |
| C1I310 | 1.39 | 30.50 | 0.88 | 17.33 | 0.59 | 44.86 | 0.89 | 36.92 |
| Average | 2.20 | −9.58 | 0.65 | −12.94 | 1.65 | −16.92 | 0.34 | −45.89 |
| Stations Inside the Watershed Boundary | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | QPESUMS | Rainfall Data Adjusted by RK | Rainfall Data Adjusted by Merging | |||||||
| RMSE (mm) | CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | |
| 1510P030 | 1.41 | 0.59 | 0.86 | 39.01 | 0.85 | 44.07 | 0.87 | 38.30 | 0.85 | 44.07 |
| 1510P087 | 1.36 | 0.59 | 0.67 | 50.74 | 0.90 | 52.54 | 0.68 | 50.00 | 0.90 | 52.54 |
| C0H9A0 | 1.78 | 0.74 | 1.13 | 36.52 | 0.90 | 21.62 | 1.23 | 30.90 | 0.88 | 18.92 |
| C1I060 | 1.33 | 0.63 | 0.61 | 54.14 | 0.92 | 46.03 | 0.61 | 54.14 | 0.92 | 46.03 |
| C1I070 | 1.41 | 0.62 | 0.97 | 31.21 | 0.82 | 32.26 | 1.01 | 28.37 | 0.80 | 29.03 |
| C1I080 | 1.15 | 0.65 | 0.68 | 40.87 | 0.88 | 35.38 | 0.68 | 40.87 | 0.88 | 35.38 |
| C1I160 | 1.09 | 0.65 | 0.60 | 44.95 | 0.89 | 36.92 | 0.63 | 42.20 | 0.88 | 35.38 |
| C1I290 | 1.36 | 0.57 | 0.89 | 34.56 | 0.82 | 43.86 | 0.90 | 33.82 | 0.81 | 42.11 |
| C1I300 | 0.94 | 0.64 | 0.64 | 31.91 | 0.83 | 29.69 | 0.67 | 28.72 | 0.82 | 28.13 |
| C1I340 | 1.79 | 0.70 | 1.14 | 36.31 | 0.88 | 25.71 | 1.11 | 37.99 | 0.88 | 25.71 |
| C1I350 | 1.32 | 0.62 | 0.71 | 46.21 | 0.89 | 43.55 | 0.74 | 43.94 | 0.88 | 41.94 |
| C1M440 | 1.83 | 0.70 | 1.27 | 30.60 | 0.86 | 22.86 | 1.36 | 25.68 | 0.84 | 20.00 |
| Average | 1.40 | 0.64 | 0.85 | 39.75 | 0.87 | 36.21 | 0.87 | 37.91 | 0.86 | 34.94 |
| Stations Outside or on the Watershed Boundary | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | QPESUMS | Rainfall Data Adjusted by RK | Rainfall Data Adjusted by Merging | |||||||
| RMSE (mm) | CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | RMSE (mm) | % Red. of RMSE | CE | % Imp. of CE | |
| C1M630 | 1.91 | 0.71 | 1.77 | 7.33 | 0.75 | 5.63 | 1.83 | 4.19 | 0.74 | 4.23 |
| C1V170 | 1.76 | 0.25 | 1.58 | 10.23 | 0.39 | 56.00 | 1.60 | 9.09 | 0.37 | 48.00 |
| C1V460 | 2.12 | 0.56 | 1.72 | 18.87 | 0.71 | 26.79 | 1.94 | 8.49 | 0.64 | 14.29 |
| 1510P088 | 1.39 | 0.44 | 1.13 | 18.71 | 0.63 | 43.18 | 1.12 | 19.42 | 0.64 | 45.45 |
| 1730P132 | 2.10 | 0.46 | 1.74 | 17.14 | 0.63 | 36.96 | 1.86 | 11.43 | 0.58 | 26.09 |
| 467530 | 2.51 | 0.69 | 2.09 | 16.73 | 0.78 | 13.04 | 2.25 | 10.36 | 0.75 | 8.70 |
| 467550 | 1.65 | 0.63 | 1.41 | 14.55 | 0.73 | 15.87 | 1.61 | 2.42 | 0.65 | 3.17 |
| C0I090 | 1.41 | 0.70 | 1.12 | 20.57 | 0.81 | 15.71 | 1.19 | 15.60 | 0.79 | 12.86 |
| C1I040 | 1.34 | 0.68 | 0.99 | 26.12 | 0.82 | 20.59 | 1.08 | 19.40 | 0.79 | 16.18 |
| C1I100 | 0.86 | 0.49 | 0.88 | −2.33 | 0.46 | −6.12 | 0.88 | −2.33 | 0.47 | −4.08 |
| C1I120 | 0.81 | 0.48 | 0.83 | −2.47 | 0.45 | −6.25 | 0.88 | −8.64 | 0.38 | −20.83 |
| C1I150 | 1.07 | 0.51 | 0.75 | 29.91 | 0.76 | 49.02 | 0.84 | 21.50 | 0.70 | 37.25 |
| C1I170 | 0.94 | 0.61 | 0.83 | 11.70 | 0.70 | 14.75 | 1.00 | −6.38 | 0.56 | −8.20 |
| C1I270 | 0.94 | 0.57 | 0.61 | 35.11 | 0.82 | 43.86 | 0.77 | 18.09 | 0.71 | 24.56 |
| C1I310 | 1.07 | 0.65 | 0.57 | 46.73 | 0.90 | 38.46 | 0.54 | 49.53 | 0.91 | 40.00 |
| Average | 1.46 | 0.56 | 1.20 | 17.93 | 0.69 | 24.50 | 1.29 | 11.48 | 0.65 | 16.51 |
| Typhoon Fungwong | |||
| RK | Merging | OK | |
| Averaged RMSE Reduction (%) | 26.13 | 22.60 | 19.41 |
| Averaged CE Improvement (%) | 28.64 | 25.70 | 24.05 |
| Typhoon Sinlaku | |||
| RK | Merging | OK | |
| Averaged RMSE Reduction (%) | 24.57 | 22.22 | 15.49 |
| Averaged CE Improvement (%) | 29.43 | 24.08 | 18.46 |
| Typhoon Fanapi | |||
| RK | Merging | OK | |
| Averaged RMSE Reduction (%) | 18.12 | 6.19 | −11.58 |
| Averaged CE Improvement (%) | 11.29 | −11.20 | −50.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.-H.; Chu, T.; Yang, M.-D.; Chen, M.-C. Geostatistical Based Models for the Spatial Adjustment of Radar Rainfall Data in Typhoon Events at a High-Elevation River Watershed. Remote Sens. 2020, 12, 1427. https://doi.org/10.3390/rs12091427
Wang K-H, Chu T, Yang M-D, Chen M-C. Geostatistical Based Models for the Spatial Adjustment of Radar Rainfall Data in Typhoon Events at a High-Elevation River Watershed. Remote Sensing. 2020; 12(9):1427. https://doi.org/10.3390/rs12091427
Chicago/Turabian StyleWang, Keh-Han, Ted Chu, Ming-Der Yang, and Ming-Cheng Chen. 2020. "Geostatistical Based Models for the Spatial Adjustment of Radar Rainfall Data in Typhoon Events at a High-Elevation River Watershed" Remote Sensing 12, no. 9: 1427. https://doi.org/10.3390/rs12091427
APA StyleWang, K.-H., Chu, T., Yang, M.-D., & Chen, M.-C. (2020). Geostatistical Based Models for the Spatial Adjustment of Radar Rainfall Data in Typhoon Events at a High-Elevation River Watershed. Remote Sensing, 12(9), 1427. https://doi.org/10.3390/rs12091427