An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area
Abstract
:1. Introduction
2. The Principle of the Voxel-Based Troposphere Tomography
2.1. General Approach
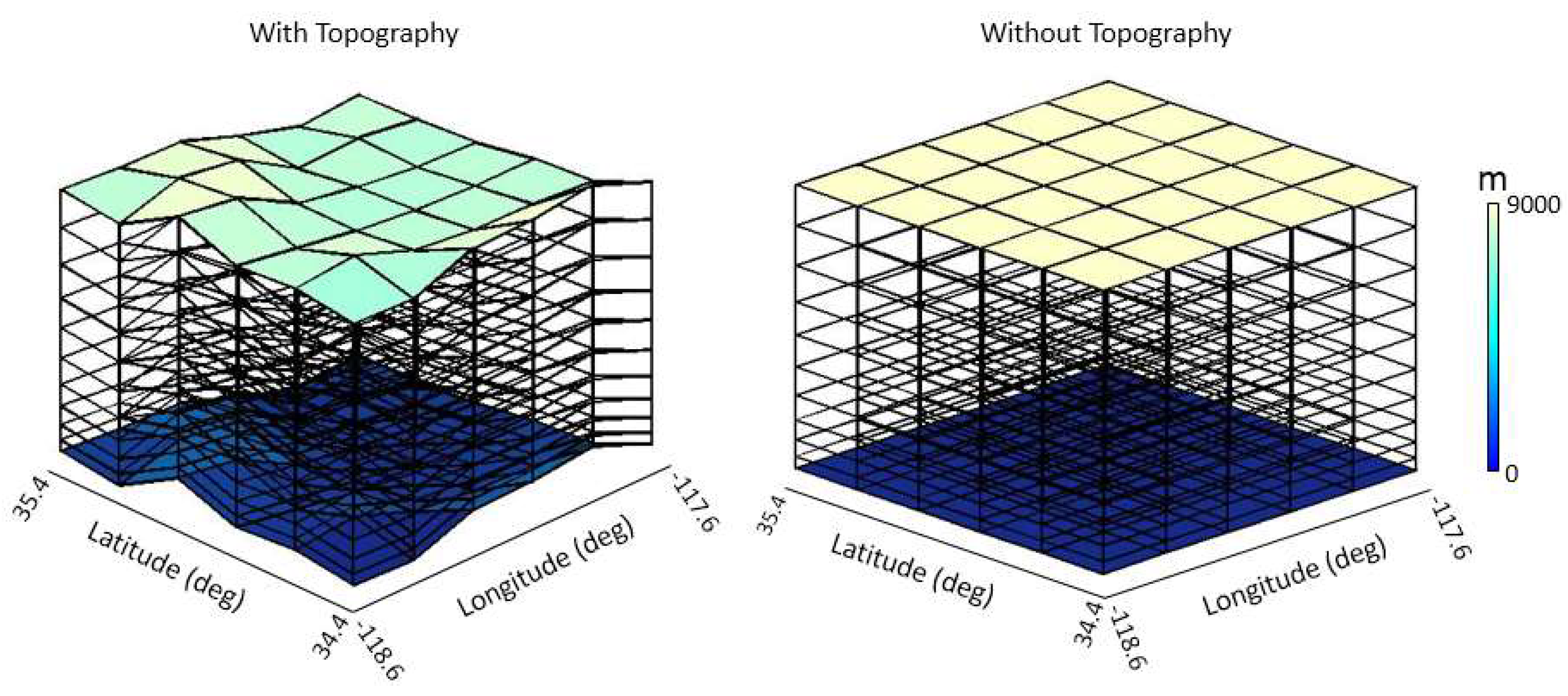
2.2. Optimal Approach Based on the WRF Model and Topography of the Area
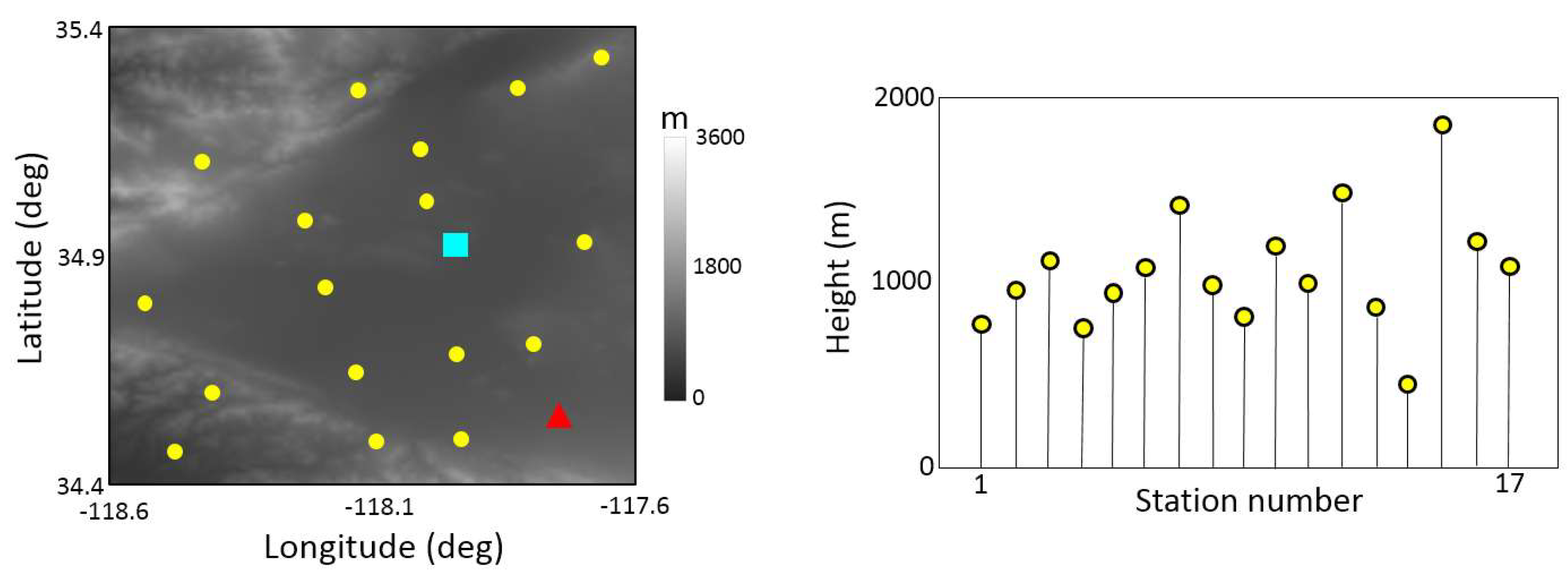
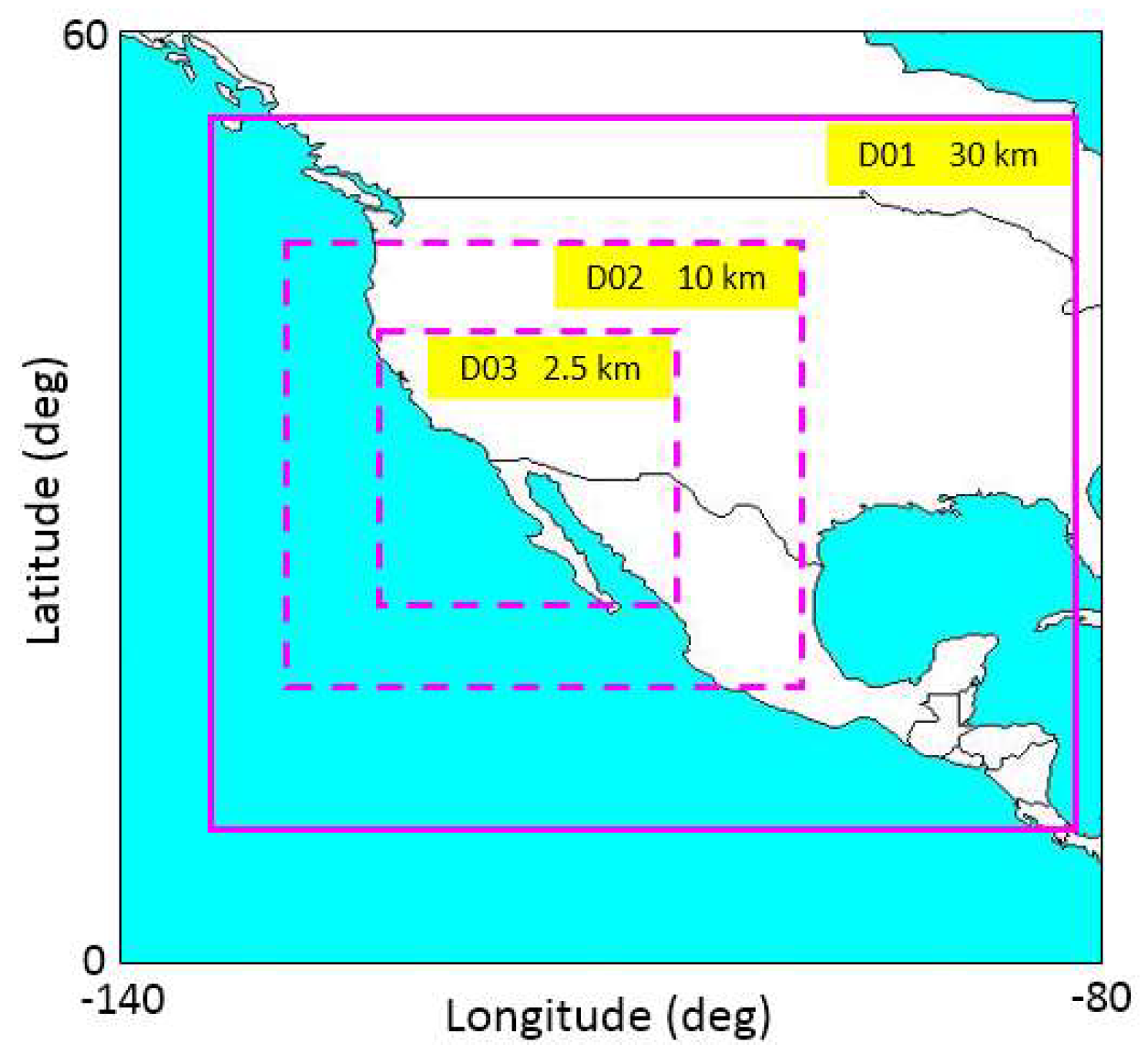
3. Study Area and Data Set
4. Configuration and Processing
4.1. GPS Processing
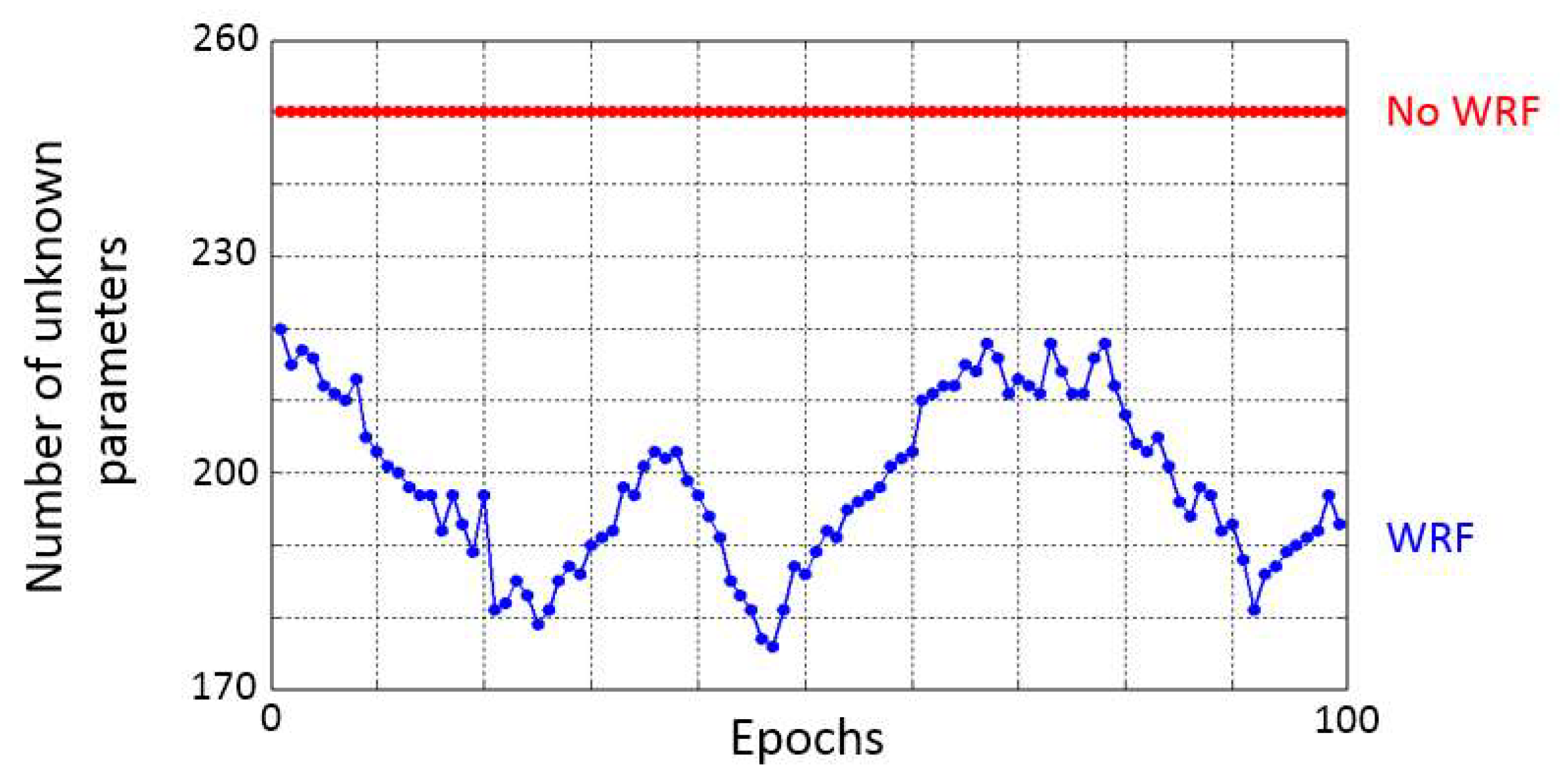
4.2. Design of Tomography Model
4.3. WRF Model Configuration
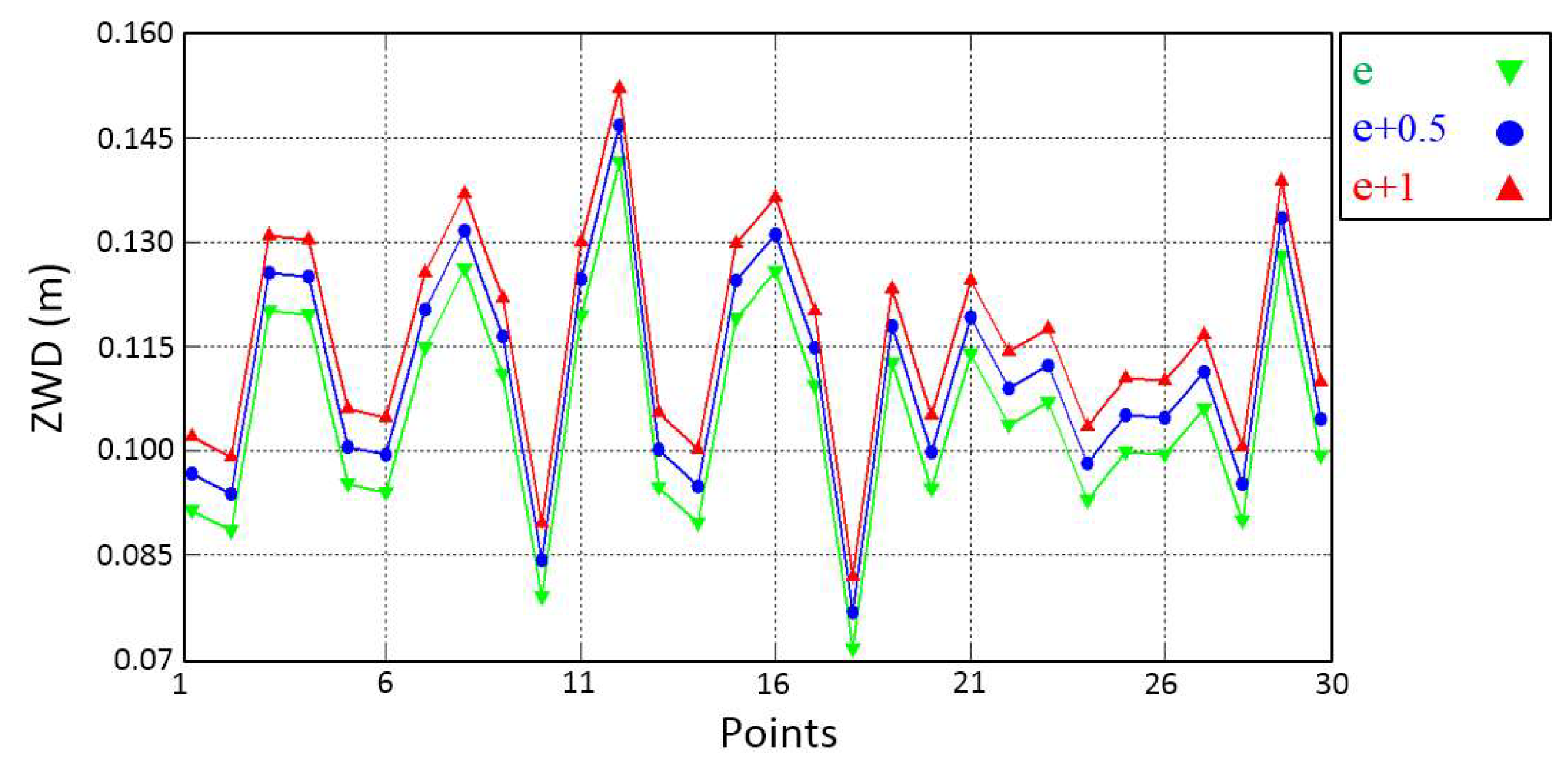
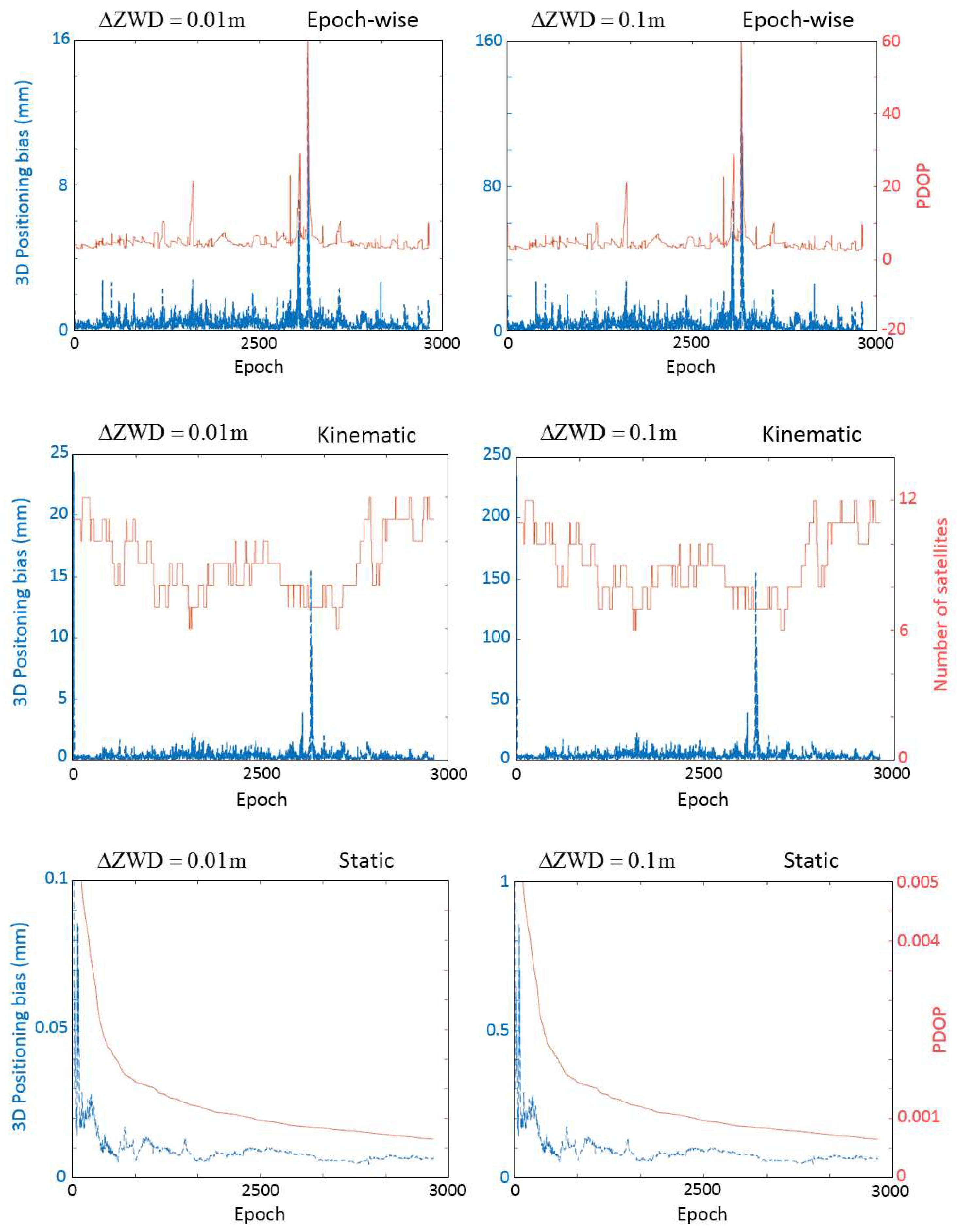
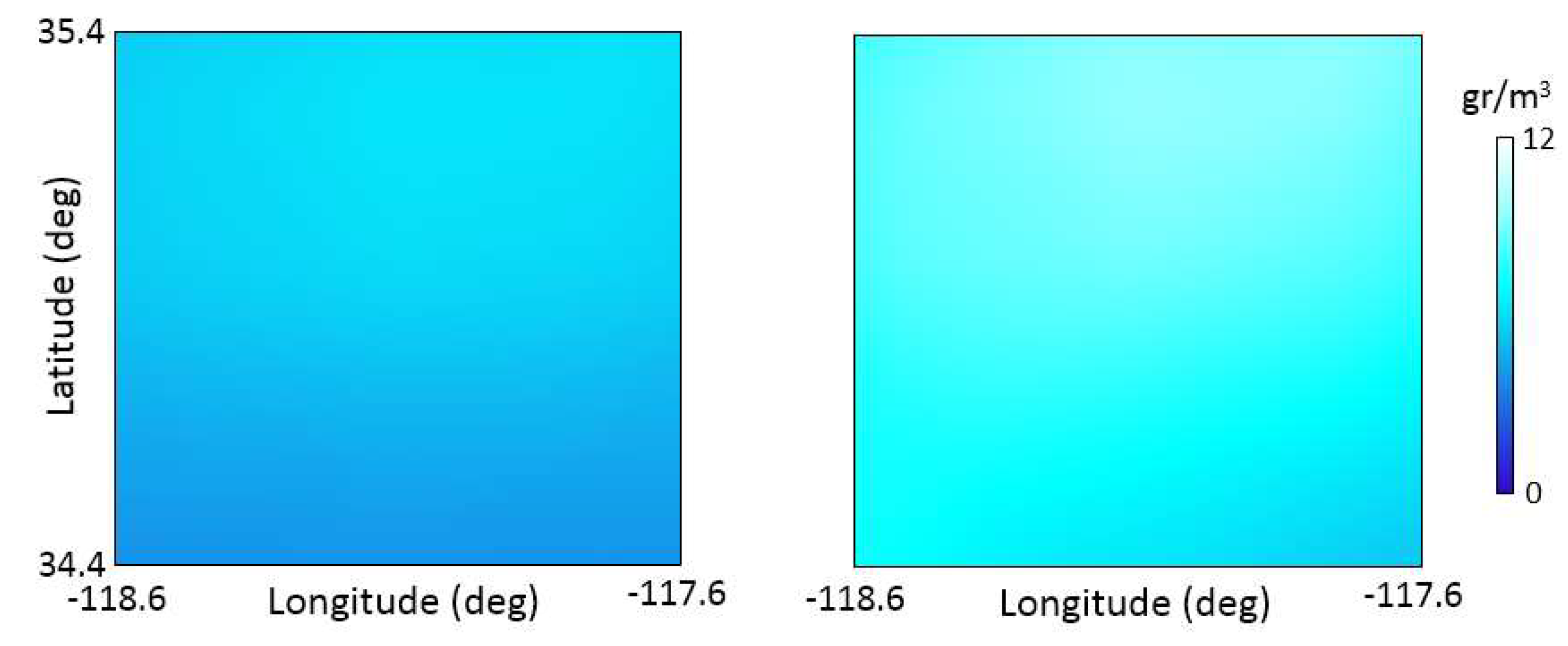
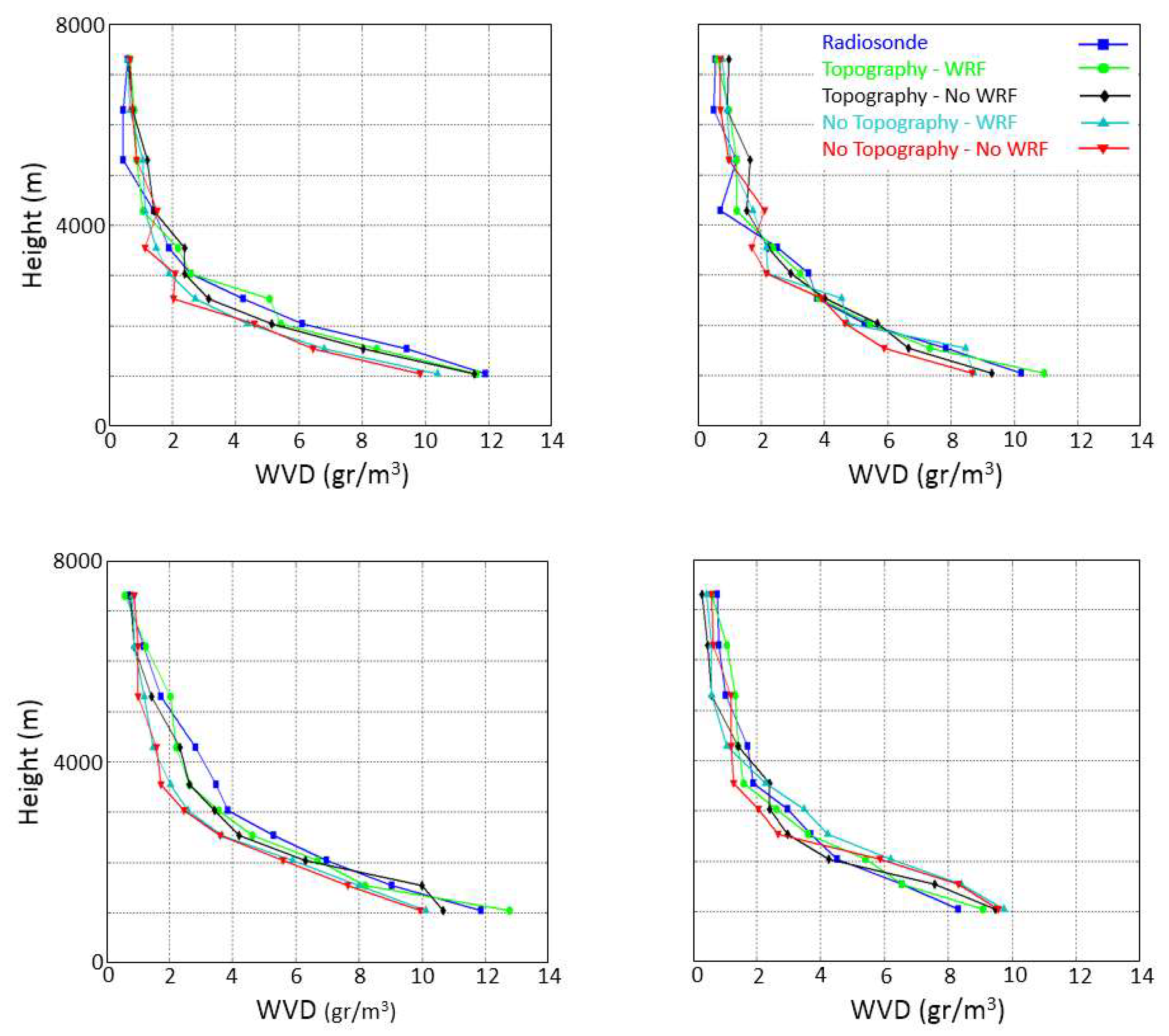
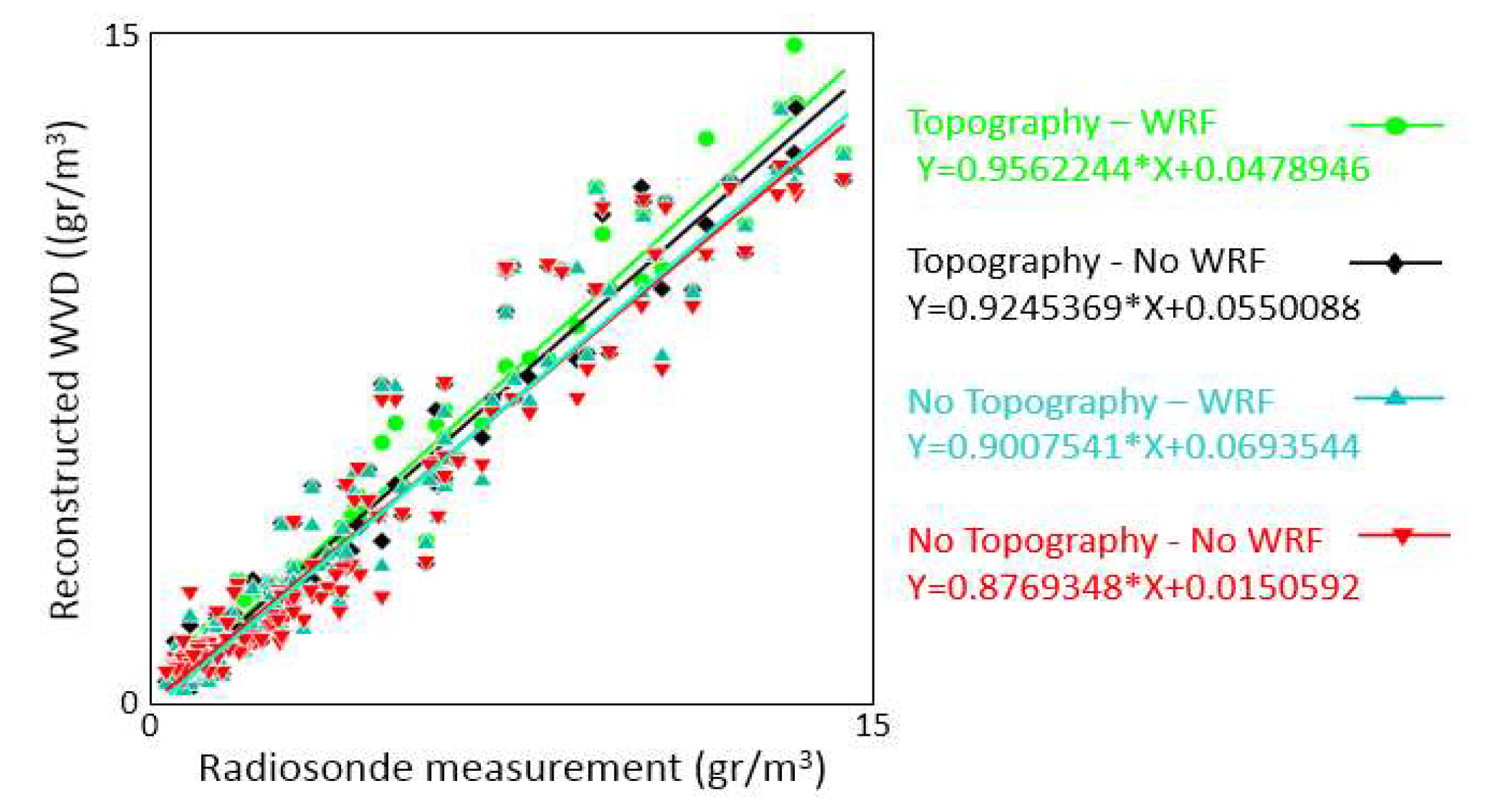
5. Results and Discussion
- Scheme 1: using the topography and WRF model outputs.
- Scheme 2: considering the topography of the area without using the WRF model.
- Scheme 3: by applying the WRF model without using the topography.
- Scheme 4: without the use of the topography and WRF model outputs.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merrikhpour, M.H.; Rahimzadegan, M. Improving the Algorithm of Extracting Regional Total Precipitable Water Vapor Over Land from MODIS Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5889–5898. [Google Scholar] [CrossRef]
- Merrikhpour, M.H.; Rahimzadegan, M. Analysis of temporal and spatial variations of total precipitable water vapor in western Iran using radiosonde and MODIS measurements. J. Appl. Remote Sens. 2019, 13, 044508. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. Ger. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Hirahara, K. Local GPS tropospheric tomography. Earth Planets Space 2000, 52, 935–939. [Google Scholar] [CrossRef] [Green Version]
- Razin, M.R.G.; Voosoghi, B. Modeling of ionosphere time series using wavelet neural networks (case study: N-W of Iran). Adv. Space Res. 2016, 58, 74–83. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. Local tomography troposphere model over mountains area. Atmos. Res. 2009, 93, 777–783. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust Kalman filtering for GNSS troposphere tomography. Atmos. Meas. Tech. 2014, 7, 1475–1486. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Zhao, Q. Maximally Using GPS Observation for Water Vapor Tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7185–7196. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Cao, X.; Zhou, F.; Xia, P. An Optimal Tropospheric Tomography Method Based on the Multi-GNSS Observations. Remote Sens. 2018, 10, 234. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Yao, W.; Xia, P. An optimal tropospheric tomography approach with the support of an auxiliary area. Ann. Geophys. 2018, 36, 1037–1046. [Google Scholar] [CrossRef] [Green Version]
- Haji-Aghajany, S.; Amerian, Y. Three dimensional ray tracing technique for tropospheric water vapor tomography using GPS measurements. J. Atmos. Solar Terr. Phys. 2017, 164, 81–88. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y. Hybrid Regularized GPS Tropospheric Sensing Using 3-D Ray Tracing Technique. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1475–1479. [Google Scholar] [CrossRef]
- Heublein, M.; AlShawaf, F.; Erdnüß, B.; Zhu, X.X.; Hinz, S. Compressive sensing reconstruction of 3D wet refractivity based on GNSS and InSAR observations. J. Geod. 2018, 93, 197–217. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y. An improved troposphere tomographic approach considering the signals coming from the side face of the tomographic area. Ann. Geophys. 2017, 35, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Zhang, K.; Yao, Y.; Li, X. A new troposphere tomography algorithm with a truncation factor model (TFM) for GNSS networks. GPS Solut. 2019, 23, 64. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, W.; Yao, Y.; Li, X. An improved GNSS tropospheric tomography method with the GPT2w model. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Brenot, H.; Rohm, W.; Kačmařík, M.; Möller, G.; Sá, A.; Tondaś, D.; Rapant, L.; Biondi, R.; Manning, T.; Champollion, C. Cross-Comparison and Methodological Improvement in GPS Tomography. Remote Sens. 2019, 12, 30. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Space Phys. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. J. Geod. 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Chen, B.; LiuiD, Z. Voxel-optimized regional water vapor tomography and comparison with radiosonde and numerical weather model. J. Geod. 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Voosoghi, B.; Yazdian, A. Estimation of north Tabriz fault parameters using neural networks and 3D tropospherically corrected surface displacement field. Geomat. Nat. Hazards Risk 2017, 8, 918–932. [Google Scholar] [CrossRef] [Green Version]
- Haji-Aghajany, S.; Voosoghi, B.; Amerian, Y. Estimating the slip rate on the north Tabriz fault (Iran) from InSAR measurements with tropospheric correction using 3D ray tracing technique. Adv. Space Res. 2019, 64, 2199–2208. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 Reanalysis is in Production; ECMWF Newsletter 147; ECMWF: Reading, UK, 2016. [Google Scholar]
- Michalakes, J.; Dudhia, J.; Gill, D.; Henderson, T.; Klemp, J.; Skamarock, W.; Wang, W. The Weather Reseach and Forecast Model: Software Architecture and Performance. In Proceedings of the 11th ECMWF Workshop on the Use of High Performance Computing in Meteorology, 25−29 October 2004; Mozdzynski, G., Ed.; ECMWF: Reading, UK, 2004. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2. User Manual, Astronomical Institute; Open Publishing; University of Bern: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar] [CrossRef]
- Bender, M.; Stosius, R.; Zus, F. GNSS water vapour tomography – Expected improvements by combining GPS, GLONASS and Galileo observations. Adv. Space Res. 2011, 47, 886–897. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, M.; Duda, K.G.; Huang, Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF; Version 3; National Center for Atmospheric Research Boulder Co Mesoscale and Microscale Meteorology Div: Boulder, CO, USA, 2008; pp. 1–113. [Google Scholar]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-Y.; Lim, J.-O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Space Phys. 2008, 113, 13103. [Google Scholar] [CrossRef]
- Chou, M.-D.; Suarez, M.J. A Solar Radiation Parameterization for Atmospheric Studies. In Technical Report Series on Global Modeling and Data Assimilation; NASA/TM-1999-104606; NASA: Washington, DC, USA, 1999; Volume 15. [Google Scholar]
- Niu, G.-Y.; Yang, Z.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical di_usion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]



| Category | Scheme | Reference |
|---|---|---|
| Longwave radiation | WRF single-moment 6 class | [30] |
| Shortwave radiation | Rapid Radiative Transfer Model | [31] |
| Land surface | Goddard | [32] |
| Planetary boundary layer | Noah-MP (multi physics) | [33] |
| microphysics | Yonsei University | [34] |
| Scheme | RMSE (gr/m3) | Bias (gr/m3) | Min-Diff (gr/m3) | Max-Diff (gr/m3) | PCC |
|---|---|---|---|---|---|
| Topography–WRF | 0.612 | 0.009 | 0.061 | 0.961 | 0.981 |
| Topography–No WRF | 0.971 | 0.014 | 0.082 | 1.378 | 0.972 |
| No Topography–WRF | 1.234 | 0.021 | 0.123 | 2.618 | 0.944 |
| No Topography–No WRF | 1.415 | 0.024 | 0.137 | 2.96 | 0.931 |
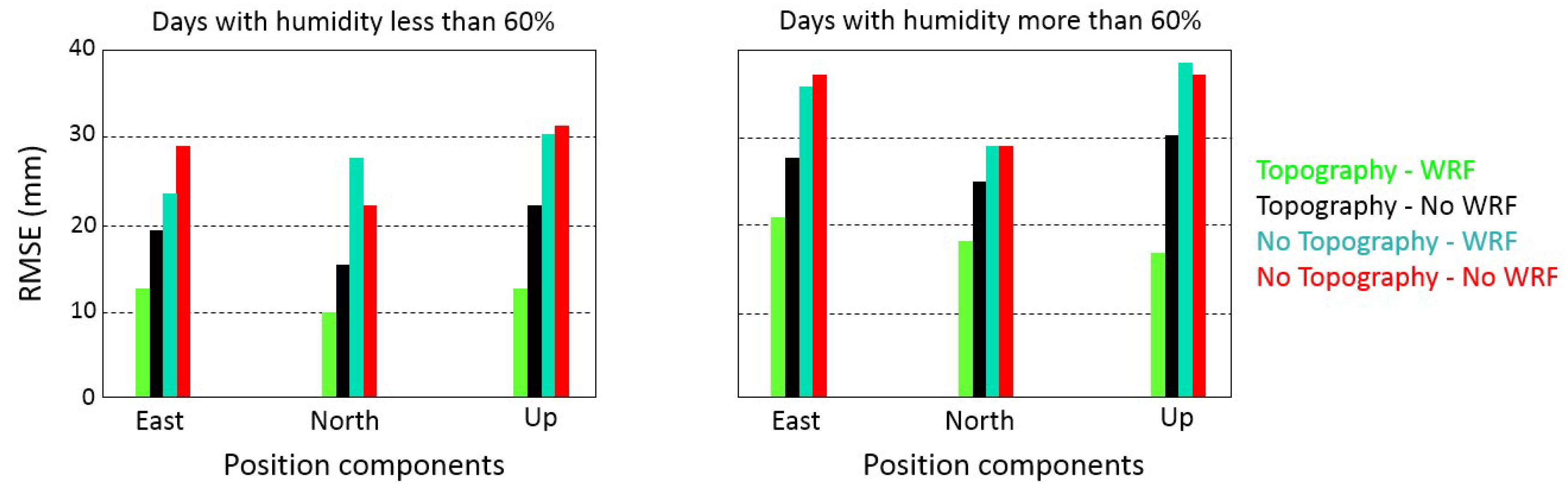
| RMSE in Days with Humidity Less than 60% (mm) | RMSE in Days with Humidity More than 60% (mm) | |||||
|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | |
| Topography–WRF | 12.92 | 10.13 | 14.01 | 20.44 | 18.77 | 17.11 |
| Topography–No WRF | 19.81 | 16.63 | 21.19 | 27.91 | 25.53 | 30.67 |
| No Topography–WRF | 23.84 | 28.14 | 30.15 | 36.45 | 29.48 | 38.65 |
| No Topography–No WRF | 29.05 | 21.59 | 31.87 | 37.86 | 29.23 | 37.14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Ma, H. An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area. Remote Sens. 2020, 12, 1442. https://doi.org/10.3390/rs12091442
Haji-Aghajany S, Amerian Y, Verhagen S, Rohm W, Ma H. An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area. Remote Sensing. 2020; 12(9):1442. https://doi.org/10.3390/rs12091442
Chicago/Turabian StyleHaji-Aghajany, Saeid, Yazdan Amerian, Sandra Verhagen, Witold Rohm, and Hongyang Ma. 2020. "An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area" Remote Sensing 12, no. 9: 1442. https://doi.org/10.3390/rs12091442
APA StyleHaji-Aghajany, S., Amerian, Y., Verhagen, S., Rohm, W., & Ma, H. (2020). An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area. Remote Sensing, 12(9), 1442. https://doi.org/10.3390/rs12091442







