1. Introduction
Soil moisture is an important factor affecting the global climate and environment. Its existence in the earth system and its spatial transmission mode play a vital role in the global energy balance. It controls the exchange of hydrothermal energy between the land and the atmosphere. Related studies have shown that there is a strong feedback relationship between soil moisture and abnormal climate. Soil moisture is an important index parameter in the fields of hydrology, meteorology, and agricultural scientific research. Large-scale soil moisture monitoring and retrieval is an important part of agricultural research and ecological environment assessment. At the same time, soil moisture is also the link between surface water and groundwater, and it is an important part of the land surface ecosystem and water cycle. Therefore, soil moisture information plays an important role in improving regional and even global climate model forecasts, global water cycle laws, water resource management, watershed hydrological models, crop growth monitoring, crop yield estimation, environmental disaster monitoring, and other related natural and ecological environmental issues [
1].
Traditional observation methods mainly use observations at discrete stations or corresponding meteorological stations, which can only represent a limited observation area (≈10–100 cm). They are also time-consuming and labor-intensive and cannot meet the needs of large-scale and high-efficiency soil moisture observation. Using this traditional monitoring method makes it difficult to match the corresponding weather and hydrological model (0.1–10 km) in terms of spatial scale and time accuracy, so this method cannot effectively study the effect of soil moisture on environmental changes.
Remote sensing methods can obtain soil moisture information with high efficiency and at a large scale. Optical, infrared, and microwave remote sensing are the main remote sensing methods for earth observation. The corresponding sensors work in the visible, infrared, and microwave bands of the electromagnetic spectrum, but these remote sensing methods have their own limitations. Optical and infrared remote sensing are limited to weather conditions and cannot work all day and under all weather conditions; microwave remote sensing overcomes this shortcoming and has the advantages of all-day, all-weather, and strong penetration. The real part of the dielectric constant of water is 80, and that of dry soil is 3.5. An increase in soil moisture will cause an increase in the dielectric constant, and thus a decrease in emissivity or an increase in reflectivity. The basic principle of microwave remote sensing soil moisture detection is the large dielectric constant difference between water and dry soil [
2]. Among them, the P-band and L-band are particularly favorable for soil moisture observation. In these bands, the atmospheric attenuation decreases, and the vegetation penetration increases.
Traditional active and passive microwave methods (microwave radiometer and radar) have their own advantages and disadvantages. The radiometer measures the surface brightness temperature, and then can use the emissivity information to retrieve soil moisture. Radiation measurement is not sensitive to surface roughness, but is easily affected by background brightness and artificial RFI (Radio Frequency Interference). Its spatial resolution is high, while data processing is simple, but its time resolution is low. Compared with the radiometer, in the radar, the larger the soil moisture content, the larger the backscattering coefficient, the lower the sensitivity of the single station radar to the soil moisture, and the more easily the backscattering is affected by surface characteristics, such as surface roughness, soil dielectric constant, and vegetation structure. Its data processing is complex and the spatial resolution is low [
3]. The unique observation geometry model of the bistatic radar has become a new method and technology for remote sensing monitoring of soil moisture and vegetation. However, in the general sense, bistatic radars need to develop special transmitters and receivers, which have limitations such as high cost, heavy load, and low power consumption.
The emerging signal of opportunity (SoOP) technology uses the existing navigation satellite group or communication satellites as the signal transmission sources, and only needs to develop a special reflected signal receiver to achieve effective monitoring of soil moisture in bistatic radar mode [
4,
5,
6]. Opportunity signal reflection remote sensing provides new opportunities for root zone soil moisture acquisition in the P-band. The P-band penetration has an advantage, with a penetration depth of about 40 cm at soil moisture of no more than 2–3 volumetric % when there is no vegetation cover, while its penetration depth is 10–15 cm and L-band signal is no more than 5 cm with vegetation presence [
7]. Because digital communication satellites are used as signal sources, there is no need to develop a special transmitter. Therefore, P-band opportunity signal reflection remote sensing has many advantages, such as low cost, low power consumption, cheap price, and high spatiotemporal resolution [
8].
GNSS-R (Global Navigation Satellite System-Reflectometry) uses navigation satellites as its signal source and uses its reflected signals to remotely sense ground feature parameters [
9]. At present, the earliest and more extensive study of GNSS-R technology on land surface is remote sensing of soil moisture, and the existing research is mostly carried out from an experimental perspective [
10,
11,
12].
Most of the existing scattering models were aimed at the backscattering of a monostatic radar, or the radiation characteristics of passive microwaves. Studies focusing solely on SoOP scattering characteristics have been paid less attention, and most of them are concentrated in one plane [
13,
14]. Although recent studies have pointed out that scattering azimuth will affect the polarization characteristics of bare soil, only linear polarization characteristics were considered in the model, and relatively few studies on SoOP circular polarization characteristics have been made. In order to overcome the influence of the ionosphere, the signals were transmitted by navigation satellites’ RHCP (Right Hand Circular Polarization) signal. After the signal is reflected from the ground, the polarization characteristics will change. However, making full use of its polarization characteristics is an urgent problem for SoOP application. At the same time, research on the ocean also found that the theoretical simulation of the co-polarized scattering component and the actual waveform were poorly matched, and a theoretical model needs to be established to simulate and analyze the co-polarized scattering component. Relevant research on the parameters of bare soil, especially the bistatic radar scattering mechanism model that focuses on various polarizations, including circular polarization characteristics, has been studied less. Due to the lack of the mechanism model, the full polarization of its bistatic scattering (circular and linear polarization) lacks awareness of sensitivity, which limits the further development of the technology. Therefore, for SoOP soil moisture remote sensing, it is important to fully excavate the polarization characteristic information of navigation satellite signals. Carrying out the circular polarization theory research of the bistatic radar scattering model is important for space-borne load design, experimental data analysis, and backward inversion algorithm development [
15].
In this paper, we will develop the surface scattering model to simulate the bistatic scattering characteristics at circular polarization for SoOP applications. In
Section 2, the theoretical formulations are presented. The simulations and analysis are given in
Section 3. In
Section 4, discussion is shown, and finally the conclusions are presented in
Section 5.
4. Discussion
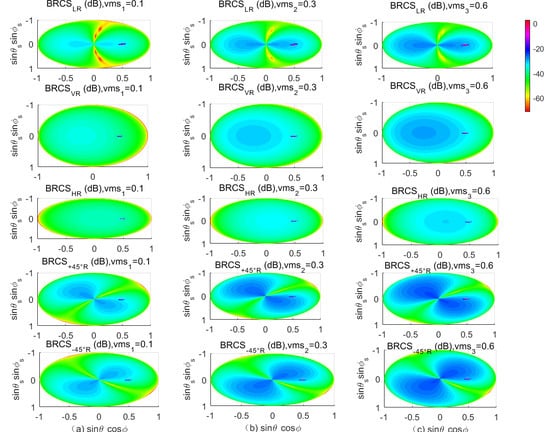
As for GNSS-R remote sensing, it only takes the coherent scattering part at the specular direction for analysis. From the present analysis of the space-borne data, such as TDS-1 and CYGNSS, most are focused on the analysis of the coherent scattering from the first Fresnel zone, and always ignored the diffuse scattering powers. As for SoOP applications, the transmitter and the corresponding receivers form the typical bistatic-radar working mode, so the influence of the observation geometry on the scattering characteristics is critical. We can also see from our simulations that strong scattering values at the specular direction do exist, especially at the specular plane. This energy should be taken into account for future data analysis, but we should note that the random rough surface will not be very flat, and the surface roughness must result in the diffuse scattering. It can be seen from the analysis that the scattering value will peak at the mirror angle, but in this case the angle needs to be in a plane. When the scattering azimuth changes, the peak of the scattering disappears. It can also be seen through simulation, that the scattering value will have troughs at different scattering azimuths, but this scattering groove is related to the scattering azimuth of different polarizations. The scattering peaks and scattering grooves in the simulation analysis are of great significance for soil moisture inversion and are the angles that need attention in the subsequent soil moisture inversion. With the development of the algorithm and the improvement of the receiver’s ability to receive signals, the bistatic scattering properties out of the specular plane must be taken good care of in the future analysis. Only by fully considering and effectively utilizing the bistatic scattering characteristics of various observation geometries, can we make better use of the advantages of SoOP remote sensing bistatic radar to observe the geophysical parameters. Our analysis and simulations give us the illustrations of these properties to some extent.
From our analysis, we can also see that the scattering properties vary a lot for different polarizations. The polarization mode is an important parameter for characterization of electromagnetic waves and is determined by the receiver antenna. Polarization is an important characteristic of electromagnetic waves. The polarization information of the surface reflection signal carries important information on the surface. The polarization ratio is an important information parameter for soil moisture inversion and vegetation state research. Common polarization methods are linear polarization and circular polarization. The antenna polarization of SoOP remote sensing receivers are different, which causes the amplitude and phase characteristics of the target echo to be different, which will affect the detection sensitivity of the receiver. The model developed in this paper can simulate the reflection signal of arbitrary polarization. According to the simulation results, it was seen that the scattering characteristics of random rough surfaces were significantly different under different polarizations. Studying the target scattering characteristics has important guiding significance for SoOP antenna design. The calculation ability of our models for any polarizations will give guidance for future data analysis.
5. Conclusions
In the past two decades, we witnessed the promising development of GNSS-R remote sensing. With the same fundamentals, the SoOP technique employs the signals of a communication satellite system as the free transmitters, which has shown in recent years that SoOP is a promising remote sensing technique for the detection of geophysical parameters. With unique frequency advantages at the P-band, we employed SoOP for our analysis. The transmitters and the corresponding receivers of SoOP form the typically bistatic radar. Here, we simulated and analyzed the bistatic scattering properties at different scattering geometries (both scattering zenith angle and azimuth angles). Scattering peak values exist at the specular plane, and the information coming from the first Fresnel Zone should be taken, especially used as in the GNSS-R technique. Scattering grooves also exist, and this information could be useful for the development of soil moisture retrieval and vegetation corrections. From the simulations, we can see that these grooves were related to the scattering azimuth at different polarizations, which is related to other features of the development models. These models can simulate and analyze five different circularly polarized scattering characteristics of random rough surfaces, namely the transmitted polarization (RHCP) and the receiving polarizations (LHCP, H, V, +45°, and −45°) characteristics, respectively. Through the simulation analysis of the models, it was seen that different frequencies and soil moisture parameters can affect the circular polarization bistatic scattering characteristics. The scattering characteristics of the scattering zenith angle and scattering azimuth angle in the observation geometry at the five different polarizations were also different. We can find and determine the optimal observation combination by using different polarizations and different observation angles. It was also conducive to a more systematic and in-depth analysis of the scattering characteristics of random rough surfaces from a physical perspective, which will contribute to the design of more effective SoOP remote sensing inversion models in the future.