Sea Surface Salinity Seasonal Variability in the Tropics from Satellites, Gridded In Situ Products and Mooring Observations
Abstract
:1. Introduction
2. Data and Methods
2.1. Datasets Used
2.2. Harmonic Analysis
3. Results
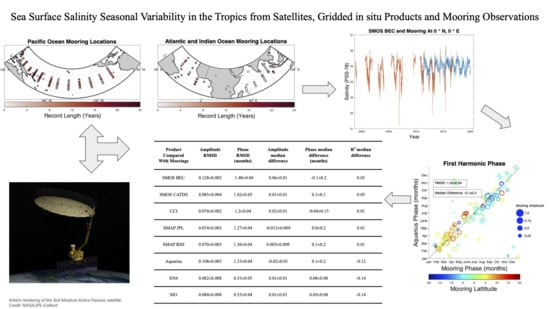
3.1. Amplitude and Phase Maps
3.2. Amplitude and Phase Comparisons
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
| Dataset | URL/DOI | Example File Name |
| Moorings | https://www.pmel.noaa.gov/tao/drupal/disdel/ | N/A |
| SMOS BEC | http://bec.icm.csic.es/ocean-global-sss/ | BEC_SSS___SMOS__GLO_L3__B_20110124T120000_0.25d_9d_REP_v002.nc |
| SMOS CATDS | DOI:10.17882/52804 | SMOS_L3_DEBIAS_LOCEAN_AD_20100116_EASE_09d_25km_v04.nc |
| CCI | DOI:10.5285/9ef0ebf847564c2eabe62cac4899ec41 | ESACCI-SEASURFACESALINITY-L4-SSS-MERGED_OI_7DAY_RUNNINGMEAN_DAILY_25km-20100101-fv2.31.nc |
| SMAP JPL | DOI:10.5067/SMP43-3TPCS | SMAP_L3_SSS_20150627_8DAYS_V4.3.nc |
| SMAP RSS (70 km) | DOI:10.5067/SMP40-3SPCS | RSS_smap_SSS_L3_8day_running_2015_090_FNL_v04.0.nc |
| Aquarius | DOI:10.5067/AQR50-3YQCE | Q20112312011237.L3m_R7_SCI_V5.0.RAIN_MASK_SSS_1deg |
| EN4 | https://www.metoffice.gov.uk/hadobs/en4/ | EN.4.2.1.f.analysis.g10.200001.nc |
| SIO | http://sio-argo.ucsd.edu/RG_Climatology.html | RG_ArgoClim_Psal.nc |
Acknowledgments
Conflicts of Interest
References
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; Decharon, A.; et al. The Aquarius/SAC-D Mission: Designed to Meet the Salinity Remote-Sensing Challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Wentz, F.J.; Le Vine, D.M. The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sens. 2018, 10, 1121. [Google Scholar] [CrossRef] [Green Version]
- Abe, H.; Ebuchi, N. Evaluation of sea-surface salinity observed by Aquarius. J. Geophys. Res. Oceans 2014, 119, 8109–8121. [Google Scholar] [CrossRef]
- Bao, S.; Wang, H.; Li, M.; Yan, H.; Chen, J. Comparison of Satellite-Derived Sea Surface Salinity Products from SMOS, Aquarius, and SMAP. J. Geophys. Res. Oceans 2019, 124, 1932–1944. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Gomez-Valdes, J.; Bouali, M.; Miranda, L.E.; Van Der Stocken, T.; Tang, W.; Gentemann, C.L. Using Saildrones to Validate Satellite-Derived Sea Surface Salinity and Sea Surface Temperature along the California/Baja Coast. Remote Sens. 2019, 11, 1964. [Google Scholar] [CrossRef] [Green Version]
- Kao, H.; Lagerloef, G.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Assessment of Aquarius Sea Surface Salinity. Remote Sens. 2018, 10, 1341. [Google Scholar] [CrossRef] [Green Version]
- Kao, H.-Y.; Lagerloef, G.; Lee, T.; Melnichenko, O.; Hacker, P. Aquarius Salinity Validation Analysis; Data Version 5.0; Aquarius/SAC-D: Seattle, WA, USA, 2018; p. 45. [Google Scholar]
- Olmedo, E.; Martinez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Olmedo, E.; González-Haro, C.; Hoareau, N.; Umbert, M.; González-Gambau, V.; Martínez, J.; Gabarró, C.; Turiel, A. Nine years of SMOS Sea Surface Salinity global maps at the Barcelona Expert Center. Earth Syst. Sci. Data Discuss. 2020, 2020, 1–49. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D.M.; Boutin, J.; Meissner, T.; Lagerloef, G. Remote Sensing of Sea Surface Salinity: Comparison of Satellite and In Situ Observations and Impact of Retrieval Parameters. Remote Sens. 2019, 11, 750. [Google Scholar] [CrossRef] [Green Version]
- Qin, S.; Wang, H.; Zhu, J.; Wan, L.; Zhang, Y.; Wang, H. Validation and correction of sea surface salinity retrieval from SMAP. Acta Oceanol. Sin. 2020, 39, 148–158. [Google Scholar] [CrossRef]
- Tang, W.; Fore, A.G.; Yueh, S.; Lee, T.; Hayashi, A.; Sanchez-Franks, A.; Martinez, J.; King, B.; Baranowski, D. Validating SMAP SSS with in situ measurements. Remote Sens. Environ. 2017, 200, 326–340. [Google Scholar] [CrossRef] [Green Version]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Drucker, R.; Riser, S.C. Validation of Aquarius sea surface salinity with Argo: Analysis of error due to depth of measurement and vertical salinity stratification. J. Geophys. Res. Oceans 2014, 119, 4626–4637. [Google Scholar] [CrossRef]
- Kuusela, M.; Stein, M.L. Locally stationary spatio-temporal interpolation of Argo profiling float data. Proc. R. Soc. A 2018, 474, 20180400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bingham, F.M.; Foltz, G.R.; McPhaden, M.J. Seasonal cycles of surface layer salinity in the Pacific Ocean. Ocean Sci. 2010, 6, 775–787. [Google Scholar] [CrossRef] [Green Version]
- Bingham, F.M.; Foltz, G.R.; McPhaden, M.J. Characteristics of the seasonal cycle of surface layer salinity in the global ocean. Ocean Sci. 2012, 8, 915–929. [Google Scholar] [CrossRef] [Green Version]
- Boyer, T.; Levitus, S. Harmonic analysis of climatological sea surface salinity. J. Geophys. Res. Space Phys. 2002, 107, 8006. [Google Scholar] [CrossRef]
- Yu, L.; Bingham, F.M.; Dinnat, E.; Fournier, S.; Lee, T.; Melnichenko, O. Seasonality in Sea Surface Salinity Revisited. J. Geophys. Res. Ocean. 2020. in review. [Google Scholar]
- Bingham, F.M.; Lee, T. Space and time scales of sea surface salinity and freshwater forcing variability in the global ocean (60°S–60°N). J. Geophys. Res. Oceans 2017, 122, 2909–2922. [Google Scholar] [CrossRef]
- Martins, M.S.; Serra, N.; Stammer, D. Spatial and temporal scales of sea surface salinity variability in the Atlantic Ocean. J. Geophys. Res. Oceans 2015, 120, 4306–4323. [Google Scholar] [CrossRef]
- Melnichenko, O.; Hacker, P.; Bingham, F.M.; Lee, T. Patterns of SSS Variability in the Eastern Tropical Pacific: Intraseasonal to Interannual Timescales from Seven Years of NASA Satellite Data. Oceanography 2019, 32, 20–29. [Google Scholar] [CrossRef]
- Kessler, W. The circulation of the eastern tropical Pacific: A review. Prog. Oceanogr. 2006, 69, 181–217. [Google Scholar] [CrossRef]
- Guimbard, S.; Reul, N.; Chapron, B.; Umbert, M.; Maes, C. Seasonal and interannual variability of the Eastern Tropical Pacific Fresh Pool. J. Geophys. Res. Oceans 2017, 122, 1749–1771. [Google Scholar] [CrossRef]
- Fiedler, P.C.; Talley, L.D. Hydrography of the eastern tropical Pacific: A review. Prog. Oceanogr. 2006, 69, 143–180. [Google Scholar] [CrossRef]
- Foltz, G.R.; McPhaden, M.J. Seasonal mixed layer salinity balance of the tropical North Atlantic Ocean. J. Geophys. Res. Space Phys. 2008, 113, 02013. [Google Scholar] [CrossRef] [Green Version]
- Grodsky, S.A.; Carton, J.A.; Bryan, F.O. A curious local surface salinity maximum in the northwestern tropical Atlantic. J. Geophys. Res. Ocean. 2014, 119, 484–495. [Google Scholar] [CrossRef]
- McPhaden, M.; Busalacchi, A.; Anderson, D. A TOGA Retrospective. Oceanography 2010, 23, 86–103. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Yueh, S.H.; Fore, A.G.; Hayashi, A.; Lee, T.; Lagerloef, G. Uncertainty of Aquarius sea surface salinity retrieved under rainy conditions and its implication on the water cycle study. J. Geophys. Res. Ocean. 2014, 119, 4821–4839. [Google Scholar] [CrossRef] [Green Version]
- Reul, N.; Grodsky, S.; Arias, M.; Boutin, J.; Catany, R.; Chapron, B.; D’Amico, F.; Dinnat, E.; Donlon, C.; Fore, A.; et al. Sea surface salinity estimates from spaceborne L-band radiometers: An overview of the first decade of observation (2010–2019). Remote Sens. Environ. 2020, 242, 111769. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Oceans 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.; Manaseter, A. Remote Sensing Systems SMAP Ocean Surface Salinities Level 3 Running 8-Day; Version 3.0 validated release; Systems, R.S., Ed.; Remote Sensing Systems: Santa Rosa, CA, USA, 2018. [Google Scholar]
- Millero, F.J. What is PSU? Oceanography 1993, 6, 67. [Google Scholar]
- Freitag, H.P.; McPhaden, M.J.; Connell, K.J. Comparison of ATLAS and T-FLEX Mooring Data. Available online: https://www.pmel.noaa.gov/pubs/PDF/frei4747/frei4747.pdf (accessed on 24 December 2020).
- Olmedo, E.; González-Haro, C.; González-Gambau, V.; Martínez, J.; Turiel, A. Global SMOS-BEC SSS L3 and L4 Product V2 Description. Available online: http://bec.icm.csic.es/doc/BEC-SMOS-PD-SSSv2-v1.pdf (accessed on 24 December 2020).
- Boutin, J.; Vergely, J.-L.; Khvorostyanov, D. SMOS SSS L3 maps generated by CATDS CEC LOCEAN. debias V5.0. Available online: https://www.seanoe.org/data/00417/52804/ (accessed on 24 December 2020).
- Boutin, J.; Vergely, J.; Marchand, S.; D’Amico, F.; Hasson, A.; Kolodziejczyk, N.; Reul, N.; Reverdin, G.; Vialard, J. New SMOS Sea Surface Salinity with reduced systematic errors and improved variability. Remote Sens. Environ. 2018, 214, 115–134. [Google Scholar] [CrossRef] [Green Version]
- Vergely, J.-L.; Boutin, J. SMOS OS Level 3 Algorithm Theoretical Basis Document (v300). Available online: https://www.catds.fr/content/download/78841/file/ATBD_L3OS_v3.0.pdf (accessed on 24 December 2020).
- Rouffi, F. Climate Change Initiative+ (CCI+) Phase 1: Sea Surface Salinity [D4.3] Product User Guide. Available online: https://res.mdpi.com/data/mdpi_references_guide_v5.pdf (accessed on 24 December 2020).
- Fore, A.; Yueh, S.; Tang, W.; Hayashi, A. SMAP Salinity and Wind Speed Users Guide, Version 5.0. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/smap/docs/%20JPL-CAP_V5/SMAP-SSS_JPL_V5.0_Documentation.pdf (accessed on 30 December 2020).
- Yi, D.L.; Melnichenko, O.; Hacker, P.; Potemra, J. Remote Sensing of Sea Surface Salinity Variability in the South China Sea. J. Geophys. Res. Oceans 2020, 125, e2020JC016827. [Google Scholar] [CrossRef]
- Drushka, K.; Asher, W.; Jessup, A.; Thompson, E.; Iyer, S.; Clark, D. Capturing Fresh Layers with the Surface Salinity Profiler. Oceanography 2019, 32, 76–85. [Google Scholar] [CrossRef]
- D’Addezio, J.M.; Bingham, F.M.; Jacobs, G.A. Sea surface salinity subfootprint variability estimates from regional high-resolution model simulations. Remote Sens. Environ. 2019, 233, 111365. [Google Scholar] [CrossRef]
- Bingham, F.M. Subfootprint Variability of Sea Surface Salinity Observed during the SPURS-1 and SPURS-2 Field Campaigns. Remote Sens. 2019, 11, 2689. [Google Scholar] [CrossRef] [Green Version]
- Boutin, J.; Martin, N.; Reverdin, G.; Yin, X.; Gaillard, F. Sea surface freshening inferred from SMOS and ARGO salinity: Impact of rain. Ocean Sci. 2013, 9, 183–192. [Google Scholar] [CrossRef] [Green Version]
- Boutin, J.; Chao, Y.; Asher, W.E.; Delcroix, T.; Drucker, R.; Drushka, K.; Kolodziejczyk, N.; Lee, T.; Reul, N.; Reverdin, G.; et al. Satellite and In Situ Salinity: Understanding Near-Surface Stratification and Subfootprint Variability. Bull. Am. Meteorol. Soc. 2016, 97, 1391–1407. [Google Scholar] [CrossRef] [Green Version]
- Hénocq, C.; Boutin, J.; Reverdin, G.; Petitcolin, F.; Arnault, S.; Lattes, P. Vertical Variability of Near-Surface Salinity in the Tropics: Consequences for L-Band Radiometer Calibration and Validation. J. Atmospheric Ocean. Technol. 2010, 27, 192–209. [Google Scholar] [CrossRef]
- Rainville, L.; Centurioni, L.; Asher, W.; Clayson, C.A.; Drushka, K.; Edson, J.; Hodges, B.; Hormann, V.; Farrar, J.T.; Schanze, J.J.; et al. Novel and Flexible Approach to Access the Open Ocean: Uses of Sailing Research Vessel Lady Amber During SPURS-2. Oceanography 2019, 32, 116–121. [Google Scholar] [CrossRef]
- Drushka, K.; Asher, W.E.; Sprintall, J.; Gille, S.T.; Hoang, C. Global Patterns of Submesoscale Surface Salinity Variability. J. Phys. Oceanogr. 2019, 49, 1669–1685. [Google Scholar] [CrossRef]
- Thyng, K.; Greene, C.; Hetland, R.; Zimmerle, H.; DiMarco, S. True Colors of Oceanography: Guidelines for Effective and Accurate Colormap Selection. Oceanography 2016, 29, 9–13. [Google Scholar] [CrossRef] [Green Version]










| Dataset | Time Resolution | Spatial Grid | Time Span | References |
|---|---|---|---|---|
| Moorings | Hourly | N/A | various | [35] |
| SMOS BEC | Daily values with a 9-day running mean | 0.25° | 2011–2019 | [9,10,36] |
| SMOS CATDS | 4-day values with a 9-day running mean | Lon: 0.2594° Lat: varies from 0.1962° to 1.5341° | 2010–2019 | [37,38,39] |
| CCI | Daily values with a 7-day running mean | Lon: 0.2594° Lat: varies from 0.1962° to 1.5341° | 2010–2018 | [40] |
| SMAP JPL | 8-day running mean | 0.25° | 2015–2020 | [41] |
| SMAP RSS (70 km) | 8-day running mean | 0.25° | 2015–2020 | [3,33] |
| Aquarius | Daily values with a 7-day running mean | 1° | 2011–2015 | [2,8] |
| EN4 | Monthly | 1° | 2000–2018 | [32] |
| SIO | Monthly | 1° | 2004–2020 | [14] |
| Product | Amplitude RMSD | Phase RMSD (months) | Amplitude Median Difference | Phase Median Difference (months) | R2 Median Difference |
|---|---|---|---|---|---|
| SMOS BEC | 0.128 ± 0.002 | 1.48 ± 0.04 | 0.06 ± 0.01 | −0.1 ± 0.2 | 0.03 |
| SMOS CATDS | 0.085 ± 0.004 | 1.02 ± 0.05 | 0.01 ± 0.01 | 0.1 ± 0.1 | 0.05 |
| CCI | 0.074 ± 0.002 | 1.2 ± 0.04 | 0.02 ± 0.01 | −0.04 ± 0.15 | 0.01 |
| SMAP JPL | 0.074 ± 0.003 | 1.27 ± 0.04 | −0.013 ± 0.009 | 0.0 ± 0.2 | 0.01 |
| SMAP RSS | 0.070 ± 0.003 | 1.30 ± 0.04 | 0.003 ± 0.009 | 0.1 ± 0.2 | 0.01 |
| Aquarius | 0.108 ± 0.003 | 1.33 ± 0.04 | −0.02 ± 0.01 | 0.1 ± 0.2 | −0.12 |
| EN4 | 0.082 ± 0.008 | 0.53 ± 0.05 | 0.01 ± 0.01 | 0.08 ± 0.08 | −0.14 |
| SIO | 0.080 ± 0.008 | 0.55 ± 0.04 | 0.01 ± 0.01 | 0.05 ± 0.08 | −0.14 |
| Median R2 | |
|---|---|
| Moorings | 0.190 |
| SMOS BEC | 0.103 |
| SMOS CATDS | 0.187 |
| CCI | 0.1842 |
| SMAP JPL | 0.198 |
| SMAP RSS | 0.203 |
| Aquarius | 0.316 |
| EN4 | 0.351 |
| SIO | 0.430 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bingham, F.M.; Brodnitz, S.; Yu, L. Sea Surface Salinity Seasonal Variability in the Tropics from Satellites, Gridded In Situ Products and Mooring Observations. Remote Sens. 2021, 13, 110. https://doi.org/10.3390/rs13010110
Bingham FM, Brodnitz S, Yu L. Sea Surface Salinity Seasonal Variability in the Tropics from Satellites, Gridded In Situ Products and Mooring Observations. Remote Sensing. 2021; 13(1):110. https://doi.org/10.3390/rs13010110
Chicago/Turabian StyleBingham, Frederick M., Susannah Brodnitz, and Lisan Yu. 2021. "Sea Surface Salinity Seasonal Variability in the Tropics from Satellites, Gridded In Situ Products and Mooring Observations" Remote Sensing 13, no. 1: 110. https://doi.org/10.3390/rs13010110
APA StyleBingham, F. M., Brodnitz, S., & Yu, L. (2021). Sea Surface Salinity Seasonal Variability in the Tropics from Satellites, Gridded In Situ Products and Mooring Observations. Remote Sensing, 13(1), 110. https://doi.org/10.3390/rs13010110