Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery
Abstract
:1. Introduction
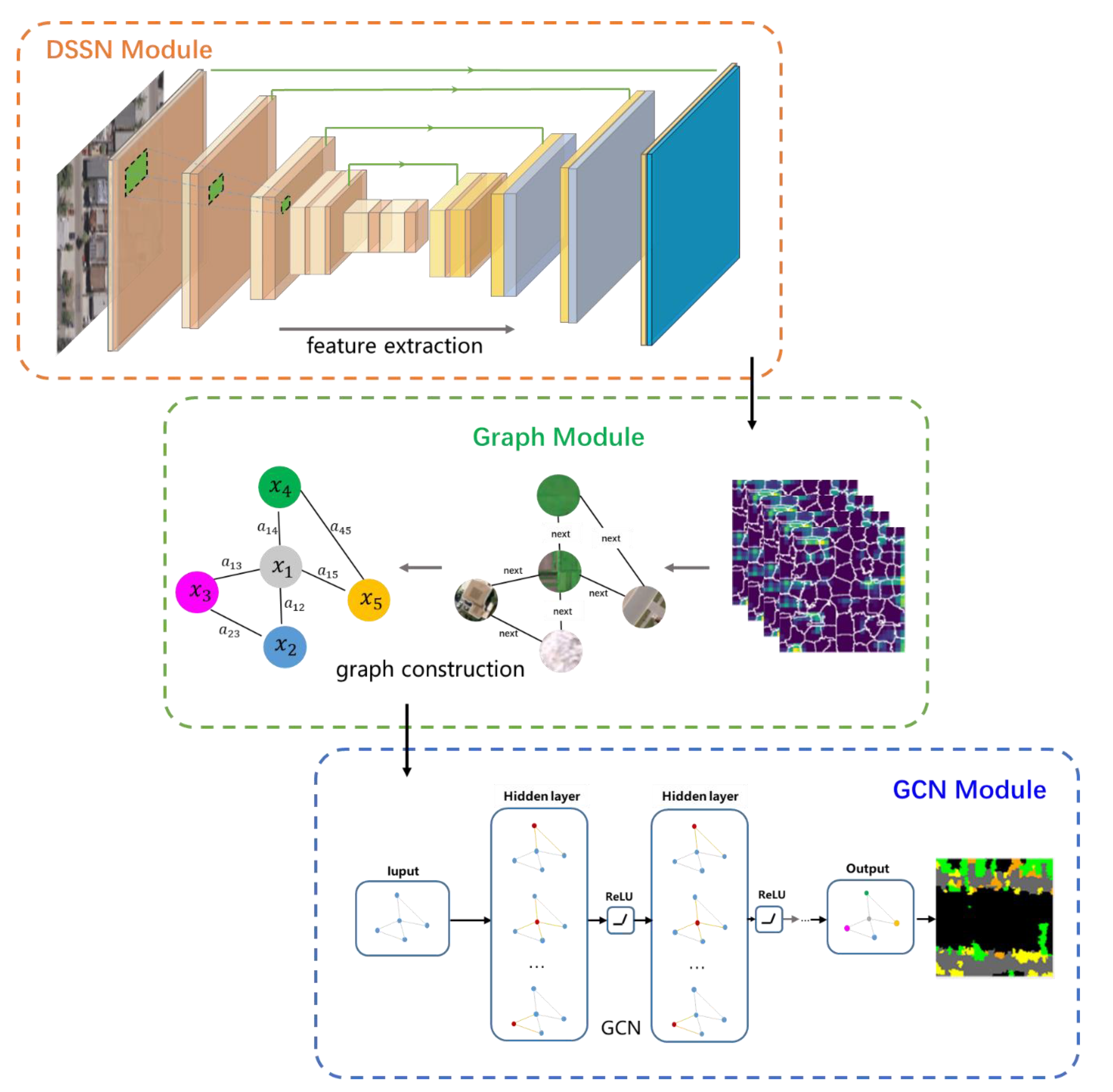
2. Materials and Methods
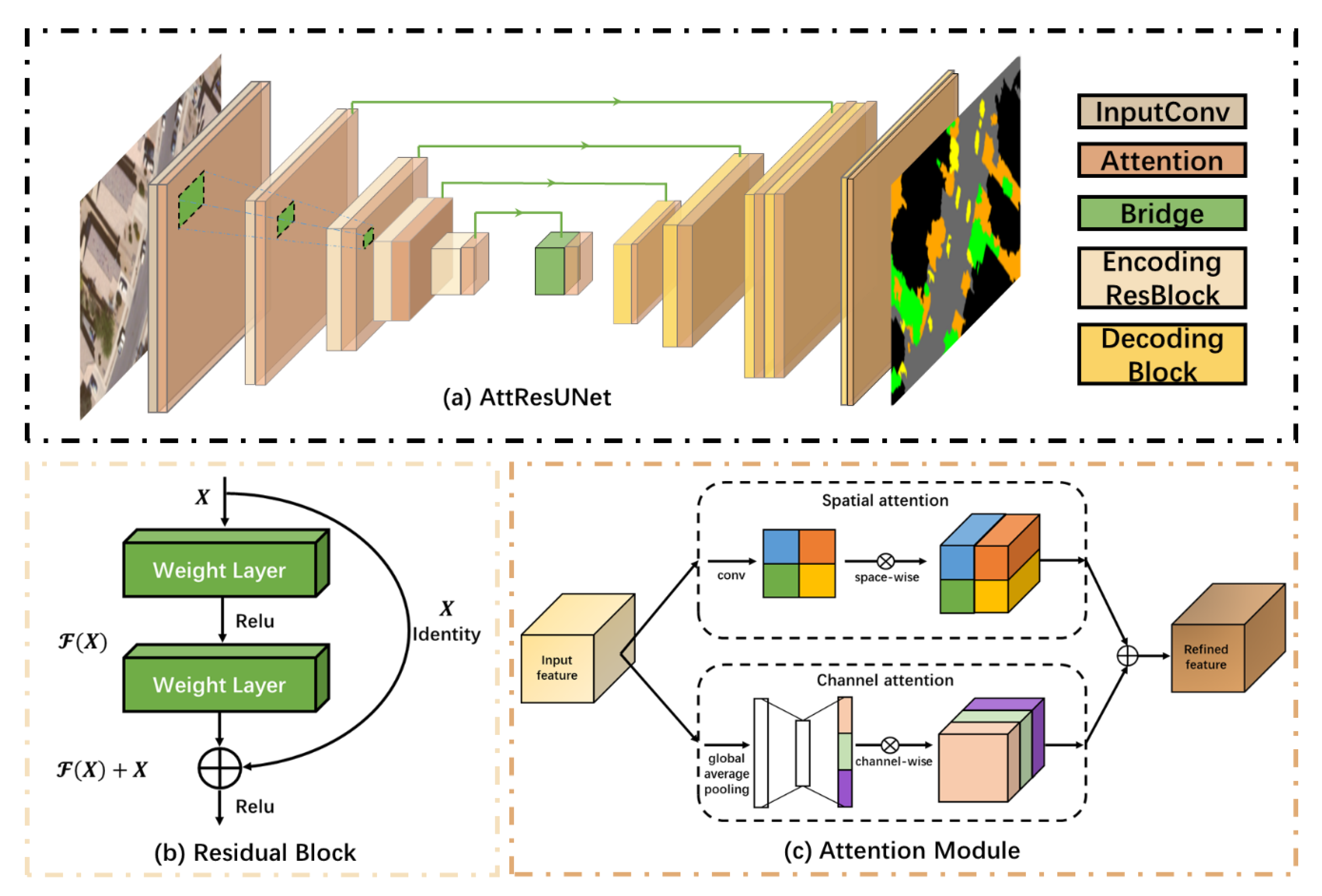
2.1. The Proposed DSSN: AttResUNet
2.2. Feature Extraction Based on DSSN
2.3. Graph Construction
2.4. Node Classification via GCN
| Algorithm 1. Combining DSSN and GCN for Semantic Segmentation of Remote Sensing Imagery |
| Input: the remote sensing image dataset ; the number of superpixels . 1. Train DSSN with samples from . 2. Use the DSSN to extract high-level features . 3. Construct the graph nodes . Regions segmented by the unsupervised segmentation algorithm are used as graph nodes . Use features to semantically initialize the intrinsic content of the graph nodes, represented as . 4. Construct the graph edges . Take the first-order adjacency relationships (with common edge) between the graph nodes as the graph edges and calculate the strength of the edges. 5. After the training of the GCN, adopt the GCN to perform classification on the graph nodes. 6. Get the maps of semantic segmentation. Assign the category of each node to the pixels located in the node. Output: the maps of semantic segmentation. |
3. Experiments
3.1. Datasets and Evaluation Metrics
3.2. Implementation Details
3.3. Sensitivity Analysis of Critical Parameters
3.4. Comparison with the State-of-the-Art Method
3.4.1. Results on the UCM Dataset
3.4.2. Results on the DeepGlobe Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, J.; Anderson, D.; Chan, C.S. A Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Du, S.; Du, S.; Zhang, X. Incorporating Deep Features into GEOBIA Paradigm for Remote Sensing Imagery Classification: A Patch-Based Approach. Remote Sens. 2020, 12, 3007. [Google Scholar] [CrossRef]
- Mountrakis, G.; Li, J.; Lu, X.; Hellwich, O. Deep learning for remotely sensed data. J. Photogramm. Remote Sens. 2018, 145, 1–2. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y. Deep learning in remote sensing applications: A meta-analysis and review. J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Zhang, Y.; Tao, C.; Xiao, R.; Tan, Y. Accurate cloud detection in high-resolution remote sensing imagery by weakly supervised deep learning. Remote Sens. Environ. 2020, 250, 112045. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Yuille, A.L. Deep networks under scene-level supervision for multi-class geospatial object detection from remote sensing images. J. Photogramm. Remote Sens. 2018, 146, 182–196. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing. IEEE Geosci. Remote Sens. Lett. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chao, T.; Yihua, T.; Ke, S.; Jinwen, T. Unsupervised multilayer feature learning for satellite image scene classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 157–161. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Zhang, Y. Image retrieval from remote sensing big data: A survey. Inf. Fusion. 2021, 67, 94–115. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhu, Z. Error-tolerant deep learning for remote sensing image scene classification. IEEE Trans. Cybern. 2020, in press. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, Y.; Huang, X.; Ma, J. Learning source-invariant deep hashing convolutional neural networks for cross-source remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6521–6536. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Huang, X.; Zhu, H.; Ma, J. Large-scale remote sensing image retrieval by deep hashing neural networks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 950–965. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Basaeed, E.; Bhaskar, H.; Al-Mualla, M. Supervised remote sensing image segmentation using boosted convolutional neural networks. Knowl. Based Syst. 2016, 99, 19–27. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolutional network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1520–1528. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 40, 834–848. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Chen, L.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Roy, A.G.; Navab, N.; Wachinger, C. Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M. Attention U-Net: Learning Where to Look for the Pancreas. In Proceedings of the International Conference on Medical Imaging with Deep Learning, Amsterdam, The Netherlands, 4–6 July 2018. [Google Scholar]
- Li, H.; Qiu, K.; Chen, L.; Mei, X.; Hong, L.; Tao, C. SCAttNet: Semantic Segmentation Network with Spatial and Channel Attention Mechanism for High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wurm, M.; Stark, T.; Zhu, X.X.; Weigand, M.; Taubenbock, H. Semantic segmentation of slums in satellite images using transfer learning on fully convolutional neural networks. J. Photogramm. Remote Sens. 2019, 150, 59–69. [Google Scholar] [CrossRef]
- Sherrah, J. Fully Convolutional Networks for Dense Semantic Labelling of High-Resolution Aerial Imagery. arXiv 2016, arXiv:1606.02585. [Google Scholar]
- Marmanis, D.; Wegner, J.D.; Galliani, S.; Schindler, K.; Datcu, M.; Stilla, U. Semantic segmentation of aerial images with an ensemble of CNSS. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Fully Convolutional Neural Networks for Remote Sensing Image Classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5071–5074. [Google Scholar]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic segmentation of small objects and modeling of uncertainty in urban remote sensing images using deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Wang, C.; Li, L. Multi-Scale Residual Deep Network for Semantic Segmentation of Buildings with Regularizer of Shape Representation. Remote Sens. 2020, 12, 2932. [Google Scholar] [CrossRef]
- Audebert, N.; Saux, B.L.; Lefèvre, S. Semantic Segmentation of Earth Observation Data Using Multimodal and Multi-Scale Deep Networks. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 180–196. [Google Scholar]
- Zhang, M.; Hu, X.; Zhao, L.; Lv, Y.; Luo, M.; Pang, S. Learning dual multi-scale manifold ranking for semantic segmentation of high resolution images. Remote Sens. 2017, 9, 500. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Gao, L.; Andrea, M.; Zhang, B.; Fan, Y.; Paolo, G. Semantic Labeling of High Resolution Aerial Imagery and LiDAR Data with Fine Segmentation Network. Remote Sens. 2018, 10, 743. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Fu, K.; Gao, X.; Yan, M.; Zhang, W.; Zhang, Y.; Sun, X. Effective fusion of multi-modal data with group convolutions for semantic segmentation of aerial imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 3911–3914. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.; Shenglin, L.; Dehui, X.; Peizhang, F.; Mingsheng, L. Remote Sensing Image Semantic Segmentation Based on Edge Information Guidance. Remote Sens. 2020, 12, 1501. [Google Scholar]
- Alirezaie, M.; Längkvist, M.; Sioutis, M. Semantic referee: A neural-symbolic framework for enhancing geospatial semantic segmentation. Semant. Web. 2019, 10, 863–880. [Google Scholar] [CrossRef] [Green Version]
- Yong, L.; Wang, R.; Shan, S.; Chen, X. Structure inference net: Object detection using scene-level context and instance-level relationships. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6985–6994. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, Canada, 31 July–4 August 2005. [Google Scholar]
- Kipf, T.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the international conference on learning representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Li, G.; Müller, M.; Thabet, A.; Ghanem, B. DeepGCNs: Can GCNs Go as Deep as CNNs? In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lu, Y.; Chen, Y.; Zhao, D.; Chen, J. Graph-FCN for image semantic segmentation. arXiv 2020, arXiv:2001.00335. [Google Scholar]
- Li, Y.; Chen, R.; Zhang, Y. A CNN-GCN framework for multi-label aerial image scene classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Hawaii, HI, USA, 19–24 July 2020. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Shao, Z.; Yang, K.; Zhou, W.; Hu, B. Performance evaluation of single-label and multi-label remote sensing image retrieval using a dense labeling dataset. Remote Sens. 2018, 10, 964. [Google Scholar] [CrossRef] [Green Version]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raska, R. Deepglobe 2018: A challenge to parse the earth through satellite images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 172–17209. [Google Scholar]
- Arvor, D.; Belgiu, M.; Falomir, Z.; Mougenot, I.; Durieux, L. Ontologies to interpret remote sensing images: Why do we need them? Gisci. Remote Sens. 2019, 56, 911–939. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Li, H.; Yan, L. An Object-Based Semantic Classification Method for High Resolution Remote Sensing Imagery Using Ontology. Remote Sens. 2017, 9, 329. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.O.; Villena-Martinez, V.; Garcia-Rodriguez, J. A Review on Deep Learning Techniques Applied to Semantic Segmentation. arXiv 2017, arXiv:1704.06857v1. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K. SLIC Superpixels Compared to State-of-the-art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed] [Green Version]










| UCM | Vegetation | Pavement | Ground | Building | Water | Car | Ship | Airplane |
|---|---|---|---|---|---|---|---|---|
| all | 28.59 | 27.38 | 17.63 | 13.65 | 7.87 | 2.88 | 1.62 | 0.36 |
| train | 29.23 | 27.17 | 17.37 | 13.58 | 7.84 | 2.84 | 1.61 | 0.35 |
| validation | 25.65 | 30.62 | 16.71 | 13.38 | 8.61 | 2.63 | 1.80 | 0.60 |
| test | 26.43 | 25.77 | 20.66 | 14.51 | 7.39 | 3.47 | 1.55 | 0.21 |
| DeepGlobe | Agriculture | Urban | Forest | Rangeland | Barren | Water | Unknown |
|---|---|---|---|---|---|---|---|
| all | 57.88 | 10.80 | 11.11 | 8.41 | 8.43 | 3.33 | 0.05 |
| train | 58.42 | 10.93 | 9.98 | 8.51 | 8.80 | 3.31 | 0.06 |
| validation | 56.16 | 7.50 | 19.27 | 7.78 | 5.04 | 4.23 | 0.01 |
| test | 55.29 | 13.05 | 11.99 | 8.26 | 8.82 | 2.59 | 0.01 |
| Layers | Ouput Size | |
|---|---|---|
| Input | input | H W 3 |
| InputConv | conv 7 7, stride 2 | H/2 W/2 64 |
| attention module | H/2 W/2 64 | |
| maxpool 3 3, stride 2 | H/4 W/4 64 | |
| Encoder1 | ResBlock1 | H/4 W/4 256 |
| attention module | H/4 W/4 256 | |
| Encoder2 | ResBlock2 | H/8 W/8 512 |
| attention module | H/8 W/8 512 | |
| Encoder3 | ResBlock3 | H/16 W/16 1024 |
| attention module | H/16 W/16 1024 | |
| Encoder4 | ResBlock4 | H/32 W/32 2048 |
| attention module | H/32 W/32 2048 | |
| Bridge | conv 3 3, stride 1 | H/32 W/32 192 |
| attention module | H/32 W/32 192 | |
| Decoder1 | deconv 4 4, stride 2 | H/16 W/16 128 |
| concatenation | H/16 W/16 (1024 + 128) | |
| conv 3 3, stride 1 | H/16 W/16 128 | |
| attention module | H/16 W/16 128 | |
| Decoder2 | deconv 4 4, stride 2 | H/8 W/8 96 |
| concatenation | H/8 W/8 (512 + 96) | |
| conv 33, stride 1 | H/8 W/8 96 | |
| attention module | H/8 W/8 96 | |
| Decoder3 | deconv 4 4, stride 2 | H/4 W/4 64 |
| concatenation | H/4 W/4 (256 + 64) | |
| conv 3 3, stride 1 | H/4 W/4 64 | |
| attention module | H/4 W/4 64 | |
| Decoder4 | deconv 44, stride 2 | H/2 W/2 48 |
| conv 3 3, stride 1 | H/2 W/2 48 | |
| attention module | H/2 W/2 48 | |
| Decoder5 | deconv 4 4, stride 2 | H W 32 |
| conv 3 3, stride 1 | H W 32 | |
| conv 1 1, stride 1 | H W C | |
| attention module | H W C | |
| Output | output | H W |
| Model | Vegetation | Ground | Pavement | Building | Water | Car | Ship | Airplane | Overall (OA) |
|---|---|---|---|---|---|---|---|---|---|
| U-Net | 81.21 | 73.13 | 90.03 | 65.10 | 89.58 | 72.61 | 87.52 | 0 | 79.72 |
| DSSN-GCN v1 | 84.22 | 80.76 | 85.69 | 71.85 | 89.16 | 69.79 | 80.25 | 0 | 81.71 |
| SegNet | 81.35 | 77.34 | 83.31 | 75.97 | 87.94 | 70.74 | 85.45 | 10.00 | 80.28 |
| DSSN-GCN v2 | 83.44 | 76.52 | 84.18 | 80.01 | 88.16 | 63.99 | 82.02 | 0 | 81.17 |
| DeepLab v3+ | 80.13 | 77.85 | 80.97 | 86.05 | 87.07 | 75.63 | 93.73 | 57.27 | 81.25 |
| DSSN-GCN v3 | 82.30 | 78.87 | 85.45 | 80.78 | 86.18 | 68.35 | 91.02 | 0 | 81.94 |
| AttResUNet | 85.77 | 75.62 | 86.44 | 86.76 | 92.30 | 82.04 | 87.60 | 58.43 | 84.31 |
| DSSN-GCN V4 | 86.67 | 77.06 | 88.08 | 86.80 | 93.57 | 75.72 | 81.29 | 33.78 | 85.00 |
| Model | Vegetation | Ground | Pavement | Building | Water | Car | Ship | Airplane | Overall (FWIoU) |
|---|---|---|---|---|---|---|---|---|---|
| U-Net | 70.20 | 61.14 | 68.71 | 56.73 | 79.65 | 62.02 | 68.45 | 0 | 66.23 |
| DSSN-GCN v1 | 71.33 | 64.03 | 73.08 | 62.80 | 81.32 | 59.65 | 68.29 | 0 | 69.17 |
| SegNet | 68.47 | 65.14 | 69.16 | 60.31 | 80.60 | 59.82 | 63.95 | 9.62 | 67.18 |
| DSSN-GCN v2 | 69.32 | 66.17 | 70.77 | 62.53 | 81.84 | 58.45 | 66.05 | 0 | 68.41 |
| DeepLab v3+ | 68.34 | 65.17 | 71.77 | 65.54 | 81.93 | 61.54 | 58.14 | 37.62 | 68.71 |
| DSSN-GCN v3 | 69.33 | 65.64 | 72.87 | 67.21 | 82.25 | 61.25 | 59.67 | 0 | 69.55 |
| AttResUNet | 72.42 | 65.72 | 77.11 | 71.02 | 86.01 | 70.67 | 76.09 | 49.53 | 72.99 |
| DSSN-GCN V4 | 73.47 | 67.03 | 77.87 | 73.24 | 87.36 | 68.18 | 72.87 | 33.07 | 73.99 |
| Model | Urban | Agriculture | Rangeland | Forest | Water | Barren | Unknown | Overall (OA) |
|---|---|---|---|---|---|---|---|---|
| U-Net | 71.67 | 87.03 | 47.06 | 90.65 | 73.74 | 63.96 | 0 | 79.77 |
| DSSN-GCN v1 | 85.43 | 88.87 | 50.53 | 87.91 | 75.38 | 55.64 | 0 | 81.86 |
| SegNet | 82.68 | 90.00 | 52.33 | 84.65 | 73.16 | 57.37 | 0 | 81.97 |
| DSSN-GCN v2 | 83.79 | 91.95 | 46.30 | 85.42 | 74.52 | 53.76 | 0 | 82.51 |
| DeepLab v3+ | 88.67 | 89.21 | 55.39 | 90.09 | 77.48 | 70.18 | 0 | 84.46 |
| DSSN-GCN v3 | 86.63 | 92.03 | 55.66 | 86.81 | 76.12 | 66.98 | 0 | 85.07 |
| AttResUNet | 84.56 | 91.37 | 56.35 | 89.64 | 81.71 | 75.16 | 0 | 85.70 |
| DSSN-GCN V4 | 84.60 | 91.16 | 56.61 | 89.95 | 82.09 | 76.90 | 0 | 85.81 |
| Model | Urban | Agriculture | Rangeland | Forest | Water | Barren | Unknown | Overall (FWIoU) |
|---|---|---|---|---|---|---|---|---|
| U-Net | 65.61 | 80.65 | 28.02 | 69.39 | 59.08 | 41.67 | 0 | 68.99 |
| DSSN-GCN v1 | 72.72 | 81.91 | 29.49 | 74.16 | 59.41 | 43.94 | 0 | 71.52 |
| SegNet | 72.57 | 81.76 | 29.89 | 75.53 | 61.64 | 44.66 | 0 | 71.74 |
| DSSN-GCN v2 | 73.34 | 82.15 | 28.74 | 75.94 | 62.69 | 43.86 | 0 | 71.96 |
| DeepLab v3+ | 74.53 | 83.23 | 37.66 | 79.52 | 60.89 | 52.82 | 0 | 74.62 |
| DSSN-GCN v3 | 75.58 | 84.17 | 37.92 | 79.40 | 61.67 | 53.28 | 0 | 75.35 |
| AttResUNet | 75.32 | 84.71 | 38.69 | 79.18 | 69.53 | 58.34 | 0 | 76.30 |
| DSSN-GCN V4 | 75.60 | 84.77 | 39.09 | 79.29 | 69.48 | 58.95 | 0 | 76.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, S.; Li, Y. Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery. Remote Sens. 2021, 13, 119. https://doi.org/10.3390/rs13010119
Ouyang S, Li Y. Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery. Remote Sensing. 2021; 13(1):119. https://doi.org/10.3390/rs13010119
Chicago/Turabian StyleOuyang, Song, and Yansheng Li. 2021. "Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery" Remote Sensing 13, no. 1: 119. https://doi.org/10.3390/rs13010119
APA StyleOuyang, S., & Li, Y. (2021). Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery. Remote Sensing, 13(1), 119. https://doi.org/10.3390/rs13010119






