Deriving Tree Size Distributions of Tropical Forests from Lidar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
- (a)
- h = (57.4 × d)/(0.43 + d),
- (b)
- andcr = 9.08 × d0.68
- (c)
- vertical tree crown length cl (m) is linearly related to the tree height by [23]cl = 0.4 × h.
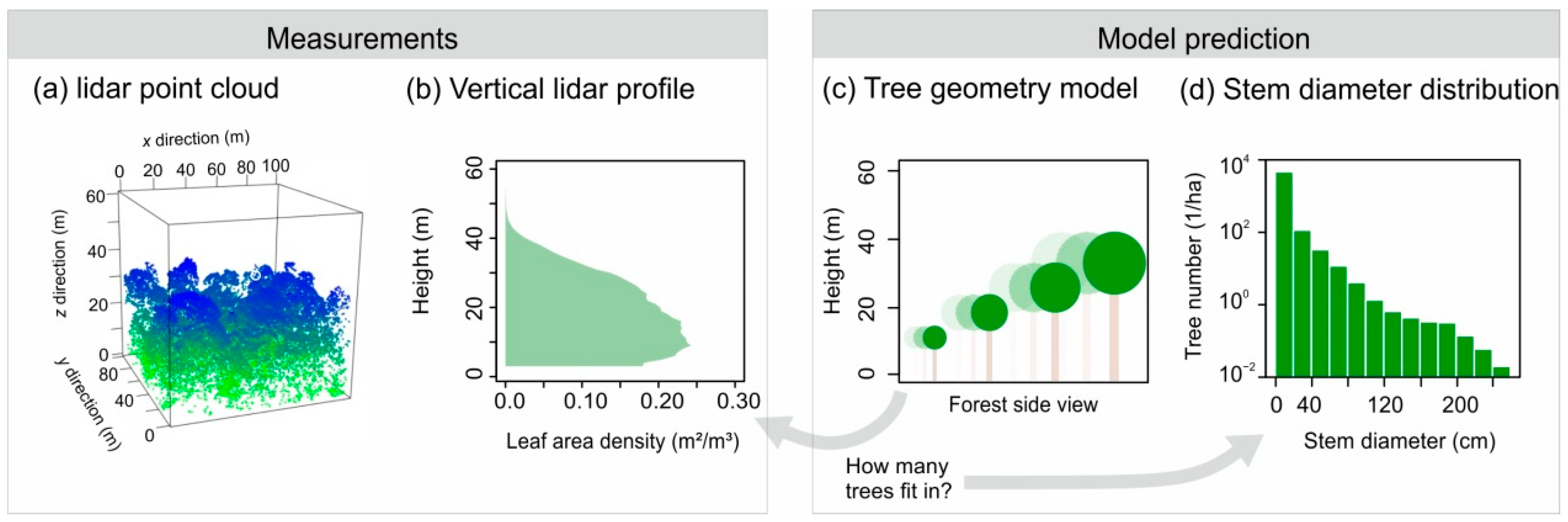
2.2. Derivation of Leaf Area Profiles from lidar
2.3. ‘Leaf–Tree Matrix’ of the Tree Geometry Model
2.4. Linear Equation Solving to Derive Forest Structure from lidar Profiles
2.5. Analysis and Statistics of Results
3. Results
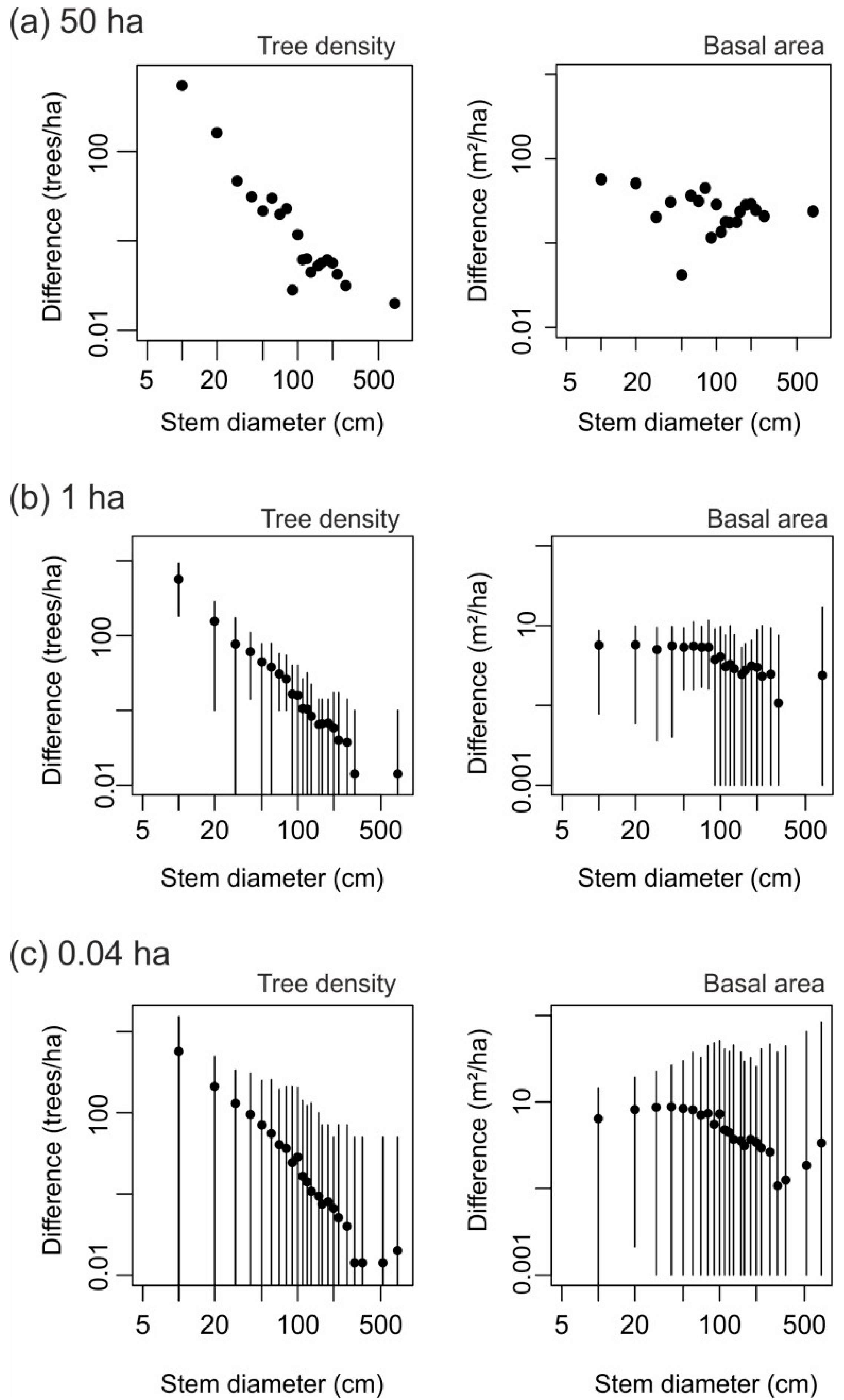
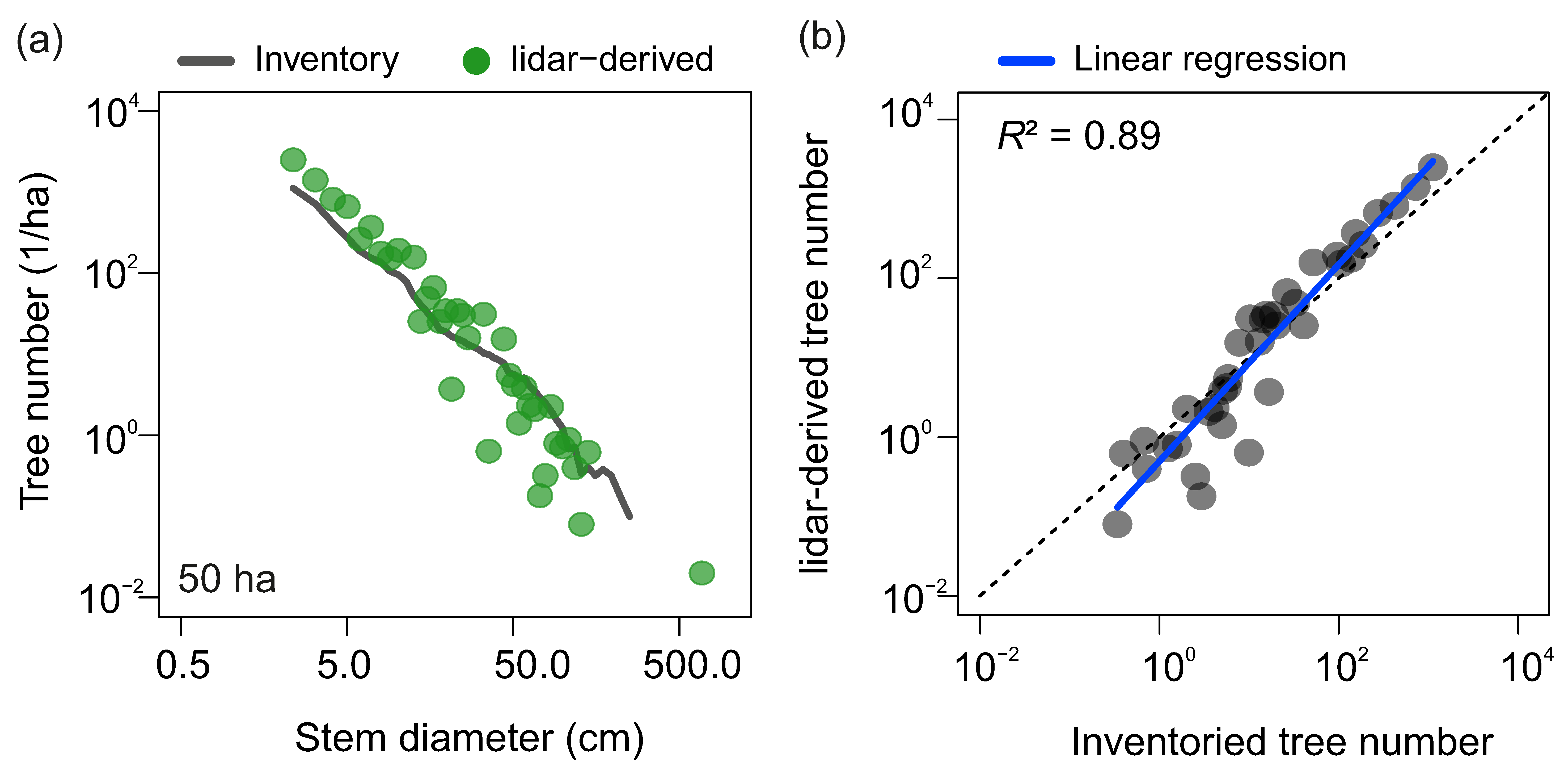
3.1. Stem Diameter Distribution Derived at the 50-ha Scale
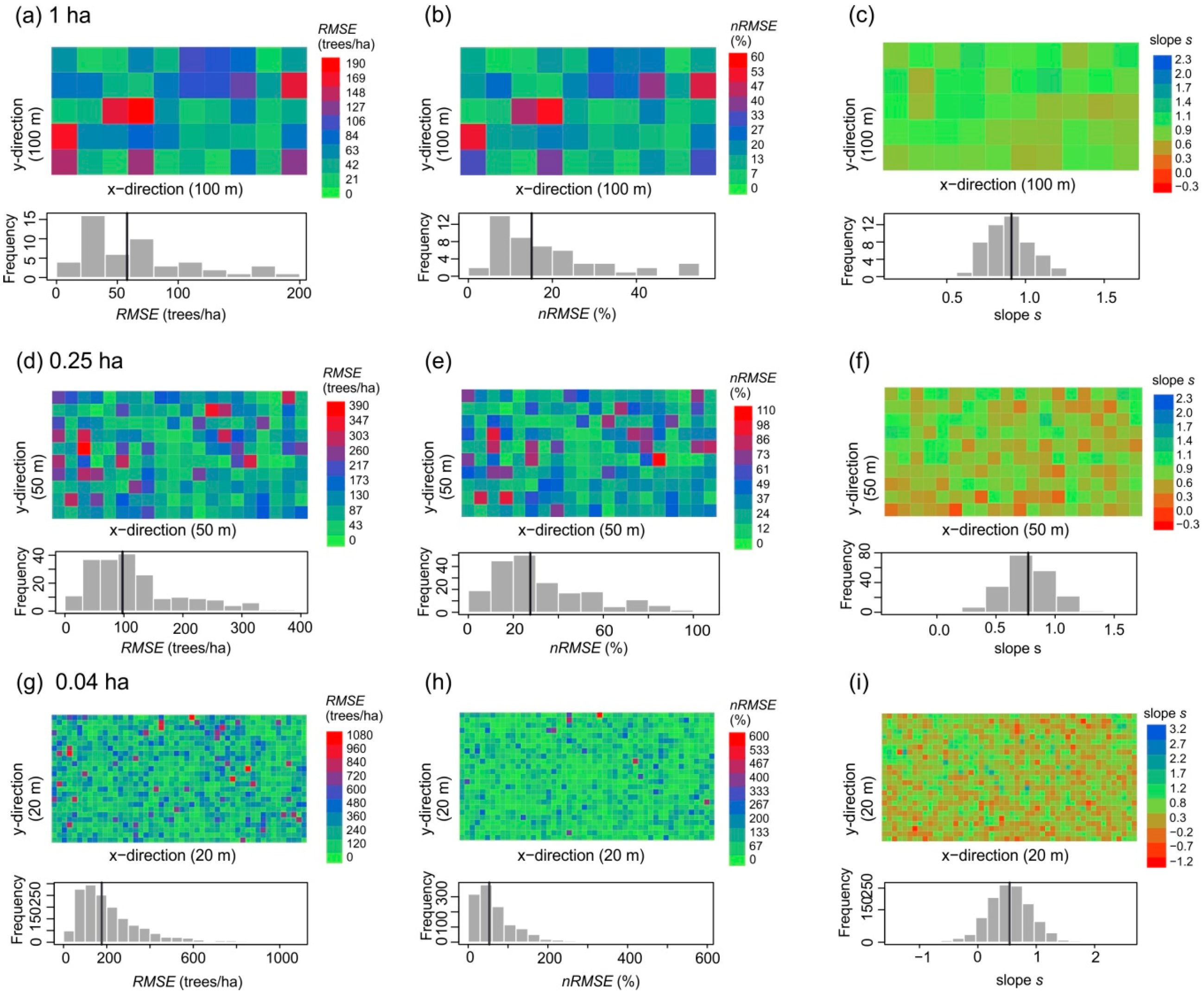
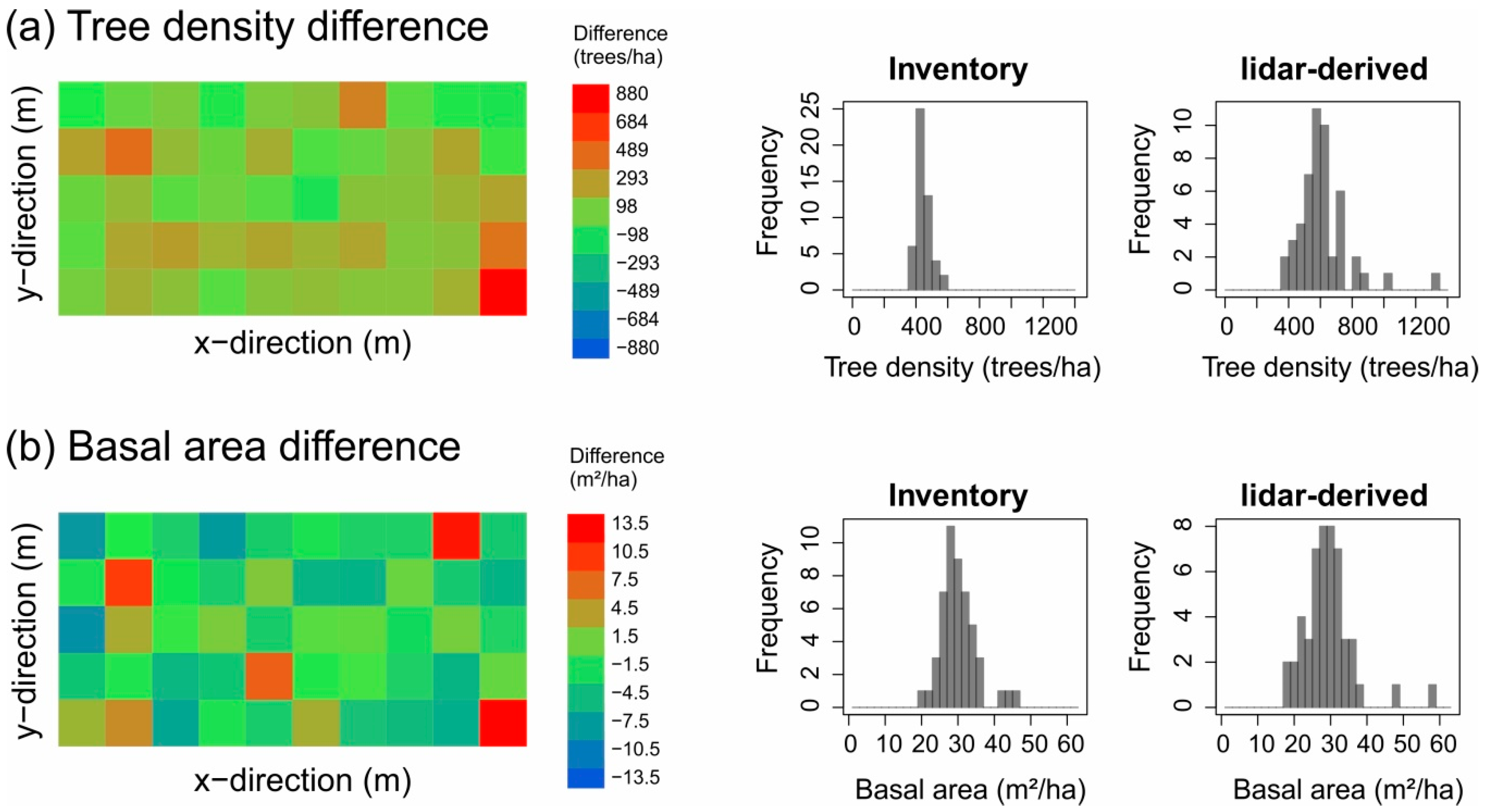
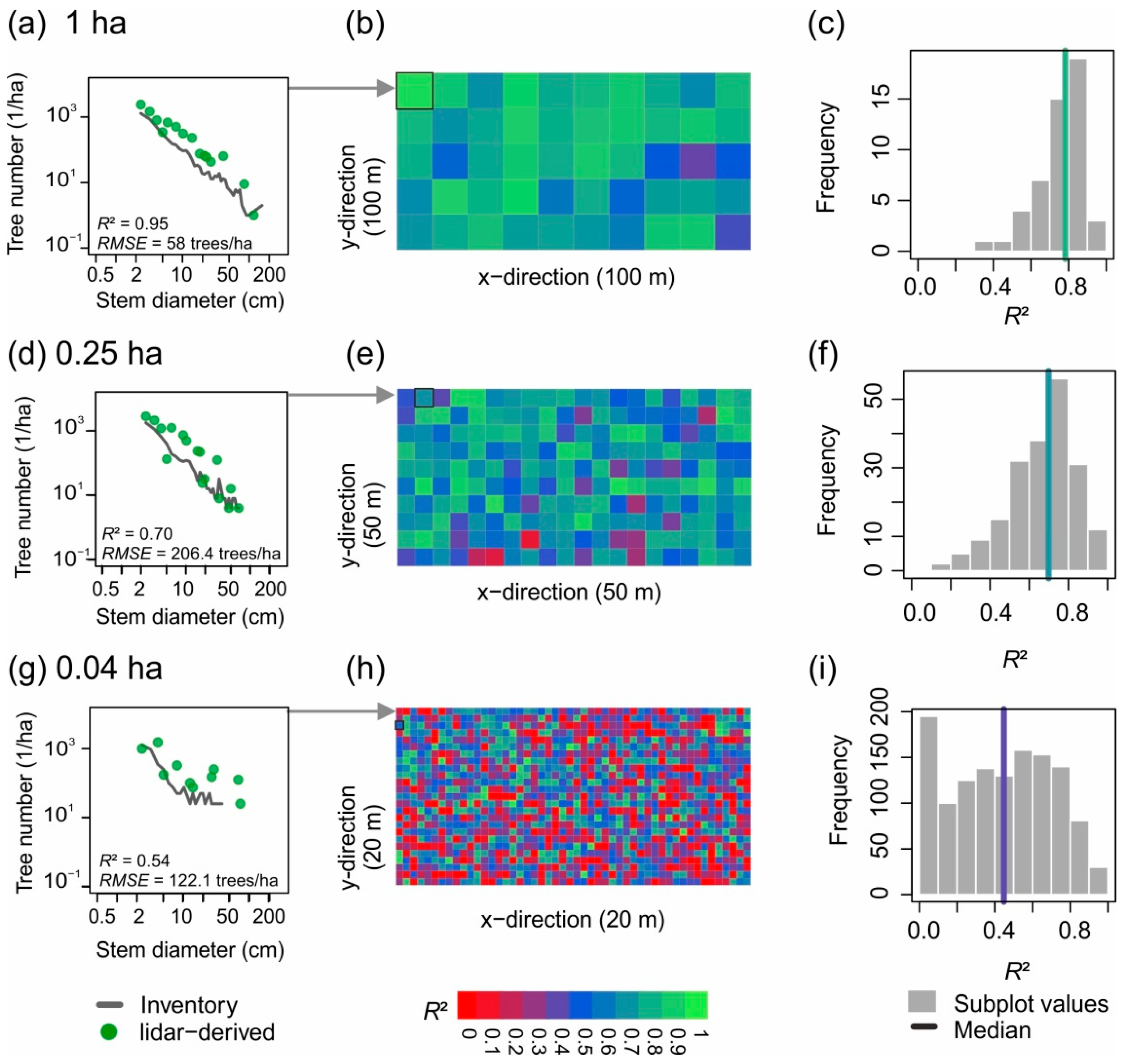
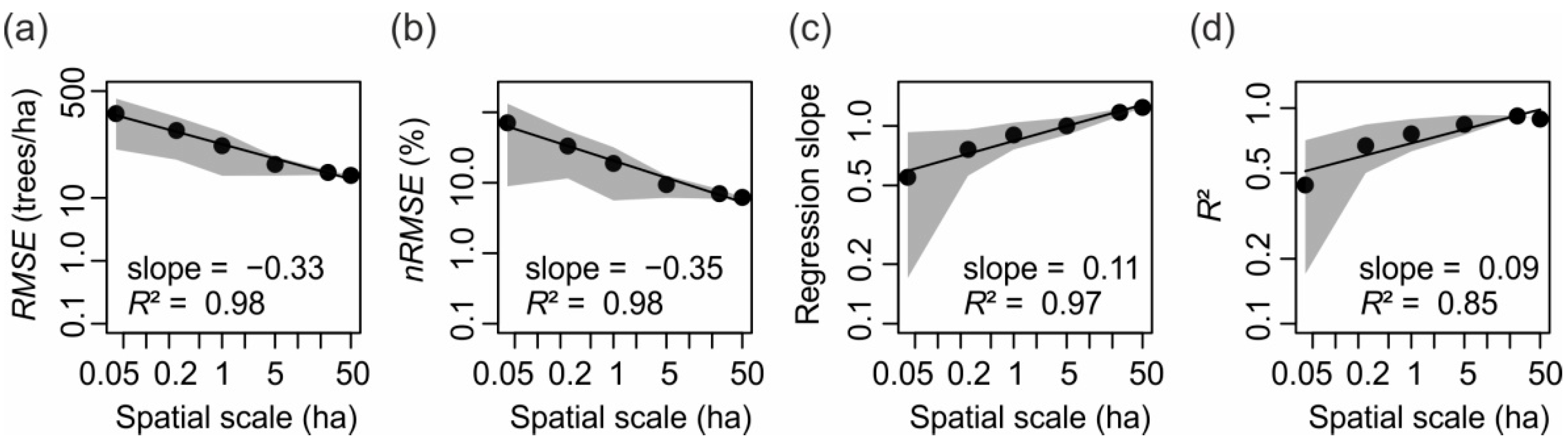
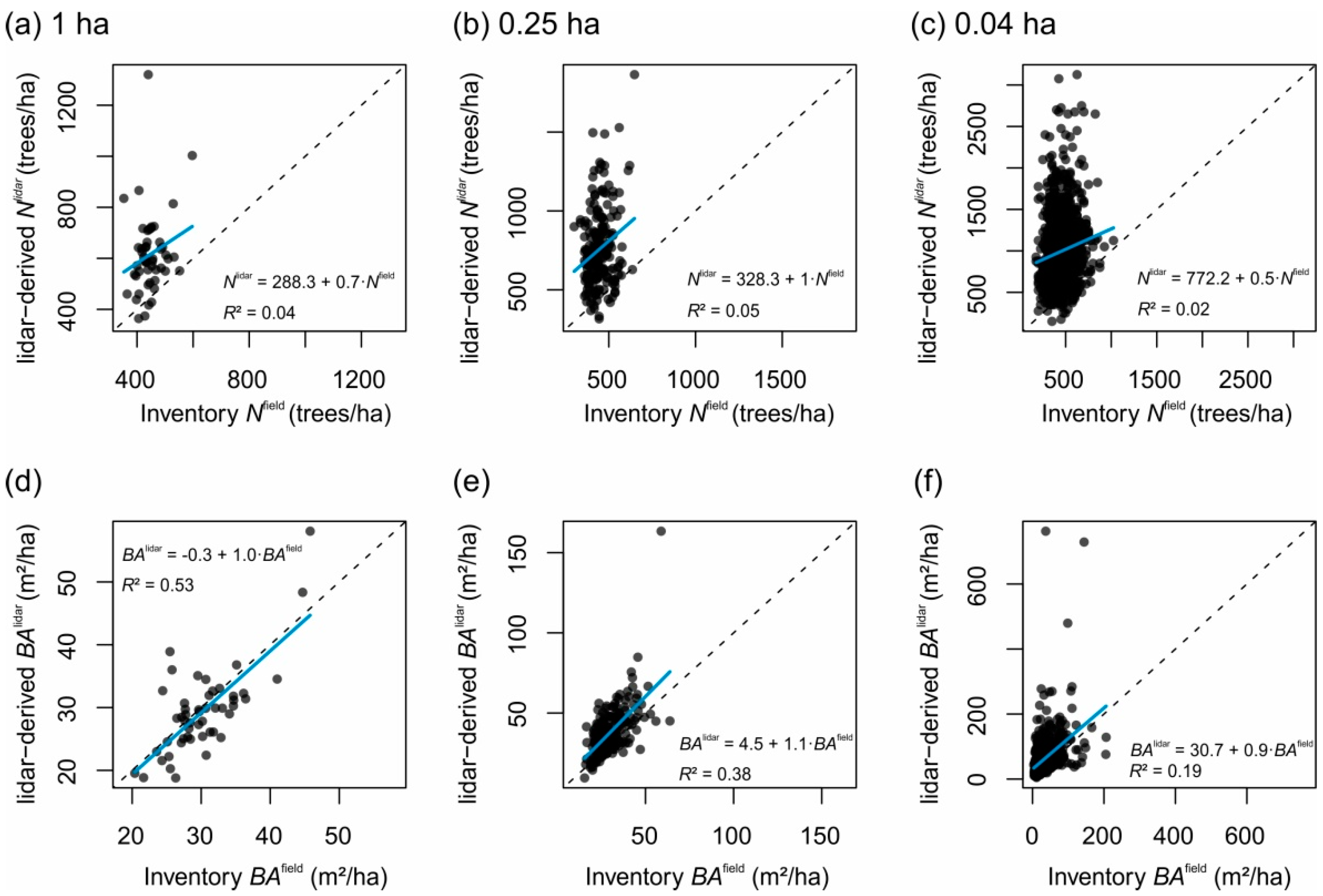
3.2. Small-Scale Derivations of Stem Diameter Distributions
4. Discussion
4.1. Strengths and Limitations of the Presented Approach
4.2. Future Applications and Challenges
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Method | Direct Calculation | Numerical Backward Solving |
|---|---|---|
| Regression slope | 1.22 | 1.24 |
| Coefficient of determination R² | 0.88 | 0.89 |
| Number of stem classes with negative predictions (%) | 26.9 | 0 |
| RMSE (trees/ha) | 29.6 | 22.8 |
| nRMSE (%) | 8.1 | 6.2 |
| Plot Size (ha) | 25 | 5 | |
|---|---|---|---|
| Side length (m) in x-direction | 500 | 200 | |
| Side length (m) in y-direction | 500 | 250 | |
| Number of plots | 2 | 10 | |
| Overall quality | Regression slope | 1.17 ± 0.05 (1.14, 1.21) | 1.0 ± 0.1 (0.8, 1.1) |
| R² | 0.92 ± 0.005 (0.91, 0.92) | 0.84 ± 0.09 (0.65, 0.94) | |
| RMSE (trees/ha) | 25.4 ± 2.3 (23.8, 27.0) | 34.1 ± 11.5 (17.1, 50.8) | |
| nRMSE (%) | 7.0 ± 1.1 (6.2, 7.7) | 9.4 ± 3.3 (4.9, 14.1) | |
| RMSE per size group | Small trees 1 | 596.2 ± 192.2 (460.3, 732.1) | 622.6 ± 240.2 (402.2, 1191.5) |
| Mid-sized trees 2 | 36.0 ± 1.4 (35.0, 37.0) | 45.9 ± 7.3 (36.8, 55.0) | |
| Large trees 3 | 2.1 ± 0.6 (1.6, 2.5) | 3.3 ± 1.4 (1.5, 5.1) | |
| Tree density 4 (trees/ha) | Inventory-based | 447.3 ± 3.0 (445.2, 449.4) | 447.3 ± 25.1 (420.0, 489.4) |
| lidar-derived | 562.3 ± 29.4 (541.5, 583.1) | 561.4 ± 65.4 (476.2, 715.4) | |
| bias | −115.0 | −114.1 | |
| RMSE | 116.5 | 128.3 | |
| nRMSE (%) | 26.1 | 28.7 | |
| Basal area 4 (m²/ha) | Inventory-based | 30.1 ± 2.4 (28.4, 31.8) | 30.1 ± 2.8 (25.5, 34.7) |
| lidar-derived | 24.3 ± 1.3 (23.4, 25.2) | 25.3 ± 3.4 (19.6, 31.8) | |
| bias | 5.8 | 4.7 | |
| RMSE | 5.8 | 4.9 | |
| nRMSE (%) | 19.4 | 16.4 | |
| Category | Measure | Spatial Scale | ||
|---|---|---|---|---|
| 1 ha | 0.25 ha | 0.04 ha | ||
| Statistical measures | Regression slope | 0.63 | 0.54 | 0.73 |
| RMSE | 0.09 | −0.15 | −0.20 | |
| nRMSE (%) | 0.05 | −0.19 | −0.18 | |
| lidar data | Profile height—median | −0.06 | −0.09 | −0.06 |
| Profile height—maximum | −0.03 | −0.10 | −0.05 | |
| Profile height—variance | −0.05 | −0.09 | −0.05 | |
| Leaf area density—median | −0.13 | −0.03 | −0.01 | |
| Leaf area density—maximum | 0.17 | −0.03 | −0.03 | |
| Leaf area density—variance | 0.21 | 0 | −0.04 | |
| WMPH | −0.31 | −0.25 | −0.19 | |
| WVPH | −0.11 | 0.03 | 0.08 | |
| Number of lidar returns | −0.12 | 0.09 | −0.04 | |
| Forest inventory | Basal area (m²/ha) | −0.15 | −0.14 | −0.09 |
| (for stem diameter d ≥ 10 cm) | −0.15 | −0.16 | −0.10 | |
| Tree density (ha−1) | 0.12 | 0.27 | 0.21 | |
| (for stem diameter d ≥ 10 cm) | 0.17 | −0.02 | −0.06 | |
| Standard deviation of tree height (m) | −0.16 | −0.28 | −0.19 | |
| Median tree height (m) | 0.09 | −0.10 | −0.09 | |
Appendix B
Numerical Backward Calculation to Solve the Linear Equation System (Equation (10))
- If the leaf area Li in height layer i is larger than the corresponding entry fii in the leaf–tree matrix, we calculate the number of stems in the corresponding stem diameter class by Ni = ⎣Li/(fii)⎦.
- 1a.
- If tolerance is not yet reached, i.e., (Li – N × fii) > ε × Li then Ni = Ni + 1.
- 1b.
- The leaf area corresponding to the calculated number of trees Ni in the respective stem diameter class i is then subtracted from all height layers j (below layer i) in which those trees also reach in with their crown: Lj = Lj − Ni × fij.
- If the leaf area Li in height layer i is lower than the corresponding entry fii in the leaf–tree matrix F, we set the number of stems in stem diameter class i to zero (i.e., Ni = 0).
References
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, O.T. Biodiversity change and ecosystem function in tropical forests. Basic Appl. Ecol. 2009, 10, 97–102. [Google Scholar] [CrossRef]
- Lewis, S.L.; Edwards, D.P.; Galbraith, D. Increasing human dominance of tropical forests. Science 2015, 349, 827–832. [Google Scholar] [CrossRef]
- Trumbore, S.; Brando, P.; Hartmann, H. Forest health and global change. Science 2015, 349, 814–818. [Google Scholar] [CrossRef] [Green Version]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Mitchard, E.T. The tropical forest carbon cycle and climate change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef]
- Taubert, F.; Fischer, R.; Groeneveld, J.; Lehmann, S.; Müller, M.S.; Rödig, E.; Wiegand, T.; Huth, A. Global patterns of tropical forest fragmentation. Nature 2018, 554, 519–522. [Google Scholar] [CrossRef]
- Curtis, P.G.; Slay, C.M.; Harris, N.L.; Tyukavina, A.; Hansen, M.C. Classifying drivers of global forest loss. Science 2018, 361, 1108–1111. [Google Scholar] [CrossRef]
- Chaplin-Kramer, R.; Ramler, I.; Sharp, R.; Haddad, N.M.; Gerber, J.S.; West, P.C.; Mandle, L.; Engstrom, P.; Baccini, A.; Sim, S.; et al. Degradation in carbon stocks near tropical forest edges. Nat. Commun. 2015, 6, 10185. [Google Scholar] [CrossRef] [PubMed]
- Brinck, K.; Fischer, R.; Groeneveld, J.; Lehmann, S.; Dantas De Paula, M.; Pütz, S.; Sexton, J.O.; Song, D.; Huth, A. High resolution analysis of tropical forest fragmentation and its impact on the global carbon cycle. Nat. Commun. 2017, 8, 14855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Wright, S.J.; Salim, K.A.; Zambrano, A.M.A.; Alonso, A.; Baltzer, J.L.; et al. CTFS-Forest GEO: A worldwide network monitoring forests in an era of global change. Glob. Chang. Biol. 2015, 21, 528–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frolking, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Cheng, X.; Gong, P.; Huang, H.; Li, Z.; Li, X. Earth science applications of ICESat/GLAS: A review. Int. J. Remote Sens. 2011, 32, 8837–8864. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef] [Green Version]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A pathfinder mission for global-scale monitoring of the environment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3307–3316. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Gascon, F.; Cadau, E.; Colin, O.; Hoersch, B.; Isola, C.; López Fernández, B.; Martimort, P. Copernicus Sentinel-2 mission: Products, algorithms and Cal/Val. In Proceedings of the SPIE 9218, Earth Observing Systems XIX, 92181E, San Diego, CA, USA, 26 September 2014. [Google Scholar]
- Justice, C.O.; Townsend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and products. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking lidar and forest modeling to assess biomass estimation across scales and disturbance states. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Cazcarra-Bes, V.; Huth, A. Structure metrics to generalize biomass estimation from lidar across forest types from different continents. Remote Sens. Environ. 2020, 237, 111597. [Google Scholar] [CrossRef]
- Magnussen, S.; Næsset, E.; Gobakken, T.; Frazer, G. A fine-scale model for area-based predictions of tree-size-related attributes derived from LiDAR canopy heights. Scand. J. For. Res. 2012, 27, 312–322. [Google Scholar] [CrossRef]
- Magnussen, S.; Renaud, J.P. Multidimensional scaling of first-return airborne laser echoes for prediction and model-assisted estimation of a distribution of tree stem diameters. Ann. For. Sci. 2016, 73, 1089–1098. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Duan, G.; Ye, Q.; Meng, X.; Luo, P.; Sharma, R.P.; Sun, H.; Wang, G.; Liu, Q. Prediction of Individual Tree Diameter Using a Nonlinear Mixed-Effects Modeling Approach and Airborne LiDAR Data. Remote Sens. 2020, 12, 1066. [Google Scholar] [CrossRef] [Green Version]
- Maltamo, M.; Gobakken, T. Predicting tree diameter distributions. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherlands, 2014; pp. 177–191. [Google Scholar]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Spriggs, R.A.; Coomes, D.A.; Jones, T.A.; Caspersen, J.P.; Vanderwel, M.C. An alternative approach to using LiDAR remote sensing data to predict stem diameter distributions across a temperate forest landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef] [Green Version]
- Antonarakis, A.S.; Munger, J.W.; Moorcroft, P.R. Imaging spectroscopy-and lidar-derived estimates of canopy composition and structure to improve predictions of forest carbon fluxes and ecosystem dynamics. Geophys. Res. Lett. 2014, 41, 2535–2542. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Longo, M.; Clark, D.B. Tropical tree size–frequency distributions from airborne lidar. Ecol. Appl. 2020. [Google Scholar] [CrossRef] [PubMed]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A Local Projection-Based Approach to Individual Tree Detection and 3-D Crown Delineation in Multistoried Coniferous Forests Using High-Density Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1168–1182. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A comparative assessment of the performance of individual tree crowns delineation algorithms from ALS data in tropical forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar. Remote Sens. Environ. 2011, 115, 2965–2974. [Google Scholar] [CrossRef]
- Condit, R.; Perez, R.; Aguilar, S.; Lao, S.; Foster, R.; Hubbell, S. Complete data from the Barro Colorado 50-ha plot: 423617 trees, 35 years. Dryad 2019. [Google Scholar] [CrossRef]
- Condit, R.; Perez, R.; Aguilar, S.; Lao, S.; Foster, R.; Hubbell, S. BCI 50-ha plot taxonomy. Dryad 2019. [Google Scholar] [CrossRef]
- Condit, R. Tropical Forest Census Plots; Springer: Berlin, Germany; R. G. Landes Company: Georgetown, TX, USA, 1998. [Google Scholar]
- Hubbell, S.P.; Foster, R.B.; O’Brien, S.T.; Harms, K.E.; Condit, R.; Wechsler, B.; Wright, S.J.; Loo de Lao, S. Light gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1999, 283, 554557. [Google Scholar] [CrossRef] [Green Version]
- ForestGeo Global Earth Observatory Network. Available online: https://forestgeo.si.edu/explore-data/barro-colorado-island-termsconditionsrequest-forms (accessed on 18 December 2020).
- Dryad. Available online: https://datadryad.org/stash/dataset/doi:10.15146/5xcp-0d46 (accessed on 18 December 2020).
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Bohlman, S.; O’Brien, S. Allometry, adult stature and regeneration requirement of 65 tree species on Barro Colorado Island, Panama. J. Trop. Ecol. 2006, 123–136. [Google Scholar] [CrossRef] [Green Version]
- Taubert, F.; Jahn, M.W.; Dobner, H.J.; Wiegand, T.; Huth, A. The structure of tropical forests and sphere packings. Proc. Natl. Acad. Sci. USA 2015, 112, 15125–15129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobo, E.; Dalling, J.W. Spatial scale and sampling resolution affect measures of gap disturbance in a lowland tropical forest: Implications for understanding forest regeneration and carbon storage. Proc. R. Soc. B Biol. Sci. 2014, 281, 20133218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campbell, G.S.; Norman, J. An Introduction to Environmental Biophysics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Strang, G. Introduction to linear algebra. Wellesley-Cambridge Press: Wellesley, MA, USA, 2016. [Google Scholar]
- Zenner, E.K. Development of tree size distributions in Douglas-fir forests under differing disturbance regimes. Ecol. Appl. 2005, 15, 701–714. [Google Scholar] [CrossRef]
- Purves, D.W.; Lichstein, J.W.; Pacala, S.W. Crown plasticity and competition for canopy space: A new spatially implicit model parameterized for 250 North American tree species. PLoS ONE 2007, 2, e870. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S.C.; Zhao, K. A voxel-based lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Martinez Cano, I.M.; Muller-Landau, H.C.; Wright, S.J.; Bohlman, S.A.; Pacala, S.W. Tropical tree height and crown allometries for the Barro Colorado Nature Monument, Panama: A comparison of alternative hierarchical models incorporating interspecific variation in relation to life history traits. Biogeosciences 2019, 16, 847–862. [Google Scholar] [CrossRef] [Green Version]
- Disney, M.; Burt, A.; Calders, K.; Schaaf, C.; Stovall, A. Innovations in Ground and Airborne Technologies as Reference and for Training and Validation: Terrestrial Laser Scanning (TLS). Surv. Geophys. 2019. [Google Scholar] [CrossRef] [Green Version]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Ma, X.; Migliavacca, M.; Wirth, C.; Bohn, F.J.; Huth, A.; Richter, R.; Mahecha, M.D. Monitoring Plant Functional Diversity Using the Reflectance and Echo from Space. Remote Sens. 2020, 12, 1248. [Google Scholar] [CrossRef] [Green Version]
- Hancock, S.; Armston, J.; Hofton, M.; Sun, X.; Tang, H.; Duncanson, L.I.; Kellner, J.R.; Dubayah, R. The GEDI simulator: A large-footprint waveform lidar simulator for calibration and validation of spaceborne missions. Earth Space Sci. 2019, 6, 294–310. [Google Scholar] [CrossRef]
- Blair, J.B.; Hofton, M.A. Modeling laser altimeter return waveforms over complex vegetation using high-resolution elevation data. Geophys. Res. Lett. 1999, 26, 2509–2512. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Swatantran, A.; Hofton, M.; Sheldon, S.; Clark, D.B.; Blair, B. Retrieval of vertical LAI profiles over tropical rain forests using waveform lidar at La Selva, Costa Rica. Remote Sens. Environ. 2012, 124, 242–250. [Google Scholar] [CrossRef]
- Stark, S.C.; Leitold, V.; Wu, J.L.; Hunter, M.O.; de Castilho, C.V.; Costa, F.R.C.; McMahon, S.M.; Parker, G.G.; Shimabukuro, M.T.; Lefsky, M.A.; et al. Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment. Ecol. Lett. 2012, 15, 1406–1414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harding, D.J.; Lefsky, M.A.; Parker, G.G.; Blair, J.B. Laser altimeter canopy height profiles: Methods and validation for closed-canopy, broadleaf forests. Remote Sens. Environ. 2001, 76, 283–297. [Google Scholar] [CrossRef]
- Detto, M.; Asner, G.P.; Muller-Landau, H.C.; Sonnentag, O. Spatial variability in tropical forest leaf area density from multireturn lidar and modeling. J. Geophys. Res. Biogeosci. 2015, 120, 294–309. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Horn, H.S. Foliage profile by vertical measurements. Ecology 1969, 50, 802–804. [Google Scholar] [CrossRef] [Green Version]
- Ni-Meister, W.; Jupp, D.L.; Dubayah, R. Modeling lidar waveforms in heterogeneous and discrete canopies. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1943–1958. [Google Scholar] [CrossRef] [Green Version]
- Adams, T.; Beets, P.; Parrish, C. Another dimension from LiDAR–Obtaining foliage density from full waveform data. Int. Conf. Lidar Appl. Assess. For. Ecosyst. 2011, 798. Available online: https://scholars.unh.edu/ccom/798 (accessed on 1 January 2021).
- Rödig, E.; Knapp, N.; Fischer, R.; Bohn, F.J.; Dubayah, R.; Tang, H.; Huth, A. From small-scale forest structure to Amazon-wide carbon estimates. Nat. Commun. 2019, 10, 5088. [Google Scholar] [CrossRef]
- Rammer, W.; Seidl, R. A scalable model of vegetation transitions using deep neural networks. Methods Ecol. Evol. 2019, 10, 879–890. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI lidar observations for forest structure mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Houghton, R.A.; Dos Santos Alvala, R.C.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Chang. Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]


| Data Source | Attribute | Unit | Calculations |
|---|---|---|---|
| lidar data | Profile height | m | Maximum, Median, Variance |
| Leaf area density | m²/m³ | Maximum, Median, Variance | |
| Number of lidar returns | 1/m2 | - | |
| profile height weighted by leaf area | m | Median (WMPH 1), Variance (WVPH 2) | |
| Forest inventory | Basal area 3,4 | m²/ha | Sum |
| Tree density 3,4 | 1/m2 | Sum | |
| Tree height 3 | m | Median, Standard deviation |
| Sensitivity Scenario | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Crown shape | Sphere | Cylinder | Ellipsoid | Ellipsoid |
| Height allometry | Asymptotic | Asymptotic | Asymptotic | Power law |
| Crown length | Crown radius | 0.4 × height | 0.4 × height | 0.4 × height |
| Crown leaf density | 0.44 m²/m³ | 0.44 m²/m³ | 1 m²/m³ | 0.44 m²/m³ |
| Regression slope | 1.22 | 1.29 | 1.21 | 1.1 |
| R² | 0.89 | 0.98 | 0.92 | 0.89 |
| RMSE (trees/ha) | 32.0 | 4.5 | 15.0 | 15.3 |
| nRMSE (%) | 8.8 | 1.2 | 4.1 | 3.8 |
| Plot Size (ha) | 50 | 1 | 0.25 | 0.04 | |
|---|---|---|---|---|---|
| Side length (m) in x-direction | 1000 | 100 | 50 | 20 | |
| Side length (m) in y-direction | 500 | 100 | 50 | 20 | |
| Number of plots | 1 | 50 | 200 | 1250 | |
| Overall quality | Regression slope | 1.24 | 0.9 ± 0.14 (0.66, 1.23) | 0.76 ± 0.2 (0.11, 1.3) | 0.55 ± 0.38 (−0.94, 2.17) |
| R² | 0.89 | 0.76 ± 0.13 (0.38, 0.95) | 0.67 ± 0.17 (0.13, 0.94) | 0.44 ± 0.27 (0.00005, 1) | |
| RMSE (trees/ha) | 22.8 | 67.6 ± 45.1 (15.2, 187.4) | 118.1 ± 77.6 (13.4, 385.6) | 219.2 ± 160.4 (17.7, 1074.6) | |
| nRMSE (%) | 6.2 | 18.8 ± 13.2 (4.2, 55.0) | 33.2 ± 21.7 (3.0, 105.7) | 70.9 ± 62.0 (3.2, 590.1) | |
| RMSE per size group (trees/ha) | Small trees 1 | 590.5 | 719.5 ± 379.6 (188.6, 1844.9) | 796.8 ± 492.6 (153.6, 3028.1) | 902.2 ± 751.6 (128.4, 5423.6) |
| Mid-sized trees 2 | 39.4 | 77.1 ± 30.5 (28.0, 175.3) | 112.9 ± 43.1 (39.9, 267.6) | 153.9 ± 73.9 (33.5, 606.7) | |
| Large trees 3 | 1.2 | 5.1 ± 2.5 (2.2, 15.9) | 9.1 ± 5.5 (2.4, 36.1) | 26.2 ± 21.2 (0, 230.3) | |
| Tree density 4 (trees/ha) | Inventory-based | 447.3 | 447.3 ± 46.1 (353, 597) | 447.3 ± 60.4 (300, 648) | 447.3 ± 115.7 (175, 1025) |
| lidar-derived | 516.7 | 615.5 ± 159.3 (364, 1320) | 758.9 ± 249.2 (316, 1864) | 992.6 ± 402.5 (150, 3125) | |
| bias | −69.4 | −168.2 | −311.6 | −545.3 | |
| RMSE | 69.4 | 228.4 | 394.4 | 677.8 | |
| nRMSE (%) | 15.5 | 51.1 | 88.2 | 151.5 | |
| Basal area 4 (m²/ha) | Inventory-based | 30.1 | 30.1 ± 5.1 (20.4, 45.8) | 30.1 ± 8.3 (15.5, 67.9) | 30.1 ± 20.9 (3.5, 206.1) |
| lidar-derived | 23.6 | 29.3 ± 6.9 (18.8, 58.1) | 38.1 ± 15.0 (9.5, 163.4) | 59.0 ± 45.0 (4.7, 762.5) | |
| bias | 6.5 | 0.8 | −8.0 | −28.9 | |
| RMSE | 6.5 | 4.7 | 14.3 | 49.8 | |
| nRMSE (%) | 21.6 | 15.7 | 47.4 | 165.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taubert, F.; Fischer, R.; Knapp, N.; Huth, A. Deriving Tree Size Distributions of Tropical Forests from Lidar. Remote Sens. 2021, 13, 131. https://doi.org/10.3390/rs13010131
Taubert F, Fischer R, Knapp N, Huth A. Deriving Tree Size Distributions of Tropical Forests from Lidar. Remote Sensing. 2021; 13(1):131. https://doi.org/10.3390/rs13010131
Chicago/Turabian StyleTaubert, Franziska, Rico Fischer, Nikolai Knapp, and Andreas Huth. 2021. "Deriving Tree Size Distributions of Tropical Forests from Lidar" Remote Sensing 13, no. 1: 131. https://doi.org/10.3390/rs13010131
APA StyleTaubert, F., Fischer, R., Knapp, N., & Huth, A. (2021). Deriving Tree Size Distributions of Tropical Forests from Lidar. Remote Sensing, 13(1), 131. https://doi.org/10.3390/rs13010131





