Estimation of Liquid Fraction of Wet Snow by Using 2-D Video Disdrometer and S-Band Weather Radar
Abstract
:1. Introduction
2. Data and Methods
2.1. Observational Instruments
2.2. Physical Variables of Particle
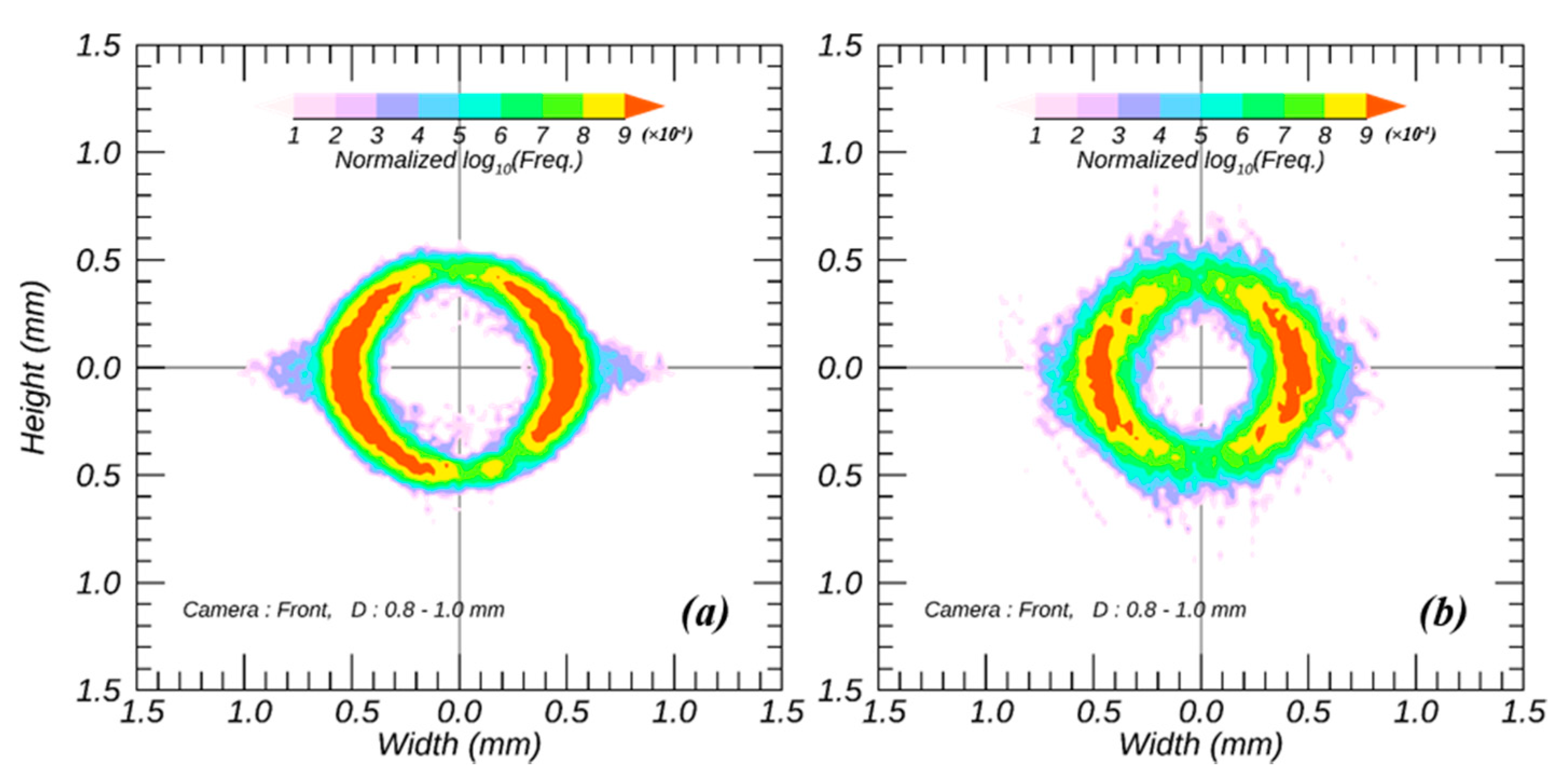
2.3. Particle Shape Irregularity
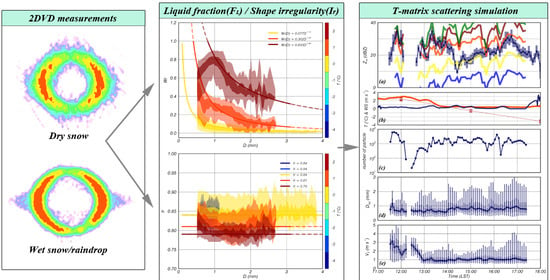
2.4. Liquid Fraction of a Snowflake
2.5. T-Matrix Scattering Simulation
3. Results
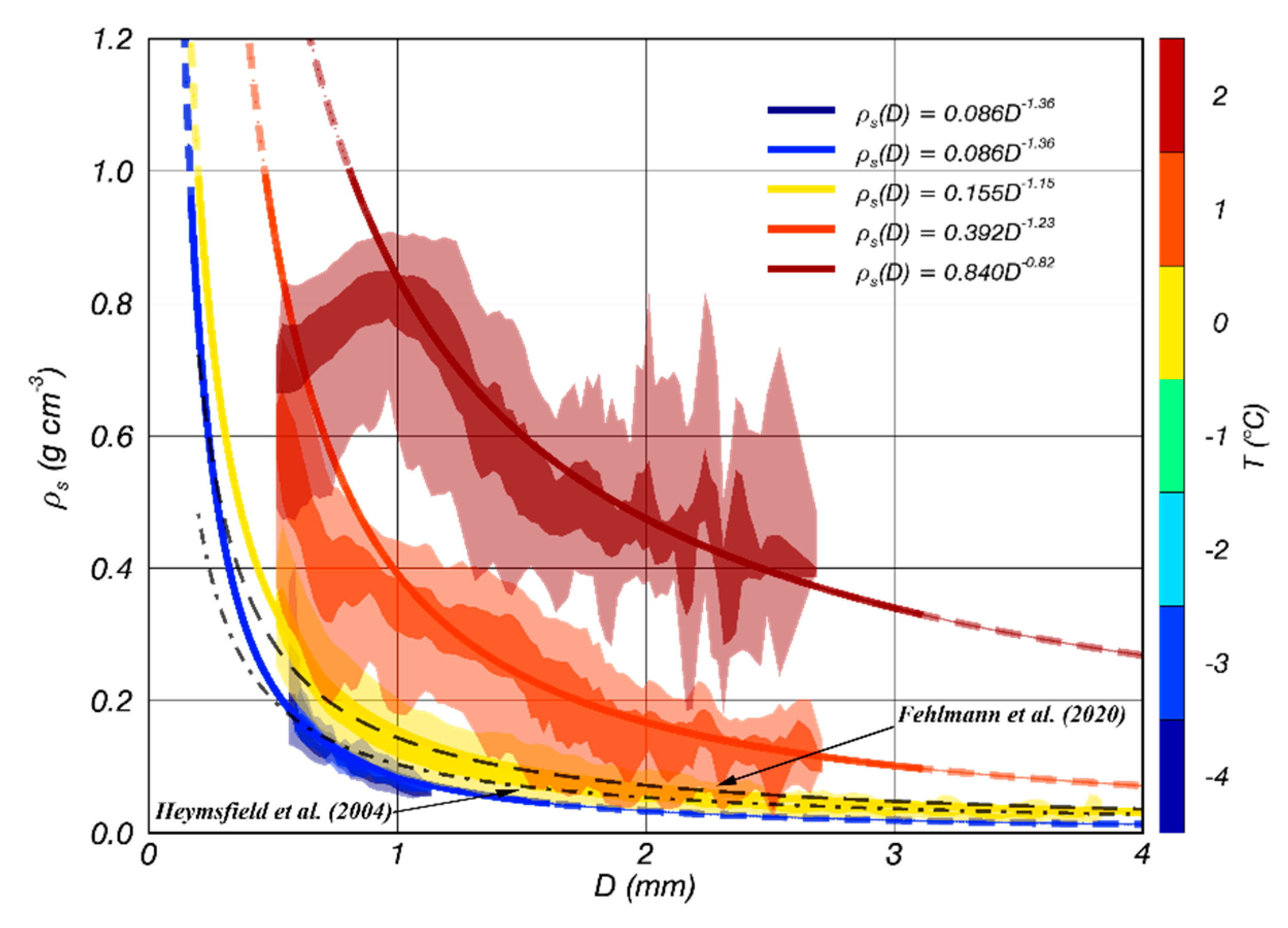
3.1. Temperature Dependence of Physical Features of Wet Snow
3.2. Dependence of Shape Irregularity of Wet Snow on Temperature and Liquid Fraction
4. Verifications
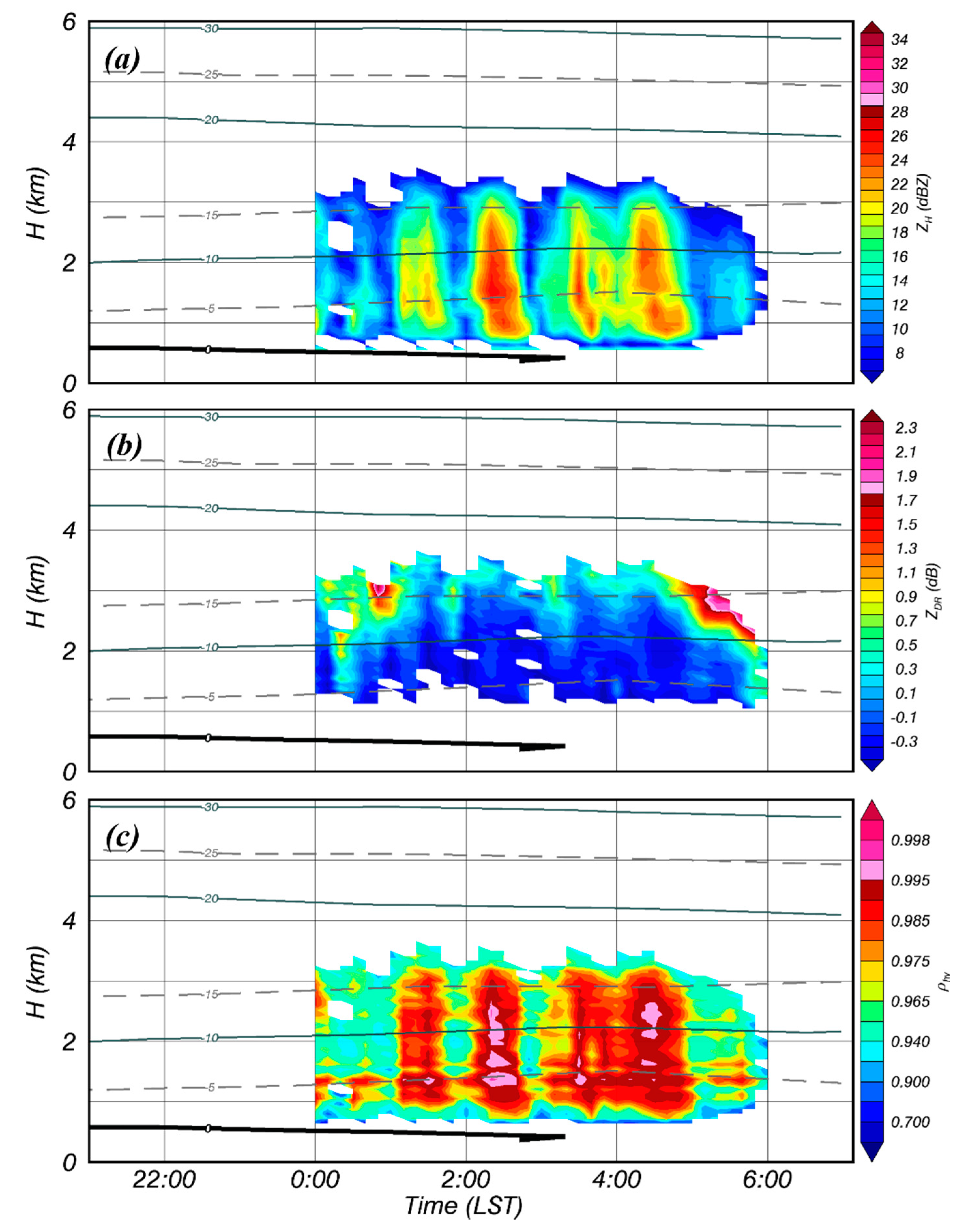
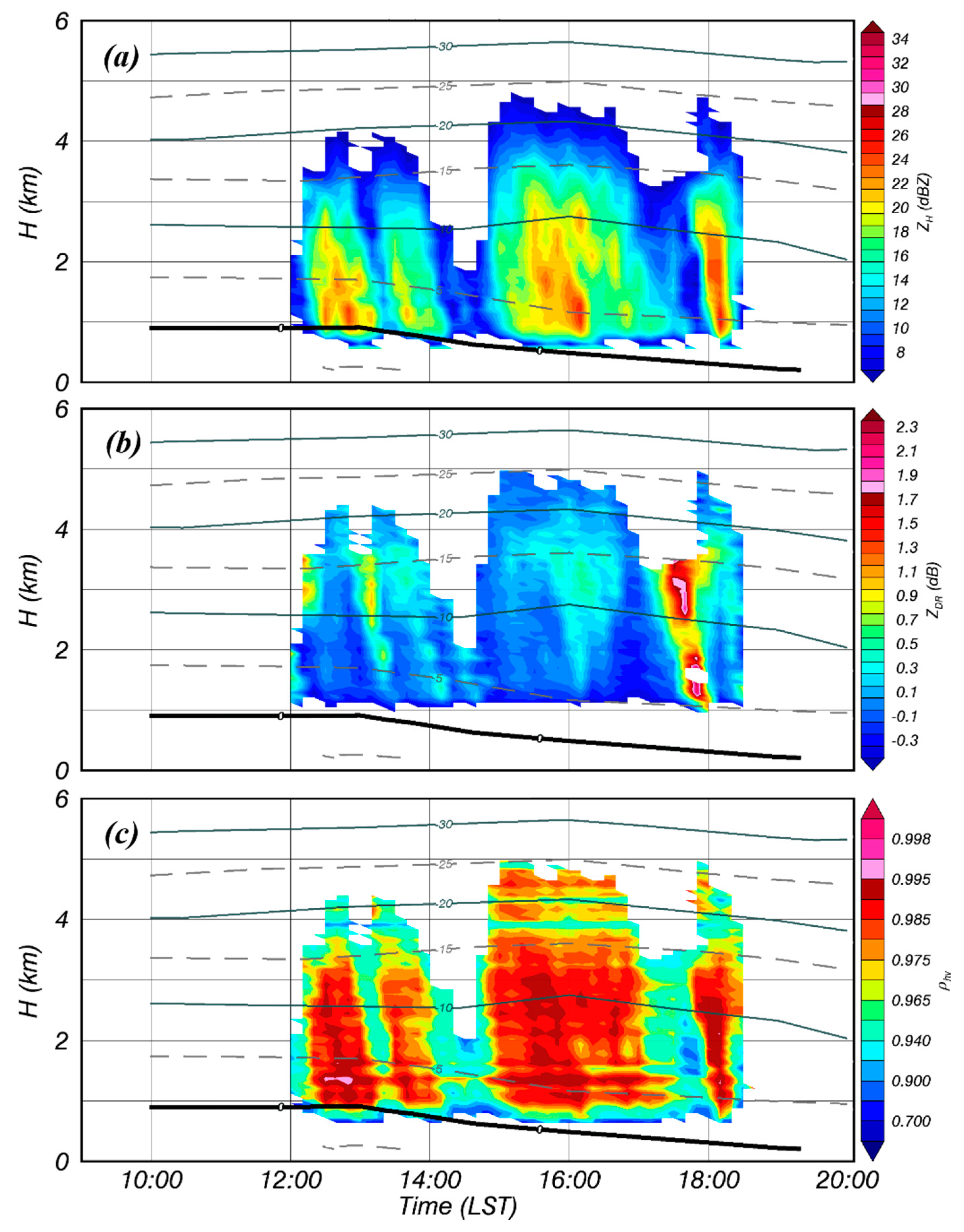
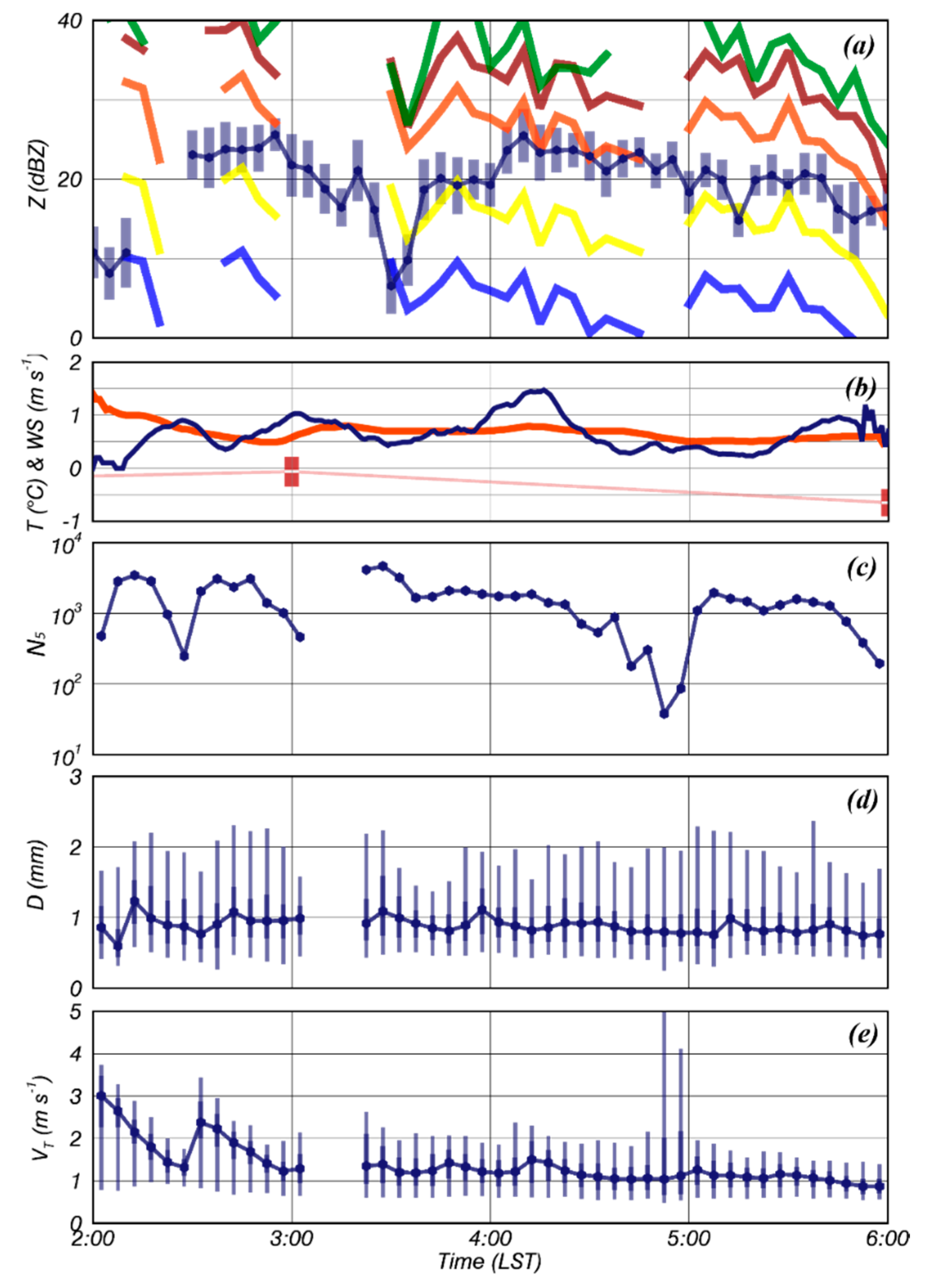
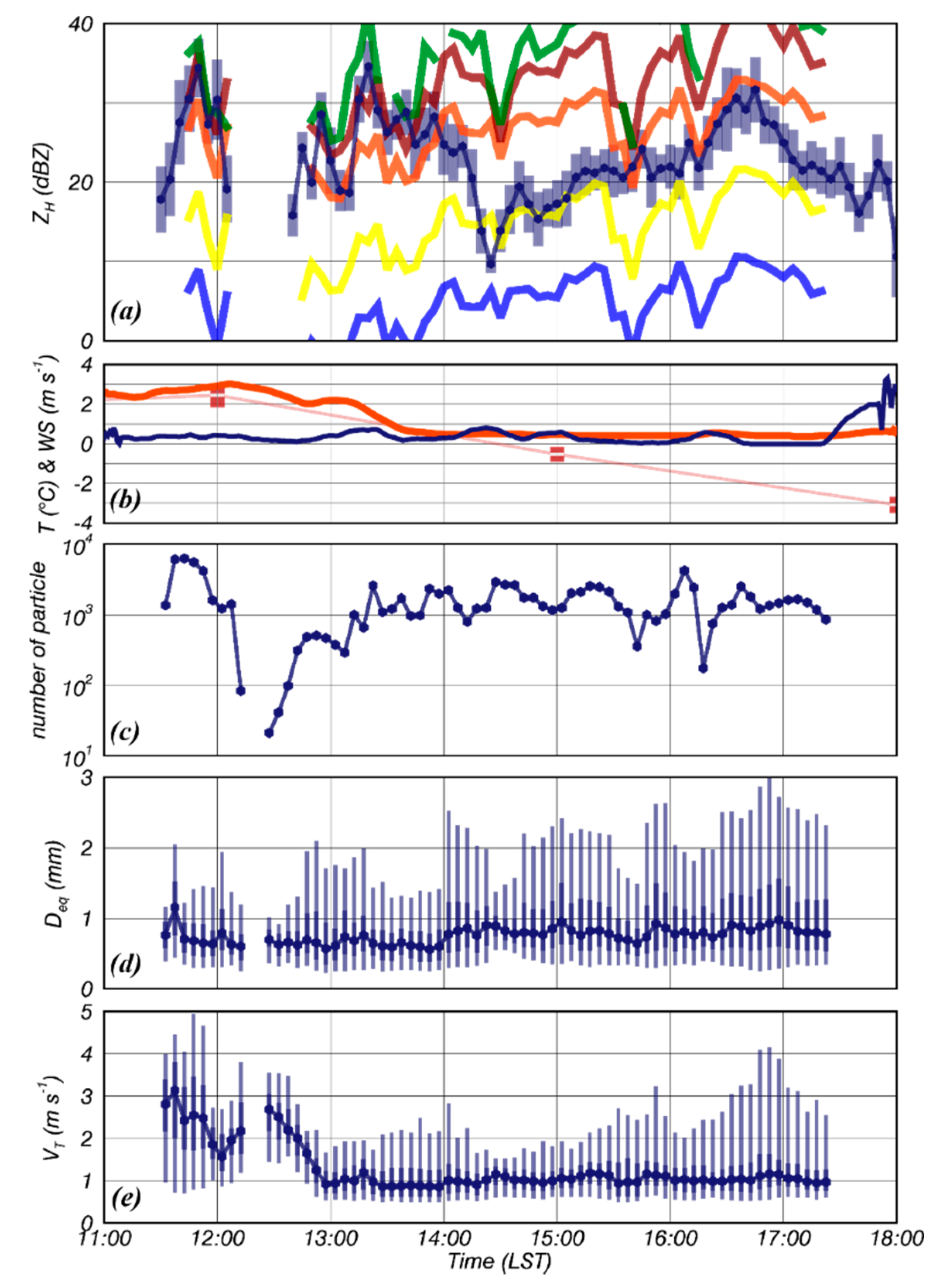
4.1. Spatiotemporal Structure of Analyzed Cases
4.2. Verification of Simulated Radar Variables
5. Discussions
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stewart, R.; Crawford, R. Some characteristics of the precipitation formed within winter storms over eastern Newfoundland. Atmos. Res. 1995, 36, 17–37. [Google Scholar] [CrossRef]
- Knight, C.A. Observations of the morphology of melting snow. J. Atmos. Sci. 1979, 36, 1123–1130. [Google Scholar] [CrossRef]
- Houston, T.G.; Changnon, S.A. Freezing rain events: A major weather hazard in the conterminous US. Nat. Hazards 2006, 40, 485–494. [Google Scholar] [CrossRef]
- Frick, C.; Wernli, H. A Case Study of High-Impact Wet Snowfall in Northwest Germany (25–27 November 2005): Observations, Dynamics, and Forecast Performance. Weather. Forecast. 2012, 27, 1217–1234. [Google Scholar] [CrossRef]
- Cober, S.G.; Isaac, G.A.; Strapp, J.W. Characterizations of Aircraft Icing Environments that Include Supercooled Large Drops. J. Appl. Meteorol. 2001, 40, 1984–2002. [Google Scholar] [CrossRef]
- Rasmussen, R.M.; Baker, B.D.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.J.; et al. How Well Are We Measuring Snow: The NOAA/FAA/NCAR Winter Precipitation Test Bed. Bull. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef] [Green Version]
- Kruger, A.; Krajewski, W.F. Two-Dimensional Video Disdrometer: A Description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Brandes, E.A.; Ikeda, K.; Zhang, G.; Schönhuber, M.; Rasmussen, R.M. A Statistical and Physical Description of Hydrometeor Distributions in Colorado Snowstorms Using a Video Disdrometer. J. Appl. Meteorol. Clim. 2007, 46, 634–650. [Google Scholar] [CrossRef]
- Zhang, G.; Xue, M.; Cao, Q.; Dawson, D. Diagnosing the Intercept Parameter for Exponential Raindrop Size Distribution Based on Video Disdrometer Observations: Model Development. J. Appl. Meteorol. Clim. 2008, 47, 2983–2992. [Google Scholar] [CrossRef] [Green Version]
- Wen, L.; Zhao, K.; Zhang, G.; Liu, S.; Chen, G. Impacts of Instrument Limitations on Estimated Raindrop Size Distribution, Radar Parameters, and Model Microphysics during Mei-Yu Season in East China. J. Atmos. Ocean. Technol. 2017, 34, 1021–1037. [Google Scholar] [CrossRef]
- Hansch, M. Fall Velocity and Shape of Snowflakes. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 1999. [Google Scholar]
- Brandes, E.A.; Ikeda, K.; Thompson, G.; Schönhuber, M. Aggregate Terminal Velocity/Temperature Relations. J. Appl. Meteorol. Clim. 2008, 47, 2729–2736. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.-J.; Bringi, V.N.; Cifelli, R.; Hudak, D.; Petersen, W.A. A Methodology to Derive Radar Reflectivity–Liquid Equivalent Snow Rate Relations Using C-Band Radar and a 2D Video Disdrometer. J. Atmos. Ocean. Technol. 2010, 27, 637–651. [Google Scholar] [CrossRef]
- Huang, G.-J.; Bringi, V.; Moisseev, D.; Petersen, W.; Bliven, L.; Hudak, D. Use of 2D-video disdrometer to derive mean density–size and Ze–SR relations: Four snow cases from the light precipitation validation experiment. Atmos. Res. 2015, 153, 34–48. [Google Scholar] [CrossRef]
- Böhm, H.P. A General Equation for the Terminal Fall Speed of Solid Hydrometeors. J. Atmos. Sci. 1989, 46, 2419–2427. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zrnic, D.S.; Ellis, S.M.; Oye, R.; Ryzhkov, A.V.; Straka, J. Cloud microphysics retrieval using S-band dual-polarization radar measurements. Bull. Am. Meteorol. Soc. 1999, 80, 381–388. [Google Scholar] [CrossRef]
- Liu, H.; Chandrasekar, V. Classification of Hydrometeors Based on Polarimetric Radar Measurements: Development of Fuzzy Logic and Neuro-Fuzzy Systems, and In Situ Verification. J. Atmos. Ocean. Technol. 2000, 17, 140–164. [Google Scholar] [CrossRef]
- Lim, S.; Chandrasekar, V.; Bringi, V. Hydrometeor classification system using dual-polarization radar measurements: Model improvements and in situ verification. IEEE Trans. Geosci. Remote. Sens. 2005, 43, 792–801. [Google Scholar] [CrossRef]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K.-E. The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D: Description and Application to an MCS. Weather. Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Grazioli, J.; Tuia, D.; Monhart, S.; Schneebeli, M.; Raupach, T.H.; Berne, A. Hydrometeor classification from two-dimensional video disdrometer data. Atmos. Meas. Tech. 2014, 7, 2869–2882. [Google Scholar] [CrossRef] [Green Version]
- Fujiyoshi, Y.; Endoh, T.; Yamada, T.; Tsuboki, K.; Tachibana, Y.; Wakahama, G. Determination of a Z-R relationship for snowfall using a radar and high sensitivity snow gauges. J. Appl. Meteorol. 1990, 29, 147–152. [Google Scholar] [CrossRef] [Green Version]
- Matrosov, S.Y. A Dual-Wavelength Radar Method to Measure Snowfall Rate. J. Appl. Meteorol. 1998, 37, 1510–1521. [Google Scholar] [CrossRef]
- Matrosov, S. Radar reflectivity in snowfall. IEEE Trans. Geosci. Remote. Sens. 1992, 30, 454–461. [Google Scholar] [CrossRef]
- Rasmussen, R.; Dixon, M.; Hage, F.; Cole, J.; Wade, C.; Tuttle, J.; Mcgettigan, S.; Carty, T.; Stevenson, L.; Fellner, W.; et al. Weather Support to Deicing Decision Making (WSDDM): A Winter Weather Nowcasting System. Bull. Am. Meteorol. Soc. 2001, 82, 579–595. [Google Scholar] [CrossRef] [Green Version]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Langleben, M. The terminal velocity of snowflakes. QJR Meteorol. Soc. 1954, 80, 174–184. [Google Scholar] [CrossRef]
- Stewart, R.E.; Thériault, J.M.; Henson, W. On the Characteristics of and Processes Producing Winter Precipitation Types near 0 °C. Bull. Am. Meteorol. Soc. 2015, 96, 623–639. [Google Scholar] [CrossRef] [Green Version]
- Barthazy, E.; Schefold, R. Fall velocity of snowflakes of different riming degree and crystal types. Atmos. Res. 2006, 82, 391–398. [Google Scholar] [CrossRef]
- Mitra, S.K.; Vohl, O.; Ahr, M.; Pruppacher, H.R. A Wind Tunnel and Theoretical Study of the Melting Behavior of Atmos. Ice Particles. IV: Experiment and Theory for Snow Flakes. J. Atmos. Sci. 1990, 47, 584–591. [Google Scholar] [CrossRef] [Green Version]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Löffler-Mang, M. Observations of Precipitation Size and Fall Speed Characteristics within Coexisting Rain and Wet Snow. J. Appl. Meteorol. Clim. 2006, 45, 1450–1464. [Google Scholar] [CrossRef] [Green Version]
- Roebber, P.J.; Bruening, S.L.; Schultz, D.M.; Cortinas, J.V., Jr. Improving snowfall forecasting by diagnosing snow density. Weather Forecast. 2003, 18, 264–287. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, R.; Dixon, M.; Vasiloff, S.; Hage, F.; Knight, S.; Vivekanandan, J.; Xu, M. Snow Nowcasting Using a Real-Time Correlation of Radar Reflectivity with Snow Gauge Accumulation. J. Appl. Meteorol. 2003, 42, 20–36. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.L. Equivalent Radar Reflectivity Factors for Snow and Ice Particles. J. Clim. Appl. Meteorol. 1984, 23, 1258–1260. [Google Scholar] [CrossRef] [Green Version]
- Sihvola, A.H. Electromagnetic Mixing Formulas and Applications; Institution of Engineering and Technology: London, UK, 1999; p. 47. [Google Scholar]
- Gourley, J.J.; Tabary, P.; Du Chatelet, J.P. A Fuzzy Logic Algorithm for the Separation of Precipitating from Nonprecipitating Echoes Using Polarimetric Radar Observations. J. Atmos. Ocean. Technol. 2007, 24, 1439–1451. [Google Scholar] [CrossRef]
- Nešpor, V.; Krajewski, W.F.; Kruger, A. Wind-Induced Error of Raindrop Size Distribution Measurement Using a Two-Dimensional Video Disdrometer. J. Atmos. Ocean. Technol. 2000, 17, 1483–1492. [Google Scholar] [CrossRef]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the New Version of the Laser-Optical Disdrometer, OTT Parsivel2. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Drop Axis Ratios from a 2D Video Disdrometer. J. Atmos. Ocean. Technol. 2005, 22, 966–978. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; Szakáll, M.; Mitra, S.K.; Beard, K.V.; Borrmann, S. Drop Shapes and Axis Ratio Distributions: Comparison between 2D Video Disdrometer and Wind-Tunnel Measurements. J. Atmos. Ocean. Technol. 2009, 26, 1427–1432. [Google Scholar] [CrossRef]
- Suh, S.-H.; Maki, M.; Iguchi, M.; Lee, D.-I.; Yamaji, A.; Momotani, T. Free-fall experiments of volcanic ash particles using a 2-D video disdrometer. Atmos. Meas. Tech. 2019, 12, 5363–5379. [Google Scholar] [CrossRef] [Green Version]
- Kunii, D.; Levenspiel, O. Fluidization Engineering; John Wiley: Hoboken, NJ, USA, 1969; Volume 8, pp. 44–45. [Google Scholar]
- Tran-Cong, S.; Gay, M.; Michaelides, E.E. Drag coefficients of irregularly shaped particles. Powder Technol. 2004, 139, 21–32. [Google Scholar] [CrossRef]
- Hölzer, A.; Sommerfeld, M. New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 2008, 184, 361–365. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C.; Manzella, I.; Vonlanthen, P. On the characterization of size and shape of irregular particles. Powder Technol. 2015, 270, 141–153. [Google Scholar] [CrossRef]
- Berrezueta, E.; Cuervas-Mons, J.; Rodríguez-Rey, Á.; Ordóñez-Casado, B. Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography. Minerals 2019, 9, 768. [Google Scholar] [CrossRef] [Green Version]
- Beard, K.V.; Chuang, C. A New Model for the Equilibrium Shape of Raindrops. J. Atmos. Sci. 1987, 44, 1509–1524. [Google Scholar] [CrossRef]
- Thurai, M.; Huang, G.; Bringi, V.N.; Randeu, W.L.; Schonhuber, M. Drop Shapes, Model Comparisons, and Calculations of Polarimetric Radar Parameters in Rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Bansemer, A.; Schmitt, C.; Twohy, C.; Poellot, M.R. Effective Ice Particle Densities Derived from Aircraft Data. J. Atmos. Sci. 2004, 61, 982–1003. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Lewis, S.; Bansemer, A.; Iaquinta, J.; Miloshevich, L.M.; Kajikawa, M.; Twohy, C.; Poellot, M.R. A General Approach for Deriving the Properties of Cirrus and Stratiform Ice Cloud Particles. J. Atmos. Sci. 2002, 59, 3–29. [Google Scholar] [CrossRef]
- Fehlmann, M.; Rohrer, M.; Von Lerber, A.; Stoffel, M. Automated precipitation monitoring with the Thies disdrometer: Biases and ways for improvement. Atmos. Meas. Tech. 2020, 13, 4683–4698. [Google Scholar] [CrossRef]
- Atlas, D.; Kerker, M.; Hitschfeld, W. Scattering and attenuation by non-spherical atmospheric particles. J. Atmos. Terr. Phys. 1953, 3, 108–119. [Google Scholar] [CrossRef]
- Wang, Y. The Application of Spectral Analysis and Artificial Intelligence Methods to Weather Radar. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2010. [Google Scholar]
- Rasmussen, R.M.; Heymsfield, A.J. Melting and Shedding of Graupel and Hail. Part I: Model Physics. J. Atmos. Sci. 1987, 44, 2754–2763. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.; Zhang, P.; Reeves, H.; Kumjian, M.; Tschallener, T.; Troemel, S.; Simmer, C. Quasi-Vertical Profiles—A New Way to Look at Polarimetric Radar Data. J. Atmos. Ocean. Technol. 2016, 33, 551–562. [Google Scholar] [CrossRef]
- Saito, K.; Fujita, T.; Yamada, Y.; Ishida, J.-I.; Kumagai, Y.; Aranami, K.; Ohmori, S.; Nagasawa, R.; Kumagai, S.; Muroi, C.; et al. The Operational JMA Nonhydrostatic Mesoscale Model. Mon. Weather. Rev. 2006, 134, 1266–1298. [Google Scholar] [CrossRef]
- Schuur, T.; Ryzhkov, A.; Heinselman, P.; Zrnic, D.; Burgess, D.; Scharfenberg, K. Observations and Classification of Echoes with the Polarimetric WSR-88D Radar; Report of the National Severe Storms Laboratory; National Severe Storms Laboratory: Norman, OK, USA, 2003; Volume 46, p. 73069. [Google Scholar]
- Herzegh, P.H.; Jameson, A.R. Observing Precipitation through Dual-Polarization Radar Measurements. Bull. Am. Meteorol. Soc. 1992, 73, 1365–1374. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Ganson, S.; Khain, A.; Pinsky, M.; Pokrovsky, A. Polarimetric characteristics of melting hail at S and C bands. In Proceedings of the 34th Conference on Radar Meteorology, Williamsburg, VA, USA, 5–9 October 2009; American Meteorology Society: Boston, MA, USA, 2009; p. 4. Available online: https://ams.confex.com/ams/34Radar/techprogram/paper_155571.htm (accessed on 11 May 2021).
- Ukichiro, N. Snow Crystals, Natural and Artificial; Harvard University Press: Cambridge, MA, USA, 1954. [Google Scholar]
- Libbrecht, K.; Rasmussen, P. The Snowflake: Winter’s Secret Beauty. In Stillwater; Voyageur Press: Minneapolis, MN, USA, 2003. [Google Scholar]
- Ryzhkov, A.; Reeves, H.; Schuur, T.; Kumjian, M.; Zrnic, D. Investigations of polarimetric radar signatures in winter storms and their relation to aircraft icing and freezing rain. In Proceedings of the 35th Conference on Radar Meteorology American Meteorological Society, Pittsburgh, PA, USA, 26–30 September 2011. [Google Scholar]
- Friedrich, K.; Higgins, S.; Masters, F.J.; Lopez, C.R. Articulating and Stationary PARSIVEL Disdrometer Measurements in Conditions with Strong Winds and Heavy Rainfall. J. Atmos. Ocean. Technol. 2013, 30, 2063–2080. [Google Scholar] [CrossRef]
- Gultepe, I.; Isaac, G.A.; Joe, P.; Kucera, P.A.; Thériault, J.M.; Fisico, T. Roundhouse (RND) Mountain Top Research Site: Measurements and Uncertainties for Winter Alpine Weather Conditions. Pure Appl. Geophys. PAGEOPH 2012, 171, 59–85. [Google Scholar] [CrossRef]
- Nitu, R.; Roulet, Y.-A.; Wolff, M.; Earle, M.; Reverdin, A.; Smith, C.; Kochendorfer, J.; Morin, S.; Rasmussen, R.; Wong, K.; et al. WMO Solid Precipitation Intercomparison Experiment (SPICE) (2012–2015); World Meteorological Organization: Geneva, Switzerald, 2019; Available online: https://repositorio.aemet.es/handle/20.500.11765/10839 (accessed on 11 May 2021).
- Zhang, L.; Zhao, L.; Xie, C.; Liu, G.; Gao, L.; Xiao, Y.; Shi, J.; Qiao, Y. Intercomparison of Solid Precipitation Derived from the Weighting Rain Gauge and Optical Instruments in the Interior Qinghai-Tibetan Plateau. Adv. Meteorol. 2015, 2015, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Gultepe, I.; Rabin, R.; Ware, R.; Pavolonis, M. Light snow precipitation and effects on weather and climate. Adv. Geophys. 2016, 57, 47–210. [Google Scholar] [CrossRef]
- Zhang, Y.; Ohata, T.; Yang, D.; Davaa, G. Bias correction of daily precipitation measurements for Mongolia. Hydrol. Process. 2004, 18, 2991–3005. [Google Scholar] [CrossRef]
- Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of Raindrop Size Distribution Measurements by Collocated Disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
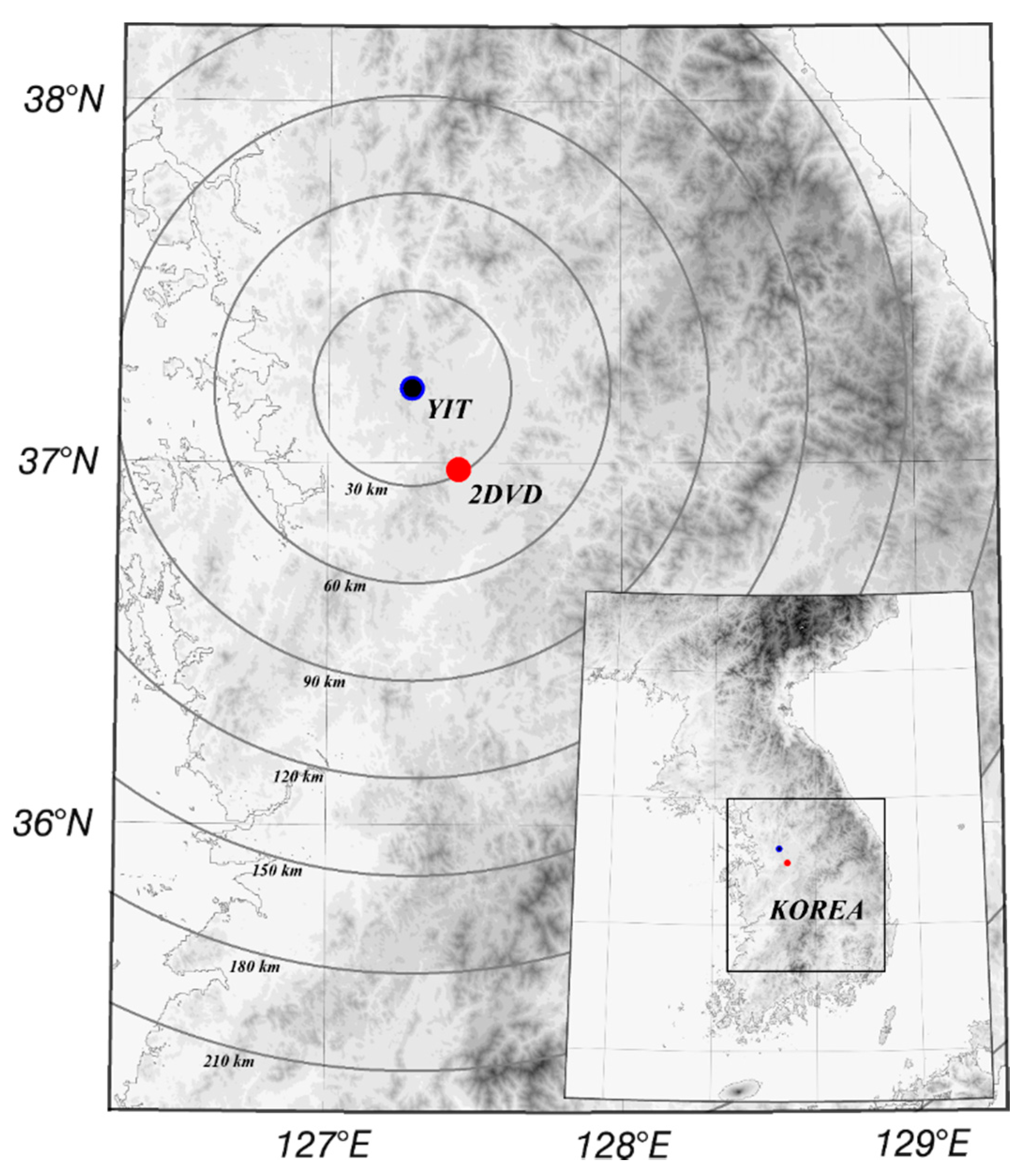




| Year | Mon | Day | Obs. Time (LST) | T0 | WS0 | YIT | |
|---|---|---|---|---|---|---|---|
| 2014 | 12 | 3 | 0017 | 1721 | −4.7 | 0.5 | O |
| 8 | 0326 | 0431 | −2.8 | 0.4 | |||
| 12 | 1612 | 2058 | −1.3 | - | |||
| 2015 | 1 | 11 | 0445 | 0523 | −0.1 | 1.8 | |
| 2016 | 1 | 14 | 2102 | 2135 | 0.1 | 2.2 | |
| 18 | 0342 | 1530 | 0.7 | - | |||
| 2 | 27 | 0027 | 0618 | 1.0 | 0.6 | O | |
| 28 | 1131 | 2155 | 2.6 | 0.9 | O | ||
| Specifications | Details |
|---|---|
| Model | DWSR-8501 S/K-SDP |
| Manufacturer | EEC (US) |
| Transmitting tube | Klystron |
| Antenna diameter | 8.5 m |
| Transmitting frequency | 2.88 GHz |
| Peak power | 850 KW |
| Effective observational range | 240 km |
| Beam/Pulse width | 0.94°/2 μs |
| Wavelength | 10.41 cm |
| Range gate size | 250 m |
| Elev. height | 473 m |
| Long./Lat. | 127.2852 °E/37.2063 °N |
| Elev. angle (°) | 0.2, 0.6, 1.1, 1.8, 2.8, 4.2, 6.2, 9.1, 13.2, 19, 80 |
| Obs. interval | 10 min |
| Specifications | Details |
|---|---|
| Resolution (horizontal) | Higher than 0.19 mm |
| Resolution (vertical) | Higher than 0.19 mm for fall velocities less than 10 m·s−1 |
| Vertical velocity accuracy | Higher than 4% for velocities less than 10 m·s−1 |
| Sampling area/rate | 100 × 100 mm2/55 kHz |
| Rain rate compared to tipping bucket | Differences typically less than 10% |
| Main voltage | 100–240 V at 50/60 Hz |
| Power consumption | Approximately 500 W |
| Long./Lat. | 127.4445 °E/36.9823 °N |
| T (°C) | Sub-Zero | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| Var. | |||||
| N | 966 | 136,969 | 17,344 | 28,620 | |
| ρs(D) | 0.086 D−1.36 | 0.155 D−1.15 | 0.392 D−1.23 | 0.840 D−0.82 | |
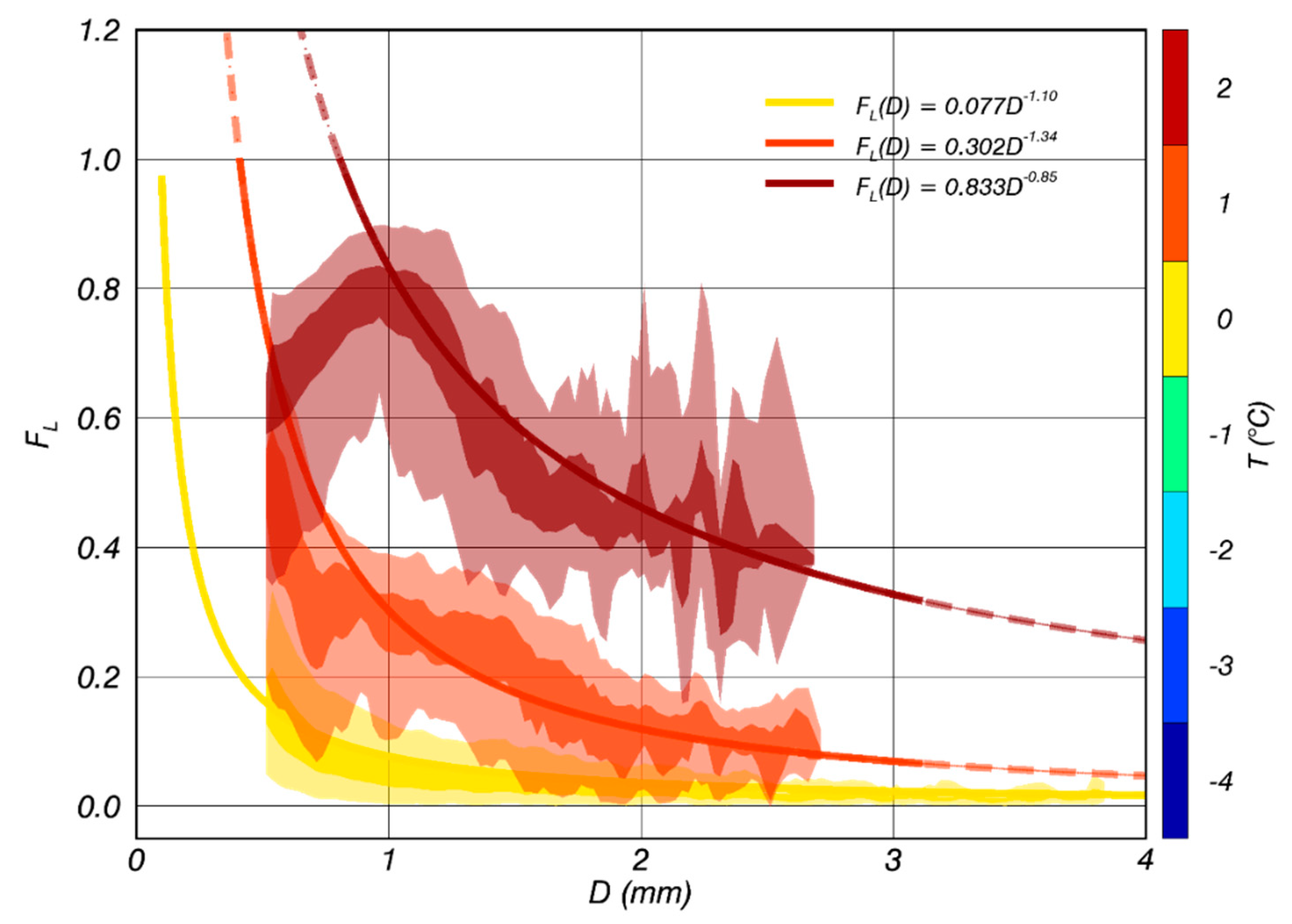
| FL(D) | 0.077 D−1.10 | 0.302 D−1.34 | 0.833 D−0.85 | ||
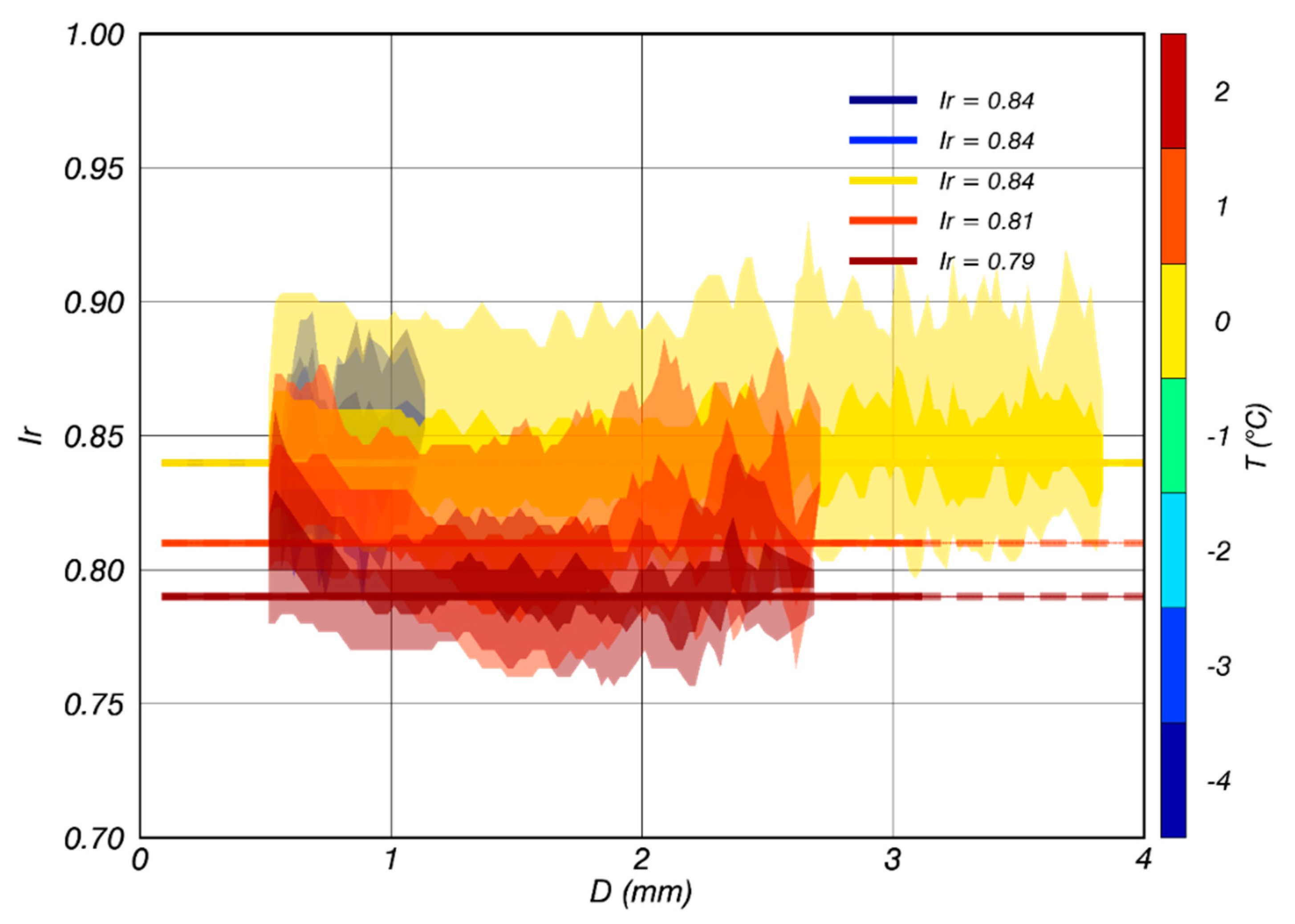
| Ir(D) | 0.84 | 0.84 | 0.81 | 0.79 | |
| FL(Ir) | 0.12exp[−0.5(0.09−1(Ir-0.75))2] | 0.37exp[−0.5(0.08−1(Ir-0.78))2] | 0.77exp[−0.5(0.1−1(Ir-0.77))2] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, S.-H.; Kim, H.-I.; Choi, E.-H.; You, C.-H. Estimation of Liquid Fraction of Wet Snow by Using 2-D Video Disdrometer and S-Band Weather Radar. Remote Sens. 2021, 13, 1901. https://doi.org/10.3390/rs13101901
Suh S-H, Kim H-I, Choi E-H, You C-H. Estimation of Liquid Fraction of Wet Snow by Using 2-D Video Disdrometer and S-Band Weather Radar. Remote Sensing. 2021; 13(10):1901. https://doi.org/10.3390/rs13101901
Chicago/Turabian StyleSuh, Sung-Ho, Hong-Il Kim, Eun-Ho Choi, and Cheol-Hwan You. 2021. "Estimation of Liquid Fraction of Wet Snow by Using 2-D Video Disdrometer and S-Band Weather Radar" Remote Sensing 13, no. 10: 1901. https://doi.org/10.3390/rs13101901
APA StyleSuh, S.-H., Kim, H.-I., Choi, E.-H., & You, C.-H. (2021). Estimation of Liquid Fraction of Wet Snow by Using 2-D Video Disdrometer and S-Band Weather Radar. Remote Sensing, 13(10), 1901. https://doi.org/10.3390/rs13101901