Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots
Abstract
:1. Introduction
2. Methods
2.1. Ground-Based Inventory Data
2.2. Ground-Based Burn Severity
2.3. Remotely-Sensed Burn Severity
2.4. Models for Burn Severity Class
3. Results
3.1. Macroplot Pixel Specific Weights
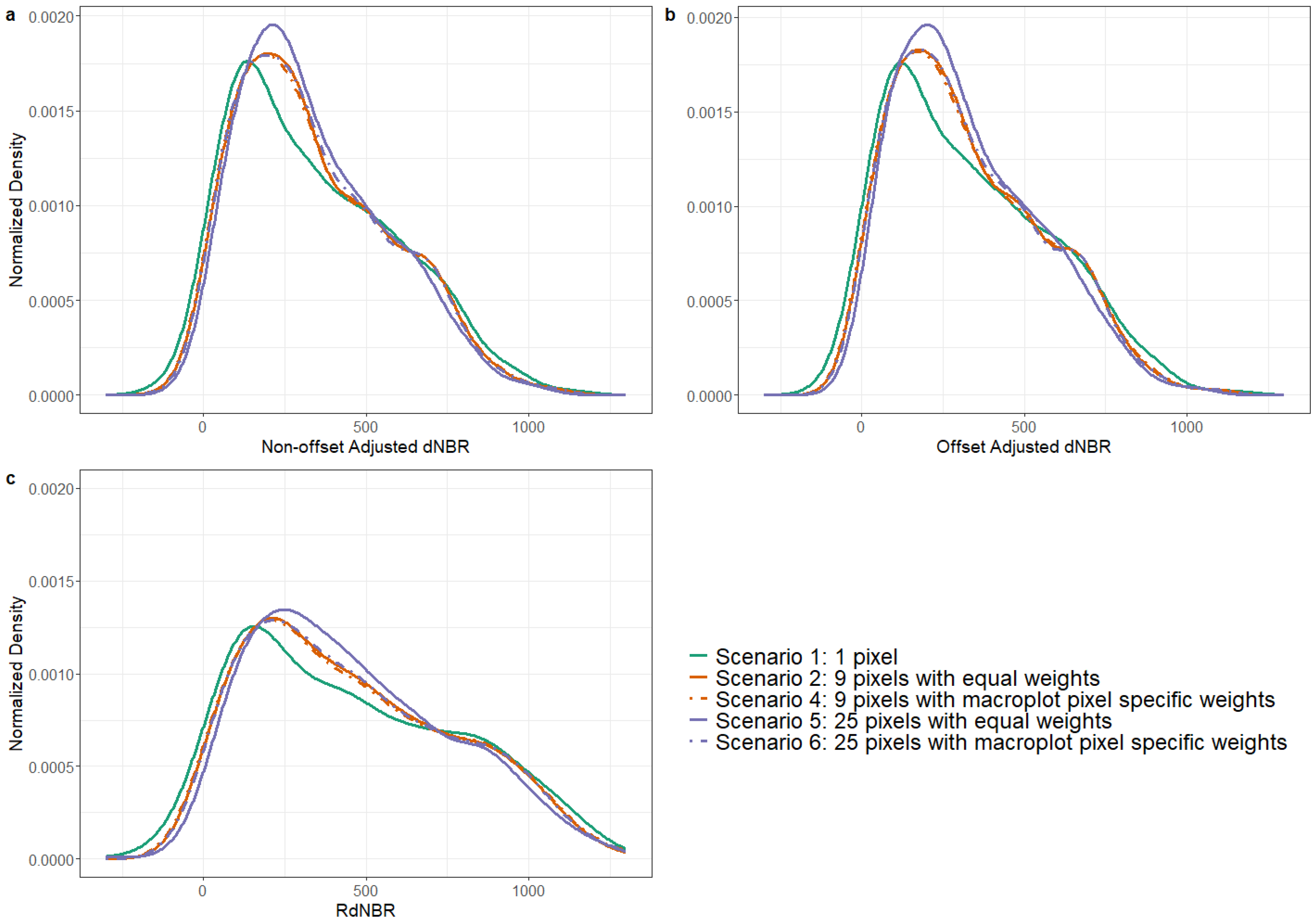
3.2. Smoothed Histograms of the Remotely-Sensed Metrics
3.3. Logistic Regression
3.4. Ordinal Regression
3.4.1. General Relationships
3.4.2. Model Fitting
3.4.3. Classification
4. Discussion
4.1. Remotely-Sensed Metrics
4.2. Pixel Configuration and Weighting
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Pixel Weight Calculation

Appendix B. Model Comparisons
Appendix B.1. Logistic Regression
| Scenario | Description | AIC | ΔAIC | RMSPE | Bias |
|---|---|---|---|---|---|
| 1 | 1 pixel | 4761.65 | 207.73 | 0.220 | −0.003 |
| 2 | 9 pixels with equal weights | 4609.45 | 55.54 | 0.216 | −0.002 |
| 3 | 9 pixels with centre pixel counted twice | 4586.63 | 32.72 | 0.215 | −0.002 |
| 4 | 9 pixels with macroplots pixel weights | 4553.91 | 0.00 | 0.214 | −0.002 |
| 5 | 25 pixels with equal weights | 5161.84 | 607.92 | 0.234 | −0.001 |
| 6 | 25 pixels with macroplots pixel weights | 4610.42 | 56.51 | 0.216 | −0.001 |
| Scenario | Description | AIC | ΔAIC | RMSPE | Bias |
|---|---|---|---|---|---|
| 1 | 1 pixel | 4696.70 | 235.30 | 0.218 | −0.004 |
| 2 | 9 pixels with equal weights | 4506.03 | 44.64 | 0.213 | −0.002 |
| 3 | 9 pixels with centre pixel counted twice | 4486.67 | 25.27 | 0.213 | −0.002 |
| 4 | 9 pixels with macroplots pixel weights | 4461.40 | 0.00 | 0.211 | −0.003 |
| 5 | 25 pixels with equal weights | 5029.62 | 568.22 | 0.231 | −0.001 |
| 6 | 25 pixels with macroplots pixel weights | 4510.42 | 49.03 | 0.213 | −0.002 |
| Scenario | Description | AIC | ΔAIC | RMSPE | Bias |
|---|---|---|---|---|---|
| 1 | 1 pixel | 5671.11 | 631.08 | 0.244 | −0.003 |
| 2 | 9 pixels with equal weights | 5040.03 | 0.00 | 0.226 | 0.000 |
| 3 | 9 pixels with centre pixel counted twice | 5045.73 | 5.70 | 0.226 | 0.000 |
| 4 | 9 pixels with macroplots pixel weights | 5056.91 | 16.88 | 0.226 | 0.000 |
| 5 | 25 pixels with equal weights | 5419.54 | 379.51 | 0.240 | 0.002 |
| 6 | 25 pixels with macroplots pixel weights | 5060.23 | 20.20 | 0.227 | 0.001 |
Appendix B.2. Ordinal Regression
Appendix B.2.1. Model Comparisons for 4-Classes Ground-Based Severity Models
| Scenario | Description | AIC | ΔAIC | Kappa | Weighted | % Correctly |
|---|---|---|---|---|---|---|
| Kappa | Classified | |||||
| 1 | 1 pixel | 801.88 | 16.46 | 0.44 | 0.62 | 62% |
| 2 | 9 pixels with equal weights | 788.99 | 3.57 | 0.45 | 0.63 | 62% |
| 3 | 9 pixels with centre pixel counted twice | 786.94 | 1.52 | 0.44 | 0.63 | 62% |
| 4 | 9 pixels with macroplots pixel weights | 785.42 | 0.00 | 0.46 | 0.64 | 63% |
| 5 | 25 pixels with equal weights | 832.57 | 47.15 | 0.41 | 0.60 | 60% |
| 6 | 25 pixels with macroplots pixel weights | 789.74 | 4.32 | 0.44 | 0.62 | 61% |
| Scenario | Description | AIC | ΔAIC | Kappa | Weighted Kappa | % Correctly Classified |
|---|---|---|---|---|---|---|
| 1 | 1 pixel | 801.55 | 18.93 | 0.45 | 0.62 | 62% |
| 2 | 9 pixels with equal weights | 785.62 | 3.00 | 0.43 | 0.63 | 61% |
| 3 | 9 pixels with centre pixel counted twice | 783.80 | 1.18 | 0.42 | 0.63 | 60% |
| 4 | 9 pixels with macroplots pixel weights | 782.62 | 0.00 | 0.43 | 0.63 | 61% |
| 5 | 25 pixels with equal weights | 827.99 | 45.37 | 0.39 | 0.59 | 59% |
| 6 | 25 pixels with macroplots pixel weights | 786.35 | 3.73 | 0.43 | 0.64 | 61% |
| Scenario | Description | AIC | ΔAIC | Kappa | Weighted Kappa | % Correctly Classified |
|---|---|---|---|---|---|---|
| 1 | 1 pixel | 870.74 | 55.15 | 0.38 | 0.56 | 58% |
| 2 | 9 pixels with equal weights | 815.59 | 0.00 | 0.41 | 0.60 | 59% |
| 3 | 9 pixels with centre pixel counted twice | 815.96 | 0.37 | 0.39 | 0.59 | 58% |
| 4 | 9 pixels with macroplots pixel weights | 817.60 | 2.01 | 0.38 | 0.58 | 58% |
| 5 | 25 pixels with equal weights | 847.05 | 31.46 | 0.36 | 0.56 | 56% |
| 6 | 25 pixels with macroplots pixel weights | 818.15 | 2.56 | 0.40 | 0.59 | 59% |
Appendix B.2.2. Model Comparisons for 5-Classes Ground-Based Severity Models
| Scenario | Description | AIC | ΔAIC | Kappa | Weighted Kappa | % Correctly Classified |
|---|---|---|---|---|---|---|
| 1 | 1 pixel | 925.08 | 28.04 | 0.41 | 0.64 | 57% |
| 2 | 9 pixels with equal weights | 898.57 | 1.53 | 0.42 | 0.65 | 57% |
| 3 | 9 pixels with centre pixel counted twice | 897.04 | hl0.00 | 0.42 | 0.65 | 57% |
| 4 | 9 pixels with macroplots pixel weights | 897.55 | 0.51 | 0.42 | 0.65 | 57% |
| 5 | 25 pixels with equal weights | 947.85 | 50.81 | 0.38 | 0.62 | 54% |
| 6 | 25 pixels with macroplots pixel weights | 900.50 | 3.46 | 0.44 | 0.65 | 58% |
| Predicted Ground Burn Severity | Actual Ground Burn Severity | ||||
|---|---|---|---|---|---|
| Very Low | Low | Moderate | Moderately Severe | Severe | |
| Very Low | 2.6% | 2.0% | 1.0% | 0% | 0% |
| Low | 79.5% | 75.0% | 41.7% | 3.3% | 1.1% |
| Moderate | 18.0% | 21.6% | 45.6% | 34.4% | 6.3% |
| Moderately Severe | 0% | 0.7% | 7.8% | 31.1% | 12.6% |
| Severe | 0% | 0.7% | 3.9% | 31.1% | 80.0% |
| Predicted Ground Burn Severity | Actual Ground Burn Severity | ||||
|---|---|---|---|---|---|
| Very Low | Low | Moderate | Moderately Severe | Severe | |
| Very Low | 0% | 0.7% | 1.0% | 0% | 0% |
| Low | 87.2% | 81.8% | 43.7% | 4.9% | 1.1% |
| Moderate | 10.3% | 15.5% | 39.8% | 47.5% | 15.8% |
| Moderately Severe | 0% | 1.4% | 6.8% | 6.6% | 7.4% |
| Severe | 2.6% | 0.7% | 8.7% | 41.0% | 75.8% |
References
- Bowman, D.M.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; D’Antonio, C.M.; DeFries, R.S.; Doyle, J.C.; Harrison, S.P.; et al. Fire in the Earth system. Science 2009, 324, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef] [PubMed]
- Dennison, P.E.; Brewer, S.C.; Arnold, J.D.; Moritz, M.A. Large wildfire trends in the western United States, 1984–2011. Geophys. Res. Lett. 2014, 41, 2928–2933. [Google Scholar] [CrossRef]
- Miller, J.D.; Skinner, C.; Safford, H.; Knapp, E.E.; Ramirez, C. Trends and causes of severity, size, and number of fires in northwestern California, USA. Ecol. Appl. 2012, 22, 184–203. [Google Scholar] [CrossRef] [PubMed]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and earlier spring increase western US forest wildfire activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beschta, R.L.; Rhodes, J.J.; Kauffman, J.B.; Gresswell, R.E.; Minshall, G.W.; Karr, J.R.; Perry, D.A.; Hauer, F.R.; Frissell, C.A. Postfire management on forested public lands of the western United States. Conserv. Biol. 2004, 18, 957–967. [Google Scholar] [CrossRef]
- Kuenzi, A.M.; Fulé, P.Z.; Sieg, C.H. Effects of fire severity and pre-fire stand treatment on plant community recovery after a large wildfire. For. Ecol. Manag. 2008, 255, 855–865. [Google Scholar] [CrossRef]
- Keith, H.; Lindenmayer, D.B.; Mackey, B.G.; Blair, D.; Carter, L.; McBurney, L.; Okada, S.; Konishi-Nagano, T. Accounting for biomass carbon stock change due to wildfire in temperate forest landscapes in Australia. PLoS ONE 2014, 9, e107126. [Google Scholar] [CrossRef] [Green Version]
- Eskelson, B.N.; Monleon, V.J.; Fried, J.S. A 6 year longitudinal study of post-fire woody carbon dynamics in California’s forests. Can. J. For. Res. 2016, 46, 610–620. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment (LA). In FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Sutherland, S., Gangi, L.J., Eds.; Gen. Tech. Rep. RMRS-GTR-164-CD; USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; p. 51. [Google Scholar]
- Lentile, L.B.; Holden, Z.A.; Smith, A.M.; Falkowski, M.J.; Hudak, A.T.; Morgan, P.; Lewis, S.A.; Gessler, P.E.; Benson, N.C. Remote sensing techniques to assess active fire characteristics and post-fire effects. Int. J. Wildland Fire 2006, 15, 319–345. [Google Scholar] [CrossRef]
- French, N.H.; Kasischke, E.S.; Hall, R.J.; Murphy, K.A.; Verbyla, D.L.; Hoy, E.E.; Allen, J.L. Using Landsat data to assess fire and burn severity in the North American boreal forest region: An overview and summary of results. Int. J. Wildland Fire 2008, 17, 443–462. [Google Scholar] [CrossRef]
- Morgan, P.; Keane, R.E.; Dillon, G.K.; Jain, T.B.; Hudak, A.T.; Karau, E.C.; Sikkink, P.G.; Holden, Z.A.; Strand, E.K. Challenges of assessing fire and burn severity using field measures, remote sensing and modelling. Int. J. Wildland Fire 2014, 23, 1045–1060. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.D.; Thode, A.E. Quantifying burn severity in a heterogeneous landscape with a relative version of the delta Normalized Burn Ratio (dNBR). Remote Sens. Environ. 2007, 109, 66–80. [Google Scholar] [CrossRef]
- Eidenshink, J.; Schwind, B.; Brewer, K.; Zhu, Z.L.; Quayle, B.; Howard, S. A project for monitoring trends in burn severity. Fire Ecol. 2007, 3, 3–21. [Google Scholar] [CrossRef]
- Kolden, C.A.; Smith, A.M.; Abatzoglou, J.T. Limitations and utilisation of Monitoring Trends in Burn Severity products for assessing wildfire severity in the USA. Int. J. Wildland Fire 2015, 24, 1023–1028. [Google Scholar] [CrossRef]
- Picotte, J.J.; Bhattarai, K.; Howard, D.; Lecker, J.; Epting, J.; Quayle, B.; Benson, N.; Nelson, K. Changes to the Monitoring Trends in Burn Severity program mapping production procedures and data products. Fire Ecol. 2020, 16, 1–12. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program-National Sampling Design and Estimation Procedures; Technical Report SRS-80; USDA Forest Service, Southern Research Station: Asheville, NC, USA, 2005.
- Shaw, J.D.; Goeking, S.A.; Menlove, J.; Werstak, C.E. Assessment of fire effects based on Forest Inventory and Analysis data and a long-term fire mapping data set. J. For. 2017, 115, 258–269. [Google Scholar] [CrossRef] [Green Version]
- Woo, H.; Eskelson, B.N.I.; Monleon, V.J. Matching methods to quantify wildfire effects on forest carbon mass in the U.S. Pacific Northwest. Ecol. Appl. 2021, 11, e02283. [Google Scholar]
- Cansler, C.A.; McKenzie, D. How robust are burn severity indices when applied in a new region? Evaluation of alternate field-based and remote-sensing methods. Remote Sens. 2012, 4, 456–483. [Google Scholar] [CrossRef] [Green Version]
- Soverel, N.O.; Perrakis, D.D.; Coops, N.C. Estimating burn severity from Landsat dNBR and RdNBR indices across western Canada. Remote Sens. Environ. 2010, 114, 1896–1909. [Google Scholar] [CrossRef]
- Hall, R.J.; Freeburn, J.T.; De Groot, W.J.; Pritchard, J.M.; Lynham, T.J.; Landry, R. Remote sensing of burn severity: Experience from western Canada boreal fires. Int. J. Wildland Fire 2008, 17, 476–489. [Google Scholar] [CrossRef]
- Kolden, C.A.; Lutz, J.A.; Key, C.H.; Kane, J.T.; van Wagtendonk, J.W. Mapped versus actual burned area within wildfire perimeters: Characterizing the unburned. For. Ecol. Manag. 2012, 286, 38–47. [Google Scholar] [CrossRef]
- Cansler, C.A. Drivers of Burn Severity in the Northern Cascade Range, Washington, USA. Master’s Thesis, University of Washington, Seattle, WA, USA, 2011. [Google Scholar]
- Parks, S.A.; Dillon, G.K.; Miller, C. A new metric for quantifying burn severity: The relativized burn ratio. Remote Sens. 2014, 6, 1827–1844. [Google Scholar] [CrossRef] [Green Version]
- Whittier, T.R.; Gray, A.N. Tree mortality based fire severity classification for forest inventories: A Pacific Northwest national forests example. For. Ecol. Manag. 2016, 359, 199–209. [Google Scholar] [CrossRef]
- Eskelson, B.N.; Monleon, V.J. Post-fire surface fuel dynamics in California forests across three burn severity classes. Int. J. Wildland Fire 2018, 27, 114–124. [Google Scholar] [CrossRef]
- Forest Inventory and Analysis National Core Field Guide Volume I: Field Data Collection Procedures for Phase 2 Plots; Technical Report; USDA Forest Service: North Bend, WA, USA, 2019.
- Miller, J.; Safford, H.; Crimmins, M.; Thode, A.E. Quantitative evidence for increasing forest fire severity in the Sierra Nevada and southern Cascade Mountains, California and Nevada, USA. Ecosystems 2009, 12, 16–32. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Bivand, R.; Lewin-Koh, N. Maptools: Tools for Handling Spatial Objects; R Package Version 0.9-9; 2019. [Google Scholar]
- Bivand, R.; Rundel, C. Rgeos: Interface to Geometry Engine—Open Source (’GEOS’); R Package Version 0.5-3; 2020. [Google Scholar]
- Bivand, R.; Keitt, T.; Rowlingson, B. Rgdal: Bindings for the ’Geospatial’ Data Abstraction Library; R Package Version 1.4-8; 2019. [Google Scholar]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling; R Package Version 3.0-12; 2020. [Google Scholar]
- Key, C.H. Ecological and sampling constraints on defining landscape fire severity. Fire Ecol. 2006, 2, 34–59. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1989. [Google Scholar]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Bolker, B. Dealing with quasi-models in R. Compare 2020, 1, 5–452. [Google Scholar]
- Temesgen, H.; Monleon, V.; Hann, D. Analysis and comparison of nonlinear tree height prediction strategies for Douglas-fir forests. Can. J. For. Res. 2008, 38, 553–565. [Google Scholar] [CrossRef] [Green Version]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0-86; 2020. [Google Scholar]
- Ferster, C.J.; Eskelson, B.N.; Andison, D.W.; LeMay, V.M. Vegetation Mortality within Natural Wildfire Events in the Western Canadian Boreal Forest: What Burns and Why? Forests 2016, 7, 187. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Cohen, J. Weighted kappa: Nominal scale agreement provision for scaled disagreement or partial credit. Psychol. Bull. 1968, 70, 213. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Hudak, A.T.; Morgan, P.; Bobbitt, M.J.; Smith, A.M.; Lewis, S.A.; Lentile, L.B.; Robichaud, P.R.; Clark, J.T.; McKinley, R.A. The relationship of multispectral satellite imagery to immediate fire effects. Fire Ecol. 2007, 3, 64–90. [Google Scholar] [CrossRef]
- Harrell, F.E., Jr. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer: Berlin/Heisenberg, Germany, 2015. [Google Scholar]
- Jain, T.B.; Battaglia, M.A.; Han, H.S.; Graham, R.T.; Keyes, C.R.; Fried, J.S.; Sandquist, J.E. A Comprehensive Guide to Fuel Management Practices for Dry Mixed Conifer Forests in the Northwestern United States; Technical Report RMRS-GTR-292; USDA Forest Service, Rocky Mountain Research Station: North Bend, WA, USA, 2012.
- San-Miguel, I.; Andison, D.W.; Coops, N.C.; Rickbeil, G.J. Predicting post-fire canopy mortality in the boreal forest from dNBR derived from time series of Landsat data. Int. J. Wildland Fire 2016, 25, 762–774. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. Application of the tasseled cap concept to simulated thematic mapper data. Photogramm. Eng. Remote Sens. 1984, 50, 343–352. [Google Scholar]



| Severity Class | Rule | Number of Plots |
|---|---|---|
| Very Low | No mortality | 39 |
| Low | % Mort Tally < 25 | 148 |
| Moderate | % Mort Tally < 60 | 103 |
| Moderately Severe | % Mort Tally < 90 | 61 |
| Severe | % Mort Tally ≥ 90 | 91 |
| Scenario | Pixel Configuration | Weighted Average |
|---|---|---|
| 1 | 1 pixel | weight only applied to centre pixel |
| 2 | 9 pixels | equal weight (1/9) applied to 9 pixels |
| 3 | 9 pixels | centre pixel has twice the weight (2/10) of other 8 pixels (1/10) |
| 4 | 9 pixels | weights for macroplots based on pixel weight calculation (Figure 2b) |
| 5 | 25 pixels | equal weight (1/25) applied to 25 pixels |
| 6 | 25 pixels | weights for macroplots based on pixel weight calculation (Figure 2c) |
| Scenario | Description | AIC | ΔAIC | RMSPE | Bias |
|---|---|---|---|---|---|
| 1 | 1 pixel | 4139.56 | 252.66 | 0.195 | 0.010 |
| 2 | 9 pixels with equal weights | 3906.68 | 19.79 | 0.188 | 0.012 |
| 3 | 9 pixels with centre pixel counted twice | 3893.69 | 6.80 | 0.187 | 0.012 |
| 4 | 9 pixels with macroplots pixel weights | 3886.89 | 0.00 | 0.187 | 0.012 |
| 5 | 25 pixels with equal weights | 4362.60 | 475.71 | 0.205 | 0.014 |
| 6 | 25 pixels with macroplots pixel weights | 3920.60 | 33.71 | 0.188 | 0.012 |
| Scenario | Description | AIC | ΔAIC | Kappa | Weighted Kappa | % Correctly Classified |
|---|---|---|---|---|---|---|
| 1 | 1 pixel | 726.26 | 24.60 | 0.50 | 0.69 | 65% |
| 2 | 9 pixels with equal weights | 703.44 | 1.78 | 0.51 | 0.70 | 66% |
| 3 | 9 pixels with centre pixel counted twice | 701.66 | 0.00 | 0.51 | 0.70 | 66% |
| 4 | 9 pixels with macroplots simulation weights | 702.28 | 0.62 | 0.50 | 0.70 | 65% |
| 5 | 25 pixels with equal weights | 745.93 | 44.27 | 0.46 | 0.66 | 62% |
| 6 | 25 pixels with macroplots simulation weights | 704.47 | 2.81 | 0.50 | 0.70 | 65% |
| Predicted Ground Burn Severity | Actual Ground Burn Severity | |||
|---|---|---|---|---|
| Very Low\Low | Moderate | Moderately Severe | Severe | |
| Very Low\Low | 81.8% | 44.7% | 3.3% | 1.1% |
| Moderate | 17.6% | 41.7% | 32.8% | 6.3% |
| Moderately Severe | 0.5% | 10.7% | 36.1% | 12.6% |
| Severe | 0.5% | 2.9% | 27.9% | 80.0% |
| Predicted Ground Burn Severity | Actual Ground Burn Severity | |||
|---|---|---|---|---|
| Very Low\Low | Moderate | Moderately Severe | Severe | |
| Very Low\Low | 82.4% | 44.7% | 3.3% | 1.1% |
| Moderate | 16.6% | 40.8% | 36.1% | 6.3% |
| Moderately Severe | 0.5% | 11.7% | 31.1% | 13.7% |
| Severe | 0.5% | 2.9% | 29.5% | 78.9% |
| Predicted Ground Burn Severity | Actual Ground Burn Severity | |||
|---|---|---|---|---|
| Very Low\Low | Moderate | Moderately Severe | Severe | |
| Very Low \Low | 82.9% | 46.6% | 9.8% | 5.3% |
| Moderate | 15.5% | 38.8% | 37.7% | 14.7% |
| Moderately Severe | 0.5% | 2.9% | 13.1% | 3.2% |
| Severe | 1.1% | 11.7% | 39.3% | 76.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelletier, F.; Eskelson, B.N.I.; Monleon, V.J.; Tseng, Y.-C. Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots. Remote Sens. 2021, 13, 1935. https://doi.org/10.3390/rs13101935
Pelletier F, Eskelson BNI, Monleon VJ, Tseng Y-C. Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots. Remote Sensing. 2021; 13(10):1935. https://doi.org/10.3390/rs13101935
Chicago/Turabian StylePelletier, Flavie, Bianca N.I. Eskelson, Vicente J. Monleon, and Yi-Chin Tseng. 2021. "Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots" Remote Sensing 13, no. 10: 1935. https://doi.org/10.3390/rs13101935
APA StylePelletier, F., Eskelson, B. N. I., Monleon, V. J., & Tseng, Y.-C. (2021). Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots. Remote Sensing, 13(10), 1935. https://doi.org/10.3390/rs13101935






