Satellite-Based Mapping of High-Resolution Ground-Level PM2.5 with VIIRS IP AOD in China through Spatially Neural Network Weighted Regression
Abstract
1. Introduction
2. Materials
2.1. Monitoring PM2.5 Data
2.2. VIIRS IP AOD Data
2.3. Meteorological Data
2.4. Geographical Data and Land Cover Data
2.5. Population Data
2.6. Data Preprocessing and Analysis
3. Methods
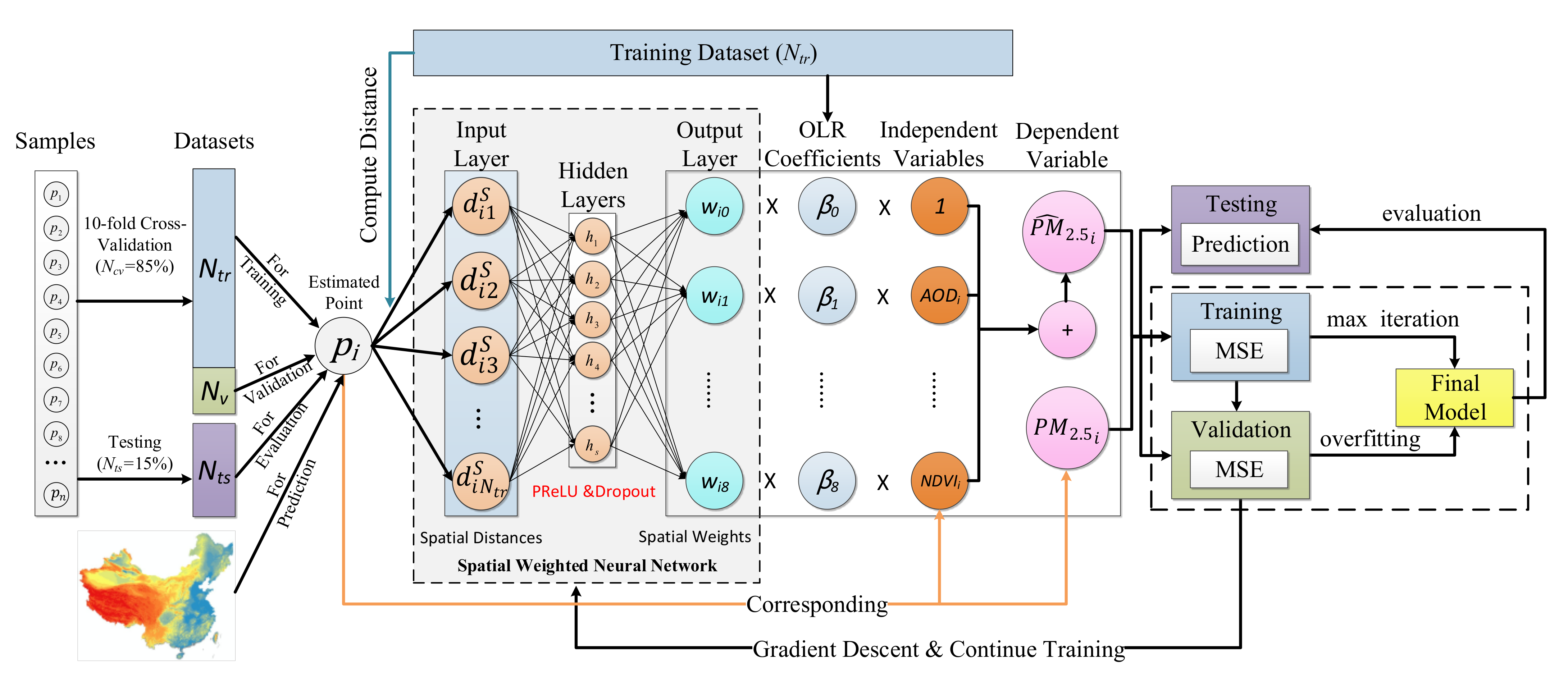
3.1. GNNWR Model
3.2. GWR Model
3.3. GRNN Model
3.4. Population Weighted PM2.5
4. Results
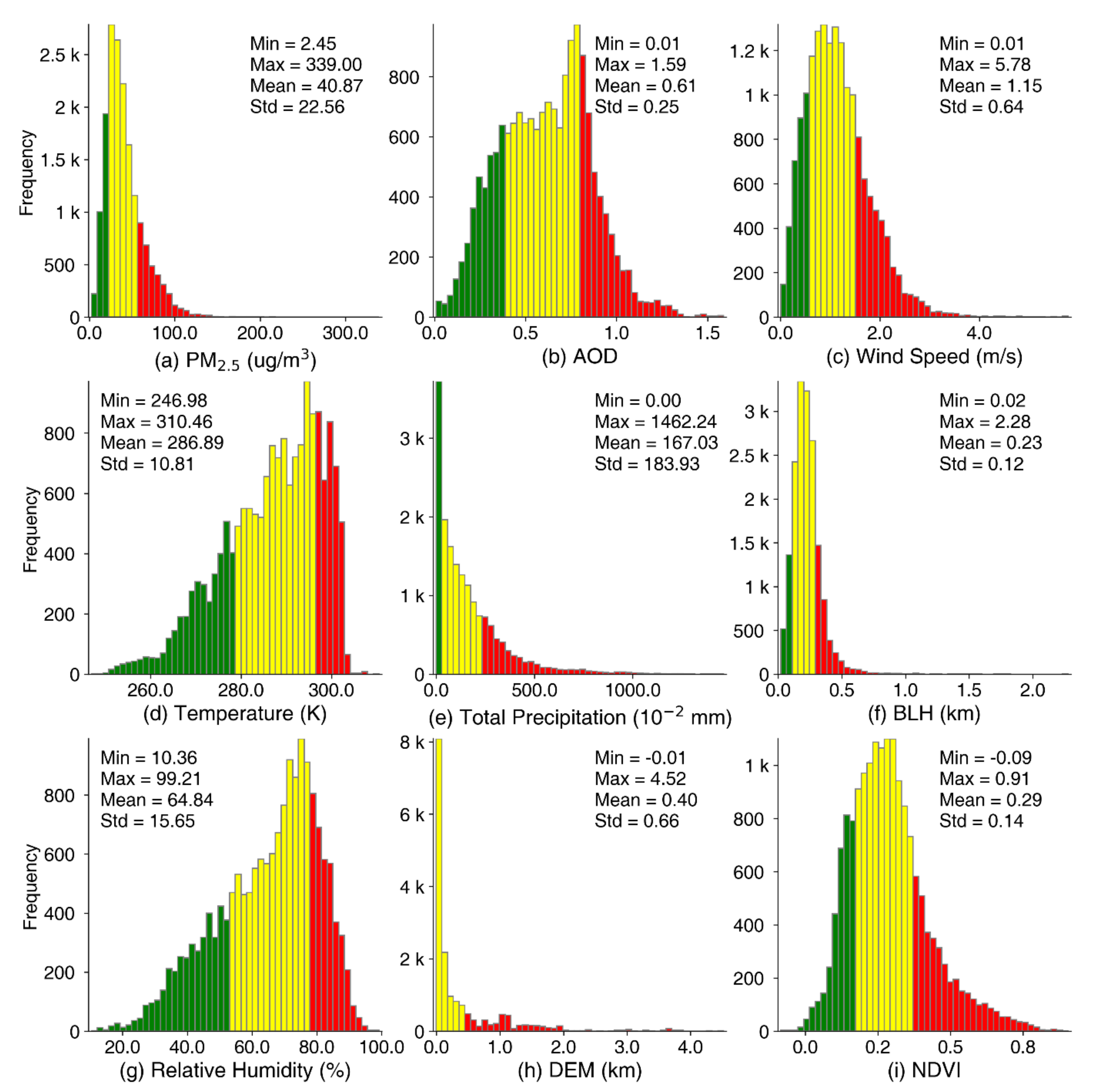
4.1. Descriptive Summary
4.2. Model Performance
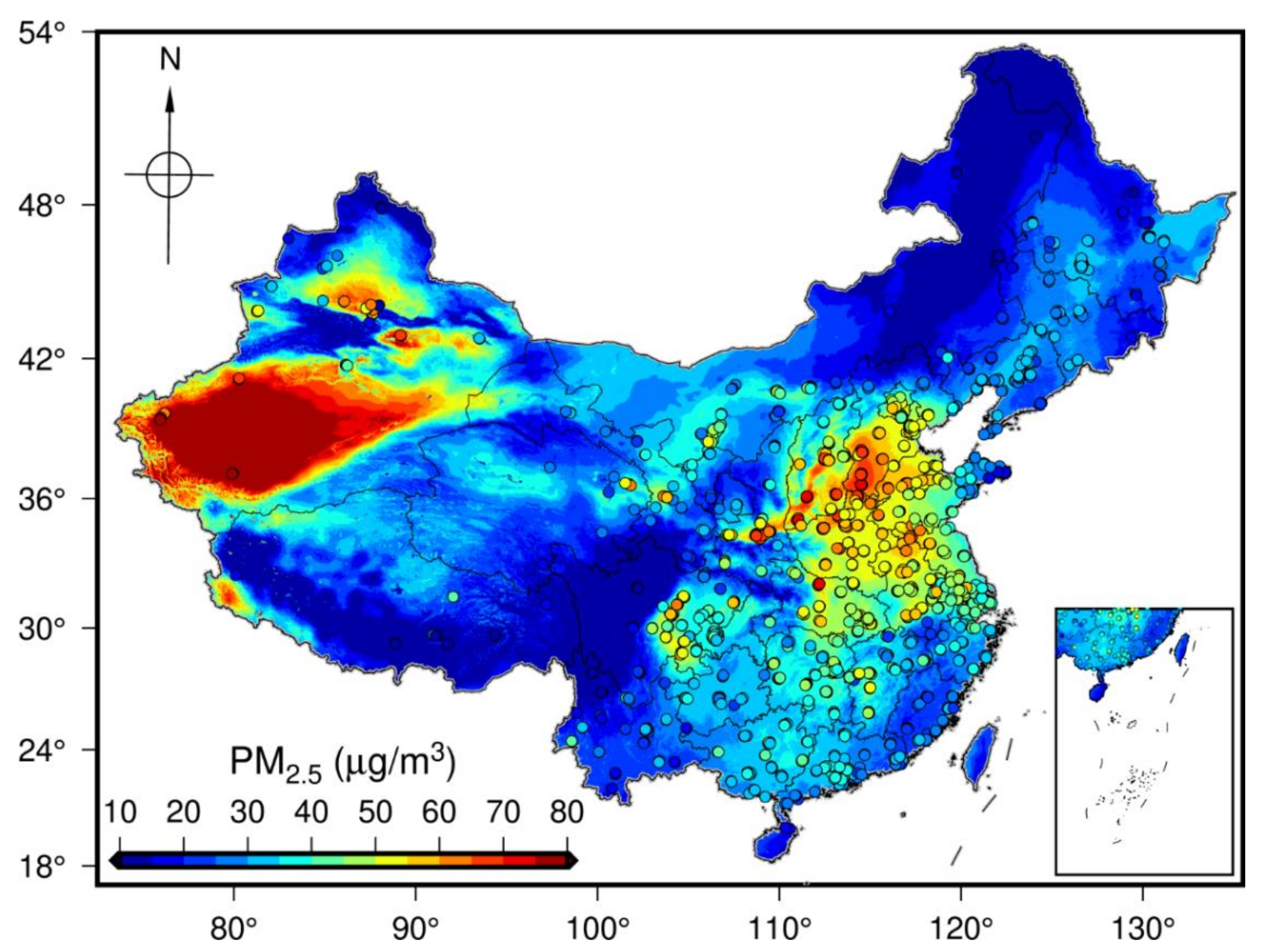
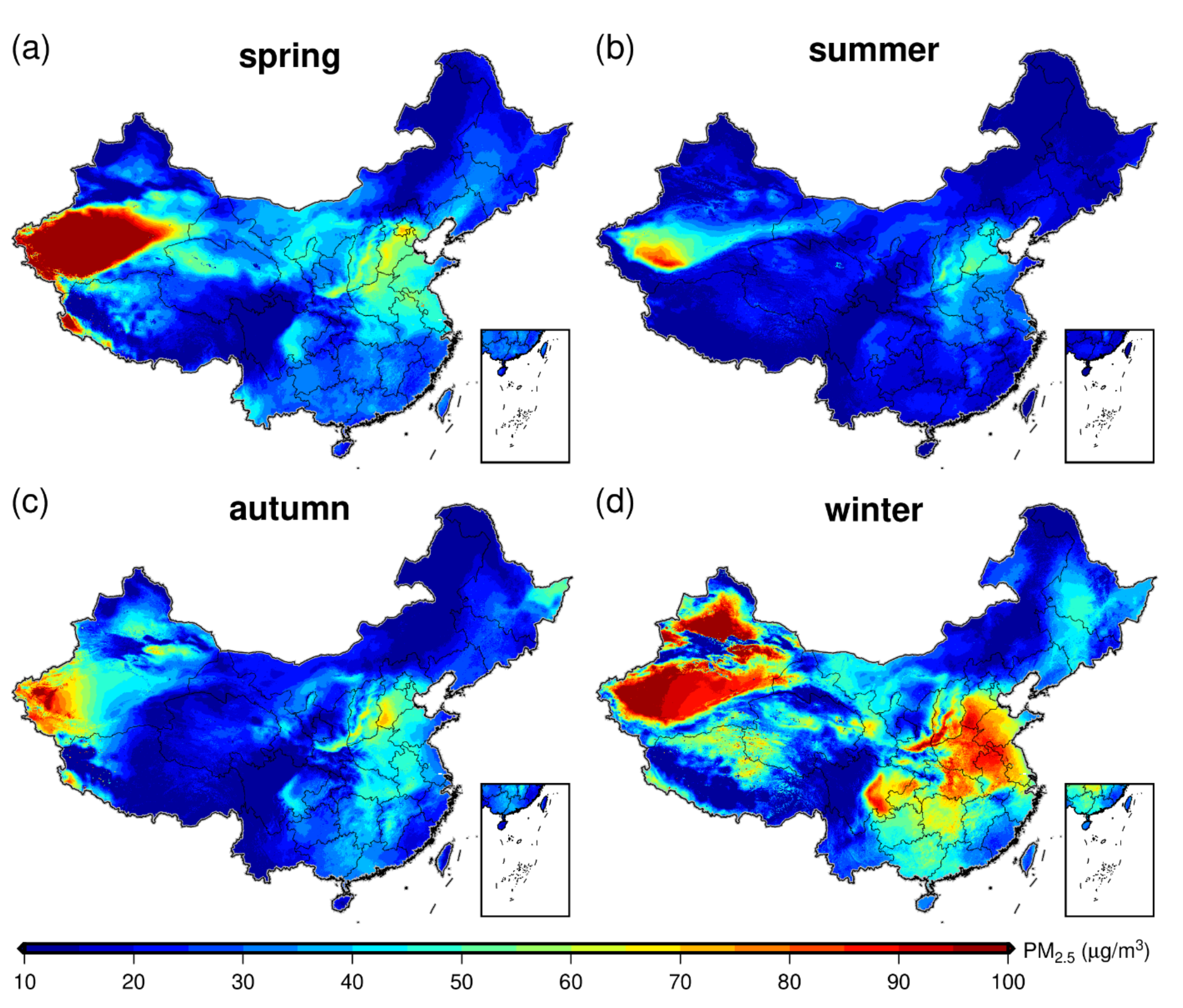
4.3. Annual Mapping and Seasonal Variations
5. Discussion
5.1. Applicability and Superiority of the GNNWR Model
5.2. Accuracy and Reasonability of Satellite-Derived PM2.5 Mappings
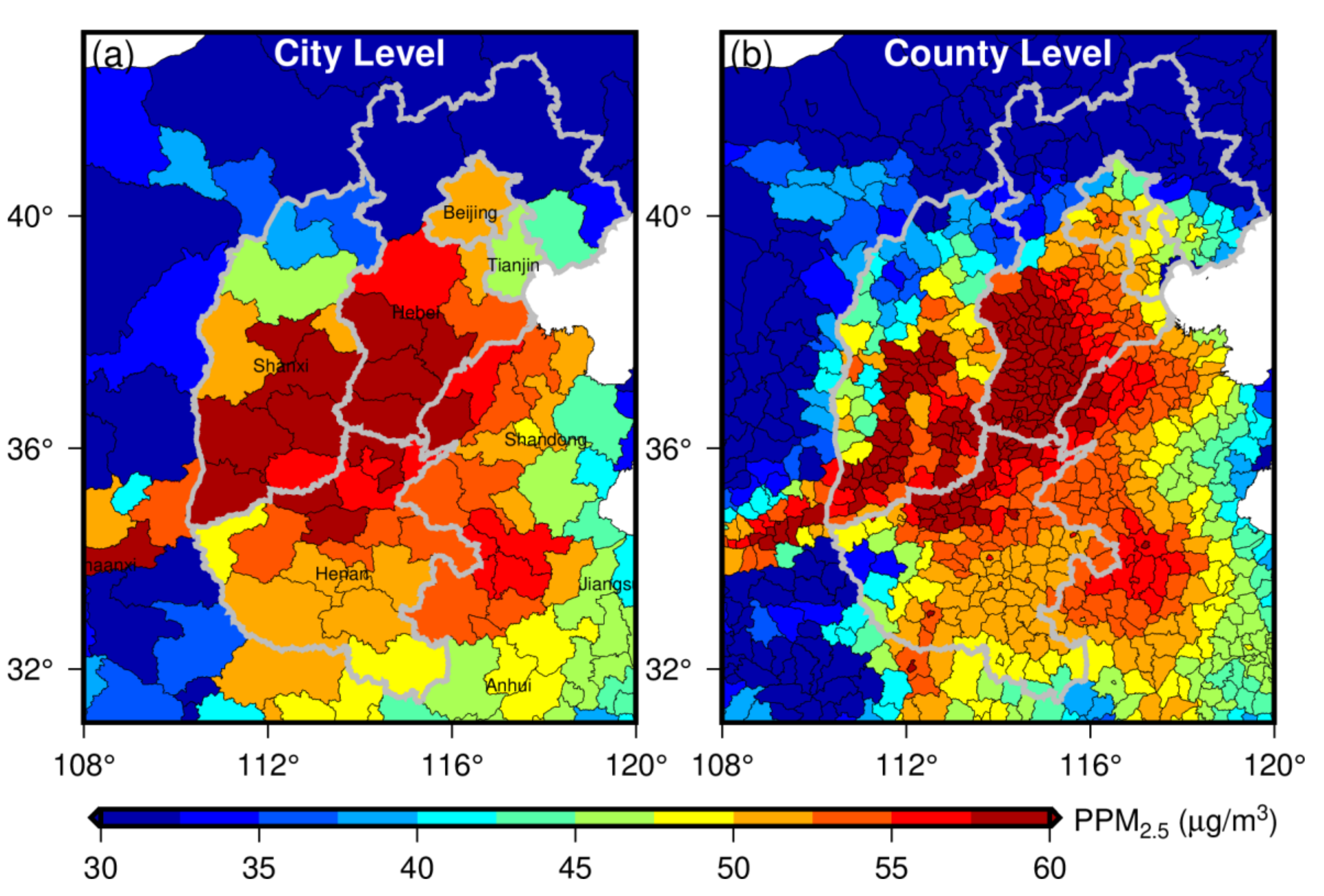
5.3. Analysis of Fine-Scale Population Exposures at Multiple Levels
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dominici, F.; Peng, R.D.; Bell, M.L.; Pham, L.; McDermott, A.; Zeger, S.L.; Samet, J.M. Fine particulate air pollution and hospital admission for cardiovascular and respiratory diseases. JAMA 2006, 295, 1127–1134. [Google Scholar] [CrossRef]
- Bartell, S.M.; Longhurst, J.; Tjoa, T.; Sioutas, C.; Delfino, R.J. Particulate air pollution, ambulatory heart rate variability, and cardiac arrhythmia in retirement community residents with coronary artery disease. Environ. Health Persp. 2013, 121, 1135–1141. [Google Scholar] [CrossRef]
- Peng, J.; Chen, S.; Lü, H.; Liu, Y.; Wu, J. Spatiotemporal patterns of remotely sensed PM2.5 concentration in China from 1999 to 2011. Remote Sens. Environ. 2016, 174, 109–121. [Google Scholar] [CrossRef]
- Chang, Y. China needs a tighter PM2.5 limit and a change in priorities. Environ. Sci. Technol. 2012, 46, 7069–7070. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, G.; Saari, R.K.; Li, S.; Liu, X.; Li, J. Quantifying PM2.5 mass concentration and particle radius using satellite data and an optical-mass conversion algorithm. ISPRS J. Photogramm. Remote Sens. 2019, 158, 90–98. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef] [PubMed]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Wang, W. Estimating national-scale ground-level PM2.5 concentration in China using geographically weighted regression based on MODIS and MISR AOD. Environ. Sci. Pollut. Res. 2016, 23, 8327–8338. [Google Scholar] [CrossRef]
- Hu, Z. Spatial analysis of MODIS aerosol optical depth, PM2.5, and chronic coronary heart disease. Int. J. Health Geogr. 2009, 8, 27. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Lv, B.; Hu, Y.; Chang, H.H.; Russell, A.G.; Bai, Y. Improving the Accuracy of Daily PM2.5 Distributions Derived from the Fusion of Ground-Level Measurements with Aerosol Optical Depth Observations, a Case Study in North China. Environ. Sci. Technol. 2016, 50, 4752–4759. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Tang, Q.; Gong, D.; Zhang, Z. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
- Yu, W.; Liu, Y.; Ma, Z.; Bi, J. Improving satellite-based PM2.5 estimates in China using Gaussian processes modeling in a Bayesian hierarchical setting. Sci. Rep. 2017, 7, 7048. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, J.; Meng, X.; Fang, Y.; Ge, Y.; Wang, J.; Wang, C.; Wu, J.; Kan, H. Estimation of PM2.5 concentrations at a high spatiotemporal resolution using constrained mixed-effect bagging models with MAIAC aerosol optical depth. Remote Sens. Environ. 2018, 217, 573–586. [Google Scholar] [CrossRef]
- Chen, W.; Ran, H.; Cao, X.; Wang, J.; Teng, D.; Chen, J.; Zheng, X. Estimating PM2. 5 with high-resolution 1-km AOD data and an improved machine learning model over Shenzhen, China. Sci. Total Environ. 2020, 746, 141093. [Google Scholar] [CrossRef]
- Yao, F.; Si, M.; Li, W.; Wu, J. A multidimensional comparison between MODIS and VIIRS AOD in estimating ground-level PM2.5 concentrations over a heavily polluted region in China. Sci. Total Environ. 2018, 618, 819–828. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Li, L. A robust deep learning approach for spatiotemporal estimation of satellite AOD and PM2.5. Remote Sens. 2020, 12, 264. [Google Scholar] [CrossRef]
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellite. Geosci. Remote 2013, 52, 1142–1156. [Google Scholar] [CrossRef]
- Yao, F.; Wu, J.; Li, W.; Peng, J. Estimating Daily PM2. 5 Concentrations in Beijing Using 750-M VIIRS IP AOD Retrievals and a Nested Spatiotemporal Statistical Model. Remote Sens. 2019, 11, 841. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. Atmos. 2013, 118, 664–678. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, B.; Gong, W.; Shi, Y.; Jin, S. Impact of environmental pollution on the retrieval of AOD products from Visible Infrared Imaging Radiometer Suite (VIIRS) over wuhan. Atmos. Pollut. Res. 2019, 10, 2063–2071. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, H.; Choi, M.; Li, S.; Kondragunta, S.; Kim, J.; Holben, B.; Levy, R.C.; Liu, Y. Evaluation of VIIRS, GOCI, and MODIS Collection 6 AOD retrievals against ground sunphotometer observations over East Asia. Atmos. Chem. Phys. 2016, 16, 1255. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. Atmos. 2009, 114, D14. [Google Scholar] [CrossRef]
- Benas, N.; Beloconi, A.; Chrysoulakis, N. Estimation of urban PM10 concentration, based on MODIS and MERIS/AATSR synergistic observations. Atmos. Environ. 2013, 79, 448–454. [Google Scholar] [CrossRef]
- Xiao, L.; Lang, Y.; Christakos, G. High-resolution spatiotemporal mapping of PM2.5 concentrations at Mainland China using a combined BME-GWR technique. Atmos. Environ. 2018, 173, 295–305. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Pan, X.; Wang, W. National-scale estimates of ground-level PM2.5 concentration in China using geographically weighted regression based on 3 km resolution MODIS AOD. Remote Sens. 2016, 8, 184. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern US using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Li, S.; Zou, B.; Sang, H.; Fang, X.; Xu, S. An improved geographically weighted regression model for PM2.5 concentration estimation in large areas. Atmos. Environ. 2018, 181, 145–154. [Google Scholar] [CrossRef]
- Memarianfard, M.; Hatami, A.M.; Memarianfard, M. Artificial neural network forecast application for fine particulate matter concentration using meteorological data. Glob. J. Environ. Sci. Manag. 2017, 3, 333–340. [Google Scholar]
- Shen, H.; Li, T.; Yuan, Q.; Zhang, L. Estimating regional ground-Level PM2.5 directly from satellite top-of-atmosphere reflectance using deep belief networks. J. Geophys. Res. Atmos. 2018, 123, 13875–13886. [Google Scholar] [CrossRef]
- Ceylan, Z.; Bulkan, S. Forecasting PM10 levels using ANN and MLR: A case study for Sakarya City. Glob. NEST J. 2018, 20, 281–290. [Google Scholar]
- Chen, Y. Prediction algorithm of PM2.5 mass concentration based on adaptive BP neural network. Computing 2018, 100, 825–838. [Google Scholar] [CrossRef]
- Lyu, H.; Dai, T.; Zheng, Y.; Shi, G.; Nakajima, T. Estimation of PM2.5 concentrations over Beijing with MODIS AODs using an artificial neural network. Sola 2018, 14, 14–18. [Google Scholar] [CrossRef]
- Li, J.; Jin, M.; Li, H. Exploring spatial influence of remotely sensed PM2.5 concentration using a developed deep convolutional neural network model. Int. J. Environ. Res. Public Health 2019, 16, 454. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, S.; Jiao, L.; Taylor, M.; Zhang, B.; Xu, G.; Hou, H. Estimation of PM2.5 Concentrations in China Using a Spatial Back Propagation Neural Network. Sci. Rep. 2019, 9, 13788. [Google Scholar]
- Mirzaei, M.; Amanollahi, J.; Tzanis, C.G. Evaluation of linear, nonlinear, and hybrid models for predicting PM2.5 based on a GTWR model and MODIS AOD data. Air Qual. Atmos. Health 2019, 12, 1215–1224. [Google Scholar] [CrossRef]
- Zang, L.; Mao, F.; Guo, J.; Gong, W.; Wang, W.; Pan, Z. Estimating hourly PM1 concentrations from Himawari-8 aerosol optical depth in China. Environ. Pollut. 2018, 241, 654–663. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- Chen, J.; de Hoogh, K.; Gulliver, J.; Hoffmann, B.; Hertel, O.; Ketzel, M.; Bauwelinck, M.; van Donkelaar, A.; Hvidtfeldt, U.A.; Katsouyanni, K.; et al. A comparison of linear regression, regularization, and machine learning algorithms to develop Europe-wide spatial models of fine particles and nitrogen dioxide. Environ. Int. 2019, 130, 104934. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Tong, D.; Zheng, B.; Li, X.; Zhu, T.; Zhang, Q. Spatiotemporal continuous estimates of PM2.5 concentrations in China, 2000–2016: A machine learning method with inputs from satellites, chemical transport model, and ground observations. Environ. Int. 2019, 123, 345–357. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J.; Zhong, C.; Ji, D.; Huang, W. Satellite-derived spatiotemporal PM2.5 concentrations and variations from 2006 to 2017 in China. Sci. Total Environ. 2020, 712, 134577. [Google Scholar] [CrossRef]
- Du, Z.; Wang, Z.; Wu, S.; Zhang, F.; Liu, R. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. Int. J. Geogr. Inf. Sci. 2020, 34, 1353–1377. [Google Scholar] [CrossRef]
- Wu, S.; Du, Z.; Wang, Y.; Lin, T.; Zhang, F.; Liu, R. Modeling spatially anisotropic nonstationary processes in coastal environments based on a directional geographically neural network weighted regression. Sci. Total Environ. 2020, 709, 136097. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Qi, J.; Wu, S.; Zhang, F.; Liu, R. A Spatially Weighted Neural Network Based Water Quality Assessment Method for Large-Scale Coastal Areas. Environ. Sci. Technol. 2021, 55, 2553–2563. [Google Scholar] [CrossRef] [PubMed]
- Beckers, J.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J.; Wang, T.; Dhital, Y.P.; Yao, R.; Yu, Y.; Lei, Z.; Zhao, R. Estimating high resolution daily air temperature based on remote sensing products and climate reanalysis datasets over glacierized basins: A case study in the Langtang Valley, Nepal. Remote Sens. 2017, 9, 959. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Integrating MODIS and CYCLOPES leaf area index products using empirical orthogonal functions. IEEE Trans. Geosci. Remote 2010, 49, 1513–1519. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Wu, J.; Yao, F.; Li, W.; Si, M. VIIRS-based remote sensing estimation of ground-level PM2.5 concentrations in Beijing-Tianjin-Hebei: A spatiotemporal statistical model. Remote Sens. Environ. 2016, 184, 316–328. [Google Scholar] [CrossRef]
- Wang, X.; Dong, Z.; Zhang, J.; Liu, L. Modern dust storms in China: An overview. J. Arid Environ. 2004, 58, 559–574. [Google Scholar] [CrossRef]
- Han, Y.; Fang, X.; Zhao, T.; Bai, H.; Kang, S.; Song, L. Suppression of precipitation by dust particles originated in the Tibetan Plateau. Atmos. Environ. 2009, 43, 568–574. [Google Scholar] [CrossRef]
- Zhu, J.; Liao, H.; Li, J. Increases in aerosol concentrations over eastern China due to the decadal-scale weakening of the East Asian summer monsoon. Geophys. Res. Lett. 2012, 39, 39. [Google Scholar] [CrossRef]
- Zhao, C.; Tie, X.; Lin, Y. A possible positive feedback of reduction of precipitation and increase in aerosols over eastern central China. Geophys. Res. Lett. 2006, 33, 33. [Google Scholar] [CrossRef]
- Yu, Y.; Schleicher, N.; Norra, S.; Fricker, M.; Dietze, V.; Kaminski, U.; Cen, K.; Stüben, D. Dynamics and origin of PM2.5 during a three-year sampling period in Beijing, China. J. Environ. Monit. 2011, 13, 334–346. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.A.S.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef]
- Chen, L.; Gao, S.; Zhang, H.; Sun, Y.; Ma, Z.; Vedal, S.; Mao, J.; Bai, Z. Spatiotemporal modeling of PM2.5 concentrations at the national scale combining land use regression and Bayesian maximum entropy in China. Environ. Int. 2018, 116, 300–307. [Google Scholar] [CrossRef]
- Yao, F.; Wu, J.; Li, W.; Peng, J. A spatially structured adaptive two-stage model for retrieving ground-level PM2.5 concentrations from VIIRS AOD in China. ISPRS J. Photogramm. 2019, 151, 263–276. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1 km resolution PM2.5 estimates across China using enhanced space-time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based high-resolution PM2.5 estimation over the Beijing-Tianjin-Hebei region of China using an improved geographically and temporally weighted regression model. Environ. Pollut. 2018, 236, 1027–1037. [Google Scholar] [CrossRef] [PubMed]
- Brauer, M.; Amann, M.; Burnett, R.T.; Cohen, A.; Dentener, F.; Ezzati, M.; Henderson, S.B.; Krzyzanowski, M.; Martin, R.V.; Van Dingenen, R. Exposure assessment for estimation of the global burden of disease attributable to outdoor air pollution. Environ. Sci. Technol. 2012, 46, 652–660. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Li, Y.; Lau, A.K.H.; Deng, X.; Tse, T.K.T.; Fung, J.C.H.; Li, C.; Li, Z.; Lu, X.; Zhang, X.; et al. Estimation of long-term population exposure to PM2.5 for dense urban areas using 1-km MODIS data. Remote Sens. Environ. 2016, 179, 13–22. [Google Scholar] [CrossRef]

| Model | 10-Fold Cross-Validation (Fitting) | Evaluation (Prediction) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | |||||||||||||
| R2 | RMSE | MAE | MAPE | Bias | R2 | RMSE | MAE | MAPE | Bias | R2 | RMSE | MAE | MAPE | Bias | |
| OLR | 0.61 | 14.27 | 9.51 | 29% | 0.00 | 0.60 | 14.43 | 9.61 | 29% | 0.01 | 0.64 | 12.86 | 9.27 | 0.265 | −0.07 |
| GWR-AFG | 0.82 | 9.60 | 6.76 | 20% | −0.26 | 0.71 | 12.20 | 7.46 | 23% | −0.19 | 0.77 | 10.17 | 7.26 | 0.203 | −0.48 |
| GWR-AAB | 0.87 | 8.36 | 5.62 | 17% | −0.06 | 0.81 | 9.87 | 6.47 | 20% | −0.10 | 0.83 | 8.78 | 6.32 | 0.183 | −0.22 |
| GRNN | 0.88 | 7.84 | 5.26 | 15% | 0.27 | 0.79 | 10.42 | 6.97 | 21% | 0.48 | 0.81 | 9.17 | 6.64 | 0.192 | 0.36 |
| GNNWR | 0.90 | 7.27 | 4.92 | 15% | 0.14 | 0.86 | 8.50 | 5.89 | 18% | 0.00 | 0.85 | 8.17 | 5.87 | 0.170 | −0.30 |
| Model | 0–50 µg/m3 | 50–100 µg/m3 | >100 µg/m3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE | Bias | RMSE | MAE | MAPE | Bias | RMSE | MAE | MAPE | Bias | |
| OLR | 10.38 | 7.77 | 32% | 3.44 | 15.21 | 11.89 | 18% | −6.92 | 58.09 | 46.54 | 35% | −46.49 |
| GWR-AFG | 8.22 | 5.67 | 23% | 1.80 | 12.12 | 9.39 | 14% | −4.75 | 30.88 | 26.05 | 21% | −24.24 |
| GWR-AAB | 6.96 | 4.90 | 20% | 1.28 | 10.20 | 7.73 | 12% | −2.93 | 28.04 | 19.87 | 15% | −17.51 |
| GRNN | 6.80 | 4.68 | 18% | 1.99 | 10.11 | 7.84 | 12% | −3.21 | 27.22 | 20.97 | 17% | −19.70 |
| GNNWR | 6.26 | 4.43 | 17% | 1.02 | 9.24 | 6.92 | 10% | −2.25 | 21.43 | 14.83 | 12% | −8.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wu, S.; Wang, Y.; Zhang, F.; Liu, R.; Du, Z. Satellite-Based Mapping of High-Resolution Ground-Level PM2.5 with VIIRS IP AOD in China through Spatially Neural Network Weighted Regression. Remote Sens. 2021, 13, 1979. https://doi.org/10.3390/rs13101979
Chen Y, Wu S, Wang Y, Zhang F, Liu R, Du Z. Satellite-Based Mapping of High-Resolution Ground-Level PM2.5 with VIIRS IP AOD in China through Spatially Neural Network Weighted Regression. Remote Sensing. 2021; 13(10):1979. https://doi.org/10.3390/rs13101979
Chicago/Turabian StyleChen, Yijun, Sensen Wu, Yuanyuan Wang, Feng Zhang, Renyi Liu, and Zhenhong Du. 2021. "Satellite-Based Mapping of High-Resolution Ground-Level PM2.5 with VIIRS IP AOD in China through Spatially Neural Network Weighted Regression" Remote Sensing 13, no. 10: 1979. https://doi.org/10.3390/rs13101979
APA StyleChen, Y., Wu, S., Wang, Y., Zhang, F., Liu, R., & Du, Z. (2021). Satellite-Based Mapping of High-Resolution Ground-Level PM2.5 with VIIRS IP AOD in China through Spatially Neural Network Weighted Regression. Remote Sensing, 13(10), 1979. https://doi.org/10.3390/rs13101979







