Remote Estimation of Trophic State Index for Inland Waters Using Landsat-8 OLI Imagery
Abstract
:1. Introduction
2. Materials and Methods
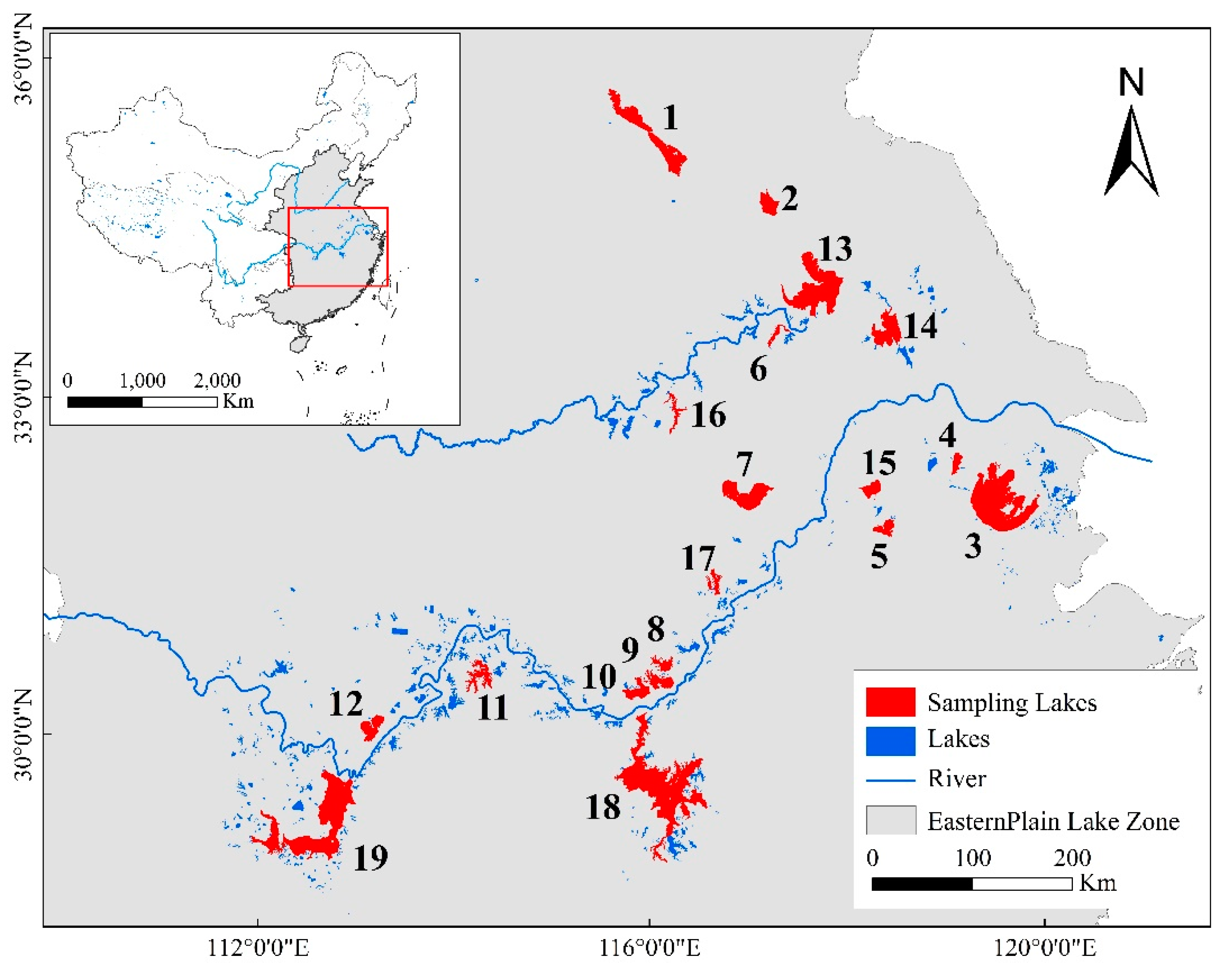
2.1. Study Area
2.2. Data Acquisition
2.2.1. Field Measurement
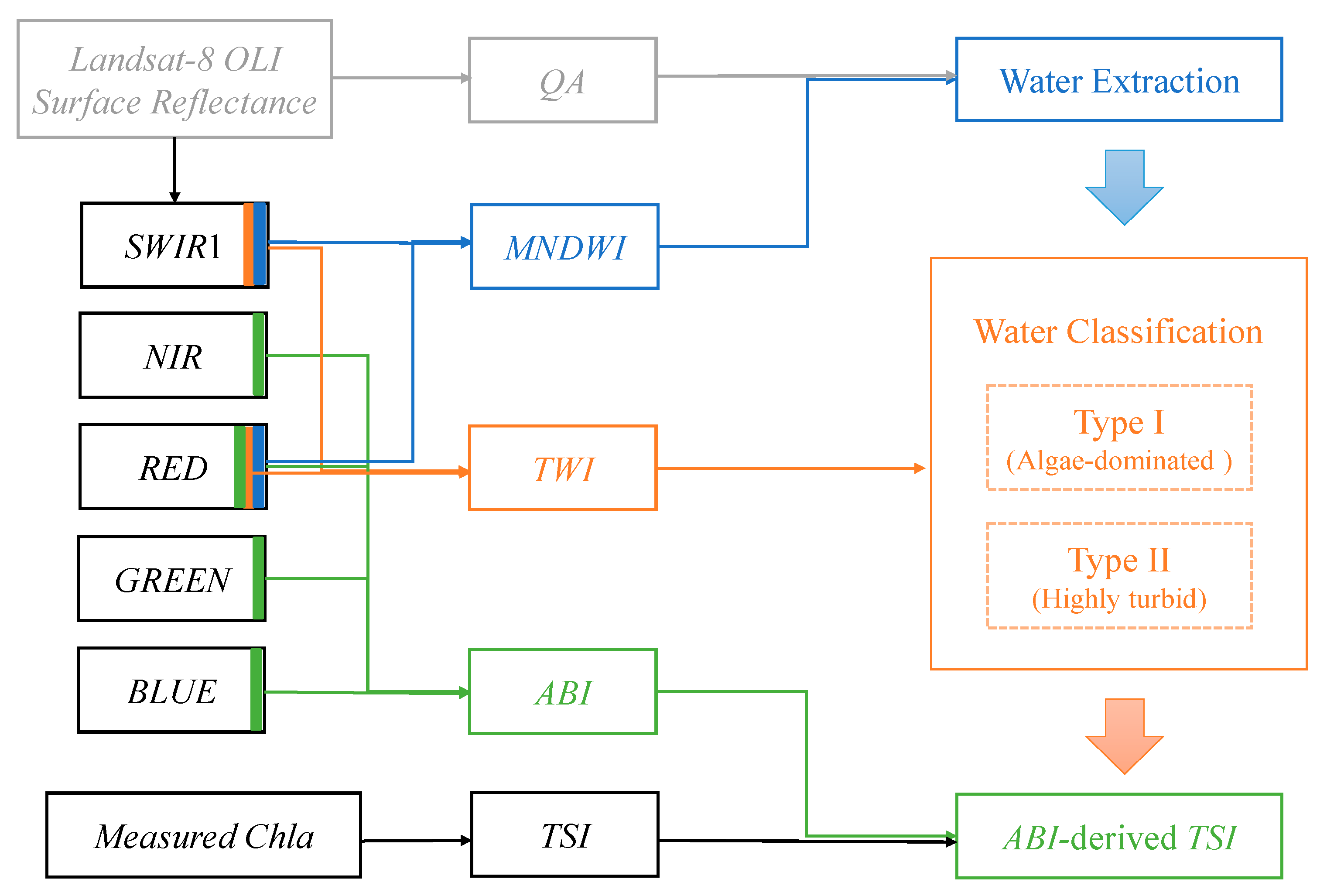
2.2.2. Satellite Images Processing
2.3. TSI Estimation from OLI Imagery
2.3.1. Turbid Water Index
2.3.2. Trophic State Index
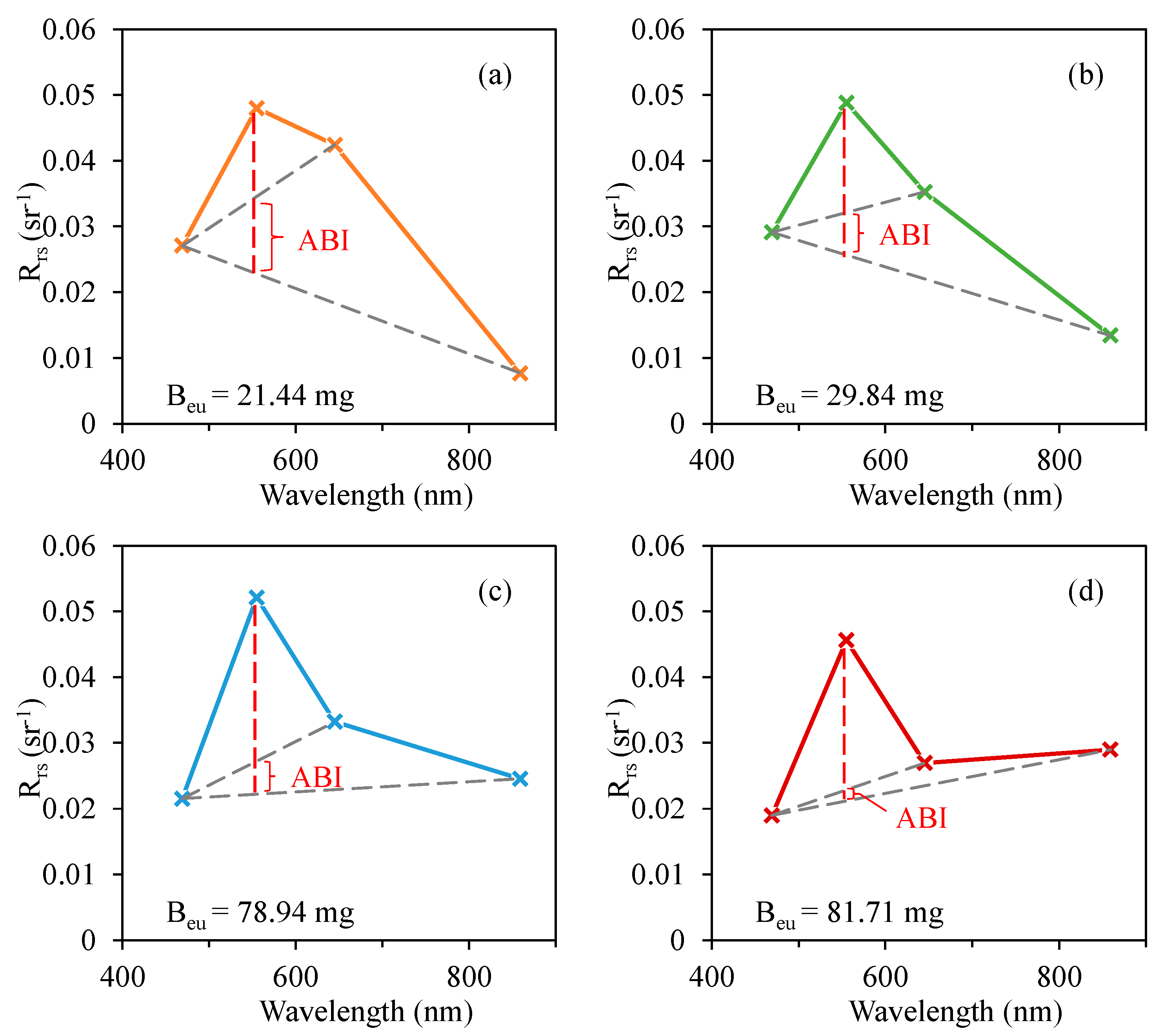
2.3.3. Algal Biomass Index
2.4. Accuracy Assessment
3. Results
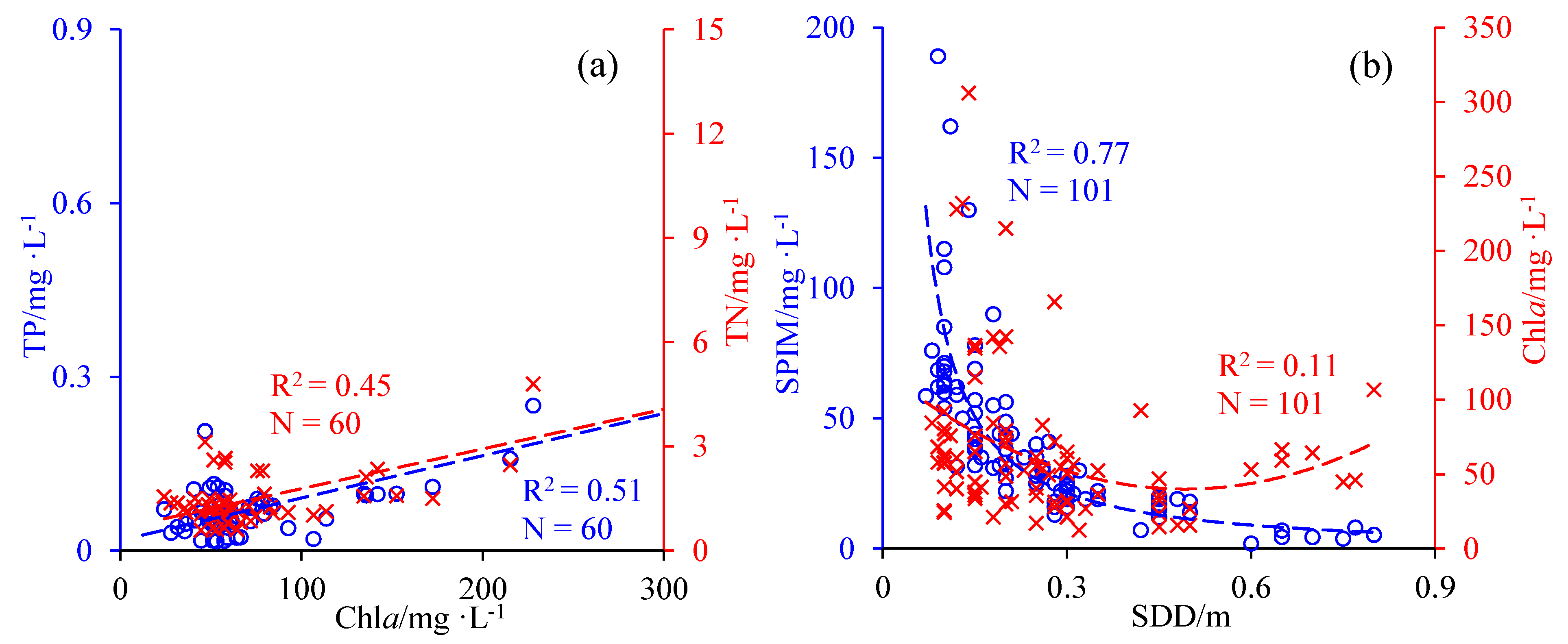
3.1. Characteristics of Water Quality Parameters in Sampling Lakes
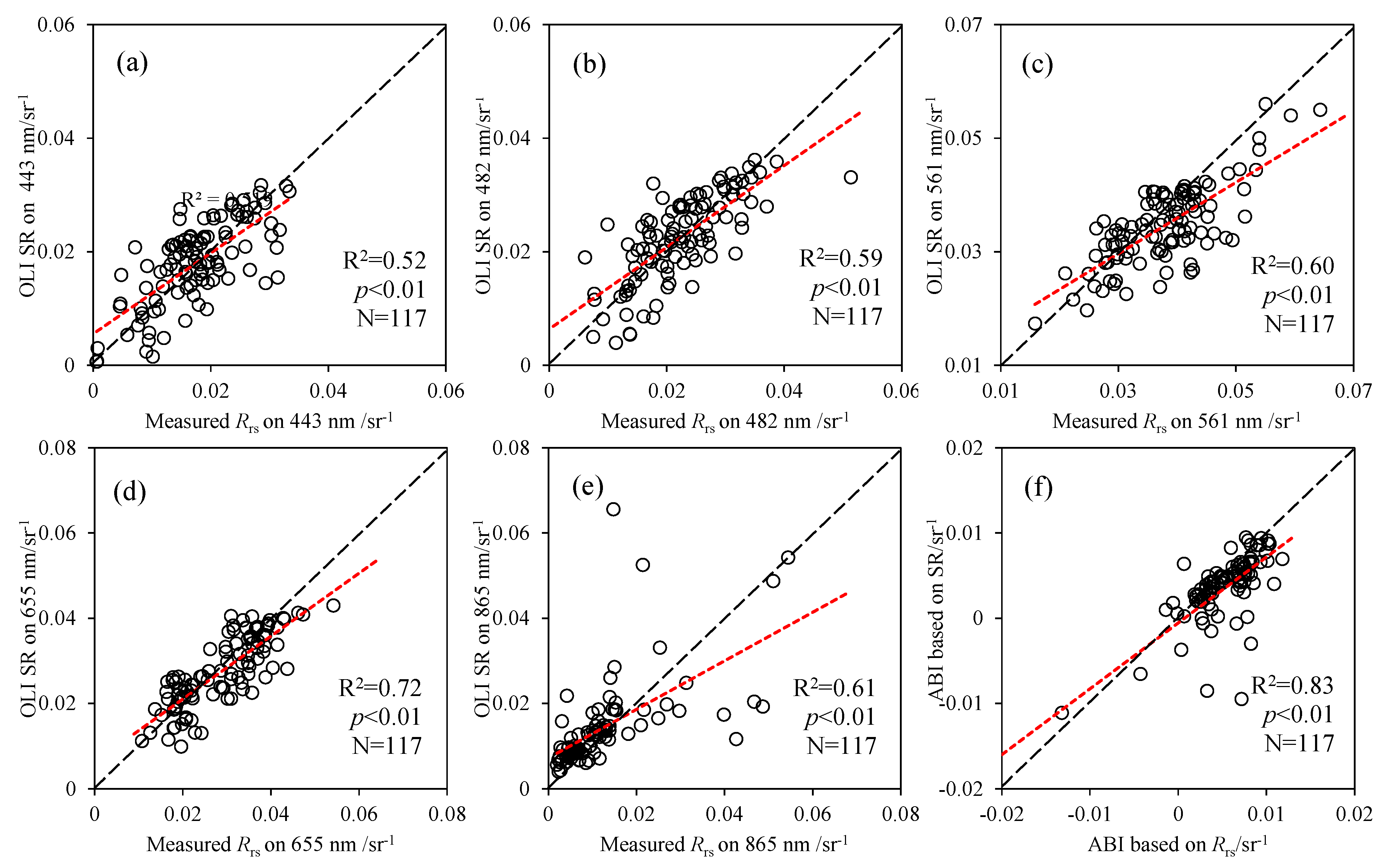
3.2. Consistency of OLI Product Data
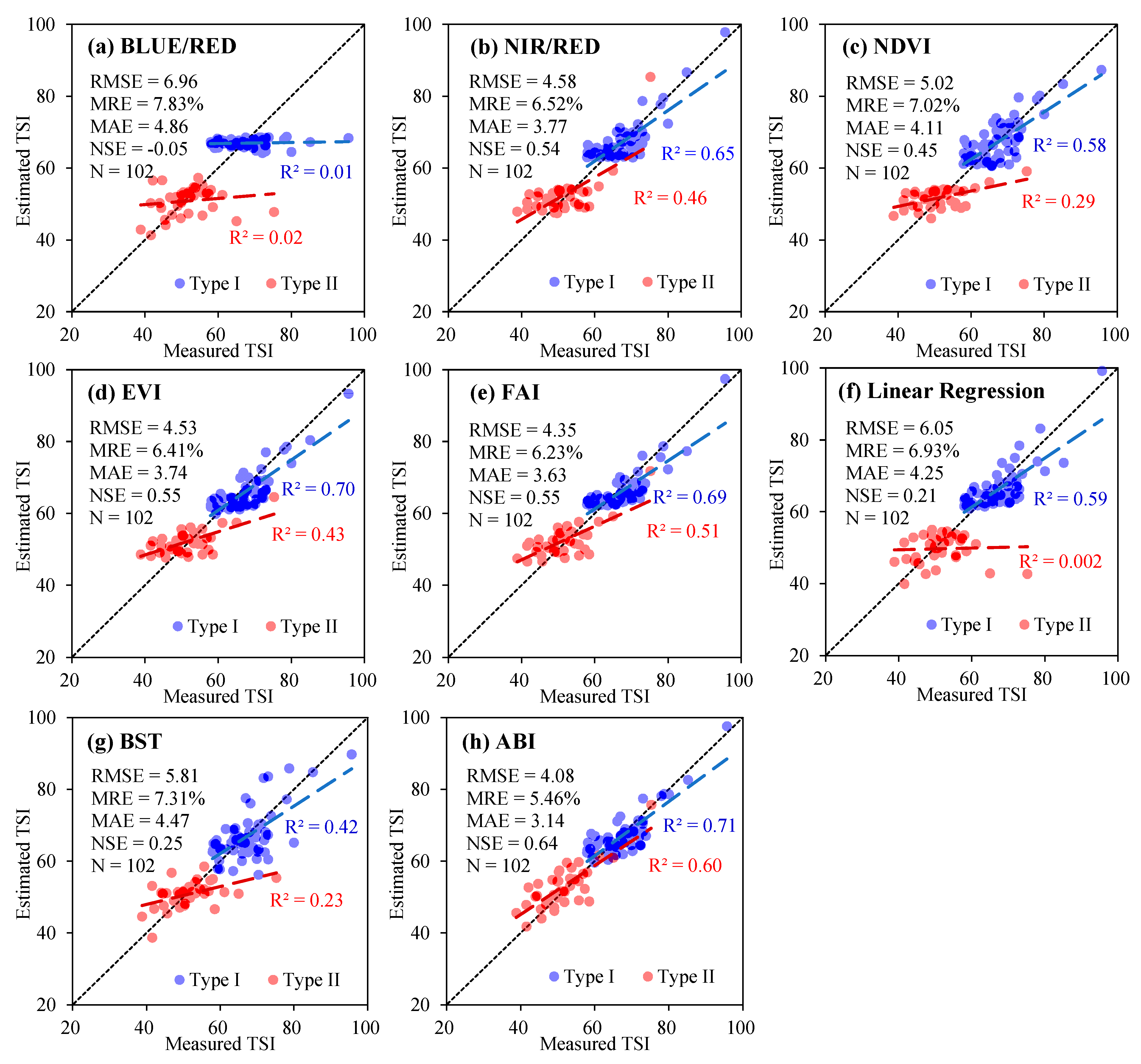
3.3. Performance of ABI-Derived TSI
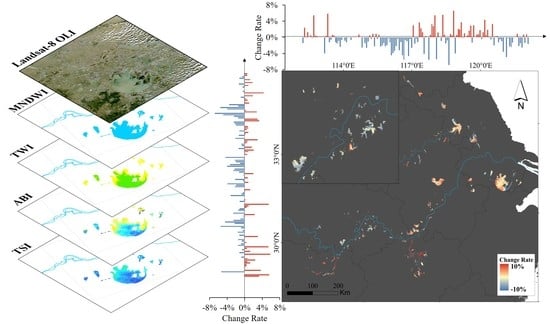
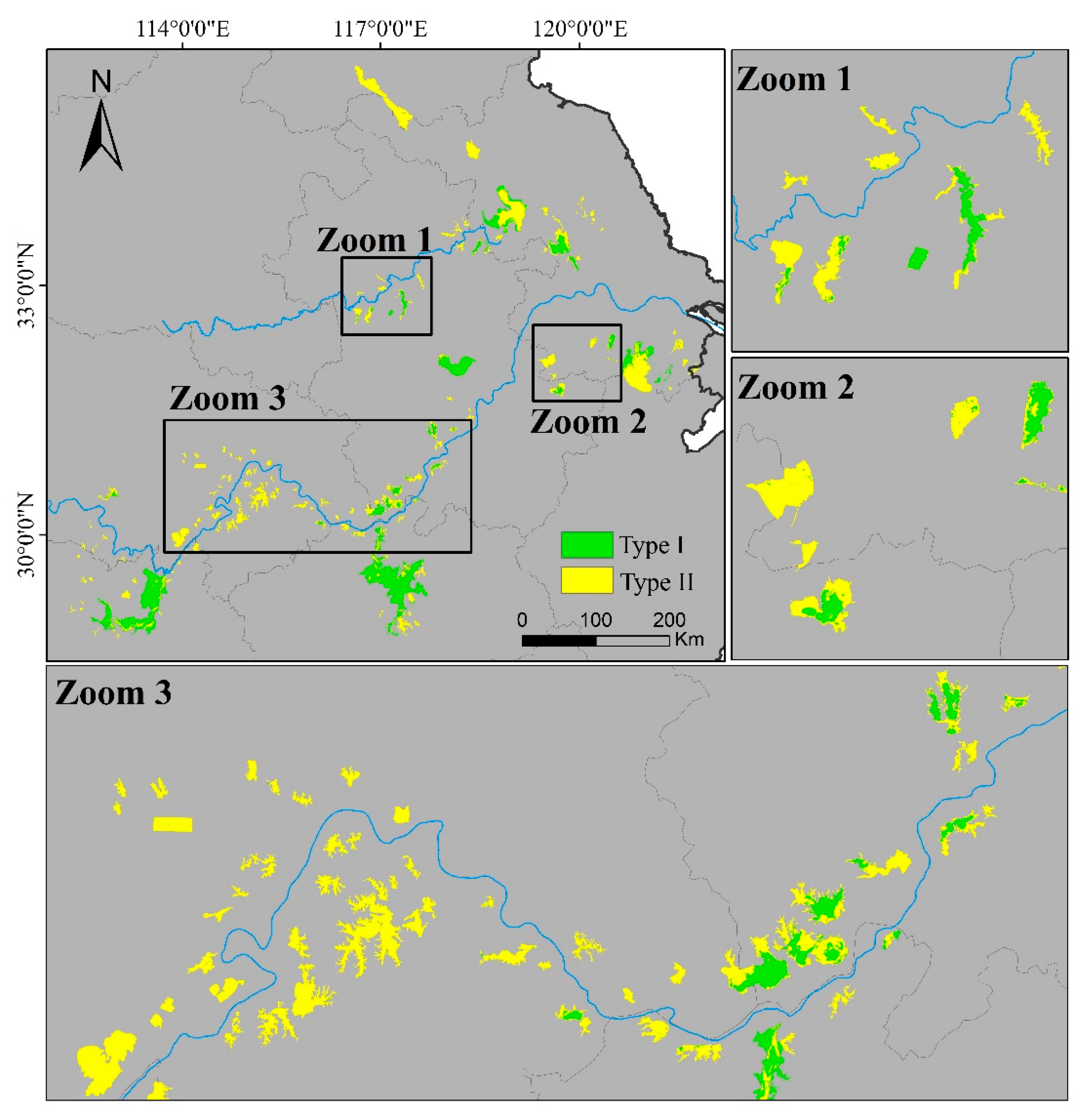
3.4. Spatial Distribution of TSI for Lakes in the EPL
3.5. Temporal Dynamics of TSI for Lakes in the EPL
4. Discussion
4.1. Limits of Algorithm
4.2. Prospects of Algorithm
4.2.1. Applicability to Other Sensors
4.2.2. Applicability to Other Lakes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, Y.; Jiang, W.; Tang, Z.; Ling, Z.; Wu, Z. Long-Term Changes of Open-Surface Water Bodies in the Yangtze River Basin Based on the Google Earth Engine Cloud Platform. Remote Sens. 2019, 11, 2213. [Google Scholar] [CrossRef] [Green Version]
- Song, K.; Liu, G.; Wang, Q.; Wen, Z.; Lyu, L.; Du, Y.; Sha, L.; Fang, C. Quantification of lake clarity in China using Landsat OLI imagery data. Remote Sens. Environ. 2020, 243, 111800. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Smith, V.H. Eutrophication of freshwater and coastal marine ecosystems a global problem. Environ. Ence Pollut. Res. Int. 2003, 10, 126. [Google Scholar] [CrossRef]
- Ho, J.C.; Michalak, A.M.; Pahlevan, N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature 2019, 574, 667–670. [Google Scholar] [CrossRef]
- Le, C.; Zha, Y.; Li, Y.; Sun, D.; Lu, H.; Yin, B. Eutrophication of Lake Waters in China: Cost, Causes, and Control. Environ. Manag. 2010, 45, 662–668. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, Y.; Ma, R.; Zhang, Y. Spatial and Temporal Dynamics of Floating Algae Blooms of Lake Chaohu in 2016 and Environmental drivers. Environ. Sci. 2018, 39, 4925–4937. [Google Scholar]
- Hatvani, I.G.; Barros, V.D.D.; Tanos, P.; Kovacs, J.; Clement, A. Spatiotemporal changes and drivers of trophic status over three decades in the largest shallow lake in Central Europe, Lake Balaton. Ecol. Eng. 2020, 151, 105861. [Google Scholar] [CrossRef]
- Adamovich, B.V.; Zhukova, T.V.; Mikheeva, T.M.; Kovalevskaya, R.Z.; Yanova, E. Long-term variations of the trophic state index in the Narochanskie Lakes and its relation with the major hydroecological parameters. Water Resour. 2016, 43, 809–817. [Google Scholar] [CrossRef]
- Dodds, W.K. Trophic state, eutrophication and nutrient criteria in streams. Trends Ecol. Evol. 2007, 22, 669–676. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Zhang, Y.; Song, K.; Liu, M.; Qin, B. A semi-analytical approach for remote sensing of trophic state in inland waters: Bio-optical mechanism and application. Remote Sens. Environ. 2019, 232, 111349. [Google Scholar] [CrossRef]
- Carlson, R.E. A Trophic State Index for Lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Aizaki, M.; Otsuki, A.; Fukushima, T.; Hosomi, M.; Muraoka, K. Application of Carlson’s trophic state index to Japanese lakes and relationships between the index and other parameters. Proc. Int. Assoc. Theor. Appl. Limnol. 1981, 16, 19–22. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H. Trophic state index and its correlation with lake parameters. Acta Sci. Circumstantiae 1993, 13, 391–397. [Google Scholar] [CrossRef]
- Vollenweider, R.A.; Kerekes, J. Eutrophication of waters. Monitoring, assessment and control. In OECD Cooperative Programme on Monitoring of Inland Waters (Eutrophication Control). Environment Directorate; OECD: Washington, DC, USA, 1982; p. 154. [Google Scholar]
- Carlson, R.E.; Havens, K.E. Simple Graphical Methods for the Interpretation of Relationships Between Trophic State Variables. Lake Reserv. Manag. 2005, 21, 107–118. [Google Scholar] [CrossRef]
- Walsh, J.R.; Carpenter, S.R.; Zanden, M.J.V. Invasive species triggers a massive loss of ecosystem services through a trophic cascade. Proc. Natl. Acad. Sci. USA 2016, 113, 201600366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.M. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Thiemann, S.; Kaufmann, H. Determination of Chlorophyll Content and Trophic State of Lakes Using Field Spectrometer and IRS-1C Satellite Data in the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2000, 73, 227–235. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, J.; Du, G. Use of satellite imagery to assess the trophic state of Miyun Reservoir, Beijing, China. Environ. Pollut. 2008, 155, 13–19. [Google Scholar]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D. Euphotic depth: Retrieval from in situ reflectance and application in assessing eutrophication. Acta Ecol. Sin. 2008, 28, 2614–2621. [Google Scholar]
- Butt, M.J.; Nazeer, M. Landsat ETM+ Secchi Disc Transparency (SDT) retrievals for Rawal Lake, Pakistan. Adv. Space Res. 2015, 56, S0273117715004780. [Google Scholar] [CrossRef]
- Liu, D.; Duan, H.; Yu, S.; Shen, M.; Xue, K. Human-induced eutrophication dominates the bio-optical compositions of suspended particles in shallow lakes: Implications for remote sensing. Sci. Total Environ. 2019, 667, 112–123. [Google Scholar] [CrossRef] [PubMed]
- Iwashita, K.; Kudoh, K.; Fujii, H.; Nishikawa, H. Satellite analysis for water flow of Lake Inbanuma. Adv. Space Res. 2004, 33, 284–289. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, M.; Tang, X. Eutrophication assessment of seasonal urban lakes in China Yangtze River Basin using Landsat 8-derived Forel-Ule index: A six-year (2013–2018) observation. Sci. Total Environ. 2020, 745, 135392. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Bing, Z.; Spyrakos, E.; Tyler, A.; Shen, Q.; Zhang, F.; Kuster, T.; Lehmann, M.; Wu, Y.; et al. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef] [Green Version]
- Wen, Z.; Song, K.; Liu, G.; Shang, Y.; Fang, C.; Du, J.; Lyu, L. Quantifying the trophic status of lakes using total light absorption of optically active components. Environ. Pollut. 2019, 245, 684–693. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.; Shi, K.; Qin, B.; Yao, B. Optical properties and composition changes in chromophoric dissolved organic matter along trophic gradients: Implications for monitoring and assessing lake eutrophication. Water Res. 2018, 131, 255–263. [Google Scholar] [CrossRef]
- Watanabe, F.S.Y.; Miyoshi, G.T.; Rodrigues, T.W.P.; Bernardo, N.; Lmai, N. Inland water’s trophic status classification based on machine learning and remote sensing data. Remote Sens. Appl. Soc. Environ. 2020, 19, 100326. [Google Scholar] [CrossRef]
- Babin, M.; Stramski, D.; Ferrari, M.G.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. Ocean. 2003, 108, C7. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 2008, 4086–4097. [Google Scholar] [CrossRef]
- Sass, G.Z.; Creed, I.F.; Bayley, S.E.; Devito, K. Understanding variation in trophic status of lakes on the Boreal Plain: A 20-year retrospective using Landsat TM imagery. Remote Sens. Environ. 2007, 109, 127–141. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral Remote Sensing of Total Phosphorus (TP) in Three Central Indiana Water Supply Reservoirs. WaterAirSoil Pollut. 2012, 223, 1481–1502. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H. Absorption characteristics of optically complex inland waters: Implications for water optical classification. J. Geophys. Res. Biogeoences 2013, 118, 860–874. [Google Scholar] [CrossRef]
- Kuhn, C.; Valerio, A.d.; Ward, N.; Loken, L.; Sawakuchi, H.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Mouw, C.B.; Greb, S.; Aurin, D.; Digiacomo, P.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Lymburner, L.; Botha, E.; Hestir, E.; Anstee, J.; Sagar, S.; Dekker, A.; Malthus, T. Landsat 8: Providing continuity and increased precision for measuring multi-decadal time series of total suspended matter. Remote Sens. Environ. 2016, 185, 108–118. [Google Scholar] [CrossRef]
- Nguyen, U.N.T.; Pham, L.T.H.; Dang, T.D. Correction to: An automatic water detection approach using Landsat 8 OLI and Google earth engine cloud computing to map lakes and reservoirs in New Zealand. Remote Sens. Environ. 2020, 191, 1–12. [Google Scholar] [CrossRef]
- Tepanosayn, G.; Muradyan, V.; Hovsepyan, A.; Minasyan, L.; Asmaryan, S. A Landsat 8 OLI Satellite Data-Based Assessment of Spatio-Temporal Variations of Lake Sevan Phytoplankton Biomass. Ann. Valahia Univ. Targoviste Geogr. 2017, 17, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Jeremy, P. Ocean color measurements with the Operational Land Imager on Landsat-8: Implementation and evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Page, B.P.; Finlay, J.C.; Brezonik, P.; Hozalski, R. Regional measurements and spatial/temporal analysis of CDOM in 10,000+ optically variable Minnesota Lakes using Landsat 8 imagery. Sci. Total Environ. 2020, 724, 138141. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Ma, R.; Duan, H.; Xue, K. Effects of broad bandwidth on the remote sensing of inland waters: Implications for high spatial resolution satellite data applications. ISPRS J. Photogramm. Remote Sens. 2019, 153, 110–122. [Google Scholar] [CrossRef]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Gilerson, A.; Gitelson, A.; Zhou, J.; Gurlin, D.; Ahmed, S. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109. [Google Scholar] [CrossRef] [Green Version]
- Gower, J.; King, S. Use of satellite images of chlorophyll fluorescence to monitor the spring bloom in coastal waters. Int. J. Remote Sens. 2012, 33, 7469–7481. [Google Scholar] [CrossRef]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- Han, L.; Jordan, K.J. Estimating and mapping chlorophyll-a concentration in Pensacola Bay, Florida using Landsat ETM+ data. Int. J. Remote Sens. 2005, 26, 5245–5254. [Google Scholar] [CrossRef]
- Ma, R.; Tang, J.; Dai, J. Bio-optical model with optimal parameter suitable for Taihu Lake in water colour remote sensing. Int. J. Remote Sens. 2006, 27, 4305–4328. [Google Scholar] [CrossRef]
- Duan, H.; Tao, M.; Loiselle, S.A.; Zhao, W.; Cao, Z.; Ma, R.; Tang, X. MODIS observations of cyanobacterial risks in a eutrophic lake: Implications for long-term safety evaluation in drinking-water source. Water Res. 2017, 122, 455–470. [Google Scholar] [CrossRef] [PubMed]
- Fernanda, W.; Enner, A.; Thanan, R.; Nilton, I.; Claudio, B.; Liuz, R. Estimation of Chlorophyll-a Concentration and the Trophic State of the Barra Bonita Hydroelectric Reservoir Using OLI/Landsat-8 Images. Int. J. Environ. Res. Public Health 2015, 12, 10391–10417. [Google Scholar]
- Hu, C.; He, M.X. Origin and Offshore Extent of Floating Algae in Olympic Sailing Area. Eos Trans. Am. Geophys. Union 2008, 89, 302–303. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; van Leeuwen, W. MODIS vegetation index (MOD13). Algorithm Theor. Basis Doc. 1999, 3, 295–309. [Google Scholar]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Erhan, A.; Gonca, C.H.; Ugur, A. Water Quality Determination of Küükekmece Lake, Turkey by Using Multispectral Satellite Data. Sci. World J. 2015, 9, 1215–1229. [Google Scholar]
- Mohammad, G.; Assefa, M.; Lakshmi, R. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Stumpf, R. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Prasad, S.; Saluja, R.; Garg, J.K. Assessing the efficacy of Landsat-8 OLI imagery derived models for remotely estimating chlorophyll-a concentration in the Upper Ganga River, India. Int. J. Remote Sens. 2020, 41, 2439–2456. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T.; Canh, B.D.; Thao, N.; Parsons, M. Landsat 8/OLI Two Bands Ratio Algorithm for Chlorophyll-A Concentration Mapping in Hypertrophic Waters: An Application to West Lake in Hanoi (Vietnam). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4919–4929. [Google Scholar] [CrossRef]
- Fernanda, W.; Enner, A.; Thanan, R.; Luiz, R.; Nariane, B.; Nilton, I. Remote sensing of the chlorophyll-a based on OLI/Landsat-8 and MSI/Sentinel-2A (Barra Bonita reservoir, Brazil). An. Da Acad. Bras. De Cienc. 2018, 90, 1987–2000. [Google Scholar]
- Shang, S.; Lee, Z.; Wei, G. Characterization of MODIS-derived euphotic zone depth: Results for the China Sea. Remote Sens. Environ. 2011, 115, 180–186. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Liu, X.; Wang, M.; Qin, B. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in Lake Taihu using MERIS data. Remote Sens. Environ. 2014, 140, 365–377. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Y.; Duan, H.; Ma, R. Variability of light absorption properties in optically complex inland waters of Lake Chaohu, China. J. Great Lakes Res. 2017, 43, 17–31. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, Y.; Ma, R.; Xue, K.; Cao, Z.; Chu, Q.; Jing, Y. Optimized remote sensing estimation of the lake algal biomass by considering the vertically heterogeneous chlorophyll distribution: Study case in Lake Chaohu of China. Sci. Total Environ. 2021, 771, 144811. [Google Scholar] [CrossRef] [PubMed]
- Harding, L.W.; Itsweire, E.C.; Esaias, W.E. Determination of phytoplankton chlorophyll concentrations in the Chesapeake Bay with aircraft remote sensing. Remote Sens. Environ. 1992, 40, 79–100. [Google Scholar] [CrossRef]
- Frolov, S.; Ryan, J.P.; Chavez, F.P. Predicting euphotic-depth-integrated chlorophyll-a from discrete-depth and satellite-observable chlorophyll-a off central California. J. Geophys. Res. Ocean. 2012, 117, C5. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Ocean. 2006, 111, C8. [Google Scholar] [CrossRef]
- Silulwane, N.F.; Richardson, A.J.; Shillington, F.A.; Mitchell-Innes, B. Identification and classification of vertical chlorophyll patterns in the Benguela upwelling system and Angola-Benguela front using an artificial neural network. S. Afr. J. Mar. Sci. 2001, 23, 37–51. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Ma, R.; Duan, H.; Liang, Q. Satellite-Based Estimation of Column-Integrated Algal Biomass in Nonalgae Bloom Conditions: A Case Study of Lake Chaohu, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 450–462. [Google Scholar] [CrossRef]
- Li, J.; Ma, R.; Xue, K.; Zhang, Y.; Loiselle, S. A Remote Sensing Algorithm of Column-Integrated Algal Biomass Covering Algal Bloom Conditions in a Shallow Eutrophic Lake. ISPRS Int. J. Geo-Inf. 2018, 7, 466. [Google Scholar] [CrossRef] [Green Version]
- Shen, M.; Duan, H.; Cao, Z.; Xue, K.; Qi, T.; Ma, J.; Liu, D.; Song, K.; Huang, C.; Song, X. Sentinel-3 OLCI observations of water clarity in large lakes in eastern China: Implications for SDG 6.3.2 evaluation. Remote Sens. Environ. 2020, 247, 111950. [Google Scholar] [CrossRef]
- Ma, R.; Yang, G.; Duan, H.; Jiang, J.; Wang, S.; Feng, X.; Li, A.; Kong, F.; Xue, B.; Wu, J.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2011, 54, 283–289. [Google Scholar] [CrossRef]
- Qin, B. Mechanism and control of eutrophication in shallow lakes in the middle and lower reaches of the Yangtze River. J. Lake Sci. 2002, 14, 193–202. [Google Scholar]
- Jiang, X.; Wu, Y.; Liu, G.; Liu, W.; Lu, B. The effects of climate, catchment land use and local factors on the abundance and community structure of sediment ammonia-oxidizing microorganisms in Yangtze lakes. AMB Express 2017, 7, 173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, L.-J.; Li, J.; Zhang, Y.; Kong, L.; Miao, J.; Yang, X.; Wu, Q. Trends in the occurrence and risk assessment of antibiotics in shallow lakes in the lower-middle reaches of the Yangtze River basin, China. Ecotoxicol. Environ. Saf. 2019, 183, 109511. [Google Scholar] [CrossRef]
- Liu, W.; Yao, L.; Wang, Z.; Xiong, Z.; Liu, G. Human land uses enhance sediment denitrification and N2O production in Yangtze lakes primarily by influencing lake water quality. Biogeosciences 2015, 12, 7815–7844. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Yuan, H.; Sun, R.; Yang, C. Streamflow simulations using error correction ensembles of satellite rainfall products over the Huaihe river basin. J. Hydrol. 2020, 589, 125179. [Google Scholar] [CrossRef]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-year monitoring of the turbidity dynamics in large lakes and reservoirs in the middle and lower basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Su, B.D.; Jiang, T.; Jin, W.B. Recent trends in observed temperature and precipitation extremes in the Yangtze River basin, China. Theor. Appl. Climatol. 2006, 83, 139–151. [Google Scholar] [CrossRef]
- Cui, L.; Gao, C.; Zhao, X.; Ma, Q.; Zhang, M. Dynamics of the lakes in the middle and lower reaches of the Yangtze River basin, China, since late nineteenth century. Environ. Monit. Assess. 2013, 185, 4005–4018. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Shi, X.; Xu, H.; Jing, Q.; Pan, X.; Liu, T.; Wang, H.; Hou, H. A GIS-based spatial multi-index model for flood risk assessment in the Yangtze River Basin, China. Environ. Impact Assess. Rev. 2020, 83, 106397. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Tian, L.; Chen, L. Human induced turbidity changes in Poyang Lake between 2000 and 2010: Observations from MODIS. J. Geophys. Res. Ocean. 2012, 117, C7. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, X.; Kong, F.; Zhang, S.; Kong, W.; Hao, J.; Shang, L. Two-Decade Reconstruction of Algal Blooms in China’s Lake Taihu. Environ. Sci. Technol. 2009, 43, 3522–3528. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.; Ma, R.; Wang, D.; Shen, M. Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes. Remote Sens. 2019, 11, 184. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Li, J.; Shen, Q.; Zhang, B.; Wu, C.; Wu, Y.; Wang, G.; Wang, S.; Lu, Z. Algorithms and Schemes for Chlorophyll a Estimation by Remote Sensing and Optical Classification for Turbid Lake Taihu, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 8, 350–364. [Google Scholar] [CrossRef]
- Xu, X.; Huang, X.; Zhang, Y.; Yu, D. Long-Term Changes in Water Clarity in Lake Liangzi Determined by Remote Sensing. Remote Sens. 2018, 10, 1441. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.P.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Doron, M.; Babin, M.; Hembise, O.; Mangin, A.; Garnesson, P. Ocean transparency from space: Validation of algorithms estimating Secchi depth using MERIS, MODIS and SeaWiFS data. Remote Sens. Environ. 2011, 115, 2986–3001. [Google Scholar] [CrossRef]
- Holm-Hansen, O. Chlorophyll-a determinations: Improvement in methodology. Oikos 1978, 30, 438–447. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Barnes, B. An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sens. 2014, 6, 10694–10715. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Wei, Y.; Lv, G.; Yuan, Z. Remote estimation of chlorophyll-a concentration in turbid water using a spectral index: A case study in Taihu Lake, China. J. Appl. Remote Sens. 2013, 7, 073465. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Duan, H.; Feng, L.; Cao, Z.; Xue, K. Climate- and human-induced changes in suspended particulate matter over Lake Hongze on short and long timescales. Remote Sens. Environ. 2017, 192, 98–113. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Ma, R.; Zheng, G. The total P estimation with hyper-spectrum—A novel insight into different P fractions. Catena 2019, 187, 104309. [Google Scholar] [CrossRef]
- Xu, H.; Paerl, H.W.; Qin, B.; Zhu, G.; Gao, G. Nitrogen and Phosphorus Inputs Control Phytoplankton Growth in Eutrophic Lake Taihu, China. Limnol. Oceanogr. 2010, 55, 420–432. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, Z.; Zeng, C.; Xia, G.; Shen, H. An Urban Water Extraction Method Combining Deep Learning and Google Earth Engine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 768–781. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, J.; Tian, L.; Feng, L.; Xing, Q. Remotely sensed water turbidity dynamics and its potential driving factors in an urbanizing city. J. Hydrol. 2020, 593, 125893. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar]
- Wang, S.; Li, J.; Zhang, B.; Shen, Q.; Zhang, F.; Lu, Z. A simple correction method for the MODIS surface reflectance product over typical inland waters in China. Int. J. Remote Sens. 2016, 37, 6076–6096. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; IIyushichenko, S.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine Applications Since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef] [Green Version]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Zhang, B.; Shen, Q.; Ye, H.; Wang, S.; Lu, Z. A simple automated dynamic threshold extraction method for the classification of large water bodies from landsat-8 OLI water index images. Int. J. Remote Sens. 2018, 39, 3429–3451. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, Y.; Ma, R.; Loiselle, S.; Hu, M. A MODIS-Based Novel Method to Distinguish Surface Cyanobacterial Scums and Aquatic Macrophytes in Lake Taihu. Remote Sens. 2017, 9, 133. [Google Scholar] [CrossRef] [Green Version]
- Bekteshi, A.; Cupi, A. Use of Trophic State Index (Carlson, 1977) For assessment of Trophic Status of the Shkodra lake. J. Environ. Prot. Ecol. 2015, 15, 359–365. [Google Scholar]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Improving Wave Model Validations Based on RMSE. 2013. Available online: https://www.researchgate.net/publication/258177596_Improving_wave_model_validations_based_on_RMSE (accessed on 28 February 2021).
- Safonov, M.G.; Chiang, R.Y. Model reduction for robust control: A schur relative error method. International. J. Adapt. Control Signal Process. 2010, 2, 259–272. [Google Scholar] [CrossRef]
- Coyle, E.J.; Lin, J.-H. Stack filters and the mean absolute error criterion. IEEE Trans Acoust. Speech Signal Process. 1988, 36, 1244–1254. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J. River Flow Forecasting Through Conceptual Models: Part 1.—A Discussion of Principles. J. Hydrol. 1970, 10, 282. [Google Scholar] [CrossRef]
- Topál, D.; Hatvani, I.G.; Kern, Z. Refining projected multidecadal hydroclimate uncertainty in East-Central Europe using CMIP5 and single-model large ensemble simulations. Theor. Appl. Climatol. 2020, 142, 1147–1167. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Shen, M.; Li, Y.; Duan, H.; Cao, Z.; Wang, D.; Xiong, J. Variations of suspended particulate concentration and composition in Chinese lakes observed from Sentinel-3A OLCI images. Sci. Total Environ. 2020, 721, 137774. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, C.; Ma, R.; Cao, Z. Remote Sensing Estimation of Lake Total Phosphorus Concentration Based on MODIS: A Case Study of Lake Hongze. Remote Sens. 2019, 11, 2068. [Google Scholar] [CrossRef] [Green Version]
- Zou, W.; Zhu, G.; Cai, Y.; Vilmi, A.; Xu, H.; Zhu, M.; Gong, Z.; Zhang, Y.; Qin, B. Relationships between nutrient, chlorophyll a and Secchi depth in lakes of the Chinese Eastern Plains ecoregion: Implications for eutrophication management. J. Environ. Manag. 2020, 260, 109923. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Zhu, G.; Cai, Y.; Xu, H.; Zhu, M.; Gong, Z.; Zhang, Y.; Qin, B. The limitations of comprehensive trophic level index (TLI) in the eutrophication assessment of lakes along the middle and lower reached of the Yangtze River during summer season and reccomdation for its improvement. J. Lake Sci. 2020, 32, 36–47. [Google Scholar]
- Morel, A. Optical Properties of Pure Water and Pure Sea Water. 1974, pp. 1–24. Available online: https://www.researchgate.net/publication/247934859_Optical_properties_of_pure_water (accessed on 20 March 2021).
- Ni, Z.; Wang, S.; Jin, X.; Jiao, L.; Li, Y. Study on the evolution and characteristics of eutrophication in the typical lakes on Yunnan-Guizhou Plateau. Acta Sci. Circumstantiate 2011, 31, 2681–2689. [Google Scholar]
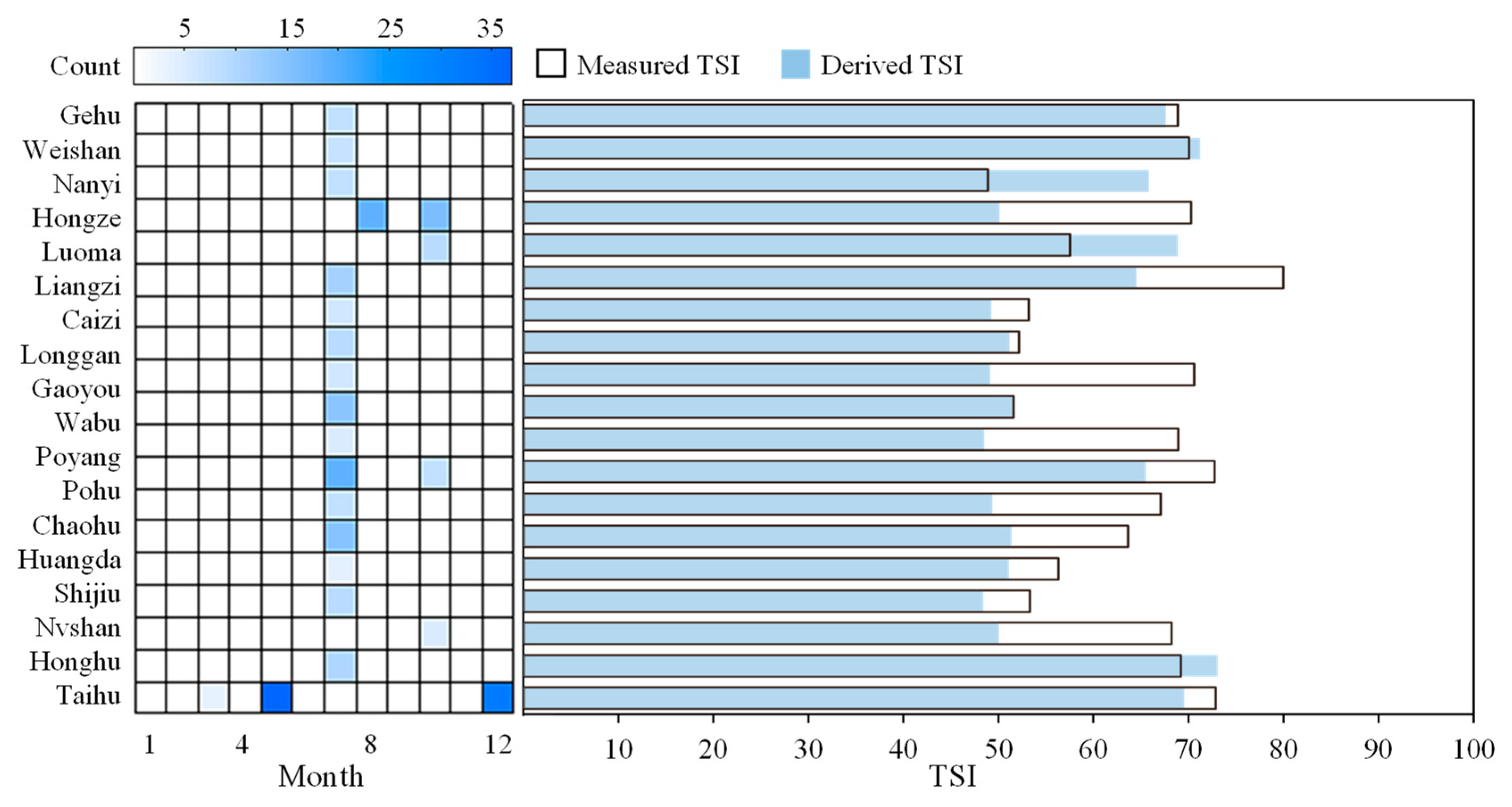
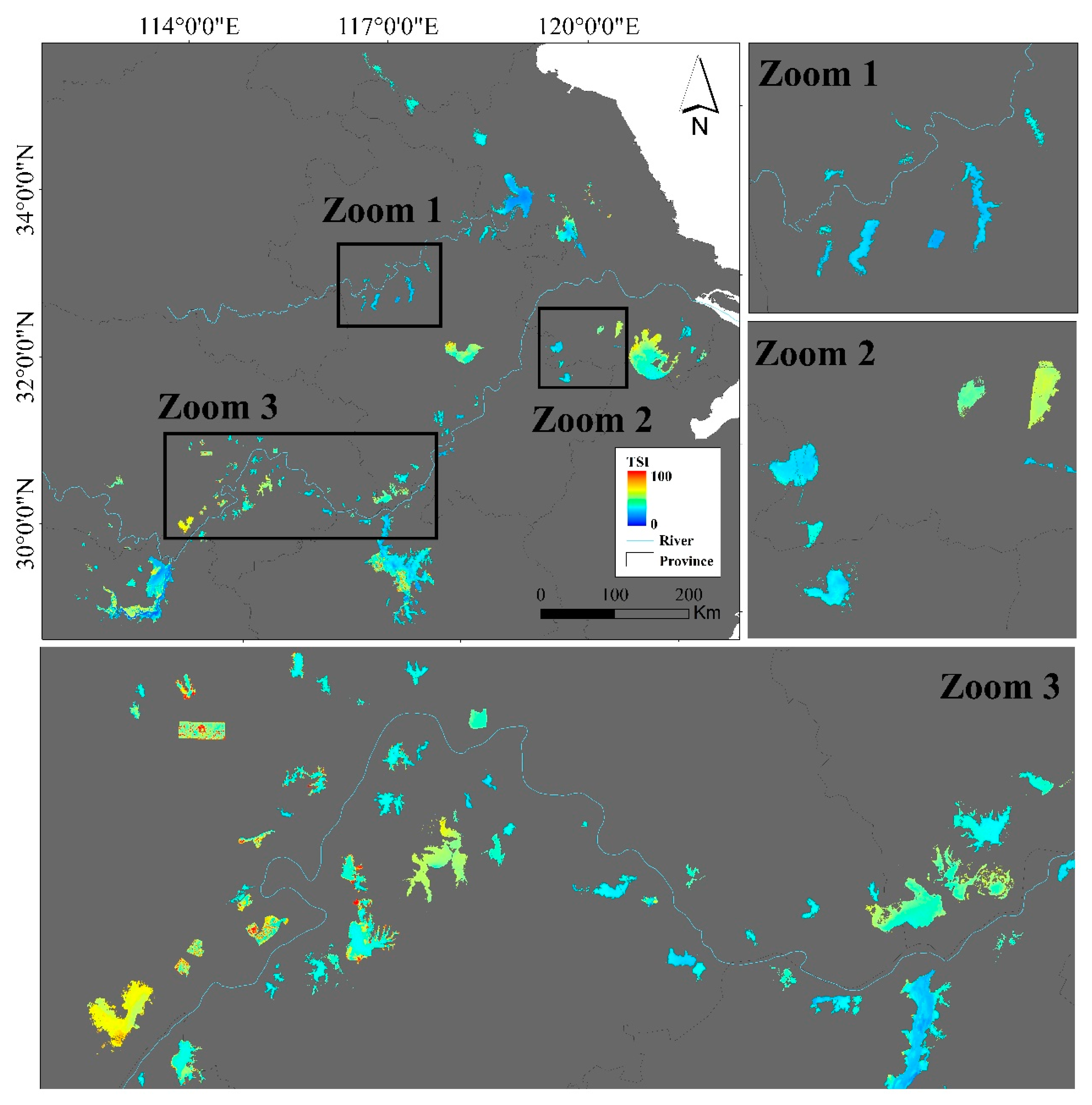

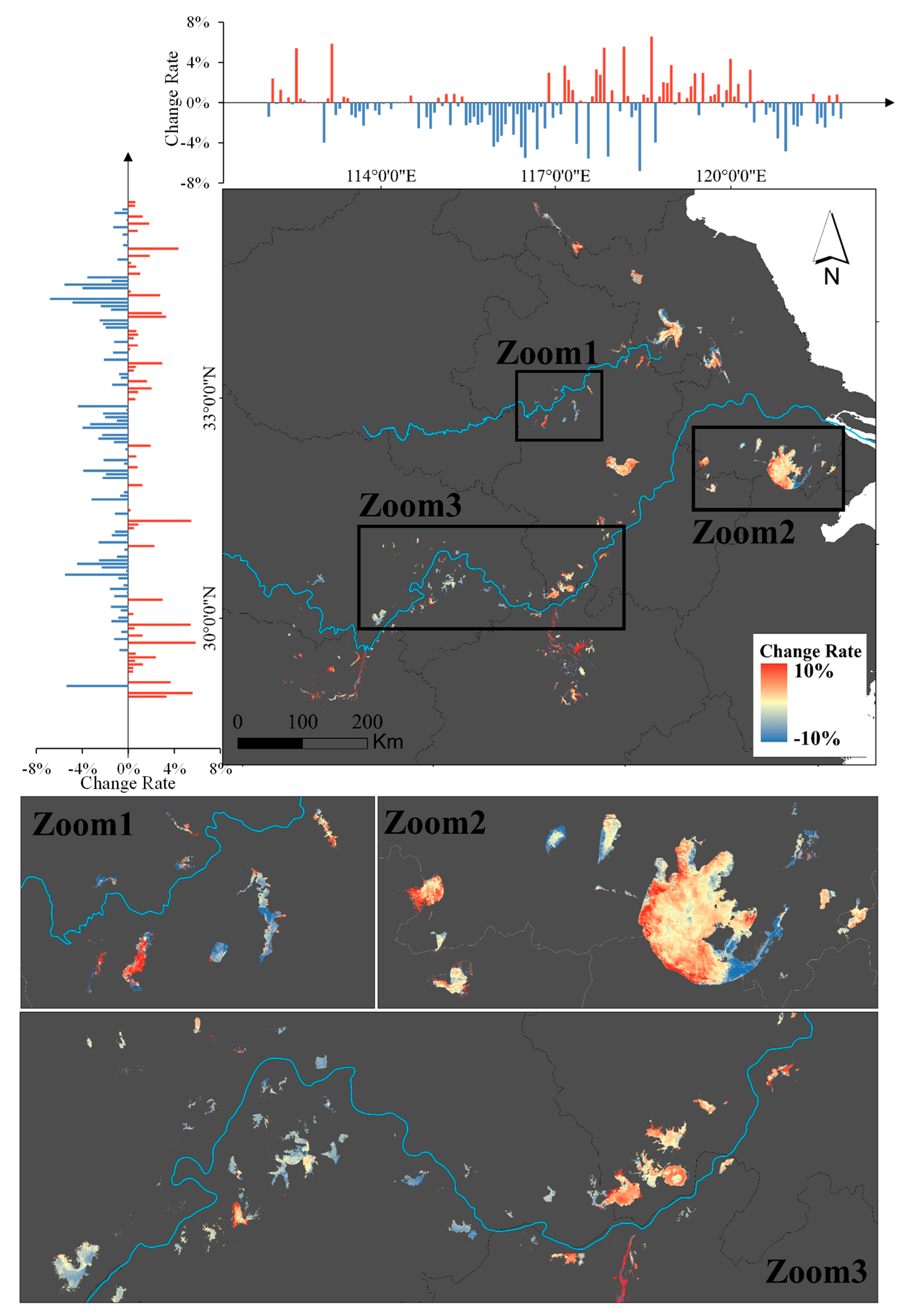
| ID | Lake | Depth (m) | Area (km2) | Number of Samples |
|---|---|---|---|---|
| 1 | Weishan | 1.5 | 1106.45 | 15 |
| 2 | Luoma | 3.3 | 290.94 | 9 |
| 3 | Taihu | 2.1 | 2444.75 | 156 |
| 4 | Gehu | 1.2 | 139.03 | 8 |
| 5 | Nanyi | 2.3 | 197.83 | 26 |
| 6 | Nvshan | 1.7 | 107.31 | 5 |
| 7 | Chaohu | 2.7 | 787.97 | 126 |
| 8 | Pohu | 4.4 | 176.67 | 12 |
| 9 | Huangda | 3.9 | 287.01 | 12 |
| 10 | Longgan | 3.8 | 280.29 | 24 |
| 11 | Liangzi | 4.2 | 349.76 | 21 |
| 12 | Honghu | 1.9 | 336.646 | 20 |
| 13 | Hongze | 1.8 | 1663.31 | 65 |
| 14 | Gaoyou | 1.5 | 639.17 | 13 |
| 15 | Shijiu | 4.1 | 214.31 | 14 |
| 16 | Wabu | 2.4 | 162.11 | 5 |
| 17 | Caizi | 1.7 | 168.49 | 12 |
| 18 | Poyang | 5.1 | 3192 | 26 |
| 19 | Dongting | 6.4 | 2607.46 | 26 |
| Lake | SDD (m) | Chla (µg/L) | SPM (mg/L) | SPIM (mg/L) | ||||
|---|---|---|---|---|---|---|---|---|
| Min–Max | Mean ± S.D. | Min–Max | Mean ± S.D. | Min–Max | Mean ± S.D. | Min–Max | Mean ± S.D. | |
| Weishan | 0.08–0.58 | 0.31 ± 0.15 | 20.97–116.92 | 65.25 ± 24.96 | 16.00–93.00 | 34.24 ± 19.90 | 1.33–76.0 | 19.13 ± 18.40 |
| Luoma | 0.36–1.12 | 0.59 ± 0.23 | 4.15–27.96 | 16.65 ± 7.45 | 12.00–24.00 | 17.69 ± 3.87 | 7.20–17.60 | 12.18 ± 3.24 |
| Taihu | 0.15–0.95 | 0.20 ± 0.14 | 1.38–33.18 | 9.12 ± 7.31 | 18.00–139.00 | 53.25 ± 22.20 | 9.00–120.0 | 39.90 ± 20.65 |
| Gehu | 0.01–1.54 | 0.31 ± 0.36 | 3.24–74.53 | 28.29 ± 28.04 | 44.00–106.67 | 68.18 ± 20.47 | 38.67–98.67 | 62.10 ± 18.98 |
| Nanyi | 0.10–1.75 | 0.41 ± 0.26 | 1.37–432.95 | 56.08 ± 74.67 | 2.09–210.67 | 60.92 ± 35.83 | 0.50–173.33 | 38.51 ± 31.31 |
| Nvshan | 0.09–0.18 | 0.13 ± 0.03 | 51.59–152.55 | 93.83 ± 39.29 | 33.00–239.00 | 140 ± 32.88 | 16.00–218.0 | 123.75 ± 60.75 |
| Chaohu | 0.50–0.80 | 0.64 ± 0.08 | 3.90–106.63 | 40.62 ± 31.42 | 9.38–24.00 | 14.25 ± 5.25 | 4.67–8.12 | 6.73 ± 1.07 |
| Pohu | 0.15–0.50 | 0.29 ± 0.15 | 8.12–135.63 | 28.54 ± 27.38 | 17.33–58.67 | 40.64 ± 9.62 | 13.33–44.00 | 33.99 ± 7.53 |
| Huangda | 0.30–0.40 | 0.34 ± 0.04 | 6.43–7.12 | 6.75 ± 0.29 | 26.67–30.67 | 29.07 ± 1.55 | 20.0–24.0 | 22.40 ± 1.55 |
| Longgan | 0.25–0.42 | 0.31 ± 0.05 | 50.43–92.74 | 64.30 ± 14.73 | 16.00–35.00 | 28.40 ± 6.62 | 7.00–28.00 | 20.00 ± 7.21 |
| Liangzi | 0.07–0.60 | 0.16 ± 0.09 | 5.60–415.40 | 65.55 ± 84.56 | 12.00–216.00 | 59.37 ± 29.74 | 6.00–120.00 | 37.10 ± 26.52 |
| Honghu | 0.20–0.45 | 0.33 ± 0.10 | 28.04–56.88 | 44.86 ± 10.13 | 10.67–33.33 | 24.67 ± 10.22 | 5.00–26.00 | 17.39 ± 8.84 |
| Hongze | 0.20–0.75 | 0.62 ± 0.19 | 5.72–24.51 | 12.95 ± 5.92 | 4.00–50.67 | 19.55 ± 15.53 | 2.00–40.00 | 12.33 ± 13.08 |
| Gaoyou | 0.10–1.40 | 0.64 ± 0.45 | 8.79–34.21 | 21.73 ± 8.20 | 2.00–24.00 | 14.33 ± 9.18 | 1.00–15.00 | 7.67 ± 6.13 |
| Shijiu | 0.05–0.41 | 0.33 ± 0.14 | 20.86–127.14 | 64.58 ± 36.99 | 14.00–37.00 | 24.89 ± 6.84 | 7.00–30.00 | 18.00 ± 7.39 |
| Wabu | 0.15–1.30 | 0.51 ± 0.27 | 2.25–11.01 | 7.75 ± 4.05 | 2.00–245.00 | 33.50 ± 48.45 | 0.50–232.00 | 28.50 ± 45.64 |
| Caizi | 0.30–0.70 | 0.49 ± 0.10 | 12.63–69.15 | 35.72 ± 18.12 | 5.00–29.14 | 16.17 ± 7.57 | 1.00–22.29 | 10.14 ± 6.86 |
| Poyang | 0.10–0.60 | 0.34 ± 0.12 | 9.96–149.65 | 74.32 ± 38.48 | 9.00–95.00 | 29.48 ± 21.15 | 1.55–77.00 | 20.32 ± 17.85 |
| Dongting | 0.35–1.45 | 0.74 ± 0.33 | 0.70–14.44 | 8.34 ± 7.65 | 4.50–27.60 | 15.42 ± 6.77 | 2.00–28.00 | 11.85 ± 7.12 |
| MAE (%) | MRE (%) | RMSE (sr−1) | NSE | |
|---|---|---|---|---|
| Rrs (443) | 0.43 | 34.42 | 0.0055 | 0.44 |
| Rrs (482) | 0.41 | 24.01 | 0.0053 | 0.65 |
| Rrs (561) | 0.46 | 13.96 | 0.0060 | 0.92 |
| Rrs (655) | 0.38 | 14.60 | 0.0047 | 0.89 |
| Rrs (865) | 0.56 | 38.45 | 0.0097 | 0.38 |
| ABI(Rrs) | 0.16 | 13.76 | 0.0022 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Ma, R.; Cao, Z.; Xiong, J.; Xue, K. Remote Estimation of Trophic State Index for Inland Waters Using Landsat-8 OLI Imagery. Remote Sens. 2021, 13, 1988. https://doi.org/10.3390/rs13101988
Hu M, Ma R, Cao Z, Xiong J, Xue K. Remote Estimation of Trophic State Index for Inland Waters Using Landsat-8 OLI Imagery. Remote Sensing. 2021; 13(10):1988. https://doi.org/10.3390/rs13101988
Chicago/Turabian StyleHu, Minqi, Ronghua Ma, Zhigang Cao, Junfeng Xiong, and Kun Xue. 2021. "Remote Estimation of Trophic State Index for Inland Waters Using Landsat-8 OLI Imagery" Remote Sensing 13, no. 10: 1988. https://doi.org/10.3390/rs13101988
APA StyleHu, M., Ma, R., Cao, Z., Xiong, J., & Xue, K. (2021). Remote Estimation of Trophic State Index for Inland Waters Using Landsat-8 OLI Imagery. Remote Sensing, 13(10), 1988. https://doi.org/10.3390/rs13101988