Assessing Past Climate Biases and the Added Value of CORDEX-CORE Precipitation Simulations over Africa
Abstract
:1. Introduction
2. Materials and Methods
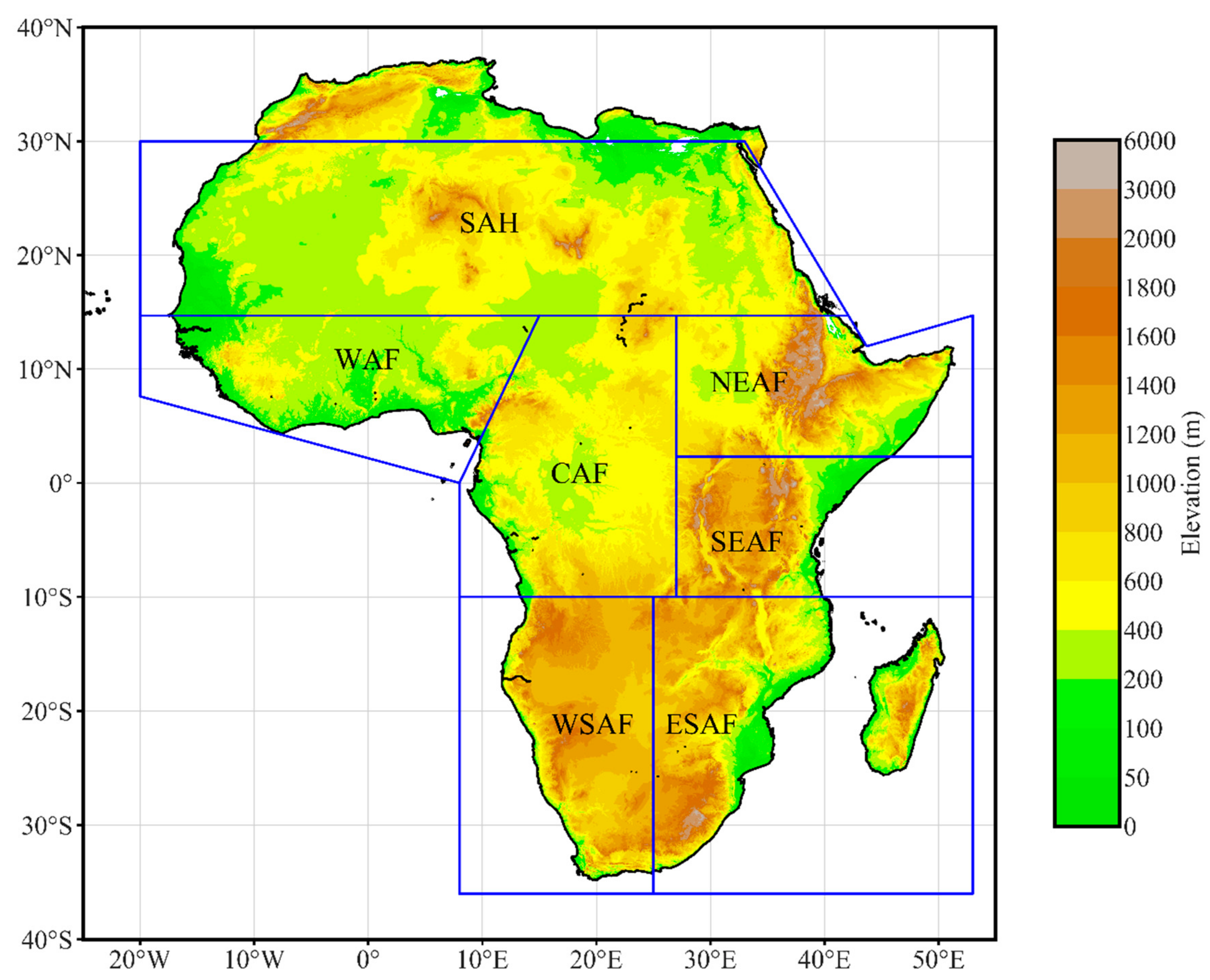
2.1. Study Area
2.2. Climate Simulation and Observation Datasets
2.3. Methodology
3. Results
3.1. Spatial Seasonal Bias and Added Value
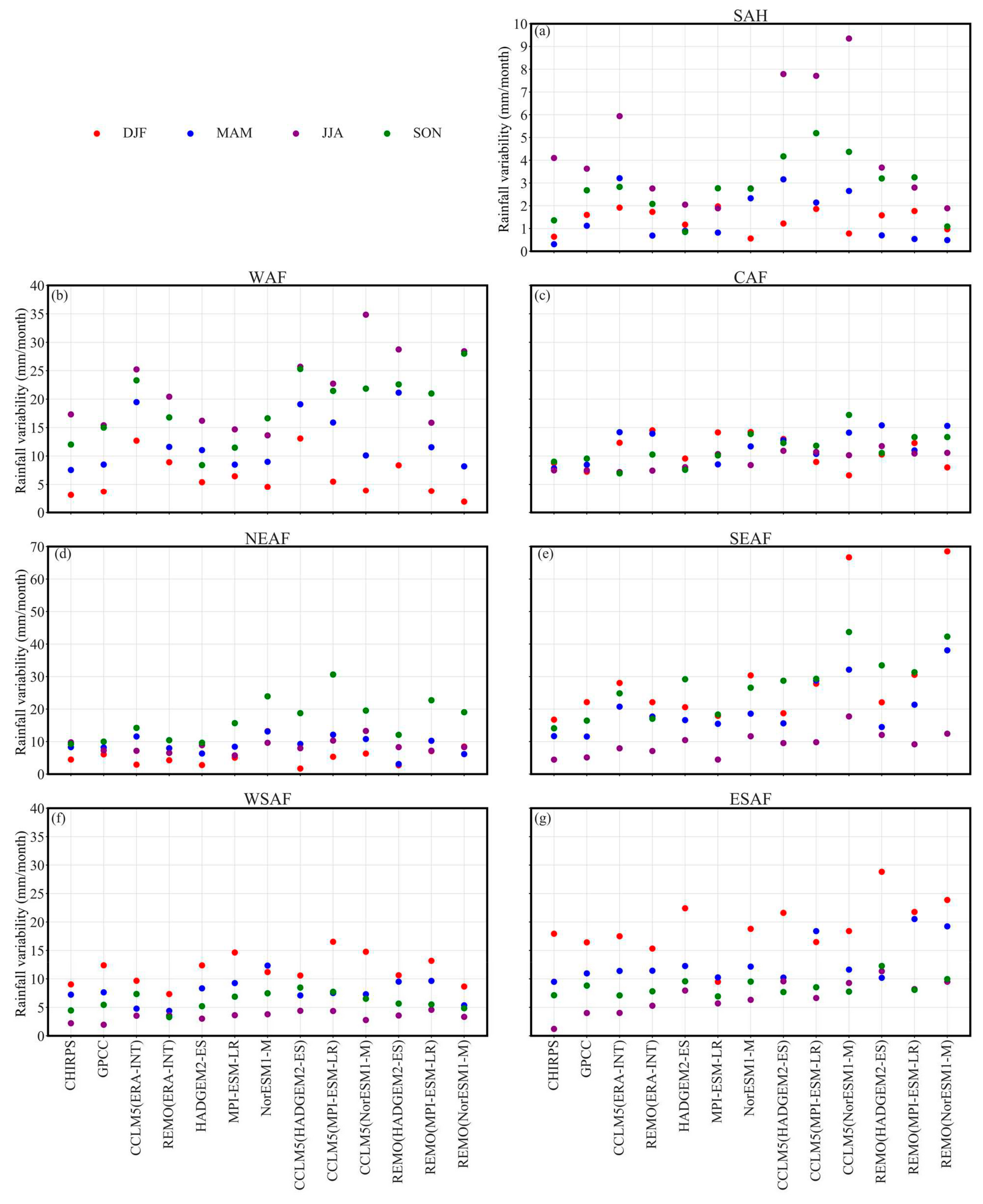
3.2. Sub Regional Annual Cycles, Interannual Variability and Added Value
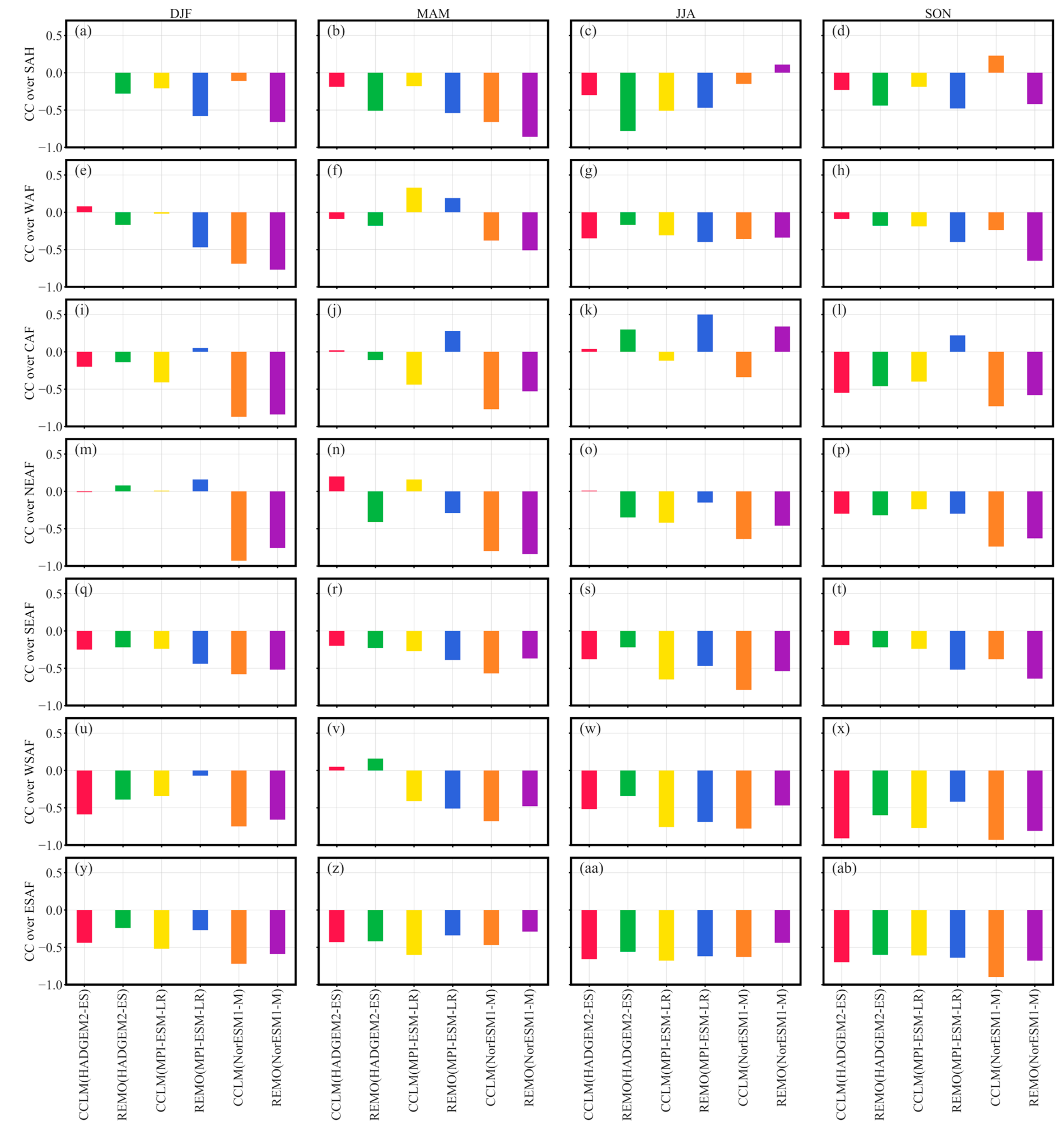
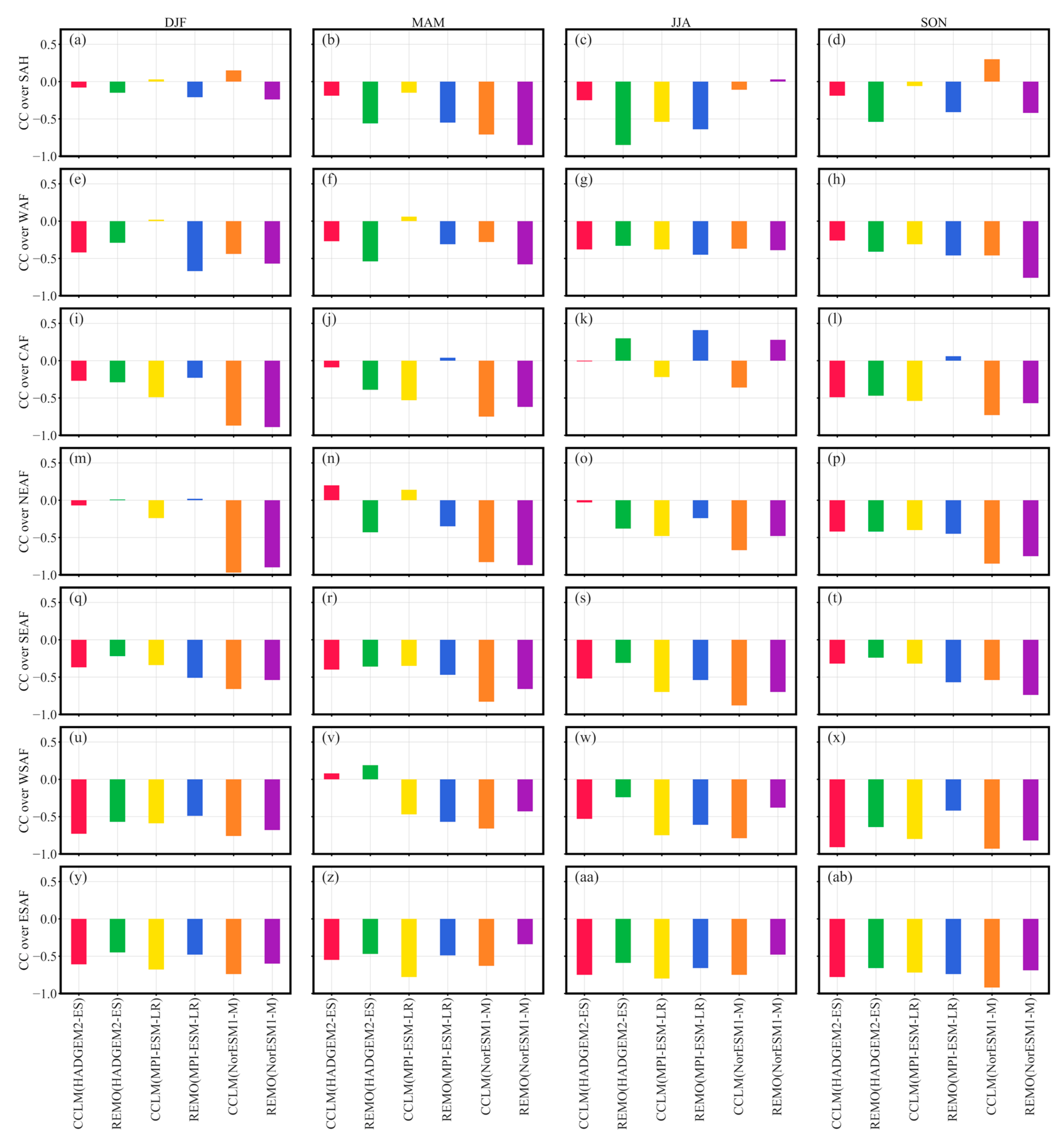
3.3. Seasonal Model Contribution Analysis
4. Discussion
5. Conclusions
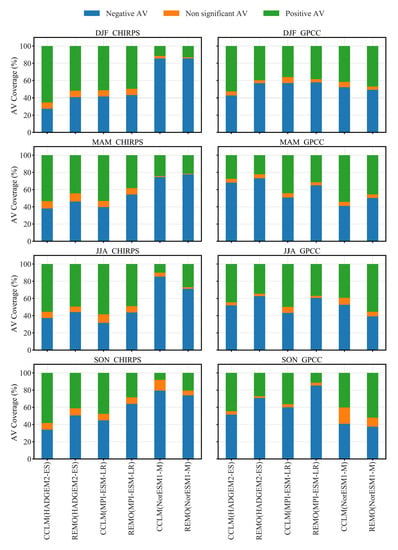
- AV by CCLM and REMO simulations can be positive, negative, or non-significant (10% significance level), based on the season, the sub-area, and the GCM–RCM combination. The biases observed over rain abundant areas result in the dominance of negative AV over such areas. CCLM and REMO have shown a systematic correction potential to spatially misplaced rain bands, which contribute to a high AV, especially over Central and South Africa in some seasons.
- The regional result revealed that REMO RCM outputs reported the best performances over SAH, WAF, and CAF, while CCLM results were superior over NEAF, SEAF, WSAF, and ESAF, in terms of spatial AV coverage for all the seasons. As AV results were proven to be highly influenced by the RCM signals in the model contribution analysis, one could be confident when using this RCM for local studies and applications, where good seasonal performances are needed.
- Beyond the meaning of the model contribution analysis for the choice between RCMs and GCMs, further implications for the GCM–RCM model chains were found. For instance, the GCMs were influential to the RCMs’ outputs AV, especially in the DJF and MAM seasons. The analysis also revealed the impact of observational uncertainty on such statistical attribution approaches. It indicated, based on the mixed results obtained per season, regions, and GCM–RCM combination, that the good integration of the GCMs’ physics and the RCM ones, as well as how they both accommodate the high-resolution settings of the downscaling experiments, could be major factors of AV. However, missing and misrepresented processes in the RCMs should not be discarded.
- It is important to recall that the AV results obtained in this study are exclusively targeting seasonal mean statistics and that these results cannot be generalized. We recommend that the AV studies for climate features and statistics relevant for VIA-CS applications should be carried out both at the continental and regional level as a continuum of the AV debate. It remains important to investigate AV concerning key processes as a first step toward going beyond AV targeting general statistics.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giorgi, F. Thirty Years of Regional Climate Modeling: Where Are We and Where Are We Going next? J. Geophys. Res. Atmos. 2019, 124, 5696–5723. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F. Producing actionable climate change information for regions: The distillation paradigm and the 3R framework. Eur. Phys. J. Plus 2020, 135, 1–15. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; Moreno, R.; Sánchez, J.L.; García-Ortega, E. Regional climate models: 30 years of dynamical downscaling. Atmos. Res. 2020, 235, 104785. [Google Scholar] [CrossRef]
- Rummukainen, M. Added value in regional climate modeling. Wiley Interdiscip. Rev. Clim. Chang. 2015, 7, 145–159. [Google Scholar] [CrossRef]
- Di Luca, A.; De Elía, R.; Laprise, R. Challenges in the Quest for Added Value of Regional Climate Dynamical Downscaling. Curr. Clim. Chang. Rep. 2015, 1, 10–21. [Google Scholar] [CrossRef]
- Kerkhoff, C.; Kunsch, H.R.; Schär, C. A Bayesian Hierarchical Model for Heterogeneous RCM–GCM Multimodel Ensembles. J. Clim. 2015, 28, 6249–6266. [Google Scholar] [CrossRef]
- Sørland, S.L.; Schär, C.; Luethi, D.; Kjellström, E. Bias patterns and climate change signals in GCM-RCM model chains. Environ. Res. Lett. 2018, 13, 074017. [Google Scholar] [CrossRef]
- Takle, E.S.; Gutowski, W.J.; Arritt, R.W.; Pan, Z.; Anderson, C.J.; Da Silva, R.R.; Caya, D.; Chen, S.-C.; Giorgi, F.; Christensen, J.H.; et al. Project to Intercompare Regional Climate Simulations (PIRCS): Description and initial results. J. Geophys. Res. Atmos. 1999, 104, 19443–19461. [Google Scholar] [CrossRef]
- Mearns, L.O.; Arritt, R.; Biner, S.; Bukovsky, M.S.; McGinnis, S.; Sain, S.; Caya, D.; Correia, J.; Flory, D.; Gutowski, W.; et al. The North American Regional Climate Change Assessment Program: Overview of Phase I Results. Bull. Am. Meteorol. Soc. 2012, 93, 1337–1362. [Google Scholar] [CrossRef]
- Christensen, J.H.; Carter, T.R.; Rummukainen, M.; Amanatidis, G. Evaluating the performance and utility of regional climate models: The PRUDENCE project. Clim. Chang. 2007, 81, 1–6. [Google Scholar] [CrossRef]
- van der Linden, P.; Mitchell, J.F.B. ENSEMBLES: Climate Change and its Impacts: Summary of Research and Results from the ENSEMBLES Project; Met Office Hadley Centre: Exeter, UK, 2009; ISBN 2003505539. [Google Scholar]
- Redelsperger, J.-L.; Thorncroft, C.D.; Diedhiou, A.; Lebel, T.; Parker, D.J.; Polcher, J. African Monsoon Multidisciplinary Analysis: An International Research Project and Field Campaign. Bull. Am. Meteorol. Soc. 2006, 87, 1739–1746. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Jones, C.; Giorgi, F.; Asrar, G. The Coordinated Regional Downscaling Experiment: CORDEX an International Downscaling Link to CMIP5; World Climate Research Programme: Geneva, Switzerland, 2011. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Sylla, M.B.; Coppola, E.; Mariotti, L.; Giorgi, F.; Ruti, P.M.; Dell’Aquila, A.; Bi, X. Multiyear simulation of the African climate using a regional climate model (RegCM3) with the high resolution ERA-interim reanalysis. Clim. Dyn. 2009, 35, 231–247. [Google Scholar] [CrossRef]
- Buontempo, C.; Mathison, C.; Jones, R.; Williams, K.; Wang, C.; McSweeney, C. An ensemble climate projection for Africa. Clim. Dyn. 2014, 44, 2097–2118. [Google Scholar] [CrossRef] [Green Version]
- Akinsanola, A.; Ajayi, V.; Adejare, A.; Adeyeri, O.; Gbode, I.; Ogunjobi, K.; Nikulin, G.; Abolude, A. Evaluation of rainfall simulations over West Africa in dynamically downscaled CMIP5 global circulation models. Theor. Appl. Clim. 2018, 132, 437–450. [Google Scholar] [CrossRef]
- Gbobaniyi, E.; Sarr, A.; Sylla, M.B.; Diallo, I.; Lennard, C.; Dosio, A.; Diedhiou, A.; Kamga, A.; Klutse, N.A.B.; Hewitson, B.; et al. Climatology, annual cycle and interannual variability of precipitation and temperature in CORDEX simulations over West Africa. Int. J. Clim. 2013, 34, 2241–2257. [Google Scholar] [CrossRef]
- Ajibola, F.; Zhou, B.; Gnitou, G.T.; Onyejuruwa, A. Evaluation of the Performance of CMIP6 HighResMIP on West African Precipitation. Atmosphere 2020, 11, 1053. [Google Scholar] [CrossRef]
- Ayugi, B.; Tan, G.; Gnitou, G.T.; Ojara, M.; Ongoma, V. Historical evaluations and simulations of precipitation over East Africa from Rossby centre regional climate model. Atmospheric Res. 2020, 232, 104705. [Google Scholar] [CrossRef]
- Dosio, A.; Panitz, H.-J.; Schubert-Frisius, M.; Lüthi, D. Dynamical downscaling of CMIP5 global circulation models over CORDEX-Africa with COSMO-CLM: Evaluation over the present climate and analysis of the added value. Clim. Dyn. 2014, 44, 2637–2661. [Google Scholar] [CrossRef] [Green Version]
- Dosio, A.; Panitz, H.-J. Climate change projections for CORDEX-Africa with COSMO-CLM regional climate model and differences with the driving global climate models. Clim. Dyn. 2016, 46, 1599–1625. [Google Scholar] [CrossRef] [Green Version]
- Dosio, A.; Turner, A.G.; Tamoffo, A.T.; Sylla, M.B.; Lennard, C.; Jones, R.G.; Terray, L.; Nikulin, G.; Hewitson, B. A tale of two futures: Contrasting scenarios of future precipitation for West Africa from an ensemble of regional climate models. Environ. Res. Lett. 2020, 15, 064007. [Google Scholar] [CrossRef]
- Gibba, P.; Sylla, M.B.; Okogbue, E.C.; Gaye, A.T.; Nikiema, M.; Kebe, I. State-of-the-art climate modeling of extreme precipitation over Africa: Analysis of CORDEX added-value over CMIP5. Theor. Appl. Clim. 2018, 137, 1041–1057. [Google Scholar] [CrossRef]
- Gnitou, G.T.; Ma, T.; Tan, G.; Ayugi, B.; Nooni, I.K.; Alabdulkarim, A.; Tian, Y. Evaluation of the Rossby Centre Regional Climate Model Rainfall Simulations over West Africa Using Large-Scale Spatial and Temporal Statistical Metrics. Atmosphere 2019, 10, 802. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Gutowski, W.J. Coordinated Experiments for Projections of Regional Climate Change. Curr. Clim. Chang. Rep. 2016, 2, 202–210. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Gutowski, W.J. Regional Dynamical Downscaling and the CORDEX Initiative. Annu. Rev. Environ. Resour. 2015, 40, 467–490. [Google Scholar] [CrossRef]
- Gutowski, W.J., Jr.; Giorgi, F.; Timbal, B.; Frigon, A.; Jacob, D.; Kang, H.-S.; Raghavan, K.; Lee, B.; Lennard, C.; Nikulin, G.; et al. WCRP COordinated Regional Downscaling EXperiment (CORDEX): A diagnostic MIP for CMIP6. Geosci. Model Dev. 2016, 9, 4087–4095. [Google Scholar] [CrossRef] [Green Version]
- Ciarlo, J.M.; Coppola, E.; Fantini, A.; Giorgi, F.; Gao, X.; Tong, Y.; Glazer, R.H.; Alavez, J.A.T.; Sines, T.; Pichelli, E.; et al. A new spatially distributed added value index for regional climate models: The EURO-CORDEX and the CORDEX-CORE highest resolution ensembles. Clim. Dyn. 2020, 1–22. [Google Scholar] [CrossRef]
- Washington, R.; Harrison, M.; Conway, D.; Black, E.; Challinor, A.; Grimes, D.; Jones, R.; Morse, A.; Kay, G.; Todd, M. African Climate Change: Taking the Shorter Route. Bull. Am. Meteorol. Soc. 2006, 87, 1355–1366. [Google Scholar] [CrossRef]
- Iturbide, M.; Gutiérrez, J.M.; Alves, L.M.; Bedia, J.; Cerezo-Mota, R.; Cimadevilla, E.; Cofiño, A.S.; Di Luca, A.; Faria, S.H.; Gorodetskaya, I.V.; et al. An update of IPCC climate reference regions for subcontinental analysis of climate model data: Definition and aggregated datasets. Earth Syst. Sci. Data 2020, 12, 2959–2970. [Google Scholar] [CrossRef]
- Teichmann, C.; Jacob, D.; Remedio, A.R.; Remke, T.; Buntemeyer, L.; Hoffmann, P.; Kriegsmann, A.; Lierhammer, L.; Bülow, K.; Weber, T.; et al. Assessing mean climate change signals in the global CORDEX-CORE ensemble. Clim. Dyn. 2020, 1–24. [Google Scholar] [CrossRef]
- Jacob, D.; Elizalde, A.; Haensler, A.; Hagemann, S.; Kumar, P.; Podzun, R.; Rechid, D.; Remedio, A.R.; Saeed, F.; Sieck, K.; et al. Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions. Atmosphere 2012, 3, 181–199. [Google Scholar] [CrossRef] [Green Version]
- Remedio, A.R.; Teichmann, C.; Buntemeyer, L.; Sieck, K.; Weber, T.; Rechid, D.; Hoffmann, P.; Nam, C.; Kotova, L.; Jacob, D. Evaluation of New CORDEX Simulations Using an Updated Köppen–Trewartha Climate Classification. Atmosphere 2019, 10, 726. [Google Scholar] [CrossRef] [Green Version]
- Panitz, H.-J.; Dosio, A.; Büchner, M.; Lüthi, D.; Keuler, K. COSMO-CLM (CCLM) climate simulations over CORDEX-Africa domain: Analysis of the ERA-Interim driven simulations at 0.44° and 0.22° resolution. Clim. Dyn. 2013, 42, 3015–3038. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M. GPCC Full Data Monthly Product Version 2018 at 0.25°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historical Data; Federal Ministry of Transport and Digital Infrastructure: Bonn, Germany, 2018.
- Earth System Grid Federation (ESGF). Available online: https://esgf-data.dkrz.de/projects/esgf-dkrz/ (accessed on 30 January 2021).
- Deutscher Wetterdienst (DWD). Available online: https://opendata.dwd.de/climate_environment/GPCC/html/fulldatamonthly_v2018_doi_download.html (accessed on 12 December 2020).
- Climate Hazard Infrared Precipitation with Stations (CHIRPS). Available online: https://data.chc.ucsb.edu/products/CHIRPS-2.0/ (accessed on 12 December 2020).
- Gutowski, W.J.; Ullrich, P.A.; Hall, A.; Leung, L.R.; O’Brien, T.A.; Patricola, C.M.; Arritt, R.W.; Bukovsky, M.S.; Calvin, K.V.; Feng, Z.; et al. The Ongoing Need for High-Resolution Regional Climate Models: Process Understanding and Stakeholder Information. Bull. Am. Meteorol. Soc. 2020, 101, E664–E683. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-Y.; Kanamitsu, M. Dynamical downscaling: Fundamental issues from an NWP point of view and recommendations. Asia-Pac. J. Atmos. Sci. 2014, 50, 83–104. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Ruti, P.M.; Calmanti, S.; Dellaquila, A. The impact of deep convection on the West African summer monsoon climate: A regional climate model sensitivity study. Q. J. R. Meteorol. Soc. 2011, 137, 1417–1430. [Google Scholar] [CrossRef]
- Nikulin, G.; Jones, C.; Giorgi, F.; Asrar, G.; Büchner, M.; Cerezo-Mota, R.; Christensen, O.B.; Déqué, M.; Fernandez, J.; Hänsler, A.; et al. Precipitation Climatology in an Ensemble of CORDEX-Africa Regional Climate Simulations. J. Clim. 2012, 25, 6057–6078. [Google Scholar] [CrossRef] [Green Version]




| Model Type | Name | Institution | Spatial Resolution | Vertical Levels |
|---|---|---|---|---|
| GCM | HadGEM2-ES | Met Office Hadley Centre (MOHC) | 1.25° × 1.85° | 38 |
| GCM | MPI-ESM-LR | Max Plank Institute for Meteorology (MPI-M) | 1.8653° × 1.875° | 47 |
| GCM | NorESM1-M | Norwegian Climate Centre (NCC) | 1.8947° × 2.5° | 26 |
| REANALYSIS | ERA-INTERIM | European Centre for Medium-Range Weather Forecasts (ECMWF) | 0.75° × 0.75° | 60 |
| RCM | REMO2015 | Climate Service Center Germany (GERICS) | 0.22° × 0.22° | 27 |
| RCM | CCLM5-0-15 | KIT, Karlsruhe, Germany in collaboration with the CLM-Community (CLMcom-KIT) | 0.22° × 0.22° | 35 |
| DJF | HadGEM2-ES | CCLM5/REMO | MPI-ESM-LR | CCLM5/REMO | NorESM1-M | CCLM5/REMO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CHIRPS | GPCC | CHIRPS | GPCC | CHIRPS | GPCC | CHIRPS | GPCC | CHIRPS | GPCC | CHIRPS | GPCC | |
| BIAS | −2.83 | −0.32 | 18.26/85.84 | 21.2/88.6 | −1.2 | 1.08 | 29.2/90.07 | 32.34/96.24 | −12.66 | −12.12 | −10.24/11.81 | −8.66/14.15 |
| RMSE | 47.56 | 56.02 | 53.27/58.61 | 61.61/70.49 | 46.83 | 53.73 | 54.3/60.37 | 62.56/70.96 | 60.38 | 65.98 | 55.31/64.37 | 62.58/72 |
| MAM | ||||||||||||
| BIAS | −12.84 | −12.77 | 22.35/54.77 | 26.24/58.34 | −2.7 | −2.15 | 24.47/65.24 | 28.66/70.43 | −1.26 | −1.76 | 8.81/34.52 | 11.39/38.54 |
| RMSE | 47.43 | 55.17 | 74.01/66.92 | 86.57/81.7 | 49.2 | 55.87 | 62.31/65.23 | 74.33/78.94 | 55.98 | 63.24 | 64.55/66.94 | 73.57/81.13 |
| JJA | ||||||||||||
| BIAS | −57.15 | −51.13 | −3.53/54.43 | 4.88/64.11 | −34 | −30.29 | 6.93/55.1 | 14.78/61.63 | −46.57 | −42.06 | −25.8/1.23 | −17.19/11.35 |
| RMSE | 35.43 | 37.98 | 79.36/68.68 | 93.73/82.72 | 36.79 | 41.1 | 62.89/53.09 | 72.51/61.92 | 59.35 | 60.05 | 64.16/54.69 | 70.47/62.8 |
| SON | ||||||||||||
| BIAS | −24.28 | −21.64 | 38.2/79.96 | 45.15/85.63 | −4.36 | −4.45 | 29.61/56.1 | 33.53/58.26 | −22.11 | −21.15 | −1.66/−3.55 | 2.2/−0.98 |
| RMSE | 40.75 | 48.6 | 88.16/73.29 | 105.35/90.68 | 38.28 | 46.55 | 65.26/57.44 | 77.13/69.15 | 54.63 | 58.08 | 56.47/47.86 | 65.64/55.81 |
| RCM Output | Negative AV | Non-Significant AV | Positive AV | |
|---|---|---|---|---|
| DJF | ||||
| CHIRPS | CCLM5/REMO(HadGEM2-ES) | 27.49/40.59 | 7.34/7.54 | 65.17/51.87 |
| CCLM5/REMO(MPI-ESM-LR) | 41.38/43.03 | 7.26/7.33 | 51.36/49.64 | |
| CCLM5/REMO(NorESM1-M) | 85.52/85.59 | 2.95/1.33 | 11.53/13.08 | |
| GPCC | CCLM5/REMO(HadGEM2-ES) | 42.52/56.87 | 4.8/3.38 | 52.68/39.75 |
| CCLM5/REMO(MPI-ESM-LR) | 56.97/57.76 | 6.96/3.71 | 36.07/38.53 | |
| CCLM5/REMO(NorESM1-M) | 52.12/49.13 | 6.16/3.82 | 41.72/47.05 | |
| MAM | ||||
| CHIRPS | CCLM5/REMO(HadGEM2-ES) | 38.02/46.13 | 8.58/9.56 | 53.39/44.31 |
| CCLM5/REMO(MPI-ESM-LR) | 39.67/54.24 | 7.08/7.43 | 53.24/38.33 | |
| CCLM5/REMO(NorESM1-M) | 74.61/77.65 | 1.12/0.86 | 24.27/21.49 | |
| GPCC | CCLM5/REMO(HadGEM2-ES) | 68.06/73.12 | 4.5/4.69 | 27.44/22.19 |
| CCLM5/REMO(MPI-ESM-LR) | 50.79/64.97 | 5.05/3.54 | 44.16/31.49 | |
| CCLM5/REMO(NorESM1-M) | 41.03/50.24 | 4.7/4.17 | 54.27/45.6 | |
| JJA | ||||
| CHIRPS | CCLM5/REMO(HadGEM2-ES) | 37.29/49.34 | 7.26/6.49 | 55.45/49.34 |
| CCLM5/REMO(MPI-ESM-LR) | 31.59/43.67 | 10.01/7.36 | 58.4/48.98 | |
| CCLM5/REMO(NorESM1-M) | 85.29/71.2 | 4.74/1.81 | 9.97/26.99 | |
| GPCC | CCLM5/REMO(HadGEM2-ES) | 51.91/62.72 | 3.6/2.78 | 44.49/35.51 |
| CCLM5/REMO(MPI-ESM-LR) | 43.17/60.63 | 7.01/2.47 | 49.82/36.9 | |
| CCLM5/REMO(NorESM1-M) | 52.68/39.13 | 8.08/5.4 | 39.25/55.47 | |
| SON | ||||
| CHIRPS | CCLM5/REMO(HadGEM2-ES) | 34.02/50.59 | 7.75/8.24 | 58.23/41.17 |
| CCLM5/REMO(MPI-ESM-LR) | 44.56/63.98 | 7.62/7.62 | 47.56/28.39 | |
| CCLM5/REMO(NorESM1-M) | 79.35/73.88 | 12.6/5.63 | 8.05/20.49 | |
| GPCC | CCLM5/REMO(HadGEM2-ES) | 51.47/70.9 | 4.03/1.93 | 44.49/27.17 |
| CCLM5/REMO(MPI-ESM-LR) | 59.99/85.27 | 3.63/3.32 | 36.38/11.41 | |
| CCLM5/REMO(NorESM1-M) | 40.81/37.42 | 19.05/10.62 | 40.14/51.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gnitou, G.T.; Tan, G.; Niu, R.; Nooni, I.K. Assessing Past Climate Biases and the Added Value of CORDEX-CORE Precipitation Simulations over Africa. Remote Sens. 2021, 13, 2058. https://doi.org/10.3390/rs13112058
Gnitou GT, Tan G, Niu R, Nooni IK. Assessing Past Climate Biases and the Added Value of CORDEX-CORE Precipitation Simulations over Africa. Remote Sensing. 2021; 13(11):2058. https://doi.org/10.3390/rs13112058
Chicago/Turabian StyleGnitou, Gnim Tchalim, Guirong Tan, Ruoyun Niu, and Isaac Kwesi Nooni. 2021. "Assessing Past Climate Biases and the Added Value of CORDEX-CORE Precipitation Simulations over Africa" Remote Sensing 13, no. 11: 2058. https://doi.org/10.3390/rs13112058
APA StyleGnitou, G. T., Tan, G., Niu, R., & Nooni, I. K. (2021). Assessing Past Climate Biases and the Added Value of CORDEX-CORE Precipitation Simulations over Africa. Remote Sensing, 13(11), 2058. https://doi.org/10.3390/rs13112058