HF Radars for Wave Energy Resource Assessment Offshore NW Spain
Abstract
:1. Introduction
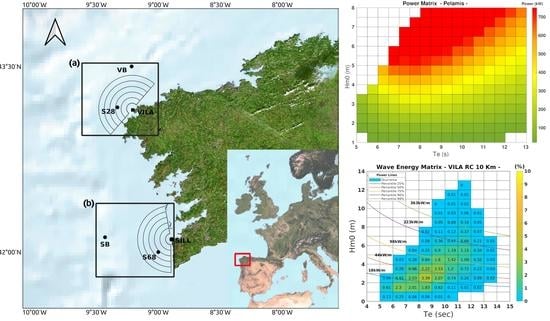
2. Materials and Methods
- VILA: North–Northwest (NNE) (–) and m;
- SILL: South (S) (–) and m.
- Vilán area: 1 January 2014–30 April 2015 + 1 January 2018–7 October 2020.
- Silleiro area: 1 January 2014–28 July 2019 + 1 August 2020–7 October 2020.
3. Results
3.1. Statistical Validation of Wave Power and Energy
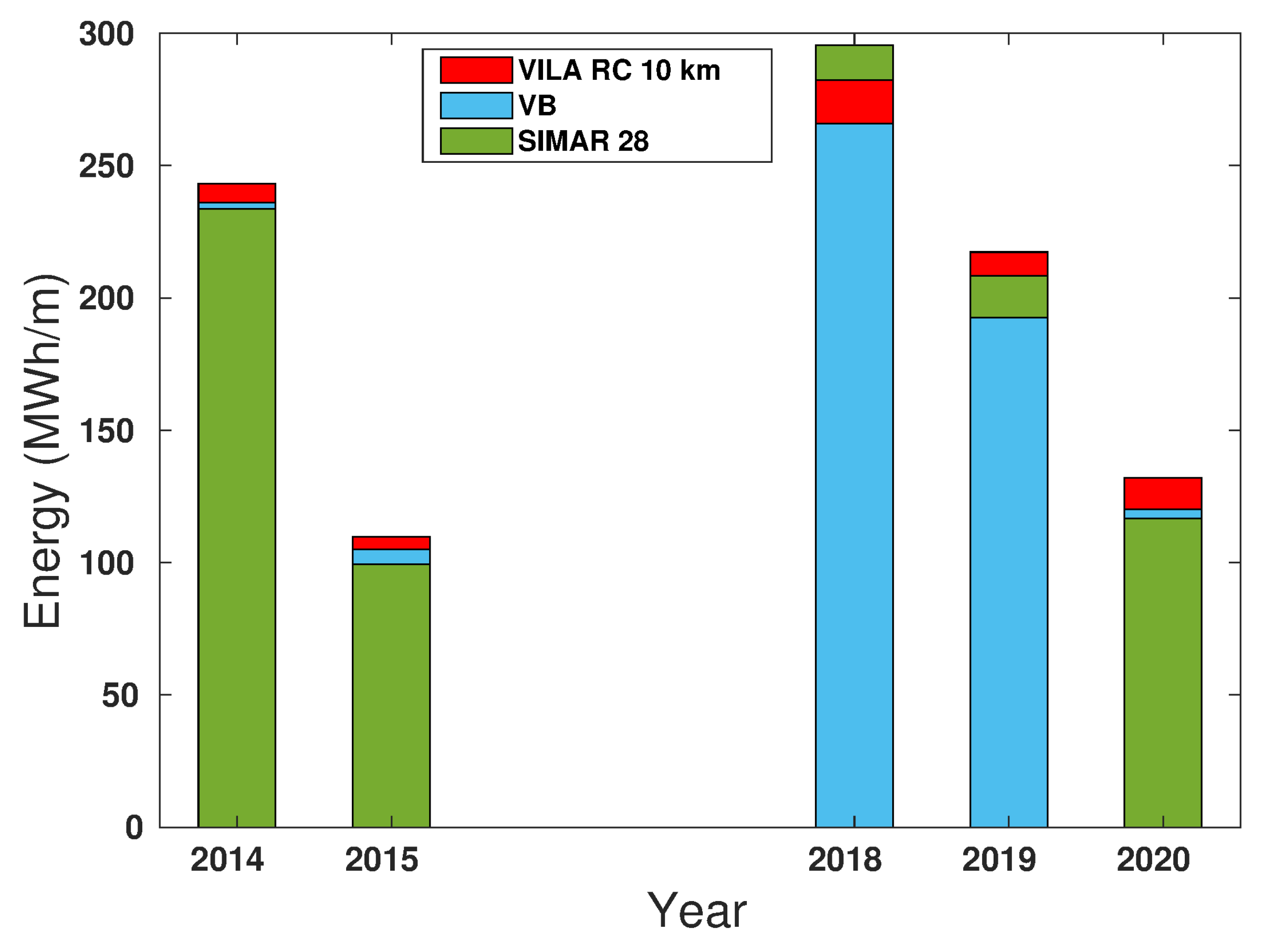
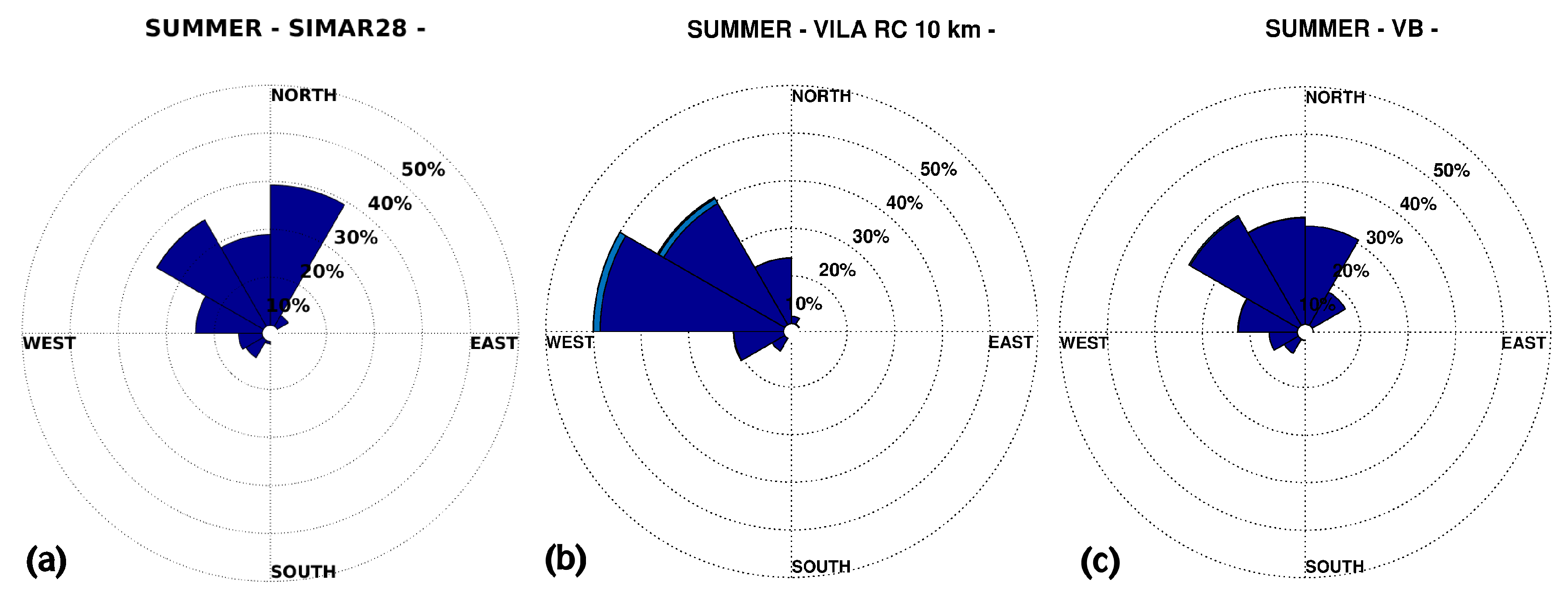
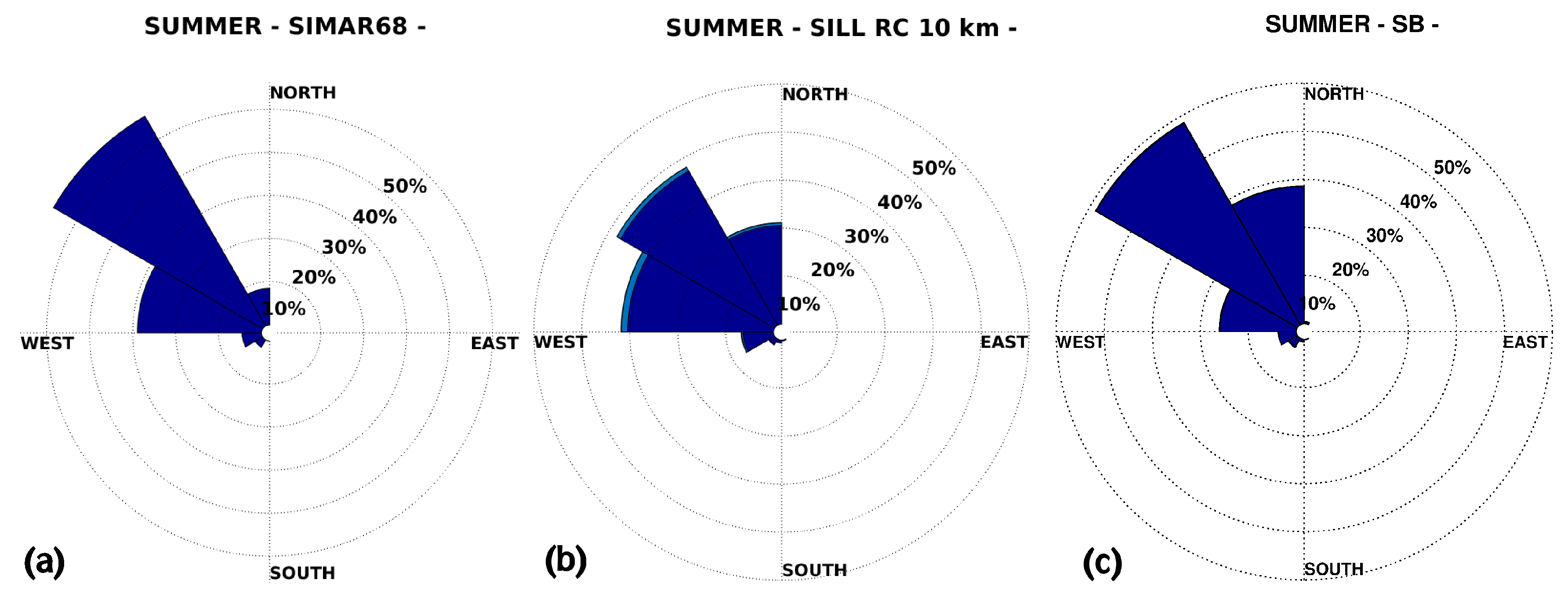
3.2. Wave Energy Resource
3.3. WEC Electricity Energy Production
3.4. Filling out Buoy Data Series
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Coefficient of variation | |
| Mean wave direction | |
| Mean wave energy | |
| Spectral significant wave height | |
| Radar centroid period | |
| Energy period | |
| Peak period | |
| AEMET | Agencia Estatal de Meteorología (Governmental Meteorological Agency in Spanish) |
| CL | Coastline limits |
| GFS | Global Forecast System |
| HF | High frequency |
| HIRLAM | High Resolution Local Area Modeling |
| P | Wave power |
| PdE | Puertos del Estado (Ports of the State in Spanish) |
| R | Lineal correlation index |
| RC | Radar range cell |
| RMSE | Root mean square error |
| S28 | SIMAR point 3004028 |
| S68 | SIMAR point 1044068 |
| SB | Silleiro buoy |
| SILL | Radar of Silleiro cape |
| SIMAR | Simulación Marina (Marine Simulation in Spanish) |
| SWAN | Simulating waves nearshore |
| VB | Vilano-Sisargas buoy |
| VILA | Radar of Vilán cape |
| WAM | Wave modeling |
| WANA | Waves analysis |
| WB | Wave bearing |
| WEC | Wave energy converter |
| WERA | Wellen radar |
| WW3 | WaveWatch III model |
References
- Rusu, E.; Venugopal, V. Special Issue. Offshore Renewable Energy: Ocean Waves, Tides and Offshore Wind. Energies 2019, 12, 182. [Google Scholar] [CrossRef] [Green Version]
- Leischman, J.M.; Scobie, G. The development of wave power—A techno-economic survey. In Report EAU M25; UK National Engineering Laboratory: East kilbride Glasgow, UK, 1976. [Google Scholar]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Esteban, M.; Leary, D. Current developments and future prospects of offshore wind and ocean energy. Appl. Energy 2012, 90, 128–136. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the Death Coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Choosing the site for the first wave farm in a region: A case study in the Galician Southwest (Spain). Energy 2011, 36, 5525–5531. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Review on Power Performance and Efficiency of Wave Energy Converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef] [Green Version]
- Mueller, M.; Wallace, R. Enabling science and technology for marine renewable energy. Energy Policy 2008, 36, 4376–4382. [Google Scholar] [CrossRef]
- Mérigaud, A.; Ringwood, J.V. Power production assessment for wave energy converters: Overcoming the perils of the power matrix. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018, 232, 50–70. [Google Scholar] [CrossRef]
- Ahn, S.; Haas, K.A.; Neary, V.S. Dominant Wave Energy Systems and Conditional Wave Resource Characterization for Coastal Waters of the United States. Energies 2020, 13, 3041. [Google Scholar] [CrossRef]
- Folley, M.; Whittaker, T.J.T. Analysis of the nearshore wave energy resource. Renew. Energy 2009, 34, 1709–1715. [Google Scholar] [CrossRef]
- Silva, D.; Rusu, E.; Soares, C.G. Evaluation of Various Technologies for Wave Energy Conversion in the Portuguese Nearshore. Energies 2013, 6, 1344–1364. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G. Annual and seasonal variabilities in the performances of wave energy converters. Energy 2018, 165, 812–823. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, A.S.; de Castro, M.; Rusu, L.; Bernardino, M.; Dias, J.M.; Gomez-Gesteira, M. Evaluating the Future Efficiency of Wave Energy Converters along the NW Coast of the Iberian Peninsula. Energies 2020, 13, 3563. [Google Scholar] [CrossRef]
- Saulnier, J.B.; Prevosto, M.; Maisondieu, C. Refinements of sea state statistics for marine renewables: A case study from simultaneous buoy measurements in Portugal. Renew. Energy 2011, 36, 2853–2865. [Google Scholar] [CrossRef] [Green Version]
- Robertson, B.; Clancy, D.; Bailey, H.; Buckham, B. Improved Energy Production Estimates from Wave Energy Converters through Spectral Partitioning of Wave Conditions In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference Kona, Big Island, HI, USA, 21–26 June 2015.
- Carballo, R.; Iglesias, G. A methodology to determine the power performance of wave energy converters at a particular coastal location. Energy Convers. Manag. 2012, 61, 8–18. [Google Scholar] [CrossRef]
- Atan, R.; Goggins, J.; Harnett, M.; Agostinho, P.; Nash, S. Assessment of wave characteristics and resource variability at a 1/4-scale wave energy test site in Galway Bay using waverider and high frequency radar (CODAR) data. Ocean. Eng. 2016, 117, 272–291. [Google Scholar] [CrossRef]
- Silva, D.; Martinho, P.; Guedes Soares, C. Wave energy distribution along the Portuguese continental coast based on a thirty three years hindcast. Renew. Energy 2018, 127, 1064–1075. [Google Scholar] [CrossRef]
- Tolman, H.L. The numerical model WaveWatch: A third generation model for the hindcasting of wind waves on tides in shelf seas. In Communications on Hydraulic and Geotechnical Engineering; Delft University of Technology: Delf, The Netherlands, 1989; Volume 89, p. 72. [Google Scholar]
- Carracedo García, P.; Balseiro, C.F.; Penabad, E.; Gómez, B.; Pérez-Muñuzuri, V. One year validation of wave forecasting at Galician coast. J. Atmos. Ocean. Sci. 2005, 10, 407–419. [Google Scholar] [CrossRef]
- Mackay, E.B.L.; Bahaj, A.S.; Challenor, P.G. Uncertainty in wave energy resource assessment. Part 1: Historic data. Renew. Energy 2010, 35, 1792–1808. [Google Scholar] [CrossRef]
- Bernardino, M.; Guedes Soares, C. Evaluating marine climate change in the Portuguese coast during the 20th century. In Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, A.P., Eds.; Taylor and Francis: London, UK, 2018; pp. 1089–1095. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Atan, R.; Goggins, J.; Nash, S. A Detailed Assessment of the Wave Energy Resource at the Atlantic Marine Energy Test Site. Energies 2016, 9, 967. [Google Scholar] [CrossRef] [Green Version]
- MeteoGalicia. Atlas de ondas de Galicia; MeteoGalicia: Santiago de Compostela, Spain, 2014.
- Soares, C.G.; Bento, A.R.; Gonçalves, M.; Silva, D.; Martinho, P. Numerical evaluation of the wave energy resource along the Atlantic European coast. Comput. Geosci. 2014, 71, 37–49. [Google Scholar] [CrossRef]
- Carballo, R.; Sánchez, M.; Ramos, V.; Taveira-Pinto, F.; Iglesias, G. A high resolution geospatial database for wave energy exploitation. Energy 2014, 68, 572–583. [Google Scholar] [CrossRef] [Green Version]
- Rusu, E. Numerical Modeling of the Wave Energy Propagation in the Iberian Nearshore. Energies 2018, 11, 980. [Google Scholar] [CrossRef] [Green Version]
- Lavidas, G.; Venugopal, V. Application of numerical wave models at European coastlines: A review. Renew. Sustain. Energy Rev. 2018, 92, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Pitt, E. Assessment of Wave Energy Resource. Report of European Marine Energy Centre LTD (EMEC); BSI: London, UK, 2009. [Google Scholar]
- Guillou, N.; Lavidas, G.; Chapalain, G. Wave Energy Resource Assessment for Exploitation—A Review. J. Mar. Sci. Eng. 2020, 8, 705. [Google Scholar] [CrossRef]
- Roarty, H.; Cook, T.; Hazard, L.; Doug, G.; Harlan, J.; Cosoli, S.; Wyatt, L.; Alvarez-Fanjul, E.; Terrill, E.; Otero, M.; et al. The Global High Frequency Radar Network. Front. Mar. Sci. 2019, 6, 164. [Google Scholar] [CrossRef]
- Hardman, R.; Wyatt, L. Inversion of HF Radar Doppler spectra using a neural network. J. Mar. Sci. Eng. 2019, 7, 255. [Google Scholar] [CrossRef] [Green Version]
- Lorente, P.; Basañez Mercader, A.; Piedracoba, S.; Pérez-Muñuzuri, V.; Montero, P.; Sotillo, M.G.; Álvarez-Fanjul, E. Long-term skill assessment of SeaSonde radar-derived wave parameters in the Galician coast (NW Spain). Int. J. Remote Sens. 2019, 10, 9208–9236. [Google Scholar] [CrossRef]
- Tian, Z.; Tian, Y.; Wen, B. Quality Control of Compact High-Frequency Radar-Retrieved Wave Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 929–939. [Google Scholar] [CrossRef]
- Anderson, S. Bistatic and Stereoscopic Configurations for HF Radar. Remote Sens. 2020, 12, 689. [Google Scholar] [CrossRef] [Green Version]
- Basañez, A.; Lorente, P.; Montero, P.; Álvarez-Fanjul, E.; Pérez-Muñuzuri, V. Quality Assessment and Practical Interpretation of the Wave Parameters Estimated by HF Radars in NW Spain. Remote Sens. 2020, 12, 598. [Google Scholar] [CrossRef] [Green Version]
- Crombie, D. Doppler spectrum of sea echo at 13.56 MHz. Nature 1955, 175, 681–688. [Google Scholar] [CrossRef]
- Hasselmann, K. Determination of ocean wave spectra from Doppler radio return from the sea surface. Nat. Phys. Sci. 1971, 229, 16–17. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D. Analysis methods for Narrow-Beam High-Frequency Radar Sea Echo; NOAA Technical Report ERL 420-WP 56; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, Environmental Research Laboratories: Boulder, CO, USA, 1982.
- Wyatt, L.R.; Green, J.; Middleditch, A.; Moorhead, M.D.; Howarth, J.; Holt, M.; Keogh, S. Operational wave, current, and wind measurements with the Pisces HF radar. IEEE J. Ocean. Eng. 2006, 31, 819–834. [Google Scholar] [CrossRef]
- Kohut, J.; Roarty, H.; Licthenwalner, S.; Glenn, S.; Barrick, D.; Lipa, B.; Allen, A. Surface Currents and Wave Validation of a Nested Regional HF radar Network in the Mid-Atlantic Bight. In Proceedings of the IEEE/OES/CMTC 9th Working Conference on Current Measurement Technology, Charleston, SC, USA, 17–19 March 2008. [Google Scholar]
- Long, R.; Barrick, D.; Largier, J.; Garfield, N. Wave observations from central California: SeaSonde Systems and in situ wave buoys. J. Sens. 2011, 2011, 728936. [Google Scholar] [CrossRef] [Green Version]
- Falco, P.; Buonocore, B.; Cianelli, D.; De Luca, L.; Giordano, A.; Iermano, I.; Kalampokis, A.; Saviano, S.; Uttieri, M.; Zambardino, G.; et al. Dynamics and sea state in the Gulf of Naples: Potential use of high-frequency radar data in an operational oceanographic context. J. Oper. Oceanogr. 2016, 9 (Suppl. S1), 33–45. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, M.; Fernandes, C.; Barroqueiro, T.; Agostinho, P.; Martins, N.; Alonso-Martirena, A. Extreme wave height events in Algarve (Portugal): Comparison between HF radar systems and wave buoys. In Proceedings of the 5th Jornadas Engenharia Hidrográfica, Lisboa, Portugal, 19–21 June 2018; pp. 222–225. [Google Scholar]
- Wyatt, L.R. Limits to the inversion of HF Radar backscatter for ocean wave measurement. J. Atmos. Ocean. Technol. 1999, 17, 1651–1665. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Essen, H.H.; Schlick, T. An empirical method to derive ocean waves from second-order bragg scattering: Prospects and limitations. IEEE J. Ocean. Eng. 2006, 31, 804–811. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B. Directional wave information from the SeaSonde. IEEE J. Ocean. Eng. 2005, 30, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Hisaki, Y. Quality control of surface wave data estimated from low signal-to-noise ratio HF radar Doppler-Spectra. J. Atmos. Ocean. Technol. 2009, 26, 2444–2461. [Google Scholar] [CrossRef]
- Lipa, B.; Daugharty, M.; Fernandes, M.; Barrick, D.; Alonso-Martirena, A.; Roarty, H.; Dicopoulos, J.; Whelan, C. Developments in Compact HF radar Ocean Wave Measurements. In Physical Sensors, Sensor Networks and Remote Sensing; Book Series: Advances in Sensors: Reviews; Yurish, S., Ed.; International Frequency Sensor Association Publishing (IFSA): Barcelona, Spain, 2018; Volume 5, Chapter 20; pp. 469–495. [Google Scholar]
- Lipa, B.; Barrick, D. Extraction of sea state from HF radar sea echo: Mathematical theory and modeling. Radio Sci. 1986, 21, 81–100. [Google Scholar] [CrossRef]
- Toffoli, A.; Onorato, M.; Monbaliu, J. Wave statistics in unimodal and bimodal seas from a second-order model. Eur. J. Mech. B/Fluids 2006, 25, 649–661. [Google Scholar] [CrossRef]
- López, G.; Conley, D.; Greaves, D. Calibration, validation and analysis if an empirical algorithm for the retrieval of wave spectra from HF radar sea echo. J. Atmos. Ocean. Technol. 2016, 33, 245–261. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Alonso-Martirena, A.; Fernandes, M.; Ferrer, M.I.; Nyden, B. The Brahan Project high frequency radar ocean measurements: Currents, winds, waves and their interactions. Remote Sens. 2014, 6, 12094–12117. [Google Scholar] [CrossRef] [Green Version]
- Saviano, P.; Kalampokis, A.; Zambianchi, E.; Uttieri, M. A year-long assessment of wave measurements retrieved from an HF radar network in the Gulf of Naples (Tyrrhenian Sea, Western Mediterranean Sea). J. Operat. Oceanogr. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Saulnier, J.B.; Maisondieu, C.; Ashton, I.; Smith, G.H. Refined sea state analysis from an array of four identical directional buoys deployed off the Northern Cornish coast (UK). Appl. Ocean. Res. 2012, 37, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Alfonso, M.; Álvarez-Fanjul, E.; López, J.D. Comparison of CODAR SeaSonde HF radar Operational Waves and Currents Measurements with Puertos Del Estado Buoys. In Final Report; Puertos Del Estado, Ministerio de Fomento: Madrid, Spain, March 2006. [Google Scholar]
- Bué, I.; Semedo, Á.; Catalão, J. Evaluation of HF Radar Wave Measurements in Iberian Peninsula by Comparison with Satellite Altimetry and in situ Wave Buoy Observations. Remote Sens. 2020, 12, 3623. [Google Scholar] [CrossRef]
- Ramos, R.J.; Graber, H.C.; Haus, B.K. Observation of Wave Energy Evolution in Coastal Areas Using HF Radar. J. Atmos. Ocean. Technol. 2009, 26, 1891–1909. [Google Scholar] [CrossRef] [Green Version]
- Wyatt, L. Wave and tidal power measurement using HF radar. Int. Mar. Energy J. 2018, 1, 123–127. [Google Scholar] [CrossRef]
- Mundaca-Moraga, V.; Abarca-del-Rio, R.; Figueroa, D.; Morales, J. A Preliminary Study of Wave Energy Resource Using an HF Marine Radar, Application to an Eastern Southern Pacific Location: Advantages and Opportunities. Remote Sens. 2021, 13, 203. [Google Scholar] [CrossRef]
- CODAR. Configuration File Formats. Available online: http://support.codar.com/ (accessed on 20 January 2020).
- Paduan, J.D.; Kim, K.C.; Cook, M.S.; Chavez, F.P. Calibration and validation of direction-finding high-frequency radar ocean surface current Observations. IEEE J. Ocean. Eng. 2006, 31, 862–875. [Google Scholar] [CrossRef]
- CODAR. Ocean Sensors SeaSonde® Remote Unit System Specification. Versión 6, Revision 06/2017. Available online: https://www.codar.com/images/products/SeaSonde/1B-CODARspec_SSRS-100_v6-20170609.pdf (accessed on 20 January 2020).
- CODAR. Ocean Sensors SeaSonde®. Available online: http://support.codar.com/Technicians_Information_Page_for_SeaSondes/Configuring_Site_files/WaveModelSetDirectionLimits.pdf (accessed on 20 January 2020).
- Copernicus Marine in situ Team. Copernicus In Situ TAC, Real Time Quality Control for WAVES; Copernicus In Situ TAC: Toulouse, France, 2017; pp. 1–19. [Google Scholar]
- Puertos del Estado. Conjunto de Datos REDEXT. Available online: http://calipso.puertos.es/BD/informes/INT_REDEXT.pdf (accessed on 20 January 2020).
- Puertos del Estado. Conjunto de Datos SIMAR. Available online: http://calipso.puertos.es/BD/informes/INT_8.pdf (accessed on 20 January 2020).
- Tucker, M.J. Analysis of records of sea waves. Proc. Inst. Civ. Eng. 1963, 262, 305–316. [Google Scholar] [CrossRef]
- The Specialist Committee on Waves Final Report and Recommendations to the 23rd ITTC. In Proceedings of the 23rd ITTC, Venice, Italy, 8–14 September 2002; Volume II.
- Carballo, R.; Sánchez, M.; Ramos, V.; Fraguela, J.A.; Iglesias, G. The intra-annual variability in the performance of wave energy converters: A comparative study in N Galicia (Spain). Energy 2015, 82, 138–146. [Google Scholar] [CrossRef]
- Iglesias, G.; López, M.; Carballo, R.; Castro, A.; Fraguela, J.A.; Frigaard, P. Wave energy potential in Galicia (NW Spain). Renew. Energy 2009, 34, 2323–2333. [Google Scholar] [CrossRef]











| (a) | VILÁN SITE | ||||
|---|---|---|---|---|---|
| Data Sets | S28 | VB | Hourly Ideal Samples | VILA 10 km | Nulls |
| Total | 35,666 | 33,637 | 35,879 | 63,839 | 51.05% |
| Spring | 9420 | 9059 | 9456 | 15,742 | 55.72% |
| Summer | 8737 | 8759 | 8832 | 13,858 | 71.40% |
| Autumn | 6734 | 6768 | 6767 | 13,497 | 45.05% |
| Winter | 10,775 | 9051 | 10,824 | 20,742 | 37.81% |
| (b) | SILLEIRO SITE | ||||
| Data Sets | S68 | SB | Hourly Ideal Samples | SILL 10 km | Nulls |
| Total | 50,377 | 49,596 | 50,471 | 95,202 | 39.38% |
| Spring | 13,092 | 13,053 | 13,104 | 25,280 | 46.01% |
| Summer | 13,188 | 12,377 | 13,199 | 25,891 | 57.01% |
| Autumn | 11,173 | 11,183 | 11,184 | 19,770 | 29.41% |
| Winter | 12,924 | 12,983 | 12,984 | 24,261 | 21.79% |
| (a) | VILÁN SITE | (b) | SILLEIRO SITE | ||
|---|---|---|---|---|---|
| Paired Clean Samples | Paired Clean Samples | ||||
| Data Sets | All Sources | Data Sets | All Sources | ||
| Total | 13,724 | Total | 27,486 | ||
| Spring | 3210 | Spring | 4656 | ||
| Summer | 1849 | Summer | 6618 | ||
| Autumn | 3650 | Autumn | 6891 | ||
| Winter | 5015 | Winter | 9321 | ||
| (a) | VILÁN SITE | (b) | SILLEIRO SITE | ||||
|---|---|---|---|---|---|---|---|
| Paired Raw Data: 29,578 Samples. | Paired Raw Data: 46,475 samples. | ||||||
| Valid Samples | Valid Samples | ||||||
| Data Sets | S28 | VILA RC 10 km | VB | Data Sets | S68 | SILL RC 10 km | SB |
| Total | 29,578 | 13,770 | 29,537 | Total | 46,475 | 27,856 | 45,768 |
| Spring | 7439 | 3224 | 7425 | Spring | 12,501 | 6627 | 12,488 |
| Summer | 6,819 | 1,859 | 6,814 | Summer | 12,076 | 4997 | 11,412 |
| Autumn | 6723 | 3657 | 6,718 | Autumn | 9848 | 6898 | 9835 |
| Winter | 8597 | 5030 | 8580 | Winter | 12,050 | 9334 | 12,033 |
| VILÁN SITE | ||||
|---|---|---|---|---|
| Wave Power Statistics (kW/m) | ||||
| Data Sets | MEAN | RMSE vs. VB | RMSE vs. S28 | |
| Total | VB | 67.00 | — | — |
| S28 | 69.48 | 29.37 | — | |
| VILA | 71.76 | 41.73 | 44.17 | |
| Spring | VB | 32.47 | — | — |
| S28 | 37.34 | 15.88 | — | |
| VILA | 39.18 | 23.75 | 23.20 | |
| Summer | VB | 22.47 | — | — |
| S28 | 22.95 | 8.74 | — | |
| VILA | 24.83 | 19.54 | 20.63 | |
| Autumn | VB | 84.06 | — | — |
| S28 | 87.92 | 33.18 | — | |
| VILA | 93.70 | 47.93 | 52.14 | |
| Winter | VB | 92.91 | — | — |
| S28 | 93.79 | 37.00 | — | |
| VILA | 93.95 | 49.93 | 52.58 | |
| SILLEIRO SITE | ||||
|---|---|---|---|---|
| Wave Power Statistics (kW/m) | ||||
| Data Sets | MEAN | RMSE vs. SB | RMSE vs. S68 | |
| Total | SB | 54.39 | — | — |
| S68 | 45.14 | 28.87 | — | |
| SILL | 66.00 | 40.02 | 46.57 | |
| Spring | SB | 29.97 | — | — |
| S68 | 27.33 | 14.59 | — | |
| SILL | 40.36 | 27.94 | 30.76 | |
| Summer | SB | 19.22 | — | — |
| S68 | 15.36 | 9.37 | — | |
| SILL | 29.40 | 24.69 | 27.54 | |
| Autumn | SB | 60.74 | — | — |
| S68 | 49.44 | 27.92 | — | |
| SILL | 76.76 | 44.23 | 53.13 | |
| Winter | SB | 84.61 | — | — |
| S68 | 69.48 | 41.07 | — | |
| SILL | 94.51 | 49.17 | 57.07 | |
| (a) | VILÁN SITE | (b) | SILLEIRO SITE | ||||
|---|---|---|---|---|---|---|---|
| Mean Wave Energy (MWh/m) | Mean Wave Energy (MWh/m) | ||||||
| Data Sets | S28 | VILA RC 10 km | VB | Data Sets | S68 | SILL RC 10 km | SB |
| Annual | 343.28 | 240.80 | 325.75 | Annual | 246.52 | 316.83 | 292.75 |
| Spring | 45.54 | 29.24 | 38.39 | Spring | 37.94 | 44.70 | 41.97 |
| Summer | 25.93 | 11.42 | 22.70 | Summer | 20.28 | 24.23 | 22.39 |
| Autumn | 145.47 | 110.81 | 138.27 | Autumn | 73.72 | 103.69 | 90.01 |
| Winter | 132.58 | 95.42 | 131.44 | Winter | 117.18 | 148.84 | 141.84 |
| (a) | VILÁN SITE | (b) | SILLEIRO SITE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coefficient of Variation () (%) | Coefficient of Variation () (%) | ||||||||
| Em | Power | Em | Power | ||||||
| Data Sets | VILA RCs | WW3 Cells Bisector | VILA RCs | WW3 Cells Bisector | Data Sets | SILL RCs | WW3 Cells Bisector | SILL RCs | WW3 Cells Bisector |
| Annual/ Total | 7.12 | 4.04 | 22.97 | 5.30 | Annual/ Total | 4.34 | 5.02 | 23.36 | 6.81 |
| Spring | 9.66 | 3.78 | 24.66 | 5.28 | Spring | 5.20 | 4.46 | 25.21 | 6.69 |
| Summer | 12.11 | 4.32 | 19.30 | 6.16 | Summer | 7.67 | 6.03 | 26.56 | 8.08 |
| Autumn | 7.40 | 3.92 | 22.21 | 4.80 | Autumn | 3.94 | 4.96 | 18.58 | 6.45 |
| Winter | 5.88 | 4.16 | 21.82 | 5.03 | Winter | 4.20 | 5.06 | 20.43 | 5.93 |
| VILAN SITE | SILLEIRO SITE | ||||||
|---|---|---|---|---|---|---|---|
| (a) | Pelamis Mean Electricity Production (MWh) | (b) | Pelamis Mean Electricity Production (MWh) | ||||
| Data Sets | S28 | VILA RC 10 km | VB | Data Sets | S68 | SILL RC 10 km | SB |
| Annual | 1107.59 | 996.00 | 1612.53 | Annual | 773.39 | 1198.51 | 1421.46 |
| Spring | 200.00 | 146.86 | 250.16 | Spring | 149.98 | 199.30 | 258.66 |
| Summer | 135.43 | 69.94 | 158.12 | Summer | 99.95 | 128.74 | 145.63 |
| Autumn | 431.36 | 443.70 | 654.90 | Autumn | 223.79 | 394.71 | 442.19 |
| Winter | 362.94 | 362.62 | 579.31 | Winter | 305.86 | 492.73 | 591.41 |
| (c) | Aquabuoy Mean Electricity Production (MWh) | (d) | Aquabuoy Mean Electricity Production (MWh) | ||||
| Data Sets | S28 | VILA RC 10 km | VB | Data Sets | S68 | SILL RC 10 km | SB |
| Annual | 362.88 | 267.22 | 442.93 | Annual | 260.83 | 350.55 | 415.74 |
| Spring | 63.90 | 43.84 | 70.39 | Spring | 48.86 | 62.29 | 76.81 |
| Summer | 41.24 | 22.03 | 45.36 | Summer | 30.94 | 42.28 | 44.79 |
| Autumn | 142.84 | 115.10 | 183.52 | Autumn | 79.71 | 120.13 | 134.78 |
| Winter | 121.95 | 93.21 | 153.82 | Winter | 104.05 | 131.34 | 164.88 |
| VILÁN SITE | |||
|---|---|---|---|
| Mean Wave Energy (MWh/m) | |||
| Data Sets | S28 | VB | VB + VILA |
| Annual | 417.28 | 350.75 | 404.00 |
| Spring | 54.63 | 44.05 | 47.05 |
| Summer | 31.78 | 28.18 | 28.29 |
| Autumn | 145.99 | 139.43 | 139.52 |
| Winter | 180.87 | 142.02 | 183.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basañez, A.; Pérez-Muñuzuri, V. HF Radars for Wave Energy Resource Assessment Offshore NW Spain. Remote Sens. 2021, 13, 2070. https://doi.org/10.3390/rs13112070
Basañez A, Pérez-Muñuzuri V. HF Radars for Wave Energy Resource Assessment Offshore NW Spain. Remote Sensing. 2021; 13(11):2070. https://doi.org/10.3390/rs13112070
Chicago/Turabian StyleBasañez, Ana, and Vicente Pérez-Muñuzuri. 2021. "HF Radars for Wave Energy Resource Assessment Offshore NW Spain" Remote Sensing 13, no. 11: 2070. https://doi.org/10.3390/rs13112070
APA StyleBasañez, A., & Pérez-Muñuzuri, V. (2021). HF Radars for Wave Energy Resource Assessment Offshore NW Spain. Remote Sensing, 13(11), 2070. https://doi.org/10.3390/rs13112070