Alternative Approach for Tsunami Early Warning Indicated by Gravity Wave Effects on Ionosphere
Abstract
1. Introduction
2. Materials
3. Methods
3.1. TEC Measurements
3.2. TEC Disturbances
3.3. Ionospheric Irregularities
4. Results
4.1. IGWs
4.1.1. Horizontal Speed Phase of IGWs
4.1.2. Ionosphere Response to IGWs
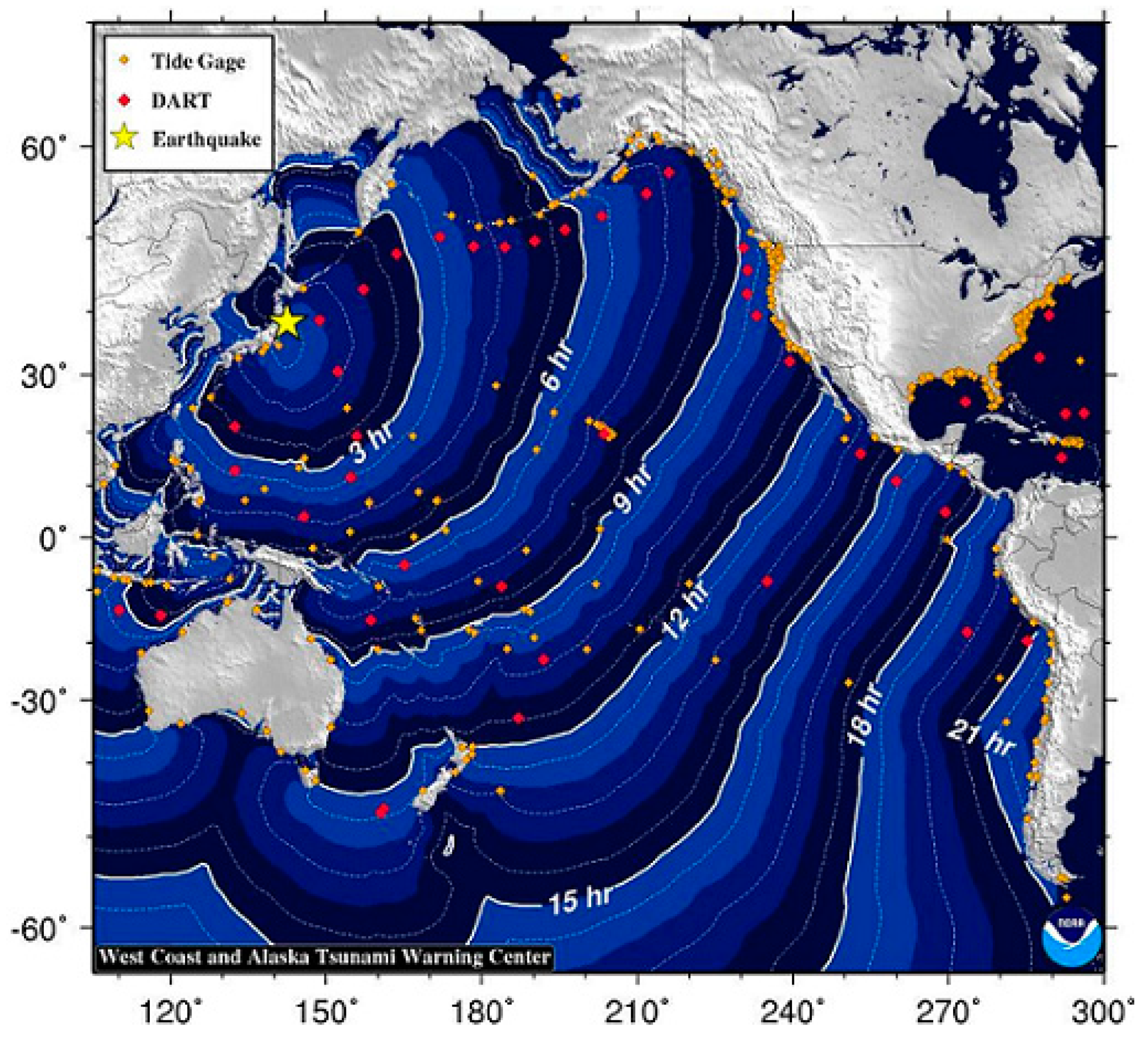
4.2. Tsunami Waves Activity
4.3. Validation of Results
4.3.1. Using Ionosonde Data
4.3.2. Using Electron Density Disturbances
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuanggen, J.; Estel, C.; Feiqin, X. GNSS Remote Sensing: Theory, Methods and Applications; Springer: Enchede, The Netherlands, 2014; Volume 19, pp. 18–21. [Google Scholar]
- Böhm, J.; David, S.; Alizadeh, M.; Wijaya, D.D. Geodetic and Atmospheric Background. In Atmospheric Effects in Space Geodesy; Böhm, J., Schuh, H., Eds.; Springer: Berlin, Germany, 2013; pp. 1–33. [Google Scholar]
- Laštovička, J. Forcing of the ionosphere by waves from below. J. Atmos. Sol. Terr. Phys. 2006, 68, 479–497. [Google Scholar] [CrossRef]
- Peltier, W.R.; Hines, C.O. On the possible detection of tsunamis by a monitoring of the ionosphere. J. Geophys. Res. (1896–1977) 1976, 81, 1995–2000. [Google Scholar] [CrossRef]
- Saha, K. The Earth’s Atmosphere: Its Physics and Dynamics; Springer: Berlin, Germany, 2008; pp. 239–244. [Google Scholar]
- Lejeune, S.; Wautelet, G.; Warnant, R. Ionospheric effects on relative positioning within a dense GPS network. GPS Solut. 2012, 16, 105–116. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, H.F.; Lin, C.H.; Kamogawa, M.; Chen, Y.I.; Lin, C.H.; Huang, B.S.; Yu, S.B.; Yeh, Y.H. Coseismic ionospheric disturbances triggered by the Chi-Chi earthquake. J. Geophys. Res. Space Phys. 2010, 115, A08303. [Google Scholar] [CrossRef]
- Artru, J.; Ducic, V.; Kanamori, H.; Lognonné, P.; Murakami, M. Ionospheric detection of gravity waves induced by tsunamis. Geophys. J. Int. 2005, 160, 840–848. [Google Scholar] [CrossRef]
- Yang, Y.-M.; Garrison, J.L.; Lee, S.-C. Ionospheric disturbances observed coincident with the 2006 and 2009 North Korean underground nuclear tests. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Hines, C.O. Gravity Waves in the Atmosphere. Nature 1972, 239, 73–78. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, Y.B.; Chen, S.W.; Lee, C.P.; Chen, Y.C.; Yen, H.Y.; Chang, W.Y.; Liu, C. Giant ionospheric disturbances excited by the M9.3 Sumatra earthquake of 26 December 2004. Geophys. Res. Lett. 2006, 33, L02103. [Google Scholar] [CrossRef]
- Occhipinti, G.; Rolland, L.; Lognonné, P.; Watada, S. From Sumatra 2004 to Tohoku-Oki 2011: The systematic GPS detection of the ionospheric signature induced by tsunamigenic earthquakes. J. Geophys. Res. Space Phys. 2013, 118, 3626–3636. [Google Scholar] [CrossRef]
- Makela, J.J.; Lognonné, P.; Hébert, H.; Gehrels, T.; Rolland, L.; Allgeyer, S.; Kherani, A.; Occhipinti, G.; Astafyeva, E.; Coïsson, P.; et al. Imaging and modeling the ionospheric airglow response over Hawaii to the tsunami generated by the Tohoku earthquake of 11 March 2011. Geophys. Res. Lett. 2011, 38, L00G02. [Google Scholar] [CrossRef]
- Rolland, L.M.; Occhipinti, G.; Lognonné, P.; Loevenbruck, A. Ionospheric gravity waves detected offshore Hawaii after tsunamis. Geophys. Res. Lett. 2010, 37, L17101. [Google Scholar] [CrossRef]
- Tang, L.; Li, Z.; Zhou, B. Large-area tsunami signatures in ionosphere observed by GPS TEC after the 2011 Tohoku earthquake. GPS Solut. 2018, 22, 93. [Google Scholar] [CrossRef]
- Tsugawa, T.; Saito, A.; Otsuka, Y.; Nishioka, M.; Maruyama, T.; Kato, H.; Nagatsuma, T.; Murata, K.T. Ionospheric disturbances detected by GPS total electron content observation after the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 66. [Google Scholar] [CrossRef]
- NOAA. Available online: http://wcatwc.arh.noaa.gov/previous.events/?p=03-11-11_Honshu (accessed on 21 March 2011).
- Perevalova, N.P.; Ishin, A.B. Effects of tropical cyclones in the ionosphere from data of sounding by GPS signals. Izv. Atmos. Ocean. Phys. 2011, 47, 1072–1083. [Google Scholar] [CrossRef]
- Cheng, Z.; Shi, J.; Zhang, T.; Dunlop, M.; Liu, Z. The relations between density of FACs in the plasma sheet boundary layers and Kp index. Sci. China Technol. Sci. 2011, 54, 2987. [Google Scholar] [CrossRef]
- Zolesi, B.; Cander, L.R. The General Structure of the Ionosphere. In Ionospheric Prediction and Forecasting; Springer: Berlin, Germany, 2014. [Google Scholar]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; University of Berne: Berne, Switzerland, 1999. [Google Scholar]
- Li, M.; Yuan, Y.; Wang, N.; Liu, T.; Chen, Y. Estimation and analysis of the short-term variations of multi-GNSS receiver differential code biases using global ionosphere maps. J. Geod. 2018, 92, 889–903. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J. Medium-scale traveling ionospheric disturbances affecting GPS measurements: Spatial and temporal analysis. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, X. A Multi-Step Multi-Order Numerical Difference Method for Traveling Ionospheric Disturbances Detection. In China Satellite Navigation Conference (CSNC) 2014 Proceedings; Sun, J., Jiao, W., Wu, H., Lu, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Pi, X.; Mannucci, A.J.; Lindqwister, U.J.; Ho, C.M. Monitoring of global ionospheric irregularities using the Worldwide GPS Network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Jacobsen, K.S.; Dähnn, M. Statistics of ionospheric disturbances and their correlation with GNSS positioning errors at high latitudes. J. Space Weather Space Clim. 2014, 4, A27. [Google Scholar] [CrossRef]
- Galvan, D.A.; Komjathy, A.; Hickey, M.P.; Mannucci, A.J. The 2009 Samoa and 2010 Chile tsunamis as observed in the ionosphere using GPS total electron content. J. Geophys. Res. Space Phys. 2011, 116, A06318. [Google Scholar] [CrossRef]
- Galvan, D.A.; Komjathy, A.; Hickey, M.P.; Stephens, P.; Snively, J.; Tony Song, Y.; Butala, M.D.; Mannucci, A.J. Ionospheric signatures of Tohoku-Oki tsunami of March 11, 2011: Model comparisons near the epicenter. Radio Sci. 2012, 47, RS4003. [Google Scholar] [CrossRef]
- Vadas, S.L.; Becker, E. Numerical Modeling of the Excitation, Propagation, and Dissipation of Primary and Secondary Gravity Waves during Wintertime at McMurdo Station in the Antarctic. J. Geophys. Res. Atmos. 2018, 123, 9326–9369. [Google Scholar] [CrossRef]
- Shalimov, S.L.; Rozhnoi, A.A.; Solov’eva, M.S.; Ol’shanskaya, E.V. Impact of Earthquakes and Tsunamis on the Ionosphere. Izv. Phys. Solid Earth 2019, 55, 168–181. [Google Scholar] [CrossRef]
- Occhipinti, G.; Lognonné, P.; Kherani, E.A.; Hébert, H. Three-dimensional waveform modeling of ionospheric signature induced by the 2004 Sumatra tsunami. Geophys. Res. Lett. 2006, 33, L20104. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 11. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chen, C.-Y.; Sun, Y.-Y.; Lee, I.T.; Chum, J. Fluctuations on vertical profiles of the ionospheric electron density perturbed by the March 11, 2011 M9.0 Tohoku earthquake and tsunami. GPS Solut. 2019, 23, 76. [Google Scholar] [CrossRef]









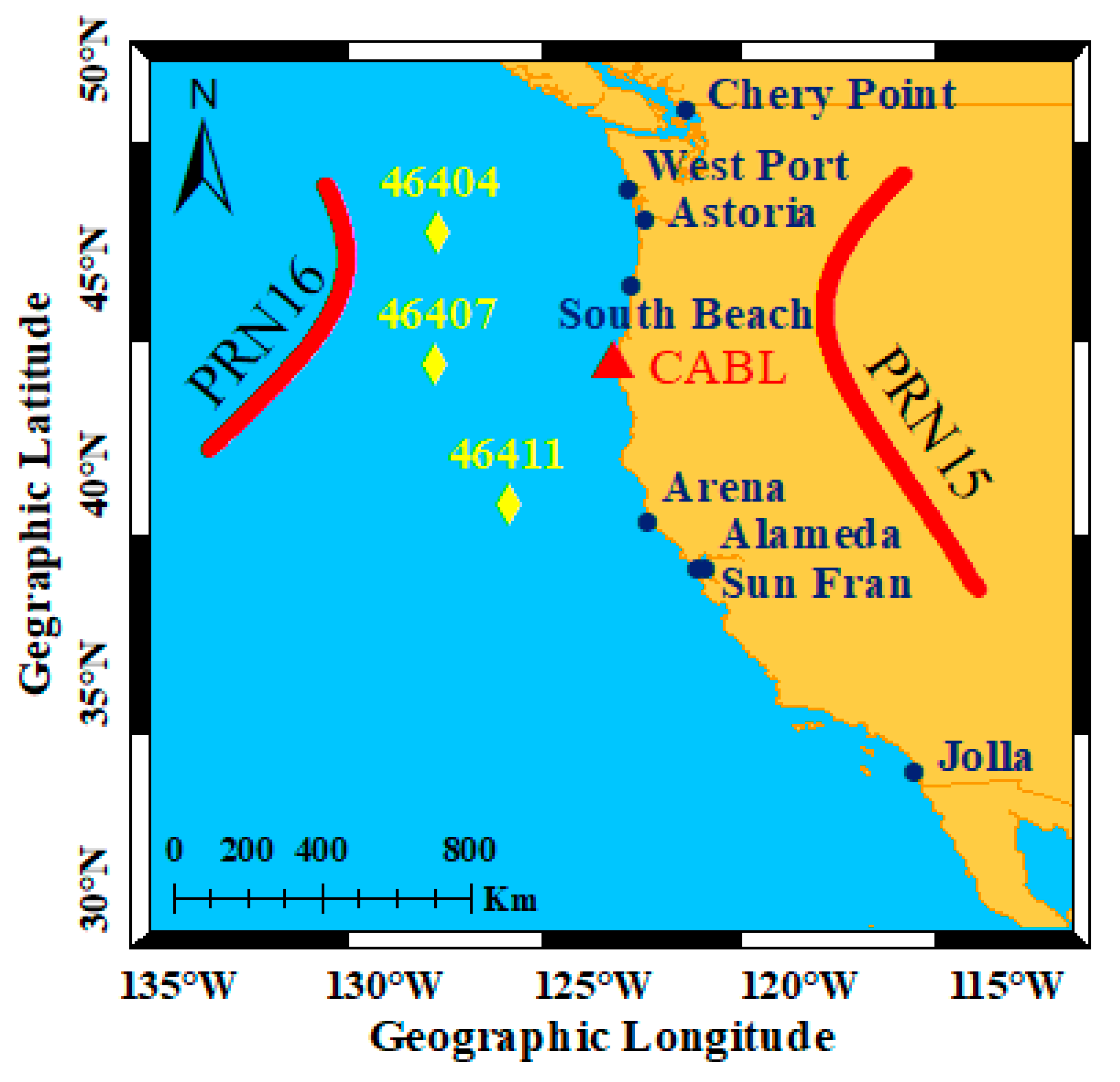








| Station | Tsunami Time Arrival (UT) | Latitude (° N) | Longitude (° W) |
|---|---|---|---|
| Alameda | 16:36 | 37.77 | −122.3 |
| Arena | 15:34 | 38.91 | −123.72 |
| Astoria | 16:24 | 46.21 | −123.77 |
| Cherry Point | 17:08 | 48.86 | −122.76 |
| Jolla | 16:22 | 32.87 | −117.26 |
| San Fran | 16:15 | 37.81 | −122.47 |
| South Beach | 15:42 | 44.63 | −124.04 |
| West Port | 15:39 | 46.91 | −124.11 |
| 46404 | 14:33 | 45.85 | −128.78 |
| 46407 | 14:39 | 42.71 | −128.83 |
| 46411 | 14:59 | 39.34 | −127.07 |
| Station | Tsunami Propagation Velocity (m/s) |
|---|---|
| 46404 | 163.8 |
| 46407 | 178.9 |
| 46411 | 204.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroodi, Z.; Alizadeh, M.; Schuh, H.; Tsai, L.-C. Alternative Approach for Tsunami Early Warning Indicated by Gravity Wave Effects on Ionosphere. Remote Sens. 2021, 13, 2150. https://doi.org/10.3390/rs13112150
Foroodi Z, Alizadeh M, Schuh H, Tsai L-C. Alternative Approach for Tsunami Early Warning Indicated by Gravity Wave Effects on Ionosphere. Remote Sensing. 2021; 13(11):2150. https://doi.org/10.3390/rs13112150
Chicago/Turabian StyleForoodi, Zahra, Mahdi Alizadeh, Harald Schuh, and Lung-Chih Tsai. 2021. "Alternative Approach for Tsunami Early Warning Indicated by Gravity Wave Effects on Ionosphere" Remote Sensing 13, no. 11: 2150. https://doi.org/10.3390/rs13112150
APA StyleForoodi, Z., Alizadeh, M., Schuh, H., & Tsai, L.-C. (2021). Alternative Approach for Tsunami Early Warning Indicated by Gravity Wave Effects on Ionosphere. Remote Sensing, 13(11), 2150. https://doi.org/10.3390/rs13112150







