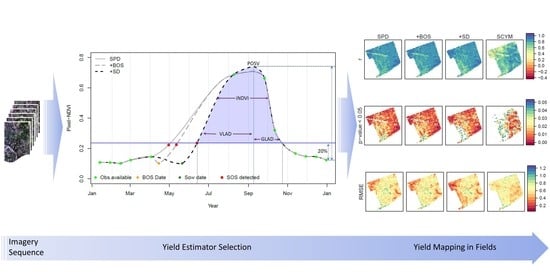
The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia
Abstract
:1. Introduction
2. Date Collection and Pre-Processing
2.1. Study Fields, On-Farm Management Records, and Yield Maps
2.2. Satellite Remote Sensing Datasets
2.3. Climate Data
3. Methodology
3.1. Models Tested
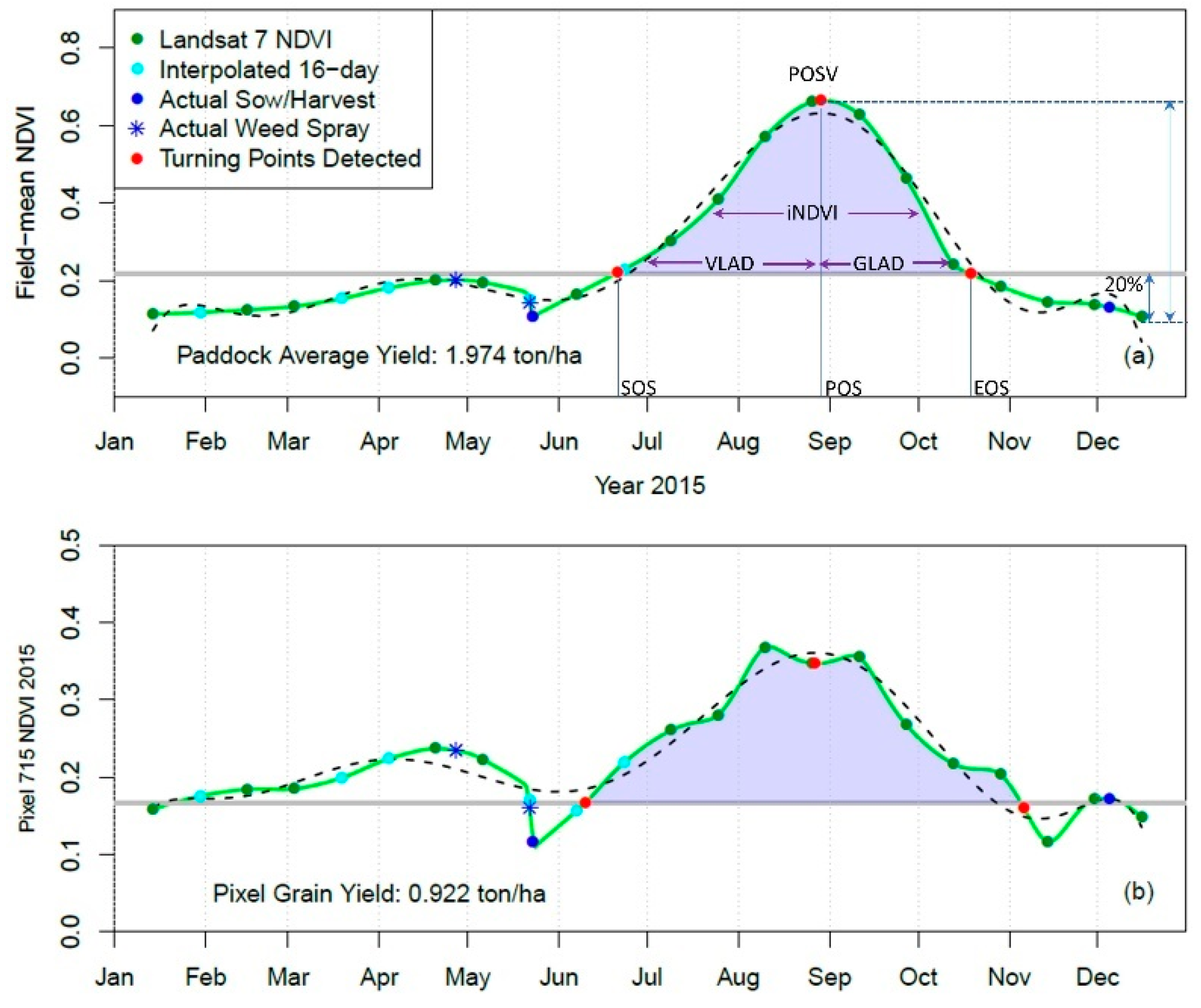
3.1.1. Statistical Phenology Detection (SPD)
- (1)
- (2)
- Repeat step 1 to interpolate the 16-day time-series NDVI to daily sequence. As a result, the daily reconstructed NDVI series was named as ‘reconstructed daily’ in the following analysis;
- (3)
- Fit a multi-polynomial with a degree of 8 to the ‘reconstructed daily’ sequences for each year to identify the peak of season (POS) date. While POSV is the value in the ‘reconstructed daily’ on the corresponding POS date (Figure 2b);
- (4)
- The start of the growing season (SOS) and end of the growing season (EOS) is identified as the date when NDVI value starts to be higher or lower than 20% of the curve amplitude. This date must be in a time window with continued positive (negative) slopes in the first (second) half curve [11,32] (Figure 2). The amplitude of the NDVI curve is calculated as the range of the ‘reconstructed daily’ NDVI sequence;
- (5)
3.1.2. Use of Additional Information in Phenology Detection (+SD and +BOS)
- (1)
- ‘Availability limits’ excluded the pixels in the years that have less than 3 available cloud-free remote sensing observations after actual/estimated sow dates;
- (2)
- ‘Sow date adding’ regulate the conditions to add additional information as there is no cloud-free NDVI value available in the ‘time windows’ before and after 11 days to the actual/estimated sow date. The ‘time window’ was defined as 2/3 of Landsat revisit time (16 days). We assume that there was no vegetation except bare soil across the fields on SD/BOS. As such, the spectral signature captured by remote sensing on SD/BOS was mostly made of soil reflectance. As the soil water and nutrient distribution were assumed to be inconsistent across the fields, we cannot simply give a single NDVI value to all the pixels on that day. Instead, we assumed that the NDVI value on SD/BOS was the lowest throughout the growing season for a certain pixel, and the value was set based on the original available NDVI sequence;
- (3)
- ‘Harvest date adding’ followed the same conditions as ‘sow date adding’. Because the harvest dates across WA wheat belt were mostly based on the farmer’s own schedule rather than a certain weather pattern [34], we then made this step optional;
- (4)
- ‘Threshold limits’ was a step for checking the rationality of the fitted curve. The 20% threshold is critical to determine the date of start of season (SOS) (see Section 3.1.1). The NDVI value on SOS date was assumed to be higher than the NDVI value on SD/BOS. However, the ‘reconstructed sequence’ contains bias due to the irregular distribution of limited available time points (Supplementary Materials File S1). In these cases, we either replace the calculated 20% threshold by SD/BOS NDVI, or exclude the pixel in a certain year, based on the comparison to the 35% limit (Figure 3).
3.1.3. Yield Estimation Using Integrated NDVI Metrics
3.1.4. The SCYM Model
- (1)
- APSIM crop model simulations: The APSIM model is a process-based model that is well-adapted to systematically simulate interactions between crop and environment at a daily time step, especially in Australia. We selected seven soil types and four winter wheat cultivars, which comprise a total of twenty-eight simulations. The soil types were selected to be geographically closest to the two fields in Merredin: acid yellow sandy earth, loamy sand, duplex sandy gravel, yellow-brown shallow loamy duplex, pale sandy earth (shallow), deep sand duplex, and shallow loamy duplex. The wheat cultivars were the main cultivars planted in the two fields: Mace, Calingiri, Arrino, and Wyalkatchem. APSIM was run from 1 January 2000 to 31 December 2018. The sowing date was allowed to vary from year to year using the break of season and was assumed to occur if 15 mm of rainfall was accumulated over 3 days after 25 April, or 5 mm over 3 days after 5 June [4]. Emergence, flowering, maturity, end of grain filling dates, leaf area index (LAI) and grain yield were output by APSIM and LAI was converted to GCVI using the approach of Lobell et al. [26] and Azzari et al. [36];
- (2)
- Yield model calibration: The simulated GCVI data at different combinations of image dates were regressed against yield. Specifically, we divided the growing season into two, two-month periods: ‘early season’ (before 5 September) and ‘late season’. The 5 September date was calculated based on the average season of GCVI sequences. The combination set of dates were one image acquisition dates in each of the two-month windows. The general form of the regression model was (Equation (3)):where, β = are the coefficients corresponding to the intercept, VI dates in early season (e) and VI dates in the late season (l), and d is one of the possible combination-sets of dates. The coefficients, β, was estimated by running the regression models using APSIM outputs and then stored in a lookup table;
- (3)
- Pixel by pixel yield estimation: The pre-processed Landsat 07 CGVI images in the ‘early season’ and ‘late season’ groups were composited into two sets of images preserving the maximum GCVI for each pixel, and the day of the year (DOY) for that maximum, respectively. Then, the spatial yields were estimated using the regression models, calibrated in the previous step, corresponding to the date combinations (d) for each pixel.
3.2. Model Assessment
4. Results
4.1. Preliminary Data Exploration and SPD Model Calibration Using Training Field J
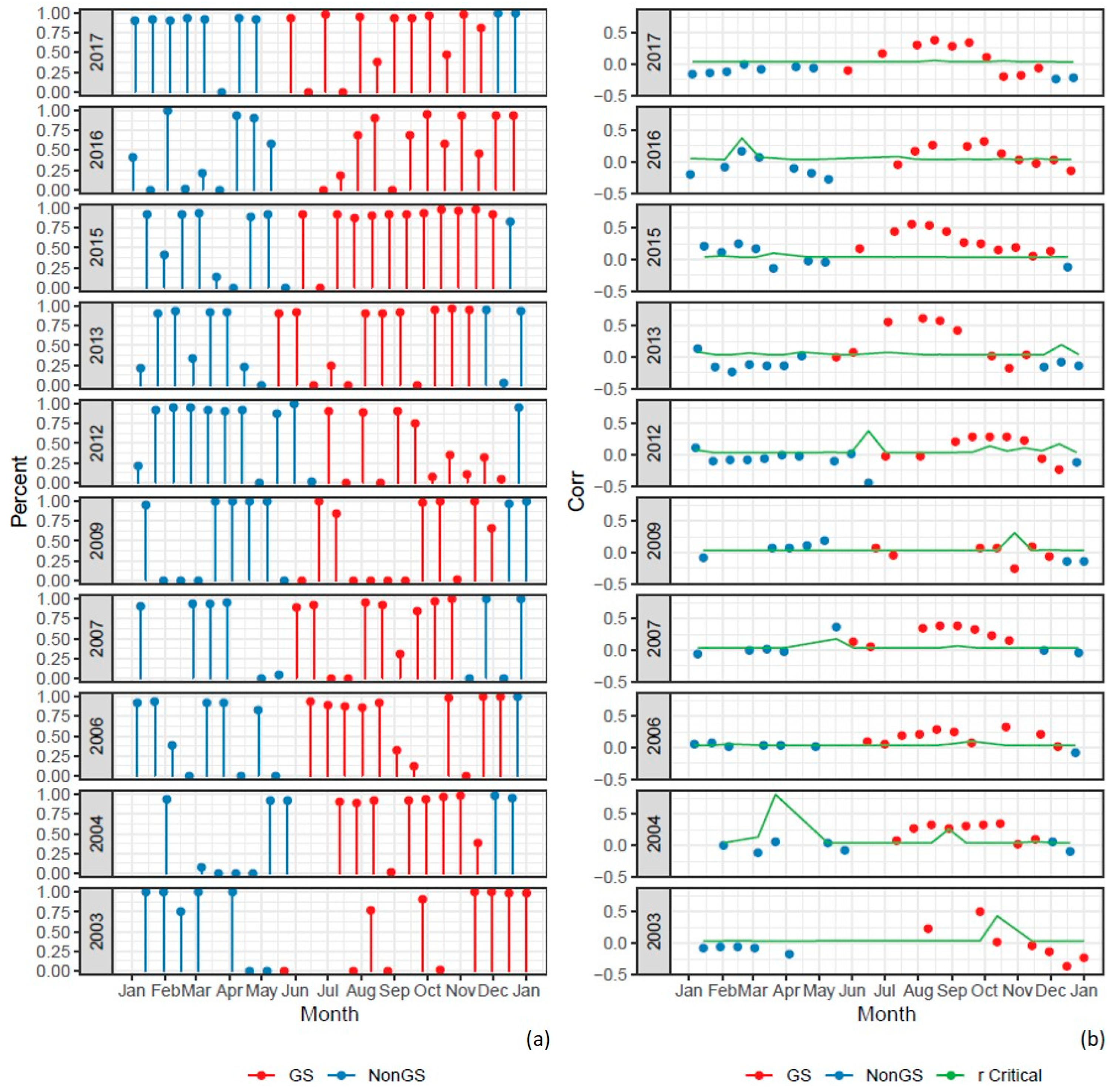
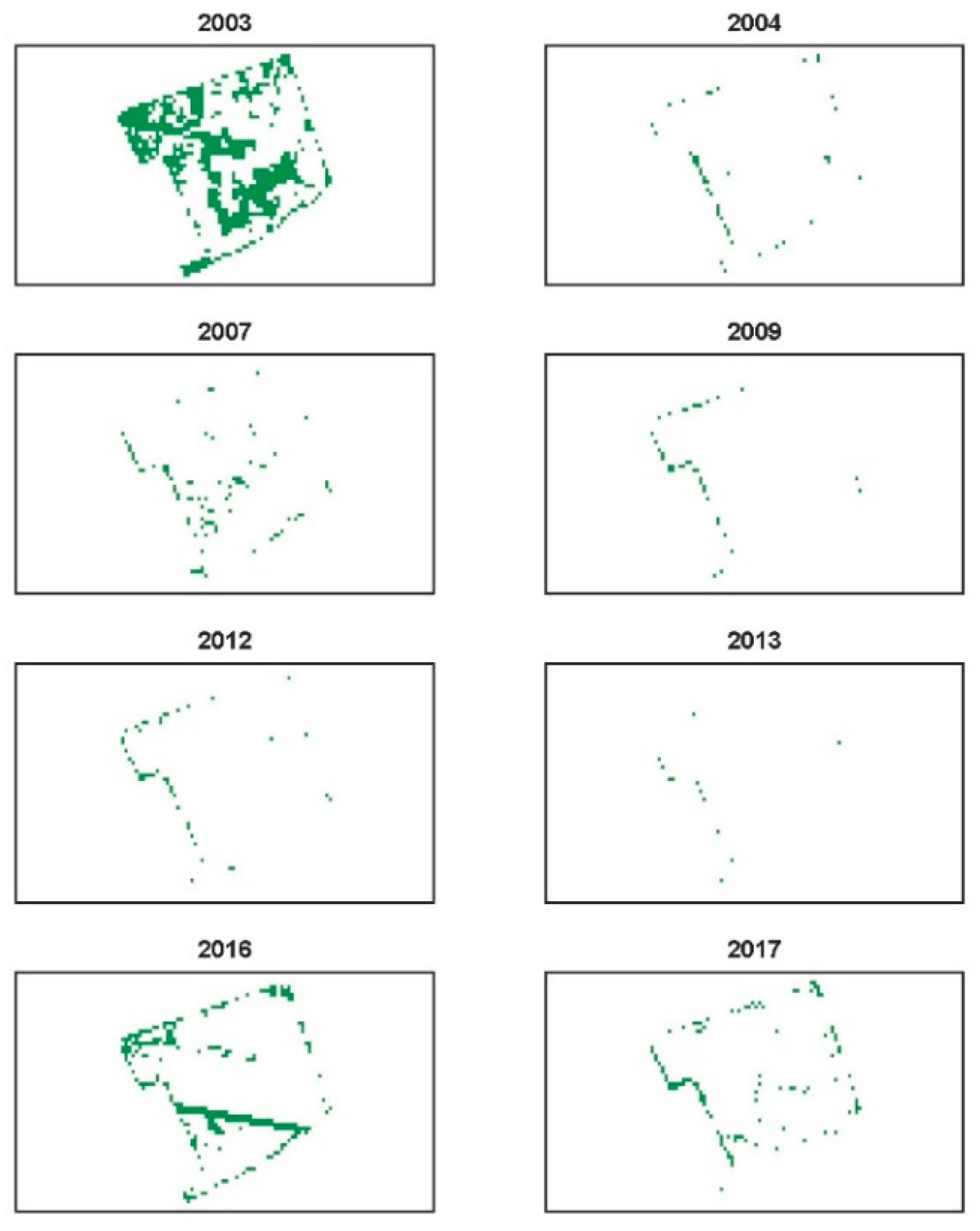
4.2. Incorporating Additional Information into Statistical Phenology Detection
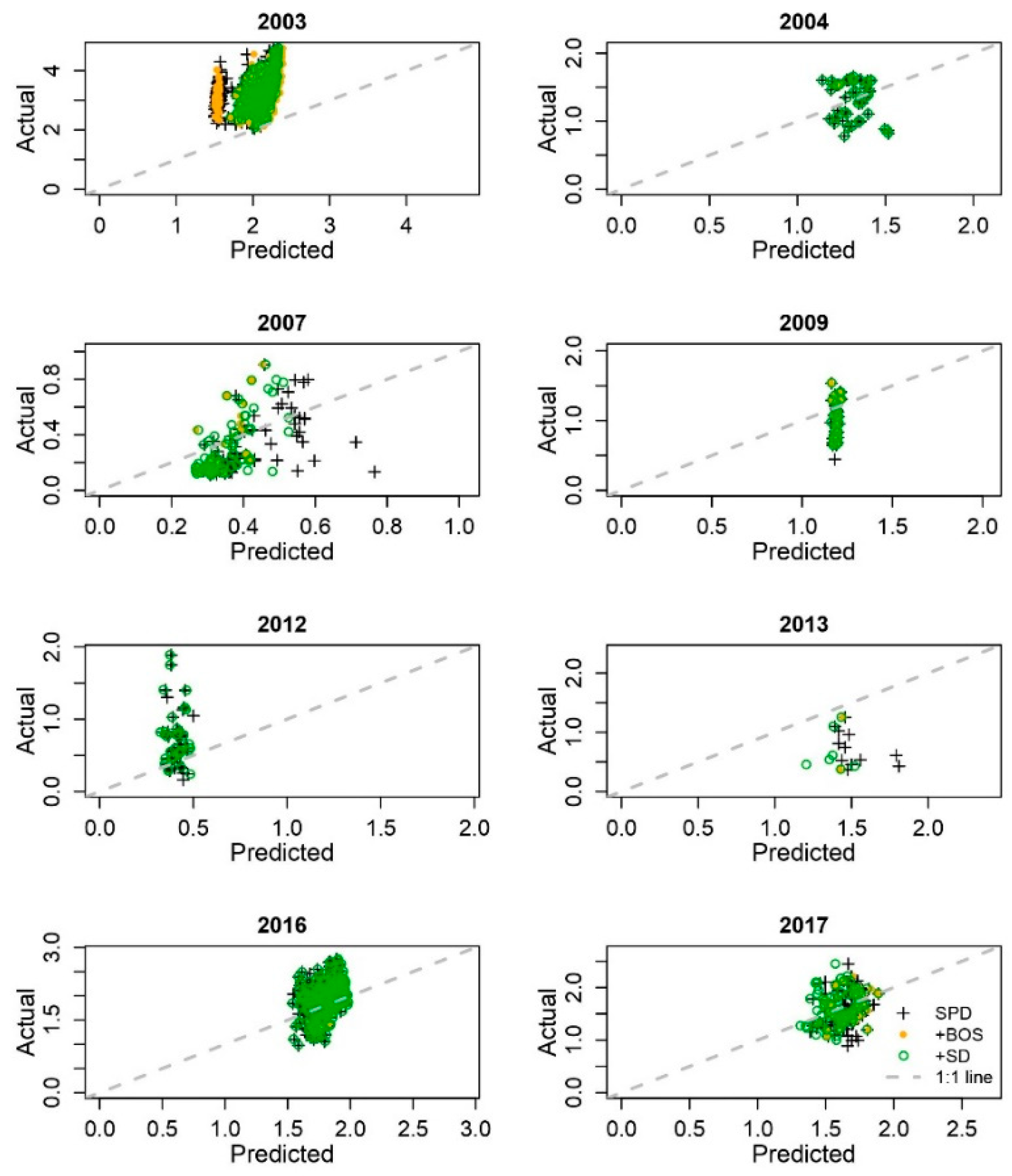
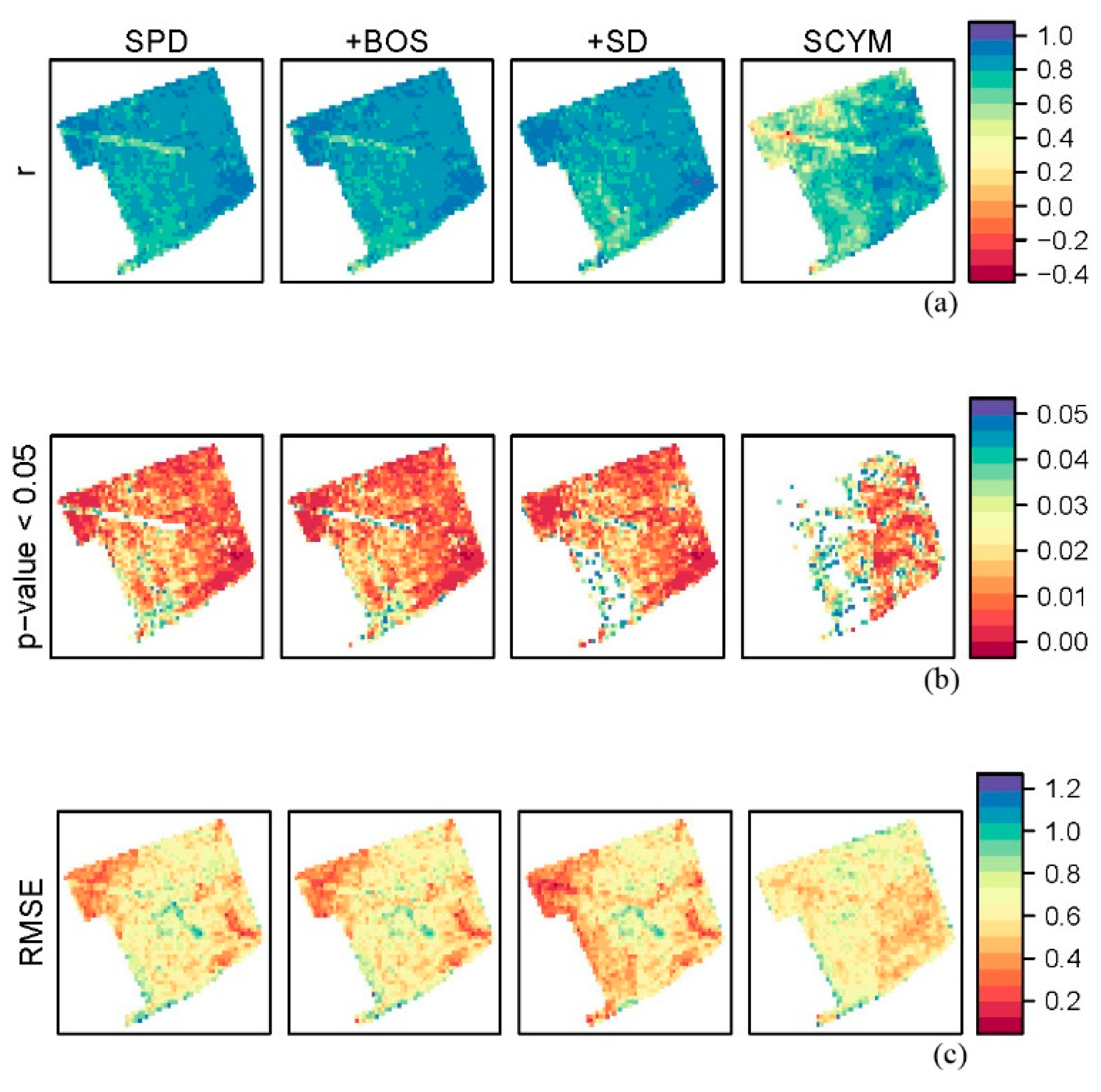
4.3. Yield Predictors Using Statistical Phenology Detection Compared to SCYM
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Department of Primary Industries and Regional Development. Western Australian Grains Industry. Available online: https://agric.wa.gov.au/n/2072 (accessed on 1 March 2021).
- Evans, F.H.; Guthrie, M.M.; Foster, I. Accuracy of six years of operational statistical seasonal forecasts of rainfall in Western Australia (2013 to 2018). Atmos. Res. 2020, 233, 104697. [Google Scholar] [CrossRef]
- McBratney, A.; Whelan, B.; Ancev, T.; Bouma, J. Future Directions of Precision Agriculture. Precis. Agric. 2005, 6, 7–23. [Google Scholar] [CrossRef]
- Asseng, S.; Turner, N.C.; Keating, B.A. Analysis of water- and nitrogen-use efficiency of wheat in a Mediterranean climate. Plant Soil 2001, 233, 127–143. [Google Scholar] [CrossRef]
- Belward, A.S.; Skøien, J.O. Who launched what, when and why; trends in global land-cover observation capacity from civilian earth observation satellites. ISPRS J. Photogramm. Remote Sens. 2015, 103, 115–128. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA/GSFC Type III Final Report: Greenbelt, MD, USA, 1974; p. 371. [Google Scholar]
- Wall, L.; Larocque, D.; Léger, P.M. The early explanatory power of NDVI in crop yield modelling. Int. J. Remote Sens. 2008, 29, 2211–2225. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Broich, M.; Huete, A.; Paget, M.; Ma, X.; Tulbure, M.; Coupe, N.R.; Evans, B.; Beringer, J.; Devadas, R.; Davies, K. A spatially explicit land surface phenology data product for science, monitoring and natural resources management applications. Environ. Model. Softw. 2015, 64, 191–204. [Google Scholar] [CrossRef]
- Araya, S.; Ostendorf, B.; Lyle, G.; Lewis, M. CropPhenology: An R package for extracting crop phenology from time series remotely sensed vegetation index imagery. Ecol. Inform. 2018, 46, 45–56. [Google Scholar] [CrossRef]
- Shen, J.; Huete, A.; Tran, N.N.; Devadas, R.; Ma, X.; Eamus, D.; Yu, Q. Diverse sensitivity of winter crops over the growing season to climate and land surface temperature across the rainfed cropland-belt of eastern Australia. Agric. Ecosyst. Environ. 2018, 254, 99–110. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Lai, Y.R.; Pringle, M.J.; Kopittke, P.M.; Menzies, N.W.; Orton, T.G.; Dang, Y.P. An empirical model for prediction of wheat yield, using time-integrated Landsat NDVI. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 99–108. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. Near real-time prediction of U.S. corn yields based on time-series MODIS data. Remote Sens. Environ. 2014, 147, 219–231. [Google Scholar] [CrossRef]
- Roy, D.P.; Yan, L. Robust Landsat-based crop time series modelling. Remote Sens. Environ. 2020, 238, 110810. [Google Scholar] [CrossRef]
- Whitcraft, A.K.; Vermote, E.F.; Becker-Reshef, I.; Justice, C.O. Cloud cover throughout the agricultural growing season: Impacts on passive optical earth observations. Remote Sens. Environ. 2015, 156, 438–447. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-scale land surface phenology from harmonized Landsat 8 and Sentinel-2 imagery. Remote Sens. Environ. 2020, 240, 111685. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Kimball, J.S.; Maneta, M.P.; Maxwell, B.D.; Moreno, A.; Beguería, S.; Wu, X. Regional Crop Gross Primary Productivity and Yield Estimation Using Fused Landsat-MODIS Data. Remote Sens. 2018, 10, 372. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; Liu, H.; Zhang, X.; Ren, C.; Ustin, S.; Qiu, Z.; Xu, M.; Guo, D. Assessment of the effectiveness of spatiotemporal fusion of multi-source satellite images for cotton yield estimation. Comput. Electron. Agric. 2019, 162, 44–52. [Google Scholar] [CrossRef]
- Chen, Y.; McVicar, T.R.; Donohue, R.J.; Garg, N.; Waldner, F.; Ota, N.; Li, L.; Lawes, R. To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction. Remote Sens. 2020, 12, 1653. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Chen, K.; O’Leary, R.A.; Evans, F.H. A simple and parsimonious generalised additive model for predicting wheat yield in a decision support tool. Agric. Syst. 2019, 173, 140–150. [Google Scholar] [CrossRef]
- Pebesma, E.; Heuvelink, G. Spatio-temporal interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time series missing value imputation in R. R J. 2017, 9, 207–218. [Google Scholar] [CrossRef] [Green Version]
- Stineman, R.W. A consistently well-behaved method of interpolation. Creat. Comput. 1980, 6, 54–57. [Google Scholar]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO-1 Hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. Remote Sens. 2020, 160, 124–135. [Google Scholar] [CrossRef]
- Smith, R.; Adams, J.; Stephens, D.; Hick, P. Forecasting wheat yield in a Mediterranean-type environment from the NOAA satellite. Aust. J. Agric. Res. 1995, 46, 113–125. [Google Scholar] [CrossRef]
- AKAIKE, H. Maximum likelihood identification of Gaussian autoregressive moving average models. Biometrika 1973, 60, 255–265. [Google Scholar] [CrossRef]
- Azzari, G.; Jain, M.; Lobell, D.B. Towards fine resolution global maps of crop yields: Testing multiple methods and satellites in three countries. Remote Sens. Environ. 2017, 202, 129–141. [Google Scholar] [CrossRef]
- Younes, N.; Joyce, K.E.; Maier, S.W. All models of satellite-derived phenology are wrong, but some are useful: A case study from northern Australia. Int. J. Appl. Earth Obs. Geoinf. 2021, 97, 102285. [Google Scholar] [CrossRef]
- Colaço, A.F.; Bramley, R.G.V. Site–Year Characteristics Have a Critical Impact on Crop Sensor Calibrations for Nitrogen Recommendations. Agron. J. 2019, 111, 2047–2059. [Google Scholar] [CrossRef]
- Wang, B.; Feng, P.; Liu, D.L.; O’Leary, G.J.; Macadam, I.; Waters, C.; Asseng, S.; Cowie, A.; Jiang, T.; Xiao, D.; et al. Sources of uncertainty for wheat yield projections under future climate are site-specific. Nat. Food 2020. [Google Scholar] [CrossRef]
- Waldner, F.; Horan, H.; Chen, Y.; Hochman, Z. High temporal resolution of leaf area data improves empirical estimation of grain yield. Sci. Rep. 2019, 9, 15714. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of Smoothing Methods for Reconstructing NDVI Time-Series and Estimating Vegetation Phenology from MODIS Data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef] [Green Version]
- Jeffries, G.R.; Griffin, T.S.; Fleisher, D.H.; Naumova, E.N.; Koch, M.; Wardlow, B.D. Mapping sub-field maize yields in Nebraska, USA by combining remote sensing imagery, crop simulation models, and machine learning. Precis. Agric. 2020, 21, 678–694. [Google Scholar] [CrossRef]
- Mbow, C.; Fensholt, R.; Rasmussen, K.; Diop, D. Can vegetation productivity be derived from greenness in a semi-arid environment? Evidence from ground-based measurements. J. Arid Environ. 2013, 97, 56–65. [Google Scholar] [CrossRef]
- Pryor, D.; Nadler, A. Examining micro-climate effects in field crop production. In Proceedings of the 7th Annual Manitoba Agronomists Conference, Winnipeg, MB, Canada, December 2008. [Google Scholar]
- Claverie, M.; Vermote, E.F.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM+ surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Simbahan, G.C.; Dobermann, A.; Ping, J.L. Screening Yield Monitor Data Improves Grain Yield Maps. Agron. J. 2004, 96, 1091–1102. [Google Scholar] [CrossRef]
- Gaso, D.V.; Berger, A.G.; Ciganda, V.S. Predicting wheat grain yield and spatial variability at field scale using a simple regression or a crop model in conjunction with Landsat images. Comput. Electron. Agric. 2019, 159, 75–83. [Google Scholar] [CrossRef]
- Whitcraft, A.K.; Becker-Reshef, I.; Killough, B.D.; Justice, C.O. Meeting Earth Observation Requirements for Global Agricultural Monitoring: An Evaluation of the Revisit Capabilities of Current and Planned Moderate Resolution Optical Earth Observing Missions. Remote Sens. 2015, 7, 1482–1503. [Google Scholar] [CrossRef] [Green Version]
- Duncan, J.; Dash, J.; Atkinson, P. The potential of satellite-observed crop phenology to enhance yield gap assessments in smallholder landscapes. Front. Environ. Sci. 2015, 3, 56. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Yang, Z.; Di, L.; Pei, Z. Evaluation of Temporal Resolution Effect in Remote Sensing Based Crop Phenology Detection Studies; Springer: Berlin/Heidelberg, Germany, 2012; pp. 135–150. [Google Scholar]
- Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Whitcraft, A.; Baruth, B.; Bonifacio, R.; Crutchfield, J.; et al. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]



| Year | Rainfall Available (mm) | Field | Yield (tons/ha) | Sow Date | Harvest Date |
|---|---|---|---|---|---|
| 2003 | 331.4 | J | 2.055 | 21 May | 15 January 2004 |
| M | 3.194 | 12 May | 12 December | ||
| 2004 | 269.3 | J | 1.600 | 26 May | 25 November |
| M | 1.610 | 10 June | 18 December | ||
| 2006 | 284.2 | J | 1.389 | 07 June | 07 December |
| 2007 | 172.9 | J | 0.483 | 31 May | 05 November |
| M | 0.677 | 03 June | 15 November | ||
| 2009 | 258.0 | J | 1.195 | 01 June | 07 December |
| M | 1.454 | 15 June | 05 December | ||
| 2012 | 178.4 | J | 0.467 | 24 June | 21 December |
| M | 1.661 | 16 June | 11 December | ||
| 2013 | 271.2 | J | 1.835 | 15 May | 20 November |
| M | 1.917 | 19 May | 12 December | ||
| 2015 | 235.5 | J | -- | 23 May | 05 December |
| 2016 | 277.2 | J | 1.618 | 20 May | 18 December |
| M | 2.031 | 18 May | 08 December | ||
| 2017 | 227.1 | J | 1.739 | 19 May | 03 December |
| M | 1.691 | 23 May | 23 November |
| Model | Predictors of Yield | Abbreviation |
|---|---|---|
| Statistical phenology detection | Single best phenological metric each year | SPD |
| Statistics phenology detection with added sowing date information | Single best phenological metric each year | +SD |
| Statistical phenology detection with added break of season information | Single best phenological metric each year | +BOS |
| Scalable crop yield mapper | NDVI values from one or two time points | SCYM |
| Model | Parameters | Year | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2003 | 2004 | 2006 | 2007 | 2009 | 2012 | 2013 | 2015 | 2016 | 2017 | ||
| SPD | Proxy | POSV | POSV | GLAD | VLAD | POSV | POSV | VLAD | iNDVI | POSV | GLAD |
| a | 1.176 | 0.918 | 0.043 | 0.031 | 0.273 | 0.594 | 0.078 | 0.043 | 0.803 | 0.065 | |
| b | 1.272 | 0.815 | 0.738 | 0.119 | 1.056 | 0.184 | 0.660 | 0.724 | 1.255 | 1.089 | |
| r | 0.253 | 0.276 | 0.350 | 0.401 | 0.073 | 0.148 | 0.596 | 0.520 | 0.249 | 0.374 | |
| AIC | 3039 | 162 | −597 | −1902 | 1249 | −666 | 2131 | 1290 | 944 | 803 | |
| RMSE | 0.397 | 0.249 | 0.219 | 0.174 | 0.297 | 0.216 | 0.346 | 0.301 | 0.284 | 0.277 | |
| ‘+SD’ | Proxy | POSV | POSV | VLAD | VLAD | POSV | POSV | VLAD | VLAD | POSV | GLAD |
| a | 1.167 | 0.917 | 0.035 | 0.029 | 0.272 | 0.700 | 0.077 | 0.079 | 0.842 | 0.065 | |
| b | 1.269 | 0.815 | 0.765 | 0.140 | 1.057 | 0.142 | 0.680 | 0.735 | 1.234 | 1.093 | |
| r | 0.249 | 0.276 | 0.326 | 0.403 | 0.073 | 0.156 | 0.592 | 0.541 | 0.258 | 0.376 | |
| AIC | 3046 | 162 | −649 | −1895 | 1249 | −550 | 2144 | 1197 | 930 | 792 | |
| RMSE | 0.397 | 0.249 | 0.216 | 0.174 | 0.298 | 0.218 | 0.347 | 0.296 | 0.283 | 0.277 | |
| ‘+BOS’ | Proxy | POSV | POSV | iNDVI | VLAD | POSV | POSV | VLAD | VLAD | POSV | GLAD |
| a | 1.199 | 0.918 | 0.022 | 0.030 | 0.293 | 0.602 | 0.078 | 0.080 | 0.781 | 0.065 | |
| b | 1.248 | 0.814 | 0.685 | 0.134 | 1.044 | 0.181 | 0.661 | 0.741 | 1.270 | 1.081 | |
| r | 0.262 | 0.276 | 0.362 | 0.402 | 0.077 | 0.150 | 0.595 | 0.545 | 0.241 | 0.374 | |
| AIC | 3024 | 162 | −628 | −1895 | 1211 | −670 | 2135 | 1181 | 930 | 803 | |
| RMSE | 0.396 | 0.249 | 0.218 | 0.174 | 0.296 | 0.216 | 0.346 | 0.295 | 0.283 | 0.277 | |
| Conditional Setting | Model | Year (Count of Pixels) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2003 | 2004 | 2007 | 2009 | 2012 | 2013 | 2016 | 2017 | ||
| Availability limits exceed | +SD/BOS | 6 | 26 | 42 | 19 | 24 | 14 | 87 | 33 |
| >35% threshold exceed | +SD | 1 | 0 | 6 | 6 | 10 | 2 | 13 | 17 |
| +BOS | 33 | 0 | 6 | 10 | 7 | 0 | 85 | 0 | |
| Have option to add sow date | +SD | 1828 | 1808 | 152 | 0 | 62 | 144 | 100 | 0 |
| +BOS | 1828 | 60 | 152 | 0 | 0 | 1820 | 111 | 1801 | |
| Have option to add harvest date | +SD | 54 | 0 | 0 | 0 | 1810 | 1471 | 0 | 170 |
| Threshold value switch | +SD | 0 | 0 | 91 | 36 | 34 | 13 | 143 | 106 |
| +BOS | 51 | 3 | 71 | 86 | 24 | 0 | 706 | 0 | |
| Estimated SOS corrected | +SD | 675 | 41 | 79 | 36 | 45 | 11 | 243 | 98 |
| +BOS | 675 | 2 | 27 | 36 | 7 | 2 | 71 | 45 | |
| Total pixels | Actual yield | 1828 | 1808 | 1792 | 1815 | 1810 | 1820 | 1747 | 1801 |
| SCYM | 1731 | 1808 | 1792 | 1815 | 1810 | 1820 | 1747 | 1801 | |
| Year | Accuracy statistic | SPD | +BOS | +SD | SCYM |
|---|---|---|---|---|---|
| 2003 | r | 0.38 | 0.41 | 0.59 | 0.58 |
| RMSE | 1.27 | 1.23 | 1.23 | 0.92 | |
| 2004 | r | 0.34 | 0.34 | 0.35 | 0.36 |
| RMSE | 0.25 | 0.25 | 0.25 | 0.49 | |
| 2007 | r | 0.76 | 0.78 | 0.79 | 0.51 |
| RMSE | 0.21 | 0.21 | 0.21 | 0.57 | |
| 2009 | r | 0.53 | 0.51 | 0.51 | 0.22 |
| RMSE | 0.33 | 0.33 | 0.33 | 0.66 | |
| 2012 | r | 0.50 | 0.50 | 0.50 | 0.34 |
| RMSE | 0.92 | 0.92 | 0.90 | 0.38 | |
| 2013 | r | 0.59 | 0.60 | 0.53 | 0.38 |
| RMSE | 0.34 | 0.34 | 0.31 | 0.40 | |
| 2016 | r | 0.23 | 0.16 | 0.21 | 0.15 |
| RMSE | 0.41 | 0.41 | 0.40 | 0.55 | |
| 2017 | r | 0.59 | 0.60 | 0.57 | 0.37 |
| RMSE | 0.23 | 0.23 | 0.23 | 0.80 | |
| Mean | r | 0.80 | 0.80 | 0.81 | 0.70 |
| RMSE | 0.61 | 0.60 | 0.56 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Evans, F.H. The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia. Remote Sens. 2021, 13, 2202. https://doi.org/10.3390/rs13112202
Shen J, Evans FH. The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia. Remote Sensing. 2021; 13(11):2202. https://doi.org/10.3390/rs13112202
Chicago/Turabian StyleShen, Jianxiu, and Fiona H. Evans. 2021. "The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia" Remote Sensing 13, no. 11: 2202. https://doi.org/10.3390/rs13112202
APA StyleShen, J., & Evans, F. H. (2021). The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia. Remote Sensing, 13(11), 2202. https://doi.org/10.3390/rs13112202