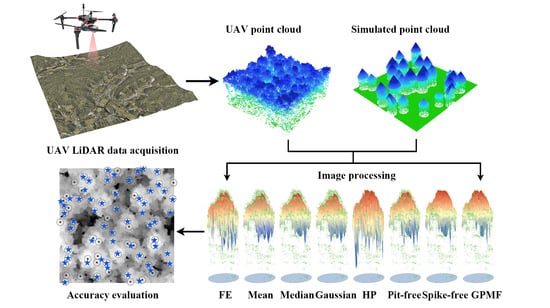
Comparison and Evaluation of Different Pit-Filling Methods for Generating High Resolution Canopy Height Model Using UAV Laser Scanning Data
Abstract
:1. Introduction
2. Materials
2.1. Simulated Data
2.2. Real-World Data
2.2.1. Study Area
2.2.2. UAV-LiDAR Data
2.2.3. Field-Measured Data
3. Methodology
3.1. UAVLS Data Pre-Processing
3.2. Description of CHM Generation Algorithms
3.2.1. Pit-Free Algorithm
3.2.2. Spike-Free Algorithm
3.2.3. Graph-Based Progressive Morphological Filtering
3.3. Accuracy Assessment
3.3.1. Accuracy Assessment of Simulated CHMs
3.3.2. Accuracy Assessment of UAVLS-Derived CHMs
4. Results
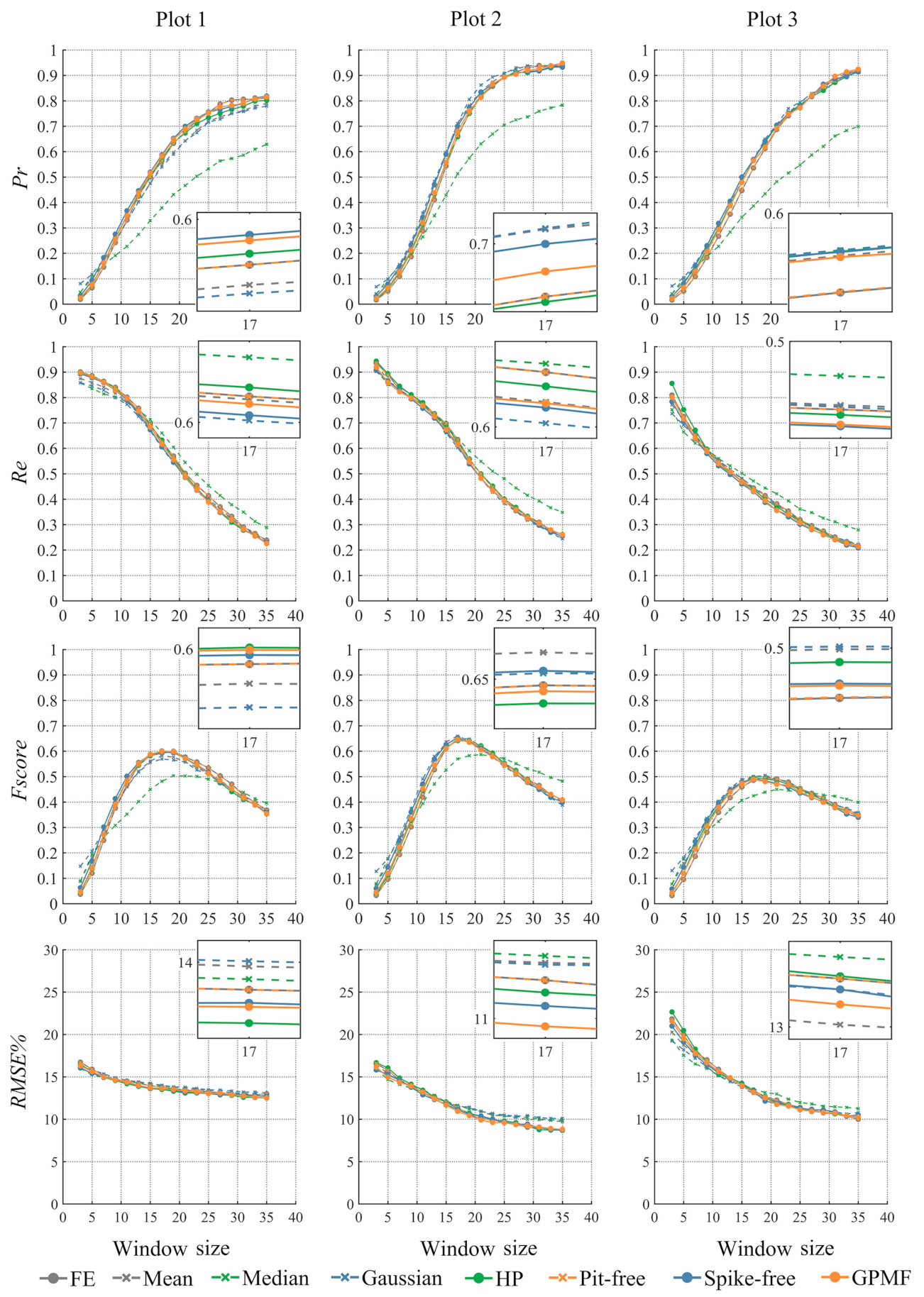
4.1. Sensitivity Analysis
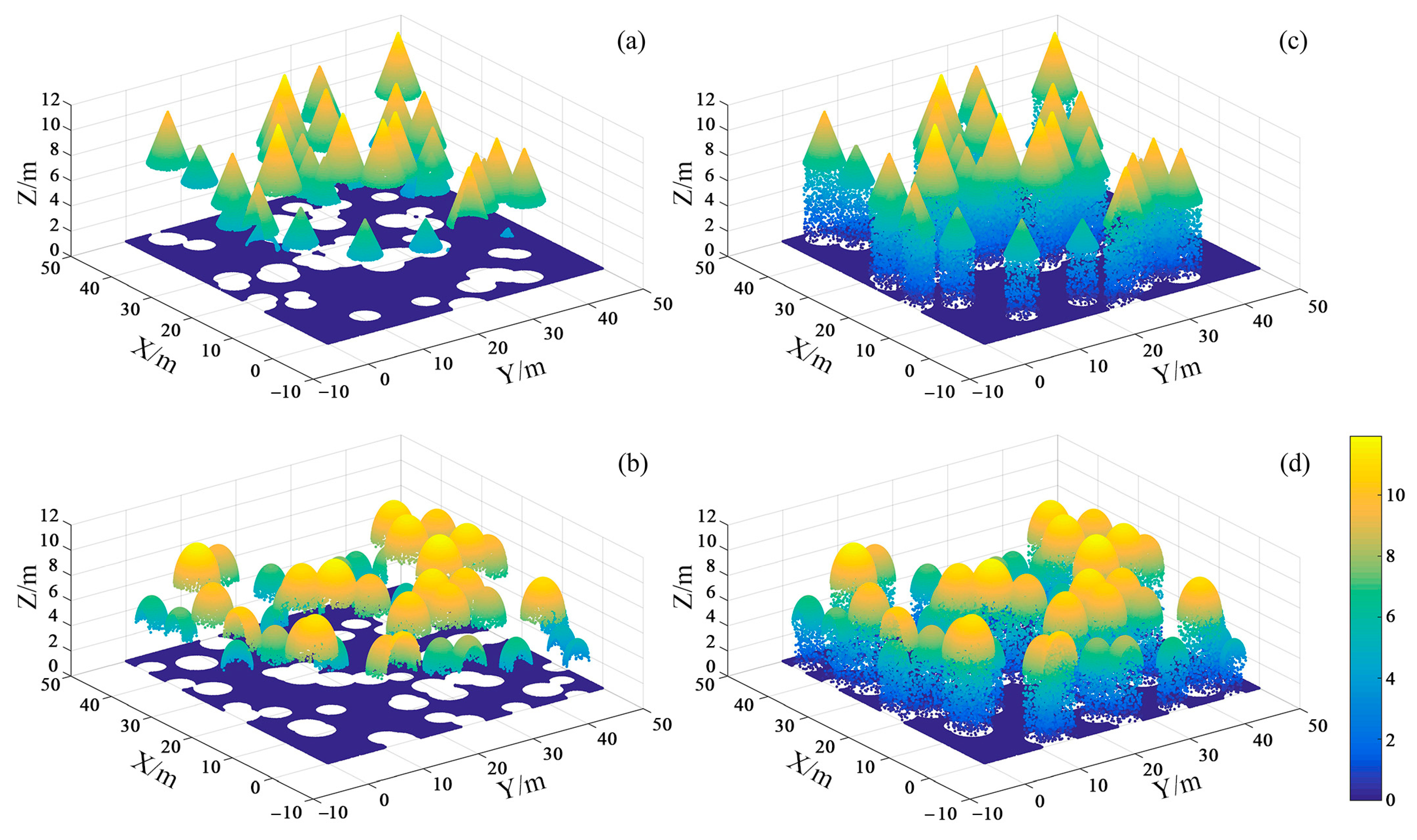
4.2. Comparison of Simulated CHMs
4.2.1. Visual Performance
4.2.2. Quantitative Analysis
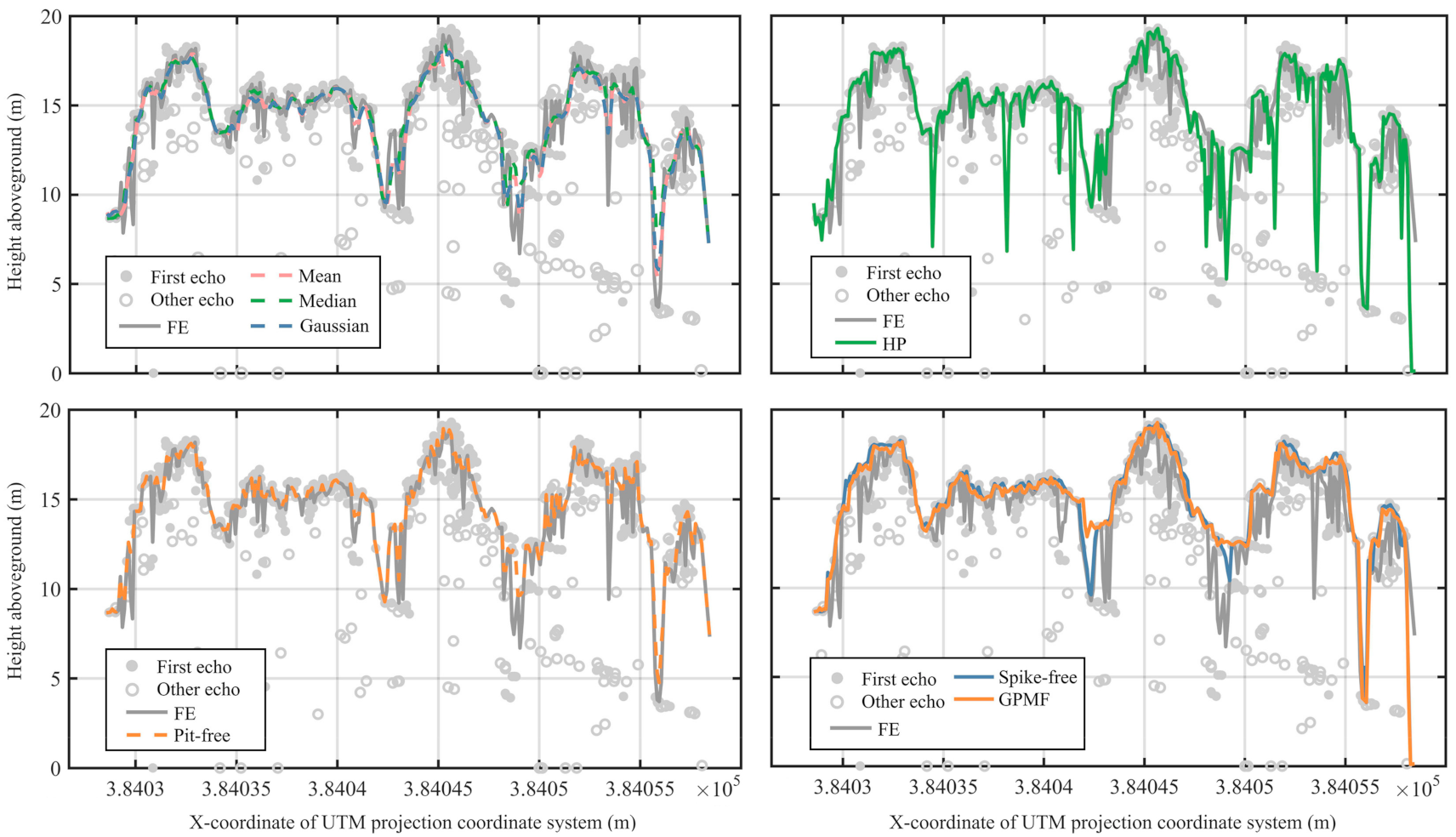
4.3. Comparison of UAVLS-Derived CHMs
4.3.1. Visual Performance
4.3.2. Quantitative Analysis
4.3.3. Individual Tree Application Evaluation
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Qiu, F. Individual Tree Segmentation from LiDAR Point Clouds for Urban Forest Inventory. Remote Sens. 2015, 7, 7892–7913. [Google Scholar] [CrossRef] [Green Version]
- Zhen, Z.; Quackenbush, L.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and evaluating different LiDAR-derived canopy height model generation methods for tree height estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Shamsoddini, A.; Turner, R.; Trinder, J.C. Improving lidar-based forest structure mapping with crown-level pit removal. J. Spat. Sci. 2013, 58, 29–51. [Google Scholar] [CrossRef]
- Ben-Arie, J.R.; Hay, G.J.; Powers, R.P.; Castilla, G.; St-Onge, B. Development of a pit filling algorithm for LiDAR canopy height models. Comput. Geosci. 2009, 35, 1940–1949. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.; Li, Y.; Yue, T.; Wang, X. Robust and Parameter-Free Algorithm for Constructing Pit-Free Canopy Height Models. ISPRS Int. J. Geo Inf. 2017, 6, 219. [Google Scholar] [CrossRef] [Green Version]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Puttonen, E.; Litkey, P.; Hyyppä, J. Individual Tree Species Classification by Illuminated—Shaded Area Separation. Remote Sens. 2010, 2, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Vosselman, G. Analysis of planimetric accuracy of airborne laser scanningsurveys. ISPRS Arch. 2008, 37, 99–104. [Google Scholar]
- Goulden, T.; Hopkinson, C. The Forward Propagation of Integrated System Component Errors within Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2010, 76, 589–601. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating spike-free digital surface models using LiDAR raw point clouds: A new approach for forestry applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote 2009, 64, 561–574. [Google Scholar] [CrossRef]
- Gaveau, D.; Hill, R.A. Quantifying canopy height underestimation by laser pulse penetration in small-footprint airborne laser scanning data. Can. J. Remote Sens. 2003, 29, 650–657. [Google Scholar] [CrossRef]
- Reuter, H.I.; Hengl, T.; Gessler, P.; Soille, P. Chapter 4 Preparation of DEMs for Geomorphometric Analysis. Dev. Soil Sci. 2009, 33, 87–120. [Google Scholar]
- Priestnall, G.; Jaafar, J.; Duncan, A. Extracting urban features from LiDAR digital surface models. Comput. Environ. Urban Syst. 2000, 24, 65–78. [Google Scholar] [CrossRef]
- Macmillan, R.A.; Martin, T.C.; Earle, T.J.; Mcnabb, D.H. Automated analysis and classification of landforms using high-resolution digital elevation data: Applications and issues. Can. J. Remote Sens. 2003, 29, 592–606. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Pang, Y.; Li, Z.; Sun, G. Filling invalid values in a lidar-derived canopy height model with morphological crown control. Int. J. Remote Sens. 2013, 34, 4636–4654. [Google Scholar] [CrossRef]
- Liu, H.; Dong, P. A new method for generating canopy height models from discrete-return LiDAR point clouds. Remote Sens. Lett. 2014, 5, 575–582. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, S.; Liang, X.; Shao, J.; Hu, R.; Yu, S.; Yan, G. Cloth simulation-based construction of pit-free canopy height models from airborne LiDAR data. For. Ecosyst. 2020, 7. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Zhen, Z.; Li, F.; Zhao, Y. A graph-based progressive morphological filtering (GPMF) method for generating canopy height models using ALS data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 84–96. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Quan, Y.; Dong, L.; Li, F. Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning. Remote Sens. 2020, 13, 24. [Google Scholar] [CrossRef]
- Quan, Y.; Li, M.; Zhen, Z.; Hao, Y.; Wang, B. The Feasibility of Modelling the Crown Profile of Larix olgensis Using Unmanned Aerial Vehicle Laser Scanning Data. Sensors 2020, 20, 5555. [Google Scholar] [CrossRef] [PubMed]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, L.; Chen, Q.; Wang, G.; Luo, P.; Sharma, R.P.; He, P.; Li, M.; Wang, M.; Duan, G. Analysis of the Spatial Differences in Canopy Height Models from UAV LiDAR and Photogrammetry. Remote Sens. 2020, 12, 2884. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2020, 13, 77. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Mizoue, N.; Fukumoto, K.; Yoshida, S. Forest Structure Estimation from a UAV-Based Photogrammetric Point Cloud in Managed Temperate Coniferous Forests. Forests 2017, 8, 343. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Liang, X.; Hyyppä, H.; Wang, Y. Autonomous Collection of Forest Field Reference—The Outlook and a First Step with UAV Laser Scanning. Remote Sens. 2017, 9, 785. [Google Scholar] [CrossRef] [Green Version]
- Dong, P. Characterization of individual tree crowns using three-dimensional shape signatures derived from LiDAR data. Int. J. Remote Sens. 2009, 30, 6621–6628. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. ISPRS Arch. 2000, 33, 110–117. [Google Scholar]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of Topographic Variability and Lidar Sampling Density on Several DEM Interpolation Methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland using Small Footprint LIDAR data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef] [Green Version]
- Zhen, Z.; Quackenbush, L.J.; Stehman, S.V.; Zhang, L. Agent-based region growing for individual tree crown delineation from airborne laser scanning (ALS) data. Int. J. Remote Sens. 2015, 36, 1965–1993. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat-2 terrain and canopy heights in boreal forests. Remote Sens. Environ. 2020, 251. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote 2015, 104, 44–52. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.E.I.; Nevalainen, O.; et al. Forest in situ observations using unmanned aerial vehicle as an alternative of terrestrial measurements. For. Ecosyst. 2019, 6. [Google Scholar] [CrossRef] [Green Version]






| Proportion of Pits | FE | Mean | Median | Gaussian | HP | Pit-Free | Spike-Free | GPMF | |
|---|---|---|---|---|---|---|---|---|---|
| Cone | 10% | 0.6624 | 0.4681 | 0.2547 | 0.4503 | 0.4320 | 0.2195 | 0.1613 | 0.0952 |
| 20% | 0.9114 | 0.6601 | 0.4087 | 0.6425 | 0.5461 | 0.3896 | 0.1602 | 0.1096 | |
| 30% | 1.0808 | 0.8103 | 0.5732 | 0.7935 | 0.6143 | 0.5254 | 0.1648 | 0.1161 | |
| 40% | 1.2115 | 0.9336 | 0.7214 | 0.9178 | 0.6521 | 0.6437 | 0.1737 | 0.1283 | |
| 50% | 1.3074 | 1.0294 | 0.8360 | 1.0146 | 0.6656 | 0.7355 | 0.1707 | 0.1337 | |
| 60% | 1.3933 | 1.1202 | 0.9507 | 1.1061 | 0.6808 | 0.8271 | 0.1707 | 0.1370 | |
| Hemisphere | 10% | 0.6350 | 0.4520 | 0.2421 | 0.4339 | 0.4338 | 0.2124 | 0.1481 | 0.0975 |
| 20% | 0.8789 | 0.6277 | 0.3715 | 0.6093 | 0.5497 | 0.3563 | 0.1554 | 0.1090 | |
| 30% | 1.0392 | 0.7683 | 0.5218 | 0.7511 | 0.6013 | 0.4817 | 0.1579 | 0.1149 | |
| 40% | 1.1699 | 0.8897 | 0.6578 | 0.8732 | 0.6429 | 0.5956 | 0.1605 | 0.1220 | |
| 50% | 1.2721 | 0.9901 | 0.7803 | 0.9747 | 0.6721 | 0.6920 | 0.1660 | 0.1311 | |
| 60% | 1.3612 | 1.0803 | 0.8928 | 1.0656 | 0.6897 | 0.7805 | 0.1659 | 0.1351 |
| Method | FE | Mean | Median | Gaussian | HP | Pit-Free | Spike-Free | GPMF | |
|---|---|---|---|---|---|---|---|---|---|
| Plot1 | FE | - | 0.0000 | −0.2798 | 0.0000 | 0.0105 | −0.3264 | −0.6280 | −0.6273 |
| Mean | 1.1291 * | - | −0.2799 | 0.0000 | 0.0104 | −0.3264 | −0.6280 | −0.6273 | |
| Median | 1.4089 | 0.7120 | - | 0.2798 | 0.2903 | −0.0466 | −0.3482 | −0.3475 | |
| Gaussian | 1.0650 * | 0.1650 * | 0.6608 | - | 0.0105 | −0.3264 | −0.6280 | −0.6273 | |
| HP | 1.8070 | 1.7031 | 1.7973 | 1.6789 | - | −0.3369 | −0.6385 | −0.6378 | |
| Pit-free | 1.1468 | 0.6940 | 0.6323 | 0.6647 | 1.6962 | - | −0.3016 | −0.3009 | |
| Spike-free | 1.7900 | 1.3391 | 1.0497 | 1.3102 | 1.8219 | 1.0789 | - | 0.0007 | |
| GPMF | 1.7425 | 1.2841 | 0.9677 | 1.2494 | 1.9408 | 1.0216 | 0.9356 * | - | |
| Plot2 | FE | - | 0.0000 | −0.3070 | 0.0000 | 0.1037 | −0.4020 | −0.8574 | −0.9324 |
| Mean | 1.3112 * | - | −0.3069 | 0.0000 | 0.1038 | −0.4019 | −0.8574 | −0.9323 | |
| Median | 1.6450 | 0.8114 | - | 0.3070 | 0.4107 | −0.0950 | −0.5505 | −0.6254 | |
| Gaussian | 1.2459 * | 0.1938 * | 0.7492 | - | 0.1037 | −0.4020 | −0.8574 | −0.9324 | |
| HP | 2.1693 | 2.0782 | 2.2074 | 2.0526 | - | −0.5057 | −0.9612 | −1.0361 | |
| Pit-free | 1.2624 | 0.8422 | 0.8646 | 0.8174 | 2.0750 | - | −0.4555 | −0.5304 | |
| Spike-free | 2.2619 | 1.7930 | 1.5187 | 1.7636 | 2.2716 | 1.5274 | - | −0.0749 | |
| GPMF | 2.2495 | 1.7740 | 1.4720 | 1.7382 | 2.4812 | 1.5107 | 1.3075 | - | |
| Plot3 | FE | - | -0.0001 | −0.2580 | 0.0000 | 0.1854 | −0.3489 | −0.7381 | −0.7485 |
| Mean | 1.1884 * | - | −0.2580 | 0.0001 | 0.1854 | −0.3488 | −0.7380 | −0.7484 | |
| Median | 1.4536 | 0.7054 | - | 0.2580 | 0.4434 | −0.0909 | −0.4801 | −0.4905 | |
| Gaussian | 1.1215 * | 0.1748 * | 0.6497 | - | 0.1854 | −0.3489 | −0.7381 | −0.7485 | |
| HP | 2.4499 | 2.3126 | 2.3662 | 2.2942 | - | −0.5343 | −0.9234 | −0.9339 | |
| Pit-free | 1.1670 | 0.7407 | 0.7105 | 0.7126 | 2.3038 | - | −0.3892 | −0.3996 | |
| Spike-free | 2.1171 | 1.7104 | 1.4729 | 1.6850 | 2.2822 | 1.4845 | - | −0.0104 | |
| GPMF | 2.0048 | 1.5767 | 1.3130 | 1.5450 | 2.4923 | 1.3449 | 1.2313 | - |
| Method | Peak | Valley | Overall | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | Bias (m) | RMSE (m) | R2 | Bias (m) | RMSE (m) | R2 | Bias (m) | RMSE (m) | ||
| Plot1 | FE | 0.82 | 0.5703 | 0.9928 | 0.93 | 0.3427 | 0.6356 | 0.88 | 0.4543 | 0.8301 |
| Mean | 0.86 | 0.8258 | 1.0654 | 0.84 | 0.8002 | 1.1172 | 0.86 | 0.8128 | 1.0921 | |
| Median | 0.91 | 0.7139 | 0.8832 | 0.98 | 0.3715 | 0.4494 | 0.95 | 0.5393 | 0.6967 | |
| Gaussian | 0.86 | 0.8668 | 1.0908 | 0.89 | 0.7329 | 0.9747 | 0.89 | 0.7986 | 1.0332 | |
| HP | 0.98 | 0.1585 | 0.3037 | 0.91 | 0.2112 | 0.6318 | 0.94 | 0.1854 | 0.4987 | |
| Pit-free | 0.95 | 0.4140 | 0.5773 | 0.95 | 0.2827 | 0.5053 | 0.95 | 0.3470 | 0.5418 | |
| Spike-free | 0.99 | 0.1801 | 0.2766 | 1.00 | 0.0829 | 0.1315 | 0.99 | 0.1306 | 0.2152 | |
| GPMF | 0.99 | 0.2186 | 0.2998 | 0.98 | 0.1453 | 0.3269 | 0.98 | 0.1812 | 0.3139 | |
| Plot2 | FE | 0.52 | 1.0193 | 2.1159 | 0.70 | 0.7952 | 1.6607 | 0.67 | 0.9058 | 1.8990 |
| Mean | 0.72 | 1.4988 | 1.8005 | 0.83 | 1.1116 | 1.4945 | 0.83 | 1.3026 | 1.6526 | |
| Median | 0.87 | 1.1726 | 1.3415 | 0.88 | 0.8567 | 1.2020 | 0.90 | 1.0126 | 1.2727 | |
| Gaussian | 0.75 | 1.4979 | 1.7743 | 0.85 | 1.1134 | 1.4524 | 0.84 | 1.3031 | 1.6192 | |
| HP | 0.90 | 0.3282 | 0.6553 | 0.88 | 0.4779 | 0.9246 | 0.92 | 0.4041 | 0.8031 | |
| Pit-free | 0.91 | 0.5997 | 0.8012 | 0.87 | 0.5869 | 1.0497 | 0.91 | 0.5932 | 0.9354 | |
| Spike-free | 0.99 | 0.2139 | 0.2895 | 0.97 | 0.2245 | 0.4448 | 0.98 | 0.2193 | 0.3763 | |
| GPMF | 0.99 | 0.3037 | 0.3710 | 0.95 | 0.2375 | 0.5728 | 0.97 | 0.2702 | 0.4839 | |
| Plot3 | FE | 0.53 | 0.5059 | 1.6823 | 0.74 | 0.4354 | 1.5109 | 0.70 | 0.9414 | 1.5983 |
| Mean | 0.69 | 0.6556 | 1.5872 | 0.82 | 0.6037 | 1.5287 | 0.81 | 1.2594 | 1.5580 | |
| Median | 0.80 | 0.5384 | 1.2751 | 0.89 | 0.4986 | 1.2282 | 0.89 | 1.0370 | 1.2517 | |
| Gaussian | 0.71 | 0.6597 | 1.5690 | 0.83 | 0.6127 | 1.5212 | 0.83 | 1.2724 | 1.5451 | |
| HP | 0.94 | 0.1181 | 0.4526 | 0.77 | 0.2761 | 1.1566 | 0.86 | 0.3942 | 0.8804 | |
| Pit-free | 0.80 | 0.3717 | 1.0157 | 0.89 | 0.3299 | 0.9703 | 0.89 | 0.7016 | 0.9931 | |
| Spike-free | 0.97 | 0.1188 | 0.3450 | 0.98 | 0.1066 | 0.3785 | 0.98 | 0.2255 | 0.3622 | |
| GPMF | 0.97 | 0.1521 | 0.4043 | 0.94 | 0.1733 | 0.6063 | 0.96 | 0.3254 | 0.5160 | |
| Avg. | FE | 0.62 | 0.6985 | 1.5970 | 0.79 | 0.5244 | 1.2691 | 0.75 | 0.7672 | 1.4425 |
| Mean | 0.76 | 0.9934 | 1.4844 | 0.83 | 0.8385 | 1.3801 | 0.83 | 1.1249 | 1.4342 | |
| Median | 0.86 | 0.8083 | 1.1666 | 0.92 | 0.5756 | 0.9599 | 0.91 | 0.8630 | 1.0737 | |
| Gaussian | 0.77 | 1.0081 | 1.4780 | 0.86 | 0.8197 | 1.3161 | 0.85 | 1.1247 | 1.3992 | |
| HP | 0.94 | 0.2016 | 0.4705 | 0.85 | 0.3217 | 0.9043 | 0.91 | 0.3279 | 0.7274 | |
| Pit-free | 0.89 | 0.4618 | 0.7981 | 0.90 | 0.3998 | 0.8418 | 0.92 | 0.5473 | 0.8234 | |
| Spike-free | 0.98 | 0.1709 | 0.3037 | 0.98 | 0.1380 | 0.3183 | 0.98 | 0.1918 | 0.3179 | |
| GPMF | 0.98 | 0.2248 | 0.3584 | 0.96 | 0.1854 | 0.5020 | 0.97 | 0.2589 | 0.4379 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, Y.; Li, M.; Hao, Y.; Wang, B. Comparison and Evaluation of Different Pit-Filling Methods for Generating High Resolution Canopy Height Model Using UAV Laser Scanning Data. Remote Sens. 2021, 13, 2239. https://doi.org/10.3390/rs13122239
Quan Y, Li M, Hao Y, Wang B. Comparison and Evaluation of Different Pit-Filling Methods for Generating High Resolution Canopy Height Model Using UAV Laser Scanning Data. Remote Sensing. 2021; 13(12):2239. https://doi.org/10.3390/rs13122239
Chicago/Turabian StyleQuan, Ying, Mingze Li, Yuanshuo Hao, and Bin Wang. 2021. "Comparison and Evaluation of Different Pit-Filling Methods for Generating High Resolution Canopy Height Model Using UAV Laser Scanning Data" Remote Sensing 13, no. 12: 2239. https://doi.org/10.3390/rs13122239
APA StyleQuan, Y., Li, M., Hao, Y., & Wang, B. (2021). Comparison and Evaluation of Different Pit-Filling Methods for Generating High Resolution Canopy Height Model Using UAV Laser Scanning Data. Remote Sensing, 13(12), 2239. https://doi.org/10.3390/rs13122239