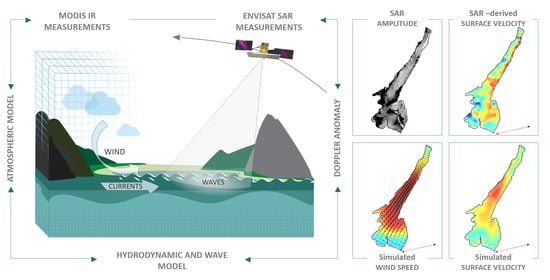
Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Sensor and Dataset
2.3. SAR Doppler Centroid Anomaly Estimation
2.4. Numerical Modeling
3. Results
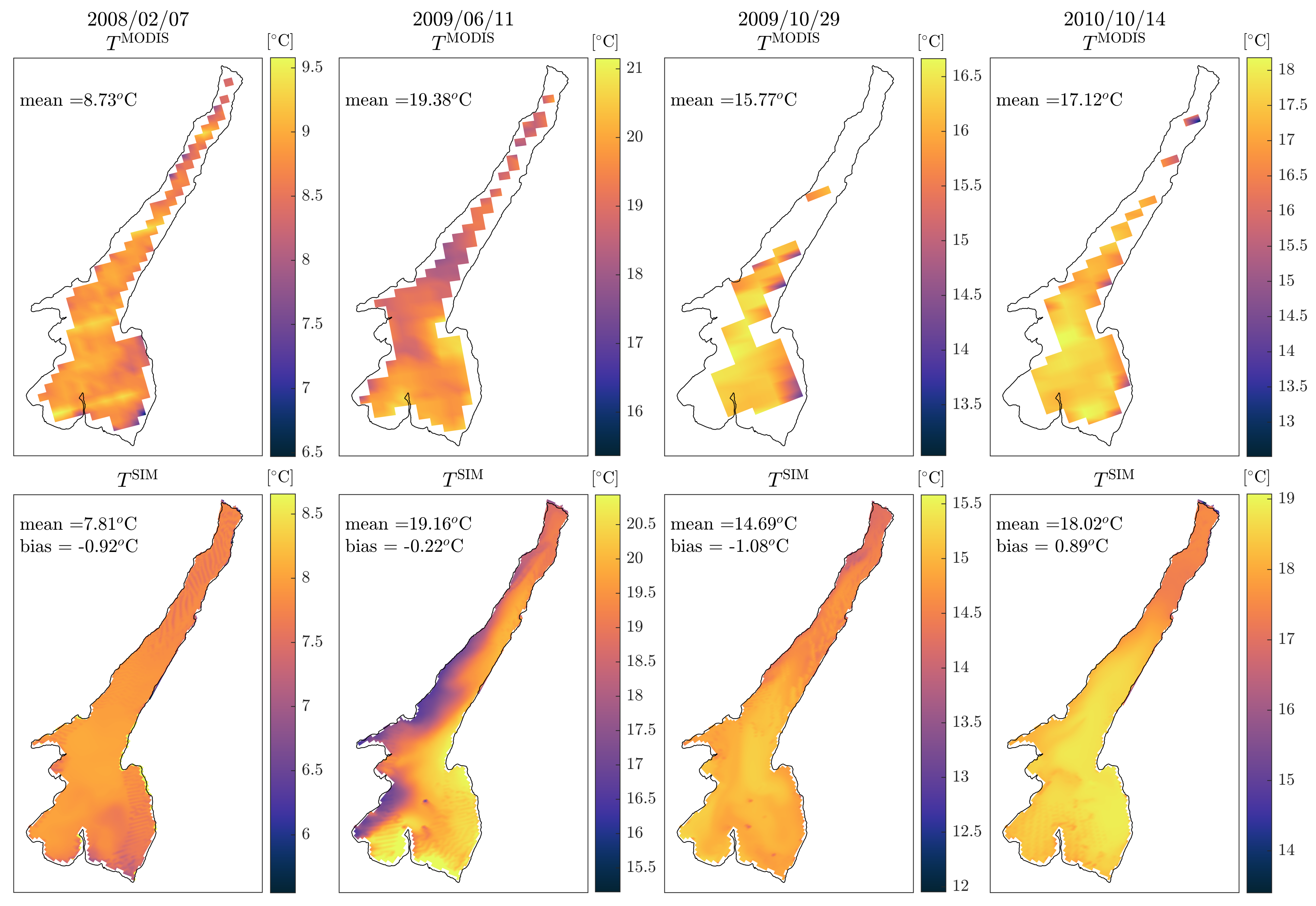
3.1. Model Verification Against MODIS
3.2. Main Features of Investigated Dates
- is processed as described at the end of Section 2.3 expressed in dB to enhance the visibility of its variation over lake;
- is obtained as in Equation (2).
- is obtained by computing the component of the simulated surface velocity along the ground range;
- is obtained by computing the component of the simulated wind velocity vector (at 10 m a.w.s.) along the ground range direction.
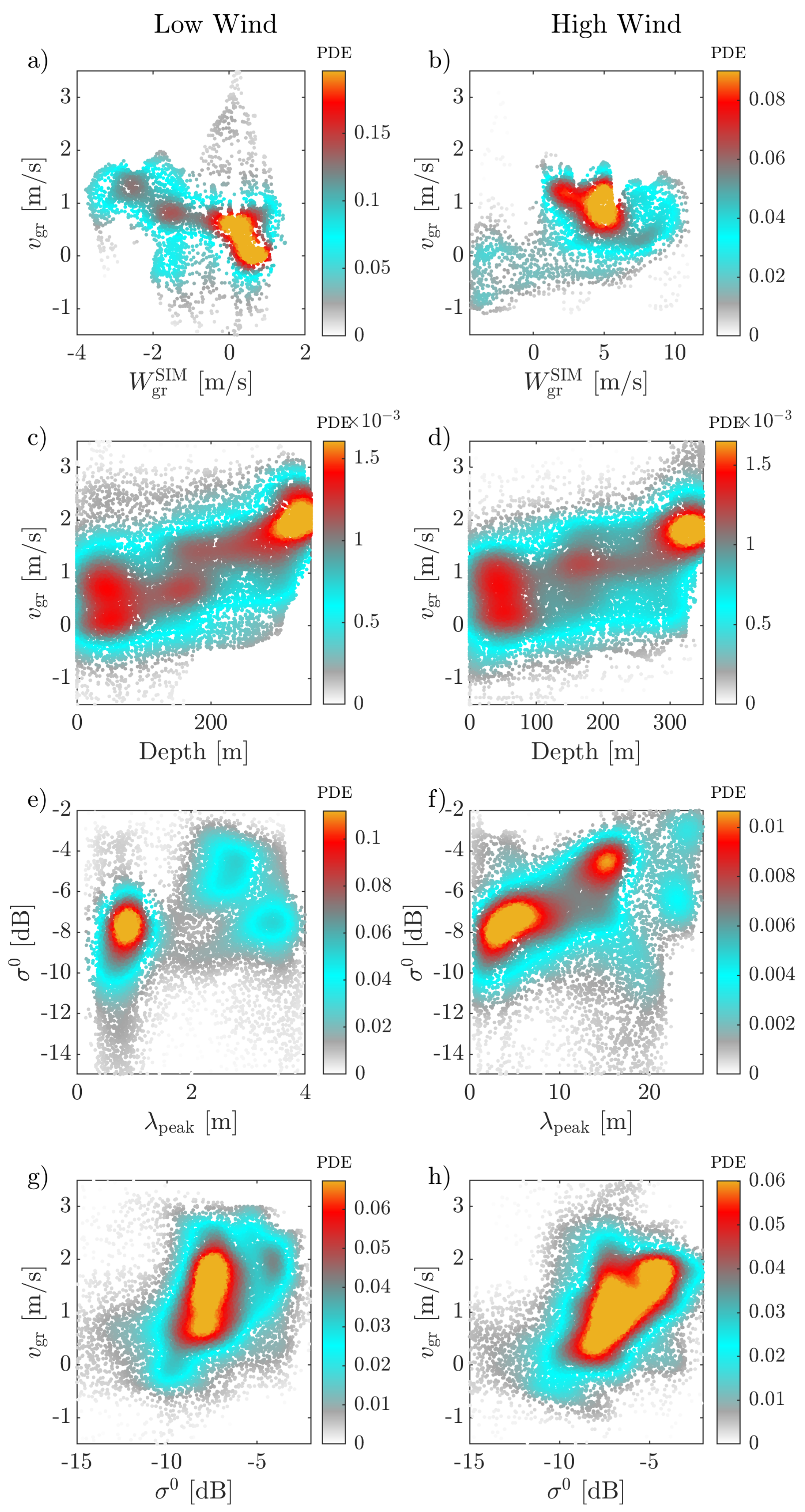
3.3. Low Wind Dates
3.4. High Wind Dates
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DCA | Doppler Centroid Anomaly |
| DRC | Doppler Resolution Cell |
| ECMWF | European Center for Medium-Range Weather Forecast |
| GMF | Geophysical Model Function |
| KDE | Kernel Density Estimation |
| LOS | Line Of Sight |
| S1 | Sentinel-1 |
| SAR | Synthetic Aperture Radar |
| SLC | Single Look Complex |
| SST | Sea Surface Temperature |
| SWAN | Simulating WAves Nearshore |
| WRF | Weather Research and Forecasting |
References
- Noviello, C.; Verde, S.; Zamparelli, V.; Fornaro, G.; Pauciullo, A.; Reale, D.; Nicodemo, G.; Ferlisi, S.; Gulla, G.; Peduto, D. Monitoring Buildings at Landslide Risk With SAR: A Methodology Based on the Use of Multipass Interferometric Data. IEEE Geosci. Remote Sens. Mag. 2020, 8, 91–119. [Google Scholar] [CrossRef]
- Cascini, L.; Peduto, D.; Reale, D.; Arena, L.; Ferlisi, S.; Verde, S.; Fornaro, G. Detection and monitoring of facilities exposed to subsidence phenomena via past and current generation SAR sensors. J. Geophys. Eng. 2013, 10, 064001. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Trivero, P.; Adamo, M.; Biamino, W.; Borasi, M.; Cavagnero, M.; De Carolis, G.; Di Matteo, L.; Fontebasso, F.; Nirchio, F.; Tataranni, F. Automatic oil slick detection from SAR images: Results and improvements in the framework of the PRIMI pilot project. Deep Sea Res. Part Top. Stud. Oceanogr. 2016, 133, 146–158. [Google Scholar] [CrossRef]
- De Carolis, G.; Olla, P.; De Santi, F. SAR image wave spectra to retrieve the thickness of grease-pancake sea ice using viscous wave propagation models. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Tello, M.; Lopez-Martinez, C.; Mallorqui, J.J. A novel algorithm for ship detection in SAR imagery based on the wavelet transform. IEEE Geosci. Remote. Sens. Lett. 2005, 2, 201–205. [Google Scholar] [CrossRef]
- Lehner, S.; Horstmann, J.; Koch, W.; Rosenthal, W. Mesoscale wind measurements using recalibrated ERS SAR images. J. Geophys. Res. Ocean. 1998, 103, 7847–7856. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Ullo, S.L.; Clemente, C.; Orlando, D. Perspectives on the Structural Health Monitoring of Bridges by Synthetic Aperture Radar. Remote Sens. 2020, 12, 3852. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Gierull, C.H. Optimum SAR/GMTI Processing and Its Application to the Radar Satellite RADARSAT-2 for Traffic Monitoring. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3868–3881. [Google Scholar] [CrossRef]
- Moiseev, A.; Johnsen, H.; Hansen, M.; Johannessen, J. Evaluation of Radial Ocean Surface Currents Derived from Sentinel-1 IW Doppler Shift Using Coastal Radar and Lagrangian Surface Drifter Observations. J. Geophys. Res. Ocean. 2020, 125, e2019JC015743. [Google Scholar] [CrossRef]
- Dagestad, K.F.; Horstmann, J.; Mouche, A.; Perrie, W.; Shen, H.; Zhang, B.; Li, X.; Monaldo, F.; Pichel, W.; Lehner, S.; et al. Wind retrieval from synthetic aperture radar-an overview. In Proceedings of the 4th SAR Oceanography Workshop (SEASAR 2012), Tromsø, Norway, 18–22 June 2012; pp. 18–22. [Google Scholar]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.F.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the use of Doppler shift for sea surface wind retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Kerbaol, V. Satellite synthetic aperture radar sea surface Doppler measurements. In Proceedings of the 2nd Workshop on SAR Coastal and Marine Applications, 2004, Svalbard, Norway, 8–12 September 2003; pp. 8–12. [Google Scholar]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. Ocean. 2005, 110. [Google Scholar] [CrossRef]
- S1 Level 2 OCN: Surface Radial Velocity (RVL) Component. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar/products-algorithms/level-2/products/surface-radial-velocity-component (accessed on 15 February 2021).
- Zamparelli, V.; De Santi, F.; Cucco, A.; Zecchetto, S.; De Carolis, G.; Fornaro, G. Surface Currents Derived from SAR Doppler Processing: An Analysis over the Naples Coastal Region in South Italy. J. Mar. Sci. Eng. 2020, 8, 203. [Google Scholar] [CrossRef] [Green Version]
- Zamparelli, V.; De Santi, F.; De Carolis, G.; Fornaro, G. On the Analysis of SAR Derived Wind and Sea Surface Currents. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5721–5724. [Google Scholar] [CrossRef]
- Romeiser, R.; Runge, H.; Suchandt, S.; Kahle, R.; Rossi, C.; Bell, P.S. Quality Assessment of Surface Current Fields from TerraSAR-X and TanDEM-X Along-Track Interferometry and Doppler Centroid Analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2759–2772. [Google Scholar] [CrossRef] [Green Version]
- Romeiser, R.; Alpers, W. An improved composite surface model for the radar backscattering cross section of the ocean surface: 2. Model response to surface roughness variations and the radar imaging of underwater bottom topography. J. Geophys. Res. Oceans 1997, 102, 25251–25267. [Google Scholar] [CrossRef]
- Gelautz, M.; Frick, H.; Raggam, J.; Burgstaller, J.; Leberl, F. SAR image simulation and analysis of alpine terrain. Isprs J. Photogramm. Remote Sens. 1998, 53, 17–38. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Leshkevich, G.A. Satellite SAR remote sensing of Great Lakes ice cover, Part 1. Ice backscatter signatures at C band. J. Great Lakes Res. 2007, 33, 722–735. [Google Scholar] [CrossRef]
- Wu, L.; Wang, L.; Min, L.; Hou, W.; Guo, Z.; Zhao, J.; Li, N. Discrimination of Algal-bloom using spaceborne SAR observations of Great Lakes in China. Remote Sens. 2018, 10, 767. [Google Scholar] [CrossRef] [Green Version]
- De Santi, F.; Luciani, G.; Bresciani, M.; Giardino, C.; Lovergine, F.P.; Pasquariello, G.; Vaiciute, D.; De Carolis, G. Synergistic Use of Synthetic Aperture Radar and Optical Imagery to Monitor Surface Accumulation of Cyanobacteria in the Curonian Lagoon. J. Mar. Sci. Eng. 2019, 7, 461. [Google Scholar] [CrossRef] [Green Version]
- McKinney, P.; Holt, B.; Matsumoto, K. Small eddies observed in Lake Superior using SAR and sea surface temperature imagery. J. Great Lakes Res. 2012, 38, 786–797. [Google Scholar] [CrossRef]
- Katona, T.; Bartsch, A. Estimation of wind speed over lakes in Central Europe using spaceborne C-band SAR. Eur. J. Remote Sens. 2018, 51, 921–931. [Google Scholar] [CrossRef] [Green Version]
- Pareeth, S.; Bresciani, M.; Buzzi, F.; Leoni, B.; Lepori, F.; Ludovisi, A.; Morabito, G.; Adrian, R.; Neteler, M.; Salmaso, N. Warming trends of perialpine lakes from homogenised time series of historical satellite and in-situ data. Sci. Total Environ. 2017, 578, 417–426. [Google Scholar] [CrossRef] [PubMed]
- Jackson, G.; Fornaro, G.; Berardino, P.; Esposito, C.; Lanari, R.; Pauciullo, A.; Reale, D.; Zamparelli, V.; Perna, S. Experiments of sea surface currents estimation with space and airborne SAR systems. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 373–376. [Google Scholar]
- Kersten, P.R.; Toporkov, J.V.; Ainsworth, T.L.; Sletten, M.A.; Jansen, R.W. Estimating Surface Water Speeds With a Single-Phase Center SAR Versus an Along-Track Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3638–3646. [Google Scholar] [CrossRef]
- Toporkov, J.V.; Perkovic, D.; Farquharson, G.; Sletten, M.A.; Frasier, S.J. Sea surface velocity vector retrieval using dual-beam interferometry: First demonstration. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2494–2502. [Google Scholar] [CrossRef]
- Steissberg, T.E.; Hook, S.J.; Schladow, S.G. Measuring surface currents in lakes with high spatial resolution thermal infrared imagery. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Amadori, M.; Giovannini, L.; Toffolon, M.; Piccolroaz, S.; Zardi, D.; Bresciani, M.; Giardino, C.; Luciani, G.; Kliphuis, M.; van Haren, H.; et al. Multi-scale evaluation of a 3D lake model forced by an atmospheric model against standard monitoring data. Environ. Model. Softw. 2021, 139, 105017. [Google Scholar] [CrossRef]
- Salmaso, N.; Mosello, R. Limnological research in the deep southern subalpine lakes: Synthesis, directions and perspectives. Adv. Oceanogr. Limnol. 2010, 1, 29–66. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Serafin, S.; Zardi, D. The thermally driven diurnal wind system of the Adige Valley in the Italian Alps. Q. J. R. Meteorol. Soc. 2017, 143, 2389–2402. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Zardi, D.; de Franceschi, M. Climatological characteristics of the Ora del Garda wind in the Alps. Int. J. Climatol. 2015, 35, 4103–4115. [Google Scholar] [CrossRef] [Green Version]
- Piccolroaz, S.; Amadori, M.; Toffolon, M.; Dijkstra, H.A. Importance of planetary rotation for ventilation processes in deep elongated lakes: Evidence from Lake Garda (Italy). Sci. Rep. 2019, 9, 8290. [Google Scholar] [CrossRef]
- Moreira, A. A golden age for spaceborne SAR systems. In Proceedings of the 2014 20th International Conference on Microwaves, Radar and Wireless Communications (MIKON), Gdansk, Poland, 16–18 June 2014; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Zamparelli, V.; Jackson, G.; Cucco, A.; Fornaro, G.; Zecchetto, S. SAR based sea current estimation in the Naples coastal area. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4665–4668. [Google Scholar] [CrossRef]
- Zamparelli, V.; Fornaro, G. SAR based sea surface currents estimation: Application to the Gulf of Trieste. In Proceedings of the ISAG-2019 International Symposium on Applied Geoinformatics, Istanbul, Turkey, 7–9 November 2019. [Google Scholar]
- Johnsen, H.; Nilsen, V.; Engen, G.; Mouche, A.A.; Collard, F. Ocean doppler anomaly and ocean surface current from Sentinel 1 tops mode. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3993–3996. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.; Kudryavtsev, V.; Chapron, B.; Johannessen, J.; Collard, F.; Dagestad, K.F.; Mouche, A. Simulation of radar backscatter and Doppler shifts of wave–current interaction in the presence of strong tidal current. Remote Sens. Environ. 2012, 120, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Kraemer, T.; Johnsen, H.; Brekke, C. Emulating Sentinel-1 Doppler Radial Ice Drift Measurements Using Envisat ASAR Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6407–6418. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhou, Y.; Ge, J.; Johannessen, J.; Shen, F. Mapping sea surface velocities in the Changjiang coastal zone with advanced synthetic aperture radar. Acta Oceanol. Sin. 2014, 33, 141–149. [Google Scholar] [CrossRef]
- Madsen, S. Estimating the Doppler centroid of SAR data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 134–140. [Google Scholar] [CrossRef] [Green Version]
- Bamler, R. Doppler frequency estimation and the Cramer-Rao bound. IEEE Trans. Geosci. Remote Sens. 1991, 29, 385–390. [Google Scholar] [CrossRef] [Green Version]
- Meyer, F.J. Performance Requirements for Ionospheric Correction of Low-Frequency SAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3694–3702. [Google Scholar] [CrossRef]
- Sansosti, E. A simple and exact solution for the interferometric and stereo SAR geolocation problem. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1625–1634. [Google Scholar] [CrossRef]
- Ghirardi, N.; Amadori, M.; Free, G.; Giovannini, L.; Toffolon, M.; Giardino, C.; Bresciani, M. Using remote sensing and numerical modelling to quantify a turbidity discharge event in Lake Garda. J. Limnol. 2020, 80, 47–52. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; Keste, T.M.V.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Oceans 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Seibt, C.; Peeters, F.; Graf, M.; Sprenger, M.; Hofmann, H. Modeling wind waves and wave exposure of nearshore zones in medium-sized lakes. Limnol. Oceanogr. 2013, 58, 23–36. [Google Scholar] [CrossRef]
- Mao, M.; Van Der Westhuysen, A.J.; Xia, M.; Schwab, D.J.; Chawla, A. Modeling wind waves from deep to shallow waters in Lake Michigan using unstructured SWAN. J. Geophys. Res. Oceans 2016, 121, 3836–3865. [Google Scholar] [CrossRef]
- Giovannini, L.; Antonacci, G.; Zardi, D.; Laiti, L.; Panziera, L. Sensitivity of simulated wind speed to spatial resolution over complex terrain. Energy Procedia 2014, 59, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R.C.; Hook, S.J.; Schneider, P.; Schladow, S.G. Skin and bulk temperature difference at Lake Tahoe: A case study on lake skin effect. J. Geophys. Res. Atmos. 2013, 118, 10–332. [Google Scholar] [CrossRef]
- Monaldo, F.; Kerbaol, V.; Clemente-Colon, P.; Furevik, B.; Horstmann, J.; Johannessen, J.; Li, X.; Pichel, W.; Sikora, T.; Thompson, D.; et al. The SAR Measurements of Ocean Surface Winds: A White Paper for the 2nd Workshop on Coastal and Marine Applications of SAR, Longyearbyen, Spitsbergen, Norway, 8–12 September 2003. ESA SP 2003, 565. [Google Scholar]
- Donelan, M.A.; Pierson, W.J., Jr. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry. J. Geophys. Res. Oceans 1987, 92, 4971–5029. [Google Scholar] [CrossRef]
- Toffoli, A.; Bitner-Gregersen, E.M. Types of Ocean Surface Waves, Wave Classification. In Encyclopedia of Maritime and Offshore Engineering; American Cancer Society: Hoboken, NJ, USA, 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Wüest, A.; Lorke, A. Small scale hydrodynamics in lakes. Annu. Rev. Fluid Mech. 2003, 35, 373–412. [Google Scholar] [CrossRef]
- Hofmann, H.; Lorke, A.; Peeters, F. The relative importance of wind and ship waves in the littoral zone of a large lake. Limnol. Oceanogr. 2008, 53, 368–380. [Google Scholar] [CrossRef]
- Amadori, M.; Piccolroaz, S.; Giovannini, L.; Zardi, D.; Toffolon, M. Wind variability and Earth’s rotation as drivers of transport in a deep, elongated subalpine lake: The case of Lake Garda. J. Limnol. 2018, 77, 505–521. [Google Scholar] [CrossRef]
- Henderson-Sellers, B. The dependence of surface velocity in water bodies on wind velocity and latitude. Appl. Math. Model. 1988, 12, 202–203. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Alpers, W.; Hennings, I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar. J. Geophys. Res. Oceans 1984, 89, 10529–10546. [Google Scholar] [CrossRef]
- Wright, J. A new model for sea clutter. IEEE Trans. Antennas Propag. 1968, 16, 217–223. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Effects of intermediate-scale waves on radar signatures of ocean fronts and internal waves. J. Geophys. Res. Oceans 1998, 103, 18759–18768. [Google Scholar] [CrossRef]






| Class | Date | [m/s] | [cm/s] | [cm] | [m] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean ± Std | Max | Mean ± Std | Max | Mean ± Std | Max | Mean ± Std | Max | ||
| low | 29 October 2009 | 2.3 ± 1.5 | 5.5 | 8.3 ± 6.8 | 30.3 | 8.6 ± 5.6 | 19.6 | 2.04 ± 1.23 | 4.40 |
| low | 5 August 2010 | 3.1 ± 0.9 | 5.1 | 10.6 ± 5.4 | 33.5 | 11.4 ± 4.2 | 17.4 | 2.34 ± 0.94 | 3.74 |
| low | 14 October 2010 | 1.3 ± 0.5 | 2.1 | 3.2 ± 2.0 | 13.6 | 3.3 ± 0.9 | 5.3 | 0.81 ± 0.18 | 1.14 |
| high | 7 February 2008 | 8.2 ± 3.2 | 16.4 | 16.4 ± 8.1 | 61.0 | 49.7 ± 24.4 | 92.4 | 9.71 ± 5.04 | 19.24 |
| high | 13 November 2008 | 10.2 ± 5.2 | 22.2 | 33.1 ± 21.2 | 117.5 | 68.1 ± 42.7 | 145.1 | 12.79 ± 8.31 | 27.8 |
| high | 11 June 2009 | 7.9 ± 4.6 | 17.2 | 17.3 ± 8.4 | 53.2 | 48.9 ± 35.0 | 109.7 | 9.34 ± 7.00 | 29.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amadori, M.; Zamparelli, V.; De Carolis, G.; Fornaro, G.; Toffolon, M.; Bresciani, M.; Giardino, C.; De Santi, F. Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy. Remote Sens. 2021, 13, 2293. https://doi.org/10.3390/rs13122293
Amadori M, Zamparelli V, De Carolis G, Fornaro G, Toffolon M, Bresciani M, Giardino C, De Santi F. Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy. Remote Sensing. 2021; 13(12):2293. https://doi.org/10.3390/rs13122293
Chicago/Turabian StyleAmadori, Marina, Virginia Zamparelli, Giacomo De Carolis, Gianfranco Fornaro, Marco Toffolon, Mariano Bresciani, Claudia Giardino, and Francesca De Santi. 2021. "Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy" Remote Sensing 13, no. 12: 2293. https://doi.org/10.3390/rs13122293
APA StyleAmadori, M., Zamparelli, V., De Carolis, G., Fornaro, G., Toffolon, M., Bresciani, M., Giardino, C., & De Santi, F. (2021). Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy. Remote Sensing, 13(12), 2293. https://doi.org/10.3390/rs13122293