Full-Wave Modeling and Inversion of UWB Radar Data for Wave Propagation in Cylindrical Objects
Abstract
:1. Introduction
2. Methods and Experimental Set-Up
2.1. Computational Methods
2.1.1. Scattering Green’s Function for Cylindrically-Layered Media with Circular Cross Section
2.1.2. Optimal Integration Path
2.1.3. Far-Field Radar-Antenna Model
2.1.4. Full-Wave Inversion Method
2.2. Numerical Experiments
Laboratory Experimental Set-Up
- The Lightweight Radar System
- Measurements on the Cylindrical Models
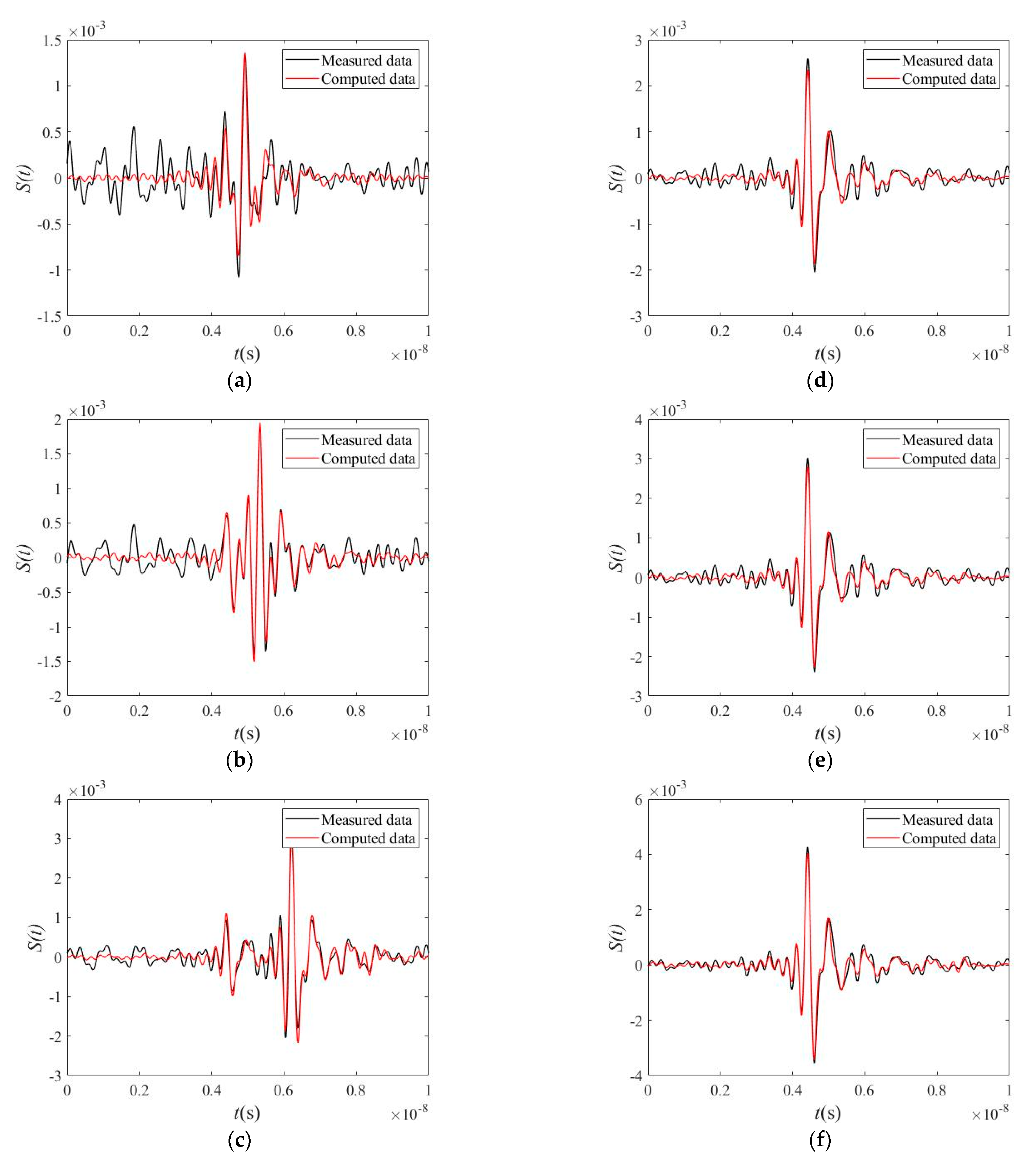
3. Results
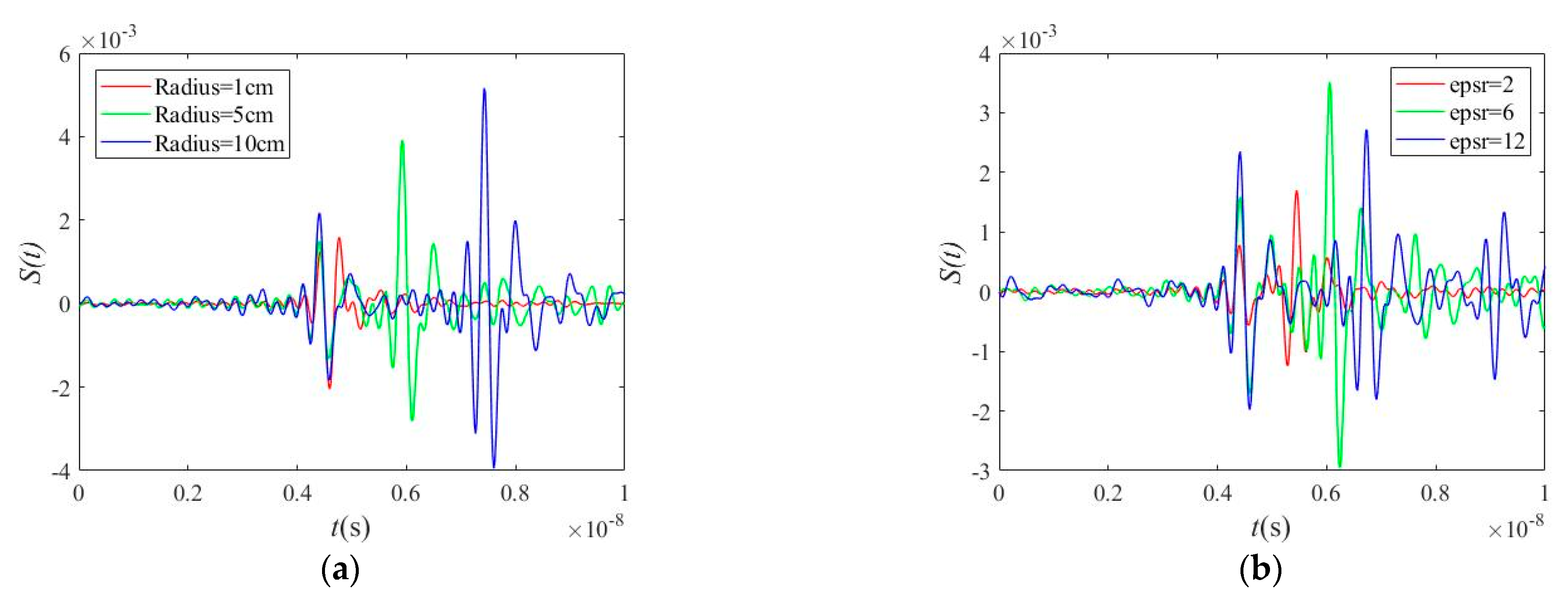
3.1. The Effects of Conductivity, Radius, and Relative Permittivity on Time Domain GPR Signals
3.2. Full-Wave Inversion Analysis
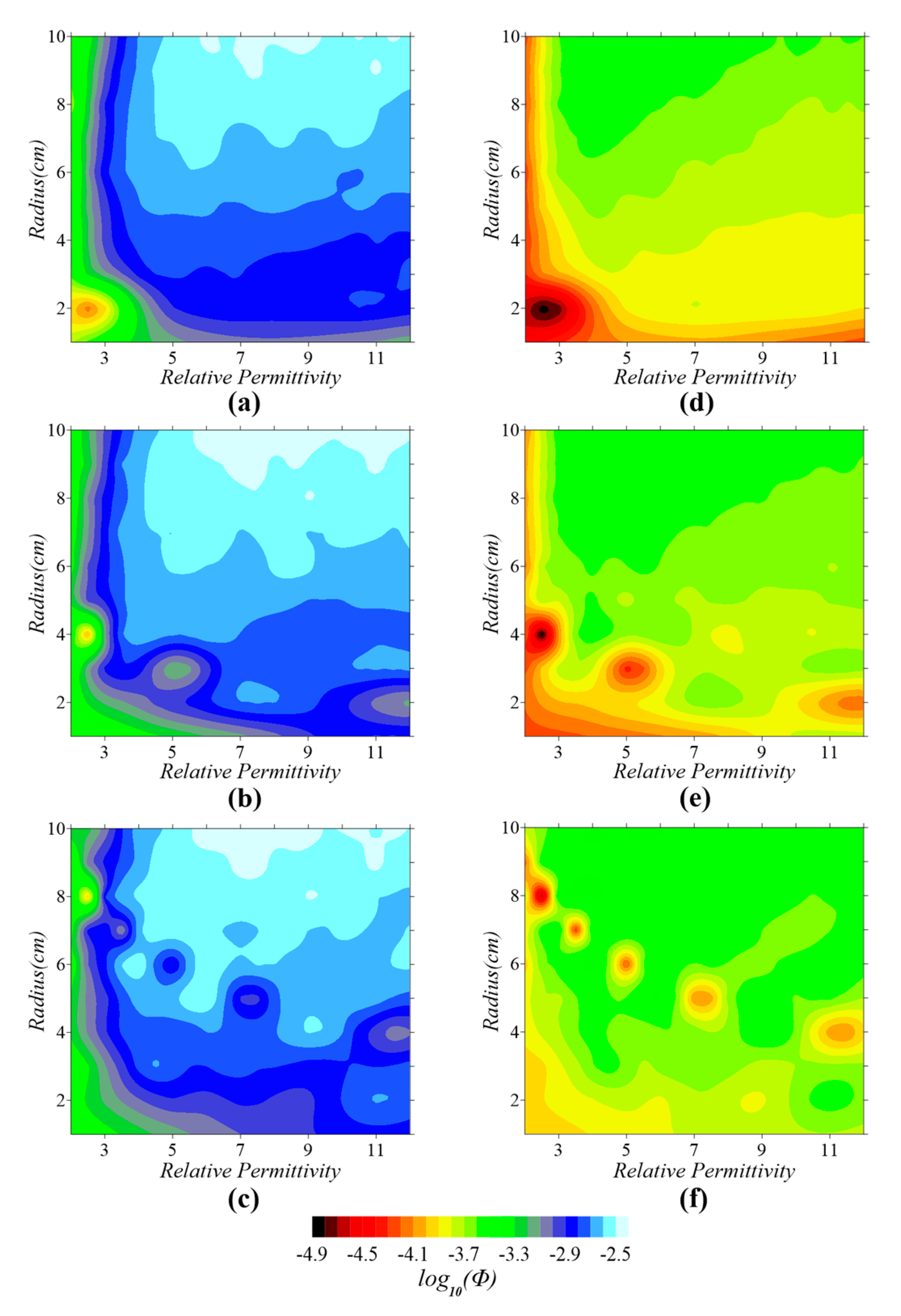
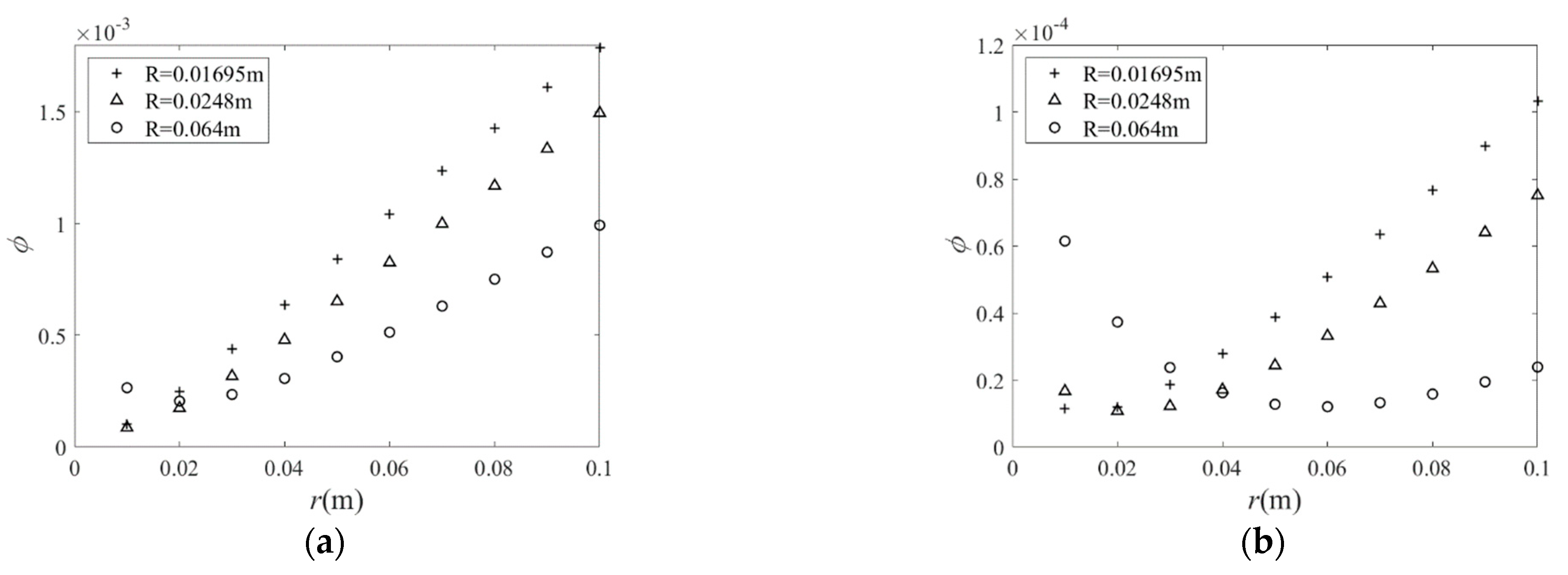
3.2.1. Topography of the Objective Functions
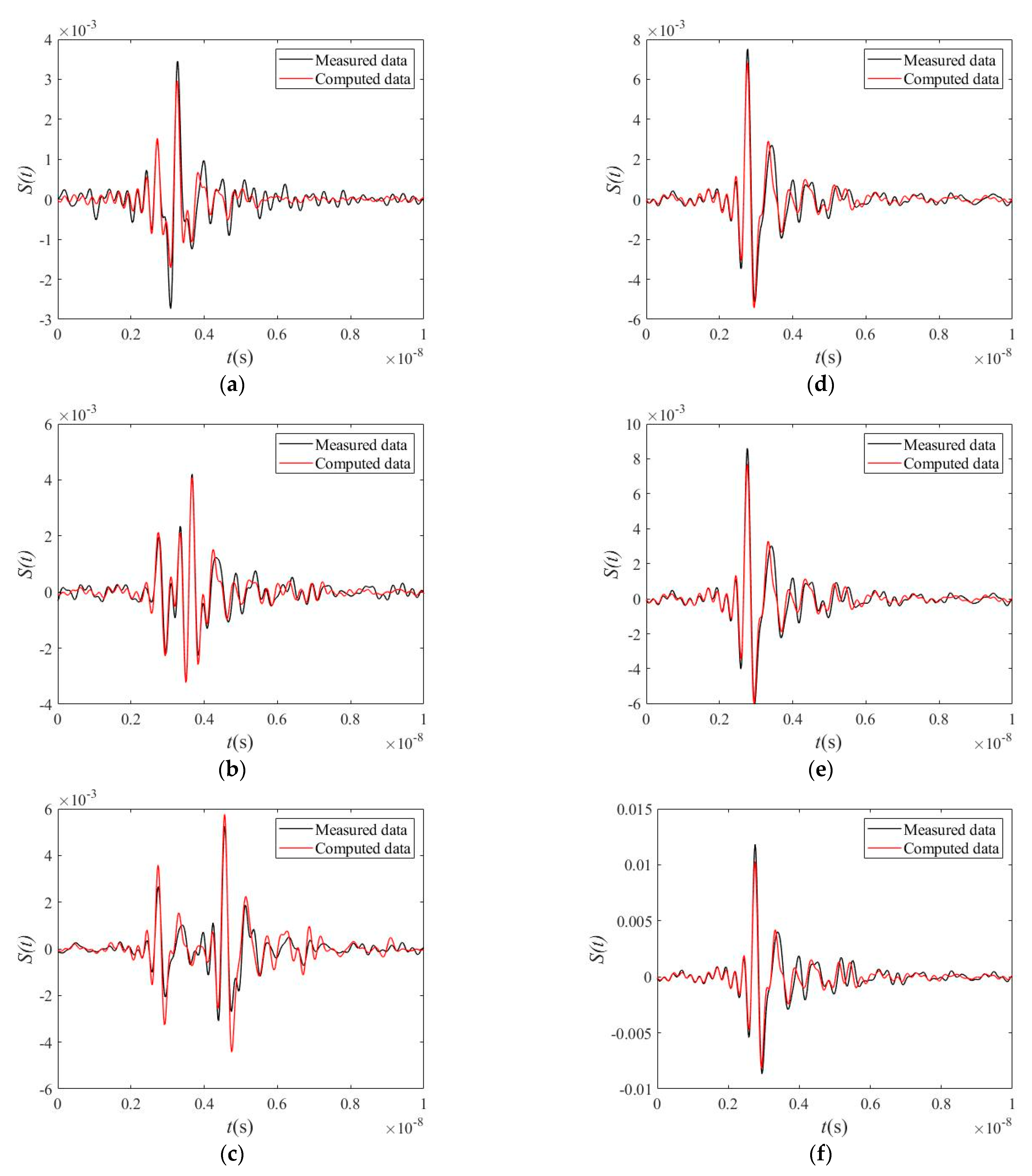
3.2.2. The Local Optimization Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Dong, X.; Xue, Q.; Leskovar, D.I.; Jifon, J.; Butnor, J.R.; Marek, T. Ground penetrating radar (GPR) detects fine roots of agricultural crops in the field. Plant Soil 2018, 423, 517–531. [Google Scholar] [CrossRef]
- Benedetto, A.; Pajewski, L. Civil Engineering Applications of Ground Penetrating Radar; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Pälli, A.; Kohler, J.C.; Isaksson, E.; Moore, J.C.; Pinglot, J.F.; Pohjola, V.A.; Samuelsson, H. Spatial and temporal variability of snow accumulation using ground-penetrating radar and ice cores on a Svalbard glacier. J. Glaciol. 2002, 48, 417–424. [Google Scholar] [CrossRef] [Green Version]
- Arcone, S.A.; Lawson, D.E.; Delaney, A.J.; Strasser, J.C.; Strasser, J.D. Ground-Penetrating Radar Reflection Profiling of Groundwater and Bedrock in an Area of Discontinuous Permafrost. Geophysics 1998, 63, 1573–1584. [Google Scholar] [CrossRef]
- Böniger, U.; Tronicke, J. Improving the interpretability of 3D GPR data using target–specific attributes: Application to tomb detection. J. Archaeol. Sci. 2010, 37, 672–679. [Google Scholar] [CrossRef]
- Neal, A.; Roberts, C.L. Applications of Ground-Penetrating Radar (GPR) to Sedimentological, Geomorphological and Geoarchaeological Studies in Coastal Environments; Geological Society, Special Publications: London, UK, 2000; Volume 175, pp. 139–171. [Google Scholar]
- Daniels, D.J. A review of GPR for landmine detection. Sens. Imag. Int. J. 2006, 7, 90–123. [Google Scholar] [CrossRef]
- Zhu, Q.; Collins, L. Application of feature extraction methods for landmine detection using the Wichmann/Niitek ground-penetrating radar. IEEE Trans. Geosci. Remote Sens. 2005, 43, 81–85. [Google Scholar] [CrossRef]
- Torrione, P.; Collins, L.M. Texture Features for Antitank Landmine Detection Using Ground Penetrating Radar. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2374–2382. [Google Scholar] [CrossRef]
- Ježová, J.; Mertens, L.; Lambot, S. Ground-penetrating radar for observing tree trunks and other cylindrical objects. Constr. Build. Mater. 2016, 123, 214–225. [Google Scholar] [CrossRef]
- Devaru, D.; Halabe, U.B.; Gopalakrishnan, B.; Agrawal, S.; Grushecky, S. Algorithm for detecting defects in wooden logs using ground penetrating radar. Proc. Spie Int. Soc. Opt. Eng. 2005, 5999, 835. [Google Scholar] [CrossRef]
- Tetuko, J.; Tateishi, R.; Wikantika, K. A method to estimate tree trunk diameter and its application to discriminate Java-Indonesia tropical forests. Int. J. Remote Sens. 2001, 22, 177–183. [Google Scholar] [CrossRef]
- Giannakis, I.; Tosti, F.; Lantini, L.; Alani, A.M. Health Monitoring of Tree Trunks Using Ground Penetrating Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8317–8326. [Google Scholar] [CrossRef]
- Boero, F.; Fedeli, A.; Lanini, M.; Maffongelli, M.; Monleone, R.; Pastorino, M.; Randazzo, A.; Salvadè, A.; Sansalone, A. Microwave Tomography for the Inspection of Wood Materials: Imaging System and Experimental Results. IEEE Trans. Microw. Theory Tech. 2018, 66, 3497–3510. [Google Scholar] [CrossRef]
- Alani, A.M.; Soldovieri, F.; Catapano, I.; Giannakis, I.; Gennarelli, G.; Lantini, L.; Ludeno, G.; Tosti, F. The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks. Remote Sens. 2019, 11, 2073. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Tofighi, M.-R.; Schreurs, D.; Horng, T.-S.J. Principles and Applications of RF/Microwave in Healthcare and Biosensing; Academic Press: New York, NY, USA, 2017. [Google Scholar]
- Conceição, R.C.; Medeiros, H.; Godinho, D.M.; O’Halloran, M.; Rodriguez-Herrera, D.; Flores-Tapia, D.; Pistorius, S. Classification of breast tumor models with a prototype microwave imaging system. Med. Phys. 2020, 47, 1860–1870. [Google Scholar] [CrossRef] [PubMed]
- Dachena, C.; Fedeli, A.; Fanti, A.; Lodi, M.B.; Pastorino, M.; Randazzo, A. Microwave Imaging for the Diagnosis of Cervical Diseases: A Feasibility Analysis. IEEE J. Electromagn. RF Microw. Med. Biol. 2020, in press. [Google Scholar] [CrossRef]
- Fedeli, A.; Schenone, V.; Randazzo, A.; Pastorino, M.; Henriksson, T.; Semenov, S. Nonlinear S-Parameters Inversion for Stroke Imaging. IEEE Trans. Microw. Theory Tech. 2021, 69, 1760–1771. [Google Scholar] [CrossRef]
- Gennarelli, G.; Ludeno, G.; Catapano, I.; Soldovieri, F. Full 3-D Imaging of Vertical Structures via Ground-Penetrating Radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8857–8873. [Google Scholar] [CrossRef]
- Negishi, T.; Gennarelli, G.; Soldovieri, F.; Liu, Y.; Erricolo, D. Radio Frequency Tomography for Nondestructive Testing of Pillars. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3916–3926. [Google Scholar] [CrossRef]
- Pastorino, M.; Randazzo, A. Microwave Imaging Methods and Applications; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Jezova, J.; Harou, J.; Lambot, S. Reflection waveforms occurring in bistatic radar testing of columns and tree trunks. Constr. Build. Mater. 2018, 174, 388–400. [Google Scholar] [CrossRef]
- Li, W.; Wen, J.; Xiao, Z.; Xu, S. Application of Ground-Penetrating Radar for Detecting Internal Anomalies in Tree Trunks with Irregular Contours. Sensors 2018, 18, 649. [Google Scholar] [CrossRef] [Green Version]
- Kiat, T.T.W.; Rahiman, M.H.F.; Jack, S.P. An initial study to investigate the potential of microwave tomography for agarwood imaging. Int. J. Agric. For. Plant. 2016, 4, 26–32. [Google Scholar]
- Chew, W.C. Waves and Fields in Inhomogenous Media; IEEE Press: Piscataway, NY, USA, 1995. [Google Scholar]
- Roberts, R.L.; Daniels, J.J. Modeling near-field GPR in three dimensions using the FDTD method. Geophysics 1997, 62, 1114–1126. [Google Scholar] [CrossRef]
- Semenov, S.; Bulyshev, A.; Abubakar, A.; Posukh, V.; Sizov, Y.; Souvorov, A.; Berg, P.V.D.; Williams, T. Microwave-tomographic imaging of the high dielectric-contrast objects using different image-reconstruction approaches. IEEE Trans. Microw. Theory Tech. 2005, 53, 2284–2294. [Google Scholar] [CrossRef]
- Scapaticci, R.; Catapano, I.; Crocco, L. Wavelet-Based Adaptive Multiresolution Inversion for Quantitative Microwave Imaging of Breast Tissues. IEEE Trans. Antennas Propag. 2012, 60, 3717–3726. [Google Scholar] [CrossRef]
- Lovell, J.R.; Chew, W.C. Response of a Point Source in a Multicylindrcally Layered Medium. IEEE Trans. Geosci. Remote Sens. 1987, GE-25, 850–858. [Google Scholar] [CrossRef]
- Liu, Q. Electromagnetic field generated by an off-axis source in a cylindrically layered medium with an arbitrary number of horizontal discontinuities. Geophysics 1993, 58, 616–625. [Google Scholar] [CrossRef]
- Wait, J.R. Electromagnetic Radiation from Cylindrical Structures; The Institution of Electrical Engineers: London, UK, 1988. [Google Scholar]
- Wait, J.R.; Hill, D.A. Excitation of a homogeneous conductive cylinder of finite length by a prescribed axial current distribution. Radio Sci. 1973, 8, 1169–1176. [Google Scholar] [CrossRef]
- Wu, J.; Khamas, S.K.; Cook, G.G. An Efficient Asymptotic Extraction Approach for the Green’s Functions of Conformal Antennas in Multilayered Cylindrical Media; IEEE Transactions on Antennas and Propagation: Piscataway, NJ, USA, 2010; Volume 58, pp. 3737–3742. [Google Scholar]
- Zhonggui, X.; Yilong, L. Electromagnetic dyadic Green’s function in cylindrically multilayered media. IEEE Trans. Microw. Theory Tech. 1996, 44, 614–621. [Google Scholar] [CrossRef]
- Fedeli, A.; Pastorino, M.; Raffetto, M.; Randazzo, A. 2-D Green’s Function for Scattering and Radiation Problems in Elliptically Layered Media With PEC Cores. IEEE Trans. Antennas Propag. 2017, 65, 7110–7118. [Google Scholar] [CrossRef]
- Tokgoz, C.; Dural, G. Closed-form Green’s functions for cylindrically stratified media. IEEE Trans. Microw. Theory Tech. 2000, 48, 40–49. [Google Scholar] [CrossRef]
- Sun, J.; Wang, C.-F.; Li, L.-W.; Leong, M.-S. A Complete Set of Spatial-Domain Dyadic Green’s Function Components for Cylindrically Stratified Media in Fast Computational Form. J. Electromagn. Waves Appl. 2002, 16, 1491–1509. [Google Scholar] [CrossRef]
- Ye, L.-F.; Zhao, F.; Xiao, K.; Chai, S.-L. A Robust Method for the Computation of Green’s Functions in Cylindrically Stratified Media’. IEEE Trans. Antennas Propag. 2012, 60, 3046–3051. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Ghosh, B.; Sarabandi, K. Evaluation of Efficient Closed-Form Green’s Function in a Cylindrically Stratified Medium. IEEE Trans. Antennas Propag. 2017, 65, 1505–1510. [Google Scholar] [CrossRef]
- Karan, S.; Ertürk, V.B.; Altintas, A. Closed-Form Green’s Function Representations in Cylindrically Stratified Media for Method of Moments Applications. IEEE Trans. Antennas Propag. 2009, 57, 1158–1168. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.F.; Xiao, K.; Qiu, L.; Chai, S.-L.; Mao, J.-J. An Efficient Method for the Computation of Mixed Potential Green’s Functions in Cylindrically Stratified Media. Prog. Electromagn. Res. 2012, 125, 37–53. [Google Scholar] [CrossRef] [Green Version]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef] [Green Version]
- Lambot, S.; Slob, E.; Bosch, I.V.D.; Stockbroeckx, B.; Vanclooster, M. Modeling of ground-penetrating Radar for accurate characterization of subsurface electric properties. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2555–2568. [Google Scholar] [CrossRef]
- Lambot, S.; Andre, F. Full-Wave Modeling of Near-Field Radar Data for Planar Layered Media Reconstruction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2295–2303. [Google Scholar] [CrossRef]
- Ježová, J.; Lambot, S. A dielectric horn antenna and lightweight radar system for material inspection. J. Appl. Geophys. 2019, 170, 3822. [Google Scholar] [CrossRef]
- Aksun, M.I.; Dural, G. Clarification of issues on the closed-form Green’s functions in stratified media. IEEE Trans. Antennas Propag. 2005, 53, 3644–3653. [Google Scholar] [CrossRef]
- Simsek, E.; Qing Huo, L.; Baojun, W. Singularity subtraction for evaluation of Green’s functions for multilayer media. IEEE Trans. Microw. Theory Tech. 2006, 54, 216–225. [Google Scholar] [CrossRef]
- He, X.; Gong, S.; Liu, Q. Fast computation of spatial Green’s functions of multilayered microstrip antennas. Microw. Opt. Technol. Lett. 2005, 45, 85–88. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.; Vereecken, H. Fast evaluation of zero-offset Green’s function for layered media with application to ground-penetrating radar. Geophys. Res. Lett. 2007, 34, 21. [Google Scholar] [CrossRef] [Green Version]
- De Coster, A.; Lambot, S. Full-Wave Removal of Internal Antenna Effects and Antenna–Medium Interactions for Improved Ground-Penetrating Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2018, 57, 93–103. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder--Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.P.; André, F.; Craeye, C.; Lambot, S. Near-Field Or Far-Field Full-Wave Ground Penetrating Radar Modeling As A Function Of The Antenna Height Above A Planar Layered Medium. Prog. Electromagn. Res. 2013, 141, 415–430. [Google Scholar] [CrossRef] [Green Version]
- De Coster, A.; Tran, A.P.; Lambot, S. Fundamental Analyses on Layered Media Reconstruction Using GPR and Full-Wave Inversion in Near-Field Conditions. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5143–5158. [Google Scholar] [CrossRef]





| Model | Radius (cm) | Relative Permittivity | Conductivity (S/m) |
|---|---|---|---|
| 1 | 1, 5, 10 | 5 | 0 |
| 2 | 5 | 2, 6, 12 | 0 |
| 3 | 1, 5, 10 | 1 | 100 |
| 4 | 5 | 1 | 1, 10, 100 |
| 5 | 1, 2, 3, … 10 | 2, 2.5, 3, … 12 | 0 |
| 6 | 1, 2, 3, … 10 | 1 | 100 |
| Model | Radius (m) | Relative permittivity | |||
|---|---|---|---|---|---|
| Estimated | Measured | Error (%) | Estimated | Measured | |
| PVC-1 | 0.0236 | 0.0201 | 17.41 | 1.8428 | 2.35–2.82 |
| PVC-2 | 0.0432 | 0.0406 | 6.40 | 2.0641 | 2.35–2.82 |
| PVC-3 | 0.0801 | 0.0805 | 0.50 | 2.4316 | 2.35–2.82 |
| Metal-1 | 0.0051 | 0.0170 | 70.00 | / | / |
| Metal-2 | 0.0082 | 0.0248 | 66.93 | / | / |
| Metal-3 | 0.0207 | 0.0640 | 67.66 | / | / |
| Model | Radius (m) | Relative permittivity | |||
|---|---|---|---|---|---|
| Estimated | Real | Error (%) | Estimated | Measured | |
| PVC-1 | 0.0210 | 0.0201 | 4.48 | 2.3283 | 2.35–2.82 |
| PVC-2 | 0.0419 | 0.0406 | 3.20 | 2.2918 | 2.35–2.82 |
| PVC-3 | 0.0815 | 0.0805 | 1.24 | 2.4057 | 2.35–2.82 |
| Metal-1 | 0.0124 | 0.0170 | 27.06 | / | / |
| Metal-2 | 0.0203 | 0.0248 | 18.15 | / | / |
| Metal-3 | 0.0528 | 0.0640 | 17.50 | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Dachena, C.; Wu, K.; Fedeli, A.; Pastorino, M.; Randazzo, A.; Wu, X.; Lambot, S. Full-Wave Modeling and Inversion of UWB Radar Data for Wave Propagation in Cylindrical Objects. Remote Sens. 2021, 13, 2370. https://doi.org/10.3390/rs13122370
Gao L, Dachena C, Wu K, Fedeli A, Pastorino M, Randazzo A, Wu X, Lambot S. Full-Wave Modeling and Inversion of UWB Radar Data for Wave Propagation in Cylindrical Objects. Remote Sensing. 2021; 13(12):2370. https://doi.org/10.3390/rs13122370
Chicago/Turabian StyleGao, Lan, Chiara Dachena, Kaijun Wu, Alessandro Fedeli, Matteo Pastorino, Andrea Randazzo, Xiaoping Wu, and Sébastien Lambot. 2021. "Full-Wave Modeling and Inversion of UWB Radar Data for Wave Propagation in Cylindrical Objects" Remote Sensing 13, no. 12: 2370. https://doi.org/10.3390/rs13122370






