Sequential Parameter Estimation of Modal Dispersion Curves with an Adaptive Particle Filter in Shallow Water: Experimental Results
Abstract
:1. Introduction
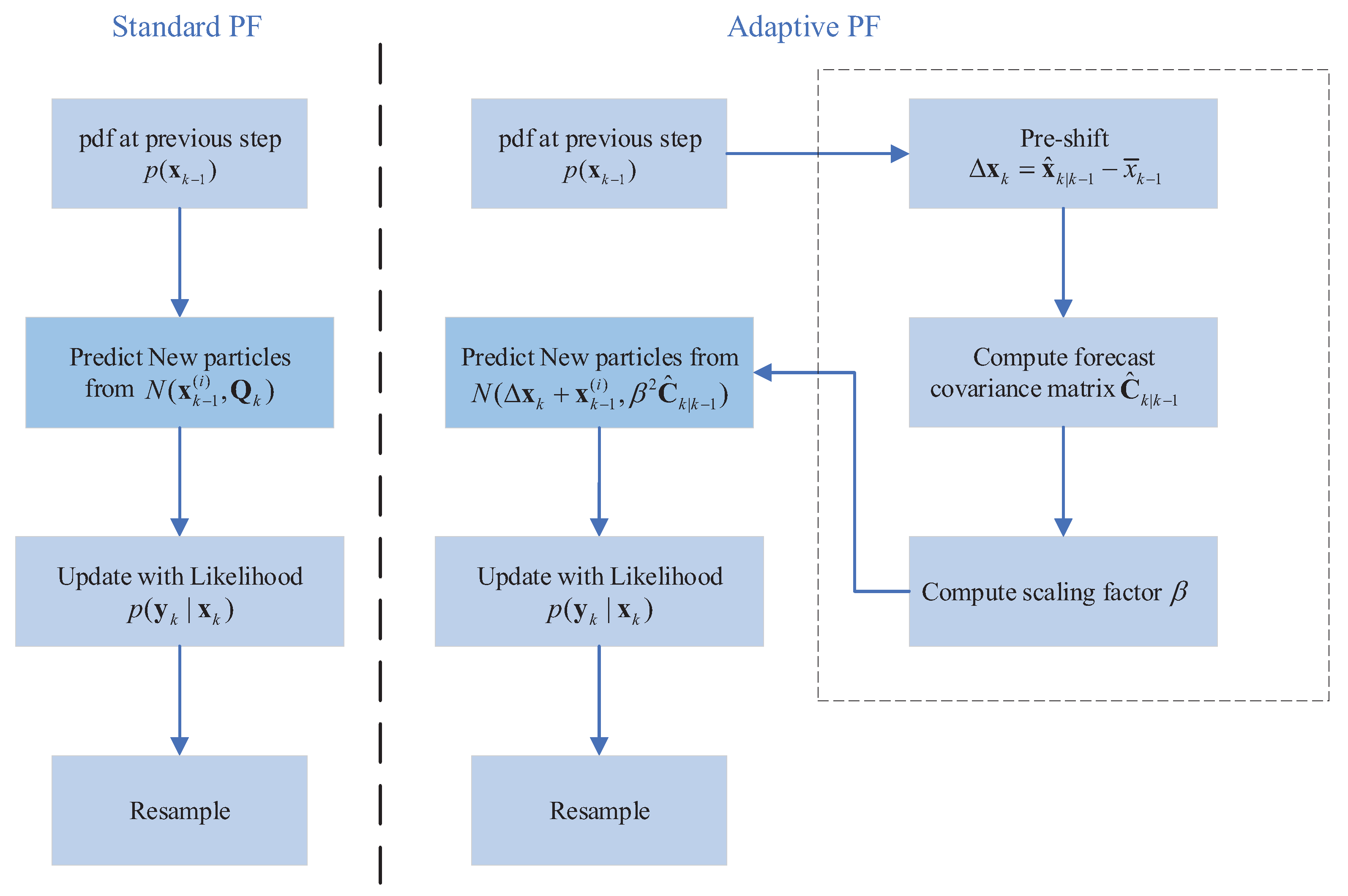
2. Sequential Estimation Method
3. Experiment Results
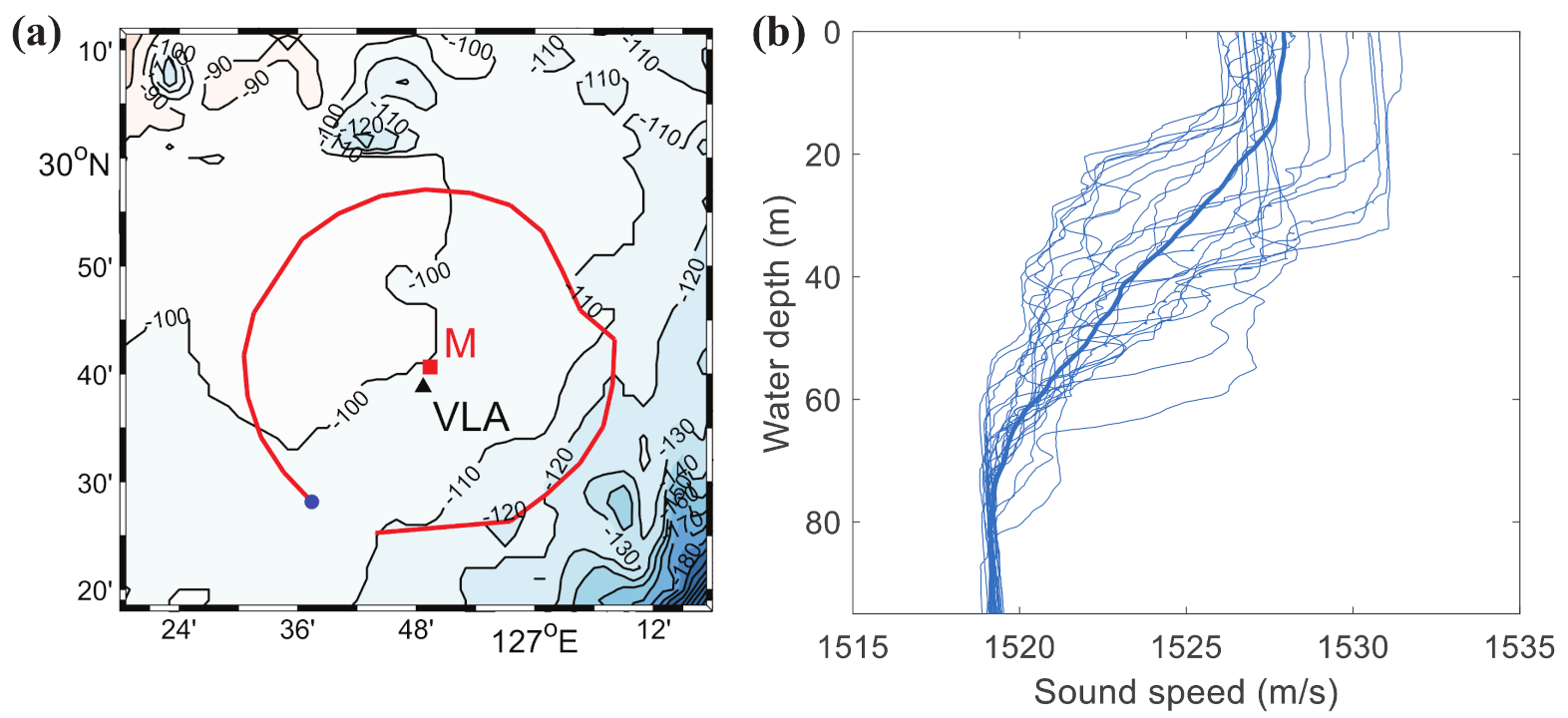
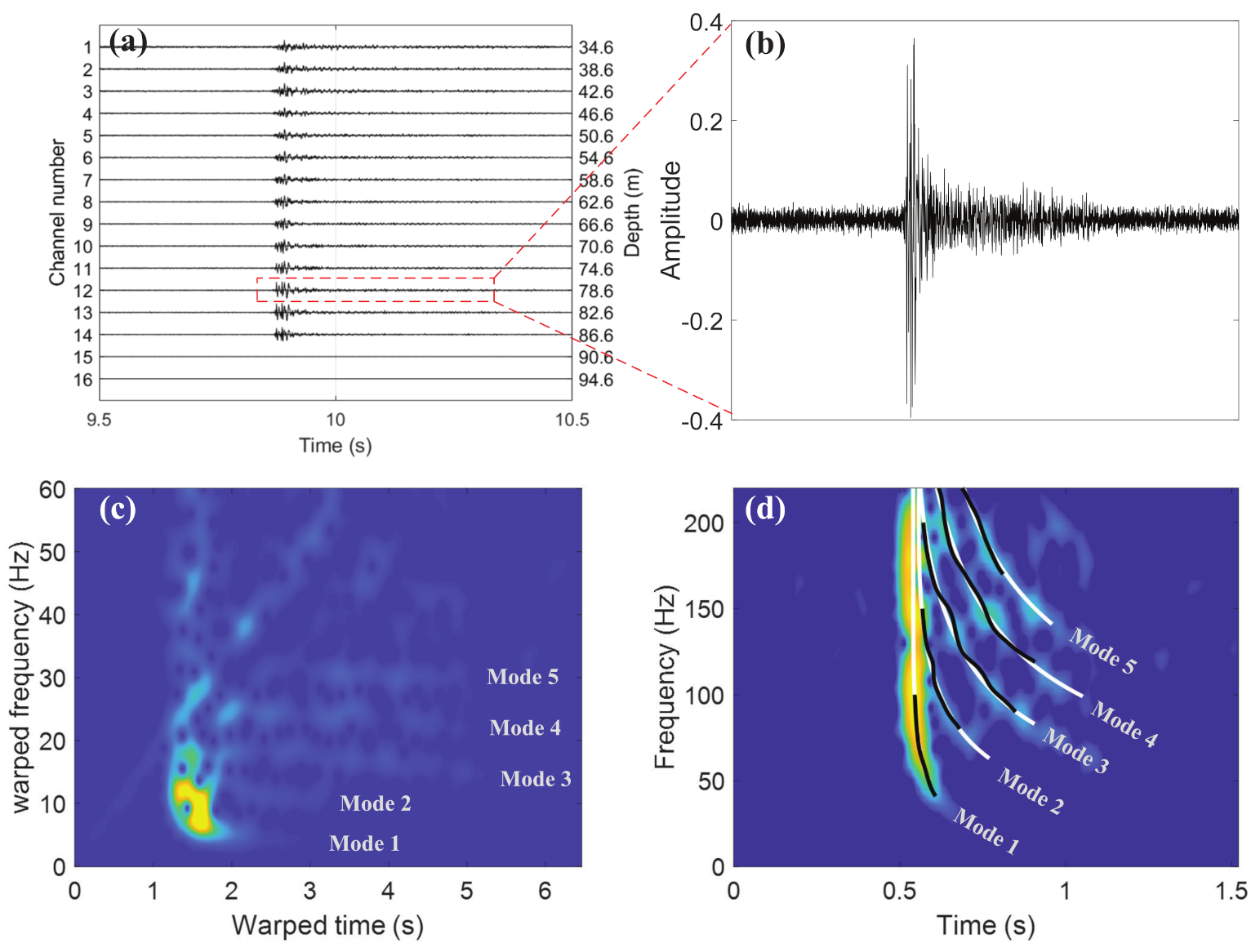
3.1. Experiment Description
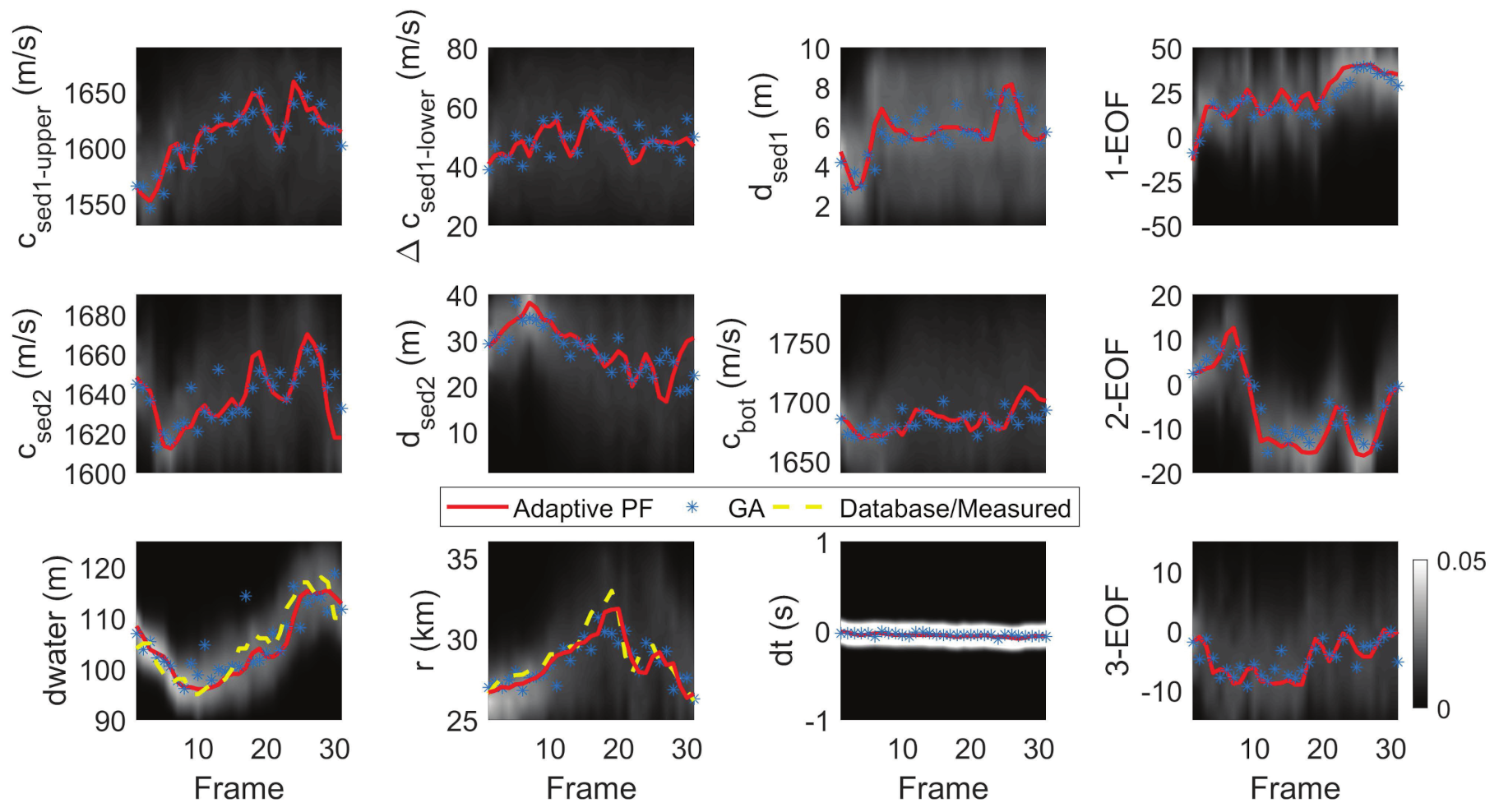
3.2. Interpretation of the Results
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Potty, G.R.; Miller, J.H.; Dahl, P.H.; Lazauski, C.J. Geoacoustic inversion results from the ASIAEX East China Sea experiment. IEEE J. Ocean. Eng. 2004, 29, 1000–1010. [Google Scholar] [CrossRef]
- Guo, X.L.; Yang, K.D.; Ma, Y.L.; Yang, Q.L. Geoacoustic Inversion Based on Modal Dispersion Curve for Range-Dependent Environment. Chin. Phys. Lett. 2015, 32, 124302. [Google Scholar] [CrossRef]
- Dahl, P.H.; Zhang, R.; Miller, J.H.; Bartek, L.R.; Peng, Z.; Ramp, S.R.; Zhou, J.-X.; Chiu, C.-S.; Lynch, J.F.; Simmen, J.A.; et al. Overview of results from the Asian Seas International Acoustics Experiment in the East China Sea. IEEE J. Ocean. Eng. 2004, 29, 920–928. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Ma, Y.; Sun, C.; Miller, J.H.; Potty, G.R. Multistep matched-field inversion for broad-band data from ASIAEX2001. IEEE J. Ocean. Eng. 2004, 29, 964–972. [Google Scholar] [CrossRef]
- Xu, L.; Yang, K.; Yang, Q. Experimental Study of Geoacoustic Inversion with Reliable Acoustic Path in the Philippine Sea. J. Theor. Comput. Acoust. 2019, 27, 1850061. [Google Scholar] [CrossRef]
- Bonnel, J.; Dosso, S.E.; Ross Chapman, N. Bayesian geoacoustic inversion of single hydrophone light bulb data using warping dispersion analysis. J. Acoust. Soc. Am. 2013, 134, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Yang, K.; Duan, R.; Ma, Y. Sequential Inversion for Geoacoustic Parameters in the South China Sea Using Modal Dispersion Curves. Acoust. Aust. 2017, 45, 1–11. [Google Scholar] [CrossRef]
- Bonnel, J.; Thode, A.; Wright, D.; Chapman, R. Nonlinear time-warping made simple: A step-by-step tutorial on underwater acoustic modal separation with a single hydrophone. J. Acoust. Soc. Am. 2020, 147, 1897–1926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Yang, K.; Ma, Y.; Yang, Q.; Huang, C. Synchrosqueezing transform for geoacoustic inversion with air-gun source in the East China Sea. Appl. Acoust. 2020, 169, 107460. [Google Scholar] [CrossRef]
- Yardim, C.; Michalopoulou, Z.; Gerstoft, P. An Overview of Sequential Bayesian Filtering in Ocean Acoustics. IEEE J. Ocean. Eng. 2011, 36, 71–89. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, N.; Gordon, N. An Introduction to Sequential Monte Carlo Methods; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Yardim, C.; Gerstoft, P.; Hodgkiss, W.S. Geoacoustic and source tracking using particle filtering: Experimental results. J. Acoust. Soc. Am. 2010, 128, 75–87. [Google Scholar] [CrossRef] [Green Version]
- Yardim, C.; Gerstoft, P.; Hodgkiss, W.S. Sequential geoacoustic inversion at the continental shelfbreak. J. Acoust. Soc. Am. 2012, 131, 1722–1732. [Google Scholar] [CrossRef]
- Cappe, O.; Godsill, S.J.; Moulines, E. An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo. Proc. IEEE 2007, 95, 899–924. [Google Scholar] [CrossRef]
- Musso, C.; Oudjane, N.; Le Gland, F. Improving Regularised Particle Filters. In Sequential Monte Carlo Methods in Practice; Doucet, A., de Freitas, N., Gordon, N., Eds.; Springer: New York, NY, USA, 2001; pp. 247–271. [Google Scholar] [CrossRef]
- Gilks, W.R.; Berzuini, C. Following a moving target—Monte Carlo inference for dynamic Bayesian models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 127–146. [Google Scholar] [CrossRef]
- Li, J.; Zhou, H. Tracking of time-evolving sound speed profiles in shallow water using an ensemble Kalman-particle filter. J. Acoust. Soc. Am. 2013, 133, 1377–1386. [Google Scholar] [CrossRef]
- Bo, L.; Xiong, J.; Ma, S. Sequential inversion of self-noise using adaptive particle filter in shallow water. J. Acoust. Soc. Am. 2018, 143, 2487–2500. [Google Scholar] [CrossRef]
- Dosso, S.E.; Dettmer, J. Bayesian matched-field geoacoustic inversion. Inverse Probl. 2011, 27, 55009. [Google Scholar] [CrossRef] [Green Version]
- Porter, M.B.; Reiss, E.L. A numerical method for bottom interacting ocean acoustic normal modes. J. Acoust. Soc. Am. 1985, 77, 1760–1767. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wu, L.X.; Niu, H.Q.; Zhang, R.H. Sequential Parameter Estimation Using Modal Dispersion Curves in Shallow Water. Chin. Phys. Lett. 2018, 35, 44301. [Google Scholar] [CrossRef]
- Hamilton, E.L.; Bachman, R.T. Sound velocity and related properties of marine sediments. J. Acoust. Soc. Am. 1982, 72, 1891–1904. [Google Scholar] [CrossRef]
- Miller, J.H.; Bartek, L.R.; Potty, G.R.; Tang, D.; Na, J.; Qi, Y. Sediments in the East China Sea. IEEE J. Ocean. Eng. 2004, 29, 940–951. [Google Scholar] [CrossRef]




| Bounds | Initial Value | Bounds | Initial Value | ||
|---|---|---|---|---|---|
| (m/s) | [1530 1690] | 1580.7 | (m) | [90 125] | 106.1 |
| (m/s) | [20 80] | 40.1 | (m) | [1 10] | 4.1 |
| (m/s) | [1600 1690] | 1647.2 | (m) | [1 40] | 29.7 |
| (m/s) | [1640 1790] | 1687.0 | 1-EOF | [−50 50] | −9.2 |
| r (km) | [25 36] | 27.10 | 2-EOF | [−20 20] | −2.2 |
| (s) | [−1 1] | 0.013 | 3-EOF | [−15 15] | −2.0 |
| Study | Geoacoustic Parameters | Result | Result in This Study |
|---|---|---|---|
| Gravity core data(Ref. [23]) | Surface sound speed | 1570–1675 m/s | 1580–1630 m/s |
| Potter et al. (Ref. [1]) | [, ] | [1590, 1665] m/s | [1580, 1630] m/s |
| Potter et al. (Ref. [1]) | 1640 m/s | 1618 m/s | |
| Potter et al. (Ref. [1]) | 1685 m/s | 1670 m/s | |
| Yang et al. (Ref. [4]) | 1594.4 m/s | 1609 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yang, K.; Yang, Q. Sequential Parameter Estimation of Modal Dispersion Curves with an Adaptive Particle Filter in Shallow Water: Experimental Results. Remote Sens. 2021, 13, 2387. https://doi.org/10.3390/rs13122387
Liu H, Yang K, Yang Q. Sequential Parameter Estimation of Modal Dispersion Curves with an Adaptive Particle Filter in Shallow Water: Experimental Results. Remote Sensing. 2021; 13(12):2387. https://doi.org/10.3390/rs13122387
Chicago/Turabian StyleLiu, Hong, Kunde Yang, and Qiulong Yang. 2021. "Sequential Parameter Estimation of Modal Dispersion Curves with an Adaptive Particle Filter in Shallow Water: Experimental Results" Remote Sensing 13, no. 12: 2387. https://doi.org/10.3390/rs13122387
APA StyleLiu, H., Yang, K., & Yang, Q. (2021). Sequential Parameter Estimation of Modal Dispersion Curves with an Adaptive Particle Filter in Shallow Water: Experimental Results. Remote Sensing, 13(12), 2387. https://doi.org/10.3390/rs13122387






