Next Article in Journal
Forest Fire Risk Prediction: A Spatial Deep Neural Network-Based Framework
Next Article in Special Issue
Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects
Previous Article in Journal
Construction and Application of a Knowledge Graph
Previous Article in Special Issue
Interpretation of Spectral LiDAR Backscattering off the Florida Coast
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 13
10.3390/rs13132512
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

Airborne Lidar Observations of a Spring Phytoplankton Bloom in the Western Arctic Ocean

by
James H. Churnside
1,2,*,
Richard D. Marchbanks
1,2 and
Nathan Marshall
3
1
Cooperative Institute for Research in Environmental Sciences (CIRES), University of Colorado, Boulder, CO 80305, USA
2
NOAA Chemical Sciences Laboratory, Boulder, CO 80305, USA
3
Scripps Institution of Oceanography, UC San Diego, San Diego, CA 92093, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(13), 2512; https://doi.org/10.3390/rs13132512
Submission received: 25 May 2021 / Revised: 23 June 2021 / Accepted: 24 June 2021 / Published: 27 June 2021
(This article belongs to the Special Issue Monitoring Aquatic Environments Using LiDAR)
Browse Figures
Versions Notes

Abstract

:
One of the most notable effects of climate change is the decrease in sea ice in the Arctic Ocean. This is expected to affect the distribution of phytoplankton as the ice retreats earlier. We were interested in the vertical and horizontal distribution of phytoplankton in the Chukchi Sea in May. Measurements were made with an airborne profiling lidar that allowed us to cover large areas. The lidar profiles showed a uniform distribution of attenuation and scattering from the surface to the limit of lidar penetration at a depth of about 30 m. Both parameters were greater in open water than under the ice. Depolarization of the lidar decreased as attenuation and scattering increased. A cluster analysis of the 2019 data revealed four distinct clusters based on depolarization and lidar ratio. One cluster was associated with open water, one with pack ice, one with the waters along the land-fast ice, and one that appeared to be scattered throughout the region. The first three were likely the result of different assemblages of phytoplankton, while the last may have been an artifact of thin fog in the atmosphere.

Graphical Abstract

1. Introduction

One of the most obvious effects of climate change is the rapidly decreasing sea ice cover in the Arctic Ocean. Perennial sea ice cover decreased by 4.0% per decade between 1978 and 2010, but by 8.3% per decade over the latter years (1996–2010) of this time period [1]. Another study found that September sea ice cover decreased by 4.8% per decade between 1979 and 1996, but by 18.6% per decade between 1997 and 2014 [2]. The decrease in the winter was less, with a decrease of 2.4% per decade from 1979 to 1999 and a decrease of 3.4% per decade from 2000 to 2017 [3]. The rate of decrease in spring and autumn lie between the summer and winter values [4]. Arctic sea ice is also getting thinner, with an average reduction of 1.75 m between 1980 and 2009 [5]. This decline in thickness also means that ice is drifting faster [6].
This decline in sea ice has been recognized as a major driver of ecological changes in the Arctic [7]. Thinner sea ice lets more light through and increases the productivity of algae growing on the bottom of the ice [8]. Loss of sea ice is also increasing phytoplankton productivity [9,10]. It has been estimated that 30% of the increase is due to a larger area of ice-free water and the remaining 70% to a longer growing season. That increase in growing season has created a new phytoplankton bloom in the fall [11]. A model suggests that the increased absorption caused by increased phytoplankton is contributing to a warming of the surface waters in the Arctic Ocean [12].
One other biological effect is an increase in large phytoplankton blooms under the ice. The first detailed report was of a massive bloom in the Chukchi Sea in July of 2011 [13], apparently fed by upwelling at the shelf break [14]. The area of these summer blooms seems to be increasing at a rate of about 2% per year [15]. One important driver is increased light levels under the ice, caused by a prevalence of thinner, first-year ice, faster snow melt, and increased areas of melt ponds [15,16,17]. Availability of nutrients is also important, and these blooms can be composed predominately of diatoms or Phaeocystis, depending on what nutrients are available [17].
We have also observed phytoplankton under the ice with airborne lidar [18,19]. These surveys found widespread, subsurface plankton layers under broken ice with as high as 90% ice cover. Lidar measurements cannot be made under complete ice cover. These layers were substantial, although shallower and with lower plankton concentrations than those in adjacent open water.
Lidars with similar characteristics have been used for shallow-water bathymetry [20,21,22]. There are significant differences, however. A bathymetric lidar has to scan to obtain a complete image of the sea bottom; our lidar measures only along a line under the aircraft and depends on this to get a statistical sample of the ocean. A bathymetric lidar has to have very accurate information about the aircraft position and attitude to get an accurate map of the bottom; our lidar measures features that are constantly in motion, so accurate positioning is not useful. A bathymetric lidar is looking for the relatively large return from a solid surface; our lidar is looking at the much smaller return from particles in the water column. The scanning and pulse positioning mean that a bathymetric lidar is much more complex than ours, although we require a larger laser pulse energy to accommodate the smaller backscattering level in the water.
In the atmosphere, backscatter lidars have been used to identify the dominant scattering particle. In the simplest scenario, dust could be distinguished from sulphate aerosol over the ocean using depolarization of the backscattered signal at 532 nm [23]. That was later extended to include identification of dust, spherical aerosols, water clouds, ice clouds, and precipitation with the addition of the vertical profiles of backscattering [24].The lidar extinction-to-backscatter ratio (or lidar ratio) adds more information, and a two-wavelength high-spectral-resolution lidar (HSRL) inversion used depolarization, lidar ratio, backscatter color ratio, and spectral depolarization ratio to distinguish between ice, pure dust, dusty mix, maritime, polluted maritime, urban, smoke, and fresh smoke aerosols [25,26]. A non-HSRL two-wavelength backscatter lidar on the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) satellite uses similar information to distinguish between desert dust, polluted continental, biomass burning, polluted dust, maritime, and clean continental aerosols [25,27]. More recently, simulated lidar signals have been used to train an artificial neural network to identify continental, continental polluted, dust, marine, smoke, and volcanic aerosols [28].
The success of the atmospheric studies on particle identification led us to investigate patterns of depolarization and lidar ratio in our Arctic Ocean data. Depolarization of oceanographic lidar returns depends primarily on the polarization characteristics of backscattering from the particles, although multiple forward scattering in the water column can have an effect under some conditions [29]. Model results suggest that the lidar ratio has a weak dependence on chlorophyll concentration, suggesting that it might also be more sensitive to the backscattering characteristics of the particles [30]. We should note that one attempt to infer particle characteristics from airborne lidar used a slightly different pair of parameters—the ratio of depolarization to the particulate backscattering coefficient and the ratio of chlorophyll concentration inferred from the diffuse attenuation coefficient and particulate backscattering coefficient [31].
The objective of this study was to demonstrate the utility of airborne lidar for measurements of the spring bloom in the Arctic Ocean. This involved lidar measurements of ice fraction, diffuse attenuation coefficient and particulate backscatter, and the relationships between these parameters. This also involved the lidar-specific parameters of depolarization and lidar ratio.

2. Materials and Methods

The primary instrument was the NOAA oceanographic lidar [18,32,33]. The source was a linearly polarized, flashlamp-pumped, Q-switched, frequency-doubled Nd:YAG laser producing 100 mJ, 12 ns pulses of 532 nm light at a repetition rate of 30 Hz. The beam was expanded to 17 mrad full angle and steered to overlap the receiver telescopes at a distance of 300 m.
Two receiver telescopes (Kepler) were used to collect light at two orthogonal polarizations. Telescope diameters were 6 cm for the co-polarized receiver and 15 cm for the cross-polarized receiver. A sheet of polaroid material on the front of each telescope was used to select the polarization. An aperture at the focus was used to set the field of view of each receiver to be slightly larger than the transmitter divergence. A 3 nm wide interference filter was used to reduce the amount of background light reaching the photomultiplier-tube (pmt) photodetectors. The detector outputs were fed through a logarithmic amplifier to increase dynamic range and digitized with an eight-bit, giga-sample-per-second digitizer. A computer recorded 2000 samples of each pulse, global-positioning system (GPS) information, and the photomultiplier gains.
The lidar was mounted over the camera port in a NOAA Twin Otter aircraft pointed about 15° forward from vertical to reduce specular reflections from the surface. The aircraft was generally flown at an altitude of 300 m and a speed of 60 m s−1. Flights were made on seven days between 19 and 28 May 2019 over the Chukchi and Beaufort Seas of the Arctic Ocean (Figure 1) out of Utqiaġvik, Alaska, USA. The objective of the flights was to make multiple passes over the ice edge, but fog and low clouds were constraints. The figure also shows the satellite-derived ice edge (ice fraction = 0.15) for 23 May 2019 and 23 July 2014 [18], each in the middle of this and of an earlier lidar survey. In the study area shown, the position of the ice edges is similar, and there were actually 9500 km2 more of open water in this area in May 2019 than in July 2014.
The lidar data were processed in several steps. First, the data were visually inspected to remove those data files contaminated by fog and low clouds. Next, lidar pulses hitting ice at the surface were identified by a saturation of the return signal in the cross-polarized channel. The ice fraction was calculated for each ~1 km section of flight track by taking the ratio of the number of these pulses to the total number of pulses in the segment, which was fixed at 500. For pulses without ice at the surface, the pmt gains and response functions of the log-amps and digitizer were used to convert digitizer count to photocathode current for each sample. The last 100 samples, which correspond to depths well below the laser penetration depth, of these pulses were averaged to provide an estimate of the background light signal, and this was subtracted from the rest of the samples in the pulse. The surface sample for each pulse was taken to be the one with the largest signal, and depths were measured from this sample. Data were converted from photocathode current to attenuated volume backscatter coefficient using calculated calibration coefficients at 300 m (422 m−1 sr−1 A−1 for the co-polarized channel and 79.2 m−1 sr−1 A−1 for the cross-polarized channel) and correcting for the difference in the range-squared loss between the actual altitude and 300 m using the GPS altitude. The co- and cross-polarized channels were added together to get the unpolarized return, and a linear regression of the logarithm of this signal against depth was performed over the depth range of 3–5 m. The volume scattering coefficient at the lidar scattering angle of 180°, β(π), is the exponential of the intercept of this regression. We converted this to an estimate of backscattering coefficient, bb, by multiplying by 2π. This is equivalent to assuming uniform scattering in the backward direction [33]. The lidar attenuation coefficient, α, is −0.5 times the slope of the regression, since the signal decays as exp(−2αz). For the conditions of these surveys, α is very nearly equal to the diffuse attenuation coefficient, Kd [34,35], and we will refer to Kd from here on. Both Kd and bb were averaged over 1 km flight segments; segments were eliminated if the variability was too great (standard deviation of bb values > 0.7 times the mean).
To convert bb into the particulate backscattering, bbp, the pure sea water value was subtracted. The pure water value of 1.08 × 10−3 m−1 was used throughout, based on an approximation [36] to temperature and salinity dependent measurements [37]. A typical value of 32 PSU was used for salinity. A variation of ±1 PSU would produce an error of 0.9%. The measured sea-surface temperature was near 0° for all flights, and this value was used for the calculation. A variation of ±1°, which is larger than what we observed, would produce an error of 0.6%.
All data, including the measured depolarization ratio, δ = β×(π)/β‖(π), and the lidar ratio, LR = Kd/β(π), were averaged into 0.3° longitude by 0.1° latitude bins for visualization. Here, β×(π) refers to the value that is cross-polarized with respect to the transmitted light and β‖(π) refers to the co-polarized value. All values, including δ and LR, were based on the 3–5 m regression. At 71° latitude, the averaging bins are nearly square (10.9 km by 11.1 km). Reported statistical properties were calculated before binning.
To check for clusters of lidar ratio and depolarization, the latter was plotted as a function of the former. The plotted data were observed to be separated into four distinct clusters. These were defined by: cluster C1 with LR < 30 and δ < 0.08, cluster C2 with LR < 30 and δ > 0.08, cluster C3 with 30 < LR < 180, and cluster C4 with LR > 180. It was clear from the figure that the separation between clusters was not complete. For example, there was more overlap between clusters C2 and C3 than others. In an attempt to quantify this, we assume that the distribution of points within each cluster is Gaussian and calculate the probability that a point from that distribution actually lies within a different cluster.

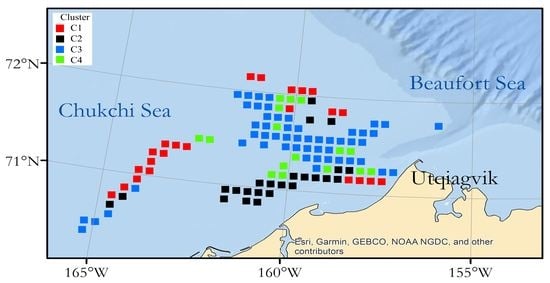
3. Results

Lidar measurements of Kd and bbp showed no vertical structure in the profiles down to the limits of lidar penetration at about 30 m. The subsurface plankton layers observed in July 2014 were completely absent in this data set.
The binned ice fractions from the lidar (Figure 2) show a pattern similar to the satellite ice edge in Figure 1. There is a large region of mostly clear water west of Utqiaġvik, with ice farther west and to the north. No lidar measurements were made in the land-fast ice along the shore, because there were no holes in this ice through with the lidar could penetrate. Note that there are some differences between the satellite-derived ice edge, which was observed on one day in the middle of the survey period, and the lidar ice cover, which was spread out over several days.
The binned diffuse attenuation data (Figure 3) show a different pattern. The largest values were found just off the land-fast ice to the southwest of Utqiaġvik. Overall (before binning), Kd was negatively correlated with ice fraction (R = −0.17, P < 10−8).
The particulate backscattering coefficient (Figure 4) has a pattern similar to Kd. In fact, the correlation between them was R = 0.66 (P < 10−99). The correlation between bbp and ice cover (R = −0.06, P = 0.03) was less than the correlation between Kd and ice cover.
The depolarization (Figure 5) was positively correlated with ice fraction (R = 0.31, P < 10−28). It was negatively correlated with Kd (R = −0.59, P < 10−99) and with bbp (R = −0.39, P < 10−46).
The lidar ratio (Figure 6) was negatively correlated with ice fraction (R = −0.08, P = 0.005). It was also negatively correlated with Kd (R = −0.42, P < 10−53) and bbp (R = −0.52, P < 10−86). However, it was positively correlated with the depolarization ratio (R = 0.18, P < 10−9). Since the lidar ratio is proportional to attenuation, it seems strange that these two quantities should be negatively correlated. The explanation is that attenuation and scattering are highly correlated, and the range of scattering values is larger than the range of attenuation values. When the attenuation increases, the scattering tends to increase by an even larger amount, so the lidar ratio actually decreases.
The scatter plot of depolarization vs. lidar ratio (Figure 7) shows the four clusters that were identified visually. These were defined by: cluster C1 with LR < 30 and δ < 0.08, cluster C2 with LR < 30 and δ > 0.08, cluster C3 with 30 < LR < 180, and cluster C4 with LR > 180. Each cluster is plotted in a different color. The heavy black lines denote the one standard deviation contour. The mean and standard deviation of each cluster lidar ratio and depolarization were: cluster C1—(13.7 ± 5.2, 0.046 ± 0.012), cluster C2—(15.3 ± 6.5, 0.126 ± 0.036), cluster C3—(61.6 ± 24.6, 0.109 ±0.035), and cluster C4—(96.53 ± 53, 0.110 ± 0.029).
It is clear from the figure that the separation between clusters was not complete. For example, there was more overlap between clusters C2 and C3 than others. In an attempt to quantify this, we assumed that the distribution of points within each cluster is Gaussian and calculated the probability that a point from that distribution actually lies within a different cluster. Based on this analysis, C1 was the tightest cluster, with a probability of extending into C2 and C3 of 3.1 × 10−5 and 4.6 × 10−6, respectively. C2 overlapped with C1 and C3 with probabilities of 0.035 and 6.9 × 10−4. C3 overlapped with C2 and C4 with probabilities of 0.033 and 2.8 × 10−12. Finally, C4 overlapped with C3 with a probability of 2.8 × 10−12. The number points in each cluster was 331, 202, 478, and 220, so C1 and C3 were the most populated clusters.
The spatial distribution of clusters (Figure 8) shows that cluster C1 was dominant in the broken ice to the west and north, cluster C2 was dominant along the edge of the land-fast ice, cluster C3 was dominant in open water, and cluster C4 was scattered geographically.

4. Discussion

One of the most surprising features of this investigation was that the ice extent in the survey area was actually less in May 2019 than it was in July 2014 (see Figure 1). This is consistent with an overall decrease in Arctic sea ice between 2014 and 2019. For example, the minimum ice extents for those two years were 4.58 × 106 km2 and 3.91 × 106 km2, which is a decrease of 14.6% in two years [38]. This decrease is much greater than the long-term trends discussed in the Introduction, and it reflects inter-annual variability more than a long-term trend.
With similar ice extent in the study area, one might expect that the stratification of the water column might be similar in July 2014 and May 2019. In fact, in July 2014, the water column was stratified and the depths of the subsurface plankton layers observed in the lidar corresponded to the depth of stratification [18]. The situation in May 2019 was different. An Alamo float in the Chukchi Sea (float 9234) reported no significant salinity stratification until about 15 June 2019 [39]. Recall that, at temperatures near freezing, density stratification closely follows salinity stratification.
Kd and bbp are important optical parameters, but they are also important because of their relationships to phytoplankton. For example, a common model relating Kd at 532 nm to the chlorophyll concentration C in mg m−3 is [30,40]
K d = 0.0452 + 0.0474 C 0.67 .
The distribution of chlorophyll concentration (Figure 9) is similar to the distribution of Kd in Figure 3. Due to the nonlinear nature of the relationship between Kd and C, the correlation coefficient between C and ice fraction (R = −0.16, P < 10−8) is slightly less than that between Kd and ice fraction.
Backscattering is more commonly related to Particulate Organic Carbon (POC) [41], and a relationship has been developed specific to the Alaskan Arctic [42],
b b p = 0.016 P O C 0.91 ,
This relationship was developed for a wavelength of 550 nm, but the difference between that and 532 nm is small. Phytoplankton, of course, are the drivers of primary productivity, and models of productivity have been developed [43,44,45,46,47,48]. Calculation of these parameters is beyond the scope of this paper.
Our data show relatively weak, negative correlations between Kd and ice fraction and between bbp and ice fraction. This suggests the strong spring phytoplankton bloom observed in open water is accompanied by an under-ice bloom that is only slightly weaker. This is consistent with a recent modeling effort that estimated that 63% of the total primary production in Arctic waters occurs in water with 50% or more ice fraction [49]. That work also estimated that 41% occurs in water with 85% or more ice fraction.
Our data also show that depolarization is positively correlated with ice fraction. This is somewhat surprising, given that the negative correlation of scattering and ice fraction. It suggests that the composition of scattering particles is different in open water than under the ice.
Since depolarization and lidar ratio depend more on the characteristics of the particulate scattering and less on the number density of particles, we expect that the different clusters represent different types of particles. Neeley et al. [50] showed that there were very distinct phytoplankton groups associated with sea ice and open water. This would seem to explain the difference in scattering properties between clusters C1 and C3 that are strongly associated with sea ice and open water, respectively. Cluster C2 is strongly associated with the edge of the land-fast ice along the northwest coast of Alaska. It is characterized by low lidar ratio and high depolarization, which suggests that this region has yet another group of phytoplankton species. The characteristics of this cluster could also be explained by a higher concentration of mineral particles than other areas.
The final cluster, C4, is spread throughout the area. It is characterized by very high lidar ratios, which might reflect another group of phytoplankton species, but might be the result of atmospheric attenuation. For example, a thin fog would reduce the energy reaching the water, thus reducing the amount of backscattered light. It would not affect the attenuation, so it would result in high attenuation-to backscatter ratios. Table 1 presents the correlations using the full data set and those without including cluster C4. The differences are small, and do not affect the overall conclusions. The relationships between ice fraction and the optical parameters Kd and bbp are slightly strengthened by removing the data in cluster C4.
There has been previous work using depolarization to distinguish between different types of scattering particles. A ship-based lidar was used to show a strong relationship between depolarization and the particulate backscattering ratio, bbp/bp, where bp is the total particulate scattering coefficient [51]. The backscattering ratio has been independently used to infer properties of scattering particles in the ocean [52,53]. Depolarization from that same lidar has been used to identify a coccolithophore bloom [54]. Another attempt used the ratio δ/bbp instead of δ to discriminate different types of scattering particles [31]. The argument for this parameter was that multiple scattering contributes to the depolarization, and dividing by bbp compensates for this effect, while retaining the differences in depolarization due to differences in particle characteristics. While this worked for the case presented, it is probably not generally valid, as the multiple-scattering component depends on the depth of the measurement and on the single-scattering albedo [29].
We did not expect the negative correlation between depolarization and bbp that was observed. If changes in bbp are a result of changes in the number density of the same particle type, we would expect this correlation to be zero. The correlation was calculated separately for each of the four clusters. In three of these, the correlation was not statistically significant. Only in cluster C1, along the ice edge, was the correlation significant (R = −0.62, P = 0.0012). This suggests that the composition of scatterers along the ice edge is changing, even within the cluster C1. On the other hand, the correlation between depolarization and Kd was significant for all of the clusters except for C2, along the edge of the landfast ice. Where the correlation with Kd is significant, but the correlation with bbp is not (e.g., C3 in open water), it is tempting to infer that the difference is due to variations in absorption by dissolved organic compounds (DOC). As the phytoplankton assemblage becomes more depolarizing, the concentration of DOC decreases. This seems to be more important at larger values of Kd. For Kd < 0.25 m−1, for example, the correlation between depolarization and Kd is actually positive (R = 0.35, P < 10−4).
The results of this study suggest that airborne lidar can be very useful for measurements of the spring bloom in the Arctic Ocean. It can measure ice fraction, diffuse attenuation coefficient and particulate backscatter, and the relationships between these parameters. With the lidar-specific parameters of depolarization and lidar ratio, it can identify regions of distinct assemblages of scattering particles. It can cover large areas of the ocean quickly, penetrate into the water in broken ice, and is unaffected by weather except for low clouds and fog. Previous work has validated lidar measurements of Kd [55] and bbp, [33] so future work in the Arctic can concentrate on converting these optical parameters to C and POC. These, in turn, can provide important information on Arctic Ocean ecosystems.

5. Conclusions

The ice edge in the Chukchi Sea in May 2019 was about the same place it was in July 2014. The vertical distribution of phytoplankton was very different, however, with strong subsurface layers in July 2014, but a uniform bloom right to the surface in May 2019. In both cases, scattering and attenuation of the lidar were greater in open water than under the ice. A cluster analysis of the 2019 data revealed four distinct clusters based on depolarization and lidar ratio. One cluster was associated with open water, one with pack ice, one with the waters along the land-fast ice, and one that appeared to be scattered throughout the region. The first three were likely the result of different assemblages of phytoplankton, but we cannot determine from the lidar return what the makeup of these assemblages might have been. The last cluster may have been an artifact of thin fog in the atmosphere, but we showed that this would not affect the main conclusions of the study.

Author Contributions

Conceptualization, J.H.C.; methodology, J.H.C. and R.D.M.; software, J.H.C., R.D.M., and N.M.; validation, J.H.C. and N.M; formal analysis, J.H.C. and N.M.; investigation, J.H.C. and N.M.; resources, J.H.C.; data curation, J.H.C.; writing—original draft preparation, J.H.C.; writing—review and editing, J.C, R.D.M., and N.M.; visualization, J.H.C.; supervision, J.H.C.; project administration, J.H.C.; funding acquisition, N.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the NOAA Cooperative Agreement with CIRES, NA17OAR4320101. Mr. Marshall was supported by a NOAA Hollings Scholarship.

Data Availability Statement

The lidar data used in this paper can be found on the NOAA Chemical Sciences Laboratory at https://csl.noaa.gov/groups/csl3/measurements/2019ArcticStratification/, accessed on 25 May 2021.

Acknowledgments

Satellite ice data downloaded from the US National Ice Center, https://www.natice.noaa.gov/products/daily_products.html, accessed on 28 April 2020. Satellite sea-surface salinity data downloaded from the NASA Jet Propulsion Laboratory, https://podaac.jpl.nasa.gov/dataset/SMAP_JPL_L3_SSS_CAP_8DAY-RUNNINGMEAN_V5, accessed on 15 May 2020.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Comiso, J.C. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2011, 25, 1176–1193. [Google Scholar] [CrossRef]
  2. Serreze, M.C.; Stroeve, J. Arctic sea ice trends, variability and implications for seasonal ice forecasting. Philos. Trans. R. Soc. A 2015, 373, 20140159. [Google Scholar] [CrossRef] [Green Version]
  3. Stroeve, J.; Notz, D. Changing state of Arctic sea ice across all seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
  4. Serreze, M.C.; Meier, W.N. The Arctic’s sea ice cover: Trends, variability, predictability, and comparisons to the Antarctic. Ann. N. Y. Acad. Sci. 2019, 1436, 36–53. [Google Scholar] [CrossRef] [PubMed]
  5. Kwok, R.; Rothrock, D.A. Decline in Arctic sea ice thickness from submarine and ICESat records: 1958–2008. Geophys. Res. Lett. 2009, 36, L15501. [Google Scholar] [CrossRef] [Green Version]
  6. Spreen, G.; Kwok, R.; Menemenlis, D. Trends in Arctic sea ice drift and role of wind forcing: 1992–2009. Geophys. Res. Lett. 2011, 38, L19501. [Google Scholar] [CrossRef] [Green Version]
  7. Post, E.; Bhatt, U.S.; Bitz, C.M.; Brodie, J.F.; Fulton, T.L.; Hebblewhite, M.; Kerby, J.; Kutz, S.J.; Stirling, I.; Walker, D.A. Ecological consequences of sea-ice decline. Science 2013, 341, 519–524. [Google Scholar] [CrossRef] [Green Version]
  8. Boetius, A.; Albrecht, S.; Bakker, K.; Bienhold, C.; Felden, J.; Fernández-Méndez, M.; Hendricks, S.; Katlein, C.; Lalande, C.; Krumpen, T. Export of algal biomass from the melting Arctic sea ice. Science 2013, 339, 1430–1432. [Google Scholar] [CrossRef] [PubMed]
  9. Arrigo, K.R.; van Dijken, G.L. Continued increases in Arctic Ocean primary production. Prog. Oceanogr. 2015, 136, 60–70. [Google Scholar] [CrossRef]
  10. Arrigo, K.R.; van Dijken, G.; Pabi, S. Impact of a shrinking Arctic ice cover on marine primary production. Geophys. Res. Lett. 2008, 35, L19603. [Google Scholar] [CrossRef]
  11. Ardyna, M.; Babin, M.; Gosselin, M.; Devred, E.; Rainville, L.; Tremblay, J.-É. Recent Arctic Ocean sea ice loss triggers novel fall phytoplankton blooms. Geophys. Res. Lett. 2014, 41, 2014GL061047. [Google Scholar] [CrossRef]
  12. Park, J.-Y.; Kug, J.-S.; Bader, J.; Rolph, R.; Kwon, M. Amplified Arctic warming by phytoplankton under greenhouse warming. Proc. Natl. Acad. Sci. USA 2015, 112, 5921–5926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Arrigo, K.R.; Perovich, D.K.; Pickart, R.S.; Brown, Z.W.; van Dijken, G.L.; Lowry, K.E.; Mills, M.M.; Palmer, M.A.; Balch, W.M.; Bates, N.R.; et al. Phytoplankton blooms beneath the sea ice in the Chukchi Sea. Deep Sea Res. II 2014, 105, 1–16. [Google Scholar] [CrossRef]
  14. Spall, M.A.; Pickart, R.S.; Brugler, E.T.; Moore, G.; Thomas, L.; Arrigo, K.R. Role of shelfbreak upwelling in the formation of a massive under-ice bloom in the Chukchi Sea. Deep Sea Res. II 2014, 105, 17–29. [Google Scholar] [CrossRef] [Green Version]
  15. Zhang, J.; Ashjian, C.; Campbell, R.; Spitz, Y.H.; Steele, M.; Hill, V. The influence of sea ice and snow cover and nutrient availability on the formation of massive under-ice phytoplankton blooms in the Chukchi Sea. Deep Sea Res. II 2015, 118, 122–135. [Google Scholar] [CrossRef] [Green Version]
  16. Palmer, M.A.; Saenz, B.T.; Arrigo, K.R. Impacts of sea ice retreat, thinning, and melt-pond proliferation on the summer phytoplankton bloom in the Chukchi Sea, Arctic Ocean. Deep Sea Res. II 2014, 105, 85–104. [Google Scholar] [CrossRef]
  17. Ardyna, M.; Mundy, C.; Mills, M.M.; Oziel, L.; Grondin, P.-L.; Lacour, L.; Verin, G.; Van Dijken, G.; Ras, J.; Alou-Font, E. Environmental drivers of under-ice phytoplankton bloom dynamics in the Arctic Ocean. Elementa 2020, 8, 30. [Google Scholar] [CrossRef]
  18. Churnside, J.H.; Marchbanks, R.D.; Vagle, S.; Bell, S.W.; Stabeno, P.J. Stratification, plankton layers, and mixing measured by airborne lidar in the Chukchi and Beaufort Seas. Deep Sea Res. II 2020, 177, 104742. [Google Scholar] [CrossRef]
  19. Churnside, J.H.; Marchbanks, R. Sub-surface plankton layers in the Arctic Ocean. Geophys. Res. Lett. 2015, 42, 4896–4902. [Google Scholar] [CrossRef]
  20. Irish, J.L.; McClung, J.; Lillycrop, W.J. Airborne Lidar Bathymetry: The SHOALS System; Bulletin of the International Navigation Association; International Navigation Association: Brussels, Belgium, 2000; pp. 43–53. [Google Scholar]
  21. Wang, C.; Li, Q.; Liu, Y.; Wu, G.; Liu, P.; Ding, X. A comparison of waveform processing algorithms for single-wavelength lidar bathymetry. ISPRS J. Photogram. 2015, 101, 22–35. [Google Scholar] [CrossRef]
  22. Klemas, V. Beach profiling and lidar bathymetry: An overview with case studies. J. Coast. Res. 2011, 27, 1019–1028. [Google Scholar] [CrossRef]
  23. Sugimoto, N.; Matsui, I.; Shimizu, A.; Uno, I.; Asai, K.; Endoh, T.; Nakajima, T. Observation of dust and anthropogenic aerosol plumes in the northwest Pacific with a two-wavelength polarization lidar on board the research vessel Mirai. Geophys. Res. Lett. 2002, 29, 7–1. [Google Scholar] [CrossRef] [Green Version]
  24. Shimizu, A.; Sugimoto, N.; Matsui, I.; Arao, K.; Uno, I.; Murayama, T.; Kagawa, N.; Aoki, K.; Uchiyama, A.; Yamazaki, A. Continuous observations of asian dust and other aerosols by polarization lidars in China and Japan during ACE-Asia. J. Geophys. Res. Atmos. 2004, 109, D19S17. [Google Scholar] [CrossRef]
  25. Burton, S.P.; Ferrare, R.A.; Vaughan, M.A.; Omar, A.H.; Rogers, R.R.; Hostetler, C.A.; Hair, J.W. Aerosol classification from airborne HSRL and comparisons with the CALIPSO vertical feature mask. Atmos. Meas. Tech. 2013, 6, 1397–1412. [Google Scholar] [CrossRef] [Green Version]
  26. Burton, S.P.; Ferrare, R.A.; Hostetler, C.A.; Hair, J.W.; Rogers, R.R.; Obland, M.D.; Butler, C.F.; Cook, A.L.; Harper, D.B.; Froyd, K.D. Aerosol classification using airborne high spectral resolution lidar measurements—Methodology and examples. Atmos. Meas. Tech. 2012, 5, 73–98. [Google Scholar] [CrossRef] [Green Version]
  27. Omar, A.H.; Winker, D.M.; Vaughan, M.A.; Hu, Y.; Trepte, C.R.; Ferrare, R.A.; Lee, K.-P.; Hostetler, C.A.; Kittaka, C.; Rogers, R.R.; et al. The CALIPSO automated aerosol classification and lidar ratio selection algorithm. J. Atm. Ocean. Tech. 2009, 26, 1994–2014. [Google Scholar] [CrossRef]
  28. Nicolae, D.; Vasilescu, J.; Talianu, C.; Binietoglou, I.; Nicolae, V.; Andrei, S.; Antonescu, B. A neural network aerosol-typing algorithm based on lidar data. Atmos. Chem. Phys. 2018, 18, 14511–14537. [Google Scholar] [CrossRef] [Green Version]
  29. Churnside, J.H. Polarization effects on oceanographic lidar. Opt. Express 2008, 16, 1196–1207. [Google Scholar] [CrossRef]
  30. Churnside, J.H.; Sullivan, J.M.; Twardowski, M.S. Lidar extinction-to-backscatter ratio of the ocean. Opt. Express 2014, 22, 18698–18706. [Google Scholar] [CrossRef] [PubMed]
  31. Schulien, J.A.; Della Penna, A.; Gaube, P.; Chase, A.P.; Haëntjens, N.; Graff, J.R.; Hair, J.W.; Hostetler, C.A.; Scarino, A.J.; Boss, E.S.; et al. Shifts in phytoplankton community structure across an anticyclonic eddy revealed from high spectral resolution lidar scattering measurements. Front. Mar. Sci. 2020, 7, 493. [Google Scholar] [CrossRef]
  32. Moore, T.S.; Churnside, J.H.; Sullivan, J.M.; Twardowski, M.S.; Nayak, A.R.; McFarland, M.N.; Stockley, N.D.; Gould, R.W.; Johengen, T.H.; Ruberg, S.A. Vertical distributions of blooming cyanobacteria populations in a freshwater lake from lidar observations. Remote Sens. Environ. 2019, 225, 347–367. [Google Scholar] [CrossRef]
  33. Churnside, J.; Marchbanks, R.; Lembke, C.; Beckler, J. Optical backscattering measured by airborne lidar and underwater glider. Remote Sens. 2017, 9, 379. [Google Scholar] [CrossRef] [Green Version]
  34. Gordon, H.R. Interpretation of airborne oceanic lidar: Effects of multiple scattering. Appl. Opt. 1982, 21, 2996–3001. [Google Scholar] [CrossRef] [PubMed]
  35. Churnside, J.H. Review of profiling oceanographic lidar. Opt. Eng. 2014, 53, 051405–051405. [Google Scholar] [CrossRef] [Green Version]
  36. Churnside, J.H.; Marchbanks, R.D. Calibration of an airborne oceanographic lidar using ocean backscattering measurements from space. Opt. Express 2019, 27, A536–A542. [Google Scholar] [CrossRef]
  37. Shifrin, K.S. Physical Optics of Ocean Water; American Institute of Physics: New York, NY, USA, 1988; 285p. [Google Scholar]
  38. Fetterer, F.; Savoie, M.; Helfrich, S.; Clement-Colon, P. Multisensor Analyzed Sea Ice Extent—Northern Hemisphere (MASIE-NH), Version 1; National Snow and Ice Data Center: Boulder, CO, USA, 2012; Available online: https://nsidc.org/data/G02186/versions/1 (accessed on 10 March 2021).
  39. Wood, K.R.; Jayne, S.R.; Mordy, C.W.; Overland, J.E. Arctic Heat Open Science Experiment; NOAA Pacific Marine Environmental Laboratory: Seattle, DC, USA, 2016.
  40. Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Oceans 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]
  41. Martinez-Vicente, V.; Dall’Olmo, G.; Tarran, G.; Boss, E.; Sathyendranath, S. Optical backscattering is correlated with phytoplankton carbon across the Atlantic Ocean. Geophys. Res. Lett. 2013, 40, 1154–1158. [Google Scholar] [CrossRef]
  42. Reynolds, R.A.; Stramski, D.; Neukermans, G. Optical backscattering by particles in Arctic seawater and relationships to particle mass concentration, size distribution, and bulk composition. Limnol. Oceanogr. 2016, 61, 1869–1890. [Google Scholar] [CrossRef] [Green Version]
  43. Campbell, J.; Antoine, D.; Armstrong, R.; Arrigo, K.; Balch, W.; Barber, R.; Behrenfeld, M.; Bidigare, R.; Bishop, J.; Carr, M.E. Comparison of algorithms for estimating ocean primary production from surface chlorophyll, temperature, and irradiance. Glob. Biogeochem. Cycles 2002, 16, 9–1. [Google Scholar] [CrossRef] [Green Version]
  44. Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
  45. Behrenfeld, M.J.; Falkowski, P.G. A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef] [Green Version]
  46. Schulien, J.A.; Behrenfeld, M.J.; Hair, J.W.; Hostetler, C.A.; Twardowski, M.S. Vertically-resolved phytoplankton carbon and net primary production from a high spectral resolution lidar. Opt. Express 2017, 25, 13577–13587. [Google Scholar] [CrossRef] [PubMed]
  47. Westberry, T.; Behrenfeld, M.J.; Siegel, D.A.; Boss, E. Carbon-based primary productivity modeling with vertically resolved photoacclimation. Glob. Biogeochem. Cycles 2008, 22, GB2024. [Google Scholar] [CrossRef] [Green Version]
  48. Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. Cycles 2005, 19, GB1006. [Google Scholar] [CrossRef]
  49. Clement Kinney, J.; Maslowski, W.; Osinski, R.; Jin, M.; Frants, M.; Jeffery, N.; Lee, Y.J. Hidden production: On the importance of pelagic phytoplankton blooms beneath Arctic sea ice. J. Geophys. Res. Oceans 2020, 125, e2020JC016211. [Google Scholar] [CrossRef]
  50. Neeley, A.R.; Harris, L.A.; Frey, K.E. Unraveling phytoplankton community dynamics in the northern Chukchi Sea under sea-ice-covered and sea-ice-free conditions. Geophys. Res. Lett. 2018, 45, 7663–7671. [Google Scholar] [CrossRef]
  51. Collister, B.L.; Zimmerman, R.C.; Sukenik, C.I.; Hill, V.J.; Balch, W.M. Remote sensing of optical characteristics and particle distributions of the upper ocean using shipboard lidar. Remote Sens. Environ. 2018, 215, 85–96. [Google Scholar] [CrossRef]
  52. Soja-Woźniak, M.; Baird, M.; Schroeder, T.; Qin, Y.; Clementson, L.; Baker, B.; Boadle, D.; Brando, V.; Steven, A.D. Particulate backscattering ratio as an indicator of changing particle composition in coastal waters: Observations from Great Barrier Reef waters. J. Geophys. Res. Oceans 2019, 124, 5485–5502. [Google Scholar] [CrossRef]
  53. Loisel, H.; Mériaux, X.; Berthon, J.-F.; Poteau, A. Investigation of the optical backscattering to scattering ratio of marine particles in relation to their biogeochemical composition in the eastern English Channel and southern North Sea. Limnol. Oceanogr. 2007, 52, 739–752. [Google Scholar] [CrossRef]
  54. Collister, B.L.; Zimmerman, R.C.; Hill, V.J.; Sukenik, C.I.; Balch, W.M. Polarized lidar and ocean particles: Insights from a mesoscale coccolithophore bloom. Appl. Opt. 2020, 59, 4650–4662. [Google Scholar] [CrossRef] [PubMed]
  55. Lee, J.H.; Churnside, J.H.; Marchbanks, R.D.; Donaghay, P.L.; Sullivan, J.M. Oceanographic lidar profiles compared with estimates from in situ optical measurements. Appl. Opt. 2013, 52, 786–794. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 13 02512 g001 550
Figure 1. Map of the Arctic Ocean north of Alaska with the lidar flight tracks shown in red. The black line shows the position of the ice edge on 23 May, in the middle of the survey. The blue line shows the position of the ice edge for a previous survey in July 2014. The bottom panel shows an expanded map showing the study region in the context of Russia, Alaska, and Canada.
Figure 1. Map of the Arctic Ocean north of Alaska with the lidar flight tracks shown in red. The black line shows the position of the ice edge on 23 May, in the middle of the survey. The blue line shows the position of the ice edge for a previous survey in July 2014. The bottom panel shows an expanded map showing the study region in the context of Russia, Alaska, and Canada.
Remotesensing 13 02512 g001
Remotesensing 13 02512 g002 550
Figure 2. Binned ice fraction from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time. The background is a rough depiction of bathymetry, with darker blue representing deeper water.
Figure 2. Binned ice fraction from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time. The background is a rough depiction of bathymetry, with darker blue representing deeper water.
Remotesensing 13 02512 g002
Remotesensing 13 02512 g003 550
Figure 3. Binned diffuse attenuation coefficient, Kd, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 3. Binned diffuse attenuation coefficient, Kd, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g003
Remotesensing 13 02512 g004 550
Figure 4. Binned particulate backscatter coefficient, bbp, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 4. Binned particulate backscatter coefficient, bbp, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g004
Remotesensing 13 02512 g005 550
Figure 5. Binned depolarization, δ, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 5. Binned depolarization, δ, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g005
Remotesensing 13 02512 g006 550
Figure 6. Binned lidar ratio, LR, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 6. Binned lidar ratio, LR, from the lidar data. The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g006
Remotesensing 13 02512 g007 550
Figure 7. Scatter plot of depolarization ratio, δ, as a function of lidar ratio, LR. Each of the four clusters is plotted as a different color, the boundaries as dashed lines, and the one standard deviation contour for each is marked with a bold black line.
Figure 7. Scatter plot of depolarization ratio, δ, as a function of lidar ratio, LR. Each of the four clusters is plotted as a different color, the boundaries as dashed lines, and the one standard deviation contour for each is marked with a bold black line.
Remotesensing 13 02512 g007
Remotesensing 13 02512 g008 550
Figure 8. Most common cluster in each of the lidar data spatial bins. The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 8. Most common cluster in each of the lidar data spatial bins. The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g008
Remotesensing 13 02512 g009 550
Figure 9. Binned chlorophyll concentration, C, calculated from Kd using Equation (1). The black line is the satellite-derived ice edge from the middle of the survey time.
Figure 9. Binned chlorophyll concentration, C, calculated from Kd using Equation (1). The black line is the satellite-derived ice edge from the middle of the survey time.
Remotesensing 13 02512 g009
Table
Table 1. Correlations between parameters calculated with/without data from cluster C4.
Table 1. Correlations between parameters calculated with/without data from cluster C4.
Ice FractionKdbbpδLR
Ice Fraction1
Kd−0.17/−0.211
bbp−0.06/−0.100.66/0.621
δ0.31/0.32−0.59/−0.58−0.39/−0.381
LR−0.08/−0.05−0.42/−0.44−0.52/−0.670.18/0.181
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Churnside, J.H.; Marchbanks, R.D.; Marshall, N. Airborne Lidar Observations of a Spring Phytoplankton Bloom in the Western Arctic Ocean. Remote Sens. 2021, 13, 2512. https://doi.org/10.3390/rs13132512

AMA Style

Churnside JH, Marchbanks RD, Marshall N. Airborne Lidar Observations of a Spring Phytoplankton Bloom in the Western Arctic Ocean. Remote Sensing. 2021; 13(13):2512. https://doi.org/10.3390/rs13132512

Chicago/Turabian Style

Churnside, James H., Richard D. Marchbanks, and Nathan Marshall. 2021. "Airborne Lidar Observations of a Spring Phytoplankton Bloom in the Western Arctic Ocean" Remote Sensing 13, no. 13: 2512. https://doi.org/10.3390/rs13132512

APA Style

Churnside, J. H., Marchbanks, R. D., & Marshall, N. (2021). Airborne Lidar Observations of a Spring Phytoplankton Bloom in the Western Arctic Ocean. Remote Sensing, 13(13), 2512. https://doi.org/10.3390/rs13132512

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop