Evaluation and Hydrological Application of a Data Fusing Method of Multi-Source Precipitation Products-A Case Study over Tuojiang River Basin
Abstract
:1. Introduction
2. Study Basin and Data Preparation
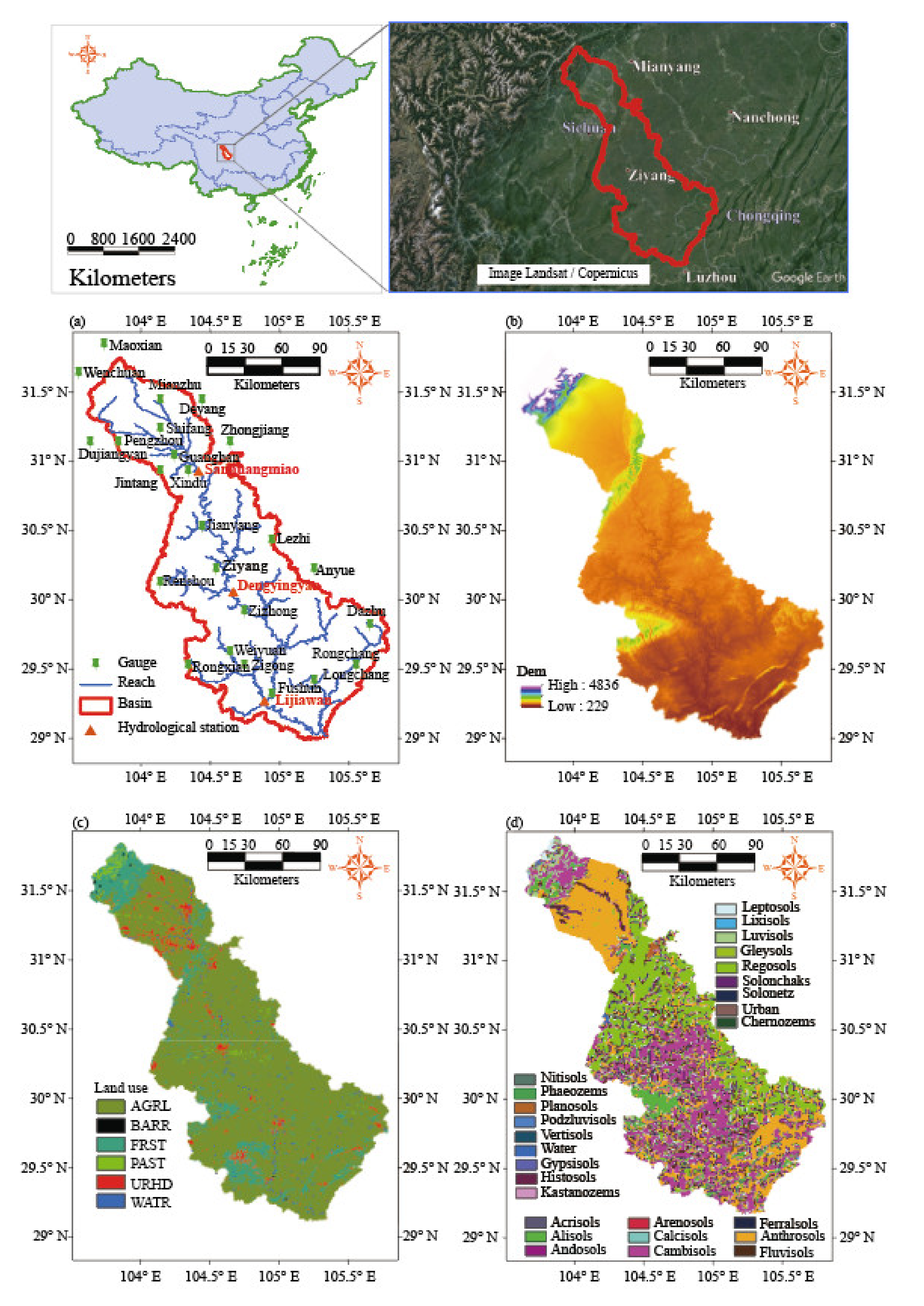
2.1. Study Basin
2.2. Precipitation Data and Other Data
3. Methodology
3.1. SWAT Model
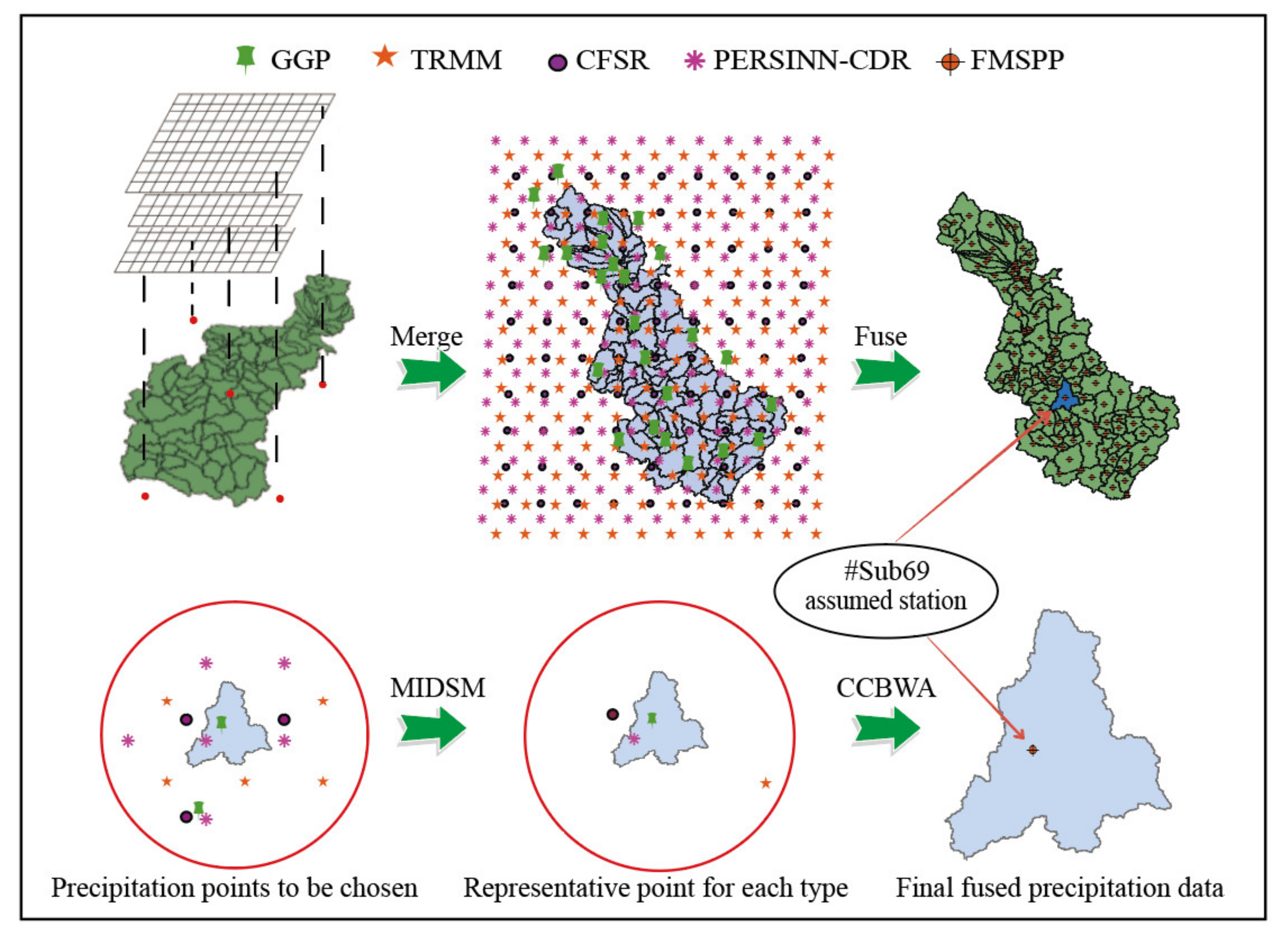
3.2. The Multi-Source Precipitation Fusing Method
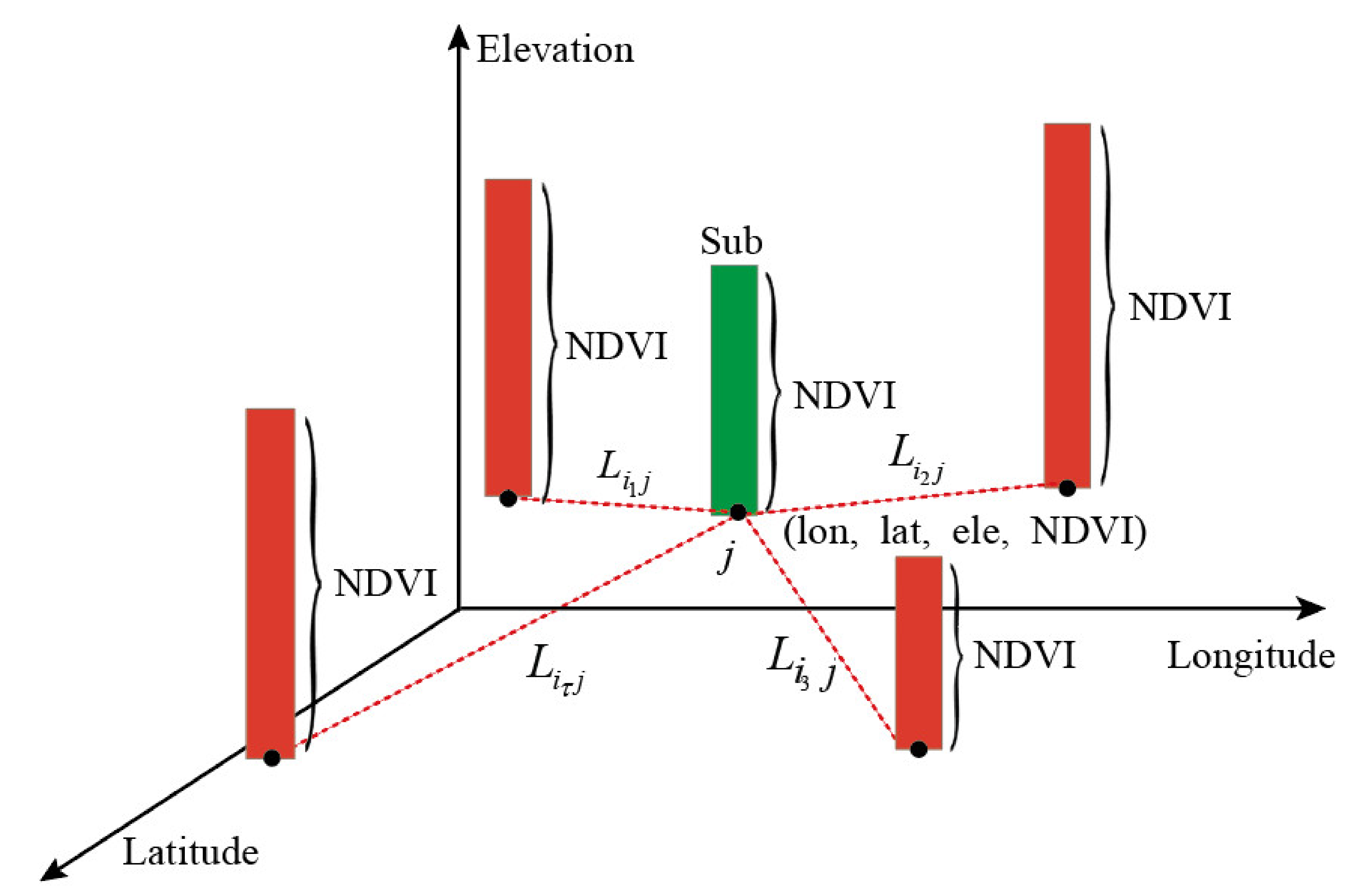
3.2.1. MIDSM
3.2.2. CCBWA
4. Result
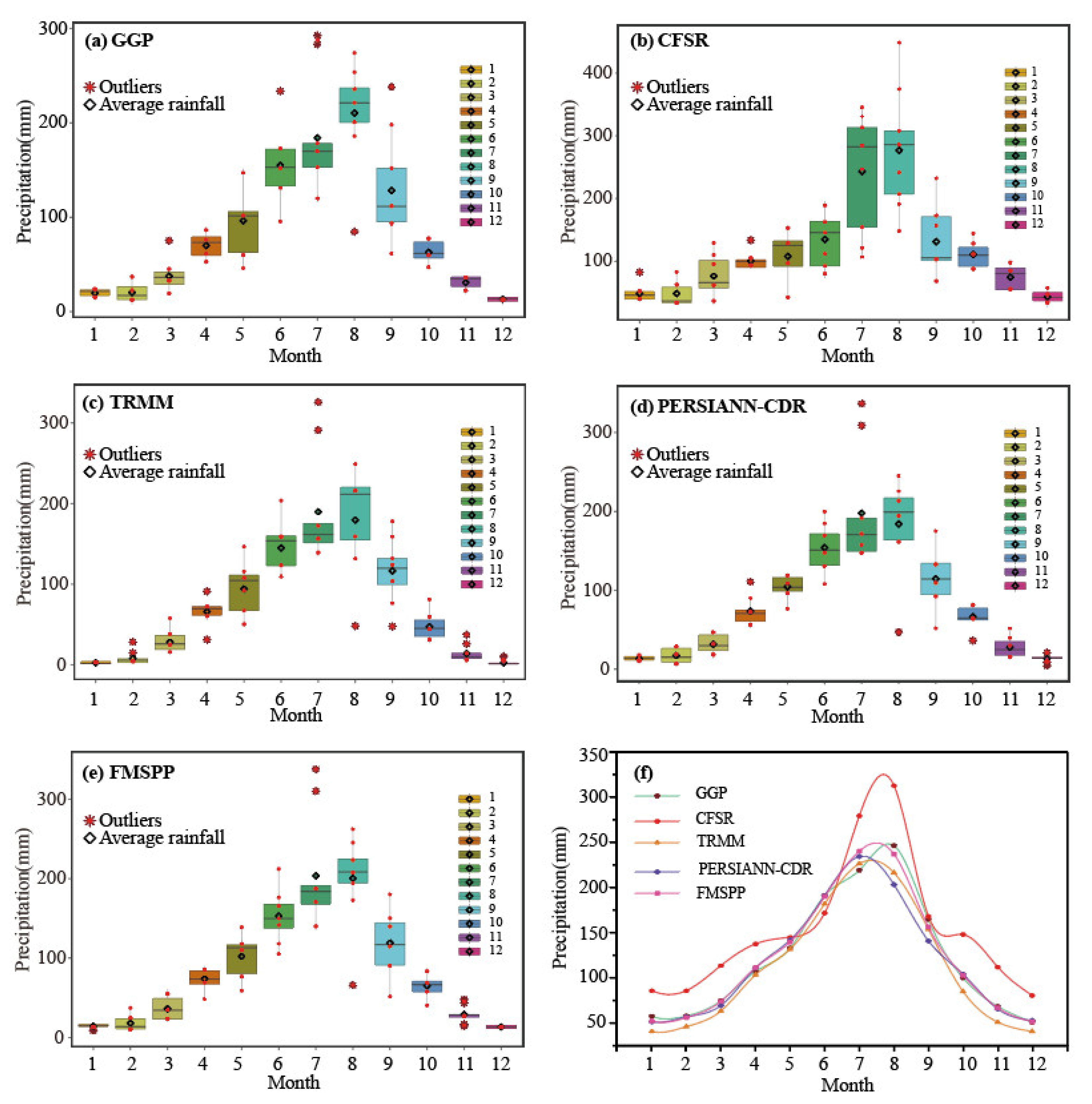
4.1. Temporal Evaluation of SPPs and FMSPP
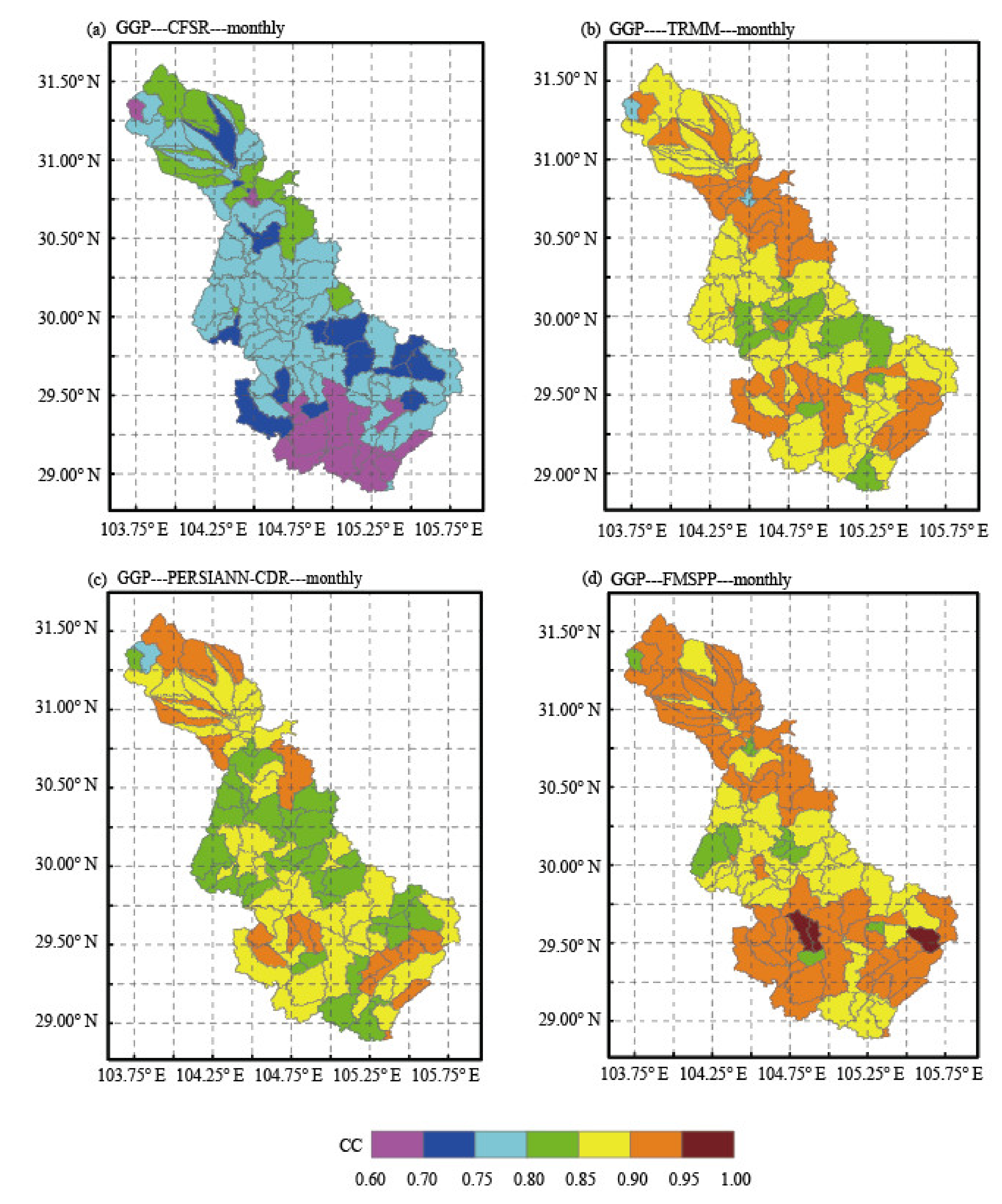
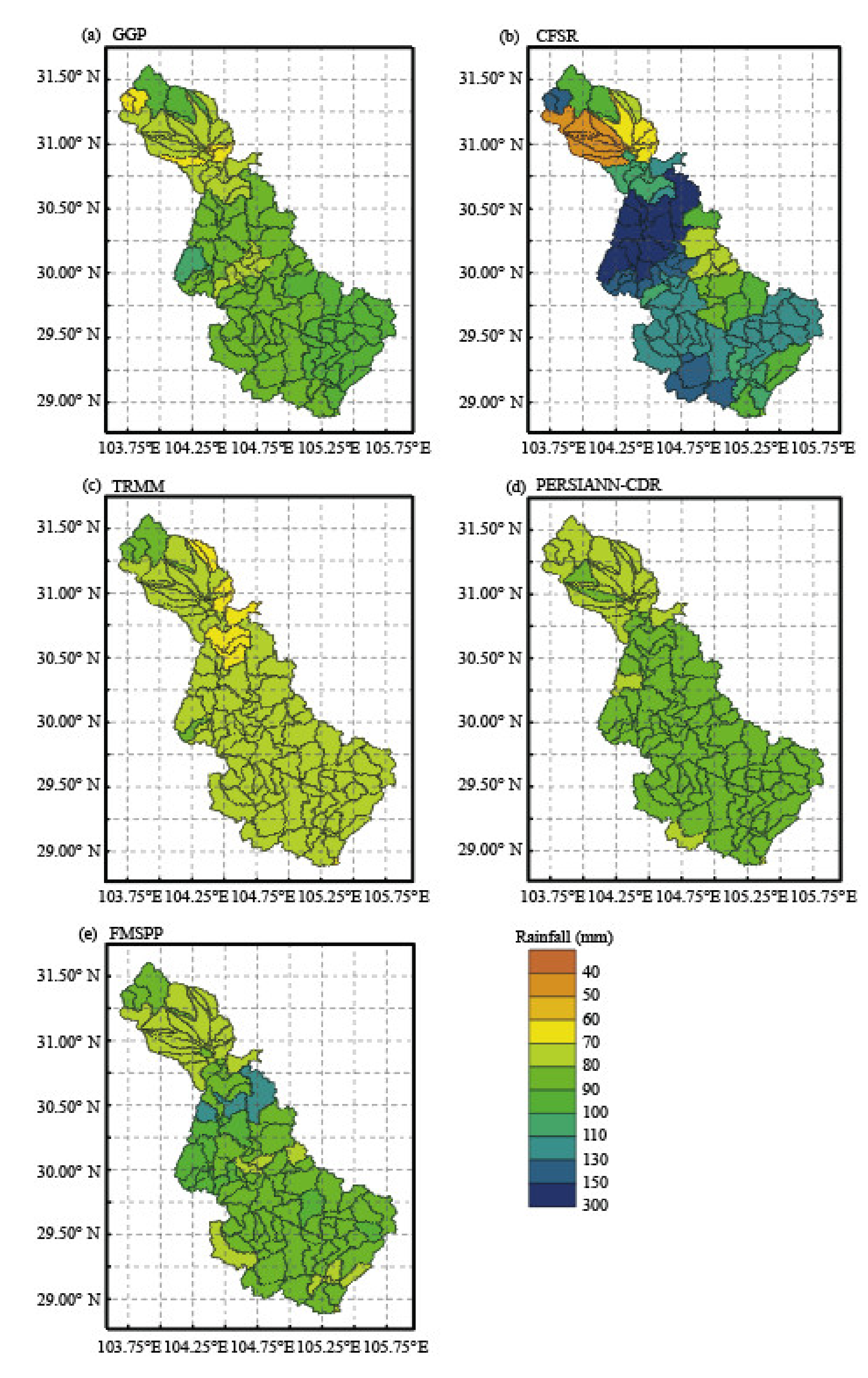
4.2. Spatial Evaluation of SPPs and FMSPP
4.3. Evaluation of the Hydrological Performance of Different Precipitation Products
4.3.1. Calibration and Validation
4.3.2. Performance Comparison of SWAT Model Forced by Different Precipitation Products
5. Discussion
6. Conclusions
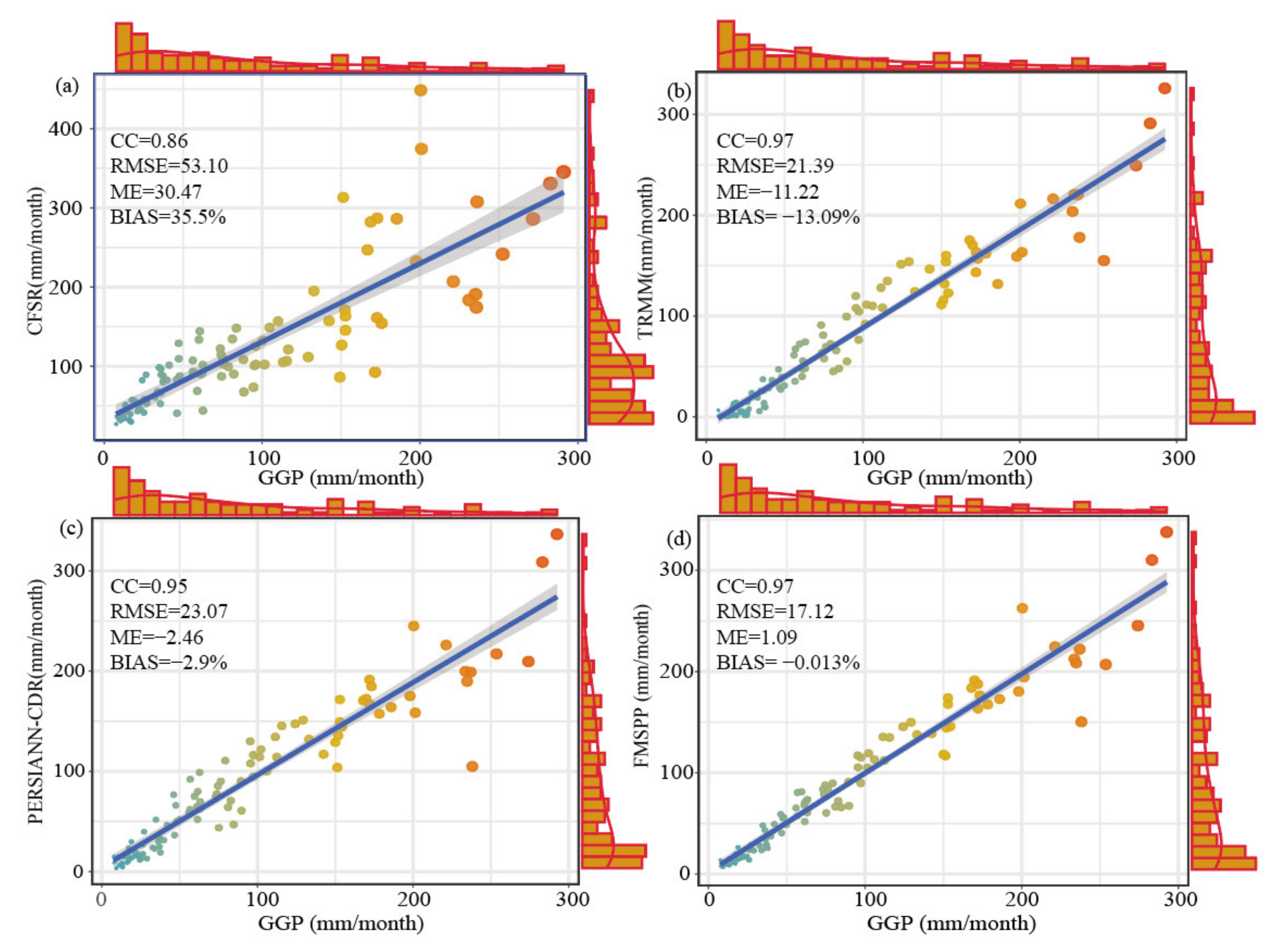
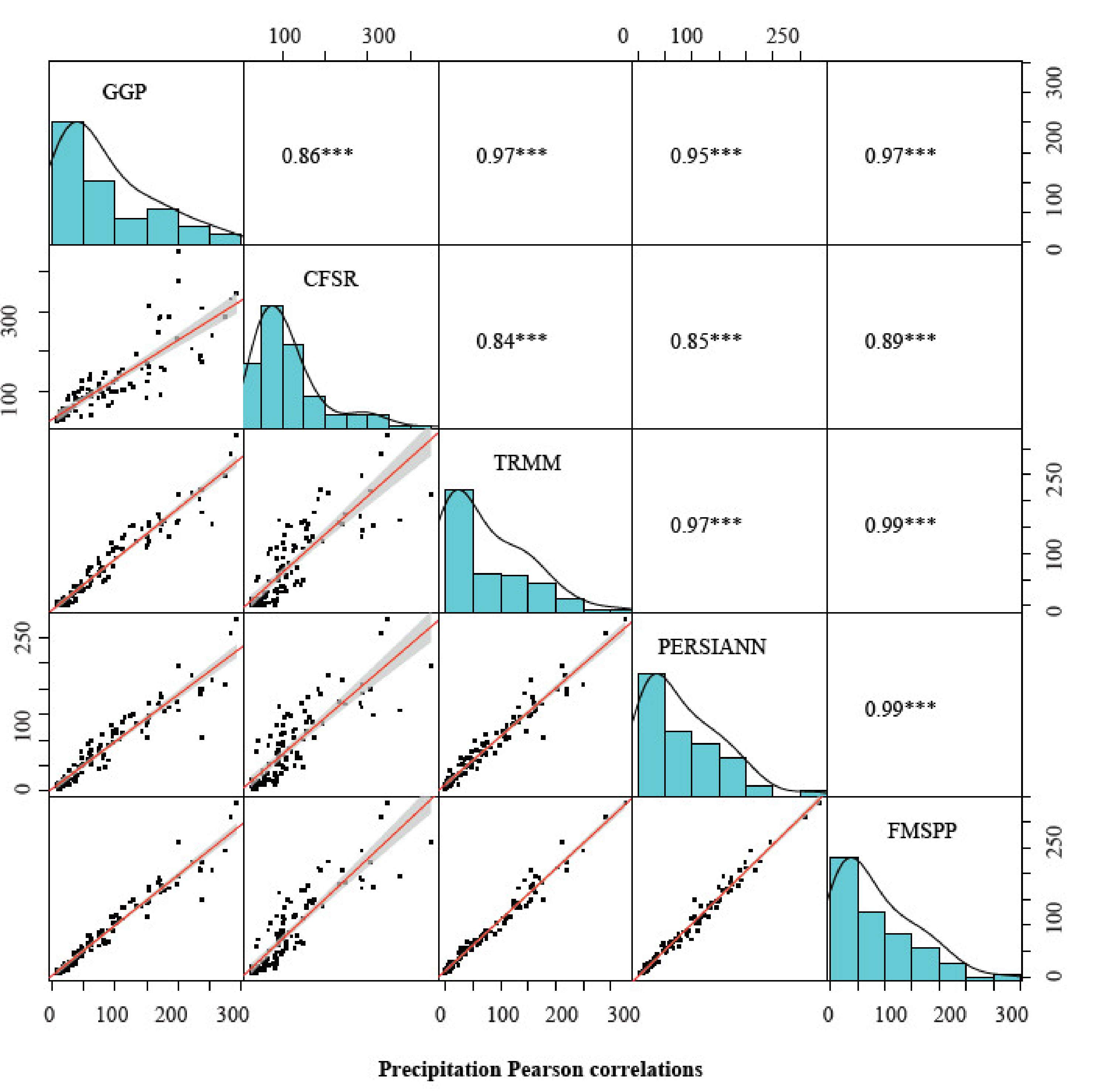
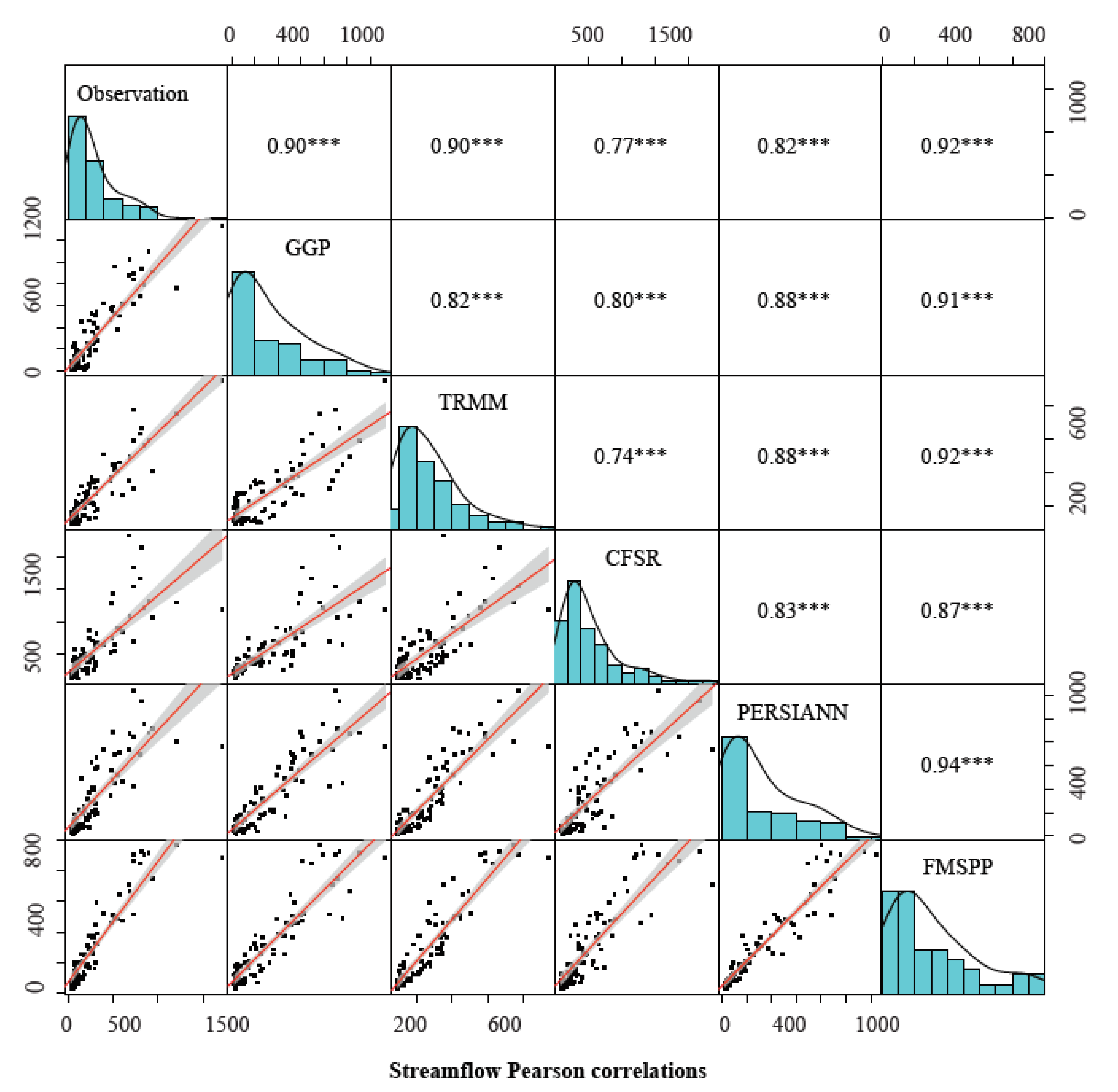
- FMSPP shows the maximum POD and minimum CSI, which proves that FMSPP can capture the occurrence of rainfall events very well. What is more, the absolute values of ME and BIAS for FMSPP are the smallest both on the daily and monthly scales over the watershed. Besides, the CC is significantly higher in most sub-basins on the monthly scale for FMSPP than the other three SPPs. Its CC changes in the range of 0.84–0.96. These results demonstrate that the performance of FMSPP is the best compared with the original SPPs.
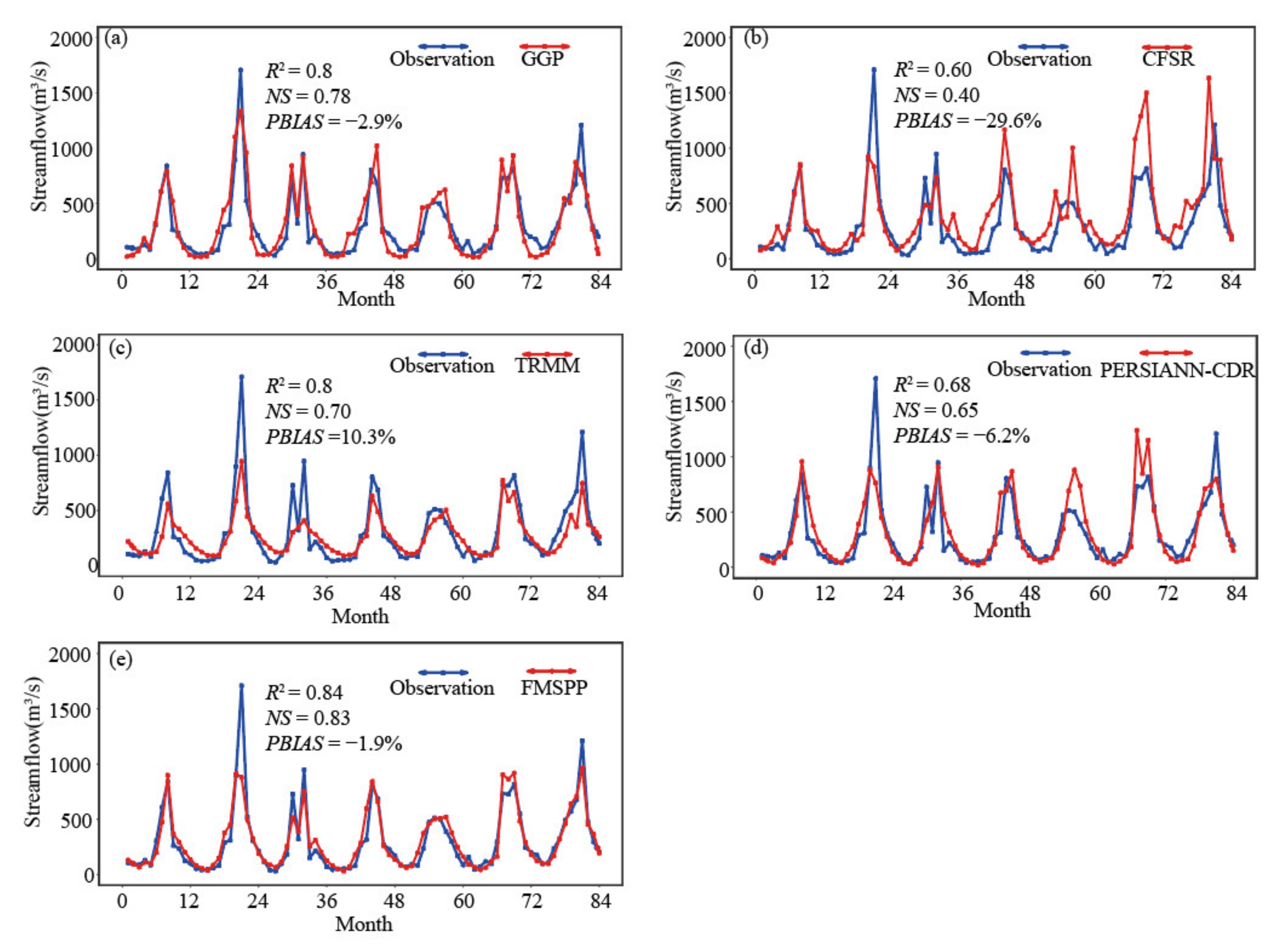
- Among the precipitation products, FMSPP shows the best simulation results, with R2 and NS both being the largest, which are 0.83 and 0.84, respectively. Moreover, its PBIAS is the smallest, at only −1.9%. The hydrological performance of GGP and TRMM is good, followed by PERSIANN-CDR, whereas CFSR is unsatisfactory.
- The proposed MIDSM-CCBWA fusion method dynamically integrates multi-source gauge-satellite precipitation over different sub-basins and forms the FMSPP, which can effectively reduce the bias induced by the random application of a single precipitation source and improve the general applicability for streamflow simulation in the data-sparse region.
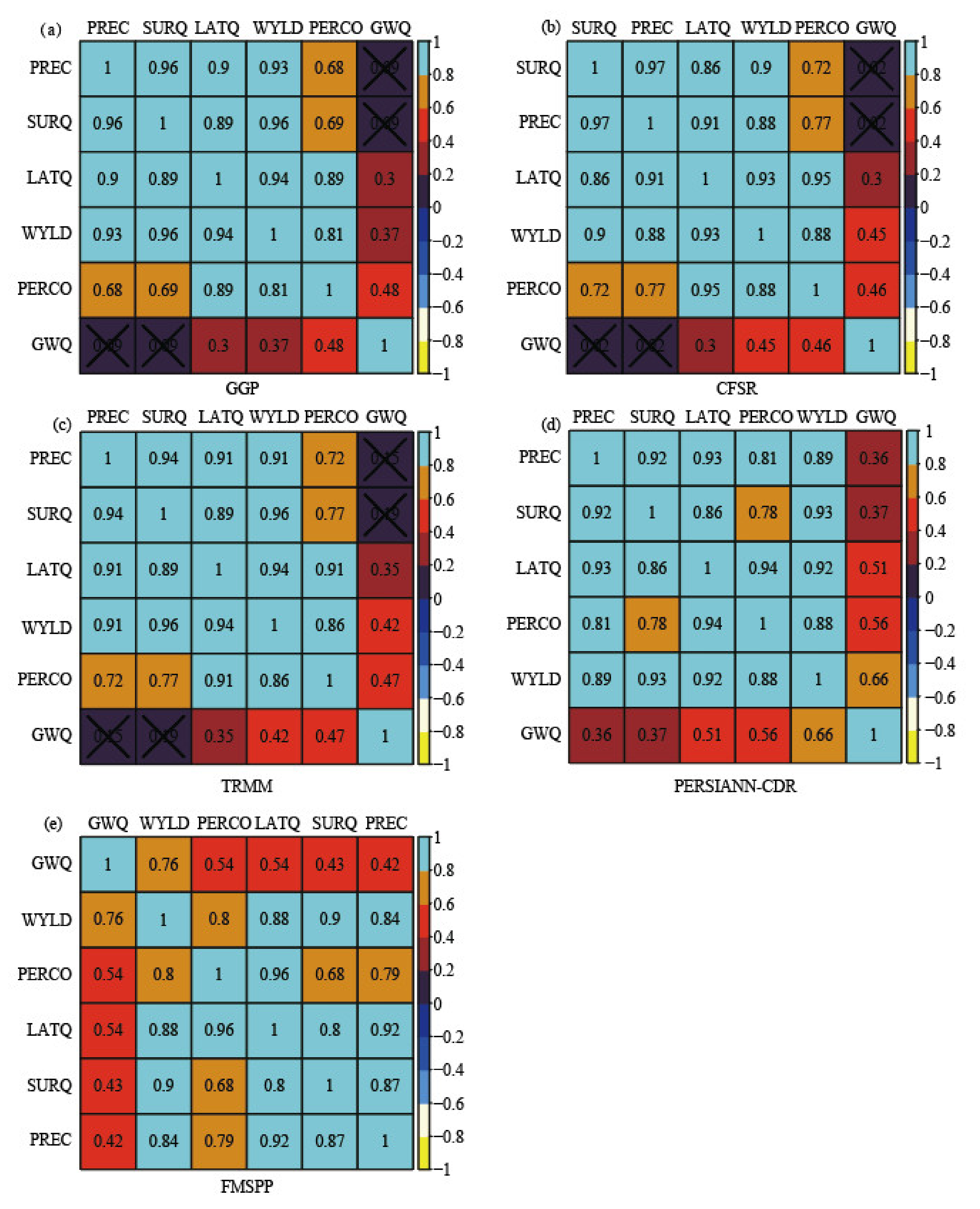
- FMSPP can preserve the characteristics of the precipitation source identified to perform well (e.g., GGP in the case study). It only has a relatively slight correlation with the precipitation source identified to perform worse (e.g., CFSR in this study).
- The rainfall deviation of SPPs from GGP over the mountainous areas on the northwest is higher than that of the southern plain, and the CC shows the opposite pattern in these areas. Thus, the satellite-based precipitation is generally more reliable in plain than in mountainous terrain for the study basin.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, N.; Zhang, K.; Hong, Y.; Zhao, Q.H.; Huang, Q.; Xu, Y.S.; Xue, X.W.; Chen, S. Evaluation of the TRMM multisatellite precipitation analysis and its applicability in supporting reservoir operation and water resources management in Hanjiang basin, China. J. Hydrol. 2017, 549, 313–325. [Google Scholar] [CrossRef]
- Hou, J.; Ye, A.; You, J.; Ma, F.; Duan, Q. An estimate of human and natural contributions to changes in water resources in the upper reaches of the Minjiang River. Sci. Total Environ. 2018, 635, 901–912. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xia, J.; She, D.X. Spatiotemporal variation and statistical characteristic of extreme precipitation in the middle reaches of the Yellow River Basin during 1960–2013. Theor. Appl. Climatol. 2018, 135, 391–408. [Google Scholar] [CrossRef]
- Xin, Z.H.; Li, Y.; Zhang, L.; Ding, W.; Ye, L.; Wu, J.; Zhang, C. Quantifying the relative contribution of climate and human impacts on seasonal streamflow. J. Hydrol. 2019, 574, 936–945. [Google Scholar] [CrossRef]
- Jeong, C.; Lee, T. Copula-based modeling and stochastic simulation of seasonal intermittent streamflows for arid regions. J. Hydro Environ. Res. 2015, 9, 604–613. [Google Scholar] [CrossRef]
- Lee, T. Multisite stochastic simulation of daily precipitation from copula modeling with a gamma marginal distribution. Theor. Appl. Climatol. 2017, 132, 1089–1098. [Google Scholar] [CrossRef]
- Parisouj, P.; Mohebzadeh, H.; Lee, T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J.; Freer, J.E.; Lamb, R. A history of TOPMODEL. Hydrol. Earth Syst. Sci. 2021, 25, 527–549. [Google Scholar] [CrossRef]
- Gou, J.; Miao, C.; Duan, Q.; Tang, Q.; Di, Z.; Liao, W.; Wu, J.; Zhou, R. Sensitivity Analysis-Based Automatic Parameter Calibration of the VIC Model for Streamflow Simulations over China. Water Resour. Res. 2020, 56, e2019WR025968. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.Y.; Xu, Z.G.; Wang, F.; He, H.; Zhou, J.H.; Wu, X.T.; Liu, Z.C. Hydrologic Evaluation of Multi-Source Satellite Precipitation Products for the Upper Huaihe River Basin, China. Remote Sens. 2018, 10, 840. [Google Scholar] [CrossRef] [Green Version]
- Hiep, N.H.; Luong, N.D.; Viet Nga, T.T.; Hieu, B.T.; Thuy Ha, U.T.; Du Duong, B.; Long, V.D.; Hossain, F.; Lee, H. Hydrological model using ground- and satellite-based data for river flow simulation towards supporting water resource management in the Red River Basin, Vietnam. J. Environ. Manag. 2018, 217, 346–355. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.L.; Li, Y.; Huang, Y.W.; Li, Y.C.; Hou, C.C.; Shi, X.L. Evaluation and hydrological application of satellite-based precipitation datasets in driving hydrological models over the Huifa river basin in Northeast China. Atmos. Res. 2018, 207, 28–41. [Google Scholar] [CrossRef]
- Chao, L.J.; Zhang, K.; Li, Z.J.; Zhu, Y.L.; Wang, J.F.; Yu, Z.B. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, Y.G.; Ji, X.; Luo, X.; Li, X. Evaluation and Hydrologic Validation of Three Satellite-Based Precipitation Products in the Upper Catchment of the Red River Basin, China. Remote Sens. 2018, 10, 1881. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.Q.; Ma, Y.Z.; Long, D.; Zhong, L.Z.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Cecinati, F.; Rico-Ramirez, M.A.; Heuvelink, G.B.M.; Han, D. Representing radar rainfall uncertainty with ensembles based on a time-variant geostatistical error modelling approach. J. Hydrol. 2017, 548, 391–405. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.Q.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.Q.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Blacutt, L.A.; Herdies, D.L.; de Gonçalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.M.; Yang, T.T.; Hsu, K.L.; Liu, C.M.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Xu, Y.P.; Gu, H.T.; Zhu, Q.; Sun, Z.L.; Xuan, W.D. Role of satellite and reanalysis precipitation products in streamflow and sediment modeling over a typical alpine and gorge region in Southwest China. Sci. Total Environ. 2019, 685, 934–950. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y.-P. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Rahman, K.; Shang, S.; Shahid, M.; Li, J. Developing an Ensemble Precipitation Algorithm from Satellite Products and Its Topographical and Seasonal Evaluations Over Pakistan. Remote Sens. 2018, 10, 1835. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Y.; Huang, J.F.; Sheng, S.X.; Mansaray, L.R.; Liu, Z.X.; Wu, H.Y.; Wang, X.Z. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Lu, B.B.; Yang, W.B.; Ge, Y.; Harris, P. Improvements to the calibration of a geographically weighted regression with parameter-specific distance metrics and bandwidths. Comput. Environ. Urban Syst. 2018, 71, 41–57. [Google Scholar] [CrossRef]
- Tang, G.Q.; Long, D.; Behrangi, A.; Wang, C.G.; Hong, Y. Exploring Deep Neural Networks to Retrieve Rain and Snow in High Latitudes Using Multisensor and Reanalysis Data. Water Resour. Res. 2018, 54, 8253–8278. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J.J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, X.; Xu, Y.-P.; Tian, Y. Merging multi-source precipitation products or merging their simulated hydrological flows to improve streamflow simulation. Hydrolog. Sci. J. 2019, 64, 910–920. [Google Scholar] [CrossRef]
- Wu, H.C.; Yang, Q.L.; Liu, J.M.; Wang, G.Q. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Yang, Y.; Han, Z.Y.; Tang, G.Q.; Maguire, L.; Chu, Z.G.; Hong, Y. Comprehensive evaluation of Ensemble Multi-Satellite Precipitation Dataset using the Dynamic Bayesian Model Averaging scheme over the Tibetan plateau. J. Hydrol. 2018, 556, 634–644. [Google Scholar] [CrossRef]
- Ur Rahman, K.; Shang, S.; Shahid, M.; Wen, Y. Hydrological evaluation of merged satellite precipitation datasets for streamflow simulation using SWAT: A case study of Potohar Plateau, Pakistan. J. Hydrol. 2020, 587, 125040. [Google Scholar] [CrossRef]
- Guan, X.X.; Zhang, J.Y.; Yang, Q.L.; Tang, X.P.; Liu, C.S.; Jin, J.L.; Liu, Y.; Bao, Z.X.; Wang, G.Q. Evaluation of Precipitation Products by Using Multiple Hydrological Models over the Upper Yellow River Basin, China. Remote Sens. 2020, 12, 4023. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Jeong, H.-G.; Ahn, J.-B.; Lee, J.; Shim, K.-M.; Jung, M.-P. Improvement of daily precipitation estimations using PRISM with inverse-distance weighting. Theor. Appl. Climato. 2019, 139, 923–934. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.G.; Wu, C.Y.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Iwasaki, H. NDVI prediction over mongolian grassland using GSMAP precipitation data and JRA-25/JCDAS temperature data. J. Arid Environ. 2009, 73, 557–562. [Google Scholar] [CrossRef]
- Bao, Z.X.; Zhang, J.Y.; Wang, G.Q.; Guan, T.S.; Jin, J.L.; Liu, Y.L.; Li, M.; Ma, T. The sensitivity of vegetation cover to climate change in multiple climatic zones using machine learning algorithms. Ecol. Indic. 2021, 124, 107443. [Google Scholar] [CrossRef]
- Pang, J.; Zhang, H.; Xu, Q.; Wang, Y.; Wang, Y.; Zhang, O.; Hao, J. Hydrological evaluation of open-access precipitation data using SWAT at multiple temporal and spatial scales. Hydrol. Earth Syst. Sci. 2020, 24, 3603–3626. [Google Scholar] [CrossRef]
- Shukla, K.; Kumar, P.; Mann, G.S.; Khare, M. Mapping spatial distribution of particulate matter using Kriging and Inverse Distance Weighting at supersites of megacity Delhi. Sustain. Cities. Soc. 2020, 54. [Google Scholar] [CrossRef]
- Tang, X.P.; Zhang, J.Y.; Gao, C.; Ruben, G.; Wang, G.Q. Assessing the Uncertainties of Four Precipitation Products for Swat Modeling in Mekong River Basin. Remote Sens. 2019, 11, 304. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xia, J.; She, D.X.; Li, L.C.; Wang, Q.; Zou, L. Evaluation of Six Satellite-Based Precipitation Products and Their Ability for Capturing Characteristics of Extreme Precipitation Events over a Climate Transition Area in China. Remote Sens. 2019, 11, 1477. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.W.; Duan, Q.Y.; Gong, W.; Gan, Y.J.; Di, Z.H.; Wang, C.; Miao, S.G. An Objective Approach to Generating Multi-Physics Ensemble Precipitation Forecasts Based on the WRF Model. J. Meteorol. Res. 2020, 34, 601–620. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Duan, Z.; Tuo, Y.; Liu, J.; Gao, H.; Song, X.; Zhang, Z.; Yang, L.; Mekonnen, D.F. Hydrological evaluation of open-access precipitation and air temperature datasets using SWAT in a poorly gauged basin in Ethiopia. J. Hydrol. 2019, 569, 612–626. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, K.K.; Derin, Y. Evaluation of Multiple Satellite-Based Precipitation Products over Complex Topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.D.; Peters-Lidard, C.D. A global map of uncertainties in satellite-based precipitation measurements. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Solano-Rivera, V.; Geris, J.; Granados-Bolaños, S.; Brenes-Cambronero, L.; Artavia-Rodríguez, G.; Sánchez-Murillo, R.; Birkel, C. Exploring extreme rainfall impacts on flow and turbidity dynamics in a steep, pristine and tropical volcanic catchment. Catena 2019, 182, 104118. [Google Scholar] [CrossRef]





| Name | Latitude (°N) | Longitude (°E) | Elevation (m) | Annual Precipitation (mm) |
|---|---|---|---|---|
| Maoxian | 31.7 | 103.8 | 1590.1 | 633.5 |
| Wenchuan | 31.5 | 103.6 | 1370.1 | 632.0 |
| Mianzhu | 31.3 | 104.2 | 589.0 | 1181.7 |
| Dujiangyan | 31.0 | 103.7 | 698.5 | 1351.2 |
| Pengzhou | 31.0 | 103.9 | 581.7 | 1017.9 |
| Shifang | 31.1 | 104.2 | 535.7 | 1049.3 |
| Deyang | 31.3 | 104.5 | 525.7 | 966.2 |
| Zhongjiang | 31.0 | 104.7 | 423.5 | 985.0 |
| Xindu | 30.8 | 104.2 | 514.5 | 966.0 |
| Guanghan | 30.9 | 104.3 | 469.0 | 913.7 |
| Jianyang | 30.4 | 104.5 | 448.5 | 939.7 |
| Jintang | 30.8 | 104.4 | 493.5 | 957.0 |
| Renshou | 30.0 | 104.2 | 436.5 | 1070.5 |
| Ziyang | 30.1 | 104.6 | 417.0 | 1025.2 |
| Zizhong | 29.8 | 104.8 | 369.4 | 1161.6 |
| Rongxian | 29.4 | 104.4 | 384.1 | 1126.1 |
| Weiyuan | 29.5 | 104.7 | 351.1 | 1083.2 |
| Zigong | 29.4 | 104.8 | 352.6 | 1162.3 |
| Fushun | 29.2 | 105.0 | 306.2 | 1150.4 |
| Lezhi | 30.3 | 105.5 | 462.6 | 1108.5 |
| Anyue | 30.1 | 105.3 | 383.6 | 1182.3 |
| Dazu | 29.7 | 105.7 | 394.7 | 1178.4 |
| Rongchang | 29.4 | 105.6 | 338.0 | 1220.5 |
| Longchang | 29.3 | 105.3 | 385.7 | 1180.2 |
| Dataset | Data Type | Spatial Resolution | Time Resolution | Period | Data Source |
|---|---|---|---|---|---|
| CFSR | Reanalysis | 0.25 × 0.25 | Daily | 1979–2014 | https://globalweather.tamu.edu/ (accessed on 3 July 2021) |
| TRMM | Satellite | 0.25 × 0.25 | Daily | 1998–2019 | https://disc.gsfc.nasa.gov/datasets?keywords=TMPA&page=1 (accessed on 3 July 2021) |
| PERSIANN-CDR | Satellite | 0.33 × 0.33 | Daily | 1983–2019 | https://chrsdata.eng.uci.edu/ (accessed on 3 July 2021) |
| GGP | in-situ measurement | 24 stations | Daily | 1978–2019 | http://data.cma.cn/ (accessed on 3 July 2021) |
| Hydrometric Station | Drainage Area (km2) | Annual Average Streamflow (m3/s) |
|---|---|---|
| Sanhuangmiao | 6590 | 230.9 |
| Dengyinyan | 14,484 | 286.7 |
| Lijiawan | 23,283 | 397.8 |
| Data Type | Spatial Resolution | Period | Data Source |
|---|---|---|---|
| Soil | 1 km | 1997 | http://www.fao.org/soils-portal/en/ (accessed on 3 July 2021) |
| Land Use | 1 km | 2005 | http://www.resdc.cn/Default.aspx (accessed on 3 July 2021) |
| DEM | 90 m | 2000 | https://portal.opentopography.org/datasets (accessed on 3 July 2021) |
| NDVI | 1 km | 1998–2008 | http://www.resdc.cn/Default.aspx (accessed on 3 July 2021) |
| Precipitation Product | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|
| CFSR | 0.72 | 4.44 | 1.02 | 35.6 | 0.92 | 0.17 | 0.83 |
| TRMM | 0.37 | 6.43 | −0.35 | −13.09 | 0.58 | 0.15 | 0.85 |
| PERSIANN-CDR | 0.36 | 6.41 | −0.06 | −2.9 | 0.68 | 0.23 | 0.77 |
| FMSPP | 0.57 | 4.92 | −0.0004 | −0.013 | 0.92 | 0.17 | 0.83 |
| Precipitation Product | CC | RMSE (mm) | ME (mm) | BIAS (%) |
|---|---|---|---|---|
| CFSR | 0.86 | 53.10 | 31.47 | 35.5 |
| TRMM | 0.97 | 21.39 | −11.56 | −13.09 |
| PERSIANN-CDR | 0.95 | 23.07 | −2.46 | −2.9 |
| FMSPP | 0.97 | 17.12 | −0.011 | −0.013 |
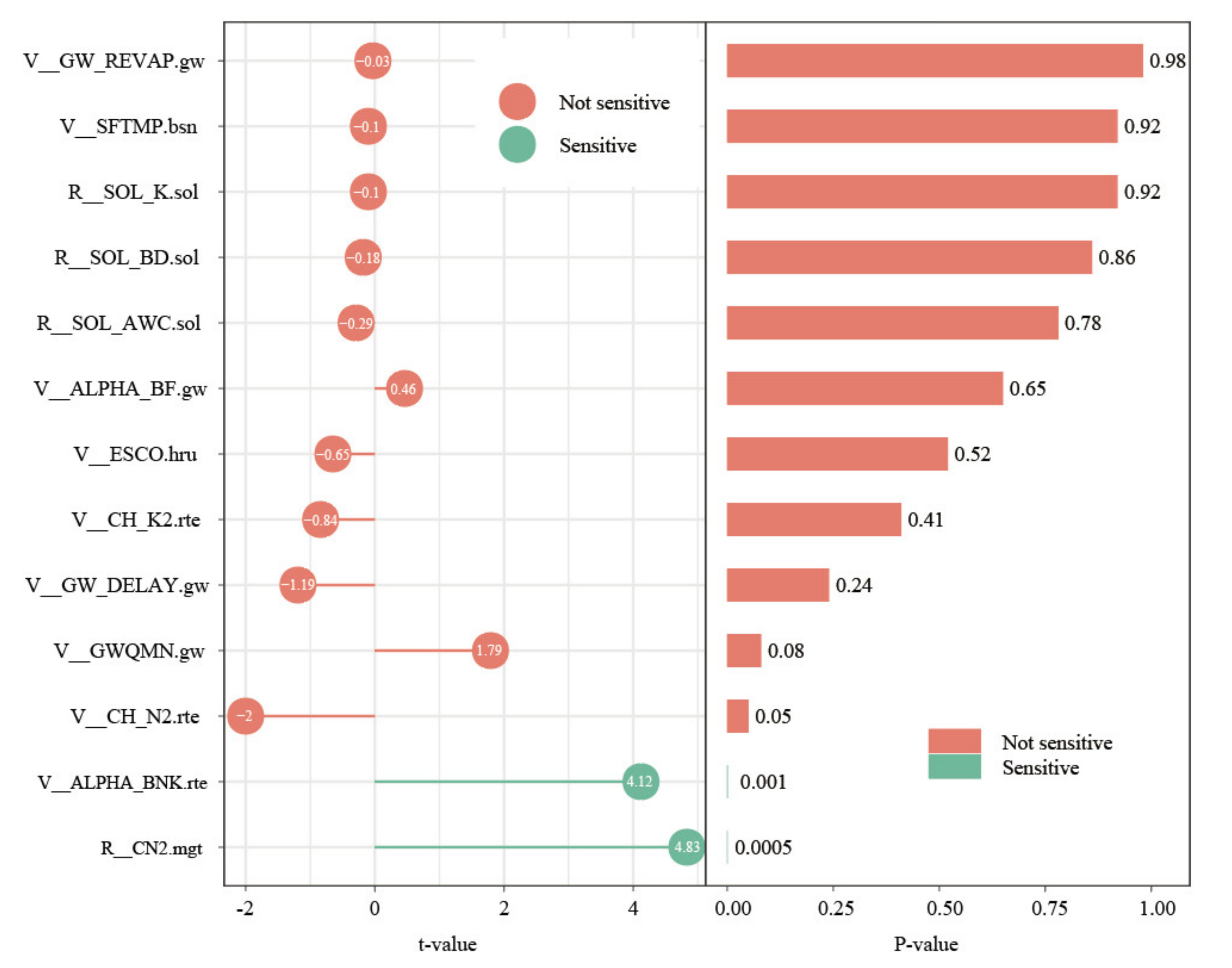
| Parameter Name | Rank | t-Value | t-Value | Fitting Value | Min Value | Max Value |
|---|---|---|---|---|---|---|
| R__CN2.mgt | 1 | 4.83 | 0.0005 | 0.18 | −0.2 | 0.2 |
| V__ALPHA_BNK.rte | 2 | 4.12 | 0.001 | 0.33 | 0 | 1 |
| V__CH_N2.rte | 3 | −2 | 0.05 | 0.09 | 0 | 0.3 |
| V__GWQMN.gw | 4 | 1.79 | 0.08 | 0.86 | 0 | 2 |
| V__GW_DELAY.gw | 5 | −1.19 | 0.24 | 210.6 | 30 | 450 |
| V__CH_K2.rte | 6 | −0.84 | 0.41 | 56.25 | 5 | 130 |
| V__ESCO.hru | 7 | −0.65 | 0.52 | 0.85 | 0.8 | 1 |
| V__ALPHA_BF.gw | 8 | 0.46 | 0.65 | 0.71 | 0 | 1 |
| R__SOL_AWC.sol | 9 | −0.29 | 0.78 | 0.14 | −0.2 | 0.4 |
| R__SOL_BD.sol | 10 | −0.18 | 0.86 | −0.45 | −0.5 | 0.6 |
| R__SOL_K.sol | 11 | −0.1 | 0.92 | 0.3 | −0.8 | 0.8 |
| V__SFTMP.bsn | 12 | −0.1 | 0.92 | 0.7 | −5 | 5 |
| V__GW_REVAP.gw | 13 | −0.03 | 0.98 | 0.01 | 0 | 2 |
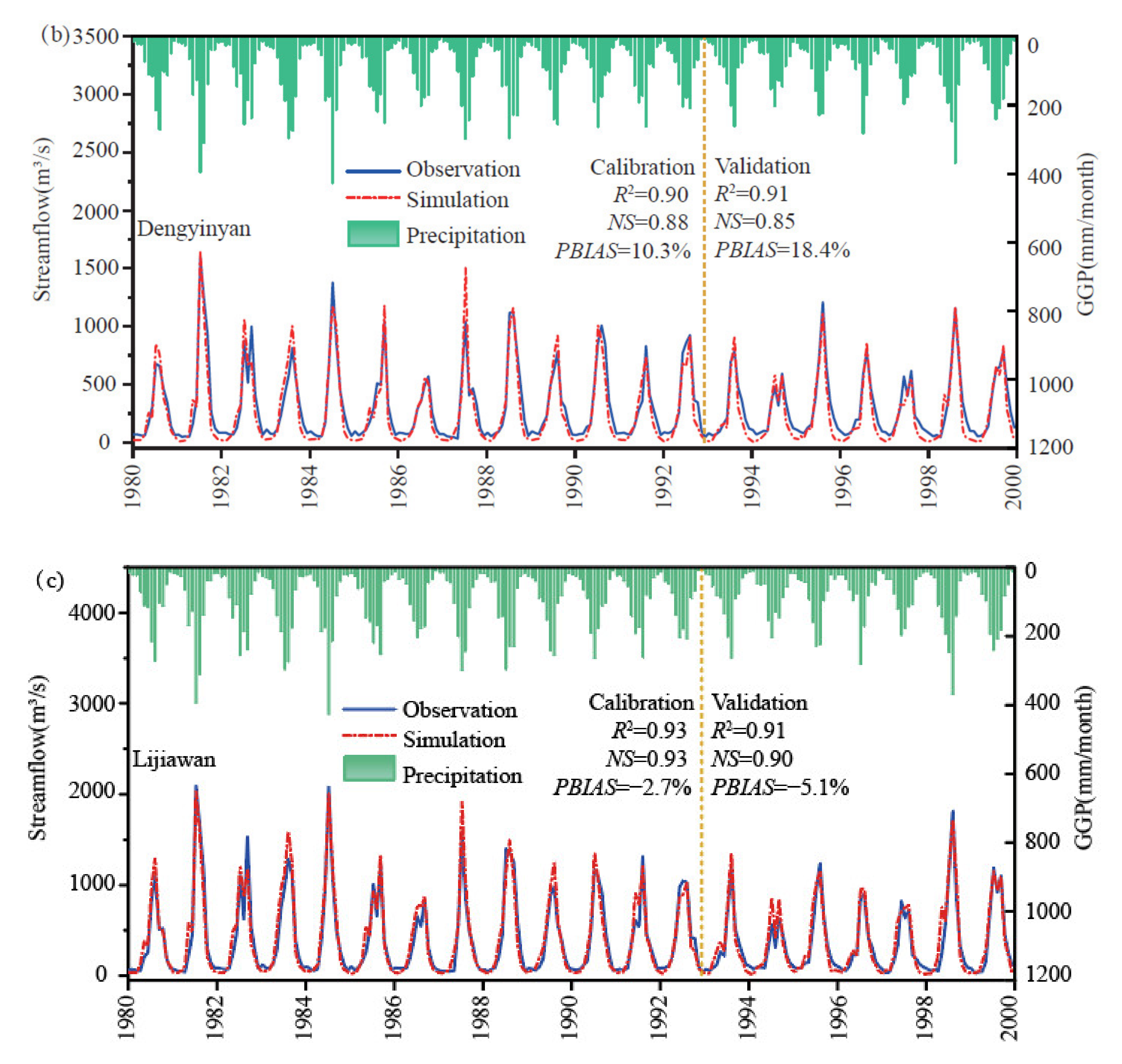
| Index | Station | Calibration | Validation |
|---|---|---|---|
| R2 | Sanhuangmiao | 0.84 | 0.85 |
| Dengyinyan | 0.90 | 0.91 | |
| Lijiawan | 0.93 | 0.91 | |
| NS | Sanhuangmiao | 073 | 0.73 |
| Dengyinyan | 0.88 | 0.85 | |
| Lijiawan | 0.93 | 0.90 | |
| PBIAS (%) | Sanhuangmiao | 12.6 | 19.1 |
| Dengyinyan | 10.3 | 18.4 | |
| Lijiawan | −2.7 | −5.1 |
| Precipitation Product | Evaluation Index | ||
|---|---|---|---|
| R2 | NS | PBIAS (%) | |
| GGP | 0.80 | 0.78 | −2.9 |
| CFSR | 0.60 | 0.40 | −29.6 |
| TRMM | 0.80 | 0.70 | 10.3 |
| PERSIANN-CDR | 0.68 | 0.65 | −6.2 |
| FMSPP | 0.84 | 0.83 | −1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, W.; Wang, G.; Yu, S. Evaluation and Hydrological Application of a Data Fusing Method of Multi-Source Precipitation Products-A Case Study over Tuojiang River Basin. Remote Sens. 2021, 13, 2630. https://doi.org/10.3390/rs13132630
Li Y, Wang W, Wang G, Yu S. Evaluation and Hydrological Application of a Data Fusing Method of Multi-Source Precipitation Products-A Case Study over Tuojiang River Basin. Remote Sensing. 2021; 13(13):2630. https://doi.org/10.3390/rs13132630
Chicago/Turabian StyleLi, Yao, Wensheng Wang, Guoqing Wang, and Siyi Yu. 2021. "Evaluation and Hydrological Application of a Data Fusing Method of Multi-Source Precipitation Products-A Case Study over Tuojiang River Basin" Remote Sensing 13, no. 13: 2630. https://doi.org/10.3390/rs13132630
APA StyleLi, Y., Wang, W., Wang, G., & Yu, S. (2021). Evaluation and Hydrological Application of a Data Fusing Method of Multi-Source Precipitation Products-A Case Study over Tuojiang River Basin. Remote Sensing, 13(13), 2630. https://doi.org/10.3390/rs13132630







