Inversion of Geothermal Heat Flux under the Ice Sheet of Princess Elizabeth Land, East Antarctica
Abstract
:1. Introduction
2. Materials and Methods
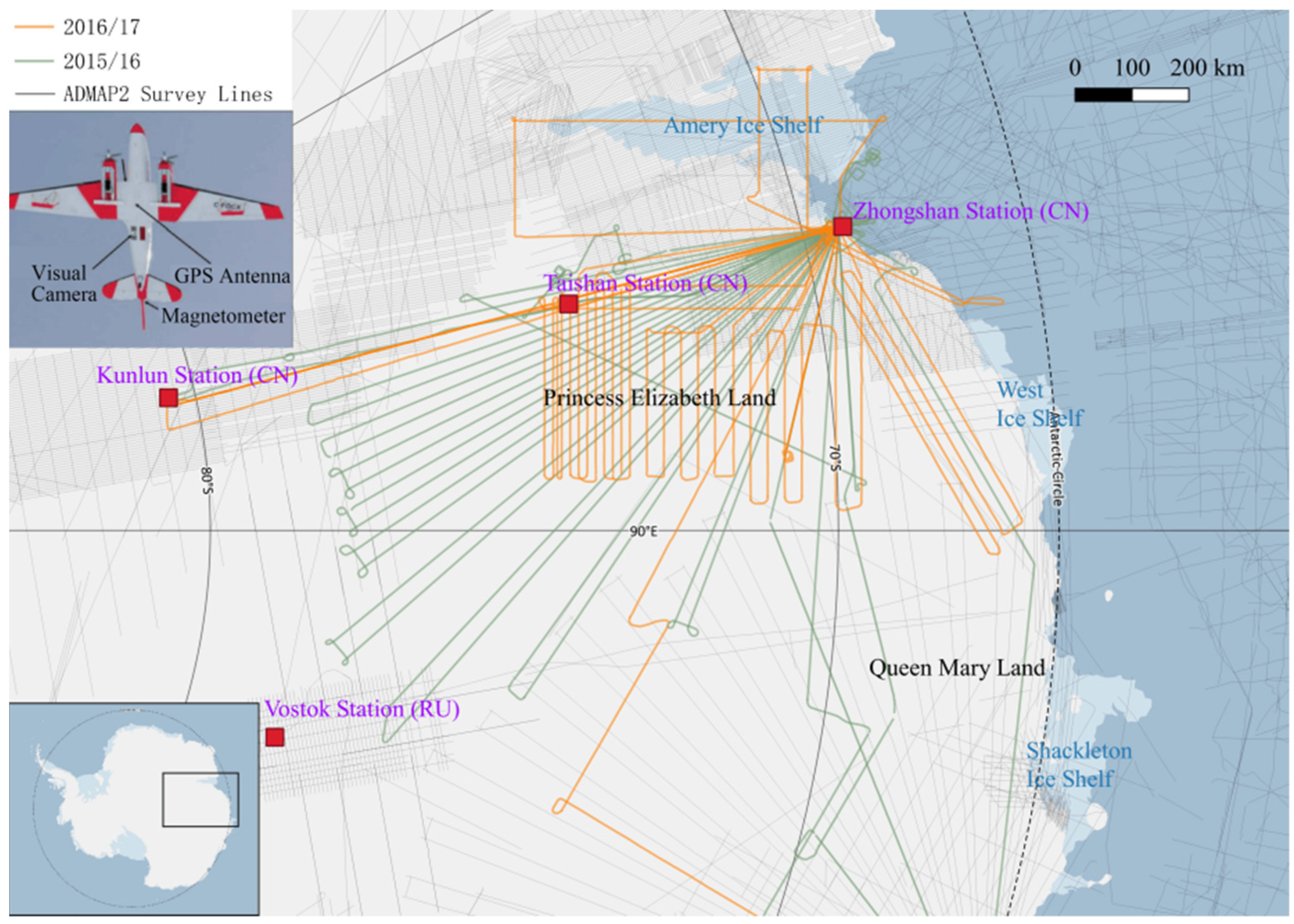
2.1. Aeromagnetic Data
2.2. Inversion Method
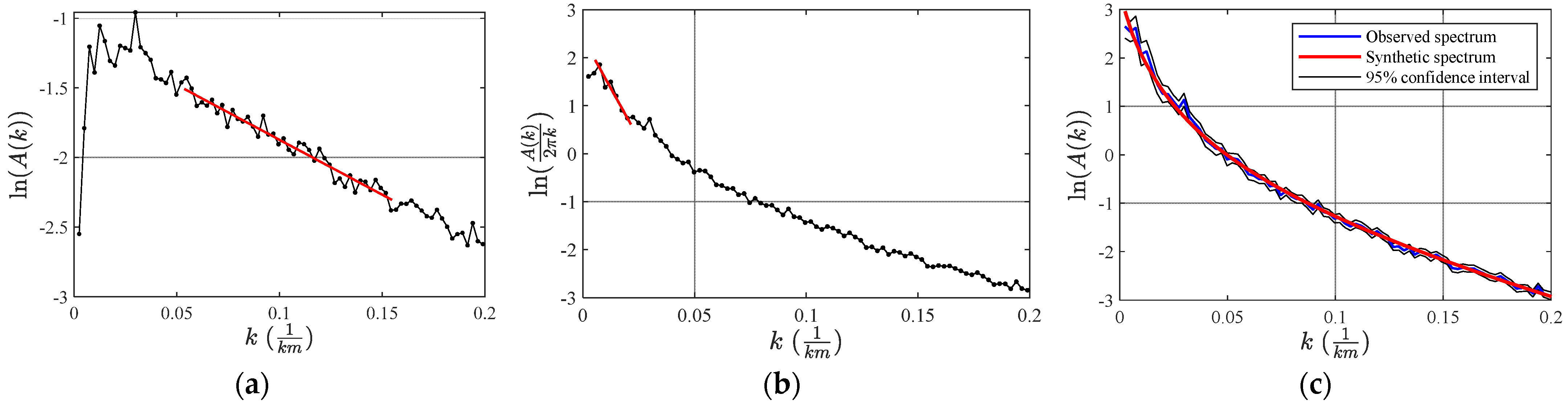
2.2.1. Using Modified Centroid Method to Invert the Curie Depth
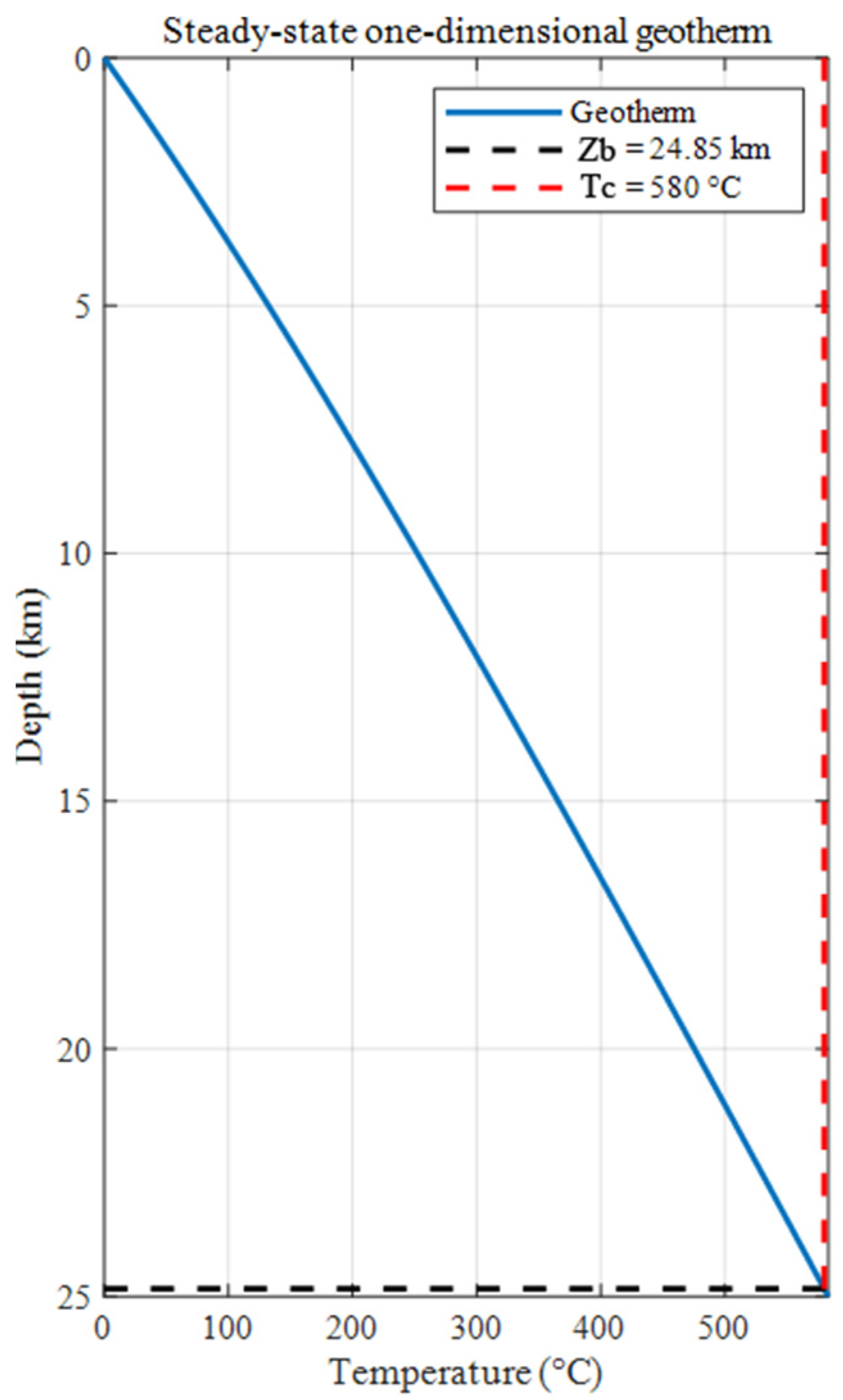
2.2.2. Calculating the Geothermal Heat Flux Based on Curie Depth
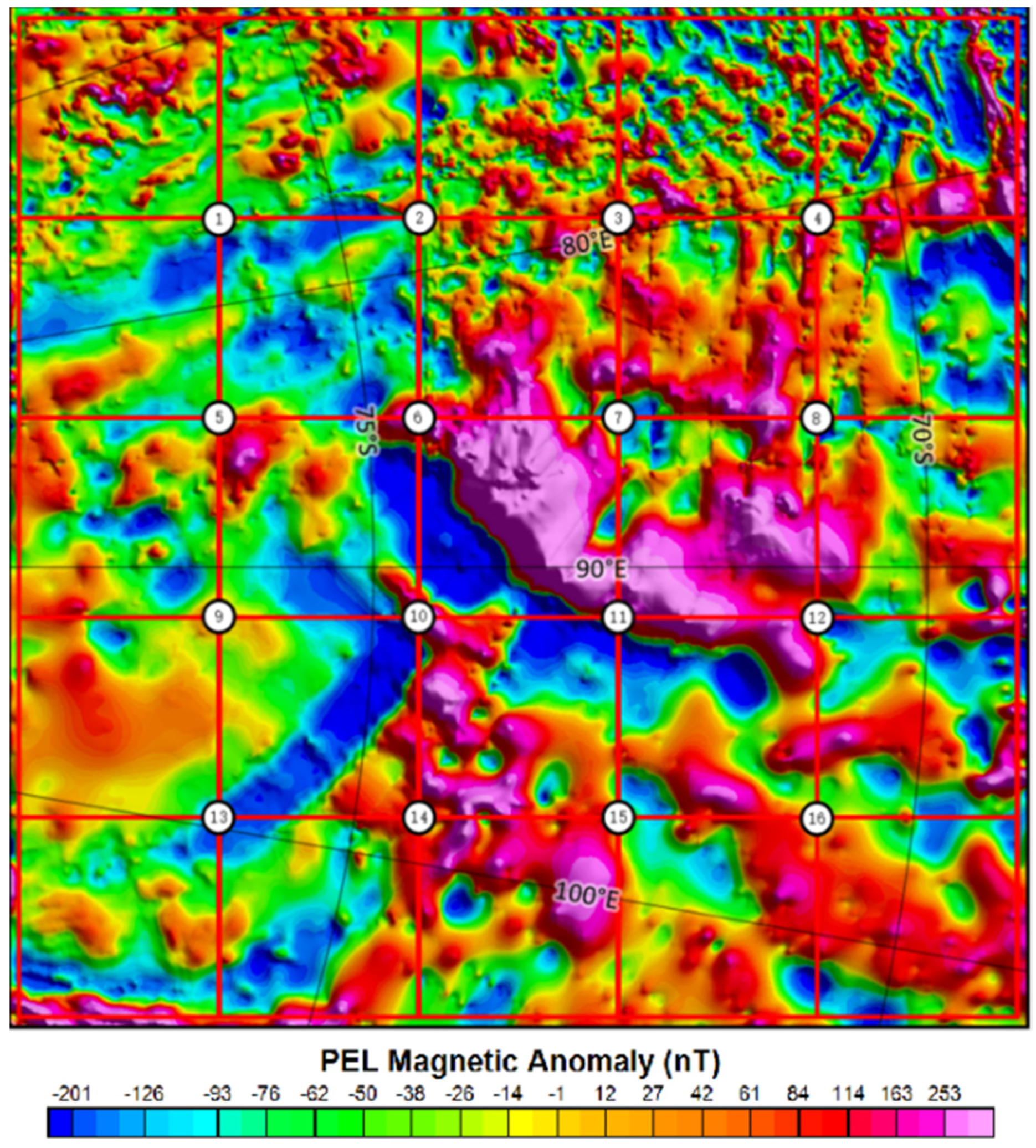
3. Results
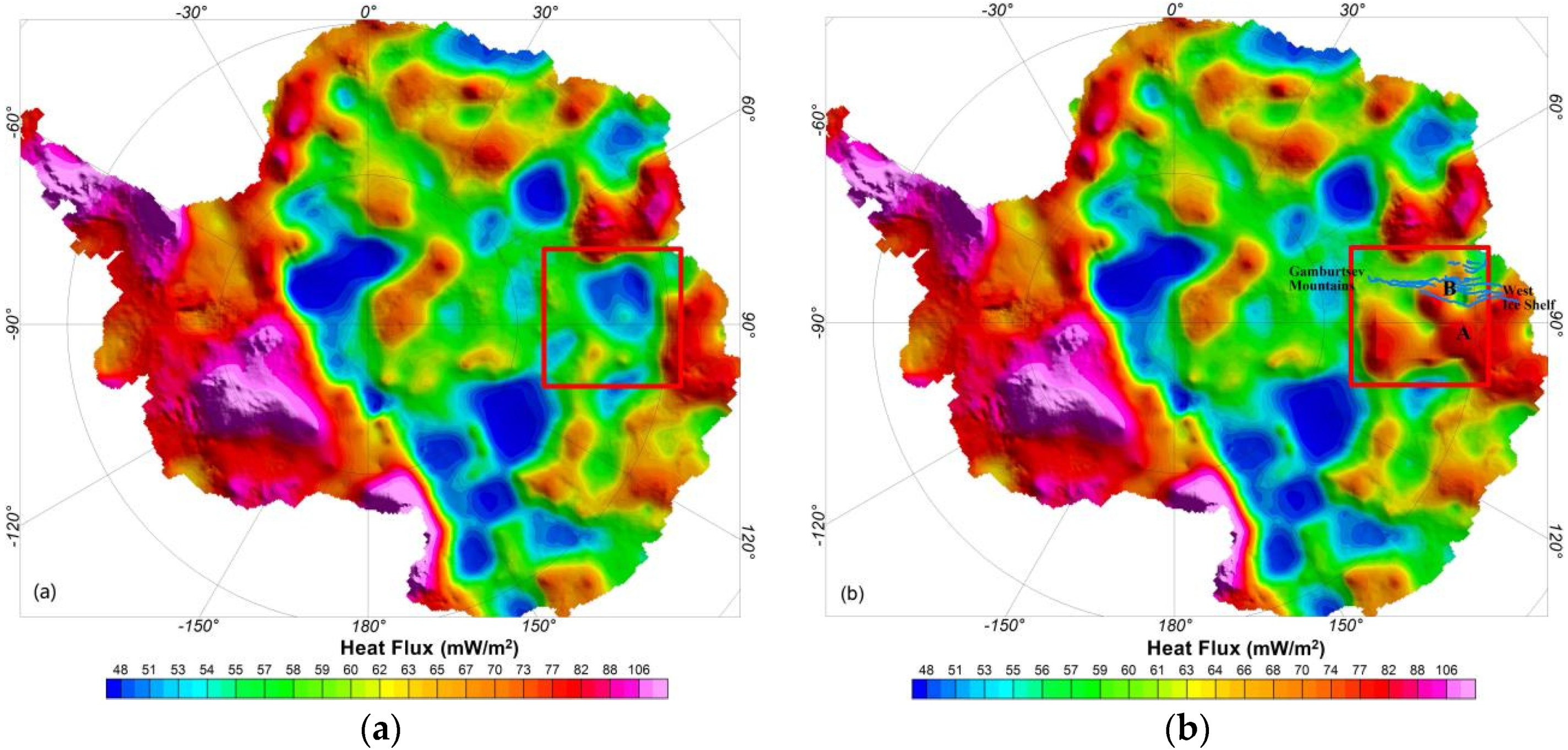
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martos, Y.M.; Catalán, M.; Jordan, T.A.; Golynsky, A.; Golynsky, D.; Eagles, G.; Vaughan, D.G. Heat Flux Distribution of Antarctica Unveiled. Geophys. Res. Lett. 2017, 44, 11417–11426. [Google Scholar] [CrossRef] [Green Version]
- Burton-Johnson, A.; Dziadek, R.; Martin, C.; Halpin, J.; Whitehouse, P.L.; Ebbing, J.; Martos, Y.M.; Martin, A.; Schroeder, D.; Shen, W.; et al. Antarctic Geothermal Heat Flow: Future Research Directions; EPIC3SCAR-SERCE White Paper; Scientific Committee on Antarctic Research (SCAR): Paris, France, 2020; Volume 2006, pp. 1–9. [Google Scholar]
- Llubes, M.; Lanseau, C.; Rémy, F. Relations between basal condition, sub-glacial hydrological networks and geothermal flux in Antarctica. Earth Planet. Sci. Lett. 2006, 241, 655–662. [Google Scholar] [CrossRef]
- Risk, G.F.; Hochstein, M.P. Heat flow at arrival heights, Ross Island, Antarctica. N. Z. J. Geol. Geophys. 1974, 17, 629–644. [Google Scholar] [CrossRef]
- Morin, R.H.; Williams, T.; Henrys, S.A.; Magens, D.; Niessen, F.; Hansaraj, D. Heat flow and hydrologic characteristics at the AND-1B borehole, ANDRILL McMurdo ice shelf project, Antarctica. Geosphere 2010, 6, 370–378. [Google Scholar] [CrossRef] [Green Version]
- Fisher, A.T.; Mankoff, K.D.; Tulaczyk, S.M.; Tyler, S.W.; Foley, N. High geothermal heat flux measured below the West Antarctic ice sheet. Sci. Adv. 2015, 1, e1500093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollack, H.N.; Hurter, S.J.; Johnson, J.R. Heat flow from the earth’s interior: Analysis of the global data set. Rev. Geophys. 1993, 31, 267–280. [Google Scholar] [CrossRef]
- Yamane, M.; Yokoyama, Y.; Abe-Ouchi, A.; Obrochta, S.; Saito, F.; Moriwaki, K.; Matsuzaki, H. Exposure age and ice-sheet model constraints on Pliocene East Antarctic ice sheet dynamics. Nat. Commun. 2015, 6, 7016. [Google Scholar] [CrossRef] [PubMed]
- Engelhardt, H. Ice temperature and high geothermal flux at Siple Dome, west Antarctica, from borehole measurements. J. Glaciol. 2004, 50, 251–256. [Google Scholar] [CrossRef] [Green Version]
- Hasterok, D. Thermal State of Continental and Oceanic Lithosphere. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA, 2010; p. 167. [Google Scholar]
- Dalziel, I.W.; Elliot, D.H. West Antarctica: Problem child of Gondwanaland. Tectonics 1982, 1, 3–19. [Google Scholar] [CrossRef]
- Block, A.E.; Bell, R.E.; Studinger, M. Antarctic crustal thickness from satellite gravity: Implications for the transantarctic and Gamburtsev Subglacial Mountains. Earth Planet. Sci. Lett. 2009, 288, 194–203. [Google Scholar] [CrossRef]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Zirizzotti, A. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef] [Green Version]
- An, M.; Wiens, D.A.; Zhao, Y.; Feng, M.; Nyblade, A.A.; Kanao, M.; Lévêque, J.J. S-velocity model and inferred Moho topography beneath the Antarctic plate from Rayleigh waves. J. Geophys. Res. Solid Earth 2015, 120, 359–383. [Google Scholar] [CrossRef]
- Shen, W.; Wiens, D.A.; Lloyd, A.J.; Nyblade, A.A. A Geothermal Heat Flux Map of Antarctica Empirically Constrained by Seismic Structure. Geophys. Res. Lett. 2020, 47, e2020GL086955. [Google Scholar] [CrossRef]
- Wolovick, M.J.; Moore, J.C.; Zhao, L. Joint Inversion for Surface Accumulation Rate and Geothermal Heat Flow From Ice-Penetrating Radar Observations at Dome A, East Antarctica. Part I: Model Description, Data Constraints and Inversion Results. J. Geophys. Res. Earth Surf. 2021, 126, 1–27. [Google Scholar] [CrossRef]
- Zagorodnov, V.; Nagornov, O.; Scambos, T.A.; Muto, A.; Mosley-Thompson, E.; Pettit, E.C.; Tyuflin, S. Borehole temperatures reveal details of 20th century warming at Bruce Plateau, Antarctic Peninsula. Cryosphere 2012, 6, 675–686. [Google Scholar] [CrossRef] [Green Version]
- Talalay, P.; Li, Y.; Augustin, L.; Clow, G.D.; Hong, J.; Lefebvre, E.; Markov, A.; Motoyama, H.; Ritz, C. Geothermal heat flux from measured temperature profiles in deep ice boreholes in Antarctica. Cryosphere 2020, 14, 4021–4037. [Google Scholar] [CrossRef]
- Golynsky, A.V.; Ferraccioli, F.; Hong, J.K.; Golynsky, D.A.; von Frese, R.R.B.; Young, D.A.; Blankenship, D.D.; Holt, J.W.; Ivanov, S.V.; Kiselev, A.V.; et al. ADMAP2 Magnetic anomaly map of the Antarctic—links to files. PANGAEA 2018. [Google Scholar] [CrossRef]
- Golynsky, A.V.; Ferraccioli, F.; Hong, J.K.; Golynsky, D.A.; von Frese, R.R.B.; Young, D.A.; Blankenship, J.W.; Holt, S.V.; Ivanov, A.V.; Kilesev, V.N.; et al. New magnetic anomaly map of the Antarctic. Geophys. Res. Lett. 45, 6437–6449. [CrossRef]
- Frost, B.R.; Shive, P.N. Magnetic mineralogy of the lower continental crust. J. Geophys. Res. Atmos. 1986, 91, 6513–6521. [Google Scholar] [CrossRef]
- Tanaka, A.; Okubo, Y.; Matsubayashi, O. Curie point depth based on spectrum analysis of the magnetic anomaly data in East and Southeast Asia. Tectonophysics 1999, 306, 461–470. [Google Scholar] [CrossRef]
- Carrillo-de la Cruz, J.L.; Prol-Ledesma, R.M.; Velázquez-Sánchez, P.; Gómez-Rodríguez, D. MAGCPD: A MATLAB-based GUI to calculate the Curie point-depth involving the spectral analysis of aeromagnetic data. Earth Sci. Inform. 2020, 13, 1539–1550. [Google Scholar] [CrossRef]
- Spector, A.; Grant, F.S. Statistical model for interpreting aeromagnetric data. Geophysics 1970, 35, 293–302. [Google Scholar] [CrossRef]
- Martos, Y.M.; Catalán, M.; Galindo-Zaldivar, J. Curie depth, heat flux and thermal subsidence reveal the Pacific mantle outflow through the Scotia Sea. J. Geophys Res. Solid Earth 2019, 124, 10735–10751. [Google Scholar] [CrossRef]
- Okubo, Y.; Matsunaga, T. Curie point depth in Northeast Japan and its correlation with regional thermal structure and seismicity. J. Geophys. Res. 1994, 99, 22363–22371. [Google Scholar] [CrossRef]
- Birch, F.; Roy, R.F.; Decker, E.R. Heat flow and thermal history in New England and New York. In Studies of Appalachian Geology: Northern and Maritime; Zen, E.-A., Ed.; Wiley Interscience: New York, NY, USA, 1968; pp. 437–451. [Google Scholar]
- Lachenbruch, A.H. Preliminary geothermal model of the Sierra Nevada. J. Geophys. Res. 1968, 73, 6977–6989. [Google Scholar] [CrossRef]
- Roy, R.F.; Blackwell, D.D.; Birch, F. Heat generation of plutonic rocks and continental heat flow provinces. Earth Planet. Sci. Lett. 1968, 5, 1–12. [Google Scholar] [CrossRef]
- Ravat, D.; Morgan, P.; Lowry, A.R. Geotherms from the temperature- depth–constrained solutions of 1-D steady-state heat-flow equation. Geosphere 2016, 12, 1187–1197. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Ritzwoller, M.H. Inferring surface heat flux distributions guided by a global seismic model: Particular application to Antarctica. Earth Planet. Sci. Lett. 2004, 223, 213–224. [Google Scholar] [CrossRef] [Green Version]
- An, M.; Wiens, D.A.; Zhao, Y.; Feng, M.; Nyblade, A.; Kanao, M.; Li, Y.; Maggi, A.; Lévêque, J.-J. Temperature, lithosphere-asthenosphere boundary, and heat flux beneath the Antarctic Plate inferred from seismic velocities. J. Geophys. Res. Solid Earth 2015, 120, 8720–8742. [Google Scholar] [CrossRef]
- Jamieson, S.S.R.; Ross, N.; Greenbaum, J.S.; Young, D.A.; Aitken, A.R.A.; Roberts, J.L.; Blankenship, D.D.; Bo, S.; Siegert, M.J. An extensive subglacial lake and canyon system in Princess Elizabeth Land, East Antarctica. Geology 2016, 44, 87–90. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Greenbaum, J.S.; Beem, L.H.; Guo, J.; Ng, G.; Li, L.; Blankenship, D.; Sun, B. The First Fixed-wing Aircraft for Chinese Antarctic Expeditions: Airframe, Modifications, Scientific Instrumentation and Applications. J. Environ. Eng. Geophys 2018, 23, 1–13. [Google Scholar] [CrossRef]
- Cui, X.; Jeofry, H.; Greenbaum, J.S.; Guo, J.; Li, L.; Lindzey, L.E.; Habbal, F.A.; Wei, W.; Young, D.A.; Ross, N.; et al. Bed topography of Princess Elizabeth Land in East Antarctica. Earth Syst. Sci. Data 2020, 12, 2765–2774. [Google Scholar] [CrossRef]
- LeMasurier, W.E.; Thomson, J.W. (Eds.) Volcanoes of the Antarctic plate and Southern Oceans. In Antarctic Research Series; American Geophysical Union: Washington, DC, USA, 1990; Volume 48, p. 487. [Google Scholar]
- Hambrey, M.J.; McKelvey, B. Major Neogene fluctuations of the East Antarctic ice sheet: Stratigraphic evidence from the Lambert glacier region. Geology 2000, 28, 887–890. [Google Scholar] [CrossRef]
- Morgan, P. Constraints on rift thermal processes from heat flow and uplift. Tectonophysics 1983, 94, 277–298. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Zhao, Y.; Liu, J.; Chen, H.; Cui, Y.; Song, B. Early Mesoproterozoic arc magmatism followed by early Neoproterozoic granulite facies metamorphism with a near-isobaric cooling path at Mount Brown, Princess Elizabeth Land, East Antarctica. Precambrian Res. 2016, 284, 30–48. [Google Scholar] [CrossRef]
- Pollett, A.; Thiel, S.; Bendall, B.; Raimondo, T.; Hand, M. Mapping the Gawler Craton–Musgrave Province interface using integrated heat flow and magnetotellurics. Tectonophysics 2019, 756, 43–56. [Google Scholar] [CrossRef]
- Liu, X.; Yue, Z.; Hong, C.; Song, B. New zircon U–Pb and Hf–Nd isotopic constraints on the timing of magmatism, sedimentation and metamorphism in the northern Prince Charles Mountains, East Antarctica. Precambrian Res. 2017, 299, 15–33. [Google Scholar] [CrossRef]
- Mueller, S.G.; Krapez, B.; Barley, M.E.; Fletcher, I.R. Giant iron-ore deposits of the Hamersley Province related to the breakup of Paleoproterozoic Australia; new insights from in situ SHRIMP dating of baddeleyite from mafic intrusions. Geology 2005, 33, 577–580. [Google Scholar] [CrossRef]
- Rogers, J.; Santosh, M. Tectonics and surface effects of the supercontinent Columbia. Gondwana Res. 2009, 15, 373–380. [Google Scholar] [CrossRef]
- Schroeder, D.M.; Blankenship, D.D.; Young, D.A.; Quartini, E. Evidence for elevated and spatially variable geothermal flux beneath the West Antarctic Ice Sheet. Proc. Natl. Acad. Sci. USA 2014, 111, 9070–9072. [Google Scholar] [CrossRef] [Green Version]
- Dziadek, R.; Gohl, K.; Diehl, A.; Kaul, N. Geothermal heat flux in the Amundsen Sea sector of West Antarctica: New insights from temperature measurements, depth to the bottom of the magnetic source estimation and thermal modeling. Geochem. Geophys. Geosyst. 2017, 18, 2657–2672. [Google Scholar] [CrossRef]
- Jordan, T.A.; Martin, C.; Ferraccioli, F.; Matsuoka, K.; Corr, H.; Forsberg, R.; Olesen, A.; Siegert, M. Anomalously high geothermal flux near the South Pole. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Tang, X.; Guo, J.; Cui, X.; Xiao, E.; Latif, K.; Sun, B.; Zhang, Q.; Shi, X. Inversion of Geothermal Heat Flux under the Ice Sheet of Princess Elizabeth Land, East Antarctica. Remote Sens. 2021, 13, 2760. https://doi.org/10.3390/rs13142760
Li L, Tang X, Guo J, Cui X, Xiao E, Latif K, Sun B, Zhang Q, Shi X. Inversion of Geothermal Heat Flux under the Ice Sheet of Princess Elizabeth Land, East Antarctica. Remote Sensing. 2021; 13(14):2760. https://doi.org/10.3390/rs13142760
Chicago/Turabian StyleLi, Lin, Xueyuan Tang, Jingxue Guo, Xiangbin Cui, Enzhao Xiao, Khalid Latif, Bo Sun, Qiao Zhang, and Xiaosong Shi. 2021. "Inversion of Geothermal Heat Flux under the Ice Sheet of Princess Elizabeth Land, East Antarctica" Remote Sensing 13, no. 14: 2760. https://doi.org/10.3390/rs13142760
APA StyleLi, L., Tang, X., Guo, J., Cui, X., Xiao, E., Latif, K., Sun, B., Zhang, Q., & Shi, X. (2021). Inversion of Geothermal Heat Flux under the Ice Sheet of Princess Elizabeth Land, East Antarctica. Remote Sensing, 13(14), 2760. https://doi.org/10.3390/rs13142760








