Spatio-Temporal Characteristics and Driving Factors of the Foliage Clumping Index in the Sanjiang Plain from 2001 to 2015
Abstract
:1. Introduction
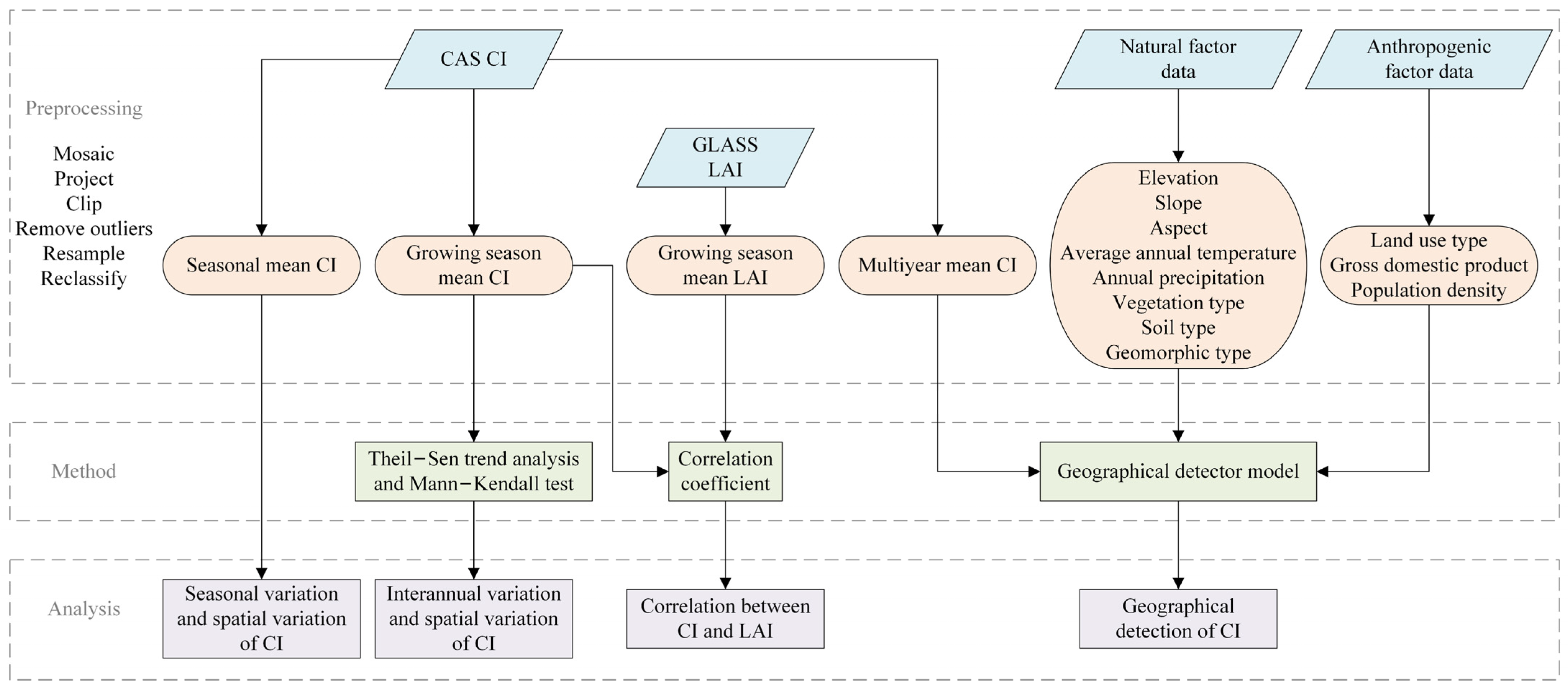
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. CI Products
2.2.2. LAI Products
2.2.3. Natural Factors
2.2.4. Anthropogenic Factors
2.3. Methods
2.3.1. Theil–Sen Trend Analysis
2.3.2. Mann−Kendall Test
2.3.3. Correlation Coefficient
2.3.4. Geographical Detector Model
2.3.5. Selection and Classification of Driving Factors
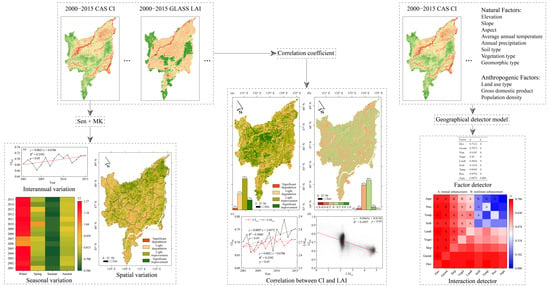
3. Results
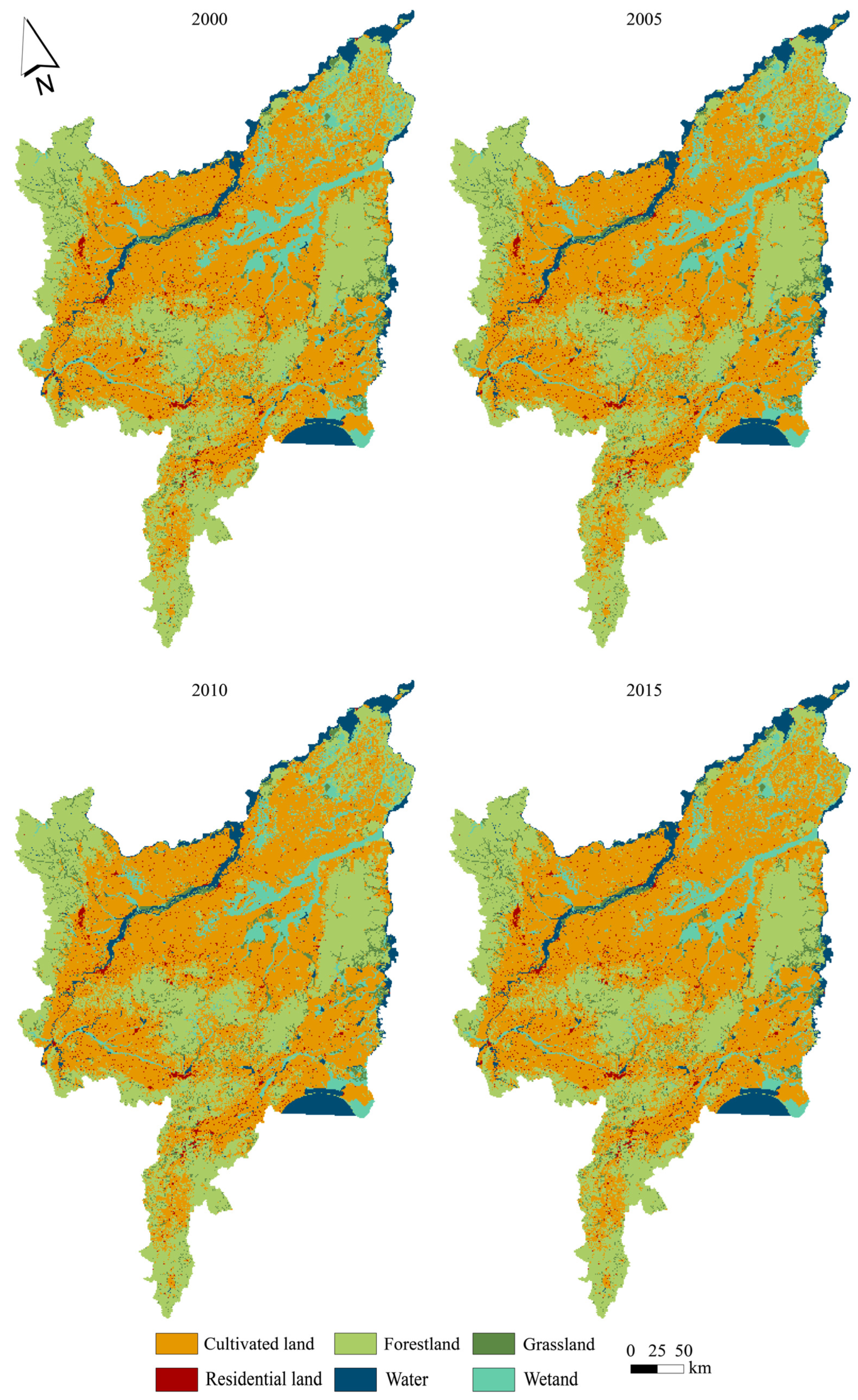
3.1. Spatial and Temporal Variations of Land Use Type in the Sanjiang Plain from 2000 to 2015
3.1.1. Temporal Variations
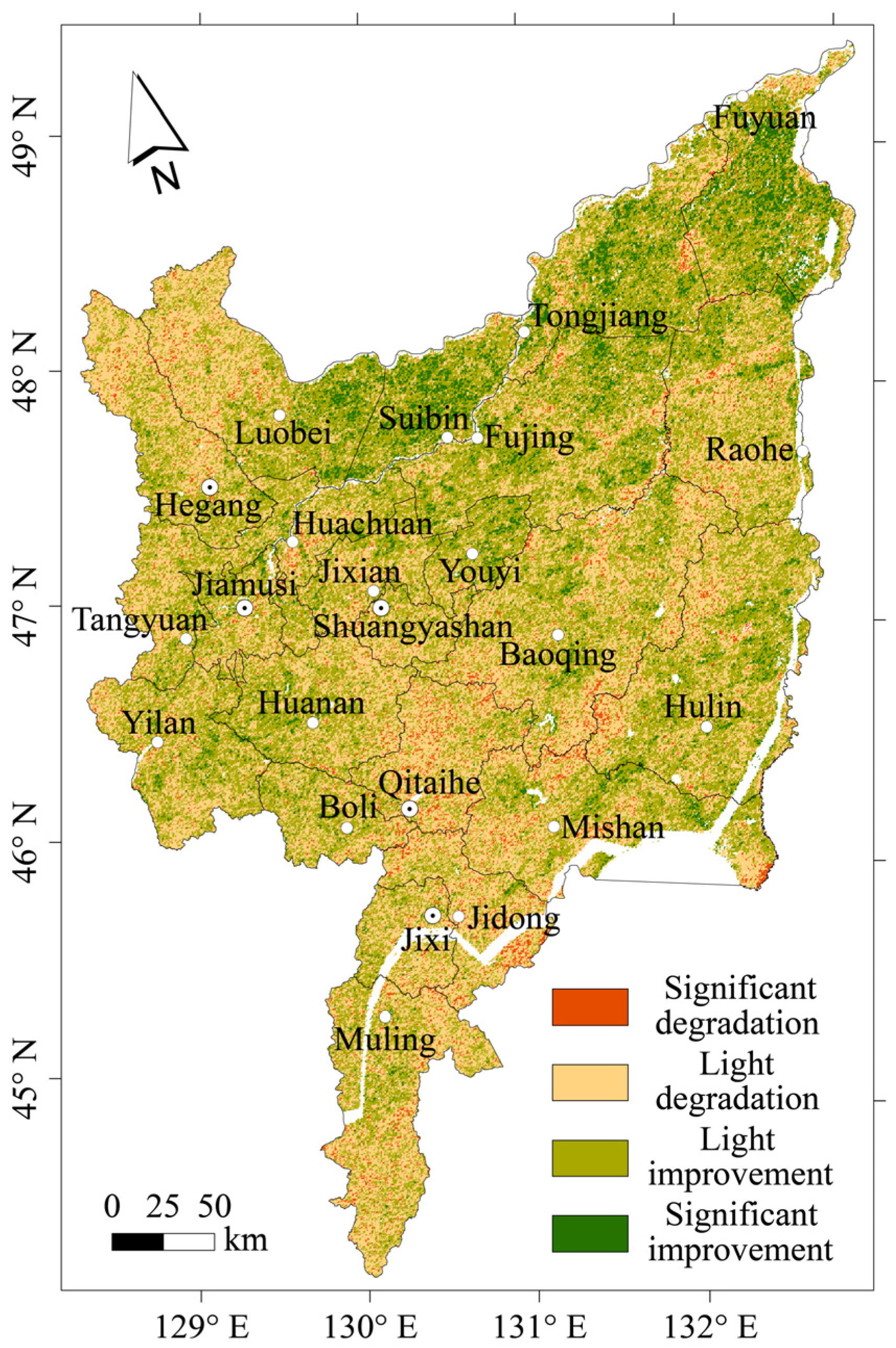
3.1.2. Spatial Variations
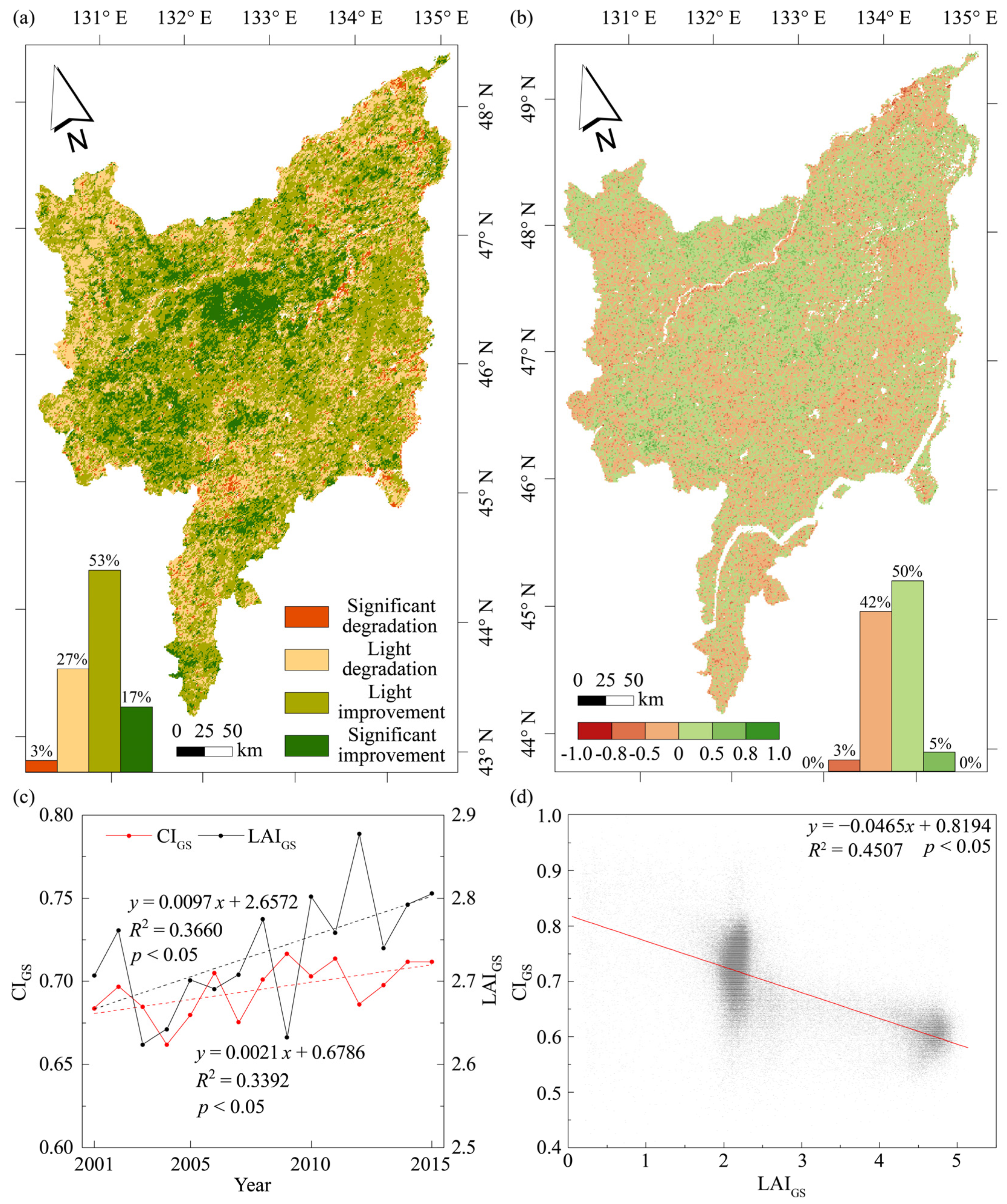
3.2. Spatial and Temporal Variations of CI in the Sanjiang Plain from 2000 to 2015
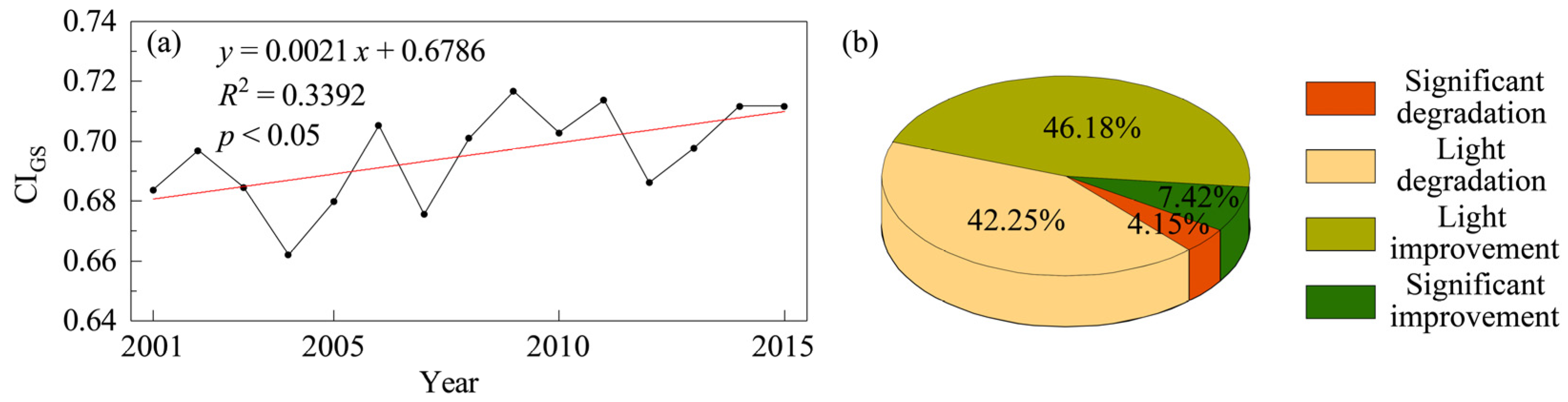
3.2.1. Interannual Variations
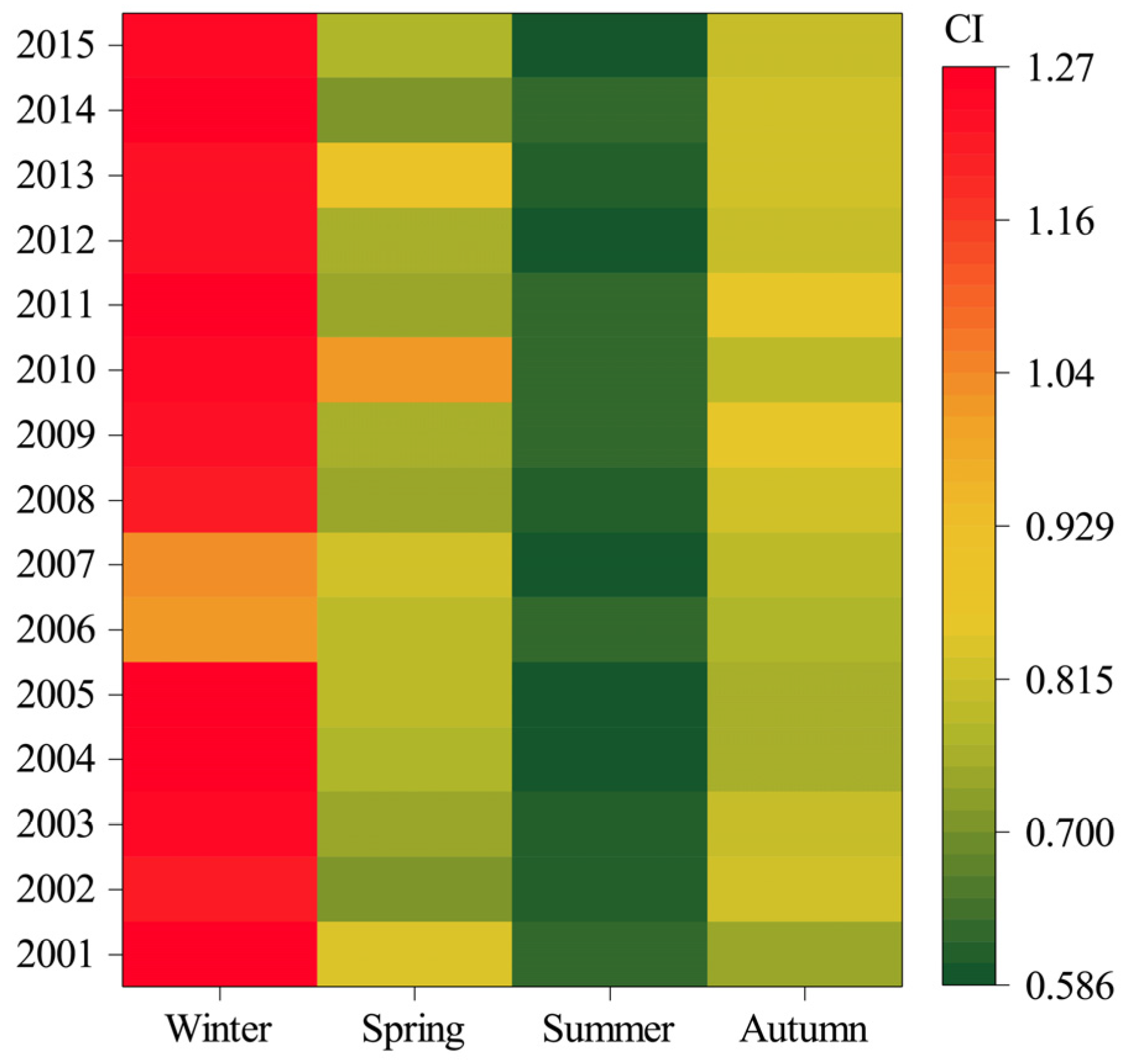
3.2.2. Seasonal Variations
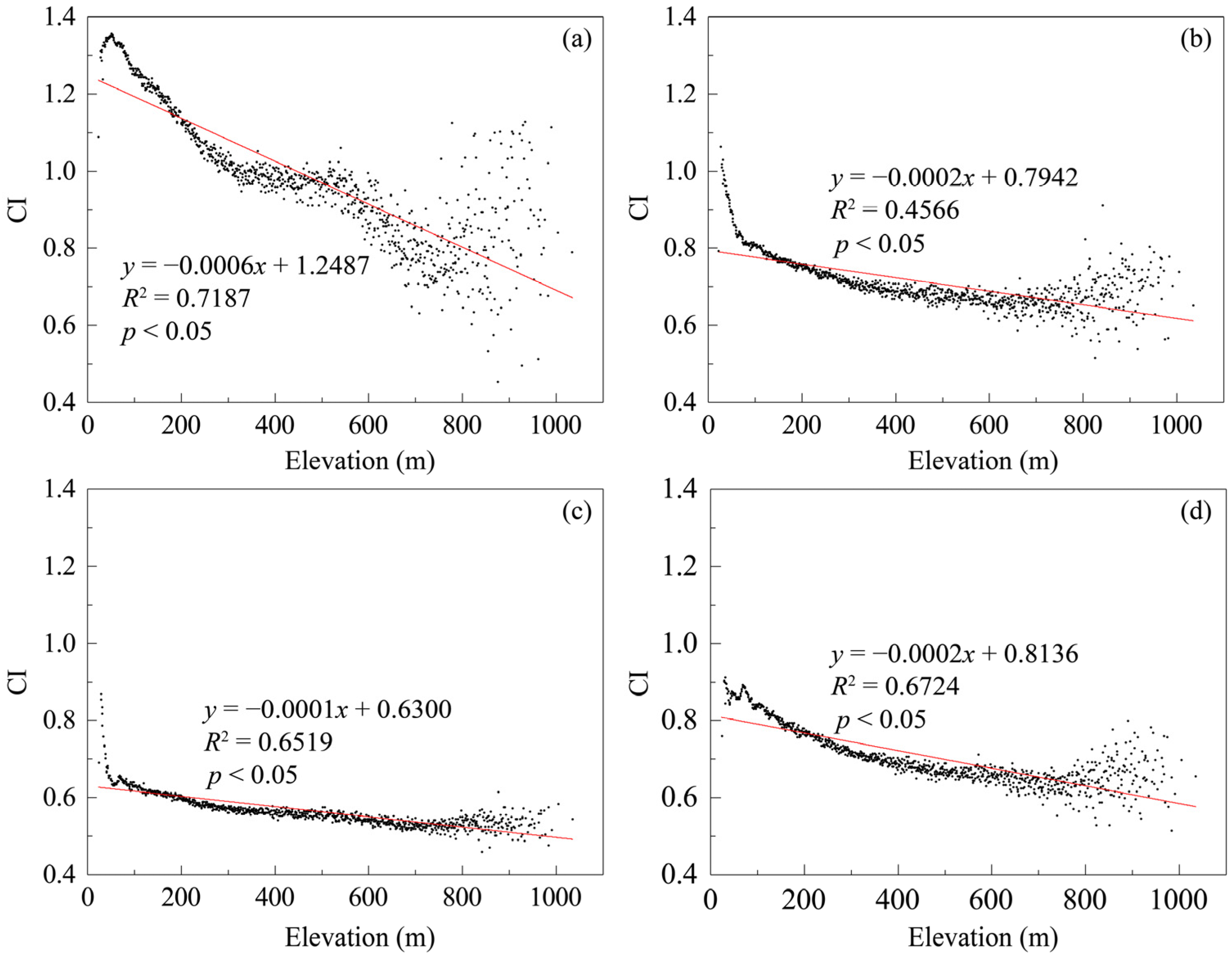
3.2.3. Spatial Variations
3.3. Correlation between CI and LAI in the Sanjiang Plain
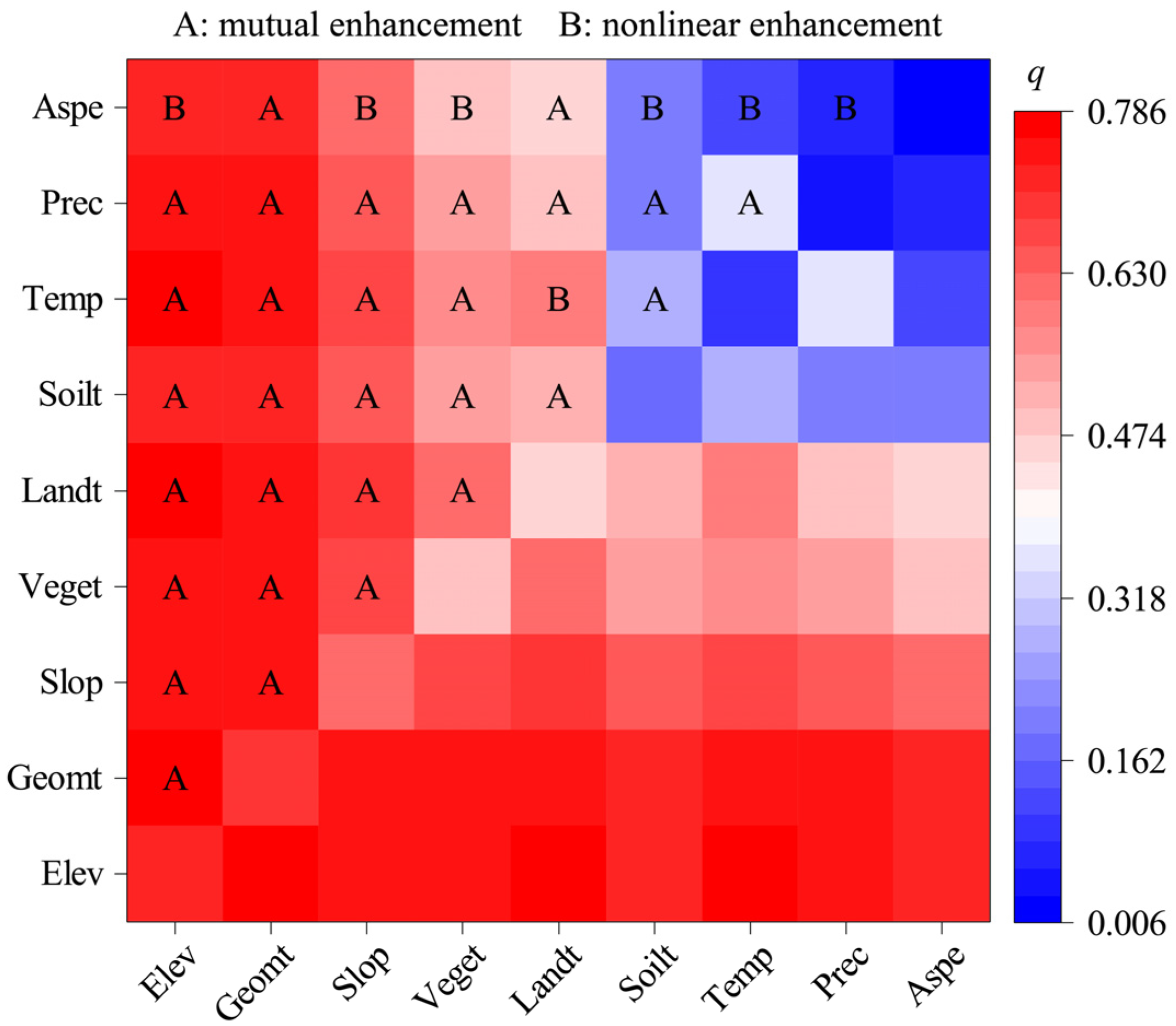
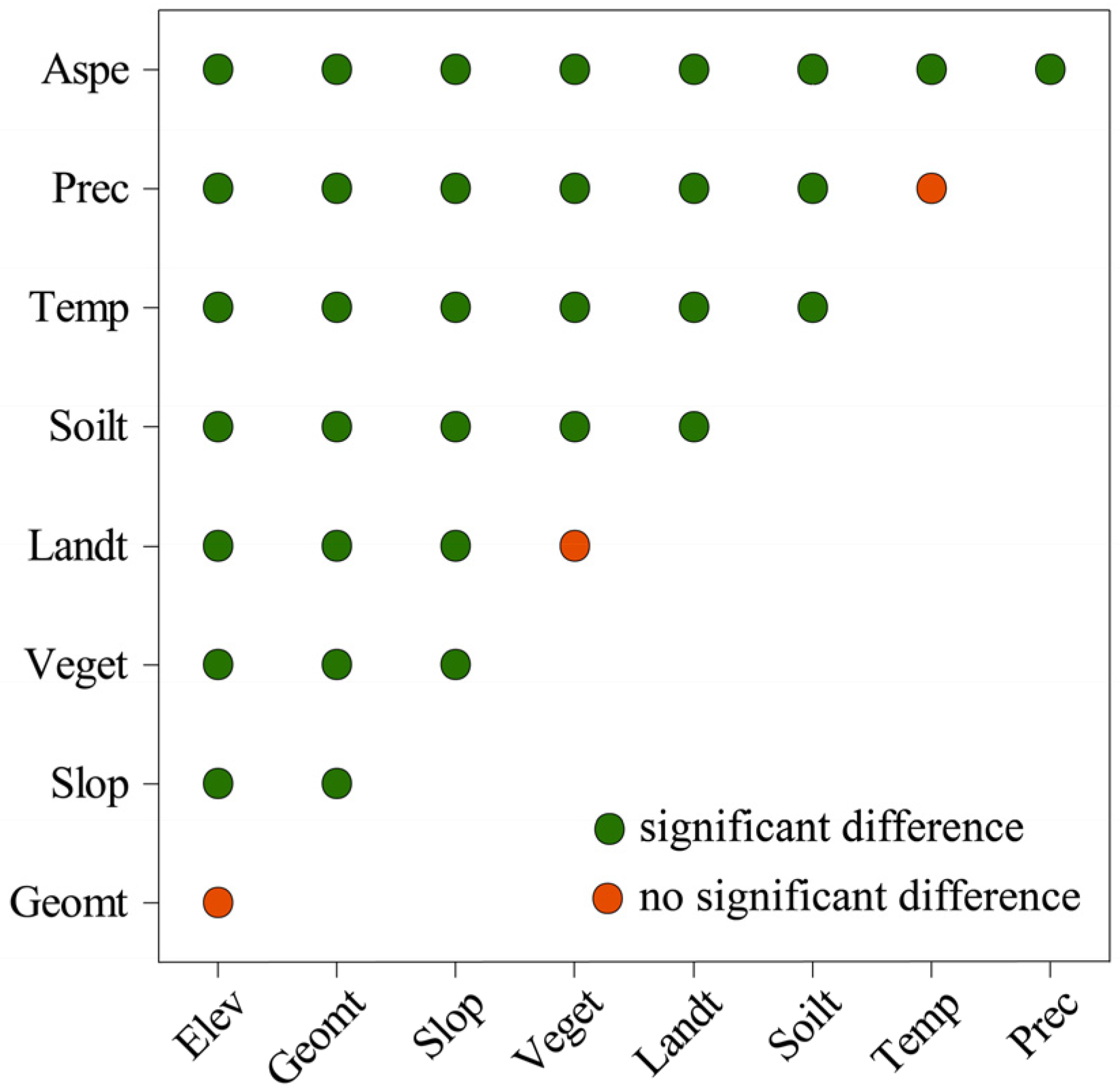
3.4. Geographical Detection of the Spatial Differentiation of CI in the Sanjiang Plain
3.4.1. Detection of the Significant Driving Factors for the Spatial Differentiation of CI
3.4.2. Detection of the Single Factors
3.4.3. Detection of the Interactions among Factors
3.4.4. Detection of the Factor Ranges/Types Suitable for Clumping Effects of Foliage
3.4.5. Detection of the Significant Differences between Factors
4. Discussion
4.1. Spatio-Temporal Variations of CI
4.2. Driving Factors of the Spatial Distribution of CI
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol. 1992, 60, 249–266. [Google Scholar] [CrossRef]
- Chen, J.M.; Rich, P.M.; Gower, S.T.; Norman, J.M.; Plummer, S. Leaf area index of boreal forests: Theory, techniques, and measurements. J. Geophys. Res. 1997, 102, 29429–29443. [Google Scholar] [CrossRef]
- Chianucci, F.; Cutini, A. Estimation of canopy properties in deciduous forests with digital hemispherical and cover photography. Agric. For. Meteorol. 2013, 168, 130–139. [Google Scholar] [CrossRef]
- Zou, J.; Zhuang, Y.; Chianucci, F.; Mai, C.; Lin, W.; Leng, P.; Luo, S.; Yan, B. Comparison of seven inversion models for estimating plant and woody area indices of leaf–on and leaf–off forest canopy using explicit 3D forest scenes. Remote Sens. 2018, 10, 1297. [Google Scholar] [CrossRef] [Green Version]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. For. Meteorol. 2007, 143, 176–188. [Google Scholar] [CrossRef]
- Chen, B.; Liu, J.; Chen, J.M.; Croft, H.; Gonsamo, A.; He, L.; Luo, X. Assessment of foliage clumping effects on evapotranspiration estimates in forested ecosystems. Agric. For. Meteorol. 2016, 216, 82–92. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, GB1019. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Wilson, K.B.; Gu, L. How the environment, canopy structure and canopy physiological functioning influence carbon, water and energy fluxes of a temperate broad-leaved deciduous forest—An assessment with the biophysical model CANOAK. Tree Physiol. 2002, 22, 1065–1077. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Baldocchi, D.; Gong, P.; Dawson, T. Modeling radiation and photosynthesis of a heterogeneous savanna woodland landscape with a hierarchy of model complexities. Agric. For. Meteorol. 2008, 148, 1005–1020. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Wilson, K.B. Modeling CO2 and water vapor exchange of a temperate broadleaved forest across hourly to decadal time scales. Ecol. Modell. 2001, 142, 155–184. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Leblanc, S.G.; Lacaze, R.; Roujean, J.-L. Multi-angular optical remote sensing for assessing vegetation structure and carbon absorption. Remote Sens. Environ. 2003, 84, 516–525. [Google Scholar] [CrossRef]
- Wang, Y.; Woodcock, C.; Buermann, W.; Stenberg, P.; Voipio, P.; Smolander, H.; Häme, T.; Tian, Y.; Hu, J.; Knyazikhin, Y.; et al. Evaluation of the MODIS LAI algorithm at a coniferous forest site in Finland. Remote Sens. Environ. 2004, 91, 114–127. [Google Scholar] [CrossRef]
- Liu, R.; Chen, J.M.; Liu, J.; Deng, F.; Sun, R. Application of a new leaf area index algorithm to China’s landmass using MODIS data for carbon cycle research. J. Environ. Manag. 2007, 85, 649–658. [Google Scholar] [CrossRef]
- Pisek, J.; Chen, J.M.; Nilson, T. Estimation of vegetation clumping index using MODIS BRDF data. Int. J. Remote Sens. 2011, 32, 2645–2657. [Google Scholar] [CrossRef]
- Zhu, G.; Ju, W.; Chen, J.M.; Gong, P.; Xing, B.; Zhu, J. Foliage clumping index over China’s landmass retrieved from the MODIS BRDF parameters product. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2122–2137. [Google Scholar] [CrossRef]
- Wei, S.; Fang, H. Estimation of canopy clumping index from MISR and MODIS sensors using the normalized difference hotspot and darkspot (NDHD) method: The influence of BRDF models and solar zenith angle. Remote Sens. Environ. 2016, 187, 476–491. [Google Scholar] [CrossRef]
- Wei, S.; Fang, H.; Schaaf, C.B.; He, L.; Chen, J.M. Global 500 m clumping index product derived from MODIS BRDF data (2001–2017). Remote Sens. Environ. 2019, 232, 111296. [Google Scholar] [CrossRef]
- Chianucci, F.; Zou, J.; Leng, P.; Zhuang, Y.; Ferrara, C. A new method to estimate clumping index integrating gap fraction averaging with the analysis of gap size distribution. Can. J. For. Res. 2019, 49, 471–479. [Google Scholar] [CrossRef]
- Pisek, J.; Lang, M.; Nilson, T.; Korhonen, L.; Karu, H. Comparison of methods for measuring gap size distribution and canopy nonrandomness at Järvselja RAMI (RAdiation transfer Model Intercomparison) test sites. Agric. For. Meteorol. 2011, 151, 365–377. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.; Wei, S.; Jiang, C. Seasonal variation of leaf area index (LAI) over paddy rice fields in NE China: Intercomparison of destructive sampling, LAI–2200, digital hemispherical photography (DHP), and AccuPAR methods. Agric. For. Meteorol. 2014, 198–199, 126–141. [Google Scholar] [CrossRef]
- García, M.; Gajardo, J.; Riaño, D.; Zhao, K.; Martín, P.; Ustin, S. Canopy clumping appraisal using terrestrial and airborne laser scanning. Remote Sens. Environ. 2015, 161, 78–88. [Google Scholar] [CrossRef]
- Wei, S. Estimation of clumping index from multi–angle remote sensing data. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2017. [Google Scholar]
- Zhu, L.; Meng, J.; Zhu, L. Applying Geodetector to disentangle the contributions of natural and anthropogenic factors to NDVI variations in the middle reaches of the Heihe River Basin. Ecol. Indic. 2020, 117, 106545. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical detectors–based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Huang, C.; Liu, K.; Zhou, L. Spatio–temporal trends and influencing factors of PM2.5 concentrations in urban agglomerations in China between 2000 and 2016. Environ. Sci. Pollut. Res. 2020, 28, 10988–11000. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Tong, C.; Huang, H. The geographical pattern and differentiational mechanism of rural poverty in China. Acta Geogr. Sin. 2021, 76, 903–920. [Google Scholar]
- Du, Z.; Zhang, X.; Xu, X.; Zhang, H.; Wu, Z.; Pang, J. Quantifying influences of physiographic factors on temperate dryland vegetation, Northwest China. Sci. Rep. 2017, 7, 40092. [Google Scholar] [CrossRef]
- Meng, X.; Gao, X.; Li, S.; Lei, J. Spatial and temporal characteristics of vegetation NDVI changes and the driving forces in Mongolia during 1982–2015. Remote Sens. 2020, 12, 603. [Google Scholar] [CrossRef] [Green Version]
- Peng, W.; Kuang, T.; Tao, S. Quantifying influences of natural factors on vegetation NDVI changes based on geographical detector in Sichuan, western China. J. Clean. Prod. 2019, 233, 353–367. [Google Scholar] [CrossRef]
- Zhao, W.; Hu, Z.; Guo, Q.; Wu, G.; Chen, R.; Li, S. Contributions of climatic factors to interannual variability of the vegetation index in Northern China grasslands. J. Clim. 2019, 33, 175–183. [Google Scholar] [CrossRef]
- Meng, Q.; Wu, Z.; Du, Z.; Zhang, H. Quantitative influence of regional fractional vegetation cover based on geodetector model—Take the Beijing–Tianjin sand source region as an example. China Environ. Sci. 2021, 41, 826–836. [Google Scholar]
- Tao, S.; Kuang, T.; Peng, W.; Wang, G. Analyzing the spatio–temporal variation and drivers of NDVI in upper reaches of the Yangtze River from 2000 to 2015: A case study of Yibin City. Acta Ecol. Sin. 2020, 40, 5029–5043. [Google Scholar]
- Liu, J.; Zhao, D.; Tian, X.; Zhao, L.; Liu, J. Landscape pattern dynamics and driving forces analysis in the Sanjiang Plain from 1954 to 2010. Acta Ecol. Sin. 2014, 34, 3234–3244. [Google Scholar]
- Zhang, B.; Lu, C.; Sun, Q.; Xiao, W.; Hou, B.; Yan, L. Effects of climate and land use change on vegetation coverage in Sanjiang Plain. Water Res. Power 2017, 35, 18–22. [Google Scholar]
- Zhang, J.; Zhang, B.; Ma, B.; Cao, B.; Liang, J.; Ma, S. Spatial–temporal variation of NDVI in Sanjiang Plain and its response to climate change. J. Des. Res. 2019, 39, 206–213. [Google Scholar]
- Yang, L.; Shen, F.; Zhang, L.; Cai, Y.; Yi, F.; Zhou, C. Quantifying influences of natural and anthropogenic factors on vegetation changes using structural equation modeling: A case study in Jiangsu Province, China. J. Clean. Prod. 2021, 280, 124330. [Google Scholar] [CrossRef]
- Li, H.; Zheng, L.; Lei, Y.; Li, C.; Zhou, K. Comparison of NDVI and EVI based on EOS/MODIS data. Prog. Geogr. 2007, 26, 26–32. [Google Scholar]
- Yan, F.; Zhang, S.; Liu, X.; Chen, D.; Chen, J.; Bu, K.; Yang, J.; Chang, L. The effects of spatiotemporal changes in land degradation on ecosystem services values in Sanjiang Plain, China. Remote Sens. 2016, 8, 917. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Yu, L.; Bu, K.; Yan, F.; Zhang, S. Seasonal local temperature responses to paddy field expansion from rain–fed farmland in the cold and humid Sanjiang Plain of China. Remote Sens. 2018, 10, 2009. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Song, C. Regional ecological risk assessment of wetlands in the Sanjiang Plain. Prog. Geogr. 2019, 38, 872–882. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time–series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef] [Green Version]
- Xu, X. Spatial Distribution Data Set of GDP in China. Data Registration and Publication System of Chinese Academy of Sciences. 2017. Available online: https://www.resdc.cn/data.aspx?DATAID=252 (accessed on 11 May 2021).
- Xu, X. Spatial Distribution Data Set of Population in China. Data Registration and Publication System of Chinese Academy of Sciences. 2017. Available online: https://www.resdc.cn/data.aspx?DATAID=251 (accessed on 11 May 2021).
- Stow, D.; Daeschner, S.; Hope, A.; Douglas, D.; Petersen, A.; Myneni, R.; Zhou, L.; Oechel, W. Variability of the seasonally integrated normalized difference vegetation index across the north slope of Alaska in the 1990s. Int. J. Remote Sens. 2003, 24, 1111–1117. [Google Scholar] [CrossRef]
- Neeti, N.; Eastman, J.R. A contextual Mann–Kendall approach for the assessment of trend significance in image time series. Trans. GIS 2011, 15, 599–611. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Li, S.; Yang, S.; Liu, X.; Liu, Y.; Shi, M. NDVI-based analysis on the influence of climate change and human activities on vegetation restoration in the Shaanxi–Gansu–Ningxia Region, Central China. Remote Sens. 2015, 7, 11163–11182. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Li, J.; Chu, L.; Wang, T.; Li, Z.; Cai, C. Analysis of spatial and temporal variations in vegetation index and its driving force in Hubei Province in the last 10 years. Acta Ecol. Sin. 2019, 39, 7722–7736. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econ. J. Econ. Soc. 1945, 13, 245–259. [Google Scholar]
- Forthofer, R.N.; Lehnen, R.G. Rank correlation methods. In Public Program Analysis: A New Categorical Data Approach; Forthofer, R.N., Lehnen, R.G., Eds.; Springer: Boston, MA, USA, 1981; pp. 146–163. [Google Scholar]
- Zhang, W.; Jin, H.; Shao, H.; Li, A.; Li, S.; Fan, W. Temporal and spatial variations in the leaf area index and its response to topography in the Three–River Source Region, China from 2000 to 2017. ISPRS Int. J. Geo Inf. 2021, 10, 33. [Google Scholar] [CrossRef]
- Guo, J.; Hu, Y.; Xiong, Z.; Yan, X.; Ren, B.; Bu, R. Spatiotemporal variations of growing–season NDVI associated with climate change in Northeastern China’s permafrost zone. Pol. J. Environ. Stud. 2017, 26, 1521–1529. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, L.; Sun, Z.; Wang, X. Spatiotemporal differentiation and the factors influencing urbanization and ecological environment synergistic effects within the Beijing–Tianjin–Hebei urban agglomeration. J. Environ. Manag. 2019, 243, 227–239. [Google Scholar] [CrossRef]
- Wang, J.F.; Hu, Y. Environmental health risk detection with GeogDetector. Environ. Model. Softw. 2012, 33, 114–115. [Google Scholar] [CrossRef]
- Chen, T.; Xia, J.; Zou, L.; Hong, S. Quantifying the influences of natural factors and human activities on NDVI changes in the Hanjiang River Basin, China. Remote Sens. 2020, 12, 3780. [Google Scholar] [CrossRef]
- Wang, W.; Samat, A.; Abuduwaili, J. Geo–detector based spatio–temporal variation characteristics and driving factors analysis of NDVI in Central Asia. Remote Sens. Land Res. 2019, 31, 32–40. [Google Scholar]
- Jenks, G.F. The data model concept in statistical mapping. Inter. Year. Carto. 1967, 7, 186–190. [Google Scholar]
- Wu, D.; Ma, Y.; Wu, H.; Xiao, Y.; Li, H. Characteristics of temporal and spatial evolution and driving forces of vegetation index in Sichuan based on MODIS–EVI. Res. Soil Water Conserv. 2020, 27, 230–236, 243. [Google Scholar]
- Zhu, G. Spatial-temporal characteristics of foliage clumping index in China during 2000–2013. Chin. Sci. Bull. 2016, 61, 1595–1603. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.; Fan, W.; Mao, X.; Yu, Y. Foliage clumping index of main vegetation types in Daxing’an Mountains, Northeast China. Chin. J. of Appl. Ecol. 2017, 28, 757–762. [Google Scholar]
- Qu, Y. MLAOS: A multi–point linear array of optical sensors for coniferous foliage clumping index measurement. Sensors 2014, 14, 9271–9289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Hu, Q.; Zou, F. Spatio-temporal changes of vegetation net primary productivity and its driving factors on the Qinghai–Tibetan Plateau from 2001 to 2017. Remote Sens. 2021, 13, 1566. [Google Scholar] [CrossRef]



| Factor Types | Abbreviations | Factors | Sources |
|---|---|---|---|
| Natural factors | Elev | Elevation | USGS (https://earthexplorer.usgs.gov/ accessed on 11 May 2021) |
| Slop | Slope | Derived from SRTM DEM | |
| Aspe | Aspect | ||
| Temp | Average annual temperature | Resource and Environment Science and Data Center, RESDC (http://www.resdc.cn/ accessed on 11 May 2021) | |
| Prec | Annual precipitation | ||
| Veget | Vegetation type | ||
| Soilt | Soil type | ||
| Geomt | Geomorphic type | ||
| Anthropogenic factors | Landt | Land use type | RESDC (http://www.resdc.cn/ accessed on 11 May 2021) |
| GDP | Gross domestic product | ||
| POP | Density of population |
| Year | Cultivated Land (%) | Forestland (%) | Grassland (%) | Water (%) | Residential Land (%) | Wetland (%) |
|---|---|---|---|---|---|---|
| 2000 | 48.29 | 33.05 | 3.89 | 4.78 | 1.92 | 8.07 |
| 2005 | 48.64 | 32.96 | 3.99 | 4.82 | 1.92 | 7.67 |
| 2010 | 49.27 | 32.66 | 3.95 | 4.83 | 1.92 | 7.37 |
| 2015 | 50.61 | 32.10 | 3.85 | 4.82 | 1.92 | 6.70 |
| 2015 | Cultivated Land | Forestland | Grassland | Residential Land | Water | Wetland | Aggregate | |
|---|---|---|---|---|---|---|---|---|
| 2000 | ||||||||
| Cultivated land | 51,956 | 155 | 100 | 76 | 11 | 16 | 52,314 | |
| Forestland | 1147 | 34,577 | 64 | 5 | 4 | 8 | 35,805 | |
| Grassland | 193 | 28 | 3941 | 1 | 28 | 24 | 4215 | |
| Residential land | 75 | 2 | 1 | 2001 | 0 | 0 | 2079 | |
| Water | 29 | 0 | 1 | 0 | 5151 | 4 | 5185 | |
| Wetland | 1430 | 15 | 70 | 3 | 25 | 7200 | 8743 | |
| Aggregate | 54,830 | 34,777 | 4177 | 2086 | 5219 | 7252 | 108,341 | |
| Factor | Elev | Geomt | Slop | Veget | Landt | Soilt | Temp | Prec | Aspe | GDP | POP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| q | 0.7118 | 0.7071 | 0.6096 | 0.4793 | 0.4657 | 0.1812 | 0.0943 | 0.0549 | 0.0077 | 0.0047 | 0.0015 |
| p | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.007 | 1.000 | 1.000 |
| Factor | Elev | Geomt | Slop | Veget | Landt | Soilt | Temp | Prec | Aspe |
|---|---|---|---|---|---|---|---|---|---|
| q | 0.7122 | 0.7073 | 0.6102 | 0.4800 | 0.4664 | 0.1818 | 0.0949 | 0.0554 | 0.0079 |
| p | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.006 |
| Factor | Optimal Range/Type | Mean Value of CIGS |
|---|---|---|
| Elev (m) | 589–1035 | 0.643 |
| Geomt | Moderate relief mountain | 0.648 |
| Slop (°) | 5.8–13 | 0.670 |
| Veget | Coniferous and broad-leaved mixed forest | 0.682 |
| Landt | Forestland | 0.746 |
| Soilt | Leached soil | 0.808 |
| Temp (°C) | 0.9–2.1 | 0.818 |
| Prec (mm) | 638.7–725.7 | 0.822 |
| Aspe (°) | 0–22.5, 337.5–360 | 0.852 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Zhang, Z.; Fang, H.; Lu, Y.; Gu, Z.; Gao, M. Spatio-Temporal Characteristics and Driving Factors of the Foliage Clumping Index in the Sanjiang Plain from 2001 to 2015. Remote Sens. 2021, 13, 2797. https://doi.org/10.3390/rs13142797
Hu K, Zhang Z, Fang H, Lu Y, Gu Z, Gao M. Spatio-Temporal Characteristics and Driving Factors of the Foliage Clumping Index in the Sanjiang Plain from 2001 to 2015. Remote Sensing. 2021; 13(14):2797. https://doi.org/10.3390/rs13142797
Chicago/Turabian StyleHu, Kehong, Zhen Zhang, Hongliang Fang, Yijie Lu, Zhengnan Gu, and Min Gao. 2021. "Spatio-Temporal Characteristics and Driving Factors of the Foliage Clumping Index in the Sanjiang Plain from 2001 to 2015" Remote Sensing 13, no. 14: 2797. https://doi.org/10.3390/rs13142797
APA StyleHu, K., Zhang, Z., Fang, H., Lu, Y., Gu, Z., & Gao, M. (2021). Spatio-Temporal Characteristics and Driving Factors of the Foliage Clumping Index in the Sanjiang Plain from 2001 to 2015. Remote Sensing, 13(14), 2797. https://doi.org/10.3390/rs13142797