4.1. Experimental Setup and Data Description
In
Table 2 we summarize the PRISMA hyperspectral sensor specifications. The hyperspectral sensor is composed of two spectrometers operating in the VNIR and the SWIR spectral range, respectively. The wavelengths covered by the two spectrometers are partially overlapped. In our experiments, we combined the data in the overlapped region of the covered spectral range thus obtaining a total number of spectral channels equal to 230.
It is worth noting that, dealing with remotely sensed data, in situ measurements for AC algorithms validation are generally not available, especially in the case of satellite missions where the acquisition of the ground truth is further complicated by the low spatial resolution of the sensor. For this reason, our analysis is carried out by comparing the results provided by the proposed algorithm with the spectral reflectance image (L2C product, [
9,
11] included in the PRISMA data product. The L2C data are obtained by a state-of-the-art PB algorithm (AC PRISMA algorithm, hereinafter) that retrieves the visibility by using the Dark Dense Vegetation technique [
28] and estimates
on a per-pixel basis by using an algorithm in the class of the differential absorption techniques [
34].
Our experiments focus on four images concerning the same scene and are collected at different times with different acquisition conditions. The scene includes several application scenarios such as urban, rural, and coastal regions and is a good test case for the proposed analysis. The scene has a spatial extent of
and is centered near the city of Grosseto, in the south of Tuscany, Italy. In
Figure 1 we show a high spatial resolution image of the region of interest taken by Google Earth. In the same image, we have marked the position of some “targets” that will be adopted to discuss the results. Selected targets include both natural surfaces and artificial surfaces.
Table 3 shows, for each image, (a) the acquisition date, (b) the solar zenith angle
, (c) the sensor viewing angle
, (d) the relative azimuth angle between the incident solar direction and the direction of propagation of the scattered radiance
, and (e) the cloud cover percentage. The angles reported in
Table 3 are averaged over all the pixels of each image. Notice that the images named DAY2, DAY3, and DAY4 were collected approximately with the same solar zenith angle and sensor viewing angle and are relatively close in time. DAY1 data were acquired at a temporal distance greater than two months from the others and with a different acquisition geometry. As an example,
Figure 2 shows the PRISMA true color (Red Green Blue: RGB) composite image taken on 8 July 2020 (DAY4).
On the basis of the acquisition time of the images, in the learning phase of the LBAC algorithm and in the visibility estimation algorithm, we adopted the LUTs derived by considering the Mid-Latitude Summer Modtran model. Furthermore, on the basis of the characteristic of the scene, we have considered two distinct aerosol models (parameter IHAZE of Modtran): the rural aerosol model for land pixels and the maritime aerosol model for pixels of the Tyrrhenian Sea. The basis matrix
of the reflectance subspace is obtained by the procedure in [
20,
35] assuming a rank of 40.
Before analyzing the results obtained on the above-mentioned images, we show the first example concerning a different image that is chosen because it is one of the rare cases in which in situ measurements are available. Specifically, we refer to the image acquired on 8 August 2020 (at 10:47) over the La Crau site in France, where one of the measurement stations of the RadCalNet network [
36] operates. RadCalNet is an initiative of the Working Group on Calibration and Validation of the Committee on Earth Observation Satellites (CEOS), aimed at collecting in situ reflectance and atmospheric measurements to aid in the post-launch radiometric calibration and validation of optical imaging sensor data. La Crau station measures data representative of a very small area (compared to the PRISMA GSD) corresponding to a disk of 30 m radius on latitude 43.55885 degrees and longitude 4.864472 degrees covered by pebbly soil with sparse vegetation. In situ spectral reflectance measurements were performed by an ASD FieldSpec-4 spectroradiometer mounted on a tripod with a time interval of 30 min between 09:00 to 15:00 local standard time. The reflectance spectra and the measurement uncertainty in the spectral range from 400 nm to 2410 nm are made available. Note that the La Crau site was not specifically conceived for validation of PRISMA L2C data products and in general for L2 data from spaceborne sensors. To the best of our knowledge, a calibration/validation site specifically designed for PRISMA data is not yet available. Consequently, La Crau data cannot be used to assess the performance of an AC algorithm applied to PRISMA data, but can only be adopted to give an example of the goodness of the AC results.
In
Figure 3, we show the true color composite (RGB) representation of a portion of the PRISMA image collected on 8 August 2020 on the La Crau site; the red box indicates the region containing the measurement field. In
Figure 4, the in situ reflectance spectra, measured at the same time of the PRISMA overpass, are compared in terms of error plot with the spectra provided by the LBAC and those included in the L2C PRISMA image. To consider the uncertainty about the pixel coordinates of the measurement field, we consider for both the LBAC results and the PRISMA L2C data an area of 5 × 5 pixels centered on the site coordinates. In the figure, the absorption bands due to CO
2 are delimited by black dashed vertical lines, and the absorption spectral window due to CH
4 is delimited by red dashed vertical lines. The blue transparent patches indicate the water absorption bands. Notice that for the spectra in
Figure 4, and for all the spectra shown in the rest of the paper, we do not consider the reflectance values in the water absorption bands near 1370 nm and 1880 nm because all the solar radiation is absorbed by the water molecules in the atmosphere.
Results in
Figure 4 show that both the LBAC and the AC PRISMA algorithm provide reflectance spectra very similar to the measured one with the mean relative errors in the order of 7% and 13%, respectively. The shape of the spectral reflectance obtained by both algorithms is very close to that measured on the ground. However, in this example, the LBAC outperforms the AC PRISMA algorithm. The LBAC reflectance closely follows the smooth behavior of the in situ reflectance, while the L2C PRISMA data exhibit artifacts (high-frequency variations) that are more evident in (a) the water absorption bands around 940 nm, 1130 nm, and above 2300 nm, and (b) in the CO
2 absorption band around 2100 nm. The possible causes of those effects will be discussed in the next section.
4.2. Reflectance Analysis
We start this sub-section by discussing the results concerning the DAY4 image and, specifically, four targets corresponding to both natural and artificial surfaces. As to the natural surfaces, we consider two pixels belonging to a beach (Sand 1) and to a holm oak forest (Holm Oak 2), respectively. The artificial surface pixels are selected from the airport runway (Airport Runway) and the rock quarry (Quarry), in the upper right part of the image.
Figure 5a–d graphically compare, for each target, the spectral reflectance obtained by the LBAC (blue plot) with the L2C PRISMA product (red plot).
Several conclusions can be drawn from the results in
Figure 5a–d. We can see that the general behavior of the spectra derived by the two AC algorithms is quite similar, and, in both the cases, the main absorption effects due to water vapor, CO
2 and CH
4 are substantially compensated. The LBAC reflectance’s are smoother than those obtained by the AC PRISMA algorithm.
It is well-known that below 2500 nm, the spectral reflectance of most natural and man-made surfaces hardly ever shows narrow absorption bands even at the high spectral resolutions characterizing hyperspectral sensors. Specifically, several studies and experimental measurements [
16,
21] show that the spectral rate of change of the reflectance is much slower than that of the corresponding radiance. PB algorithms often provide atmospherically compensated data characterized by spectral artifacts, especially in the strongest absorption bands. These artifacts are generally due to different causes [
16], such as systematic errors in the atmospheric absorption model, uncertainties in the solar reference spectrum, spectral residual calibration errors, and non-perfect radiometric calibration of the radiance data. In addition, non-systematic errors are induced by random variations due to photon noise and readout noise in the detector electronics. The presence of those artifacts motivates the practice of applying spectral polishing algorithms to the retrieved reflectance spectra in order to smooth them [
21,
33].
With reference to the experiment under consideration, we can observe that the AC PRISMA algorithm, which does not include (to the best of our knowledge) a spectral polishing procedure, seems to be not immune to the above-mentioned problems. The provided reflectance spectra exhibit systematic artifacts that suggest the possible presence of small errors in the calibration process or in the atmospheric model. We specifically refer to the sharp variations in the two water absorption bands around 940 nm and 1130 nm, and in the CO2 absorption band around 2100 nm.
Conversely, the LBAC results do not exhibit such kinds of artifacts and show better robustness to potential systematic and non-systematic spectral artifacts. This result is intrinsically related to the adopted learning strategy which relies on a database containing the measured reflectance spectrum of more than 3000 man-made materials, vegetation, water, soils, and minerals. The spectra in the database are smooth and do not have high-frequency variations in the spectral domain. Furthermore, enclosing the main sources of noise occurring in the hyperspectral data in the learning mechanism, makes the LBAC robust to incorrect calibration errors and random noise. The specific learning strategy behind the LBAC gives the algorithm an inherent polishing ability which is quite useful in many application fields such as land use/land cover, water quality, hydrology studies of snow and ice, basic mineralogical analyses, and some terrestrial and aquatic ecosystem investigations. Thus, in most applications, it is certainly a strength of LBAC and makes it a very promising approach, especially to process the low signal-to-noise ratio data and non-perfectly calibrated images. However, that intrinsic polishing effect could be a limit of LBAC in those applications where one is interested in searching materials whose reflectance is characterized by narrow-band spectral features or, in general, not well represented as a linear combination of the spectra in the database . This is, for example, the case of specific gas plumes, canopy chemistry, or environmental contaminants. In those cases, LBAC, in its current form, may not preserve the relevant spectral features. In general, when the reflectance of a given material is not well represented as a combination of the spectra in , one may lose the features that allow the discrimination of that material. This can occur also in the case of man-made target detection applications, when the signature of the target of interest could have an “anomalous” spectral behavior, in the sense that it cannot be obtained as a linear combination of the spectra in .
However, the approach in [
20] is quite general and several modifications within the learning-based framework can be made to extend the capabilities of the resulting algorithm. For instance, regression functions more complicated than linear ones (e.g., deep neural networks) can be adopted to explore non-linear structures in the data. Another possible modification may concern the database
adopted in the learning phase and for the representation of the reflectance subspace. For example, the database
could be application-driven and populated with data including the spectral features that are significant for the application of interest. Possible solutions to the drawbacks of the LBAC version considered in this paper are under investigation and they are the focus of our ongoing activity.
To provide evidence of the effectiveness of the proposed approach in the analyzed image (DAY4), we have computed the Squared Error (SE) between the reflectance of each pixel estimated by the LBAC and that given by the AC PRISMA algorithm:
In Equation (6),
and
are the coordinates of the image pixel,
is the number of spectral bands,
is the reflectance estimated by LBAC in the pixel
and
is the reflectance provided by the AC PRISMA algorithm on the same pixel. The Mean SE (MSE) obtained by averaging the SE on the whole DAY4 image is very low and equal to
. In order to provide information about the spread of the distribution of
, we consider its Probability of Exceedance (
) defined as the complement of the cumulative distribution function (
) estimated on the whole image, i.e.,
.
of
for DAY4 image (
Figure 6) shows that most of the image pixels have
lower than
, and the percentage of image pixels with
greater than
is lower than 0.47% (
).
As to the benefits linked to the inclusion of the noise sources in the learning strategy, it was deeply investigated on simulated data in [
20], by analyzing the results obtained by the version of the LBAC trained without taking into account noise. Results in
Figure 7a,b provide further evidence. In those figures, we compare the reflectance spectra obtained by applying both the LBAC and its version trained without considering noise (LBAC-NoiseFree). The poor performance of the LBAC–NoiseFree is clear proof of the importance of introducing noise in the learning phase.
Another conclusion is that, opposite to traditional PB methods, the LBAC is insensitive to bad pixels occurring in the image. This is evident in
Figure 5b,d. Specifically, the sharp and narrow transitions to zero in the PRISMA L2C spectrum of Holm Oak 2 around 700 nm and Quarry at 570 nm are caused by bad pixels that are properly flagged in the PRISMA data products. Notice that the LBAC automatically reconstructs the observed spectra in those bad bands without exploiting the information about their location in the image.
For completeness, in
Figure 8 we summarize the results obtained on all the targets considered in this experiment. Results in
Figure 8 confirm all the previous conclusions.
An analysis similar to that described in the previous part of this section has been carried out on the DAY1 image that was acquired under different atmospheric and viewing conditions. A synthesis of the results obtained is reported in the following. Specifically, in
Figure 9 we compare the spectra derived by the LBAC with those provided by the PRISMA L2C product for the same targets considered in the previous experiment: Holm Oak 2, Sand 1, Airport Runway, and Quarry. We note that the spectra derived by the LBAC and by the AC PRISMA algorithm follow the same general trend and that in both cases the main absorption effects are compensated. However, we note a slight difference in the derived spectra in the channels corresponding to wavelengths falling in the visible spectral range between 600 nm and 900 nm. In absence of ground truth data, we cannot determine which of the two results is more correct. We can only make hypotheses about the causes of that misalignment. For instance, it could be determined (1) by a difference in the derivation of the LUTs adopted by the two algorithms, (2) by the fact that the LBAC, in its current version, does not account for the terrain elevation, (3) errors in the visibility estimation. However, the MSE obtained all over the image is
and the analysis of the
shows that the percentage of image pixels with
greater than
is lower than 0.092% (
).
As in the previous experiment, we note that PRISMA L2C data exhibit possible artifacts in the water absorption bands around 940 nm and 1130 nm and in the CO2 absorption band around 2100 nm. Such artifacts seem systematic and support the thesis of potential residual errors in the radiometric calibration of the data in the absorption bands or errors in the model of the atmospheric radiometric quantities. The non-systematic variations can be generated by random noise affecting the measurements. LBAC, providing smoother spectra, confirms its robustness to both residual calibration errors and random noise. The above considerations can be extended to all the targets analyzed in our experiments whose results are not reported here for brevity.
It is worth noting that, in all the results shown (included those of the La Crau site), there is a difference between the spectra provided by the LBAC and those of the PRISMA L2C product in the 2400 nm water absorption band. The difference could be due to an imperfect compensation, in the PRISMA L2C product, of the strong water absorption effect. This possible interpretation is motivated in the following. As is shown in the next part of this section, the DAY1 image was characterized by
values (close to 0.5
) lower than those of the DAY4 image (close to 2
). Consequently, potential errors in the compensation of water absorption are supposed to have a lower impact on the results of the DAY1 image. Indeed, comparing
Figure 5 with
Figure 9, we note that the difference between the LBAC spectra and the PRISMA L2C data in the DAY1 image (
Figure 9) is strongly reduced with respect to that observed in the results concerning the DAY4 image (
Figure 5).
Another noteworthy result regards the three images named DAY2, DAY3, and DAY4. These images were collected approximately in the same period of the year and practically with the same incidence and observation angles. Therefore, the effects of seasonal changes and those of the anisotropic response of the observed surfaces to the incident radiation are expected to be negligible. This means that, if the AC algorithm works well, the reflectance spectra derived for the same surface in the scene in the three images must be very similar. The previous claim is verified by the results obtained by the LBAC on the three images. Specifically,
Figure 10 and
Figure 11 show the reflectance spectra derived by the LBAC on the three images for all the in-land targets considered in our experiments. Notice that the spectra are practically the same for almost all the targets. The only exception is represented by the targets Quarry, Holm Oak 1, and Rice Field in the DAY2 image (
Figure 11). In the case of Holm Oak 1 and Quarry, the difference in the spectra is certainly due to the fact that both the targets were covered by cloud in the DAY 2 image. For the Rice Field target, the variation in the spectra could be due to the greater presence of water in the field at the time of the acquisition of the DAY3 and DAY4 images. Of course, the above discussion also applies to the spectra of the PRISMA L2C data in the three images.
4.3. LBAC Based CWV Retrieval: Results
In this sub-section, we present the results obtained by applying the
retrieval algorithm described in
Section 3 and based on the LBAC. Such results are compared with the
estimates included in the PRISMA L2C product and with those obtained by applying the well-known Atmospherically Pre-corrected Differential Absorption (APDA) technique proposed in [
29] that is adopted by several PB atmospheric compensation algorithms. APDA was applied to the water absorption spectral window around 940 nm.
Figure 12 shows, in the form of error bars, the mean values and the standard deviations of the
estimates obtained by the means of the LBAC-based procedure, those included in the PRISMA L2C product, and those obtained by APDA. We excluded the estimates from water pixels where the three procedures do not provide reliable
results because of the low signal-to-noise ratio in the water absorption bands. In all the considered cases, the proposed algorithm provides values quite close to those included in the PRISMA L2C product and those derived by APDA. Specifically, the LBAC-based procedure attains values of
very similar to those provided by APDA. Both the algorithms give estimated values greater than (approximately 20%) those provided by the PRISMA AC algorithm. However, the estimates from the three algorithms are highly correlated. The correlation coefficients between the LBAC and the PRISMA L2C are 0.72 for DAY1, 0.93 for DAY2, 0.89 for DAY3, and 0.91 for DAY4. Those between the LBAC and APDA are 0.73 for DAY1, 0.93 for DAY2, 0.9 for DAY3, and 0.92 for DAY4. The APDA and PRISMA L2C products, both exploiting the differential absorption approach, have correlation coefficients greater than 0.95 in all the considered images. For completeness, in
Figure 13 we show the (estimated) probability density functions (pdf) for the
values obtained by the three algorithms on the four images. For each image, the pdf of the estimates obtained by the proposed procedure and by the PRISMA L2C product have approximately the same shape, but they seem to differ for a shift. This is especially true for the DAY2, DAY3, and DAY4 images. As for the comparison between the LBAC-based procedure and the APDA, we note that the pdfs are very close in shape and position.
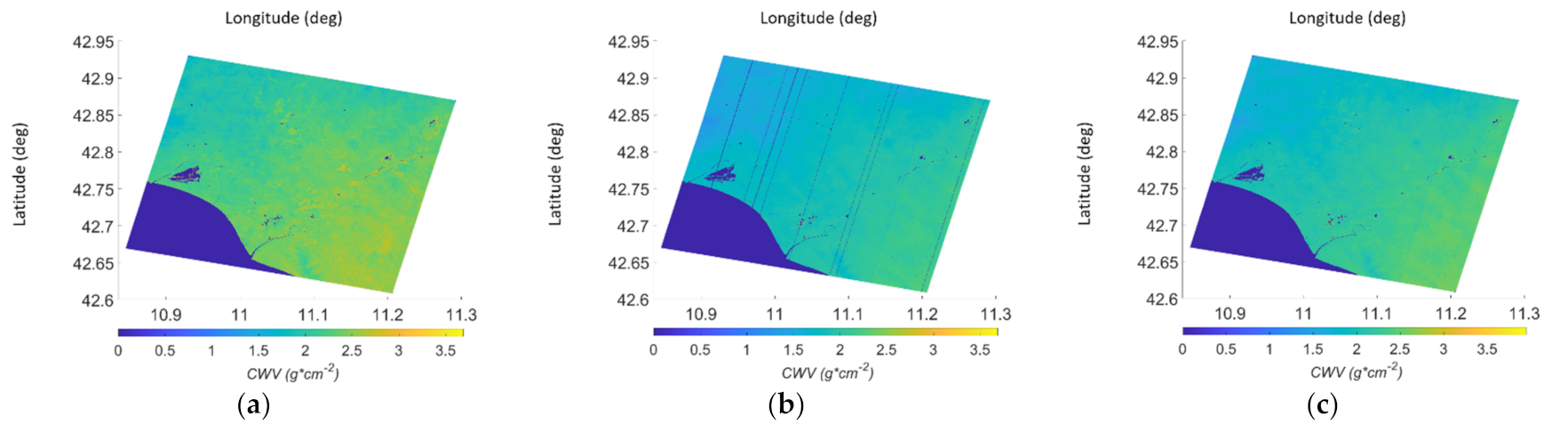
As an example, in
Figure 14 and
Figure 15 we show the
maps for the DAY1 image (
Figure 14) and the DAY4 image (
Figure 15) obtained by the proposed technique, those included in the PRISMA L2C data and those obtained by the APDA algorithm. In all the
maps, the water pixels are masked. Notice that the stripes in the cross-track direction appearing in the
map included in the PRISMA L2C product (
Figure 14b and
Figure 15b) correspond to bad pixels that are properly indicated in the provided product.