A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images
Abstract
:1. Introduction
2. Related Work
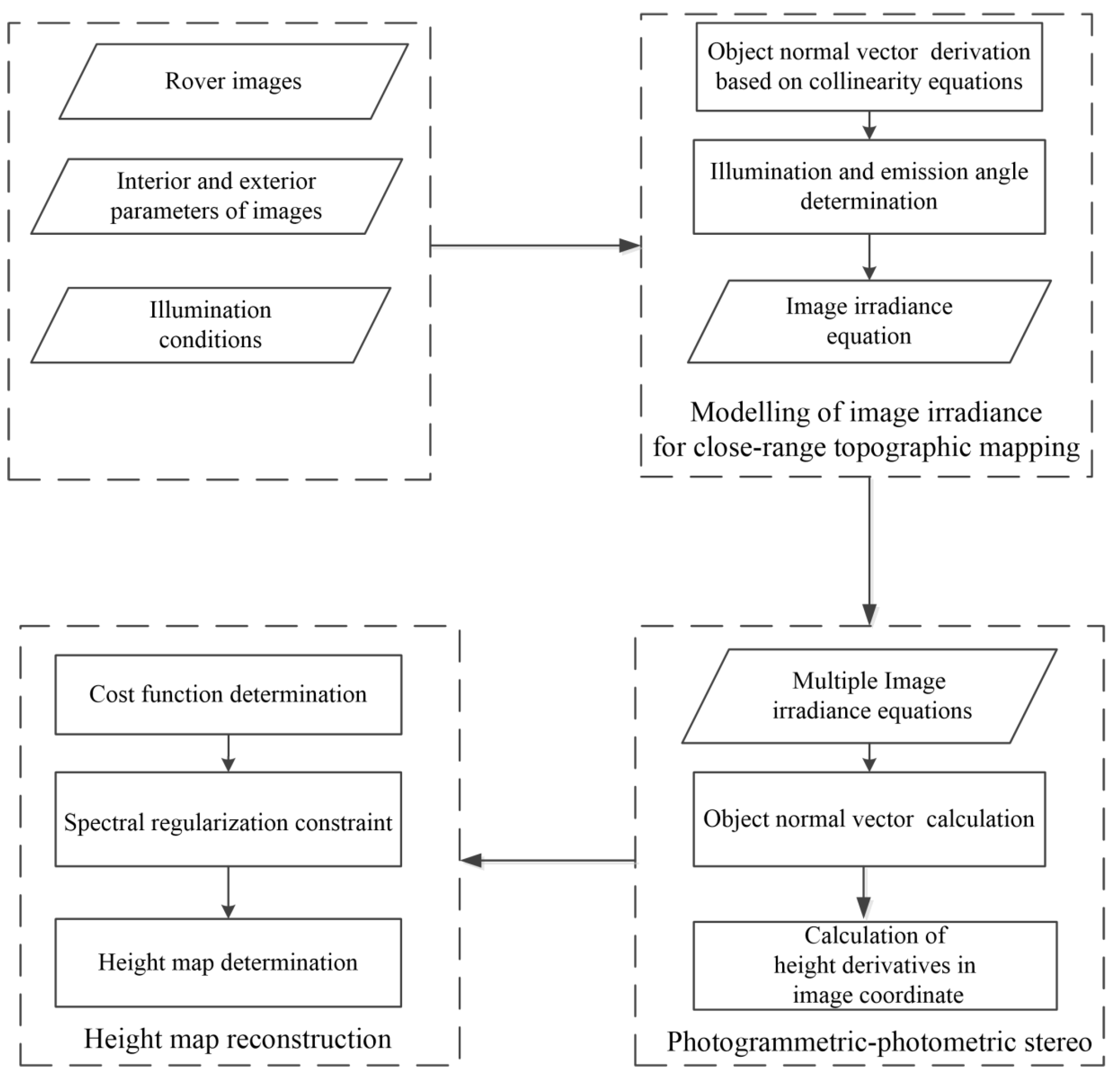
3. Photogrammetric-Photometric Stereo Method
3.1. Modelling the Image Irradiance for Close-Range Topographic Mapping
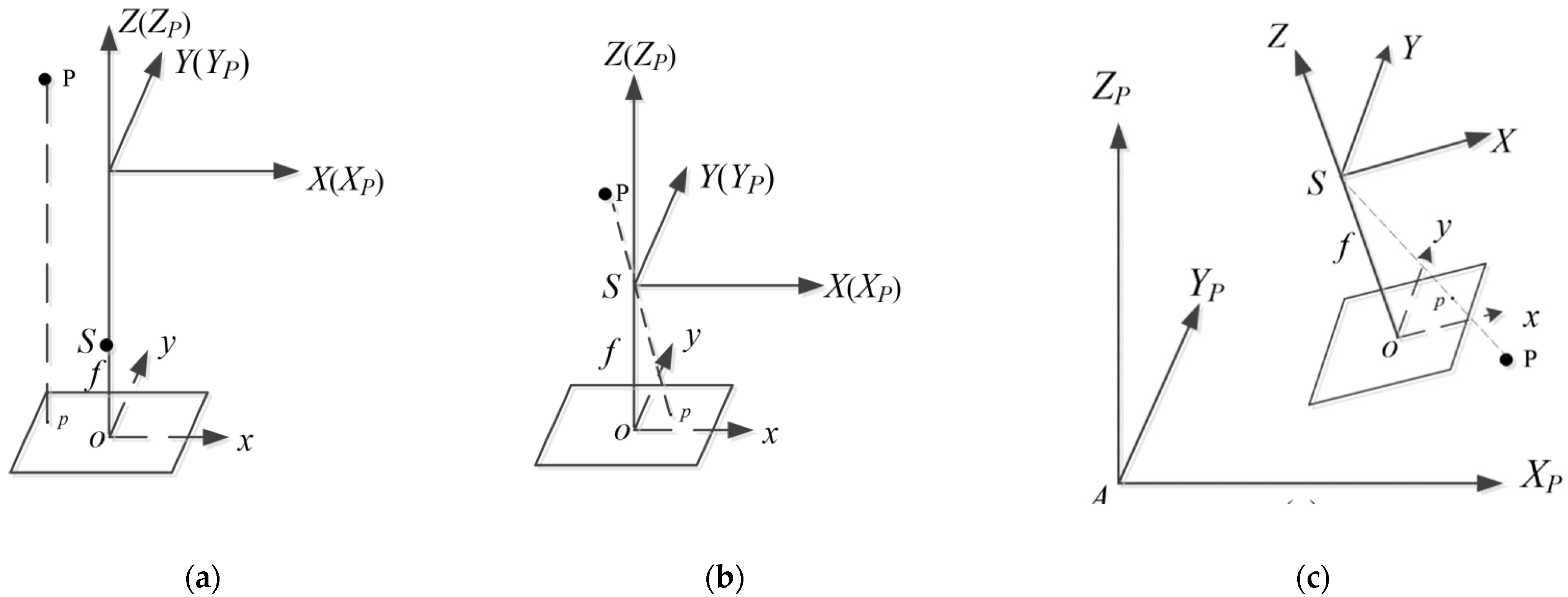
3.1.1. Coordinates in Traditional Photometric Stereo vs. Coordinates in PPS
3.1.2. Modelling of Surface Normal Based on Collinearity Equations
3.1.3. The Image Irradiance Equation
3.2. Perspective Photometric Stereo for Close-Range Topographic Mapping
3.3. Height Estimation from Estimated Height Gradient
4. Experimental Analysis
4.1. Quantitative Evaluation Measures
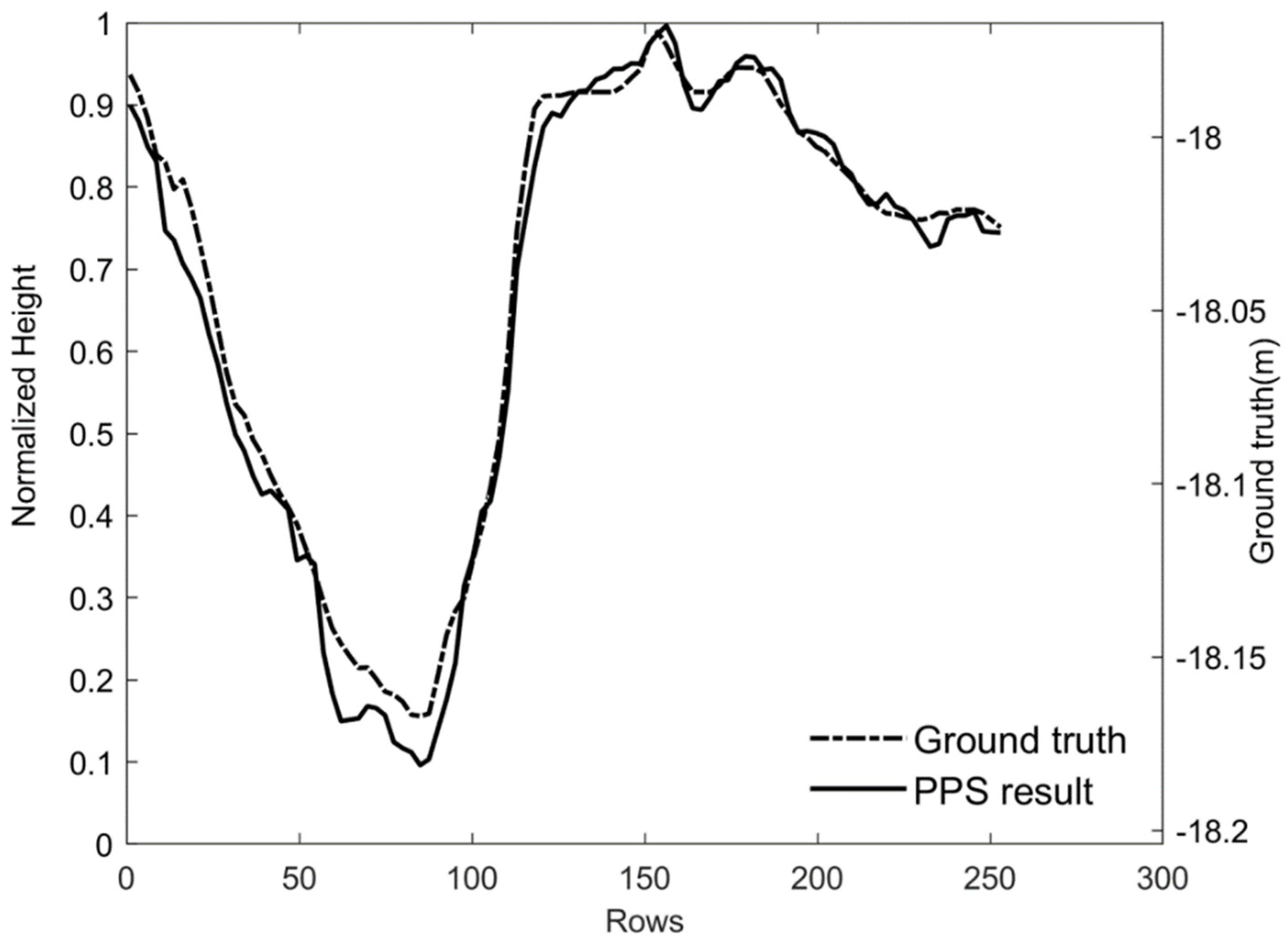
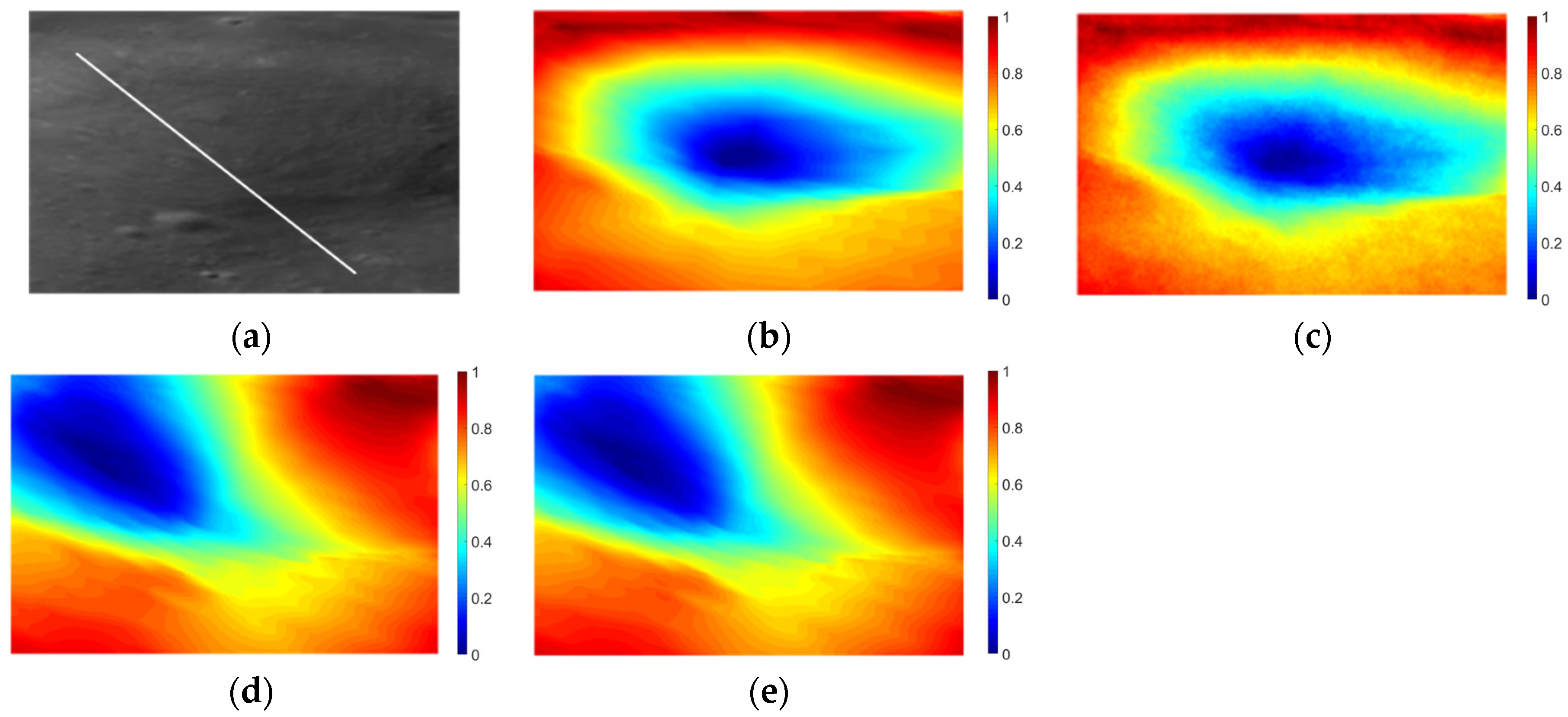
4.2. Experimental Analysis for Simulated Data
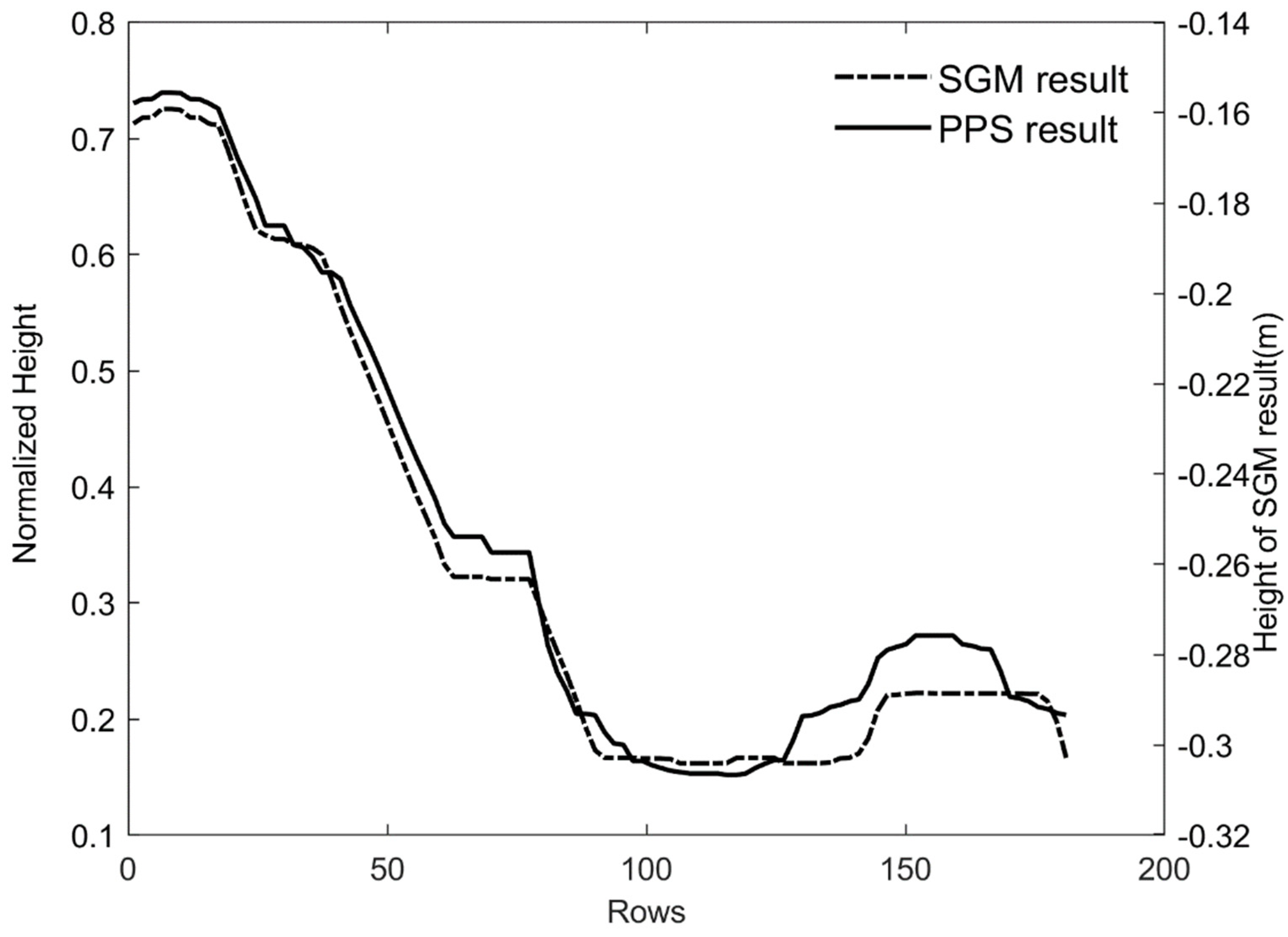
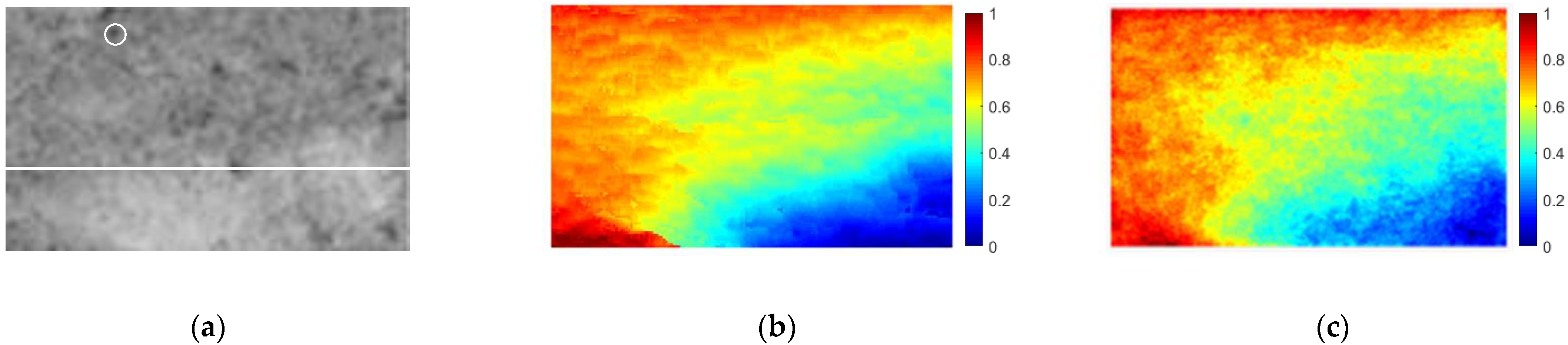
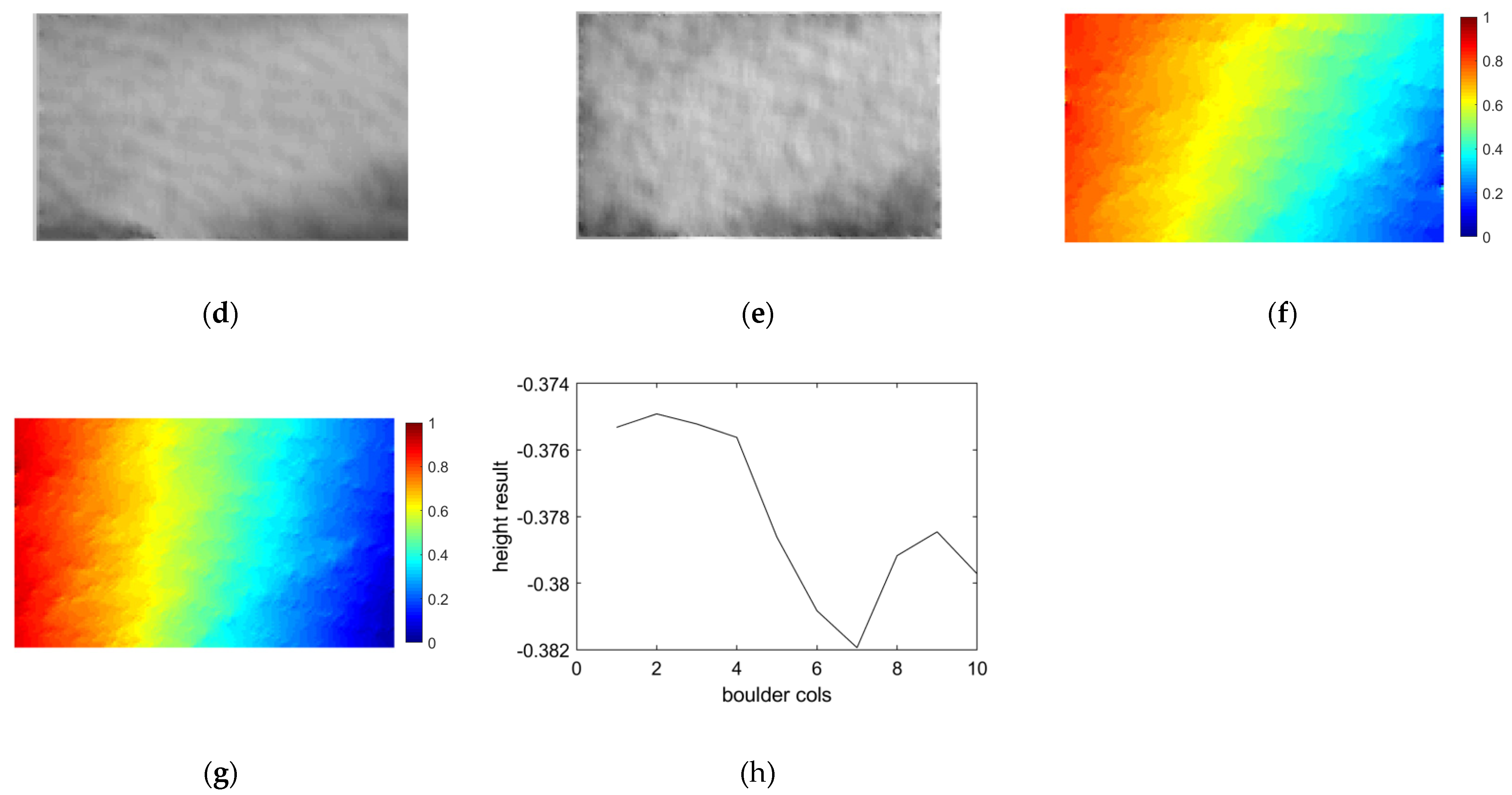
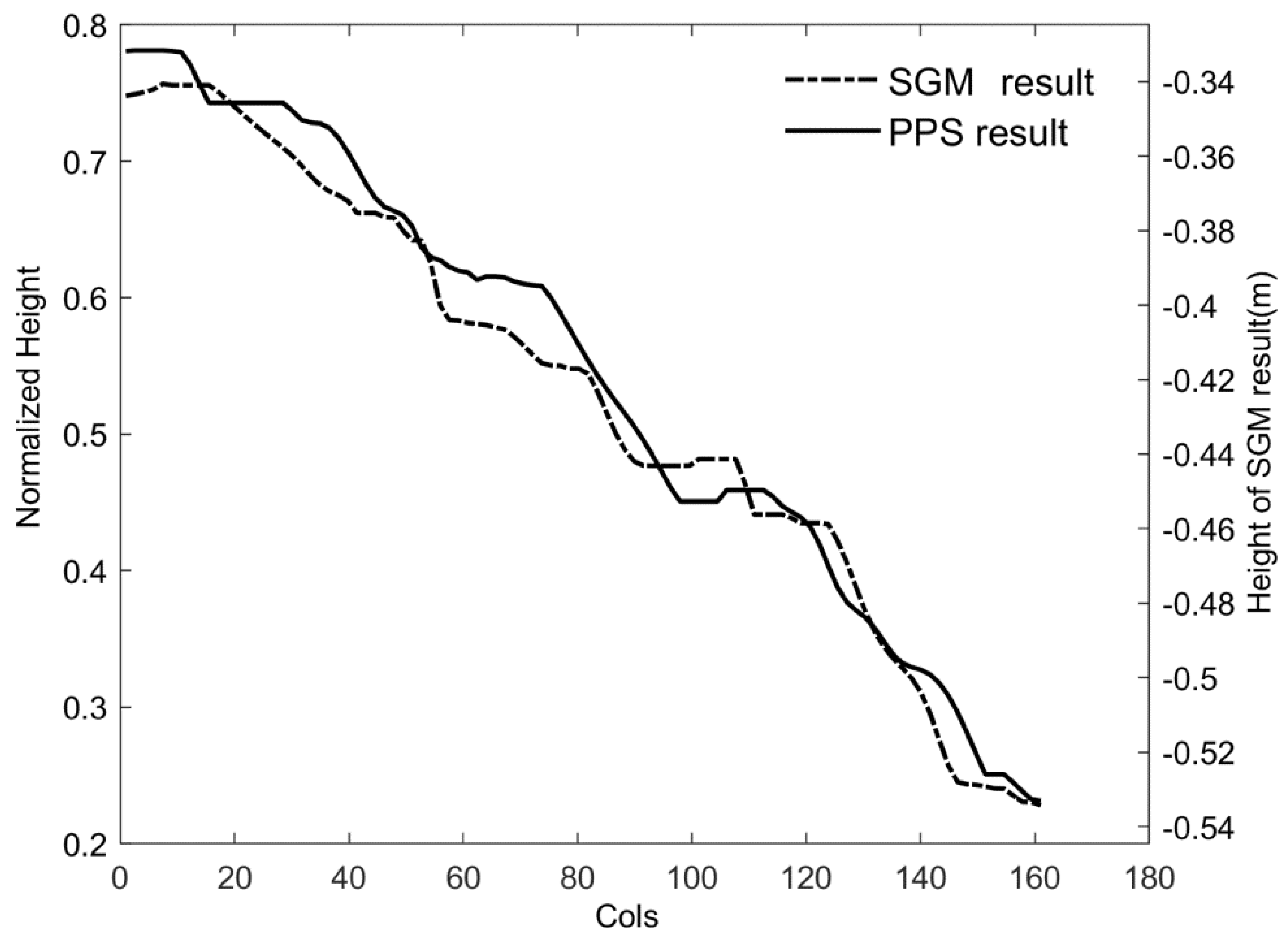
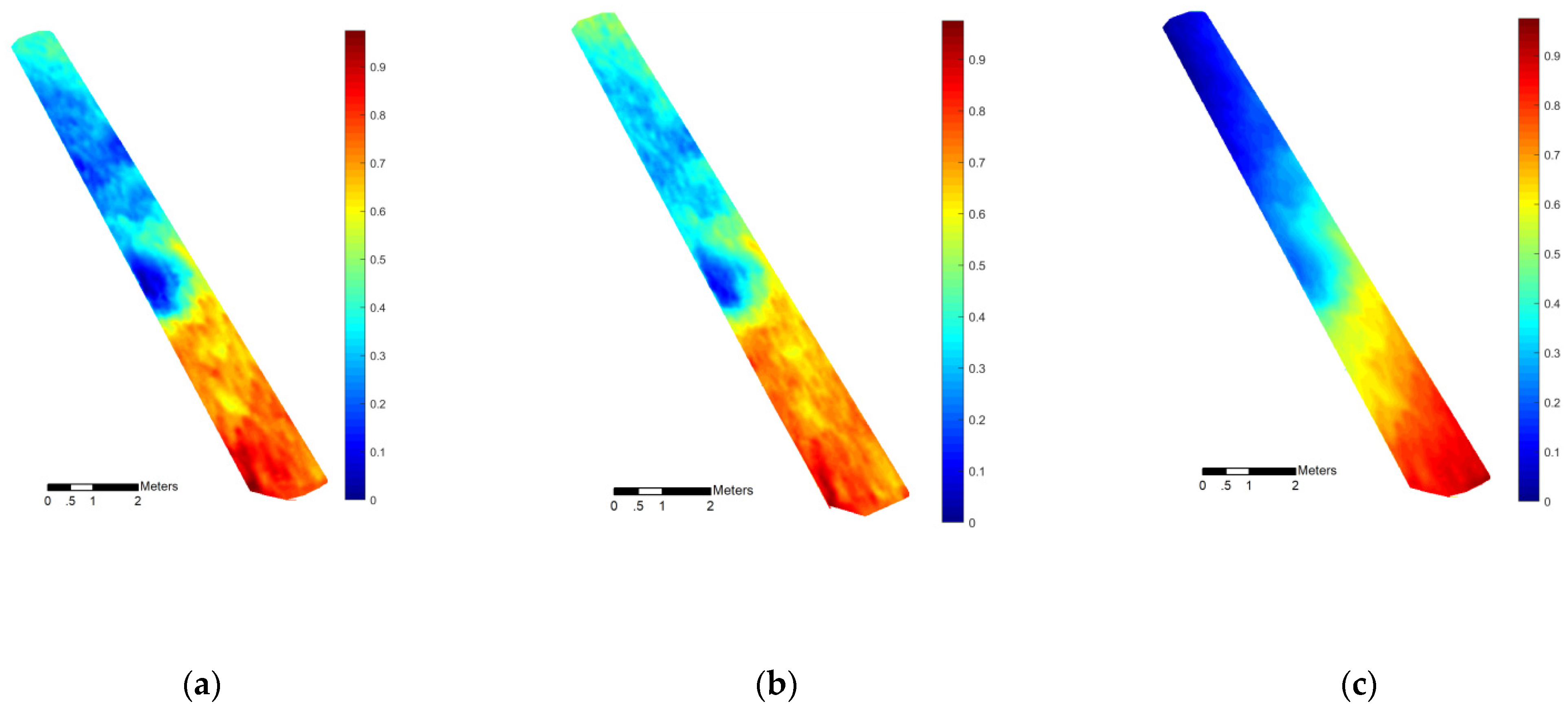
4.3. Experimental Analysis for Yutu-2 Data
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Di, K.; Zhu, M.; Yue, Z.; Lin, Y.; Wan, W.; Liu, Z.; Gou, S.; Liu, B.; Pang, M.; Wang, Y.; et al. Topographic Evolution of Von Kármán Crater Revealed by the Lunar Rover Yutu. Geophys. Res. Lett. 2019, 46, 12764–12770. [Google Scholar] [CrossRef]
- Qiao, L.; Ling, Z.; Fu, X.; Li, B. Geological characterization of the Chang’e-4 landing area on the lunar farside. Icarus 2019, 333, 37–51. [Google Scholar] [CrossRef]
- Yue, Z.; Di, K.; Liu, Z.; Michael, G.; Jia, M.; Xin, X.; Liu, B.; Peng, M.; Liu, J. Lunar regolith thickness deduced from concentric craters in the CE-5 landing area. Icarus 2019, 329, 46–54. [Google Scholar] [CrossRef]
- Liu, Z.; Di, K.; Peng, M.; Wan, W.; Liu, B.; Li, L.; Yu, T.; Wang, B.; Zhou, J.; Chen, H. High precision landing site mapping and rover localization for Chang’e-3 mission. Sci. China Ser. G Phys. Mech. Astron. 2015, 58, 1–11. [Google Scholar] [CrossRef]
- Liu, Z.; Di, K.; Li, J.; Xie, J.; Cui, X.; Xi, L.; Wan, W.; Peng, M.; Liu, B.; Wang, Y.; et al. Landing site topographic mapping and rover localization for Chang’e-4 mission. Sci. China Inf. Sci. 2020, 63, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Di, K.; Liu, Z.; Liu, B.; Wan, W.; Peng, M.; Wang, Y.; Gou, S.; Yue, Z.; Xin, X.; Jia, M.; et al. Chang’e-4 lander localization based on multi-source data. J. Remote Sens. 2019, 23, 177–184. [Google Scholar]
- Di, K.; Liu, Z.; Wan, W.; Peng, M.; Liu, B.; Wang, Y.; Gou, S.; Yue, Z. Geospatial technologies for Chang’e-3 and Chang’e-4 lunar rover missions. Geo-Spat. Inf. Sci. 2020, 23, 87–97. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, W.; Gou, S.; Peng, M.; Liu, Z.; Di, K.; Li, L.; Yu, T.; Wang, J.; Cheng, X. Vision-Based Decision Support for Rover Path Planning in the Chang’e-4 Mission. Remote Sens. 2020, 12, 624. [Google Scholar] [CrossRef] [Green Version]
- Peng, M.; Wan, W.; Wu, K.; Liu, Z.; Li, L.; Di, K.; Li, L.; Miao, Y.; Zhang, L. Topographic mapping capability analysis of Chang’e-3 Navcam stereo images and three-dimensional terrain reconstruction for mission operations. J. Remote Sens. 2014, 18, 995–1002. [Google Scholar]
- Jia, Y.; Zou, Y.; Ping, J.; Xue, C.; Yan, J.; Ning, Y. The scientific objectives and payloads of Chang’E−4 mission. Planet. Space Sci. 2018, 162, 207–215. [Google Scholar] [CrossRef]
- Horn, B.K. Understanding image intensities. Artif. Intell. 1977, 8, 201–231. [Google Scholar] [CrossRef] [Green Version]
- Horn, B.K.P. Height and gradient from shading. Int. J. Comput. Vis. 1990, 5, 37–75. [Google Scholar] [CrossRef]
- Woodham, R.J. Photometric Method For Determining Surface Orientation from Multiple Images. Opt. Eng. 1980, 19, 191139. [Google Scholar] [CrossRef]
- Lohse, V.; Heipke, C. Multi-image shape-from-shading: Derivation of planetary digital terrain models using clementine images. Int. Arch. Photogramm. Rem. Sens. 2004, 35, 828–833. [Google Scholar]
- Lohse, V.; Heipke, C.; Kirk, R.L. Derivation of planetary topography using multi-image shape-from-shading. Planet. Space Sci. 2006, 54, 661–674. [Google Scholar] [CrossRef]
- Grumpe, A.; Belkhir, F.; Wöhler, C. Construction of lunar DEMs based on reflectance modelling. Adv. Space Res. 2014, 53, 1735–1767. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.C.; Grumpe, A.; Wöhler, C. Construction of pixel-level resolution DEMs from monocular images by shape and albedo from shading constrained with low-resolution DEM. ISPRS J. Photogramm. Remote Sens. 2018, 140, 3–19. [Google Scholar] [CrossRef]
- Alexandrov, O.; Beyer, R.A. Multiview Shape-From-Shading for Planetary Images. Earth Space Sci. 2018, 5, 652–666. [Google Scholar] [CrossRef]
- Liu, W.C.; Wu, B. An integrated photogrammetric and photoclinometric approach for illumination-invariant pixel-resolution 3D mapping of the lunar surface. ISPRS J. Photogramm. Remote Sens. 2020, 159, 153–168. [Google Scholar] [CrossRef]
- Burns, K.N.; Speyerer, E.J.; Robinson, M.S.; Tran, T.; Rosiek, M.R.; Archinal, B.A.; Howington-Kraus, E. Digital elevation models and derived products from LROC NAC stereo ob-servations. ISPRS-International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2012, 39, 483–488. [Google Scholar]
- Shean, D.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef] [Green Version]
- DeVenecia, K.; Walker, A.S.; Zhang, B. New approaches to generating and processing high resolution elevation data with imagery. In Proceedings of the Photogrammetric Week, Heidelberg, Germany, 3–9 September 2007; pp. 1442–1448. [Google Scholar]
- Re, C.; Cremonese, G.; Dall’Asta, E.; Forlani, G.; Naletto, G.; Roncella, R. Performance evaluation of DTM area-based matching reconstruction of Moon and Mars. In Proceedings of the SPIE Remote Sensing, Edinburgh, UK, 24–27 September 2012; p. 8537. [Google Scholar]
- Hu, H.; Wu, B. Planetary3d: A photogrammetric tool for 3d topographic mapping of planetary bodies. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 519–526. [Google Scholar] [CrossRef] [Green Version]
- Haruyama, J.; Ohtake, M.; Matsunaga, T.; Morota, T.; Honda, C.; Yokota, Y.; Ogawa, Y. Selene (Kaguya) terrain camera observation results of nominal mission period. In Proceedings of the 40th Lunar and Planetary Science Conference, Woodlands, TX, USA, 23–27 March 2009. [Google Scholar]
- Tran, T.; Rosiek, M.R.; Beyer, R.A.; Mattson, S.; Howington-Kraus, E.; Robinson, M.S.; Archinal, B.A.; Edmunson, K.; Harbour, D.; Anderson, E. Generating digital terrain models using LROC NAC images. In Proceedings of the ASPRS/CaGIS 2010 Fall Specialty Conference, Orlando, FL, USA, 15–19 November 2010. [Google Scholar]
- Di, K.; Liu, Y.; Liu, B.; Peng, M.; Hu, W. A self calibration bundle adjustment method for photogrammetric processing of Chang’E-2 stereo lunar imager. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5432–5442. [Google Scholar]
- Wu, B.; Guo, J.; Zhang, Y.; King, B.; Li, Z.; Chen, Y. Integration of Chang’E-1 Imagery and Laser Altimeter Data for Precision Lunar Topographic Modeling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4889–4903. [Google Scholar] [CrossRef]
- Wu, B.; Hu, H.; Guo, J. Integration of Chang’E-2 imagery and LRO laser altimeter data with a combined block adjustment for precision lunar topographic modeling. Earth Planet. Sci. Lett. 2014, 391, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.; Di, K. Evaluation of Rational Function Model for Geometric Modeling of Chang’e-1 CCD Images. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 121–125. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Liu, Y.; Di, K.; Sun, X. Block adjustment of Chang’E-1 images based on rational function model. In Proceedings of the Remote Sensing of the Environment: 18th National Symposium on Remote Sensing of China, Wuhan, China, 20–23 October 2012; Volume 9158, p. 91580G. [Google Scholar]
- Liu, B.; Xu, B.; Di, K.; Jia, M. A solution to low RFM fitting precision of planetary orbiter images caused by exposure time changing. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 441–448. [Google Scholar]
- Hu, H.; Wu, B. Block adjustment and coupled epipolar rectification of LROC NAC images for precision lunar topographic mapping. Planet. Space Sci. 2018, 160, 26–38. [Google Scholar] [CrossRef]
- Liu, B.; Jia, M.; Di, K.; Oberst, J.; Xu, B.; Wan, W. Geopositioning precision analysis of multiple image triangulation using LROC NAC lunar images. Planet. Space Sci. 2018, 162, 20–30. [Google Scholar] [CrossRef]
- Wu, B.; Zeng, H.; Hu, H. Illumination invariant feature point matching for high-resolution planetary remote sensing images. Planet. Space Sci. 2018, 152, 45–54. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multi-View Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 32, 1362–1376. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Zhu, Q. Integrated point and edge matching on poor textural images constrained by self-adaptive trian-gulations. ISPRS J. Photogramm. Remote Sens. 2012, 68, 40–55. [Google Scholar] [CrossRef]
- Hirschmuller, H. Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 30, 807–814. [Google Scholar] [CrossRef]
- Hu, H.; Chen, C.; Wu, B.; Yang, X.; Zhu, Q.; Ding, Y. Texture-Aware Dense Image Matching using Ternary Census Transform. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Li, Y.; Liu, W.C.; Wang, Y.; Li, F.; Zhao, Y.; Zhang, H. Centimeter-resolution topographic modeling and fine-scale analysis of craters and rocks at the Chang’E-4 landing site. Earth Planet. Sci. Lett. 2021, 553, 116666. [Google Scholar] [CrossRef]
- Taguchi, M.; Funabashi, G.; Watanabe, S.; Fukunushi, H. Lunar albedo at hydrogen Lyman α by the NOZOMI/UVS. J. Earth Planets Space 2000, 52, 645–647. [Google Scholar] [CrossRef] [Green Version]
- Kirk, R.L. A Fast Finite-element Algorithm for Two-dimensional Photoclinometry. Ph.D. Thesis, Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA, USA, 1987; pp. 165–258. [Google Scholar]
- Kirk, R.L.; Barrett, J.M.; Soderblom, L.A. Photoclinometry Made Simple. In Proceedings of the ISPRS Commission IV, Working Group IV/9 2003, ‘‘Advances in Planetary Mapping” Workshop, Houston, TX, USA, 22 March 2003. [Google Scholar]
- O’Hara, R.; Barnes, D. A new shape from shading technique with application to Mars Express HRSC images. ISPRS J. Photogramm. Remote Sens. 2012, 67, 27–34. [Google Scholar] [CrossRef]
- Kirk, R.L.; Howington-Kraus, E.; Redding, B.; Galuszka, D.; Hare, T.M.; Archinal, B.A.; Soderblom, L.A.; Barret, J.A. High-resolution topomapping of candidate MER landing sites with Mars orbiter camera narrow-angle images. J. Geophys. Res. 2003, 108, 8088. [Google Scholar] [CrossRef]
- Beyer, R.A.; Kirk, R.L. Meter-scale slopes of candidate MSL landing sites from point photoclinometry. Space Sci. Rev. 2012, 170, 775–791. [Google Scholar] [CrossRef]
- Wu, B.; Li, F.; Hu, H.; Zhao, Y.; Wang, Y.; Xiao, P.; Li, Y.; Liu, W.C.; Chen, L.; Ge, X.; et al. Topographic and Geomorphological Mapping and Analysis of the Chang’E-4 Landing Site on the Far Side of the Moon. Photogramm. Eng. Remote Sens. 2020, 86, 247–258. [Google Scholar] [CrossRef]
- Wöhler, C.; Grumpe, A.; Berezhnoy, A.; Bhatt, M.U.; Mall, U. Integrated topographic, photometric and spectral analysis of the lunar surface: Application to impact melt flows and ponds. Icarus 2014, 235, 86–122. [Google Scholar] [CrossRef]
- Gao, Y.; Spiteri, C.; Li, C.; Zheng, Y.C. Lunar soil strength estimation based on Chang’E-3 images. Adv. Space Res. 2016, 58, 1893–1899. [Google Scholar] [CrossRef] [Green Version]
- Ding, C.; Xiao, Z.; Wu, B.; Li, Y.; Prieur, N.C.; Cai, Y.; Su, Y.; Cui, J. Fragments delivered by secondary craters at the Chang’e 4 landing site. Geophys. Res. Lett. 2020, 47, e2020GL087361. [Google Scholar] [CrossRef]
- Jiang, C.; Douté, S.; Luo, B.; Zhang, L. Fusion of photogrammetric and photoclinometric information for high-resolution DEMs from Mars in-orbit imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 418–430. [Google Scholar] [CrossRef]
- Tenthoff, M.; Wohlfarth, K.; Wöhler, C. High Resolution Digital Terrain Models of Mercury. Remote Sens. 2020, 12, 3989. [Google Scholar] [CrossRef]
- Ackermann, J.; Langguth, F.; Fuhrmann, S.; Goesele, M. Photometric stereo for outdoor webcams. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 262–269. [Google Scholar]
- Liu, W.C.; Wu, B.; Wöhler, C. Effects of illumination differences on photometric stereo shape-and-albedo-from-shading for precision lunar surface reconstruction. ISPRS J. Photogramm. Rem. Sens. 2018, 136, 58–72. [Google Scholar]
- Herbort, S.; Wöhler, C. An introduction to image-based 3D surface reconstruction and a survey of photometric stereo methods. 3D Res. 2011, 2, 1–17. [Google Scholar] [CrossRef]
- Ackermann, J.; Goesele, M. A survey of photometric stereo techniques. Found. Trends Comput. Graph. Vis. 2015, 9, 149–254. [Google Scholar] [CrossRef]
- Tankus, A.; Kiryati, N. Photometric stereo under perspective projection. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; pp. 611–616. [Google Scholar]
- Argyriou, V.; Petrou, M. Photometric Stereo: An Overview. Adv. Imaging Electron Phys. 2009, 156, 1–54. [Google Scholar]
- Tankus, A.; Sochen, N.; Yeshurun, Y. Shape-from-shading under perspective projection. Int. J. Comput. Vis. 2005, 63, 21–43. [Google Scholar] [CrossRef]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 2012; ISBN 978-1-139-21750-7. [Google Scholar]
- McEwen, A.S. Photometric functions for photoclinometry and other applications. Icarus 1991, 92, 298–311. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: The coherent backscatter opposition effect and anisotropic scattering. Icarus 2002, 157, 523–534. [Google Scholar] [CrossRef] [Green Version]
- Besse, S.; Sunshine, J.; Staid, M.; Boardman, J.; Pieters, C.; Guasqui, P.; Maralet, E.; McLaughlin, S.; Yokota, Y.; Li, J.-Y. A visible and near-infrared photometric correction for Moon Mineralogy Mapper (M3). Icarus 2013, 222, 229–242. [Google Scholar] [CrossRef]
- Hillier, J.K.; Buratti, B.J.; Hill, K. Multispectral photometry of the Moon and absolute calibration of the Clementine UV/Vis camera. Icarus 1999, 141, 205–225. [Google Scholar] [CrossRef]
- Sato, H.; Denevi, B.W.; Robinson, M.S.; Boyd, A.; Hapke, B.W.; McEwen, A.S.; Speyerer, E.J. Photometric normalization of LROC WAC global color mosaic. Lunar Planet. Sci. 2001, XLII, 636. [Google Scholar]
- Wu, Y.; Besse, S.; Li, J.Y.; Combe, J.P.; Wang, Z.; Zhou, X.; Wang, C. Photometric correction and in-flight calibration of Chang’E-1 Interference Imaging Spectrometer (IIM) data. Icarus 2013, 222, 283–295. [Google Scholar] [CrossRef]
- Bondarenko, N.V.; Dulova, I.A.; Kornienko, Y.V. Photometric Functions and the Improved Photoclinometry Method: Mature Lunar Mare Surfaces. In Proceedings of the Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2020; p. 1845. [Google Scholar]
- Lin, H.; Yang, Y.; Lin, Y.; Liu, Y.; Wei, Y.; Li, S.; Hu, S.; Yang, W.; Wan, W.; Xu, R.; et al. Photometric properties of lunar regolith revealed by the Yutu-2 rover. Astron. Astrophys. 2020, 638, A35. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W. Algorithms for the solution of the nonlinear least-squares problem. SIAM J. Numer. Anal. 1978, 15, 977–992. [Google Scholar] [CrossRef]
- Harker, M.; O’Leary, P. Least squares surface reconstruction from gradients: Direct algebraic methods with spectral, Tikhonov, and constrained regularization. In Proceedings of the IEEE Computer Vision Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2529–2536. [Google Scholar]
- Quéau, Y.; Lauze, F.; Durou, J.D. Solving uncalibrated photometric stereo using total variation. J. Math. Imaging Vis. 2015, 52, 87–107. [Google Scholar] [CrossRef] [Green Version]
- Sha, C.; Hou, J.; Cui, H. A robust 2D Otsu’s thresholding method in image segmentation. J. Vis. Commun. Image Represent. 2016, 41, 339–351. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a Completely Blind Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 3, 209–212. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-Reference Image Quality Assessment in the Spatial Domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. Referenceless Image Spatial Quality Evaluation Engine. In Proceedings of the 45th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2011. [Google Scholar]



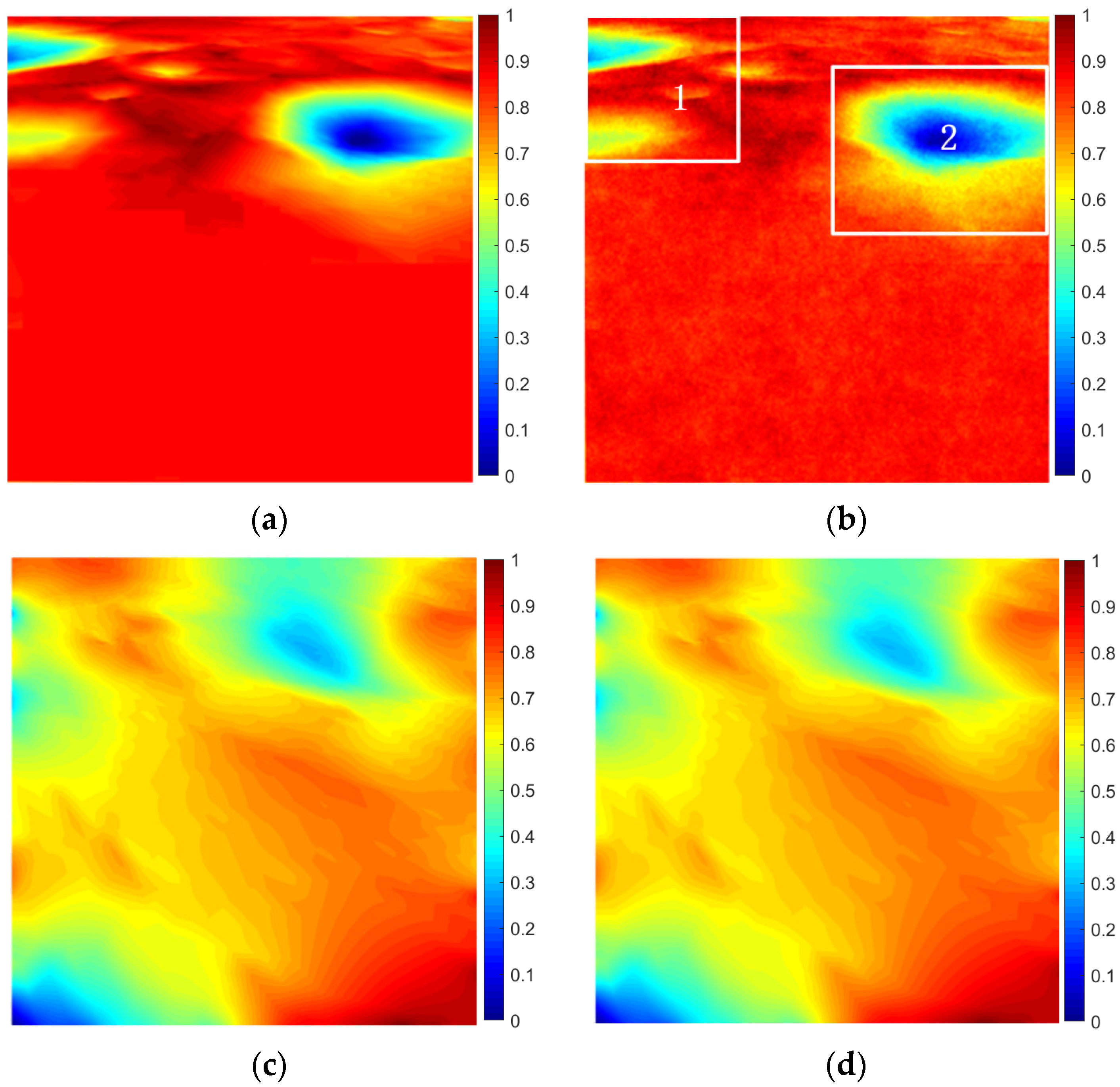
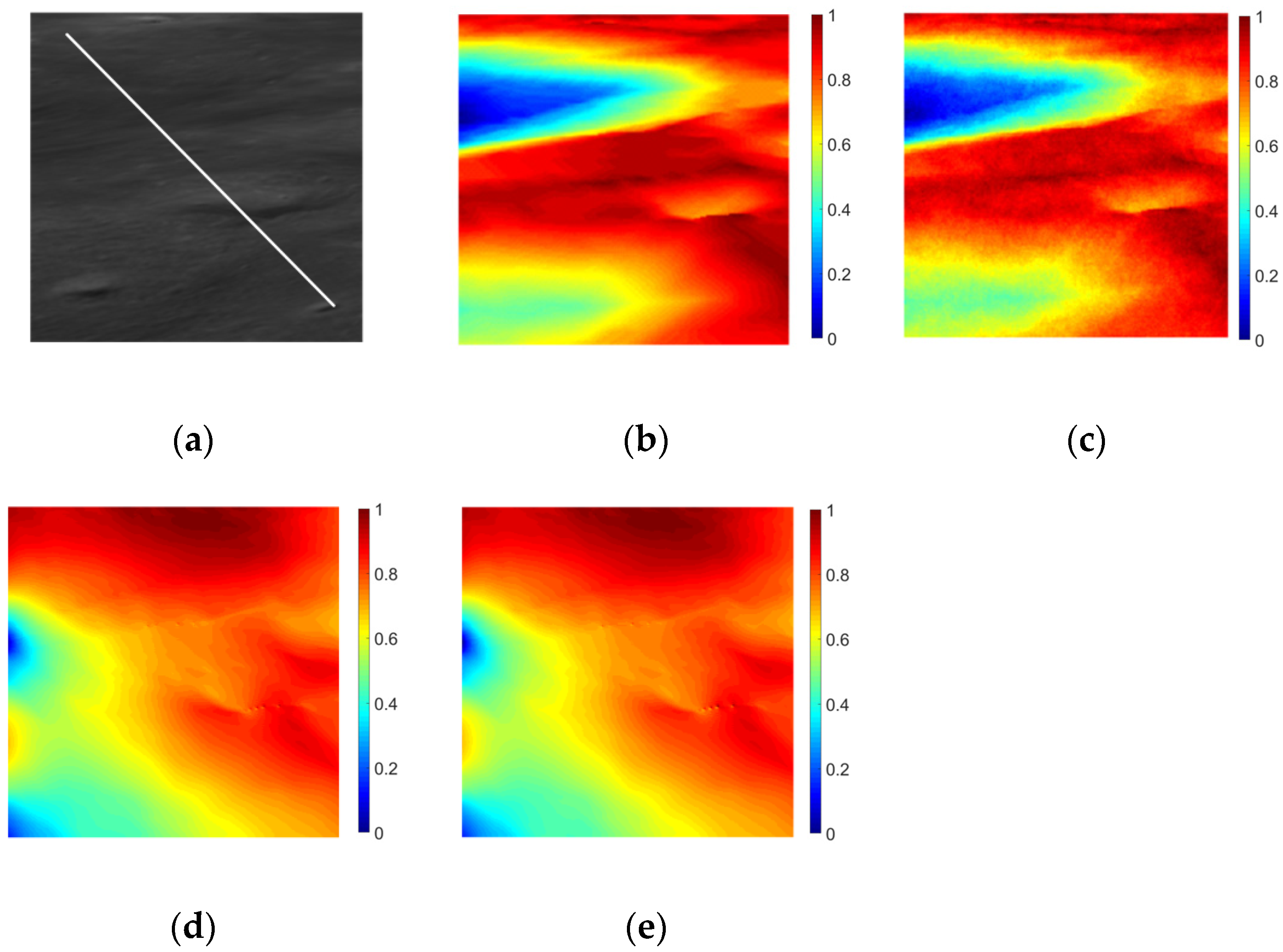





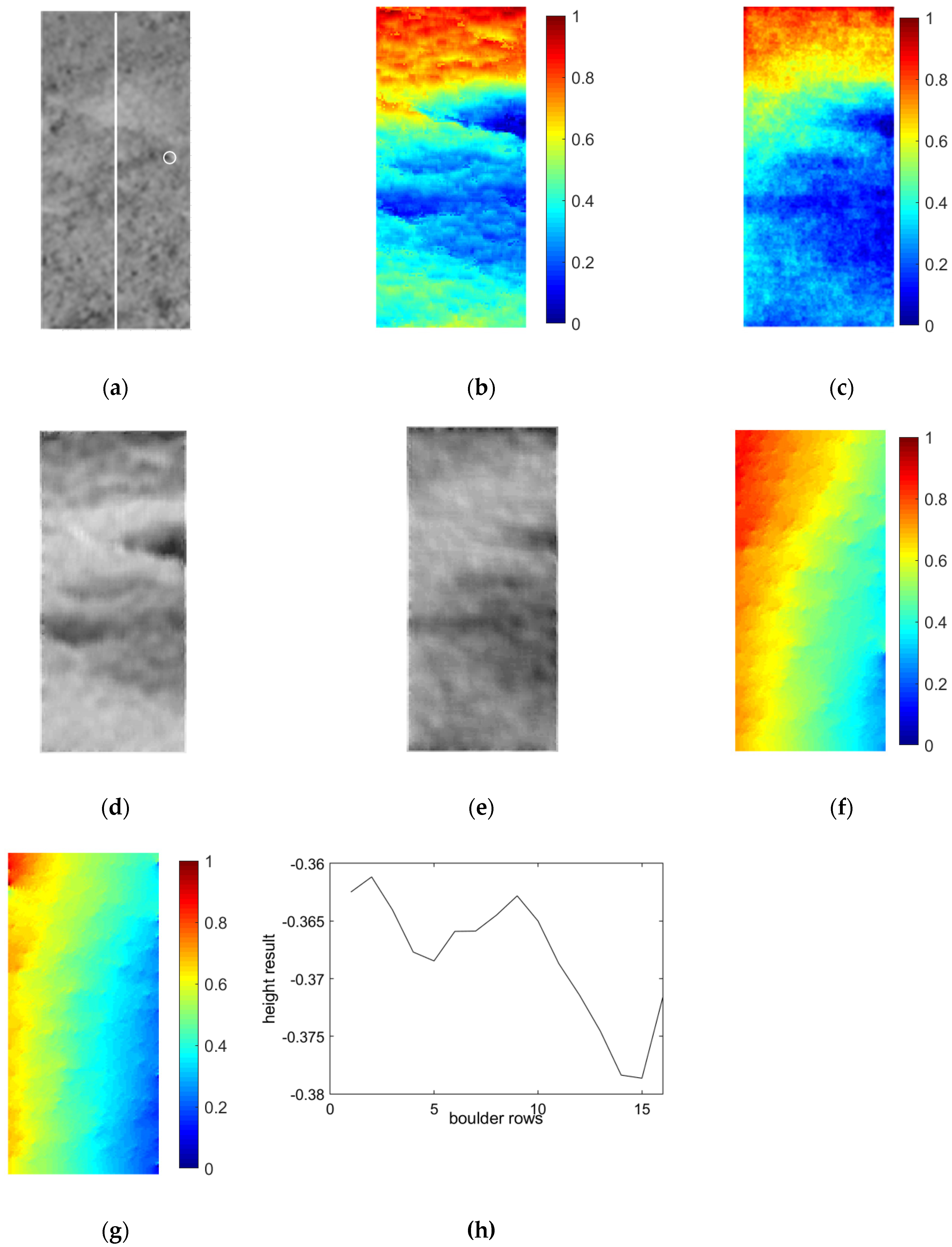


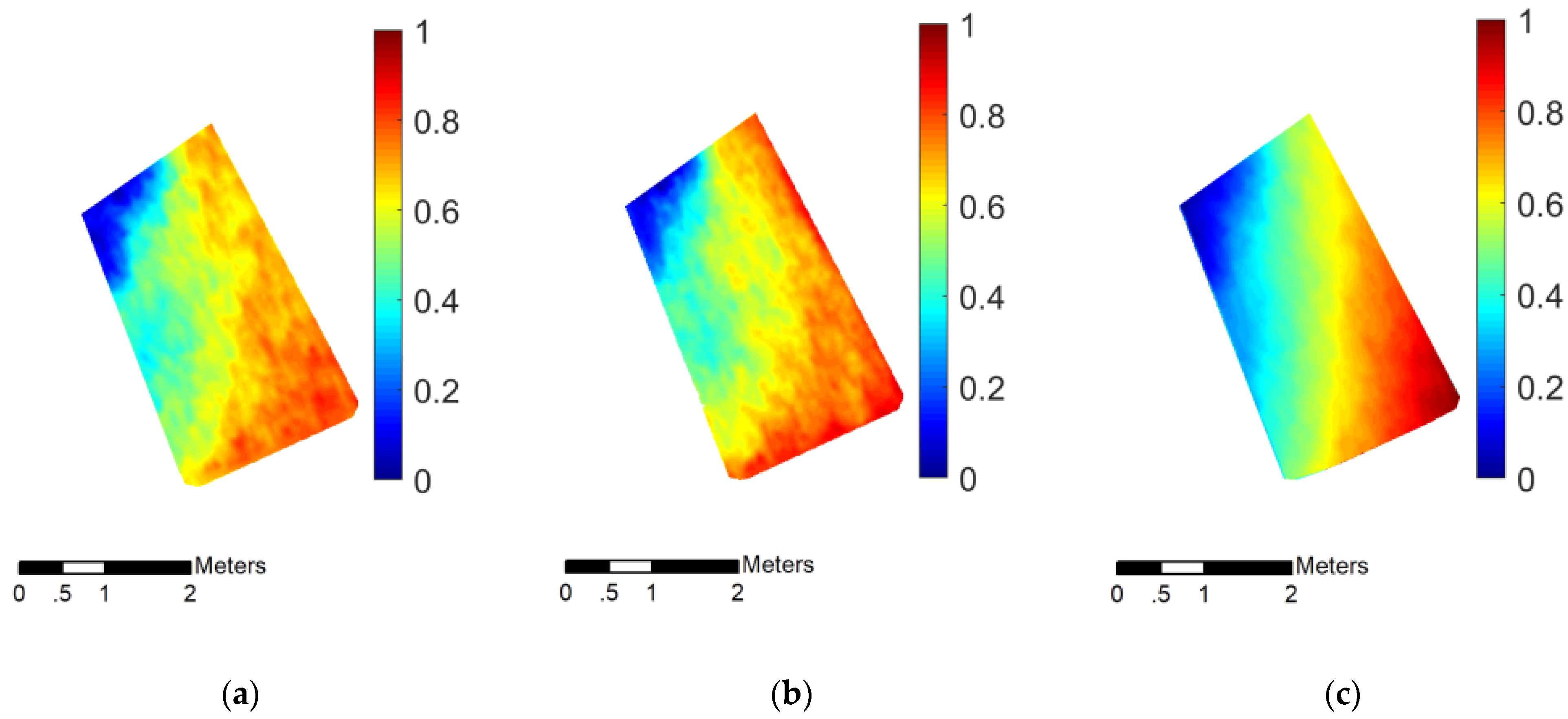
| Image ID | Solar Azimuth Angle (°) | Solar Elevation Angle (°) | Approximated Phase Angle (°) |
|---|---|---|---|
| Figure 5b | 90 | 55 | 107.5 |
| Figure 5c | 90 | 60 | 103.3 |
| Figure 5d | 90 | 65 | 99.0 |
| Methods | MEANN (°) | NFD | |
|---|---|---|---|
| ROI 1 | PPS | 0.494 | 0.003 |
| PSPP | 59.799 | - | |
| PSOP | 60.065 | - | |
| ROI 2 | PPS | 0.734 | 0.092 |
| PSPP | 59.998 | - | |
| PSOP | 59.855 | - | |
| whole image | PPS | 0.324 | 0.042 |
| PSPP | 59.963 | - | |
| PSOP | 59.960 | - |
| Stereo baseline | 0.27 m |
| Focal length | 1189 pixels |
| Pixel size | 1024 × 1024 |
| FOV | 46.4° × 46.4° |
| Image ID | Solar Azimuth Angle (°) | Solar Elevation Angle (°) | Approximated Phase Angle (°) |
|---|---|---|---|
| 94741 | −70.8 | 17 | 37.7 |
| 94914 | −71.8 | 16.2 | 38.6 |
| 95633 | −77.1 | 11.4 | 44.1 |
| Methods | MEANN (°) | NFD | |
|---|---|---|---|
| ROI 1 | PPS | 8.274 | 0.336 |
| PSPP | 93.792 | - | |
| PSOP | 102.746 | - | |
| ROI 2 | PPS | 9.459 | 0.386 |
| PSPP | 86.786 | - | |
| PSOP | 101.843 | - |
| Methods | NIQE | BRISQUE | |
|---|---|---|---|
| ROI 1 | SGM | 11.15 | 45.41 |
| PPS | 10.81 | 45.26 | |
| PSOP for orthorectified images | 11.24 | 46.15 | |
| ROI 2 | SGM | 7.819 | 47.47 |
| PPS | 7.540 | 47.37 | |
| PSOP for orthorectified images | 8.230 | 48.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, M.; Di, K.; Wang, Y.; Wan, W.; Liu, Z.; Wang, J.; Li, L. A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images. Remote Sens. 2021, 13, 2975. https://doi.org/10.3390/rs13152975
Peng M, Di K, Wang Y, Wan W, Liu Z, Wang J, Li L. A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images. Remote Sensing. 2021; 13(15):2975. https://doi.org/10.3390/rs13152975
Chicago/Turabian StylePeng, Man, Kaichang Di, Yexin Wang, Wenhui Wan, Zhaoqin Liu, Jia Wang, and Lichun Li. 2021. "A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images" Remote Sensing 13, no. 15: 2975. https://doi.org/10.3390/rs13152975
APA StylePeng, M., Di, K., Wang, Y., Wan, W., Liu, Z., Wang, J., & Li, L. (2021). A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images. Remote Sensing, 13(15), 2975. https://doi.org/10.3390/rs13152975






