Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model
Abstract
:1. Introduction
2. Self-Made Instrument of Multi-Angle Spectrometer Measurement
3. Materials Collection and Methodology
3.1. Multi-Angle Spectra Data Collection
3.2. Models and Methodology
3.2.1. Hapke Radiative Transfer Model
3.2.2. Monte Carlo Method
3.2.3. Optimization Retrieval of Photometric Parameters
4. Results and Discussion
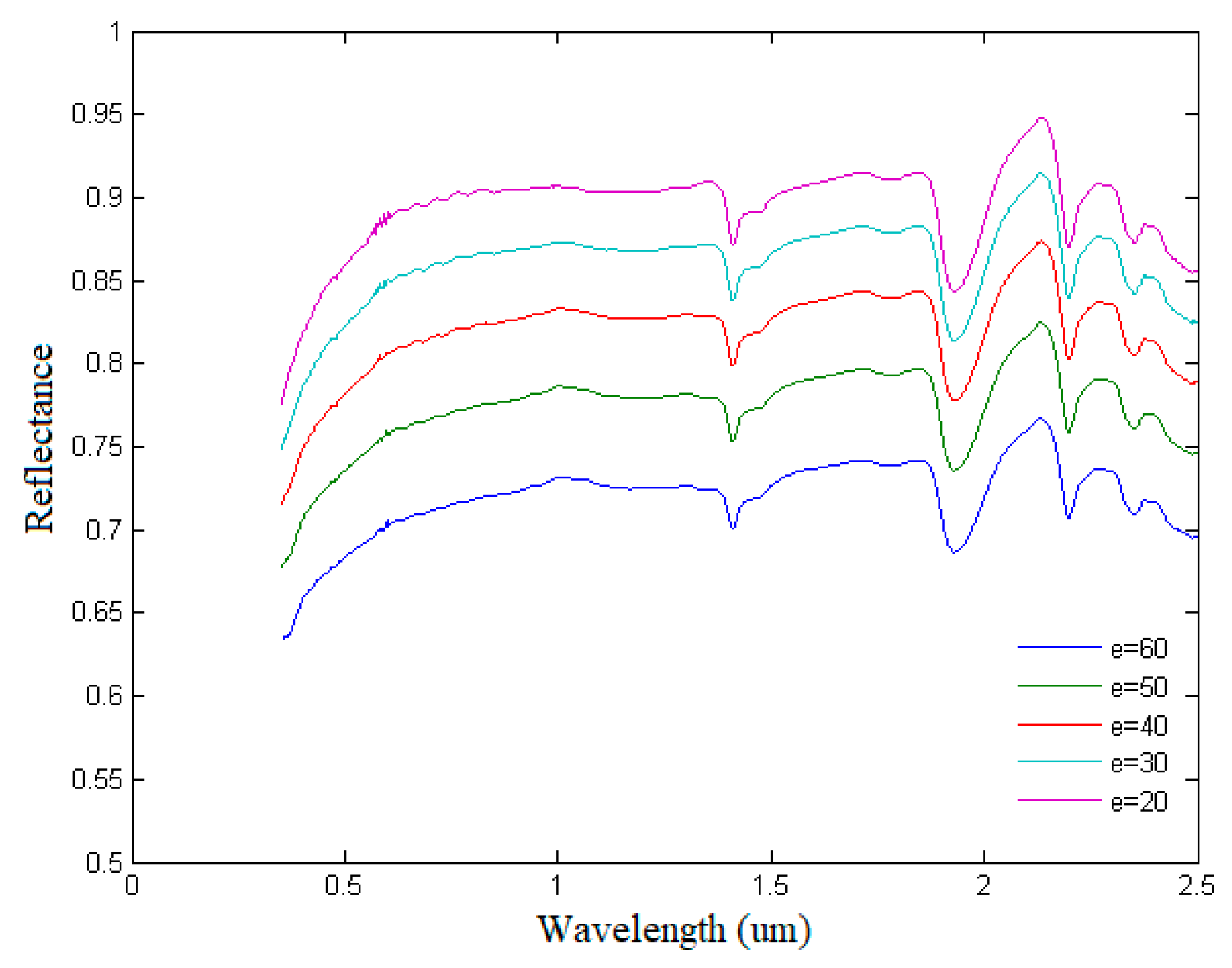
4.1. Retrieval of Photometric Parameters and Spectral Curve Simulation of Olivine
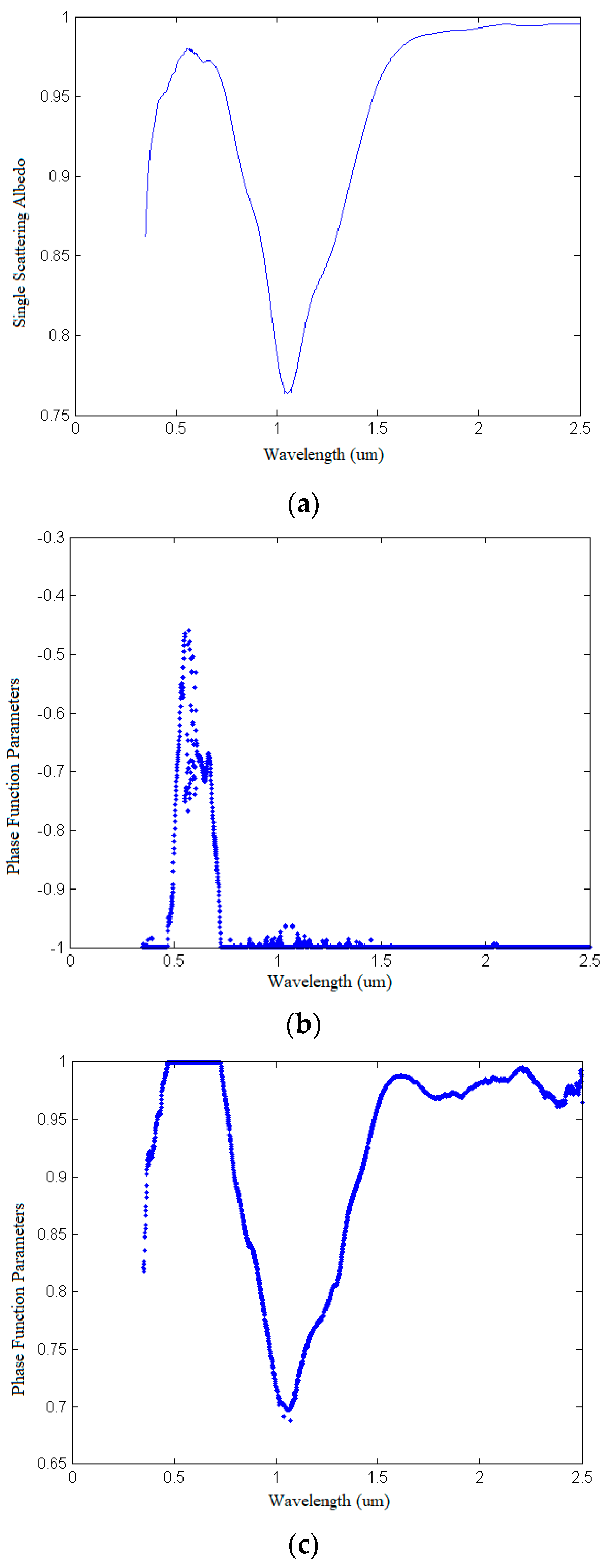
4.1.1. Photometric Parameter Retrieval of Olivine
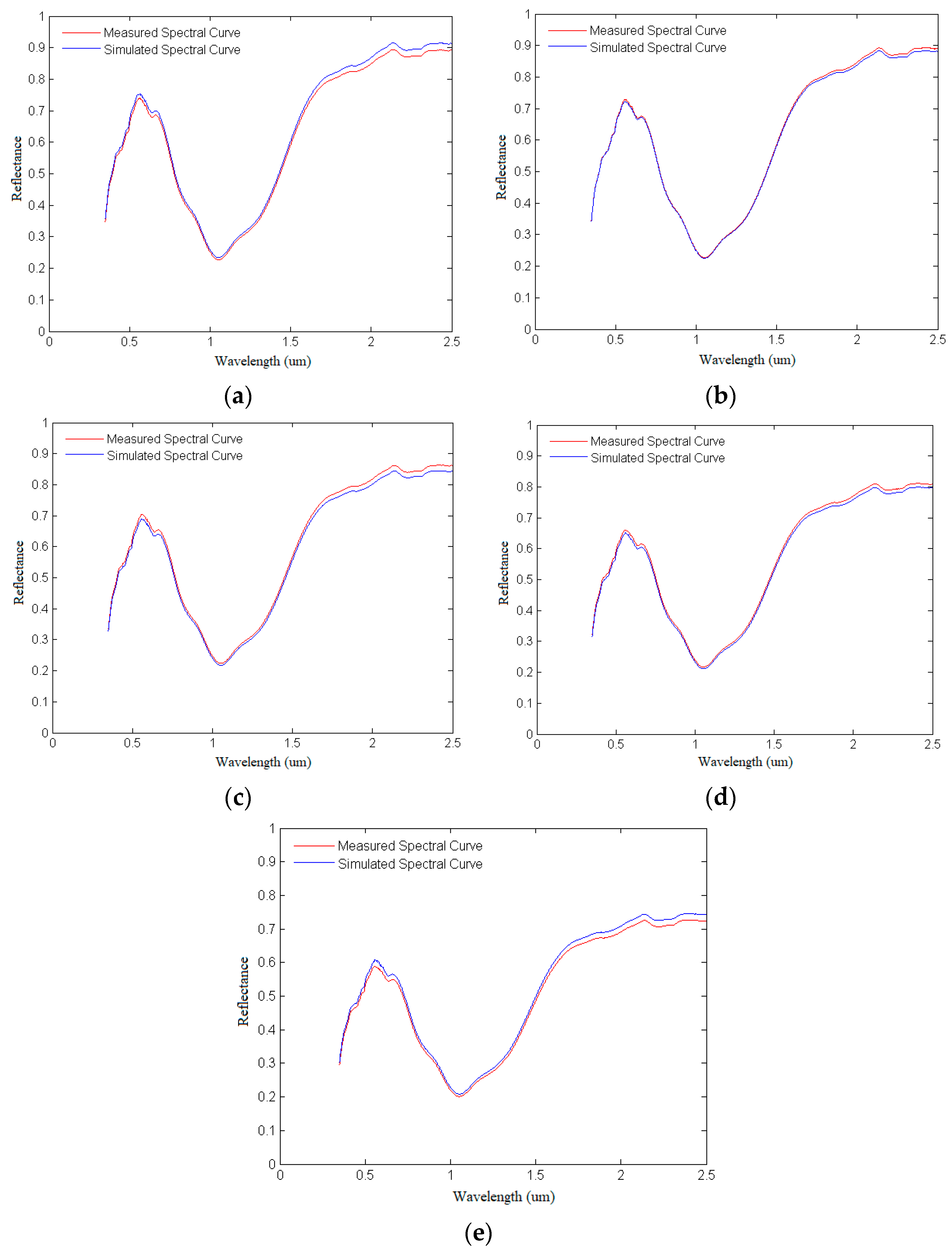
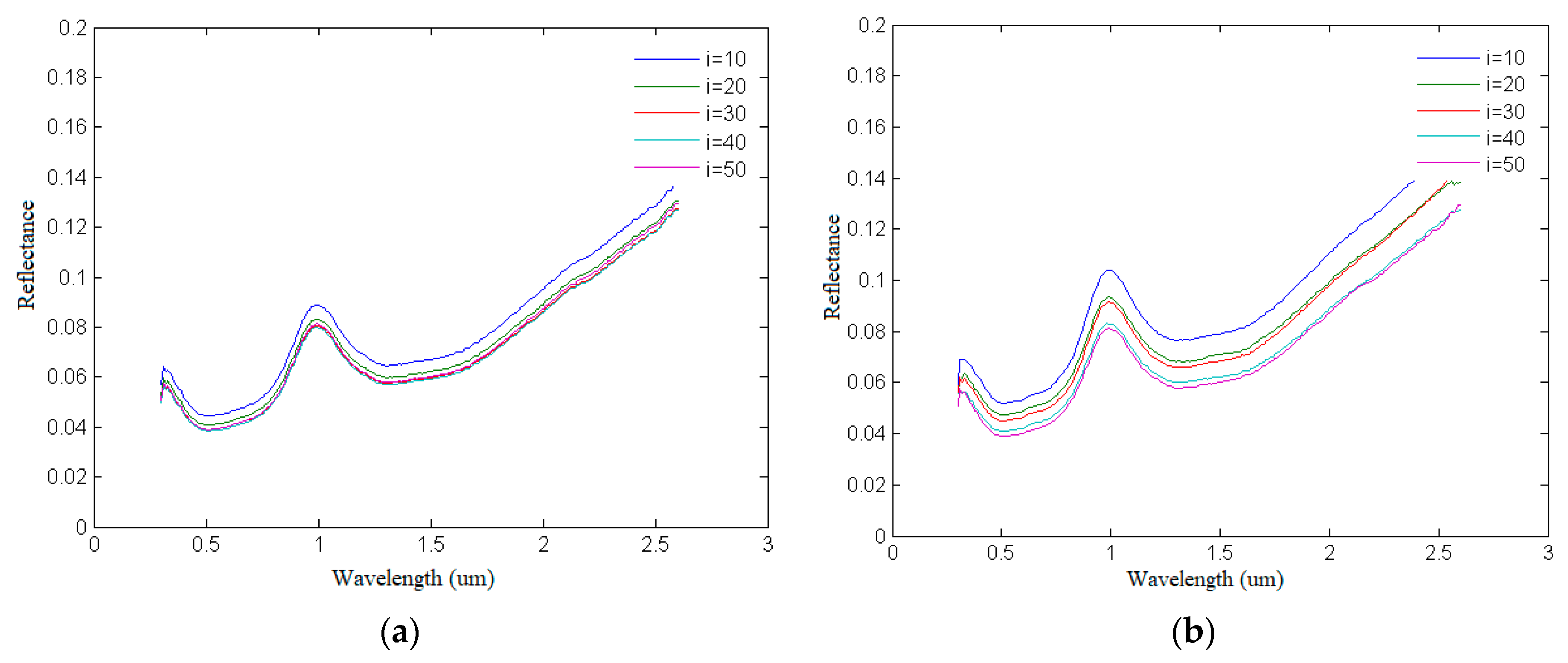
4.1.2. Spectral Curve Simulation of Olivine Based on Retrieval of Photometric Parameters
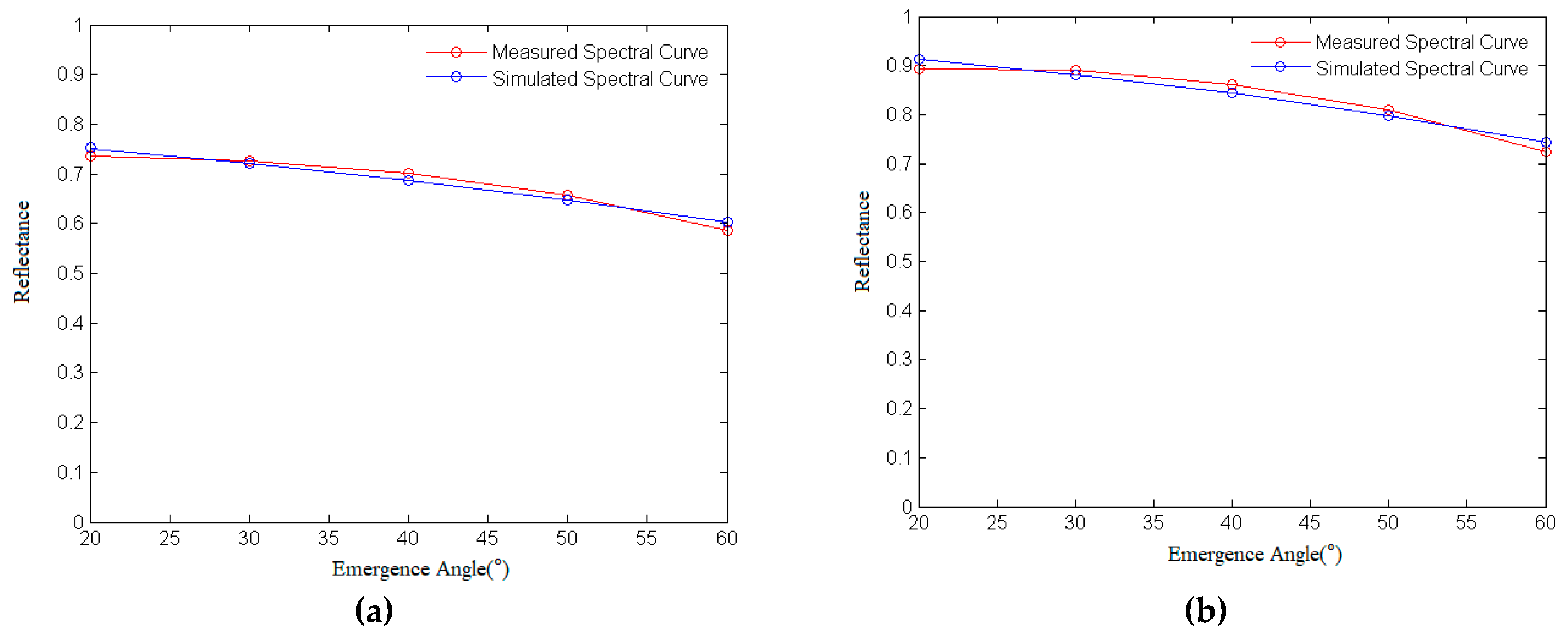
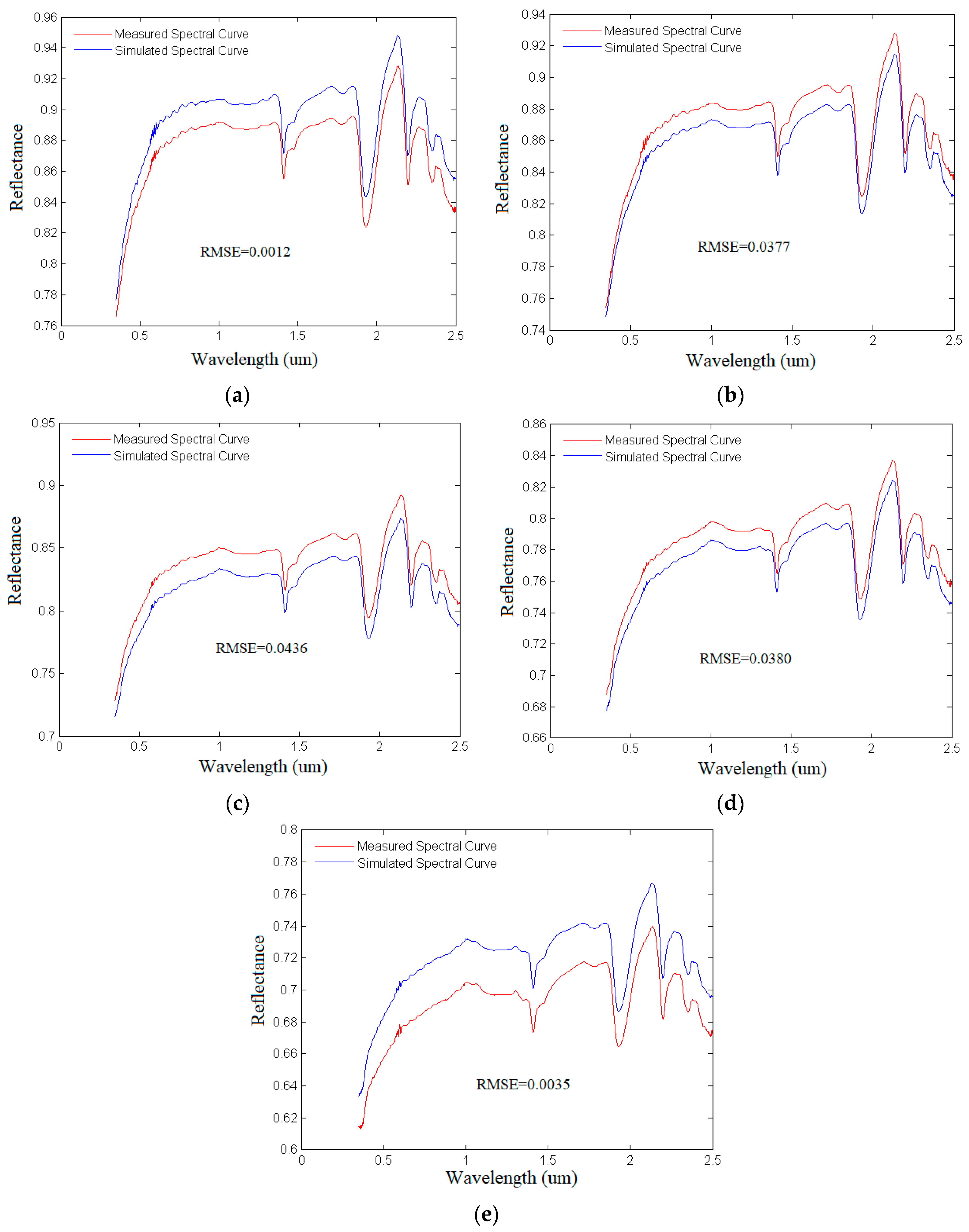
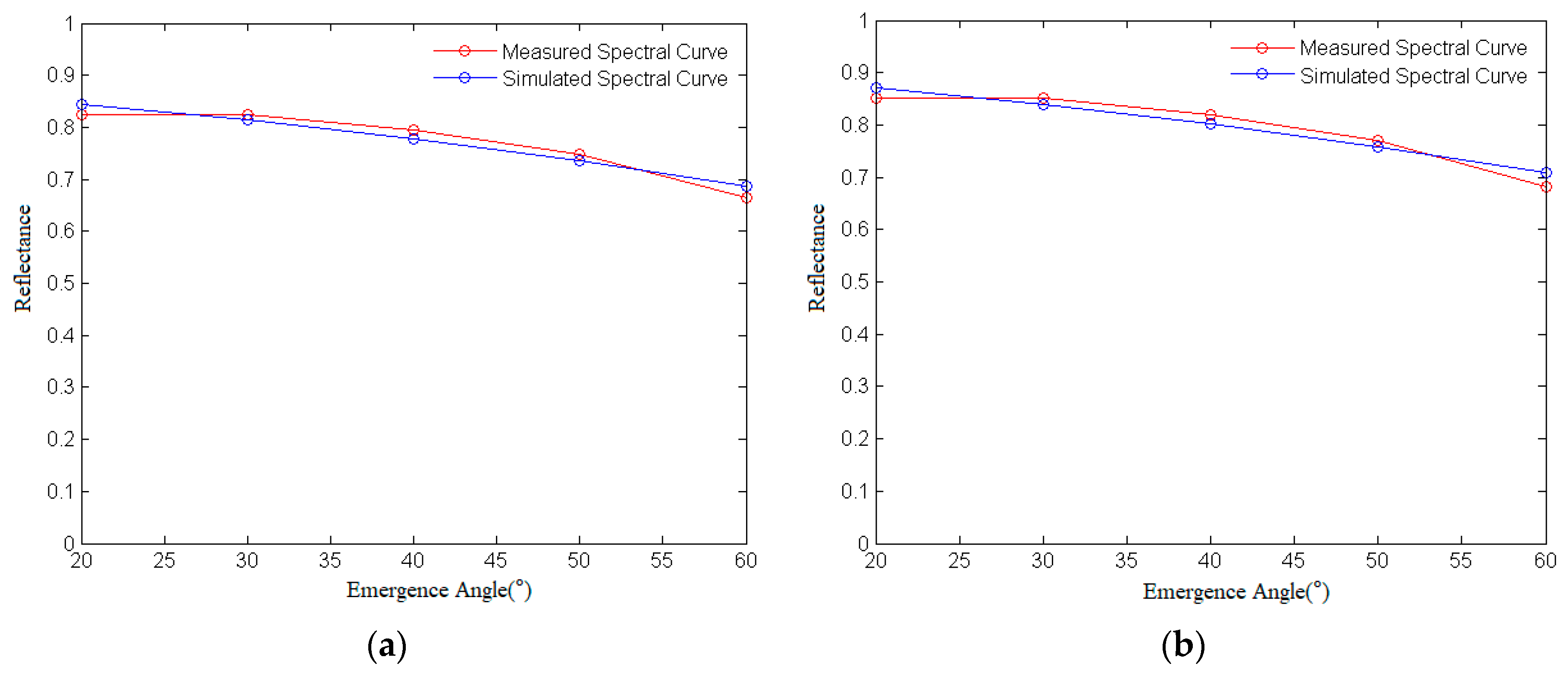
4.1.3. Comparative Analysis between the Simulated Spectra and Measured Spectra of Olivine
4.2. Retrieval of Photometric Parameters and Spectral Curve Simulation of Plagioclase
4.2.1. Photometric Parameters Retrieval of Plagioclase
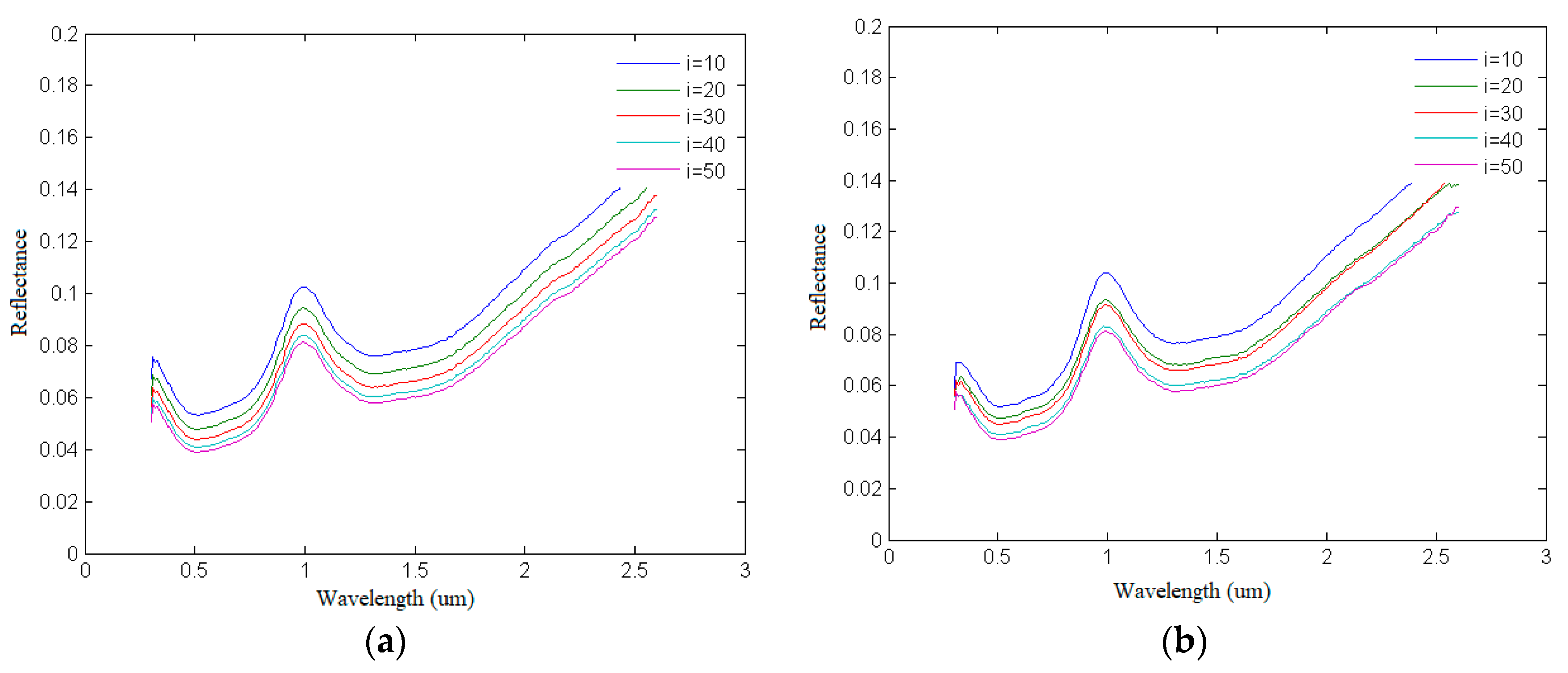
4.2.2. Spectral Curve Simulation of Plagioclase Based on Retrieval of Photometric Parameters
4.2.3. Comparative Analysis between the Simulated Spectra and Measured Spectra of Plagioclase
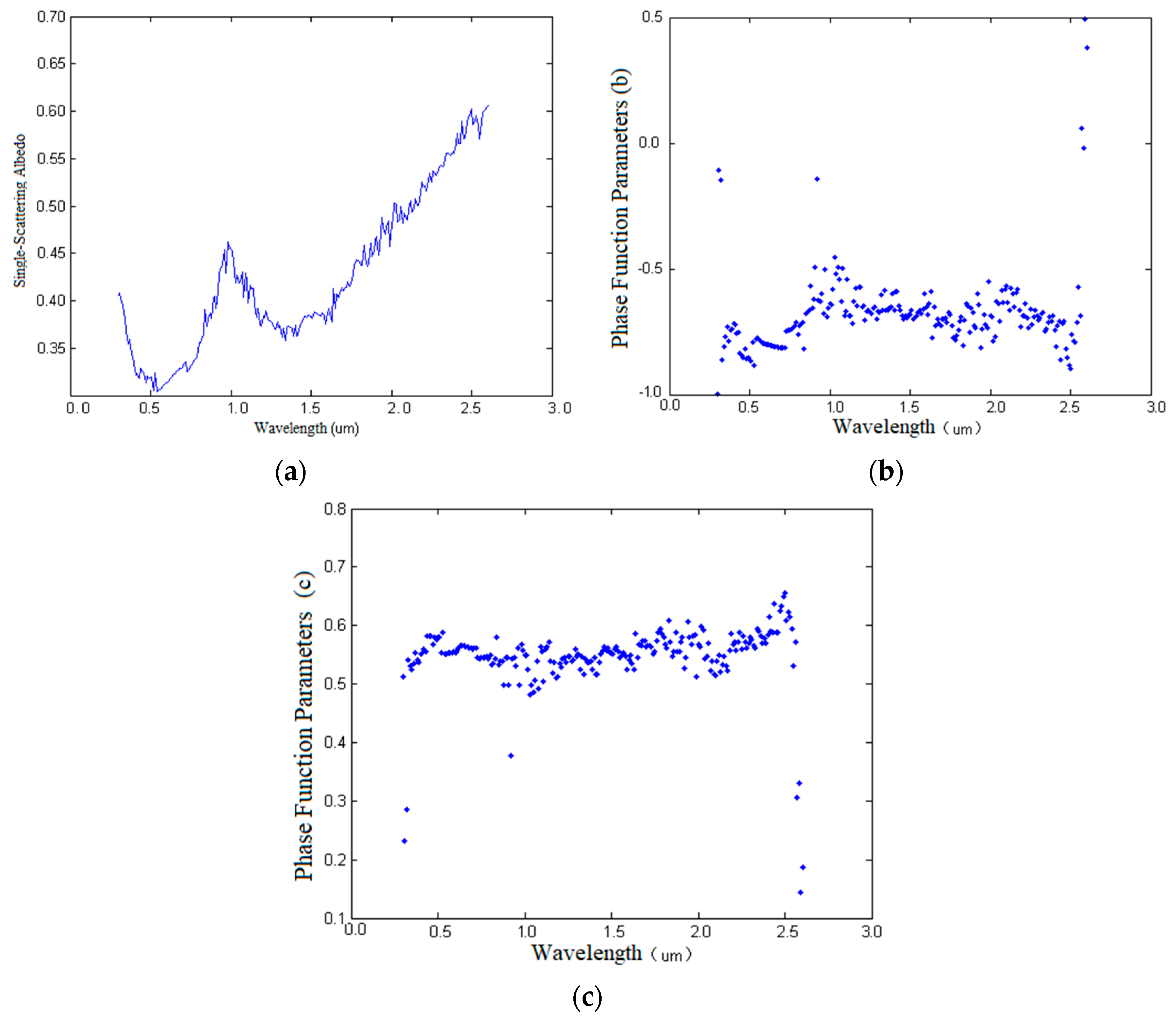
4.3. Retrieval of Photometric Parameters and Spectral Curve Simulation of Ilmenite of RELAB Spectral Library and Reliability Evaluation of Coefficient Setting of Legendre Polynomial of Scattering Phase Function
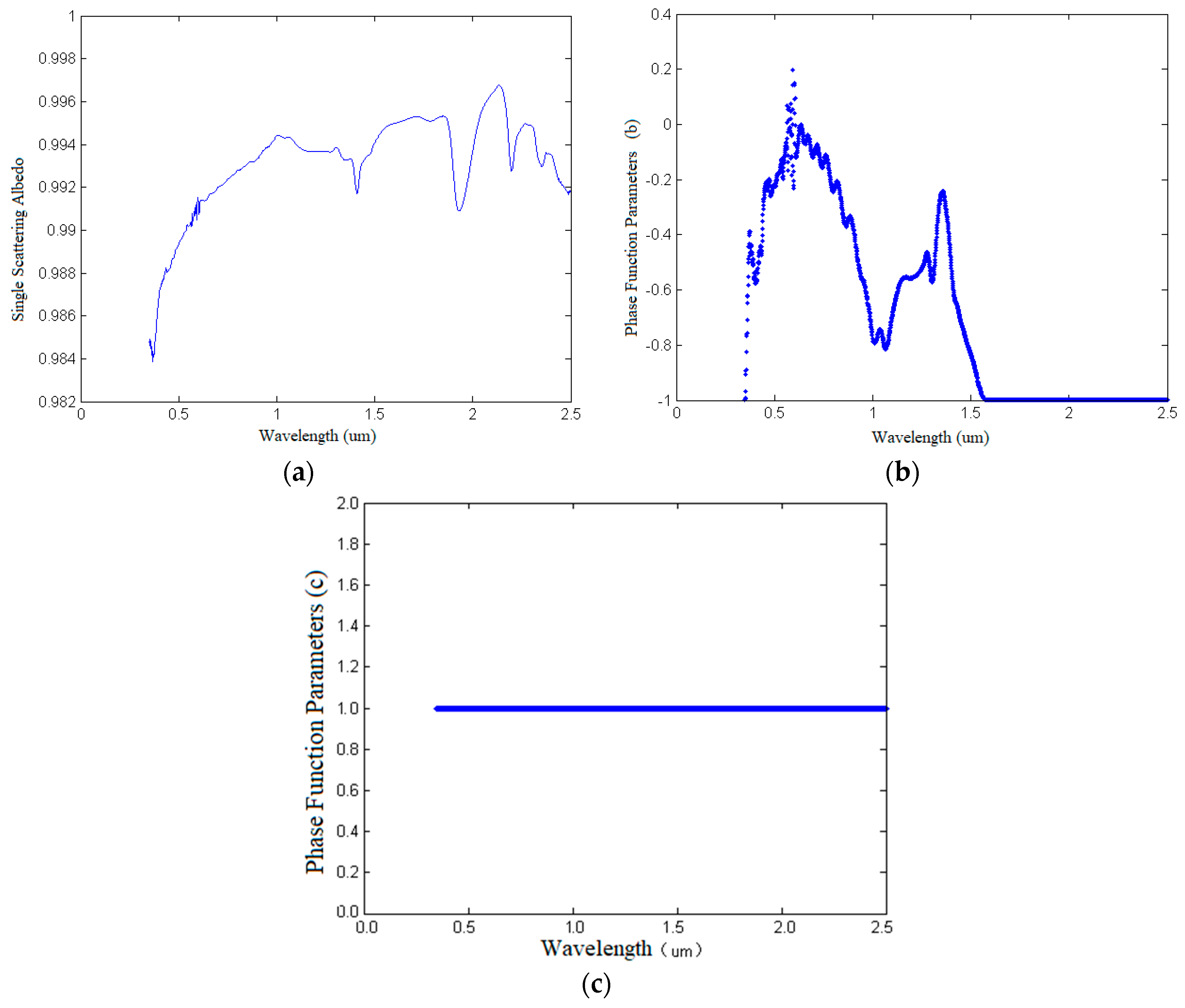
4.3.1. Retrieval of Photometric Parameters of Ilmenite of the RELAB Spectral Library
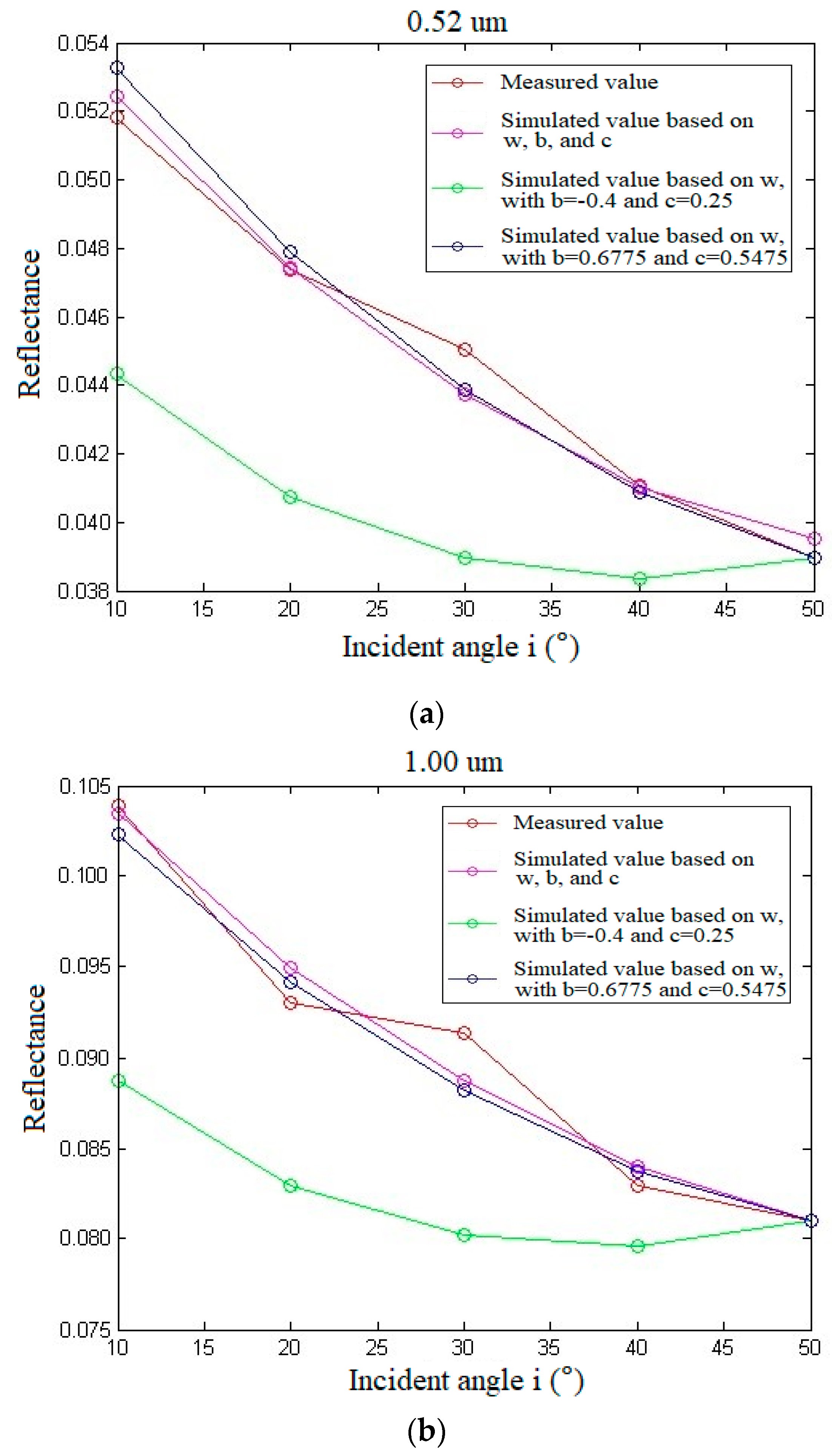
4.3.2. Spectral Curve Simulation of Ilmenite of the RELAB Spectral Library Based on Empirical Values of Photometric Parameters b and c
4.3.3. Spectral Curve Simulation of Ilmenite of the RELAB Spectrum Library Based on the Average Value of Photometric Parameters of b and c Calculated from Multi-Angle Spectrum
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shirmard, H.; Farahbakhsh, E.; Pour, A.B.; Muslim, A.M.; Müller, R.D.; Chandra, R. Integration of Selective Dimensionality Reduction Techniques for Mineral Exploration Using ASTER Satellite Data. Remote Sens. 2020, 12, 1261. [Google Scholar] [CrossRef] [Green Version]
- Sekandari, M.; Masoumi, I.; Pour, A.B.; Muslim, A.M.; Rahmani, O.; Hashim, M.; Zoheir, B.; Pradhan, B.; Misra, A. Application of Landsat-8, Sentinel-2, ASTER and WorldView-3 Spectral Imagery for Exploration of Carbonate-Hosted Pb-Zn Deposits in the Central Iranian Terrane (CIT). Remote Sens. 2020, 12, 1239. [Google Scholar] [CrossRef] [Green Version]
- Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
- Huo, H.; Ni, Z.; Jiang, X.; Zhou, P.; Liu, L. Mineral Mapping and Ore Prospecting with HyMap Data over Eastern Tien Shan, Xinjiang Uyghur Autonomous Region. Remote Sens. 2014, 6, 11829–11851. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.; Boardman, J.; Huntington, J. Comparison of airborne hyperspectral data and eo-1 hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.A.; Perry, S.L. Mineral Mapping Using Simulated Worldview-3 Short-Wave-Infrared Imagery. Remote Sens. 2013, 5, 2688–2703. [Google Scholar] [CrossRef] [Green Version]
- Ni, Z.; Lu, Q.; Xu, Y.; Huo, H. Intensity Simulation of a Fourier Transform Infrared Spectrometer. Sensors 2020, 20, 1833. [Google Scholar] [CrossRef] [Green Version]
- Yokoya, N.; Chan, J.C.-W.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Lucey, P.G. Model near-infrared optical constants of olivine and pyroxene as a function of iron content. J. Geophys. Res. Space Phys. 1998, 103, 1703–1713. [Google Scholar] [CrossRef]
- Helfenstein, P.; Veverka, J. Photometric properties of lunar terrains derived from Hapke’s equation. Icarus 1987, 72, 342–357. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Li, L. Radiative transfer modeling for quantifying lunar surface minerals, particle size, and submicroscopic metallic Fe. J. Geophys. Res. Space Phys. 2011, 116, E09001. [Google Scholar] [CrossRef]
- Masson, C.R.; Smith, I.B.; Jamieson, W.D.; McLachlan, J.L.; Volborth, A. Chromatographic and mineralogical study of Apollo 14 fines. Lunar Planet. Sci. Conf. Proc. 1972, 3, 1029. [Google Scholar]
- Egan, W.G.; Hilgeman, T. The interstellar medium—UV complex index of refraction of several candidate materials. Astron. J. 1975, 80, 587–594. [Google Scholar] [CrossRef]
- Johnson, P.; Christy, R. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Bell, P.M.; Mao, H.K.; Weeks, R.A. Optical spectra and electron paramagnetic resonance of lunar and synthetic glasses-A study of the effects of controlled atmosphere, composition, and temperature. Lunar Planet. Sci. Conf. Proc. 1976, 7, 2543–2559. [Google Scholar]
- Glotch, T.D.; Rossman, G.R. Mid-infrared reflectance spectra and optical constants of six iron oxide/oxyhydroxide phases. Icarus 2009, 204, 663–671. [Google Scholar] [CrossRef]
- Denevi, B.W.; Lucey, P.G.; Hochberg, E.; Steutel, D. Near-infrared optical constants of pyroxene as a function of iron and calcium content. J. Geophys. Res. Space Phys. 2007, 112, E05009. [Google Scholar] [CrossRef] [Green Version]
- Wenrich, M.L.; Christensen, P.R. Optical constants of minerals derived from emission spectroscopy: Application to quartz. J. Geophys. Res. Space Phys. 1996, 101, 15921–15931. [Google Scholar] [CrossRef]
- Glotch, T.D.; Rossman, G.R.; Aharonson, O. Mid-infrared (5–100 μm) reflectance spectra and optical constants of ten phyllosilicate minerals. Icarus 2007, 192, 605–622. [Google Scholar] [CrossRef]
- Denevi, B.W.; Lucey, P.G.; Sherman, S.B. Radiative transfer modeling of near-infrared spectra of lunar mare soils: Theory and measurement. J. Geophys. Res. Space Phys. 2008, 113, E02003. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Space Phys. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 3. Correction for macroscopic roughness. Icarus 1984, 59, 41–59. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hapke, B. Bidirectional Reflectance Spectroscopy: 5. The Coherent Backscatter Opposition Effect and Anisotropic Scattering. Icarus 2002, 157, 523–534. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 1993; 455p. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 6. Effects of porosity. Icarus 2008, 195, 918–926. [Google Scholar] [CrossRef] [Green Version]
- Warell, J.; Davidsson, B. A Hapke model implementation for compositional analysis of VNIR spectra of Mercury. Icarus 2010, 209, 164–178. [Google Scholar] [CrossRef]
- Ciarniello, M.; Capaccioni, F.; Filacchione, G.; Clark, R.; Cruikshank, D.; Cerroni, P.; Coradini, A.; Brown, R.; Buratti, B.; Tosi, F.; et al. Hapke modeling of Rhea surface properties through Cassini-VIMS spectra. Icarus 2011, 214, 541–555. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, S.; Milliken, R.E.; Zhang, H.; Robertson, K.; Hiroi, T. Phase Functions of Typical Lunar Surface Minerals Derived for the Hapke Model and Implications for Visible to Near-Infrared (VNIR) Spectral Unmixing. J. Geophys. Res. Planets 2019, 124, 31–60. [Google Scholar] [CrossRef]
- Mustard, J.F.; Pieters, C.M. Photometric phase functions of common geologic minerals and applications to quantitative analysis of mineral mixture reflectance spectra. J. Geophys. Res. Space Phys. 1989, 94, 13619–13634. [Google Scholar] [CrossRef]
- Pilorget, C.; Fernando, J.; Ehlmann, B.; Schmidt, F.; Hiroi, T. Wavelength dependence of scattering properties in the VIS–NIR and links with grain-scale physical and compositional properties. Icarus 2016, 267, 296–314. [Google Scholar] [CrossRef] [Green Version]
- Robertson, K.; Li, S.; Milliken, R.E.; Pieters, C. Radiative transfer modeling of laboratory derived ilmenite-silicate mixtures: Insights into the classification of high-titanium lunar basalts. Presented at the 48th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 20–24 March 2017. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons: Hoboken, NJ, USA, 2016; Volume 10. [Google Scholar]
- Sato, H.; Robinson, M.S.; Hapke, B.; Denevi, B.; Boyd, A. Resolved Hapke parameter maps of the Moon. J. Geophys. Res. Planets 2014, 119, 1775–1805. [Google Scholar] [CrossRef]
- Izawa, M.R.; Cloutis, E.A.; Rhind, T.; Mertzman, S.A.; Applin, D.M.; Stromberg, J.M.; Sherman, D.M. Spectral reflectance properties of magnetites: Implications for remote sensing. Icarus 2019, 319, 525–539. [Google Scholar] [CrossRef]


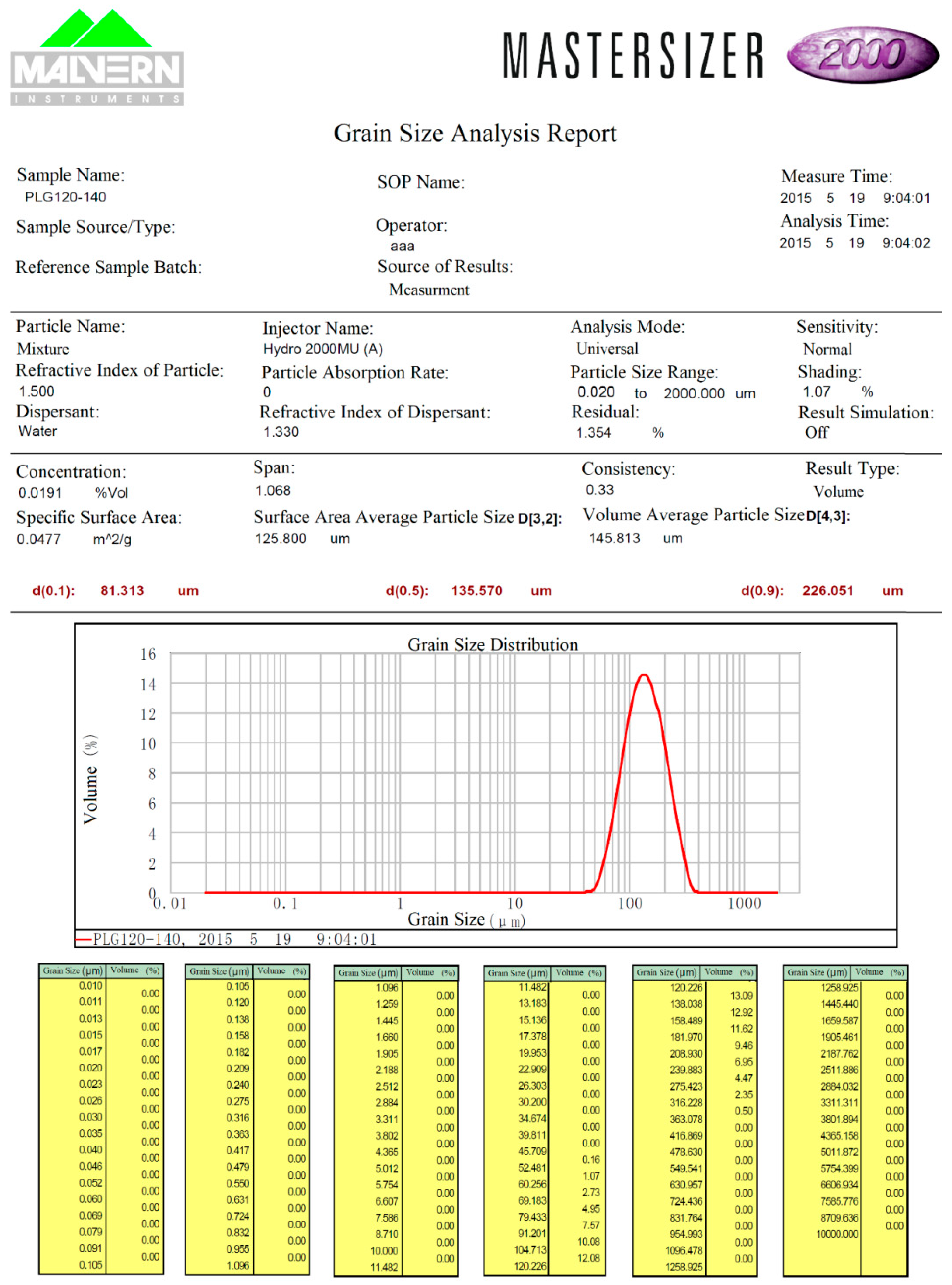

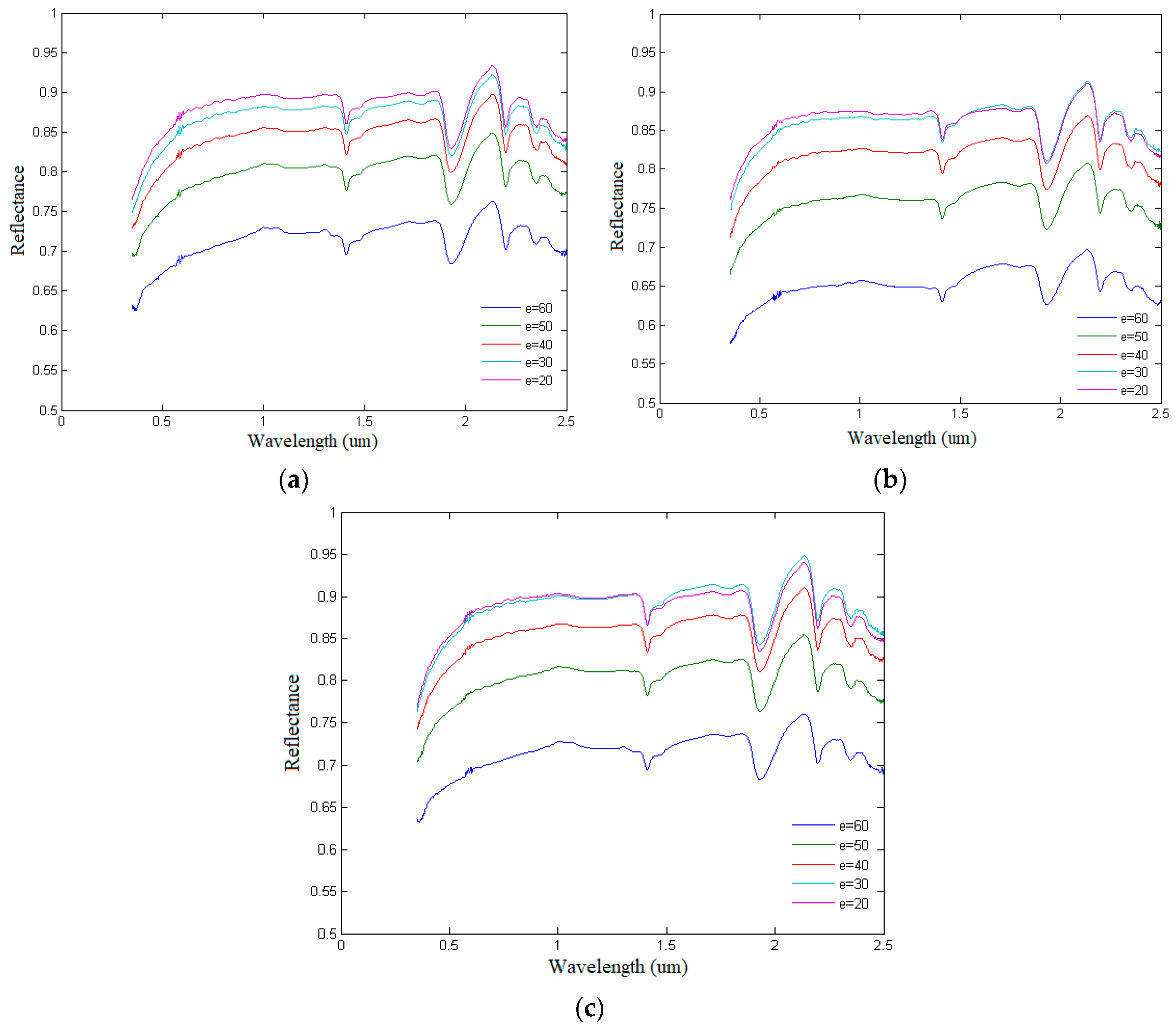
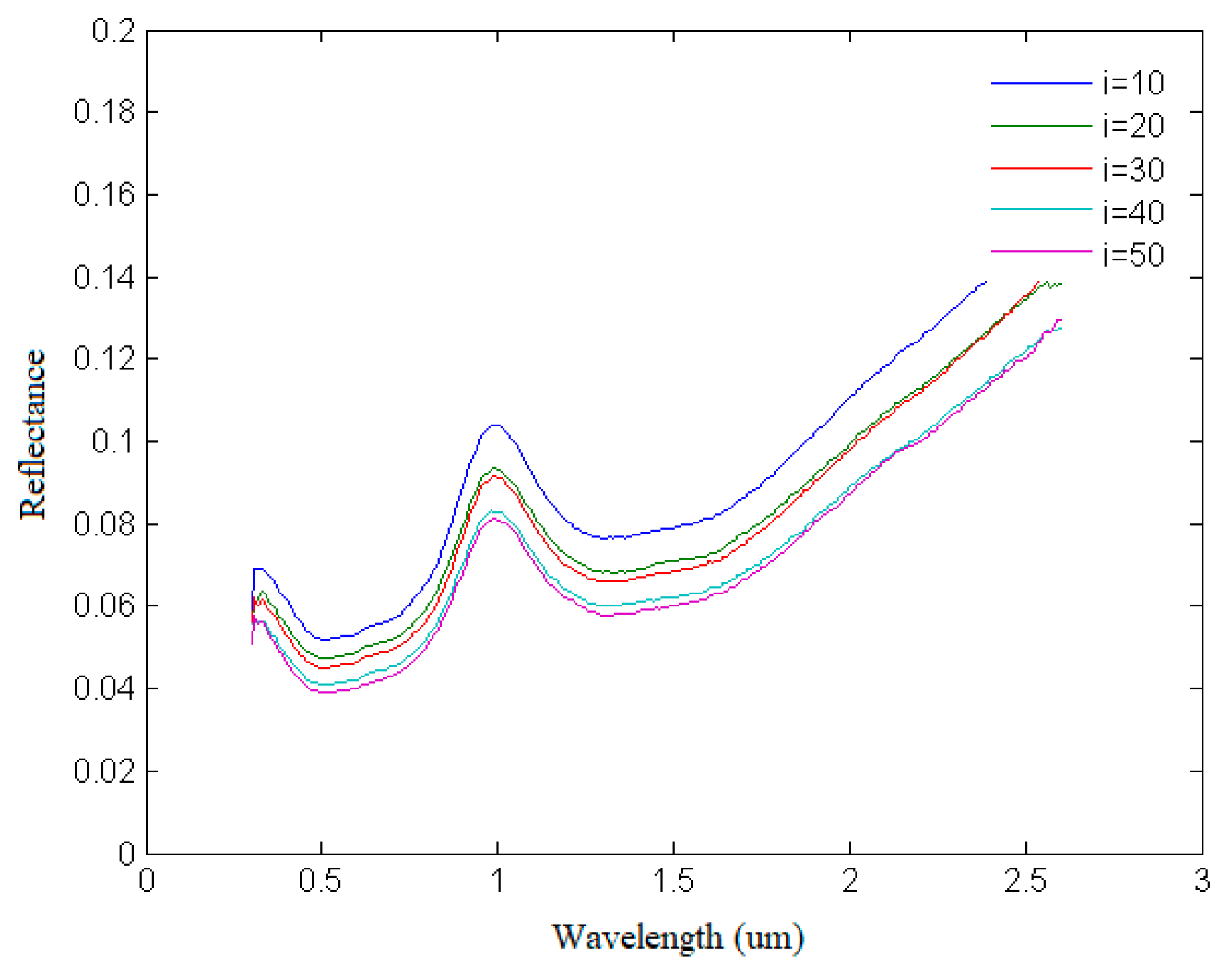

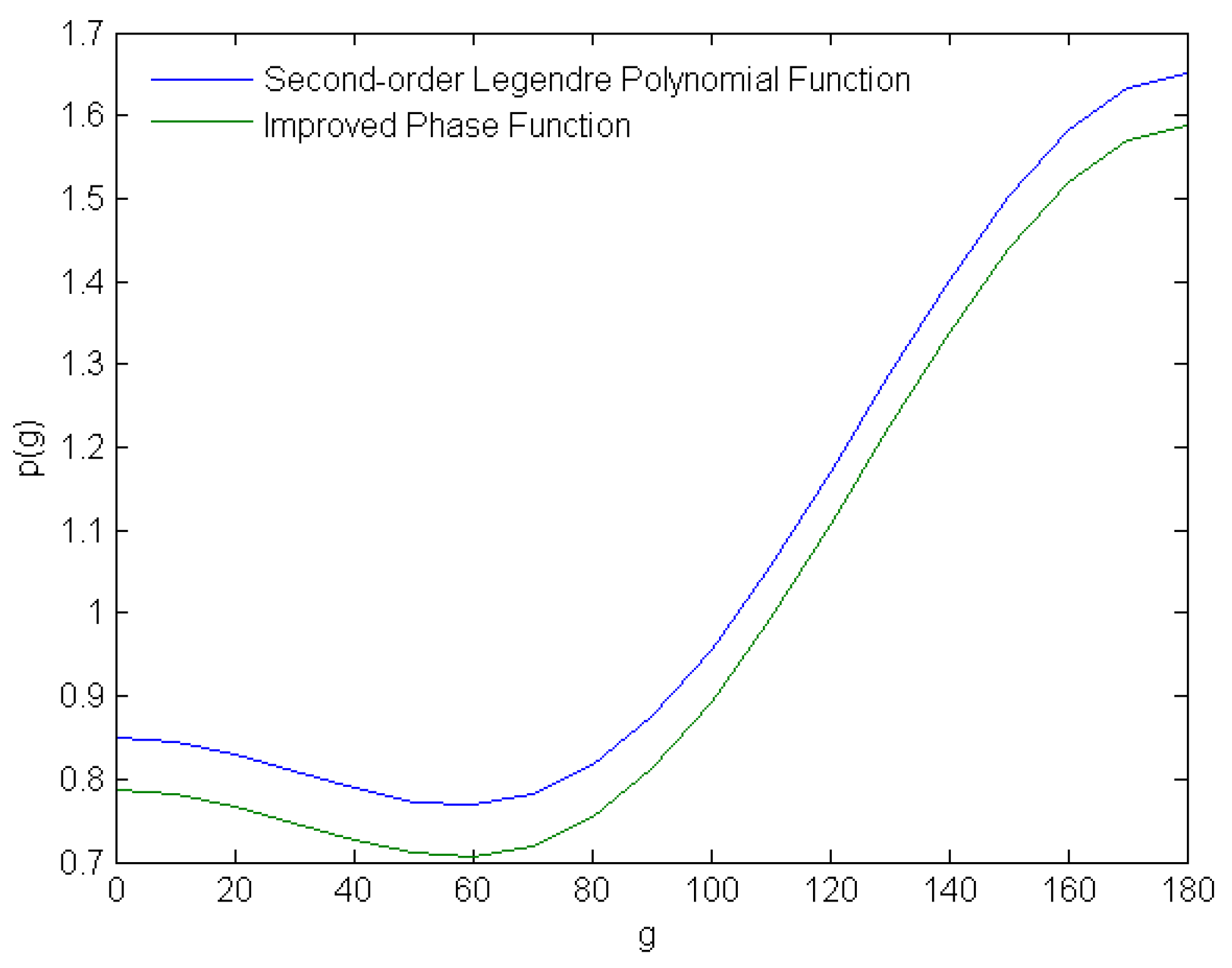

| ID | Incident Angle i | Azimuth φ | Emergence Angle e | ID | Incident Angle i | Azimuth 0φ | Emergence Angle e | ID | Incident Angle i | Azimuth φ | Emergence Angle e |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 180 | 20 | 6 | 0 | 210 | 20 | 11 | 0 | 240 | 20 |
| 2 | 30 | 7 | 30 | 12 | 30 | ||||||
| 3 | 40 | 8 | 40 | 13 | 40 | ||||||
| 4 | 50 | 9 | 50 | 14 | 50 | ||||||
| 5 | 60 | 10 | 60 | 15 | 60 |
| RMSE | e = 10 | e = 20 | e = 30 | e = 40 | e = 50 | Mean Value |
|---|---|---|---|---|---|---|
| multi-parameter simulation | 0.000436 | 0.001831 | 0.002696 | 0.001345 | 0.000345 | 0.001331 |
| single-parameter simulation (b = −0.4, c = 0.25) | 0.013568 | 0.009293 | 0.010363 | 0.00294 | 1.07 × 10−9 | 0.007233 |
| single-parameter simulation (b = −0.6775, c = 0.5475) | 0.001701 | 0.001605 | 0.003035 | 0.001328 | 1.59 × 10−8 | 0.001534 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Zhao, Z.; Huo, H.-Y.; Liu, Z. Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model. Remote Sens. 2021, 13, 3022. https://doi.org/10.3390/rs13153022
Zhou P, Zhao Z, Huo H-Y, Liu Z. Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model. Remote Sensing. 2021; 13(15):3022. https://doi.org/10.3390/rs13153022
Chicago/Turabian StyleZhou, Ping, Zhe Zhao, Hong-Yuan Huo, and Zhansheng Liu. 2021. "Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model" Remote Sensing 13, no. 15: 3022. https://doi.org/10.3390/rs13153022
APA StyleZhou, P., Zhao, Z., Huo, H.-Y., & Liu, Z. (2021). Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model. Remote Sensing, 13(15), 3022. https://doi.org/10.3390/rs13153022







