LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography
Abstract
:1. Introduction
2. Materials and Methods
2.1. LEO Constellation Simulation
2.2. Tomographic Theory and Approach
3. Experiments and Results
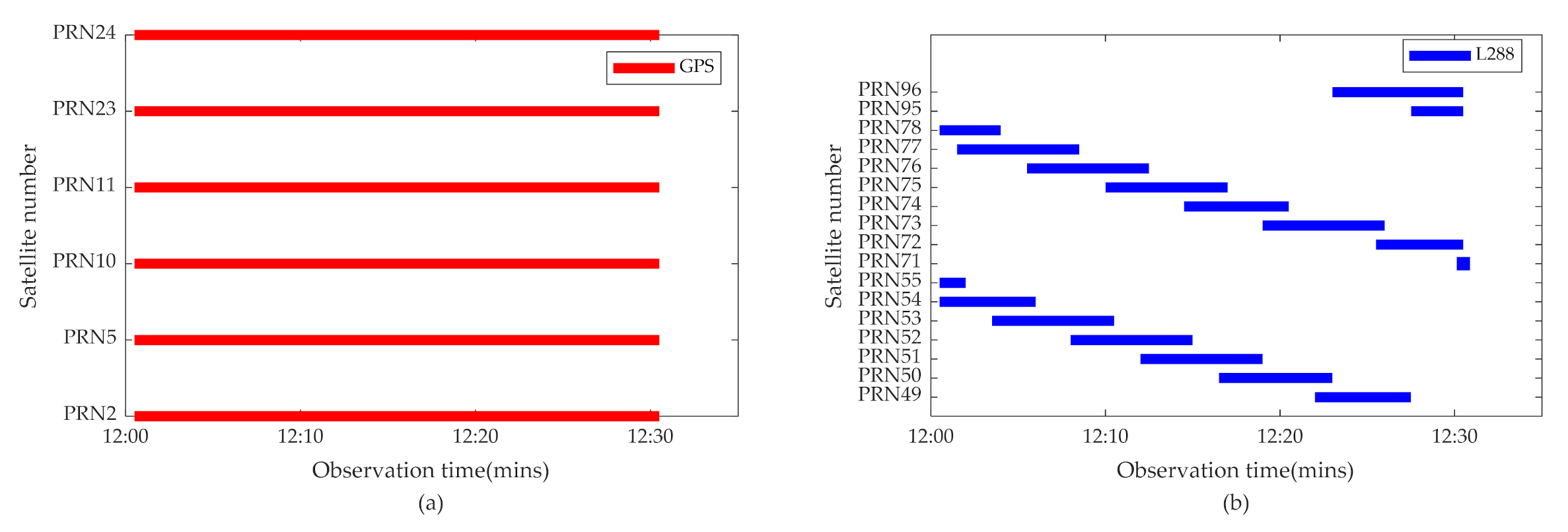
3.1. Experimental Area and Data Classification
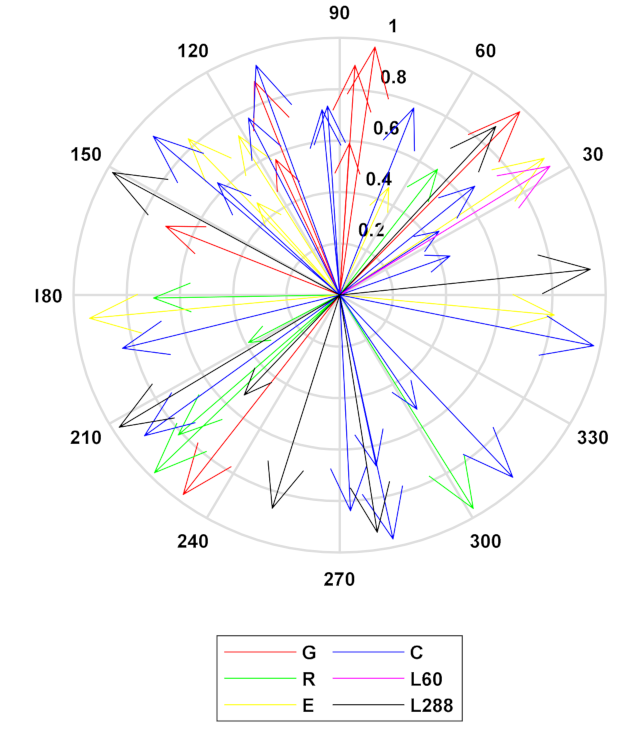
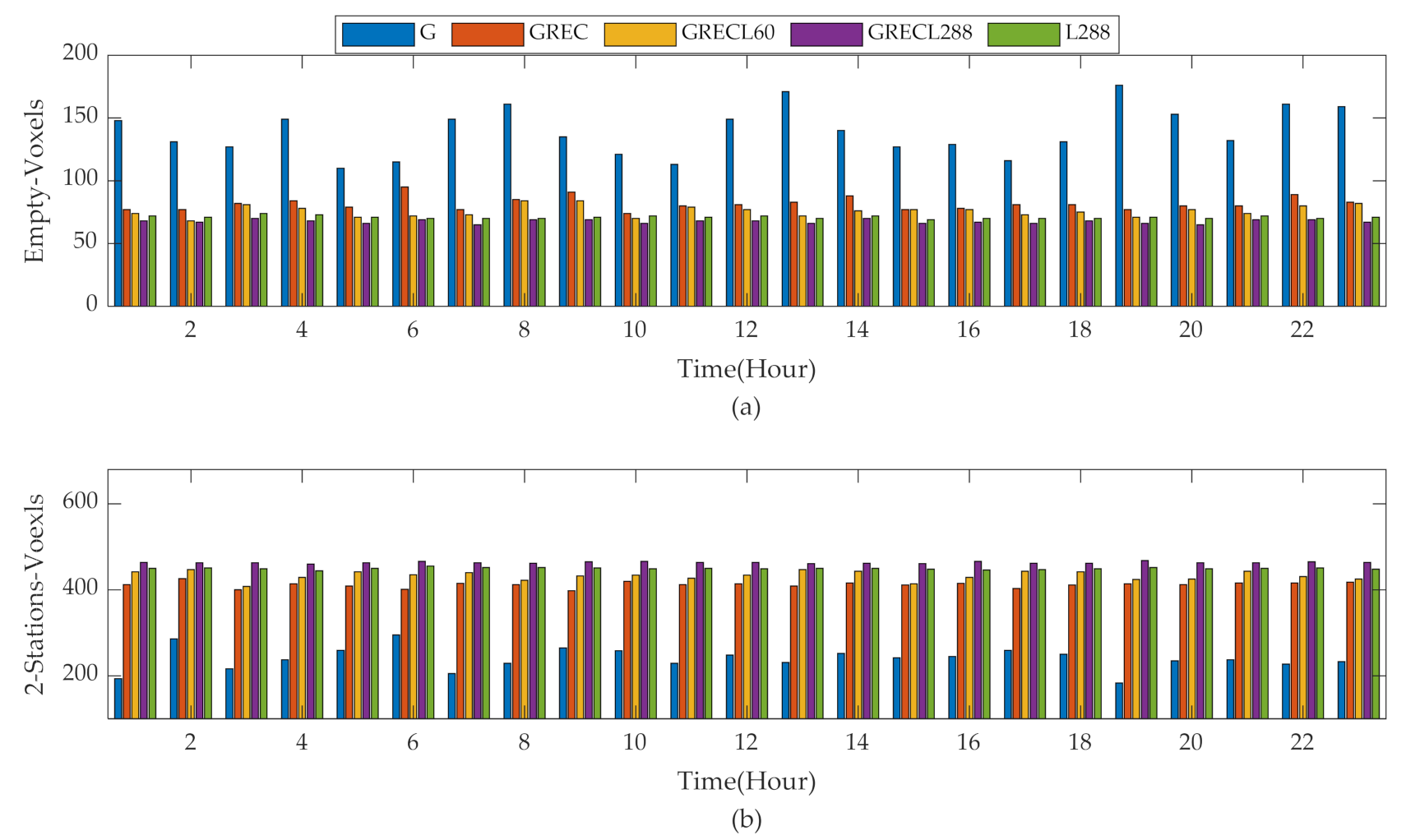
3.2. Tomographic Observation Distribution
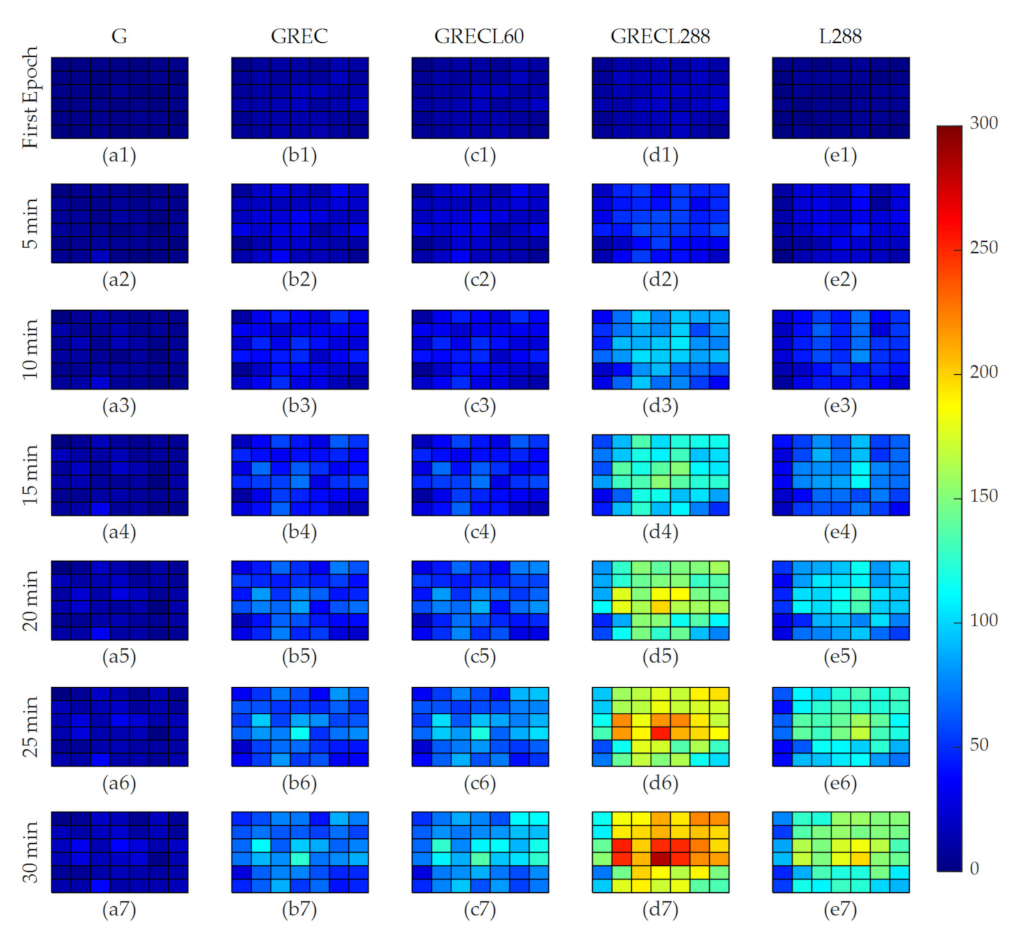
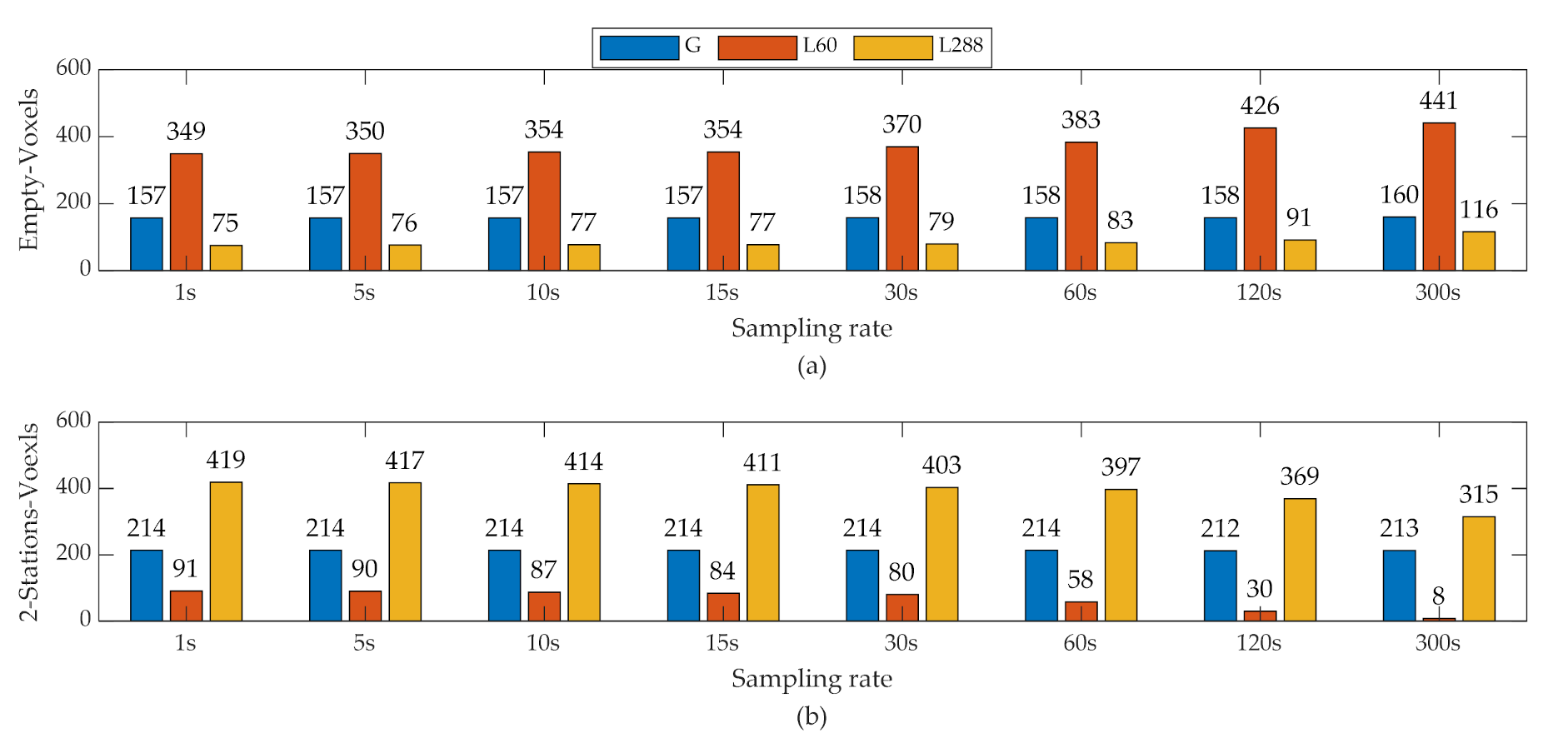
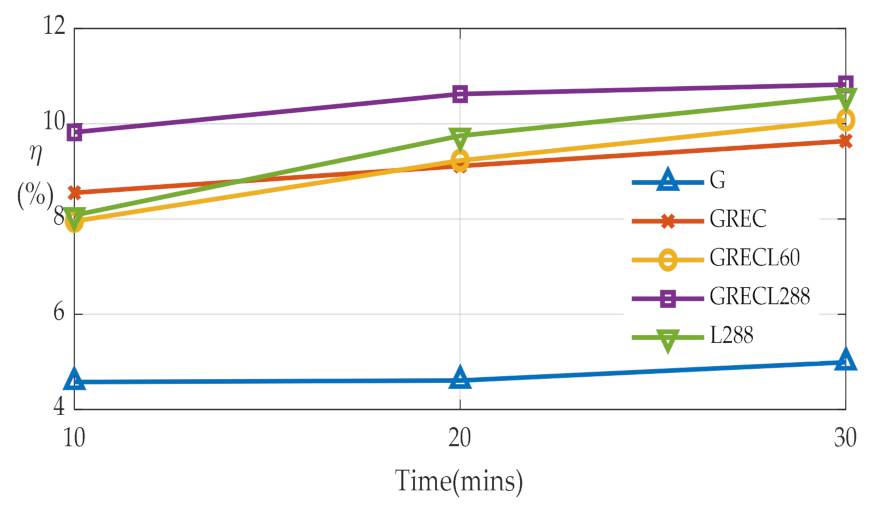
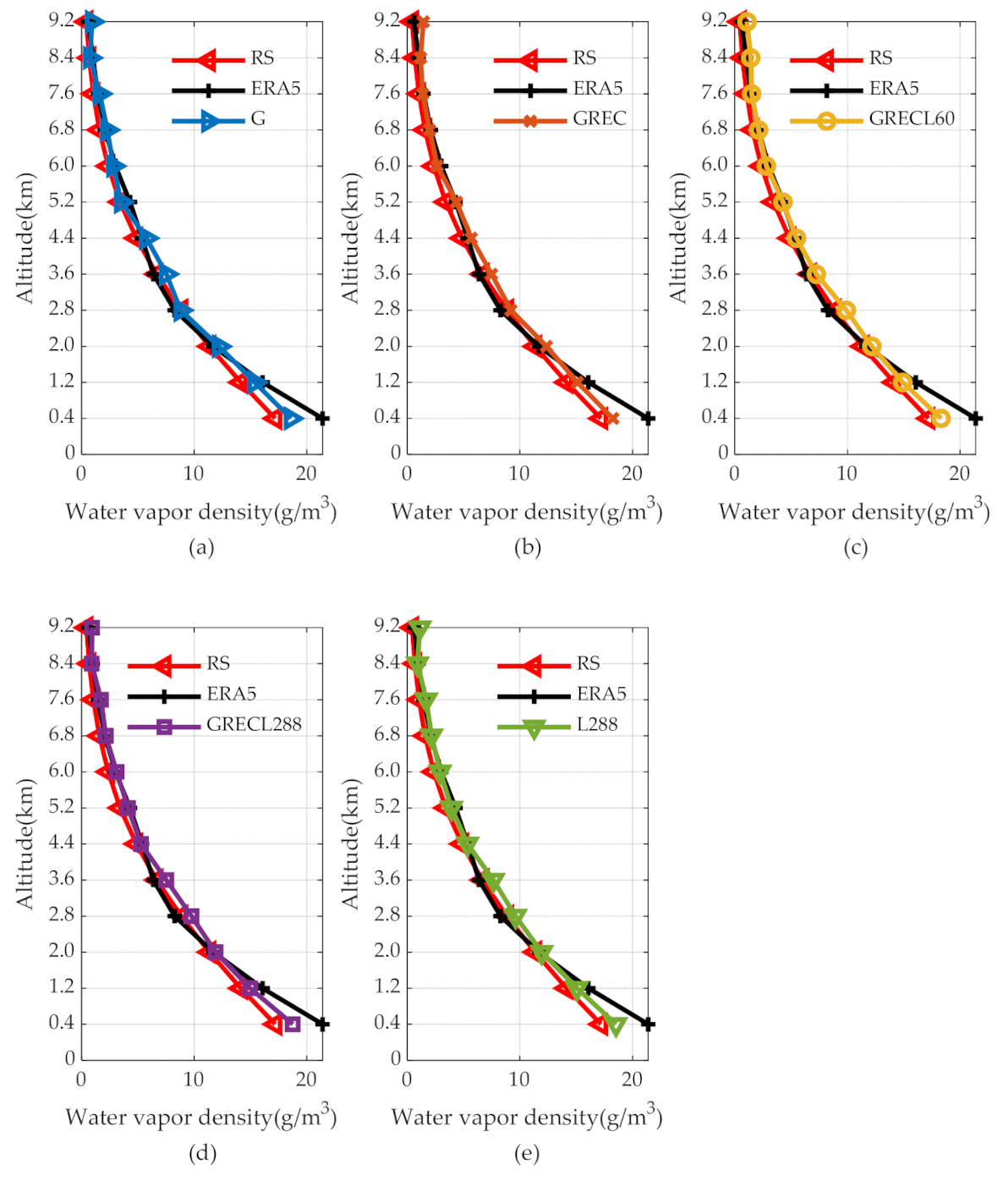
3.3. Tomographic Accuracy Evaluation
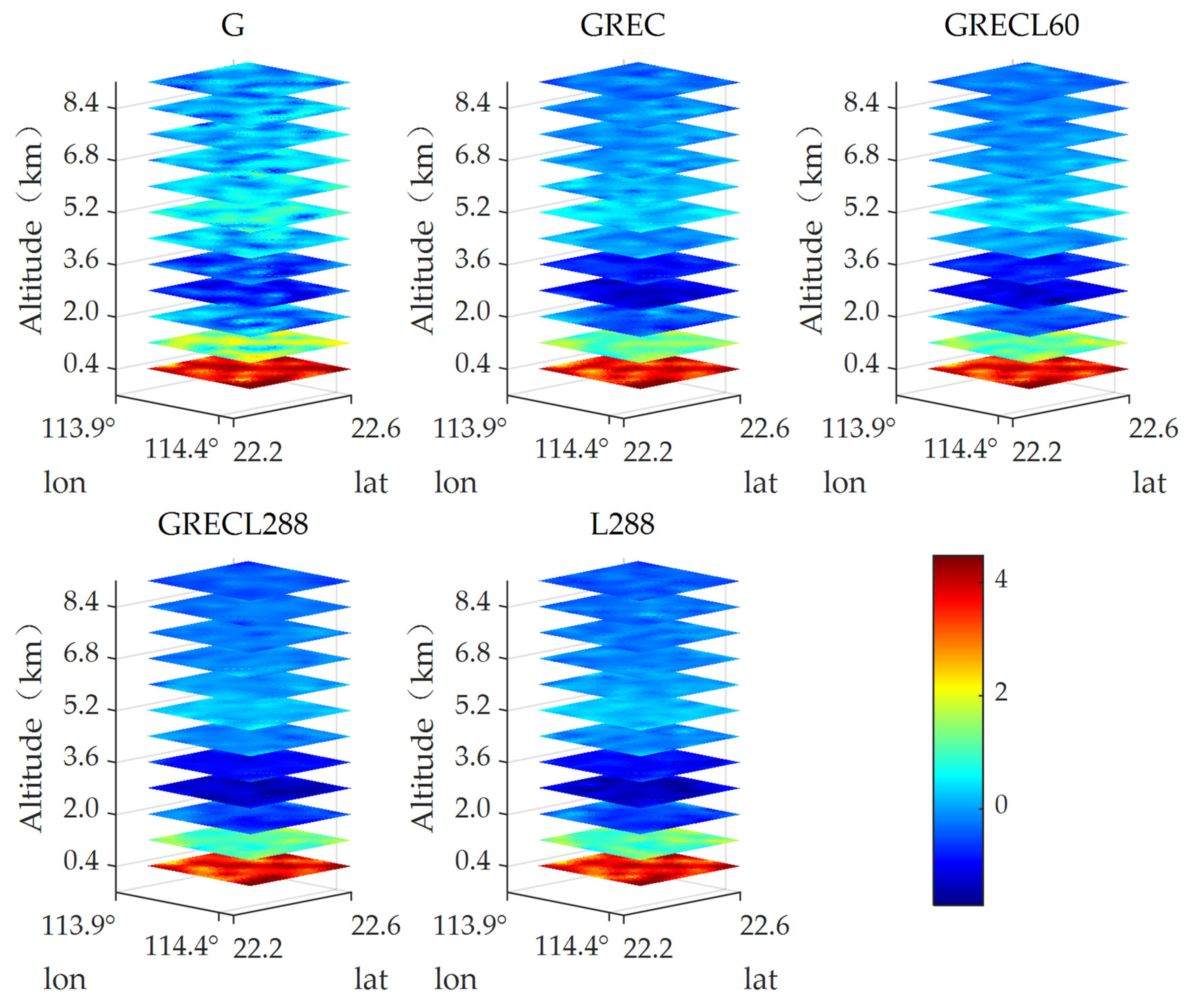
3.4. Horizontal Tomography Resolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rocken, C.; Van Hove, T.; Ware, R. Near real-time GPS sensing of atmospheric water vapor. Geophys. Res. Lett. 1997, 24, 3221–3224. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. Ger. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Troller, M.; Geiger, A.; Brockmann, E.; Bettems, J.M.; Bürki, B.; Kahle, H.G. Tomographic determination of the spatial distribution of water vapor using GPS observations. Adv. Space Res. 2006, 37, 2211–2217. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Van Baelen, J.; Walpersdorf, A.; Chery, J.; Doerflinger, E. GPS monitoring of the tropospheric water vapor distribution and variation during the 9 September 2002 torrential precipitation episode in the Cevennes (southern France). J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Ma, H. An optimal troposphere tomography technique using the WRF Model outputs and topography of the area. Remote Sens. 2020, 12, 1442. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Xia, P. An optimal tropospheric tomography approach with the support of an auxiliary area. Ann. Geophys. 2018, 36, 1037–1046. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Zhang, K.; Yao, Y.; Li, X. A new troposphere tomography algorithm with a truncation factor model (TFM) for GNSS networks. GPS Solut. 2019, 23, 64. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.; Zhang, Q. New parameterized model for GPS water vapor tomography. Ann. Geophys. 2017, 35, 311–323. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Zhang, S.; Zheng, N.; Ding, N.; Liu, X. A new integrated method of GNSS and MODIS measurements for tropospheric water vapor tomography. GPS Solut. 2021, 25. [Google Scholar] [CrossRef]
- Heublein, M.; Alshawaf, F.; Erdnüß, B.; Zhu, X.X.; Hinz, S. Compressive sensing reconstruction of 3D wet refractivity based on GNSS and InSAR observations. J. Geodesy. 2018, 93, 197–217. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Fan, Q.; Yao, Y.; Xu, C.; Li, X. An improved tomography approach based on adaptive smoothing and ground meteorological observations. Remote Sens. 2017, 9, 886. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Xia, P.; Cai, C. Optimization of GPS water vapor tomography technique with radiosonde andCOSMIC historical data. Ann. Geophys. 2016, 34, 789–799. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Ye, S.; Jiang, P.; Pan, L.; Guo, M. Assessing water vapor tomography in Hong Kong with improved vertical and horizontal constraints. Ann. Geophys. 2018, 36, 969–978. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Cai, C.; Liu, Z. GNSS troposphere tomography based on two-step reconstructions using GPS observations and COSMIC profiles. Ann. Geophys. 2013, 31, 1805–1815. [Google Scholar] [CrossRef] [Green Version]
- Benevides, P.; Nico, G.; Catalao, J.; Miranda, P.M.A. Analysis of Galileo and GPS integration for GNSS tomography. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1936–1943. [Google Scholar] [CrossRef]
- Bender, M.; Stosius, R.; Zus, F.; Dick, G.; Wickert, J.; Raabe, A. GNSS water vapour tomography—Expected improvements by combining GPS, GLONASS and Galileo observations. Adv. Space Res. 2011, 47, 886–897. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S. 3-D water vapor tomography in Wuhan from GPS, BDS and GLONASS observations. Remote Sens. 2018, 10, 62. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Cao, X.; Yao, W. Accuracy and reliability of tropospheric wet refractivity tomography with GPS, BDS, and GLONASS observations. Adv. Space Res. 2019, 63, 2836–2847. [Google Scholar] [CrossRef]
- Reid, T.G.R.; Neish, A.M.; Walter, T.F.; Enge, P.K.; Inst, N. Leveraging Commercial Broadband LEO Constellations for Navigation. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 12–16 September 2016; pp. 2300–2314. [Google Scholar]
- Ge, H.; Li, B.; Ge, M.; Nan, Z.; Nie, L.; Shen, Y.; Harald, S. Initial assessment of precise point positioning with LEO enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Chen, R.; Li, D.; Zhang, G.; Shen, X.; Yu, B.; Wu, C.; Xie, S.; Zhang, P.; Li, M.; et al. Initial assessment of the LEO Based Navigation Signal Augmentation System from Luojia-1A Satellite. Sensors 2018, 18, 3919. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Zhang, X.; Schmidt, M.; Zhao, Z.; Chen, J.; Zhang, J.; Li, X. Performance of GNSS global ionospheric modeling augmented by LEO constellation. Earth Space Sci. 2020, 7. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Chen, J.; Zhang, X.; Schmidt, M.; Li, X.; Zhang, J. Mapping topside ionospheric vertical electron content from multiple LEO satellites at different orbital altitudes. J. Geodesy. 2020, 94, 1–17. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Ge, M.; Nie, L.; Shen, Y.; Schuh, H. LEO enhanced Global Navigation Satellite System (LeGNSS) for real-time precise positioning services. Adv. Space Res. 2019, 63, 73–93. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Huang, J.; Zhu, Y.; Wu, J.; Xiong, Y.; Li, X.; Zhang, K. Galileo and QZSS precise orbit and clock determination using new satellite metadata. J. Geodesy. 2019, 93, 1123–1136. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geodesy. 2018, 92, 711–726. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Jiang, Z.; Ma, F.; Lv, H.; Yuan, Y.; Li, X. LEO precise orbit determination with inter-satellite links. Remote Sens. 2019, 11, 2117. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Lei, W.; Bian, L.; Yan, T.; Wang, Y. Clock tuning technique for a disciplined high medium–long-stability GNSS oscillator with precise clock drifts for LEO users. GPS Solut. 2020, 24, 1–15. [Google Scholar] [CrossRef]
- Lei, W.; Chen, R.; Li, D.; Guo, Z.; Xin, S. Quality assessment of the LEO navigation augmentation signals from Luojia-1A Satellite. Geomat. Inf. Wuhan Univ. 2018, 43, 2191–2196. [Google Scholar]
- AGI: Systems Tool Kit (STK). Available online: https://www.agi.com/products/stk (accessed on 6 January 2021).
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geodesy. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Copernicus Climate Data Store|Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview (accessed on 8 January 2021).
- Wallace, J. Atmospheric Science: An Introductory Survey; Elsevier: Burlington, MA, USA, 2006. [Google Scholar]
- Wexler, A. Vapor pressure formulation for water in range 0 to 100 °C. A revision. J. Res. Natl. Instit. Stand. Technol. 1976, 80A, 755–785. [Google Scholar] [CrossRef]
- Wexler, A. Vapor pressure formulation for ice. J. Res. Natl. Instit. Stand. Technol. 1977, 81A, 5–20. [Google Scholar] [CrossRef]
- Ware, R.; Alber, C.; Rocken, C.; Solheim, F. Sensing integrated water vapor along GPS ray paths. Geophys. Res. Lett. 1997, 24, 417–420. [Google Scholar] [CrossRef] [Green Version]
- B, Y.-M.; Mao, J.; Liu, X.-Y.; Fu, Y. Remote sensing of the amount of water vapor along the slant path using the ground-base GPS. Chin. J. Geophys. 2006, 49, 335–342. [Google Scholar]
- Bender, M.; Dick, G.; Wickert, J.; Schmidt, T.; Song, S.; Gendt, G.; Ge, M.; Rothacher, M. Validation of GPS slant delays using water vapour radiometers and weather models. Meteorol. Z. 2008, 17, 807–812. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.C.; Saxild-Hansen, M. AIR tools—A MATLAB package of algebraic iterative reconstruction methods. J. Comput. Appl. Math. 2012, 236, 2167–2178. [Google Scholar] [CrossRef] [Green Version]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.; Raabe, A.; Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef] [Green Version]
- Champollion, C.; Masson, F.; Bouin, M.N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS water vapour tomography: Preliminary results from the ESCOMPTE field experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, T.; Gradinarsky, L. Water vapor tomography using GPS phase observations: Simulation results. IEEE Trans. Geosci. Remote 2006, 44, 2927–2941. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. Voxel-optimized regional water vapor tomography and comparison with radiosonde and numerical weather model. J. Geodesy. 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Manning, T.; Rohm, W.; Zhang, K.; Hurter, F.; Wang, C. Determining the 4D Dynamics of Wet Refractivity Using GPS Tomography in the Australian Region; Springer: Berlin/Heidelberg, Germany, 2013; Volume 139, pp. 41–49. [Google Scholar]
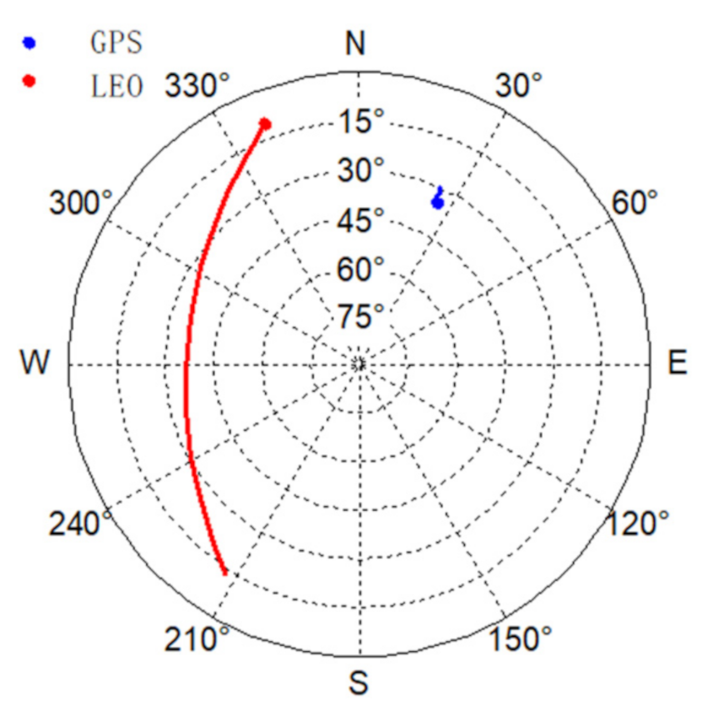
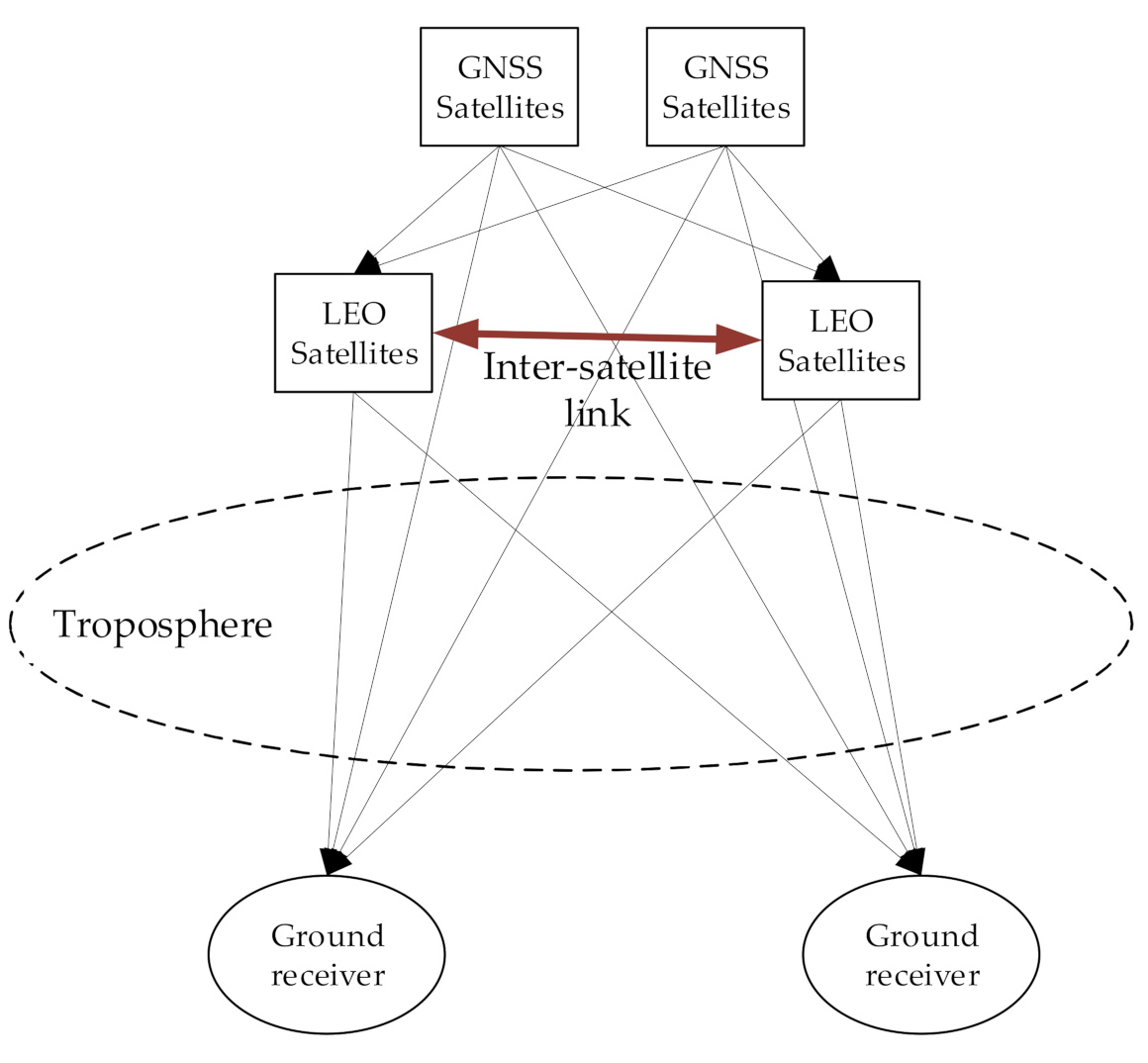
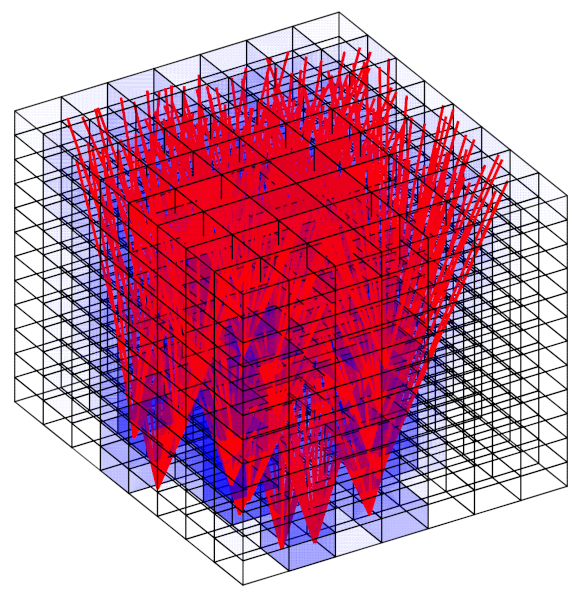
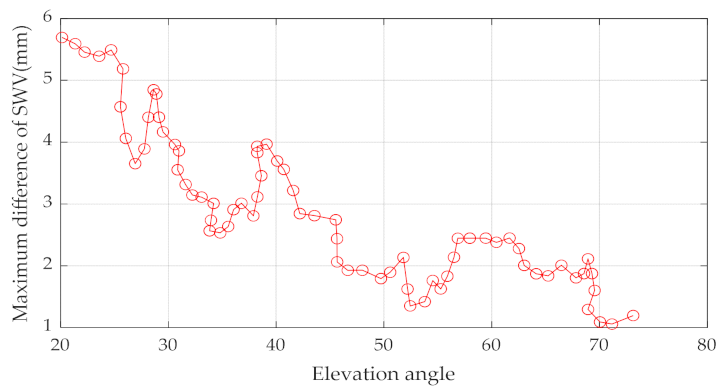
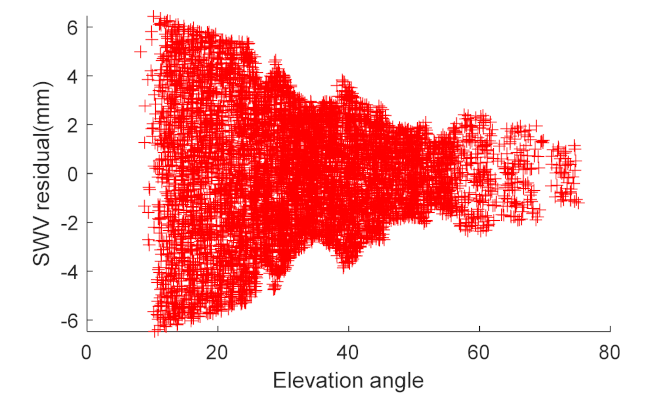
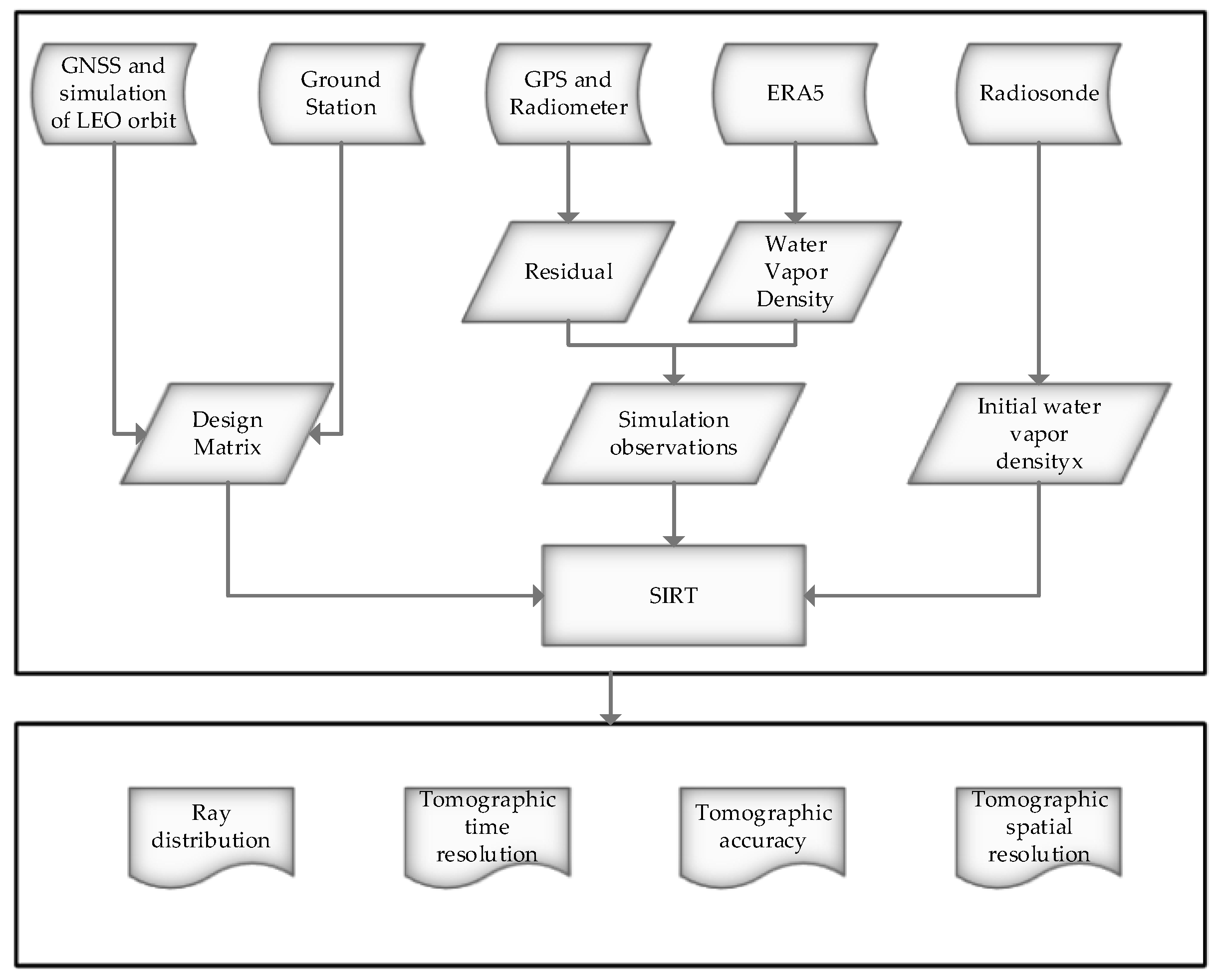
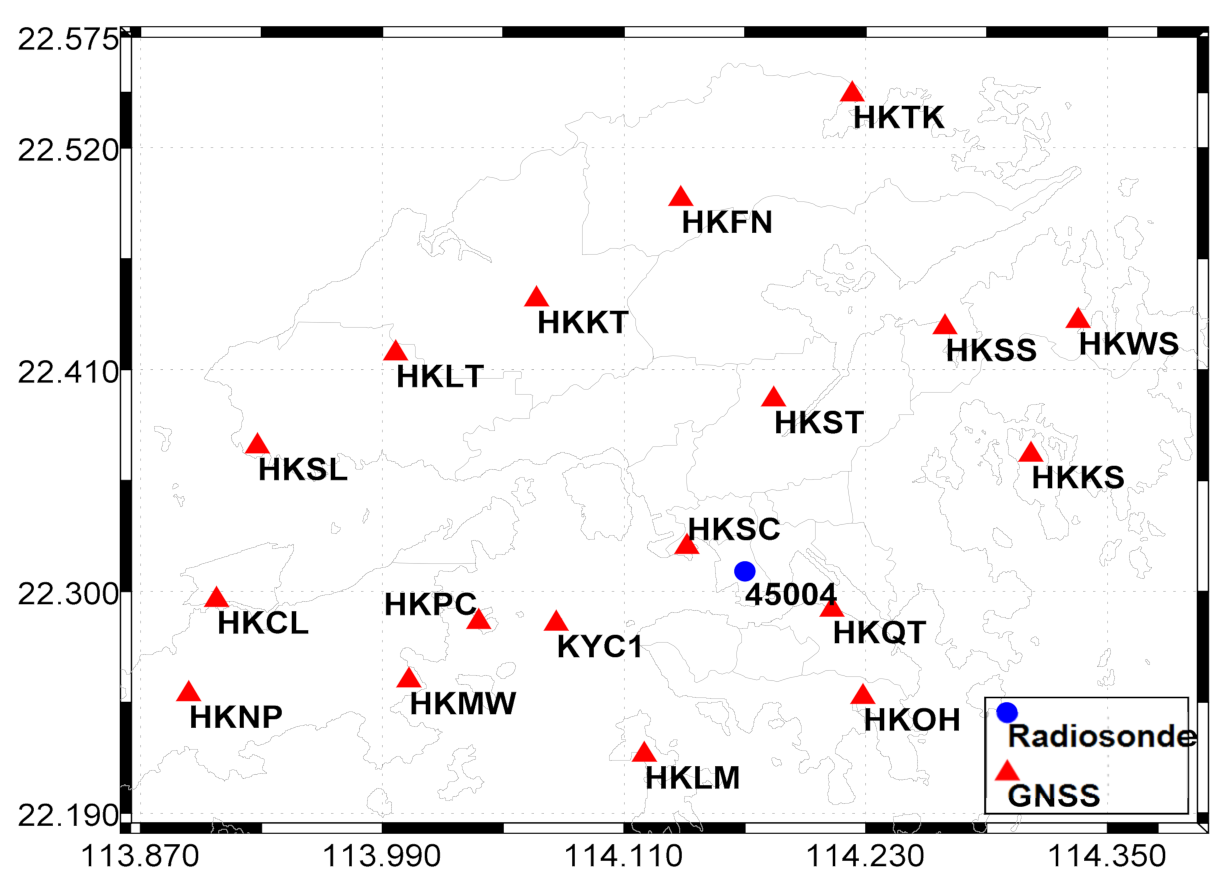
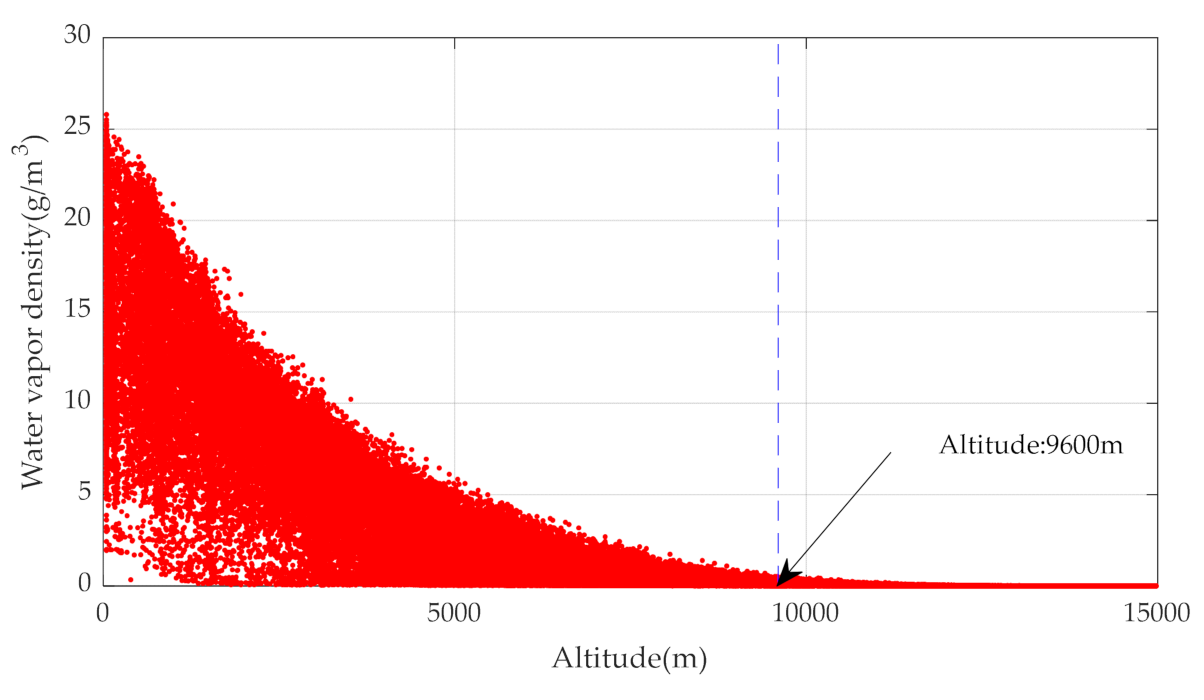



| Satellite Number | Constellation | Orbit Type | Orbit Inclination (deg) | Altitude (km) |
|---|---|---|---|---|
| 60 | 6 planes | Polar | 90 | 1000 |
| 288 | 12 planes | Polar | 90 | 1000 |
| Name | Description |
|---|---|
| Horizontal resolution | Reanalysis: 0.25° × 0.25° |
| Vertical coverage | 1000 to 1 hPa |
| Vertical resolution | 37 pressure levels |
| Temporal resolution | Hourly |
| GREC (10 min) | GREC (30 min) | GRECL288 (10 min) | GRECL288 (30 min) | |
|---|---|---|---|---|
| Effective Rays | 1192 | 2539 | 2840 | 7181 |
| Voxel Passed | 1038 | 3548 | 3834 | 9821 |
| Scheme | Lat × Lon | Lat (°) | Lon (°) | Total Voxels |
|---|---|---|---|---|
| 1 | 0.055 | 0.060 | 672 | |
| 2 | 0.055 | 0.048 | 840 | |
| 3 | 0.055 | 0.040 | 1008 | |
| 4 | 0.055 | 0.0343 | 1176 | |
| 5 | 0.04278 | 0.06 | 864 | |
| 6 | 0.0350 | 0.06 | 1056 | |
| 7 | 0.0296 | 0.06 | 1248 | |
| 8 | 0.0296 | 0.0343 | 2184 |
| Empty Voxels (%) | 2-Station Voxels (%) | (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | Max | Min | Mean | |
| GRECL288-GREC | 5.22 | 2.08 | 3.25 | 11.03 | 7.74 | 8.61 | 2.06 | 1.42 | 1.80 |
| GRECL288-G | 22.53 | 9.53 | 13.83 | 49.36 | 31.25 | 39.23 | 6.32 | 5.09 | 5.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, S.; Ma, F.; Ren, X.; Chen, J.; Zhang, X. LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography. Remote Sens. 2021, 13, 3056. https://doi.org/10.3390/rs13163056
Xiong S, Ma F, Ren X, Chen J, Zhang X. LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography. Remote Sensing. 2021; 13(16):3056. https://doi.org/10.3390/rs13163056
Chicago/Turabian StyleXiong, Si, Fujian Ma, Xiaodong Ren, Jun Chen, and Xiaohong Zhang. 2021. "LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography" Remote Sensing 13, no. 16: 3056. https://doi.org/10.3390/rs13163056
APA StyleXiong, S., Ma, F., Ren, X., Chen, J., & Zhang, X. (2021). LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography. Remote Sensing, 13(16), 3056. https://doi.org/10.3390/rs13163056







