Evaluation of GRACE/GRACE Follow-On Time-Variable Gravity Field Models for Earthquake Detection above Mw8.0s in Spectral Domain
Abstract
:1. Introduction
2. Model and Method
2.1. Coseismic Dislocation Model
2.2. GRACE Time-Variable Gravity Field Model Error
3. Data
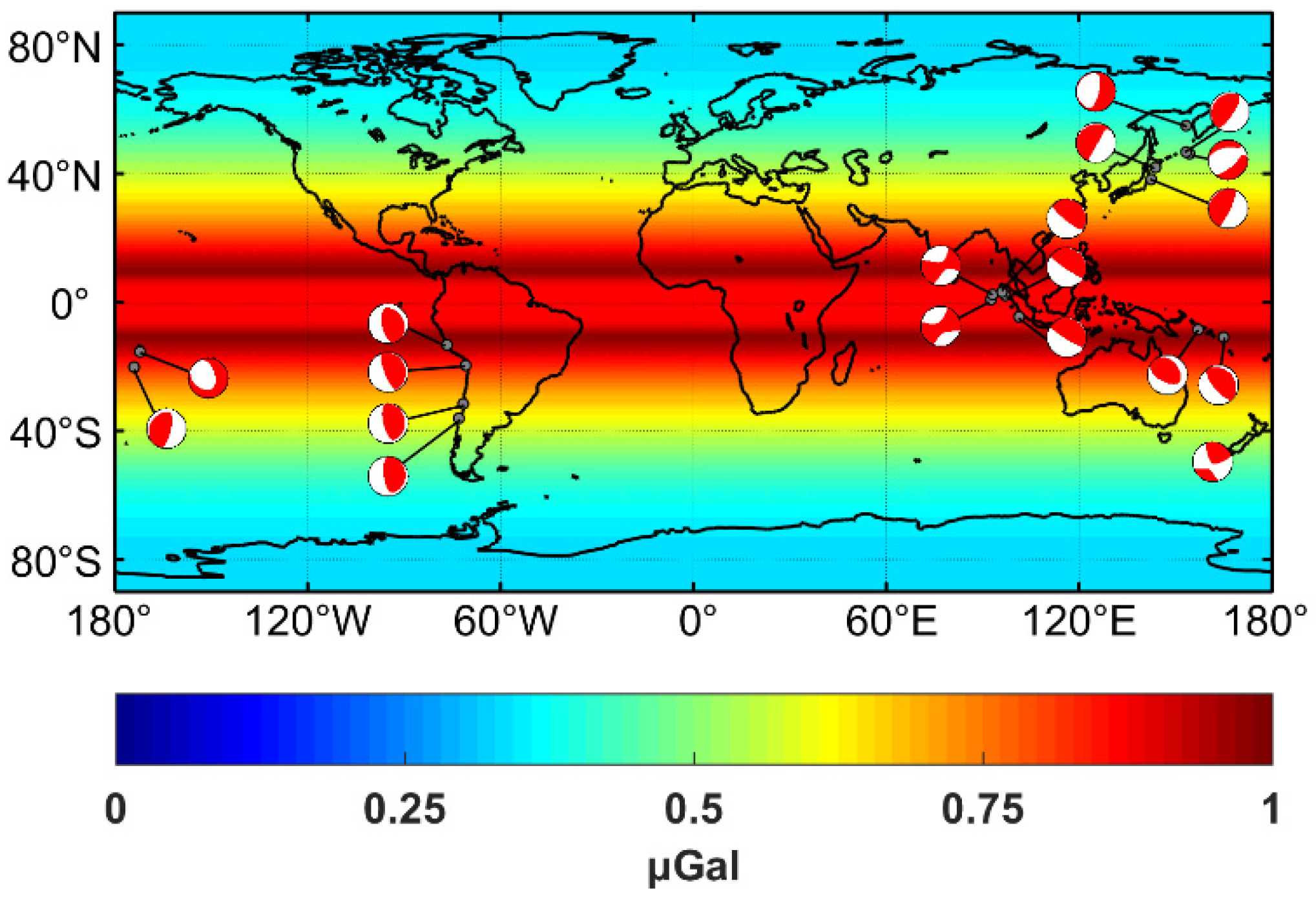
3.1. Fault Slip Models
3.2. GRACE Data
4. Results and Analysis
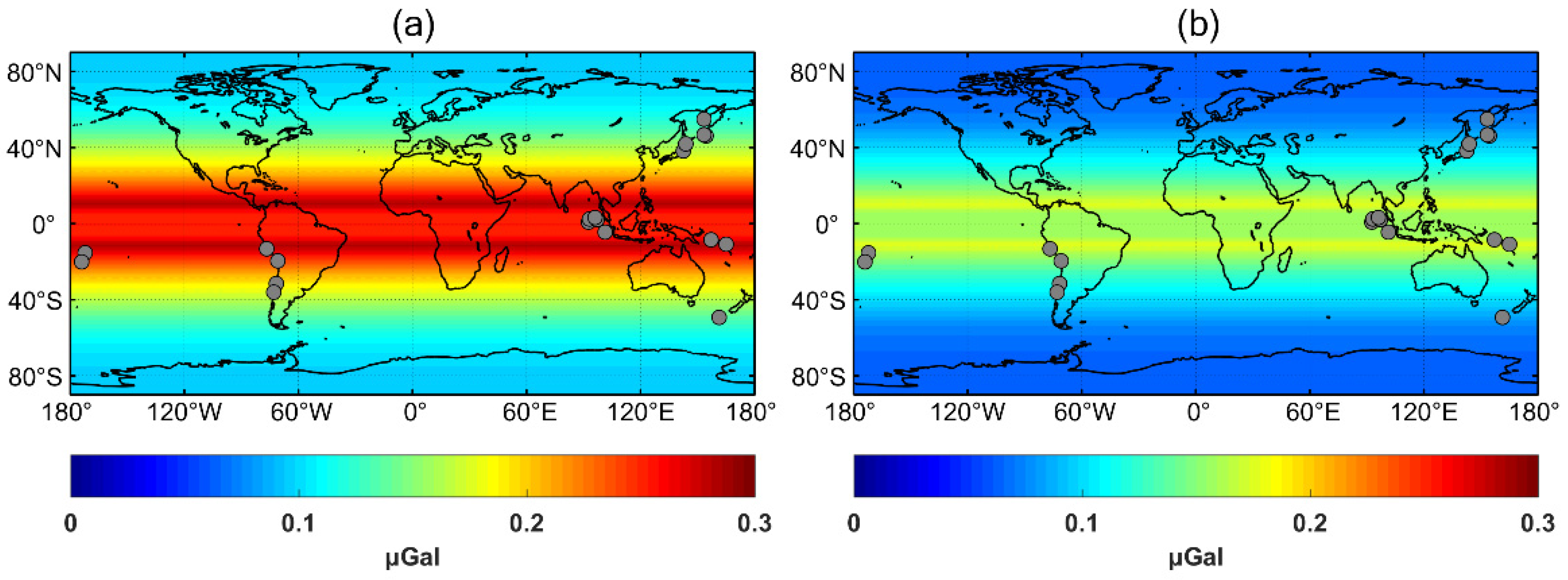
4.1. The Error of Monthly Time-Variable Field Models
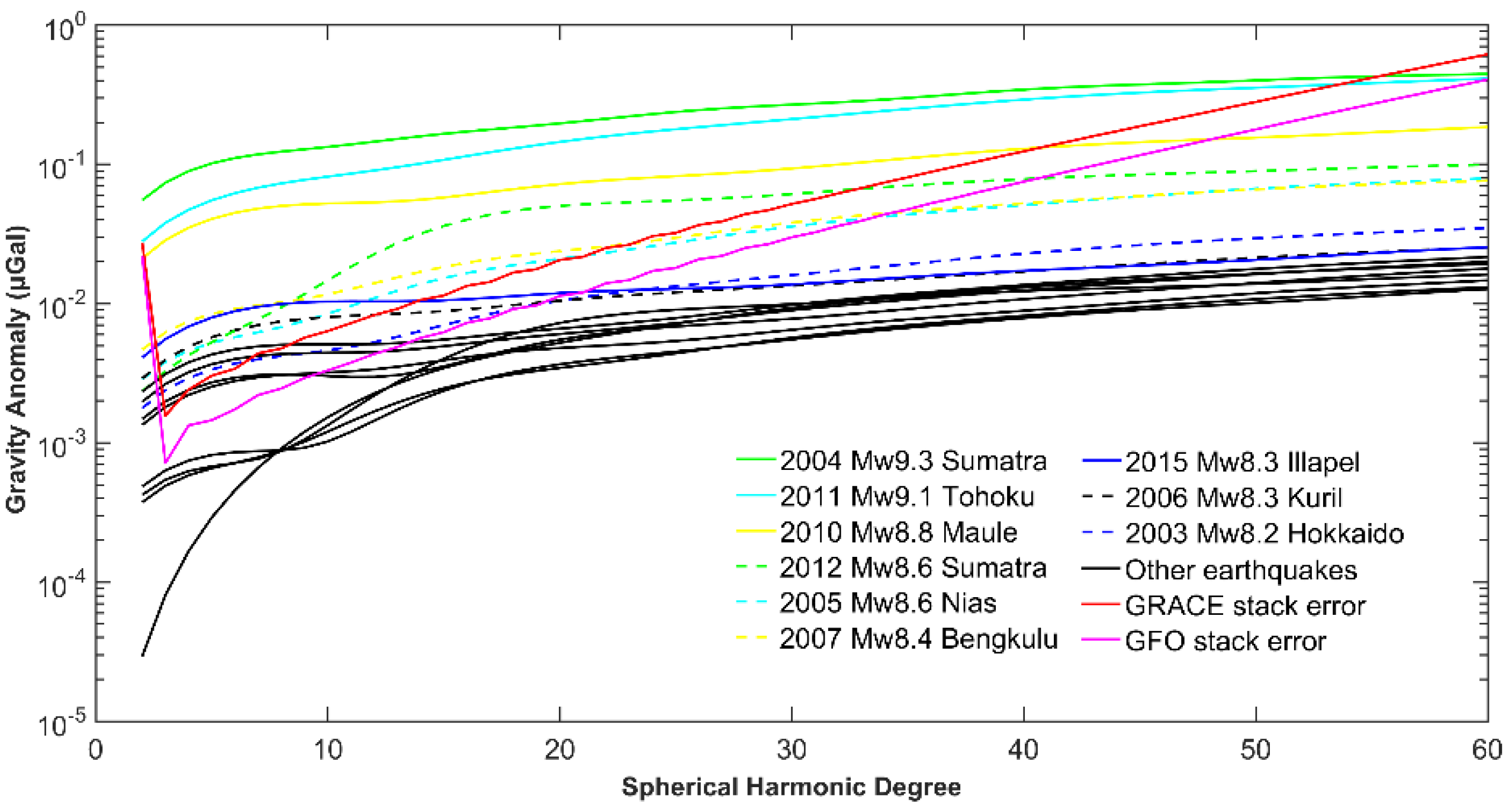
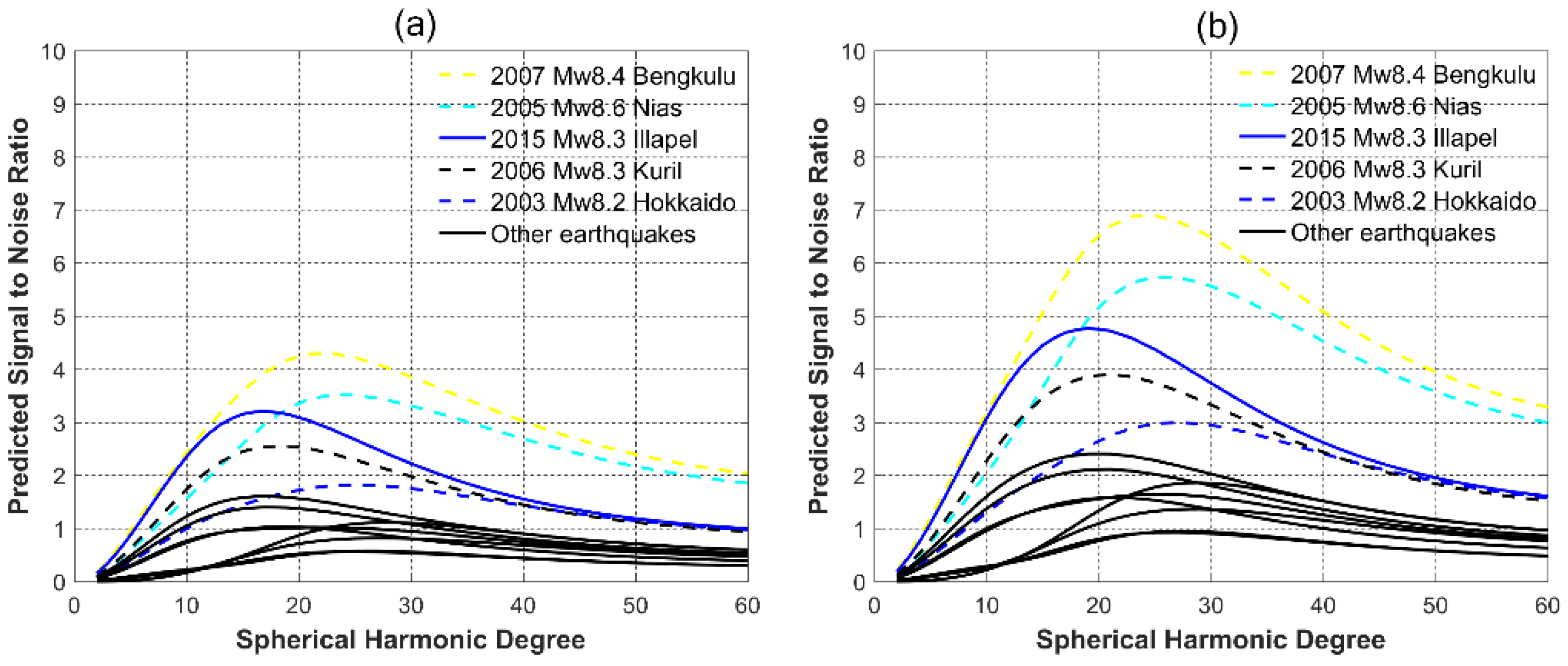
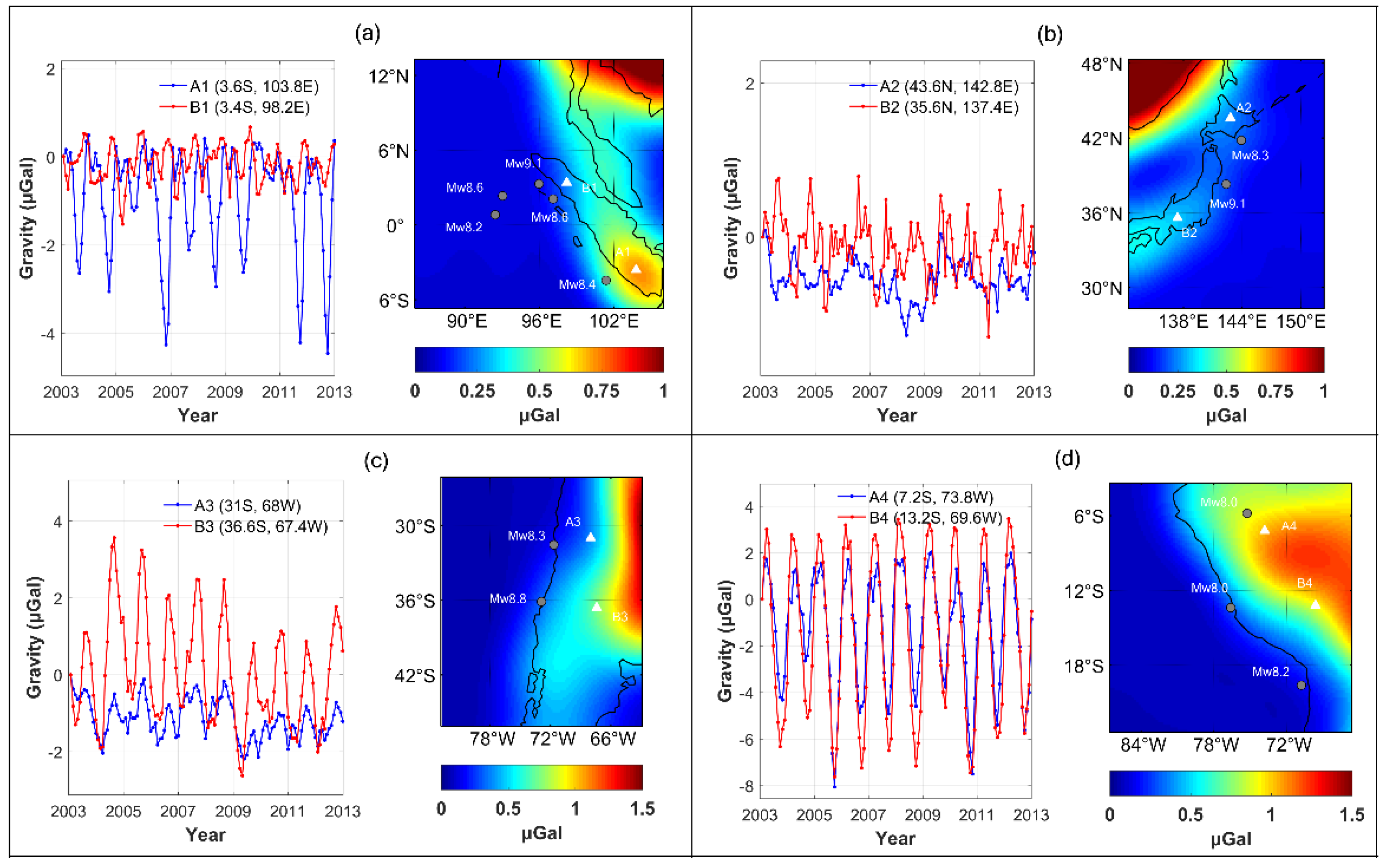
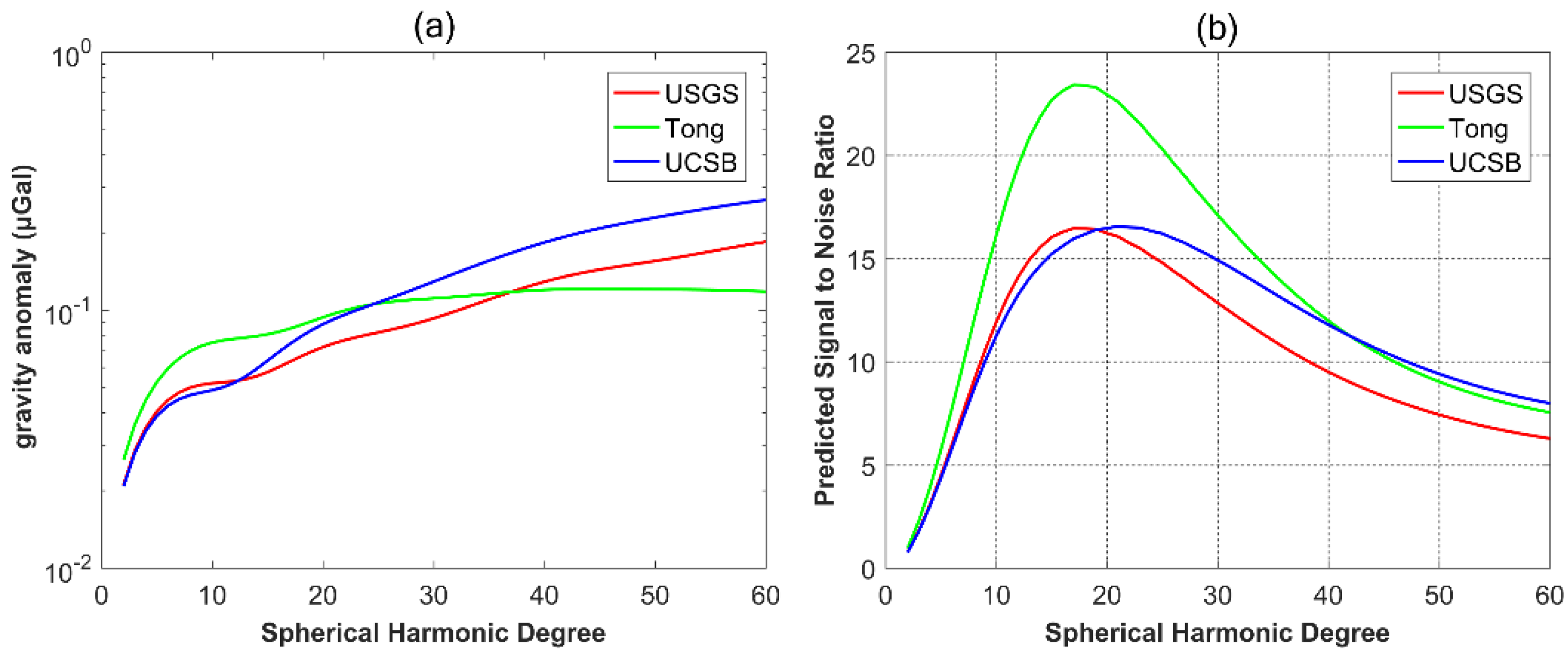
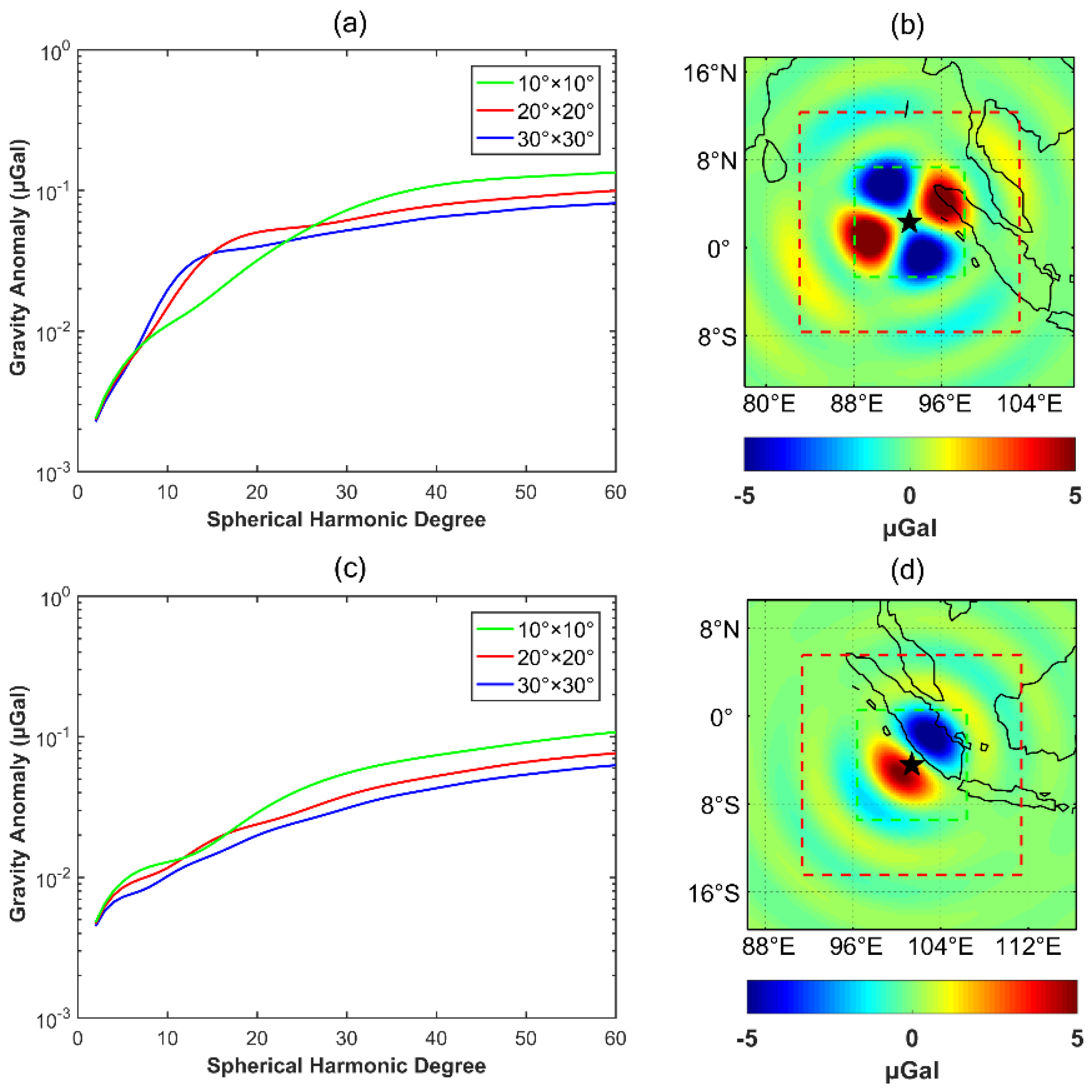
4.2. Comparison in Spectral Domain
5. Discussion
5.1. Other Factors on Extraction of Coseismic Signals
5.1.1. Strip Errors
5.1.2. Influence of Hydrological Signals
5.1.3. Influences of the Differences in Seismic Slip Models
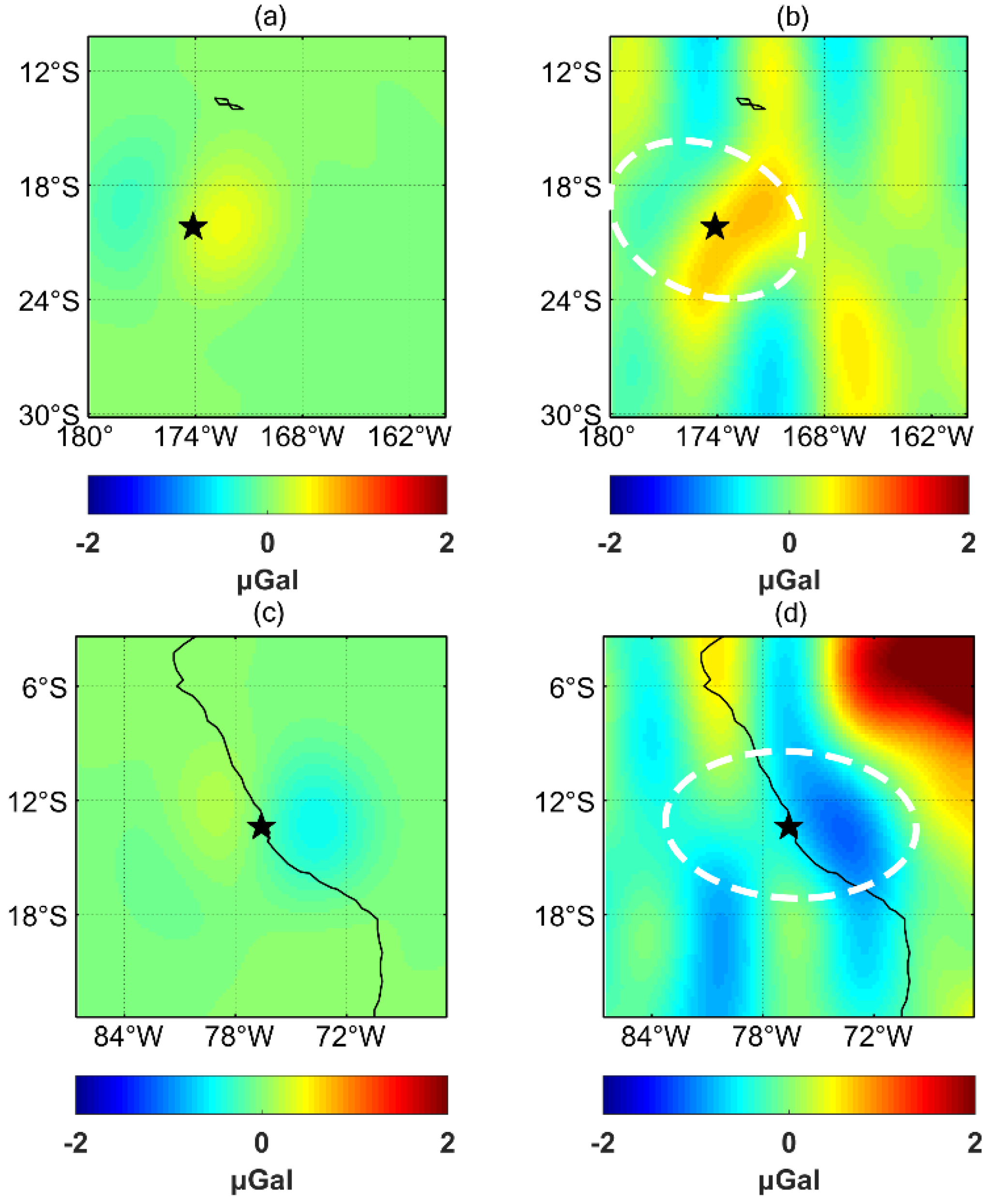
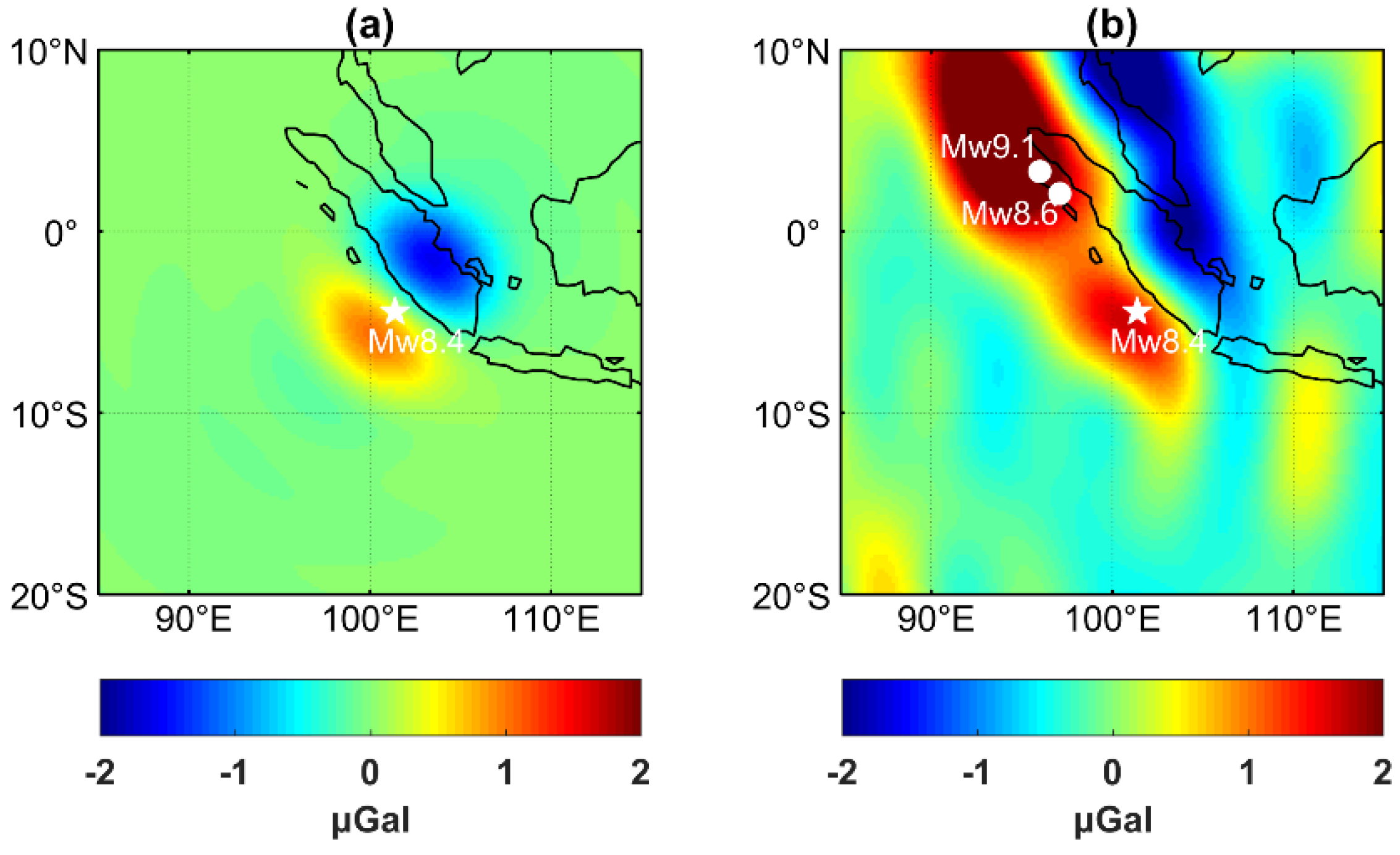
5.1.4. Influence of Earthquake Location
5.2. Influence of Spectral Leakage in Spectral Domain
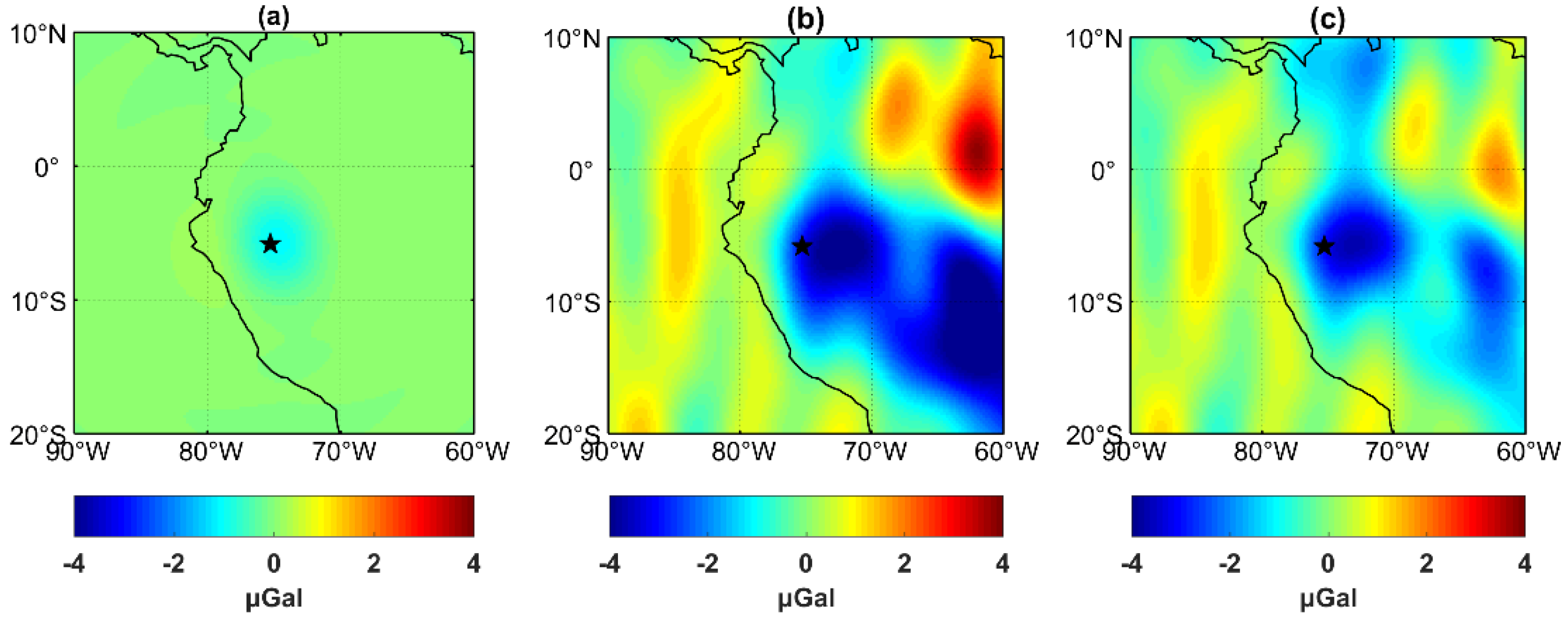
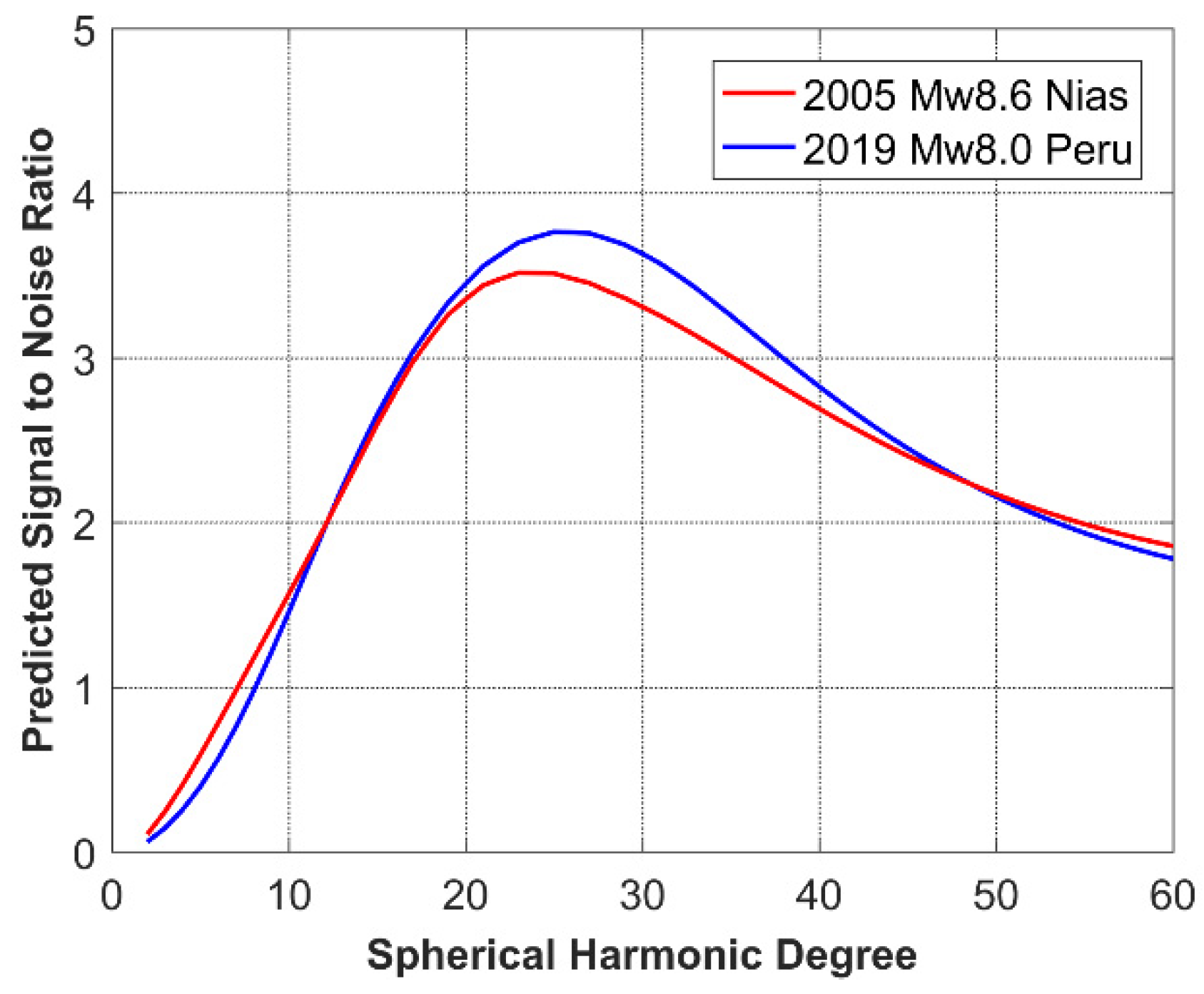
5.3. Coseismic Signal Detection of 2019 Peru Earthquake
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549–552. [Google Scholar] [CrossRef]
- Allison, I.; Alley, R.B.; Fricker, H.A.; Thomas, R.H.; Warner, R.C. Ice sheet mass balance and sea level. Antarct. Sci. 2009, 21, 413–426. [Google Scholar] [CrossRef] [Green Version]
- Quinn, K.J.; Ponte, R.M. Uncertainty in ocean mass trends from GRACE. Geophys. J. Int. 2010, 181, 762–768. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.K.; Okubo, S. Surface potential and gravity changes due to internal dislocations in a spherical earth—II. Application to a finite fault. Geophys. J. Int. 1998, 132, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Gross, R.S.; Chao, B.F. The gravitational signature of earthquakes. In Proceedings of the Gravity, Geoid and Geodynamics: GGG2000 IAG International Symposium, Banff, AB, Canada, 31 July–4 August 2000; Volume 123, pp. 205–210. [Google Scholar]
- Mikhailov, V.; Tikhotsky, S.; Diament, M.; Panet, I.; Ballu, V. Can tectonic processes be recovered from new gravity satellite data? Earth Planet. Sci. Lett. 2004, 228, 281–297. [Google Scholar] [CrossRef]
- Sun, W.K.; Okubo, S. Coseismic deformations detectable by satellite gravity missions: A case study of Alaska (1964, 2002) and Hokkaido (2003) earthquakes in the spectral domain. J. Geophys. Res. Solid Earth. 2004, 109, B04405. [Google Scholar] [CrossRef]
- Han, S.C.; Shum, C.K.; Bevis, M.; Ji, C.; Kuo, C. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake. Science 2006, 313, 658–662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007, 34, L13302. [Google Scholar] [CrossRef] [Green Version]
- Panet, I.; Mikhailov, V.; Diament, M.; Pollitz, F.; King, G.; De Viron, O.; Holschneider, M.; Biancale, R.; Lemoine, J.M. Coseismic and post-seismic signatures of the Sumatra 2004 December and 2005 March earthquakes in GRACE satellite gravity. Geophys. J. Int. 2007, 171, 177–190. [Google Scholar] [CrossRef] [Green Version]
- Heki, K.; Matsuo, K. Coseismic gravity changes of the 2010 earthquake in central Chile from satellite gravimetry. Geophys. Res. Lett. 2010, 37, L24306. [Google Scholar] [CrossRef] [Green Version]
- Han, S.C.; Sauber, J.; Luthcke, S. Regional gravity decrease after the 2010 Maule (Chile) earthquake indicates large-scale mass redistribution. Geophys. Res. Lett. 2010, 37, L23307. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, W.K.; Fu, G.Y. Gravity satellite GRACE detects coseismic gravity changes caused by 2010 Chile Mw8.8 earthquake. Chin. J. Geophys. 2011, 54, 1745–1749. (In Chinese) [Google Scholar]
- Matsuo, K.; Heki, K. Coseismic gravity changes of the 2011 Tohoku-Oki earthquake from satellite gravimetry. Geophys. Res. Lett. 2011, 38, L00G12. [Google Scholar] [CrossRef] [Green Version]
- Han, S.C.; Sauber, J.; Riva, R. Contribution of satellite gravimetry to understanding seismic source processes of the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 2011, 38, L24312. [Google Scholar] [CrossRef]
- Han, S.C.; Riva, R.; Sauber, J.; Okal, E. Source parameter inversion for recent great earthquakes from a decade-long observation of global gravity fields. J. Geophys. Res. Solid Earth 2013, 118, 1240–1267. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.J.; Jin, S.G.; Fan, L. Co-seismic deformation following the 2007 Bengkulu earthquake constrained by GRACE and GPS observations. Phys. Earth Planet. Inter. 2018, 280, 20–31. [Google Scholar] [CrossRef]
- Han, S.C.; Sauber, J.; Pollitz, F. Coseismic compression/dilatation and viscoelastic uplift/subsidence following the 2012 Indian Ocean earthquakes quantified from satellite gravity observations. Geophys. Res. Lett. 2015, 42, 3764–3772. [Google Scholar] [CrossRef]
- Tanaka, Y.; Heki, K.; Matsuo, K.; Shestakov, N.V. Crustal subsidence observed by GRACE after the 2013 Okhotsk deep-focus earthquake. Geophys. Res. Lett. 2015, 42, 3204–3209. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Shen, W.; Xu, C.; Zhu, Y. Coseismic Gravity and Displacement Signatures Induced by the 2013 Okhotsk Mw8.3 Earthquake. Sensors 2016, 16, 1410. [Google Scholar] [CrossRef] [Green Version]
- Chao, B.F.; Liau, J.R. Gravity Changes Due to Large Earthquakes Detected in GRACE Satellite Data via Empirical Orthogonal Function Analysis. J. Geophys. Res. Solid Earth 2019, 124, 3024–3035. [Google Scholar] [CrossRef]
- De Viron, O.; Panet, I.; Mikhailov, V.; Van Camp, M.; Diament, M. Retrieving earthquake signature in grace gravity solutions. Geophys. J. Int. 2008, 174, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Cambiotti, G.; Douch, K.; Cesare, S.; Haagmans, R.; Sneeuw, N.; Anselmi, A.; Marotta, A.M.; Sabadini, R. On Earthquake Detectability by the Next-Generation Gravity Mission. Surv. Geophys. 2020, 41, 1049–1074. [Google Scholar] [CrossRef]
- Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—A new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef] [Green Version]
- Bassin, C.; Laske, G.; Masters, G. The Current Limits of Resolution for Surface Wave Tomography in North America. EOS Trans. AGU 2000, 81, F897. [Google Scholar]
- Sun, W.K.; Okubo, S.; Fu, G.; Araya, A. General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric earth model-applicable to deformed earth surface and space-fixed point. Geophys. J. Int. 2009, 177, 817–833. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Chen, J.; Zhang, Z. Seismologic applications of GRACE time-variable gravity measurements. Earthq. Sci. 2014, 27, 229–245. [Google Scholar] [CrossRef] [Green Version]
- Broerse, T.; Riva, R.; Vermeersen, B. Ocean contribution to seismic gravity changes: The sea level equation for seismic perturbations revisited. Geophys. J. Int. 2014, 199, 1094–1109. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Vigny, C.; Socquet, A.; Peyrat, S.; Ruegg, J.C.; Métois, M.; Madariaga, R.; Morvan, S.; Lancieri, M.; Lacassin, R.; Campos, J.; et al. The 2010 Mw 8.8 Maule Megathrust Earthquake of Central Chile, Monitored by GPS. Science 2011, 332, 1417–1421. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Sladen, A.; The ARIA Group. Updated Result 3/11/2011 (Mw 9.0), Tohoku-Oki, Japan. Rep. Calif. Inst. of Technol. Pasadena. 2011. Available online: http://www.tectonics.caltech.edu/slip_history/2011_taiheiyo-oki/ (accessed on 4 August 2021).
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Wang, L.; Shum, C.K.; Jekeli, C. Gravitational gradient changes following the 2004 December 26 Sumatra-Andaman Earthquake inferred from GRACE. Geophys. J. Int. 2012, 191, 1109–1118. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Shen, W.-B. Monthly GRACE detection of coseismic gravity change associated with 2011 Tohoku-Oki earthquake using northern gradient approach. Earth Planets Space 2015, 67, 29. [Google Scholar] [CrossRef]
- Han, S.C.; Sauber, J.; Pollitz, F. Postseismic gravity change after the 2006–2007 great earthquake doublet and constraints on the asthenosphere structure in the central Kuril Islands. Geophys. Res. Lett. 2016, 43, 3169–3177. [Google Scholar] [CrossRef] [Green Version]
- Qu, W.; Han, Y.; Lu, Z.; An, D.; Zhang, Q.; Gao, Y. Co-Seismic and Post-Seismic Temporal and Spatial Gravity Changes of the 2010 Mw 8.8 Maule Chile Earthquake Observed by GRACE and GRACE Follow-on. Remote Sens. 2020, 12, 2768. [Google Scholar] [CrossRef]
- Dong, J.; Sun, W.; Zhou, X.; Wang, R. An analytical approach to estimate curvature effect of coseismic deformations. Geophys. J. Int. 2016, 206, 1327–1339. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Chen, J.L.; Wilson, C.R. Topographic effects on coseismic gravity change for the 2011 Tohoku-Oki earthquake and comparison with GRACE. J. Geophys. Res. Solid Earth 2016, 121, 5509–5537. [Google Scholar] [CrossRef]
- Tong, X.; Sandwell, D.; Luttrell, K.; Brooks, B.; Bevis, M.; Shimada, M.; Foster, J.; Smalley, R., Jr.; Parra, H.; Báez Soto, J.C.; et al. The 2010 Maule, Chile earthquake: Downdip rupture limit revealed by space geodesy. Geophys. Res. Lett. 2010, 37, L24311. [Google Scholar] [CrossRef] [Green Version]
- Shao, G.; Li, X.; Liu, Q.; Zhao, X.; Yano, T.; Ji, C.; UCSB. Preliminary Slip Model of the 27 February 2010 Mw 8.9 Maule, Chile Earthquake. 2010. Available online: www.geol.ucsb.edu/faculty/ji/big_earthquakes/2010/02/27/chile_2_27.html (accessed on 4 August 2021).
- Sun, W.K. Seismic Dislocation Theory; Science Press: Beijing, China, 2012; pp. 210–214. (In Chinese) [Google Scholar]



| Model Predictions | GRACE Observations | Removed GLADS | |
|---|---|---|---|
| 2003 Mw8.2 Hokkaido | −0.75~+0.44 | -- | -- |
| 2004 Mw8.1 Macquarie | −0.27~+0.30 | -- | -- |
| 2004 Mw9.1 Sumatra–Andaman | −14.00~+3.73 | −13.59~+7.45 | −13.59~+7.44 |
| 2005 Mw8.6 Nias | −1.49~+1.24 | -- | -- |
| 2006 Mw8.0 Tonga | −0.28~+0.41 | -- | -- |
| 2006 Mw8.3 Kuril | −0.74~+0.09 | -- | -- |
| 2007 Mw8.1 Solomon | −0.36~+0.11 | -- | -- |
| 2007 Mw8.0 Peru | −0.49~+0.16 | -- | -- |
| 2007 Mw8.1 Kuril | −0.13~+0.31 | -- | -- |
| 2007 Mw8.4+Mw7.9 Bengkulu | −1.76~+1.08 | −2.04~+1.67 | −2.12~+1.56 |
| 2009 Mw8.1 Samoa | −0.16~+0.20 | -- | -- |
| 2010 Mw8.8 Maule | −5.22~+1.41 | −6.13~+1.73 | −5.77~+1.70 |
| 2011 Mw9.0 Tohoku | −10.99~+3.62 | −7.86~+4.60 | −7.85~+4.56 |
| 2012 Mw8.6 Indian Ocean | −1.86~+1.85 | −3.08~+6.34 | −3.17~+6.34 |
| 2013 Mw8.0 Solomon | −0.23~+0.20 | -- | -- |
| 2013 Mw8.3 Okhotsk | −1.10~+0.60 1 | −1.07~+0.89 | −0.96~+0.90 |
| 2014 Mw8.2 Iquique | −0.54~+0.18 | -- | -- |
| 2015 Mw8.3 Illapel | −0.85~+0.02 | -- | -- |
| GRACE mean error | -- | 0.33~0.98 | -- |
| GRACE stack error | -- | 0.10~0.28 | -- |
| GFO stack error | -- | 0.06~0.18 | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Wan, X.; Chen, R.; Wu, Y.; Wang, W. Evaluation of GRACE/GRACE Follow-On Time-Variable Gravity Field Models for Earthquake Detection above Mw8.0s in Spectral Domain. Remote Sens. 2021, 13, 3075. https://doi.org/10.3390/rs13163075
Xu M, Wan X, Chen R, Wu Y, Wang W. Evaluation of GRACE/GRACE Follow-On Time-Variable Gravity Field Models for Earthquake Detection above Mw8.0s in Spectral Domain. Remote Sensing. 2021; 13(16):3075. https://doi.org/10.3390/rs13163075
Chicago/Turabian StyleXu, Ming, Xiaoyun Wan, Runjing Chen, Yunlong Wu, and Wenbing Wang. 2021. "Evaluation of GRACE/GRACE Follow-On Time-Variable Gravity Field Models for Earthquake Detection above Mw8.0s in Spectral Domain" Remote Sensing 13, no. 16: 3075. https://doi.org/10.3390/rs13163075
APA StyleXu, M., Wan, X., Chen, R., Wu, Y., & Wang, W. (2021). Evaluation of GRACE/GRACE Follow-On Time-Variable Gravity Field Models for Earthquake Detection above Mw8.0s in Spectral Domain. Remote Sensing, 13(16), 3075. https://doi.org/10.3390/rs13163075







