Comparison of Multi-GNSS Time and Frequency Transfer Performance Using Overlap-Frequency Observations

Abstract

The modernized GPS, Galileo, and BeiDou global navigation satellite system (BDS3) offers new potential for time transfer using overlap-frequency (L1/E1/B1, L5/E5a/B2a) observations. To assess the performance of time and frequency transfer with overlap-frequency observations for GPS, Galileo, and BDS3, the mathematical models of single- and dual-frequency using the carrier-phase (CP) technique are discussed and presented. For the single-frequency CP model, the three-day average RMS values of the L5/E5a/B2a clock difference series were 0.218 ns for Galileo and 0.263 ns for BDS3, of which the improvements were 36.2% for Galileo and 43.9% for BDS3 when compared with the L1/E1/B1 solution at BRUX–PTBB. For the hydrogen–cesium time link BRUX–KIRU, the RMS values of the L5/E5a/B2a solution were 0.490 ns for Galileo and 0.608 ns for BDS3, improving Galileo by 6.4% and BDS3 by 12.5% when compared with the L1/E1/B1 solution. For the dual-frequency CP model, the average stability values of the L5/E5a/B2a solution at the BRUX–PTBB time link were 3.54 × 10⁻¹² for GPS, 2.20 × 10⁻¹² for Galileo, and 2.69 × 10⁻¹² for BDS3, of which the improvements were 21.0%, 45.1%, and 52.3%, respectively, when compared with the L1/E1/B1 solution. For the BRUX–KIRU time link, the improvements were 4.2%, 30.5%, and 36.1%, respectively.

1. Introduction

Over the past few decades, the global navigation satellite system (GNSS) has been a useful and efficient spatial technique in the area of time transfer. Since the early 1980s, the global positioning system (GPS) was employed to compare remote clocks using the common-view (CV) approach [1,2], which provided precision on the order of a few nanoseconds [3]. Thereafter, the all-in-view (AV) approach was proposed to overcome the limitations of the common-view satellite condition and pseudorange measurements in the CV approach [4]. Considering that GPS carrier phase observations are two orders of magnitude more precise than that of the pseudorange measurement, a GPS carrier-phase (CP) approach was proposed for precise time and frequency transfer [5,6,7], which exhibited better performance when compared to the CV and AV approaches. Therefore, the GPS CP approach became a primary means in time laboratories worldwide.

In recent years, with the rapid development of other emerging GNSSs, such as the European Galileo and Chinese BeiDou System (BDS), research on the use of these GNSSs for precise time and frequency transfer has aroused considerable interest. Martínez-Belda et al. investigated new analysis procedures based on the E5 code plus-carrier (CPC) combination for time transfer [8,9]. Huang and Defraigne extended the standard Common GNSS Generic Time Transfer Standard (CGGTTS) software tool to the BDS regional system (BDS2) [10]. Liang et al. participated in the experiment of BDS2 time transfer in coordinated universal time (UTC), of which the stability and accuracy were evaluated by using common clock difference and multiple inter-continental baselines [11]. Tu et al. proposed a model of precise time transfer based on the BDS triple-frequency uncombined observations [12,13]. Defraigne and Verhasselt rebuilt the CGGTTS-V2E software to support the GPS, GLONASS, BeiDou, and Galileo system [14]. Zhang et al. demonstrated that the combination of GPS, BDS, and Galileo for time and frequency transfer outperforms the GPS-only, BDS-only, and Galileo-only solutions [15]. Meanwhile, the effect of the biases between the BDS global system (BDS3) and BDS2, GPS, Galileo, and GLONASS observations, on precise time and frequency transfer, were also studied [16,17,18]. Moreover, the performance of time transfer based on new-generation BDS3 triple-frequency observation was also investigated [19].

In fact, the new-generation BDS3 has a full constellation of 35 satellites, consisting of five GEO satellites, 27 MEO satellites, and three IGSO satellites. It retains the previous B1I and B3I signals of the BDS-2 satellites, but also includes the new signals B1C (1575.42 MHz) and B2a (1176.45 MHz). Considering that the E1 (1575.42 MHz) and E5a (1176.45 MHz) are equipped for the Galileo system, and the signals of L1 (1575.42 MHz) and L5 (1176.45 MHz) for the Block IIF satellites of GPS, which have formed two overlapping frequencies to enhance compatibility and interoperability between BDS3, GPS, and Galileo system. Although previous studies have focused on multi-GNSS time and frequency transfer, the performance of these overlapping frequency measurements for multi-GNSS time transfer is still unclear.

In this study, single-frequency (SF) and dual-frequency (DF) CP mathematical models were developed to assess the performance of GNSS overlap-frequency measurement time and frequency transfer. We begin with a brief description of the mathematical models of the SF and DF CP time and frequency transfer with overlapping frequency observations. Then, the experimental design and data processing strategy for assessing the performance of the models are discussed. The results and discussion are presented in this section. Finally, a summary and conclusions are drawn.

2. Principle of Multi-GNSS Time Transfer Using Overlap-Frequency Observations

2.1. Model of the SF Time and Frequency Transfer

For the SF GNSS measurement, the observation equations of phase $\phi$ and code $P$ may be written as follows [20]:

$$\{\begin{array}{l}{P}_{j,k}^s={\rho }_k^s+T_k^s+{\mu }_j{l}_k^s+d{t}_{r,k}-d{t}_k^s+D_j-d_j^s+{\epsilon }_{P_{j,k}^s}\hfill \\ {\phi }_{j,k}^s={\rho }_k^s+T_k^s-{\mu }_j{l}_k^s+d{t}_{r,k}-d{t}_k^s+B_j-b_j^s+N_j^s+{\epsilon }_{{\phi }_{j,k}^s}\hfill \end{array}$$

(1)

where the subscripts $j$ and $k$ denote the frequency and epoch, respectively, and the superscript $s$ denotes the satellite. ${\rho }_k^s$ denotes the geometric distance between the satellite and receiver, $T_k^s$ is the tropospheric delay, and $l_k^s$ denotes the ionospheric delay at the first frequency with ${\mu }_j=f_1/f_j$, $d{t}_{r,k}$ and $d{t}_k^s$ are the clock offsets for the receiver and satellite, respectively. $B_j$ and $D_j$ are the hardware delays of phase and code for the receiver, while $b_j^s$ and $d_j^s$ are the hardware delays of phase and code for the satellite. $N_j^s$ denotes the ambiguity of frequency $j$. ${\epsilon }_{{\phi }_{j,k}^s}$ and ${\epsilon }_{P_{j,k}^s}$ denote the observation noises of phase and code, respectively. It should be noted that the GNSS satellite and receiver phase center offset and variation, phase wind-up, ocean tides, and relativistic delay must be corrected in the Equation (1).

Generally, the satellite clock offset is corrected using clock products, which contain the satellite uncalibrated delay of ionosphere-free pseudorange observations.

$$d{t}^{s_{IF}}=d{t}^s+\frac{f_1^2}{f_1^2-f_2^2}{d}_1^s-\frac{f_2^2}{f_1^2-f_2^2}{d}_2^s=d{t}^s+d_1^s-\beta ·DC{B}_{12}^s$$

(2)

where $\beta =\frac{f_2^2}{f_1^2-f_2^2}$, $DC{B}_{12}^s=d_2^s-d_1^s$ is the satellite differential code bias (DCB) between different frequencies, which can be obtained from the International GNSS Service(IGS) or other GNSS analysis centers. Combining the two equations yields Equation (3):

$$\{\begin{array}{l}{P}_{j,k}^s={\rho }_k^s+T_k^s+{\mu }_j·l_k^s+d{t}_{r,k}-d{t}^{s_{IF}}+D_j-DC{B}_{1j}^s-\beta ·DC{B}_{12}^s+{\epsilon }_{P_{j,k}^s}\hfill \\ {\phi }_{j,k}^s={\rho }_k^s+T_k^s-{\mu }_j·l_k^s+d{t}_{r,k}-d{t}^{s_{IF}}+B_j-b_j^s+N_j^s+{\epsilon }_{{\phi }_{j,k}^s}\hfill \end{array}$$

(3)

The major challenge for GNSS time transfer with SF observation is the mitigation of the ionosphere delay, which cannot be precisely removed owing to the single-frequency data. Considering that ionospheric delay has opposite characteristics on code and CP observations, the GRoup And PHase Ionospheric Correction (GRAPHIC) observation combines the code and CP observations in Equation (1) to remove the ionospheric time delay, the ionosphere-free time and frequency model with SF observation can be written as:

$$G_{j,k}^s=\frac{{\phi }_{j,k}^s+P_{j,k}^s}{2}={\rho }_k^s+T_k^s-d{t}^{s_{IF}}+d{t}_{r,k}+\frac{1}{2}{D}_j-e_j^s+{\overline{N}}_j^s+\frac{1}{2}\left({\epsilon }_{{\phi }_{j,k}^s}+{\epsilon }_{P_{j,k}^s}\right)$$

(4)

where $G_{j,k}^s$ is the GRAPHIC observation; for convenience, we defined $e_j^s=DC{B}_{1j}^s+\beta ·DC{B}_{12}^s$ and ${\overline{N}}_j^s=\frac{1}{2}\left(N_j^s+B_j-b_j^s\right)$. There are many unknown parameters in Equation (4), resulting in a rank deficiency when only the SF GRAPHIC observation is used. This means that one cannot estimate all these parameters directly using Equation (4) [21,22].

Generally, the observation of phase $\phi$ or code $P$ in Equation (3) can also be combined to determine the unknown parameters. Then, the single-epoch, SF observation equation can be written as:

$$\{\begin{array}{l}{\mathit{G}}_{j,k}={\mathit{A}}_k{\mathit{x}}_k+{\mathit{t}}_k\tau -\mathit{d}{\mathit{t}}^{s_{IF}}+d{t}_{r,k}+{\overline{\mathit{N}}}_j+\frac{1}{2}{D}_j-{\mathit{e}}_{\mathit{j}}+{\mathit{\epsilon }}_{G_{j,k}}\hfill \\ {\mathit{P}}_{j,k}={\mathit{A}}_k{\mathit{x}}_k+{\mathit{t}}_k\tau -\mathit{d}{\mathit{t}}^{s_{IF}}+d{t}_{r,k}+{\mathit{I}}_{j,k}+D_j-{\mathit{e}}_{\mathit{j}}+{\mathit{\epsilon }}_{P_{j,k}}\hfill \end{array}$$

(5)

where ${\mathit{G}}_{j,k}={\left[G_{j,k}^1,\cdots ,G_{j,k}^m\right]}^T$ and ${\mathit{P}}_{j,k}={\left[P_{j,k}^1,\cdots ,P_{j,k}^m\right]}^T$ are the vectors of GRAPHIC and code observations at epoch $k$, respectively. $x$ is the station coordinate vector, and the ${\mathit{A}}_k$ is corresponding design matrix,$\tau$ is the modeling residual of tropospheric zenith delay, ${\mathit{t}}_k={\left[t_{j,k}^1,\cdots ,t_{j,k}^m\right]}^T$ is corresponding mapping coefficients, ${\mathit{e}}_{\mathit{j}}={\left[e_j^1,\cdots ,e_j^m\right]}^T$ is the vector of the DCB linear combination. ${\mathit{\epsilon }}_{G_{j,k}}$ and ${\mathit{\epsilon }}_{P_{j,k}}$ are the vectors of GRAPHIC and code observation noise, respectively. It should be noted that the hardware delay of code $D_j$ for the receiver is easily absorbed in the receiver clock offset $d{t}_{r,k}$. It should be noted that ${\mathit{I}}_{j,k}={\left[I_{j,k}^1,\cdots ,I_{j,k}^m\right]}^T$ is the vector of satellite ionospheric delay, which can be corrected using a global ionospheric map (GIM). The stochastic model is formulated as $\mathit{Q}={\mathit{Q}}_r⨂{\mathit{Q}}_k$, where ${\mathit{Q}}_r=diag\left({\sigma }_G^2,{\sigma }_P^2\right)$ with ${\sigma }_G$, and ${\sigma }_P$ is the precision of GRAPHIC and code observations. ${\mathit{Q}}_k$ is the cofactor matrix determined using the satellite-elevation-dependent model.

$$\{\begin{array}{l}{\overline{dt}}_{r,k}={dt}_{r,k}+\frac{1}{2}{D}_j\hfill \\ {\overline{N}}_j^s=\frac{1}{2}\left(N_j^s+B_j-b_j^s\right)\hfill \end{array}$$

(6)

2.2. Model of the DF Time and Frequency Transfer

For the pseudorange and carrier phase observations, the traditional CP technique using the ionosphere-free (IF) combination to eliminate the first-order ionospheric delay, which can be formulated as follows [23,24,25]:

$$\{\begin{array}{l}{P}_{IF,k}^s=a_m·P_{m,k}^s+a_n·P_{n,k}^s={\rho }_{IF,k}^s+T_k^s+d{t}_{r,k}-d{t}^{s_{IF}}+{\epsilon }_{P_{IF,k}^s}\hfill \\ {\phi }_{IF,k}^s=a_m·{\phi }_{m,k}^s+a_n·{\phi }_{n,k}^s={\rho }_{IF,k}^s+T_k^s+d{t}_{r,k}-d{t}^{s_{IF}}+N_{IF}^s+{\epsilon }_{{\phi }_{IF,k}^s}\hfill \end{array}$$

(7)

where the indices $m$ and $n$ represent the frequency indices. $a_m$ and $a_n$ are the coefficients of the IF DF combination. For the GPS and BDS, considering that the satellite clock products are determined by using L1/L2 and B1I/B3I observations, respectively, the overlapping frequency observation E1/E5a is not used, such as Galileo, because it will absorb the satellite DCB into clock products, which will require satellite DCBs among the code to extra correct and remain compatible with the current precise clock product:

$${\mathrm{DCB}}_{\mathrm{cp}}^{\mathrm{s}}\left(\mathrm{GPS}\right)={\mathsf{\beta }}_{\mathrm{L}1,\mathrm{L}2}·{\mathrm{DCB}}_{\mathrm{L}1,\mathrm{L}2}^{\mathrm{s}}-{\mathsf{\beta }}_{\mathrm{L}1,\mathrm{L}5}·{\mathrm{DCB}}_{\mathrm{L}1,\mathrm{L}5}^{\mathrm{s}}$$

(8)

$${\mathrm{DCB}}_{\mathrm{cp}}^{\mathrm{s}}\left(\mathrm{BDS}\right)={\mathsf{\beta }}_{\mathrm{B}1,\mathrm{B}3}·{\mathrm{DCB}}_{\mathrm{B}1,\mathrm{B}3}^{\mathrm{s}}-{\mathsf{\beta }}_{\mathrm{B}1,\mathrm{B}2\mathrm{a}}·{\mathrm{DCB}}_{\mathrm{B}1,\mathrm{B}2\mathrm{a}}^{\mathrm{s}}$$

(9)

Therefore, the single-epoch, DF observation equation can be written as

$$\{\begin{array}{l}{\mathit{P}}_{IF,k}={\mathit{A}}_k{\mathit{x}}_k+{\mathit{t}}_k\tau -\mathit{d}{\mathit{t}}^{s_{IF}}+d{t}_{r,k}+{\mathit{\epsilon }}_{P_{IF,k}}\hfill \\ {\mathit{\phi }}_{IF,k}={\mathit{A}}_k{\mathit{x}}_k+{\mathit{t}}_k\tau -\mathit{d}{\mathit{t}}^{s_{IF}}+d{t}_{r,k}+{\mathit{N}}_{IF,k}+{\mathit{\epsilon }}_{P_{IF,k}}\hfill \end{array}$$

(10)

where ${\mathit{P}}_{IF,k}={\left[P_{IF,k}^1,\cdots ,P_{IF,k}^m\right]}^T$ and ${\mathit{\phi }}_{IF,k}={\left[{\phi }_{IF,k}^1,\cdots ,{\phi }_{IF,k}^m\right]}^T$ are the vectors of single-epoch IF code and carrier phase observations, respectively.

For the operation of precise GNSS time and frequency transfer, this is usually carried out between two remote time and frequency references (namely, A and B). Both the SF model and DF model for time transfer, the unknown parameter of receiver clock offset $d{t}_{r,k}$ is interested, which denotes the clock difference between the individual GNSS timescale (GNSST) and the time and frequency reference. When the hardware delays caused by the receiver, antenna, and cables are calibrated [26,27], then the formula is expressed as follows:

$$\begin{gathered} T\left(A\right)-T\left(B\right)=\left(d{t}_{r,k}\left(A\right)-\mathrm{GNSST}\right)-\left(d{t}_{r,k}\left(B\right)-\mathrm{GNSST}\right) \\ =d{t}_{r,k}\left(A\right)-d{t}_{r,k}\left(B\right) \end{gathered}$$

(11)

It can be noted that the GNSS time scales plays the intermediary role in time and frequency transfer, which effectively overcome the limitation of geometric distance between two time and frequency references.

3. Time and Frequency Transfer Experiment

To assess the performance of time and frequency transfer using GPS, BDS3, and Galileo overlapping-frequency observations, three multi-GNSS stations equipped with an external atomic clock were selected, of which the attribute information are summarizes in

Table 1. Information of stations used in the experiment.

Site	GNSS Receiver	Antenna	Frequency Standard	Location
BRUX	POLARX5TR	JAVRINGANT_DM	UTC(ORB)	50.8° N, 4.4° E
PTBB	POLARX5TR	LEIAR25.R4	UTC(PTB)	52.2° N, 10.4° E
KIRU	POLARX5	SEPCHOKE_B3E6	Industrial cesium standard	67.8° N, 20.9° E

. It should be noted that the two different UTC(k) were connected to the BRUX and PTBB stations, which were maintained using a hydrogen maser. We selected BRUX as the reference station for this experiment. Hence, two time links (BRUX–PTBB and BRUX–KIRU) were formed to analyze the performance of time and frequency transfer.

During the data processing, the GNSS time and frequency transfer software named precise time transfer solution (PTTSol) was developed and employed to assess the overlap-frequency time transfer performance. Considering that most of the error models for BDS3 can be directly utilized for the other systems (GPS and Galileo), owing to the similar operation principles for these GNSSs. All observations had a sampling rate of 30 s, and the satellite elevation mask angle was set to 7°. The multi-GNSS mixed satellite orbit and clock products provided by the GNSS Research Center of Wuhan University were used at sampling intervals of 5 min and 30 s, respectively [28]. The ionospheric effect was eliminated and weakened by using the carrier phase, pseudorange combination, and CODE’s GIM for the SF model. For the DF model, the ionospheric effect was eliminated using the IF combination, which can eliminate the first-order delay [29,30]. The parameter of the satellite antenna phase center correction was temporarily unavailable for BDS3; therefore, it was not corrected. The daily multi-GNSS DCBs were derived from the Chinese Academy of Sciences [31]. Phase ambiguities were estimated as float values. The initial standard deviation values for the carrier phase and pseudorange observations were set to 0.003 and 0.3 m, respectively [32]. The tropospheric delay is typically corrected for its hydrostatic components using the Saastamoinen model, while the residual non-hydrostatic wet components are modeled as a random-walk process with noise (10⁻⁹ m²/s) [33]. The parameter of interest of the receiver clock offset was modeled as a white noise stochastic process, implying that the parameter was estimated epoch-by-epoch. The details of the observation models and data processing strategies are provided in

Table 2. Observation models and data processing strategies.

Items	Models and Strategies
Observations	Carrier phase and pseudorange measurements
Signal frequency	GPS: L1/L5; Galileo: E1/E5a; BDS3: B1/B2a
Satellite orbit and clock	Final multi-GNSS products from WUHN analysis center
Elevation cut-off	7°
Sampling rate	30 s
Tropospheric	Saastamoinen model + random-walk process for wet component (10−9 m2/s)
Ionospheric	Different Ionospheric-free linear combination for SF and DF model
Estimator	Batch least-squares estimator
Observation weight	Elevation-dependent model with cos2 (el) function
Receiver clock offset	Estimated with white noise

.

Notably, the two external atomic clocks individually equipped for one time link are still free-running during the operation of time and frequency transfer, it is impossible to evaluate the performance by repeated measurement. Generally, some smooth approaches with a certain noise are used to assess the performance of time transfer [34]. Therefore, the RMS values of the smooth residuals for the time transfer results were employed to analyze the noise levels of different solutions. Here, the Kalman filter with a process noise of 0.001 ns in the forward mode is employed to determine the RMS values. Meanwhile, the Allan variance is a measure of the fractional frequency fluctuation and offers the advantage of convergence, which is the most commonly used in the area of time and frequency to measure the frequency stability. The Allan variance can be calculated as:

$${\sigma }_y^2\left(\tau \right)=\frac{1}{2\left(N-2\right){\tau }^2}{\displaystyle \sum }_{i=1}^{N-2}{\left[x_{i+2}-2x_{i+1}+x_i\right]}^2$$

(12)

where $x_i$ is the $i$ th data, and $\tau$ is the measurement interval. In fact, the value is usually expressed as the form of square root ${\sigma }_y\left(\tau \right)$, called the Allan deviation (ADEV). The Allan variance is the same as the ordinary variance for white frequency modulation noise, but has the advantage, for more divergent noise types, such as flicker noise, of converging to a value that is independent on the number of samples.

4. Results and Discussion

In this section, based on the results obtained from different schemes, the performance of overlapping frequency observations is analyzed based on the proposed SF-CP and DF-CP models with GPS, Galileo, and BDS3 constellations. Then, some characteristics of the L1/E1/B1 and L5/E5a/B2a observations are discussed. Finally, the performance in noise level and frequency stability of two time links, including the SF and DF for overlapping frequency observations, is discussed.

4.1. SF Time and Frequency Transfer

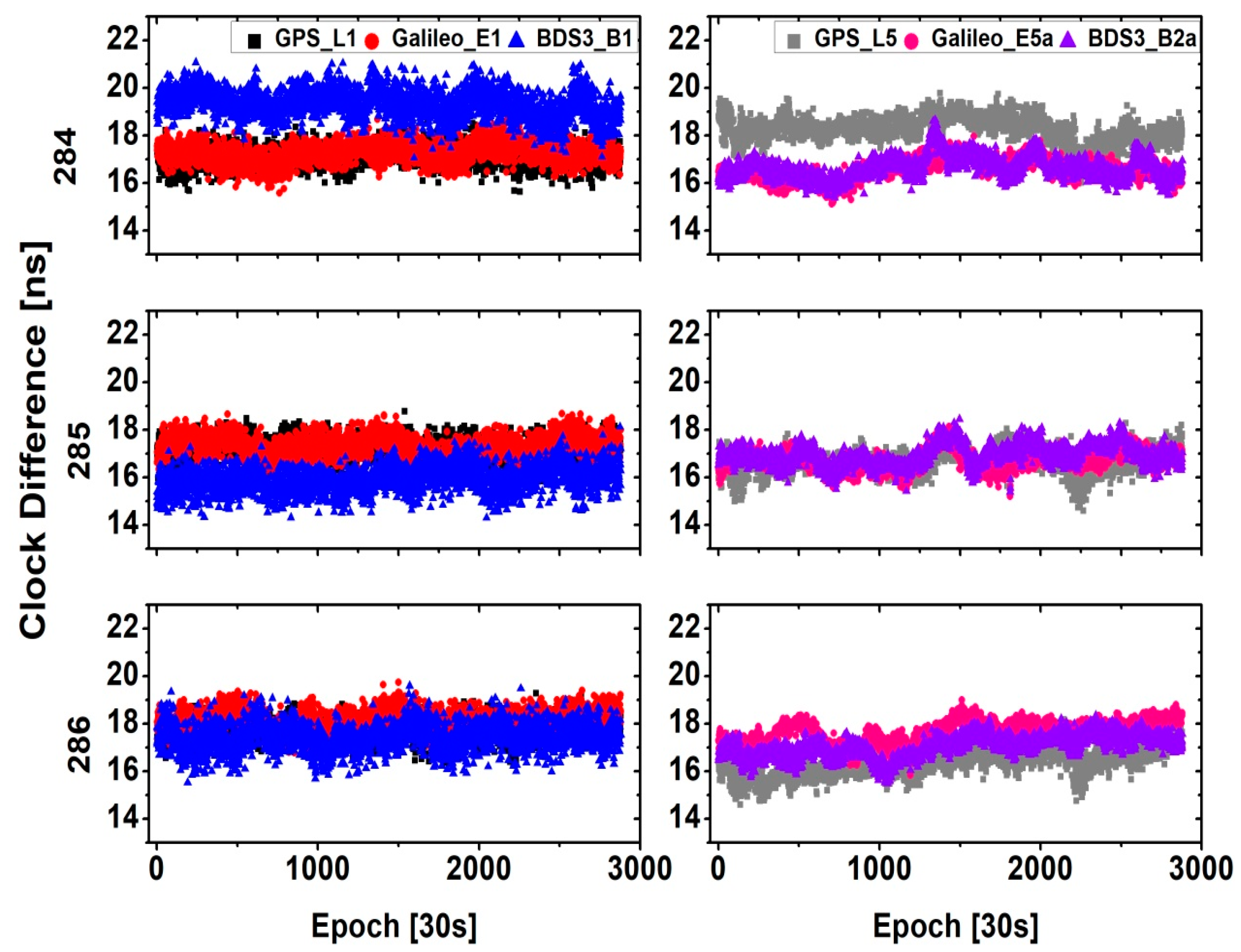
Figure 1 and Figure 2 present the SF time transfer results for GPS, Galileo, and BDS3 overlapping frequency observations at time link BRUX–PTBB and BRUX–KIRU, respectively. One can note that the variations in the time transfer values made a good match among GPS, Galileo, and BDS3 at each overlapping frequency solution. Moreover, the clear biases still existed among the GPS, Galileo, and BDS3 for each overlapping frequency solution, which is mainly caused by receiver clock offset being absorbed by different receiver DCBs as varying GNSS undergoing different time delays. Additionally, one can also note that the result of time transfer at L5/E5a/B2a exhibits better variation characteristics than L1/E1/B1 at both the time links of BRUX–PTBB and BRUX–KIRU.

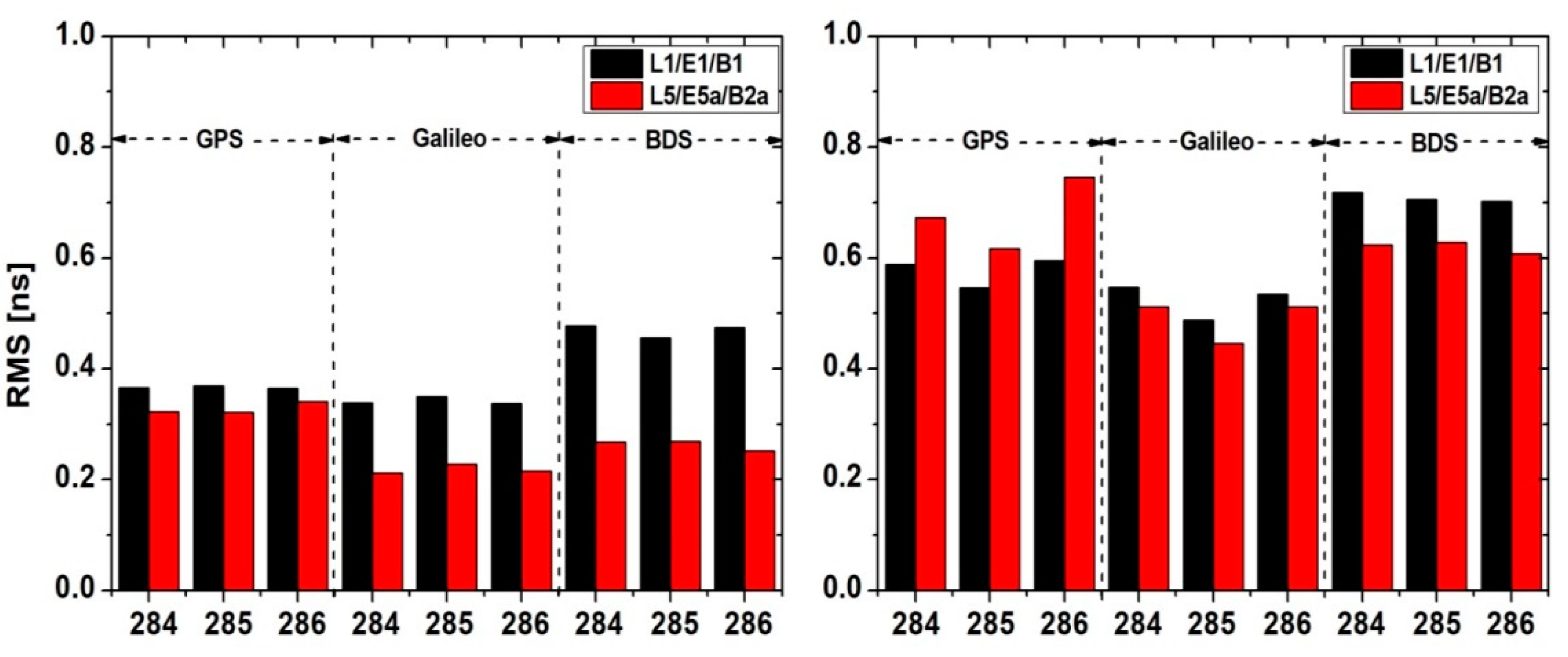
To further compare the performance of time and frequency transfer with overlapping frequency observations for GPS, Galileo, and BDS3 systems, the indicators of noise level and frequency stability of time links are employed. The RMS of smoothed residuals for the clock difference series derived by the SF models at time link BRUX–PTBB are shown in the left panel of Figure 3. For comparison, the BRUX–KIRU solutions are also presented in the right panel. One can clearly note that the time link BRUX–PTBB shows better performance than that of the BRUX–KIRU time link, the main reason is that the former one equipped with the hydrogen–hydrogen clocks, whereas the latter one is equipped with the hydrogen–cesium clocks. As shown, the L5/E5a/B2a solutions show better performance than those of the L1/E1/B1 solutions at two time links, particularly in Galileo and BDS3 solutions. The three-day averaged RMS values of the L5/E5a/B2a solution were 0.218 ns for Galileo and 0.263 ns for BDS3, improving Galileo by 36.2%, and BDS3 by 43.9% when compared with the L1/E1/B1 solution at BRUX–PTBB. For the hydrogen–cesium time link BRUX–KIRU, the corresponding RMS values of the L5/E5a/B2a solution are 0.490 ns for Galileo and 0.608 ns for BDS3, improving Galileo by 6.4% and BDS3 by 12.5% when compared with the L1/E1/B1 solution at BRUX–KIRU. From

Table 3. Average number of available satellite for different GNSS frequencies at three stations.

	BRUX	KIRU	PTBB
GPS_L1	9.2	10.1	9.2
GPS_L5	4.5	5.0	4.5
Galileo_E1	7.6	8.1	7.1
Galileo_E5a	7.6	8.1	7.1
BDS3_B1	5.2	5.7	5.2
BDS3_B2a	5.2	5.7	5.2

, it can be noted that because the limited GPS satellite is able to broadcast the L5 signals, the advantage of L5/E5a/B2a solutions is not obvious, particularly in the BRUX–KIRU time link.

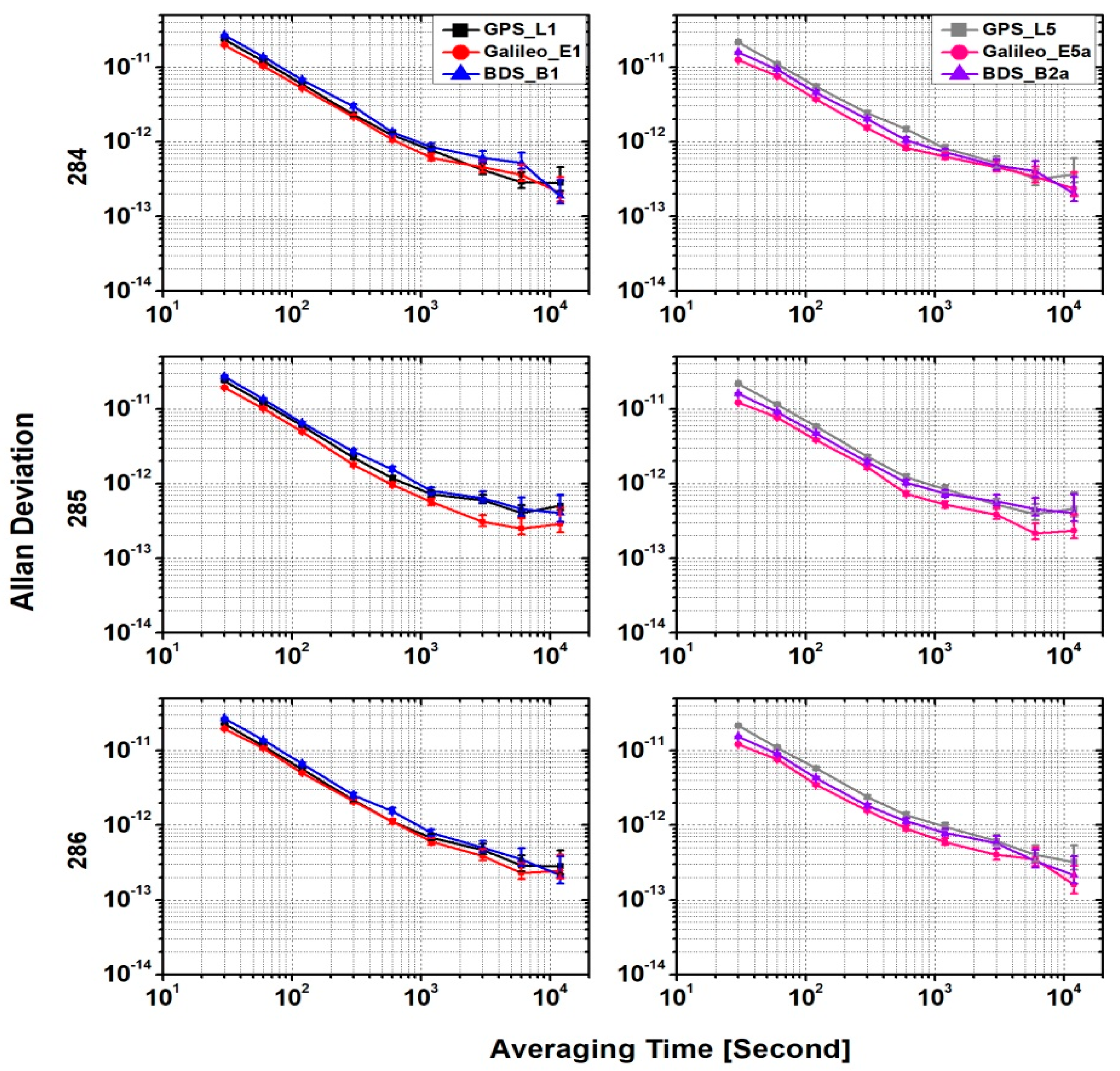
Figure 4 and Figure 5 present the ADEVs for SF time transfer results with GPS, Galileo, and BDS3 overlapping frequency observations at time link BRUX–PTBB and BRUX–KIRU. One can clearly see that the frequency stabilities of L1/E1/B1 solutions were also generally similar for the GPS, Galileo, and BDS3 both BRUX–PTBB and BRUX–KIRU time links, regardless of the averaging time interval. For the BRUX–PTBB time link, the average stability values of the L5/E5a/B2a solution at all time intervals are 3.54 × 10⁻¹² for GPS, 2.20 × 10⁻¹² for Galileo, and 2.69 × 10⁻¹² for BDS3, of which the improvements are 21.0%, 45.1%, and 52.3%, respectively, when compared with the L1/E1/B1 solution. With respect to the BRUX–KIRU time link, the average stability values of the L5/E5a/B2a solution at all time intervals are 4.94 × 10⁻¹² for GPS, 3.06 × 10⁻¹² for Galileo, and 3.82 × 10⁻¹² for BDS3, of which the improvements are 4.2%, 30.5%, and 36.1%, respectively, when compared with the L1/E1/B1 solution.

4.2. DF Time and Frequency Transfer

Figure 6 shows the DF time transfer results for GPS, Galileo, and BDS3 overlapping frequency (L1/L5, E1/E5a, B1/B2a) observations at time link BRUX–PTBB (left) and BRUX–KIRU (right), respectively. One can note that the variation of the clock difference series for GPS, Galileo, and BDS3 agreed well both at the BRUX–PTBB (Left) and BRUX–KIRU (Right), although obvious biases exist among the different series, which mainly cause by the different hardware delays for different satellite systems and can be calibrated in the time transfer campaign [35]. Meanwhile, the different estimated coordinate values of station for different satellite systems partly lead to these biases [36,37]. Therefore, we focused on the variation characteristics of the clock difference series.

Table 4. DF RMS of smoothed residuals for the clock difference series (ns).

Day	BRUX–PTBB			BRUX–KIRU
	GPS	Galileo	BDS3	GPS	Galileo	BDS3
284	0.026	0.023	0.028	0.407	0.407	0.406
285	0.023	0.020	0.020	0.345	0.344	0.344
286	0.016	0.013	0.014	0.383	0.381	0.386

presents the DF RMS of the smoothed residuals for the clock difference series. It can be noted that the RMS values are in good agreement with each GNSS at the time link of BRUX–PTBB and BRUX–KIRU, respectively. The averaged RMS improved by nearly an order of magnitude for the BRUX–PTBB time link when comparing the SF L5/E5a/B2a RMS mean values. The average improvements of RMS are 93.7%, 93.4%, and 94.0% for GPS, Galileo, and BDS3, at the BRUX–PTBB time link, and 39.7%, 25.5%, and 43.0% for GPS, Galileo, and BDS3, respectively, at the BRUX–KIRU time link.t.

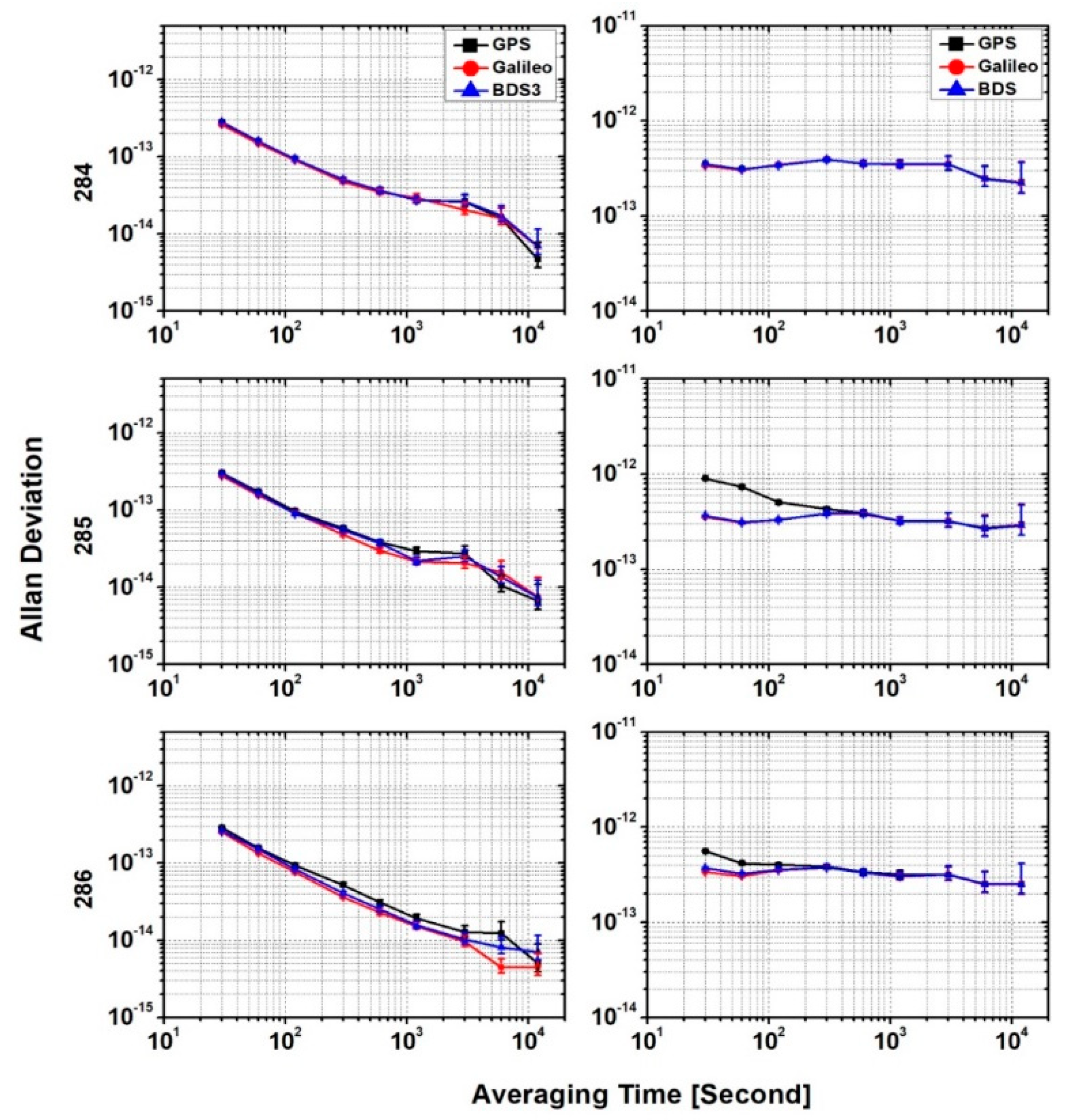
Figure 7 presents the ADEVs for DF time transfer results with GPS, Galileo, and BDS3 overlapping frequency observations at time link BRUX–PTBB and BRUX–KIRU. It can be clearly seen that the variation trends are very similar for different GNSSs at the two time links. For the BRUX–PTBB time link, the average stability values of the DF solution at all time intervals were 7.80 × 10⁻¹⁴ for GPS, 6.95 × 10⁻¹⁴ for Galileo, and 7.43 × 10⁻¹⁴ for BDS3, of which the improvements were 97.8%, 96.8%, and 97.2%, respectively, when compared with the SF L5/E5a/B2a solution. With respect to the BRUX–KIRU time link, the average stability values of the DF solution at all time intervals were 3.82 × 10⁻¹³ for GPS, 3.21 × 10⁻¹³ for Galileo, and 3.25 × 10⁻¹³ for BDS3, with improvements of 92.3%, 89.5%, and 91.5%, respectively, when compared with the SF L5/E5a/B2a solution.

5. Conclusions

The multi-GNSS overlap-frequency observation will contribute to the compatible interoperability among different GNSSs. To further exploit the potential of those GNSS overlap-frequency observation for time and frequency transfer, we studied a SF model and DF model of GNSS precise time and frequency transfer by using the CP technique. The corresponding mathematical models are analyses and presented. Moreover, numerical analyses were conducted to assess the time and frequency transfer performance of two time transfer links.

For the SF CP time transfer model, the results show that the variations in the clock difference series from the three GNSS solutions agree well, at both the L1/E1/B1 and L5/E5a/B2a overlapping frequency. With respect to the indicators of noise level and frequency stability of the time link, the L5/E5a/B2a solutions show better performance than the L1/E1/B1 solutions at two time links. In terms of noise level, the improvements in L5/E5a/B2a were 36.2% for Galileo, and 43.9% for BDS3 when compared with the L1/E1/B1 solution at hydrogen–hydrogen BRUX–PTBB, as well as the 6.4% for Galileo, and 12.5% for BDS3 at the hydrogen–cesium time link BRUX–KIRU. For the frequency stability, the improvement in the average stability value of L5/E5a/B2a solution was 21.0% for GPS, 45.1% for Galileo, and 52.3% for BDS3 at the BRUX–PTBB time link when compared with L1/E1/B1 solutions, while the improvements were 4.2% for GPS, 30.5% for Galileo, and 36.1% for BDS3 at the BRUX–KIRU time link.

For the DF CP time transfer model, the variation of the clock difference series for GPS, Galileo, and BDS3 overlapping frequency observations agreed well at two time links. The DF result shows a significant improvement over the SF time and frequency transfer results in both the noise level and frequency stability. When compared with the L5/E5a/B2a SF solutions, the average improvements in noise level were 93.7%, 93.4%, and 94.0% for GPS, Galileo, and BDS3 at the BRUX–PTBB time link, as well as the 39.7%, 25.5%, and 43.0% for GPS, Galileo, and BDS3 at the BRUX–KIRU time link, respectively. For the frequency stability, the improvements were 97.8%, 96.8%, and 97.2% for GPS, Galileo, and BDS3, respectively at the BRUX–PTBB time link. For BRUX–KIRU, the improvements were 92.3%, 89.5%, and 91.5% for GPS, Galileo, and BDS3, respectively.

In conclusion, when using the overlapping frequency observation for multi-GNSS precise time and frequency transfer, the results exhibit equivalent performance for different GNSSs based on both SF and DF models. Meanwhile, the L5/E5a/B2a frequency observations have certain advantages in terms of time and frequency transfer. Then, the DF result shows significant improvement over the SF, of which the range can reach nearly an order of magnitude. With continuous development of the GPS, Galileo, and BeiDou satellite systems, more GNSS satellites will broadcast overlapping frequency signals, which will be helpful for the compatibility of multi-system time and frequency transfer.