Abstract
In order to deal with the problem that some existing semantic segmentation networks for 3D point clouds generally have poor performance on small objects, a Spatial Eight-Quadrant Kernel Convolution (SEQKC) algorithm is proposed to enhance the ability of the network for extracting fine-grained features from 3D point clouds. As a result, the semantic segmentation accuracy of small objects in indoor scenes can be improved. To be specific, in the spherical space of the point cloud neighborhoods, a kernel point with attached weights is constructed in each octant, the distances between the kernel point and the points in its neighborhood are calculated, and the distance and the kernel points’ weights are used together to weight the point cloud features in the neighborhood space. In this case, the relationship between points are modeled, so that the local fine-grained features of the point clouds can be extracted by the SEQKC. Based on the SEQKC, we design a downsampling module for point clouds, and embed it into classical semantic segmentation networks (PointNet++, PointSIFT and PointConv) for semantic segmentation. Experimental results on benchmark dataset ScanNet V2 show that SEQKC-based PointNet++, PointSIFT and PointConv outperform the original networks about 1.35–2.12% in terms of MIoU, and they effectively improve the semantic segmentation performance of the networks for small objects of indoor scenes, e.g., the segmentation accuracy of small object “picture” is improved from 0.70% of PointNet++ to 10.37% of SEQKC-PointNet++.
1. Introduction
Since the semantic understanding and analysis of a 3D point cloud is the basis for realizing scene understanding [1,2], the application of semantic segmentation of 3D point cloud has been more and more extensive in recent years [3,4,5], such as augmented/virtual reality [6] and intelligent robot [7]. Moreover, in the field of self-driving, the accurate perception of the environment based on LIDAR point cloud data is the key to realize information decision-making and driving safely in the complex dynamic environment. Particularly, accurate segmentation of small objects can help self-driving vehicles make correct decisions in time in some cases. Semantic segmentation of 3D point clouds aims to predict the label of each point in the point clouds, making different classes of objects with corresponding labels. The performance of semantic segmentation based on deep neural networks depends on the strength of the feature extraction ability of the network [8,9,10], especially for the small objects in the scene, which requires the network to be able to extract more fine-grained local semantic information.
PointNet [11] was proposed to use raw point clouds as the input of the network at the first time, which uses Multi-Layer Perception (MLP) [12] to learn features from the point cloud adaptively. The core concept of PointNet is to approximate a general function defined on a point set by applying a symmetric function, so it can efficiently extract information from the unordered point cloud. However, it is difficult for PointNet to learn local features and the relationship between points in the point cloud. To address this problem, PointNet++ [13] uses a sampling and grouping strategy to divide the point cloud into several small local regions, so it can leverage the PointNet to extract local features. Jiang et al. [14] proposed the Orientation-Encoding and Scale-Awareness module in PointSIFT network to extract features. The orientation-encoding first integrates the feature information of the points in each of the eight spatial directions in the point cloud space, then performs a three-stage ordered convolution to encode these feature information. Meanwhile, the network connects multi-scale features by stacking orientation encoding in the process of propagation. For local regions of point clouds, Wu et al. [15] uses inverse density-weighted convolution to capture local features. The method weights the features of the points by inverse density and weight function which is generated by kernel density estimation method [16] and the coordinates of the points. PointConv gains great improvement in terms of the semantic segmentation, but the network tends to lose the information of large object edges and small objects in the sampling process.
The semantic segmentation performance of the above methods for small objects in 3D scenes is generally poor. All objects in the point cloud are composed of points connected with each other, so that the semantic segmentation of each point depends on the relationship of points. Using the MLP to extract features will treat all the points equally, and the result may be biased toward the categories that account for a larger proportion of the point cloud data. In contrast, objects with a smaller percentage of points in the scene need to be distinguished using point-to-point associations. As mentioned above, the MLP treats each point in the point cloud equally, neglecting the connection between points, and thus the extracted features of the point cloud are not distinguishable enough, resulting in low accuracy of the final 3D point cloud semantic segmentation results, especially for small objects.
Different from previous methods that use the MLP to extract features directly, the proposed Spatial Eight-Quadrant Kernel Convolution (SEQKC) algorithm generates eight kernel points with coordinates and shared weights in the neighborhood space of point cloud at first; Then, the distance between each kernel point and its neighbors are calculated, and the inverse distance is used as the coefficient of the weight; Finally, the kernel point weights are used to weight the features of each point, and all the weighted features are aggregated and input into the MLP. As a result, the proposed method can effectively extract the local fine-grained information of point clouds by modeling the relationship between points in space, which can improve the semantic segmentation accuracy of small objects in 3D scenes. Furthermore, we design a downsampling module based on the SEQKC which is combined with the existing methods (e.g., PointNet++, PointSIFT and PointConv networks) to do feature extraction for point clouds. In order to save computational time and memory, the downsampling module consists of SEQKC module and set sbstraction module. Moreover, to learn both global and local features well at the same time, the downsampling module is similar to a residual network structure, so that multi-scale semantic information of the point cloud can be extracted.
In summary, our contributions are:
- To capture point-to-point connections in point clouds for better local feature extraction, the spatial eight-quadrant kernel convolution is proposed in this paper.
- A downsampling module based on spatial eight-quadrant kernel convolution is designed, which can be combined with existing methods and further improve the semantic segmentation performance.
- Extensive experiments have been conducted on ScanNet V2 dataset [17], the experimental results show that our method can help the network effectively extract local semantic information of point clouds and improve the semantic segmentation accuracy of small objects.
2. Literature Review
In this section, we briefly review the approaches of semantic segmentation for 3D point clouds using deep learning network.
2.1. Projection-Based Semantic Segmentation Methods for Point Clouds
Some networks project 3D point clouds into 2D images, so they can use 2D convolution to process the point clouds. Tatarchenko et al. [18] proposed the tangent convolution, where a plane tangent to the local surface of each point is constructed, then the local surface is projected onto the tangent plane and convolved on the projection plane. Lawin et al. [19] observe 3D point clouds from different views, then integrate and input multiple projections to the FCN network, and synthetic image per-pixel evaluation scores are output, finally the evaluation scores are mapped back to individual views to obtain semantic labels for each point. However, the performance of this method is greatly influenced by the viewpoint selection, and it is difficult to handle the occluded point clouds, and the projection is highly prone to lose point cloud information, so these methods are not suitable for dealing with point clouds that possess complex geometric structures. Additionally, in the self-driving scenario, poor synchronization of LIDAR and camera may lead to bad point cloud projection in the image, resulting in 3D points with an erroneous semantic class [20].
2.2. Voxelization-Based Semantic Segmentation Method for Point Clouds
Since point cloud data have irregular structure in 3D space, early point clouds were often processed by voxelization methods to enable them to be processed using standard 3D convolution. Huang et al. [21] voxelized point clouds and input them into 3D convolutional neural networks for semantic segmentation, the predicted semantic labels for each point are output and compared with the real semantic labels for back-propagation learning. Due to the sparsity of point clouds, this method can only cope with some more regular point clouds. Tchapmi et al. [22] proposed SEGCloud for feature extraction in the fine-grained space of point clouds and performing semantic segmentation that encompasses the whole point cloud.
The discretization method can maintain the geometric structure of the point cloud, and the standard 3D convolution can be well adapted to this format. However, the voxelization method will inevitably make some points shift the original position and lead to discretization artifacts, and there is also the problem of information loss in the process. Since point cloud data contain variable types of objects, it is difficult to choose a suitable grid resolution, and a high resolution will make the network training slow and computationally expensive, while a low one will lose important information and lead to wrong results.
2.3. Point-Based Semantic Segmentation Method for Point Clouds
Point-based methods can directly use raw point clouds. PointNet is a pioneer work which used the point cloud data directly, but the operation of global pooling makes the network lose local information of the point cloud, which cannot meet the needs of point cloud semantic segmentation for small objects. In order to learn local features of the point cloud, subsequent work mainly uses hierarchical networks or feature weighting methods. PointNet++ is a representative work for hierarchical networks, which uses a sampling and grouping strategy to extract the point cloud local features, the iteration of downsampling to expand the receive field of the network, and feature interpolation to finally achieve point cloud semantic segmentation. In [23], a large outdoor public dataset for 3D semantic segmentation (PC-Urban) is proposed and baseline semantic segmentation results on PC-Urban are produced by PointNet++ and PointConv. Unal et al. [24] proposed a detection aware 3D semantic segmentation method which leverages localization features from an auxiliary 3D object detection task. By utilizing multitask training, the shared feature representation of the network is guided to be aware of per class detection features that aid tackling the differentiation of geometrically similar classes. Hua et al. [25] proposed a method to integrate adjacent points in the local region space of the point cloud and then convolve the integrated point cloud features using kernel point weights. Thomas et al. [26] proposed a kernel point convolution operator to construct kernel points in the 3D point cloud space, and weighted the features by calculating the Euclidean distance from the point to the kernel point. Ye et al. [27] proposed to extract multi-scale features of point clouds using a pointwise pyramid structure and apply Recurrent Neural Networks (RNNs) to achieve end-to-end learning. In order to extract the contextual features of each local region of the point cloud during the point cloud feature propagation, Engelmann et al. [28] applying RNNs to do point cloud semantic segmentation, it encodes features that contain different scales of the point cloud by [28] using merged units or recursive merged units to extract the detailed point cloud feature information.
3. Methods
3.1. Spatial Kernel Convolution Algorithm
Previous works directly use shared MLPs separately on each point, followed by the operation of global max-pooling. The shared MLP acts as a set of learning spatial encodings, and the global characteristics of the point cloud are calculated as the maximum response between all points for each of these encodings. Although the kernel of point convolution can be implemented by MLPs in this way, local spatial relationships in the data have not been considered, and it makes the convolution operator more complex and the convergence of the network harder. To this end, we propose the idea of using spatial kernel convolution, like image convolutions, whose weights are directly learned without the intermediate representation of a MLP. Furthermore, local relationships between points can be modeled by distance weighting, so that the local fine-grained feature can be extracted by the proposed method.
Specifically, multiple kernel points with shared weights are generated in the point cloud neighborhood space, and each kernel point is accompanied with coordinates. Before aggregating the neighborhood points features into the MLP, the distances between the kernel points and several points in their neighborhood are calculated, then features of each point are weighted by the distances and the kernel point weights, finally all the weighted features are aggregated and input into the MLP network.
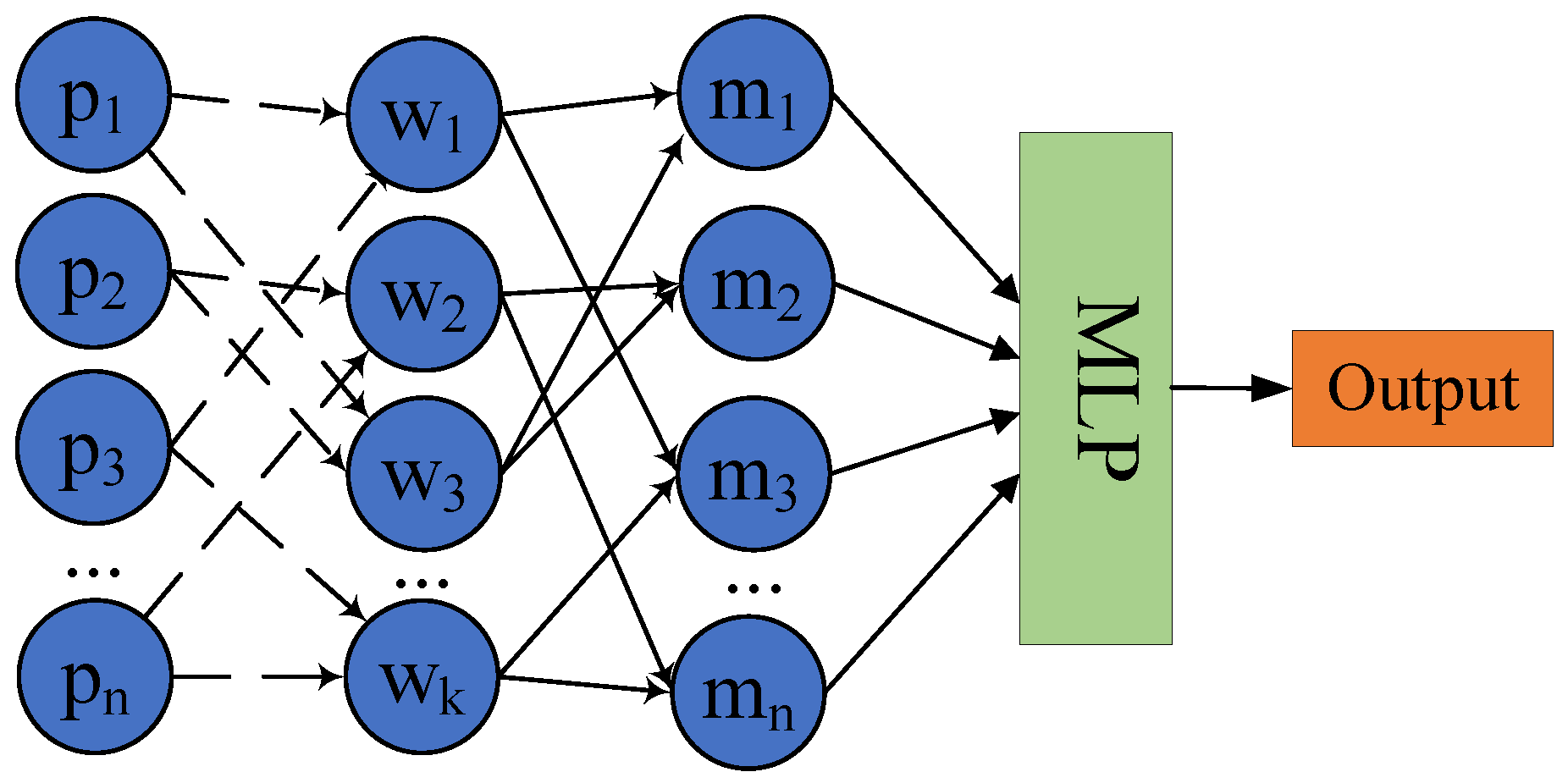
As shown in Figure 1, the represent n neighborhood points, denote the weights of the k kernel points, and the features of each point in the neighborhood are multiplied with the weights . Unlike the conventional fully connected method, features of each point are only connected to some kernel points. The dashed lines in Figure 1 which connect the features and weights indicate that the features of each point are weighted using the reverse distance from each point in the neighborhood to the kernel point, so the closer the point is to the kernel point, the greater the weight is. The method that uses inverse distance weighting features can not only well distinguish the strength of the relationship between each point and the centroid, but also extract fine-grained features of the point cloud more effectively. The features of each point are weighted by multiple spatial kernels and then combined again into new features . Then we input the new features that contain tight connections into MLP, as a result, the local point cloud features will be effectively extracted.
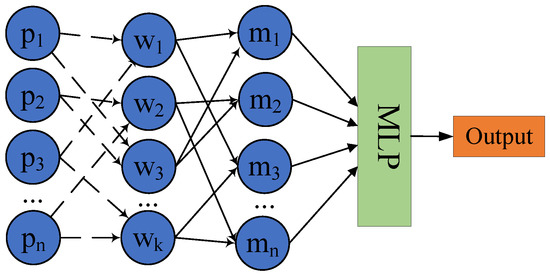
Figure 1.
The process of spatial kernel convolution, where denotes n neighborhood points, denotes weights of the k kernel points, dashed lines denote features of each point are weighted using the reverse distance from each point in the neighborhood, denotes the new feature that is combined with features weighted by multiple spatial kernels.
We study the influence of different kernel points number on ability of feature extraction. We change the number of kernel points in point cloud semantic segmentation experiments. The experimental results show that the best number of spatial kernel points is 8. Because the number of feature points in the neighborhood space is limited, and the feature information extraction of each kernel point is accompanied by distance weighting. When the number of kernel points increases, the point with the same feature may be similar to several kernel points at the same time, and the information extracted from the feature point by these kernel points may be repetitions, resulting in the entire spatial kernel convolution module doing redundant and meaningless work, which increases the network computation in vain. Since the eight kernel points are uniformly distributed in the eight quadrants of the neighborhood space, we call our point cloud feature extraction method as Spatial Eight-Quadrant Kernel Convolution (SEQKC).
3.2. Spatial Eight-Quadrant Kernel Convolution Algorithm
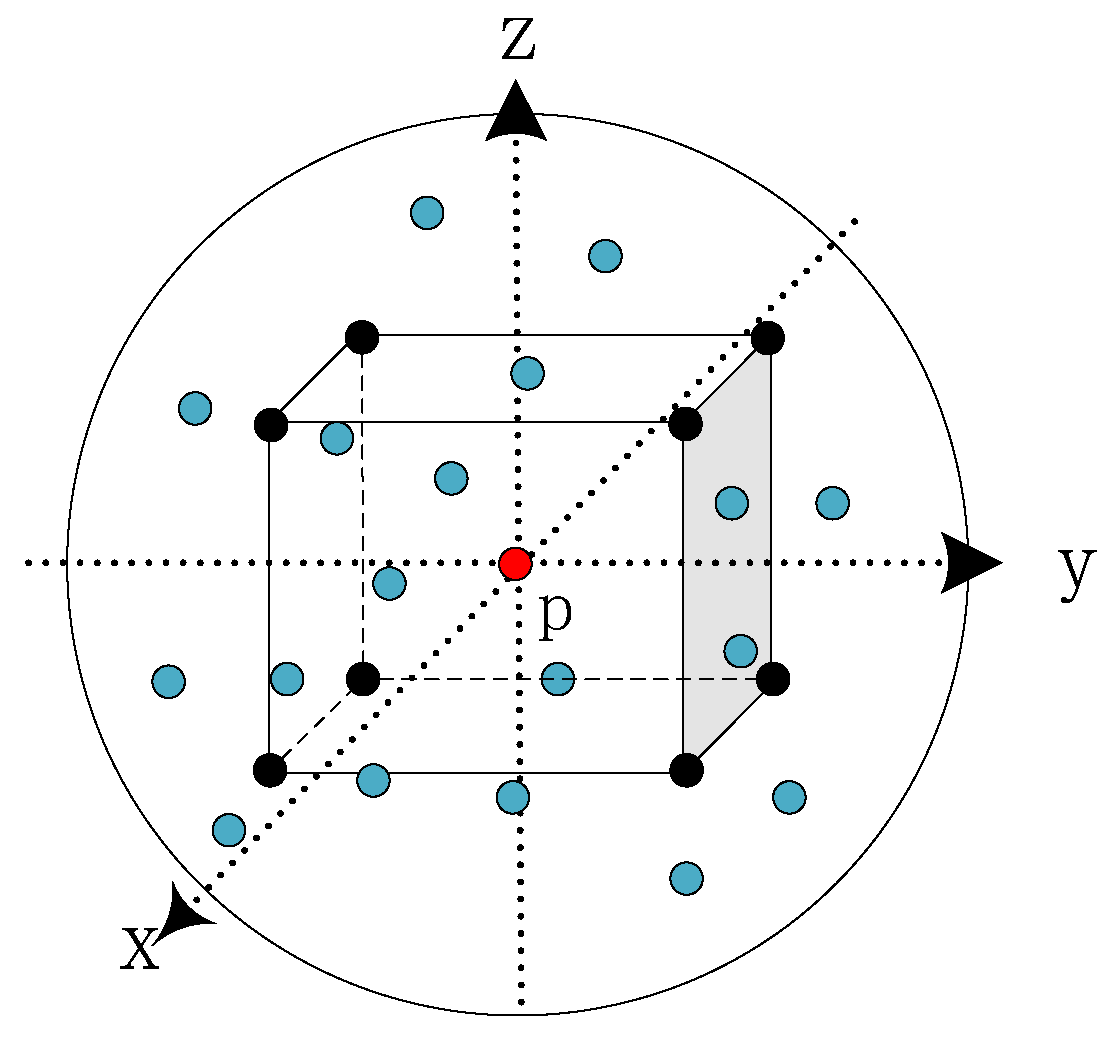
In this section we describe the details of the SEQKC. As shown in Figure 2, a spherical neighborhood space is constructed, where the center point is p and the radius is r. The SEQKC takes p as the origin and unfolds the spatial eight quadrants. In each quadrant space, there is a point with the weight , and the spatial coordinate of the kernel point is . The dimension of the weight c is matched with the dimension of current point cloud feature. The SEQKC module g is used to convolute all the point features F in the neighborhood, which can be defined as:
where denotes the points in the neighborhood, the is the feature of point , K denotes the eight quadrant kernel points. We define the kernel function g for neighborhood points as:
where is the Euclidean distance between each point in the neighborhood and the quadrant kernel point. We use it restricts the influence of kernel point to each neighborhood points, so that the weights of the points that closer to the quadrant kernel point are larger, while the points far from the quadrant kernel point are small and less affected by the weight. Using the distance-constrained weights in eight directions to dot product the feature of each point, the algorithm can aggregate the global feature from all neighborhood.
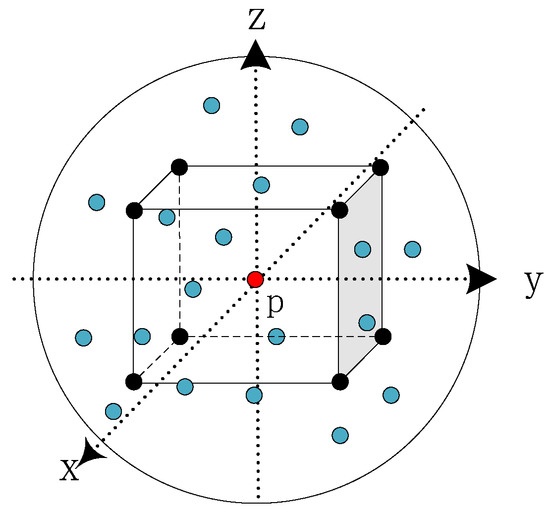
Figure 2.
The structure of spatial eight-quadrant kernel in point cloud neighborhoods. The red point is the center point p in the constructed spherical neighborhood space, the black points are kernel points of eight quadrants in the constructed spherical neighborhood space, and the blue points are neighborhood points of the center point.
3.3. Spatial Eight-Quadrant Kernel Convolution Module
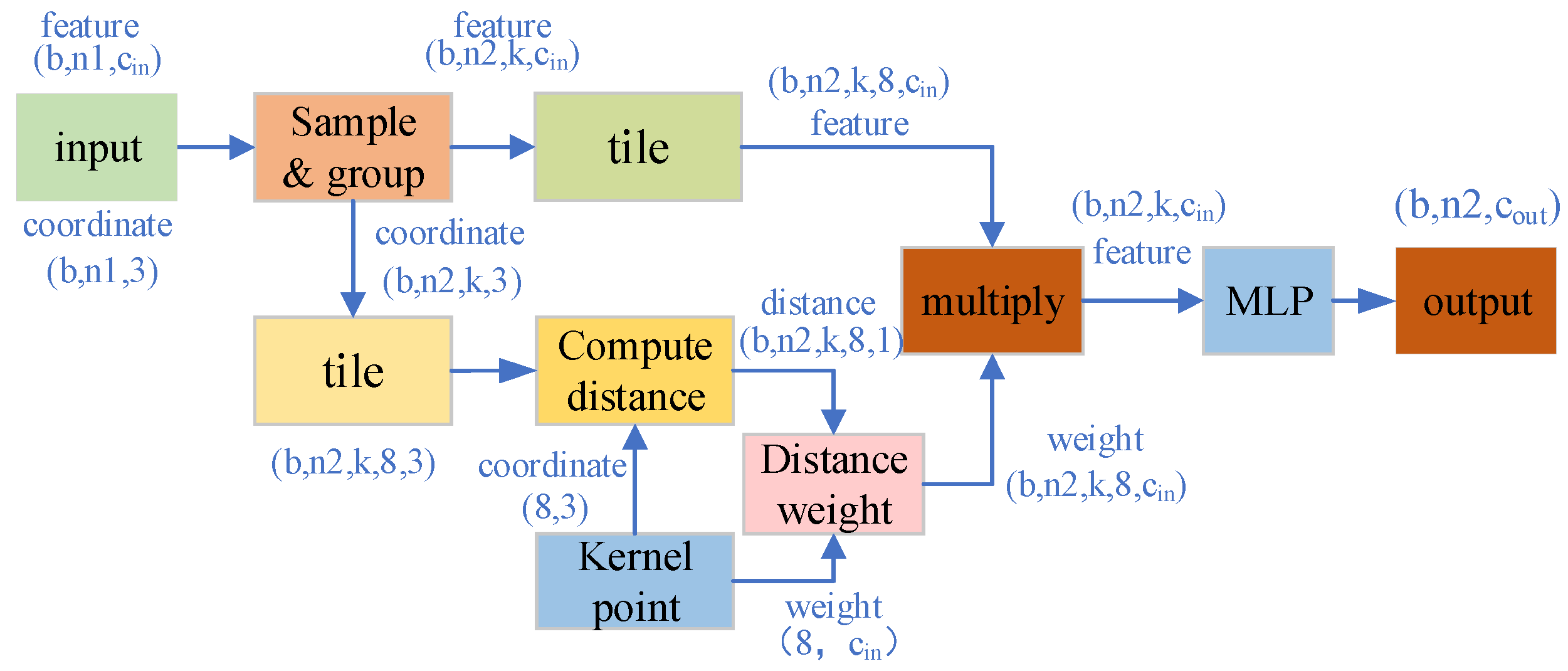
Based on the proposed SEQKC, we design a feature encoder for 3D point clouds, namely SEQKC module. The structure of SEQKC module is shown in Figure 3. The input data of the module are divided into point cloud coordinates and point clouds feature , which b denotes the batch size of input data, is the number of points for each batch, 3 indicates the coordinates of the point cloud, and is the dimension of the current point cloud feature. In addition, we employed the sampling and grouping strategy of PointNet++ to our encoder. That is to say, we use the farthest point sampling to find points, which are used to be the centroid to construct the spherical neighborhood with the radius r. In every neighborhood, we select k support points, if there are not enough points, the center point is repeatedly used instead. We combine the coordinates and features of the points in each neighborhood, so the data sizes are and respectively. The neighborhood points need to be decentered before computing with each quadrant kernel point, namely, the coordinates of each point in the neighborhood need to be subtracted from the coordinates of corresponding centroids. After that, the eight-quadrant kernel points are constructed with coordinate size and the weight dimension . We compute the distances from each point in the neighborhood to the eight-quadrant kernel points, then use them as weight coefficients for quadrant kernel point. Although the convolution kernel has only eight kernel points with eight different weights, when each weight is given a different distance weighting, it disguisedly increases the kernel point weights to the same number of points as the neighborhood points. After distance weighting, the weight dimension is raised to , which is the same as point cloud feature dimension. They are multiplied with the neighboring point cloud features, added to the bias, and followed by batch normalization layer and ReLu activation to batch normalize the features and remove the data less than zero in the features. Finally, the feature information of point cloud is extracted by MLP, and the feature information is output after dimensionality upgrading.
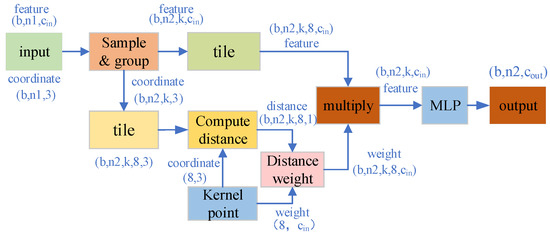
Figure 3.
The encoder module of spatial eight-quadrant kernel convolution. First, sampling and grouping the input point clouds to form the neighborhood space. Then, using the spatial eight-quadrant kernel convolution algorithm to weight the features in neighborhoods. Finally, the weighted features are aggregated and input to the MLP.
4. Spatial Eight-Quadrant Kernel Convolution Algorithm-Based Networks
We apply the proposed SEQKC module based on the spatial eight-quadrant kernel convolution algorithm to PointNet++, PointSIFT, PointConv networks as a downsampling module together with the Set Abstraction Module (SA) for feature extraction of the point cloud. The SA module consists of a sampling layer, a grouping layer, and a feature extraction layer. The sampling layer samples the point clouds globally by the farthest point sampling method; the grouping layer constructs multiple local regions by the K-nearest neighbor algorithm [29] or by specifying the radius of the sampled points; the feature extraction layer extracts the sampled and grouped point clouds using MLP to increase the feature dimension.
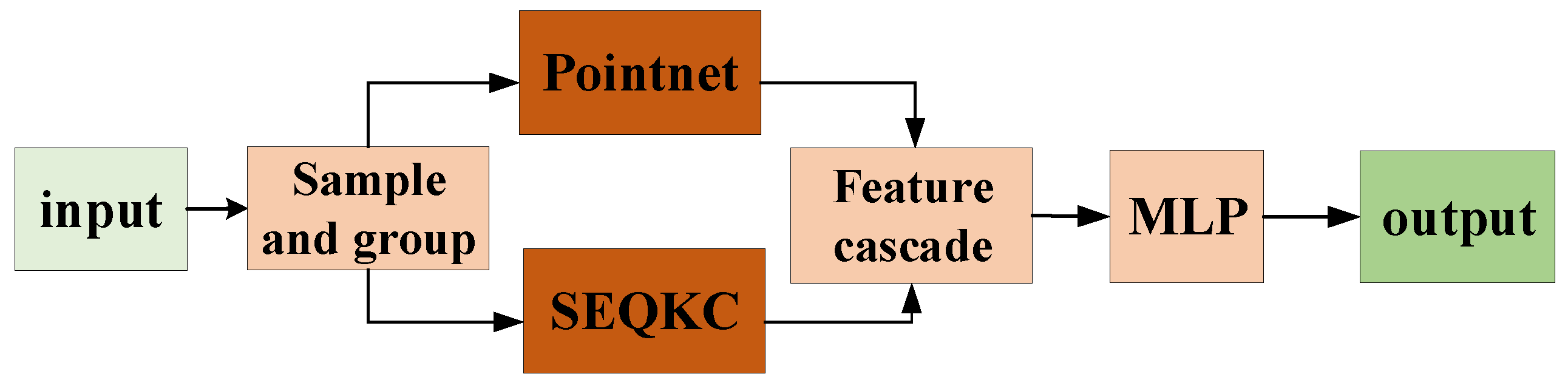
To save computational time and memory, we fused the SEQKC module with the SA module, which is shown in Figure 4. The SEQKC fusion module is similar to a residual network structure. The cascaded features contain multi-scale semantic information about the point cloud, it can allow the deep neural network to learn the global features of the grouped neighborhood as well as the shape features of small local regions.
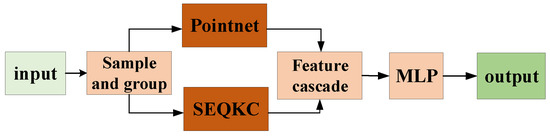
Figure 4.
The SEQKC fusion network. After sampling and grouping the point cloud, the SA module of PointNet and SEQKC module are cascaded to extract features.
4.1. Seqkc-Based Pointnnet++ Network
PointNet++ is a hierarchical neural network, by iterating the farthest point sampling to downsample point clouds, the network is able to learn features of point clouds from local to global. The network uses SA modules to extract point cloud features. Each SA module extracts the local information of the spherical neighborhood. By stacking SA modules, the number of point clouds decreases, the local information converges to global information, and the network’s receptive field changes from small to large. Subsequently, the feature propagation (FP) module is used, and the input number of points is linearly interpolated from N to . Finally, the number of point clouds is restored to the original number of point clouds while keeping the feature dimension unchanged, and the semantic segmentation is achieved.
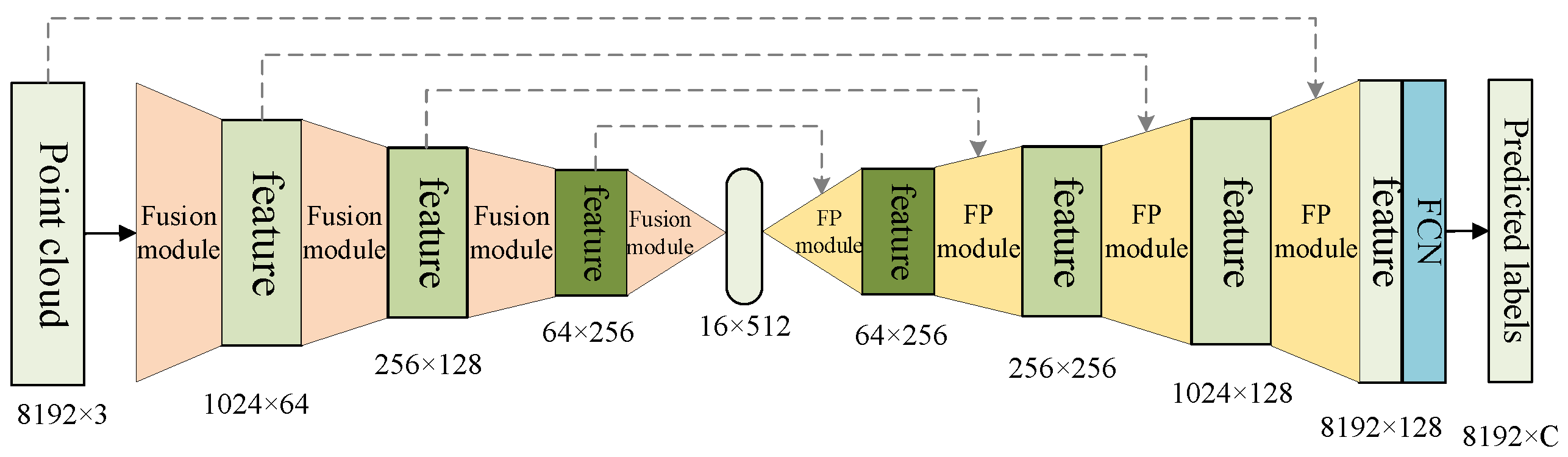
The SA module of the PointNet++ network directly inputs the sampled and grouped features into the MLP, which leads to the network learning more about the global shape information of each grouping neighborhood, lacking the processing of local area information in the neighborhood. As a result, the network is unable to segment small objects surrounded by large objects, and the robustness of the semantic segmentation for point cloud is poor. We incorporated the SEQKC module into the PointNet++ network, and the improved network structure is shown in Figure 5.
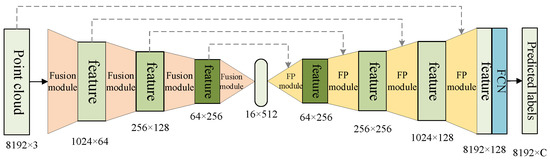
Figure 5.
The structure of SEQKC-PointNet++ nerwork. The basic structure is the same as PointNet++. Fusion module denotes the SEQKC module with the SA module, and FP module is a feature propagation module which uses linear interpolation weighted by distances to upsample the point cloud.
We directly replace the original SA module in the encoding layers of PointNet++ with SEQKC module, so that the network can extract richer features that contain more detailed contextual relationship between points. For complex environments, the network can propagate richer semantic information for the prediction of semantic labels. At the same time, the improved network is more accurate in terms of segmentation results of small objects with more natural and realistic boundary transitions due to the extracted semantic features contain more fine-grained information.
4.2. Seqkc-Based Pointsift Network
The PointSIFT network is improved based on PointNet++, which combines point cloud Orientation-Encoding and Scale-Awareness unit. In the past, point cloud local descriptors were usually unordered operations, while ordered operations may provide more information. With this in mind, PointSIFT uses Orientation-Encoding, which is a three-stage operator that convolves the 2 × 2 × 2 cube along X, Y, and Z axes successively. The PointSIFT module is used before the SA module in the network to integrate the features of point cloud. Such an approach enhances the ability of the network to extract distinguished features, so that the network has a stronger semantic segmentation capability.
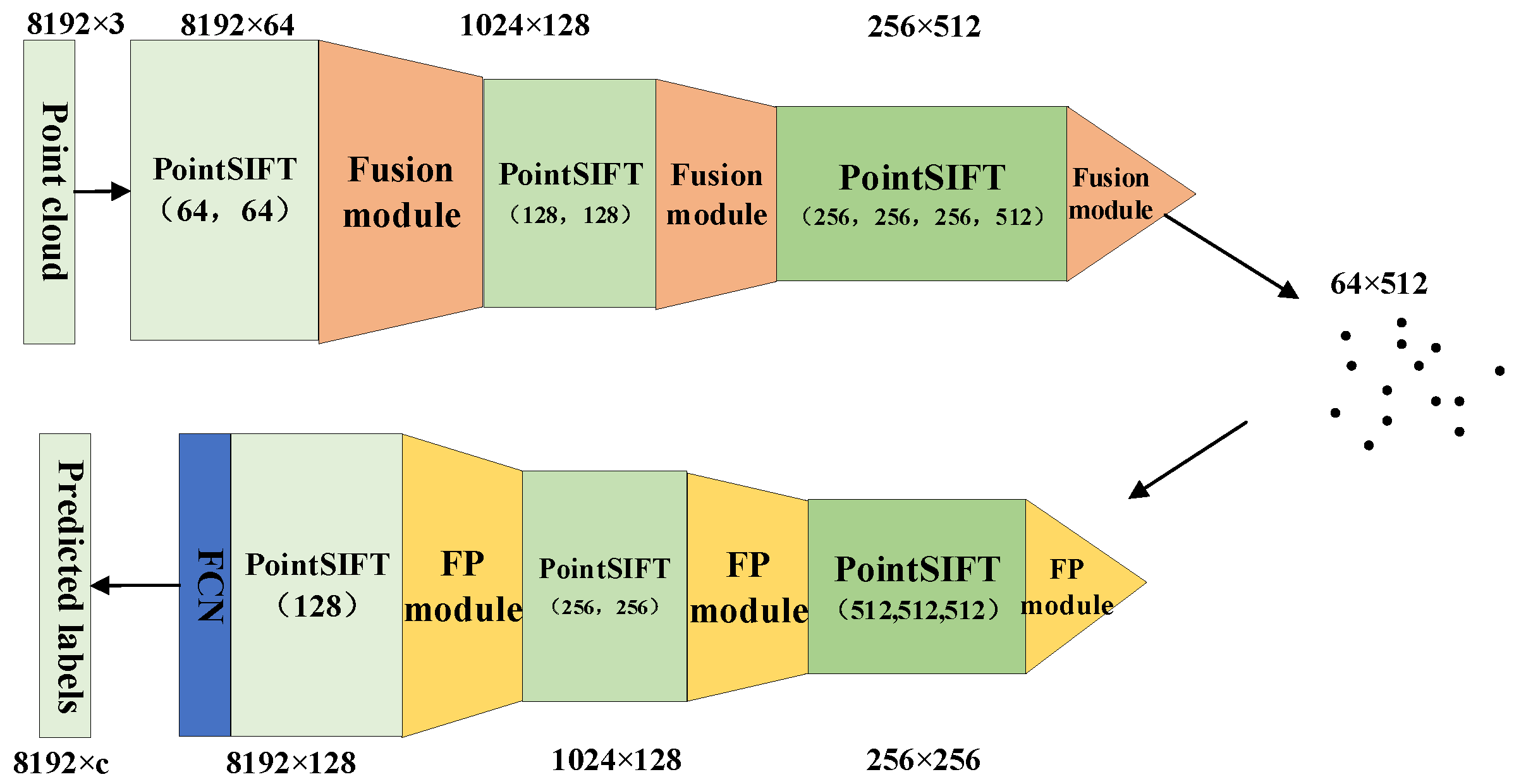
Similarly, we replace the SA module of the PointSIFT network for point cloud feature downsampling with the proposed SEQKC module. Through the interaction between the small neighborhood information contained by the features of each point and other points in the spherical neighborhood, the point cloud features output by SEQKC fusion module contain the relationship between the points. The structure of the improved PointSIFT network based on the SEQKC feature fusion module is shown in Figure 6.
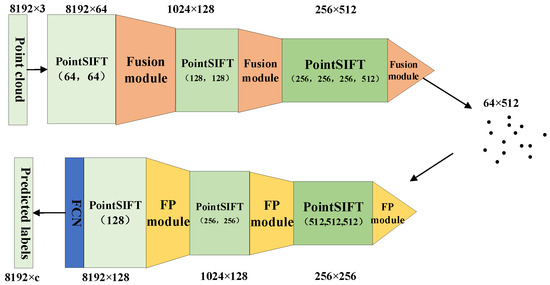
Figure 6.
The structure of SEQKC-PointSIFT network. The structure of SEQKC-PointSIFT is the same as that of PointSIFT, except that SA module is replaced with Fusion module.
With the PointSIFT module for point cloud feature preprocessing, the features obtained by the SEQKC fusion module contain more fine-grained multi-scale information about the local neighborhood of the point cloud. After three times of downsampling by the SEQKC fusion module, the acquired global features can be upsampled using the original feature decoding module of the PointSIFT network. The features obtained by downsampling with the SEQKC fusion module contain richer and more detailed semantic information than that of the original network, so the PointSIFT network with the improved downsampling module has higher semantic segmentation accuracy compared with the original PointSIFT network.
4.3. Seqkc-Based Pointconv Network
Inspired by 2D image convolution, PointConv approximates the continuous convolution operation with a discrete function that performs the convolution operation on a non-uniformly sampled point cloud. In the original PointConv network, the inverse density weighting method is used to weight the point features in the local region, and the local coordinates of the points in the region are used to construct the weights which is multiplied by the point feature. In the network based on SEQKC, the inverse distance weighting method is used to weight the point features in the local region, and the weight of the constructed kernel points is multiplied by the point features.
Since both points in sparse region and dense region are important to the whole point cloud, and the number of points in the dense region accounts for a relatively large number, so directly feeding the whole points into the network will make the network learn more information from the dense points and neglect the sparse points. To avoid this problem, the SEQKC algorithm extracts the features of the points in the region by eight spatial kernel points from the viewpoint of distance. The spatial kernel points are uniformly distributed in the local region of the point cloud, and in this region, both the points in the dense and sparse places will have their features weighted by their nearest kernel points, so that the influence of each point on the region is balanced.
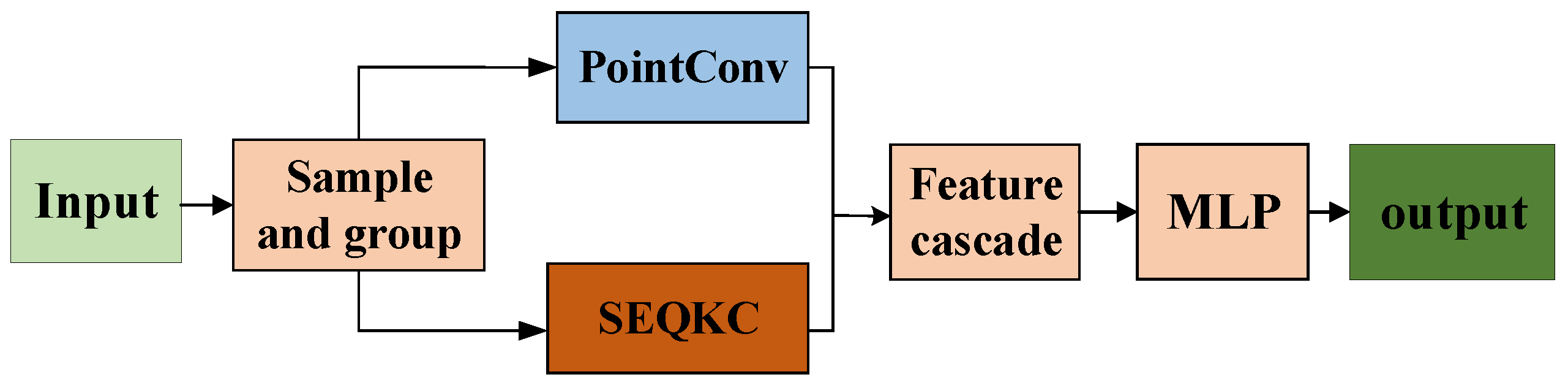
These two methods obtain balanced local space features from the viewpoint of density and distance, and have different scale point cloud semantic information. Considering the differences between these two methods, we combine them to construct a new downsampling module called the point cloud double convolution (DC) module, which is shown in Figure 7. For the input point cloud features, the improved point cloud DC module uses a sampling and grouping strategy to obtain individual local features of the point clouds.
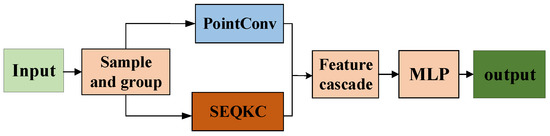
Figure 7.
The double convolution module. After sampling and grouping the point cloud, the SEQKC with PointConv convolution are cascaded to extract features.
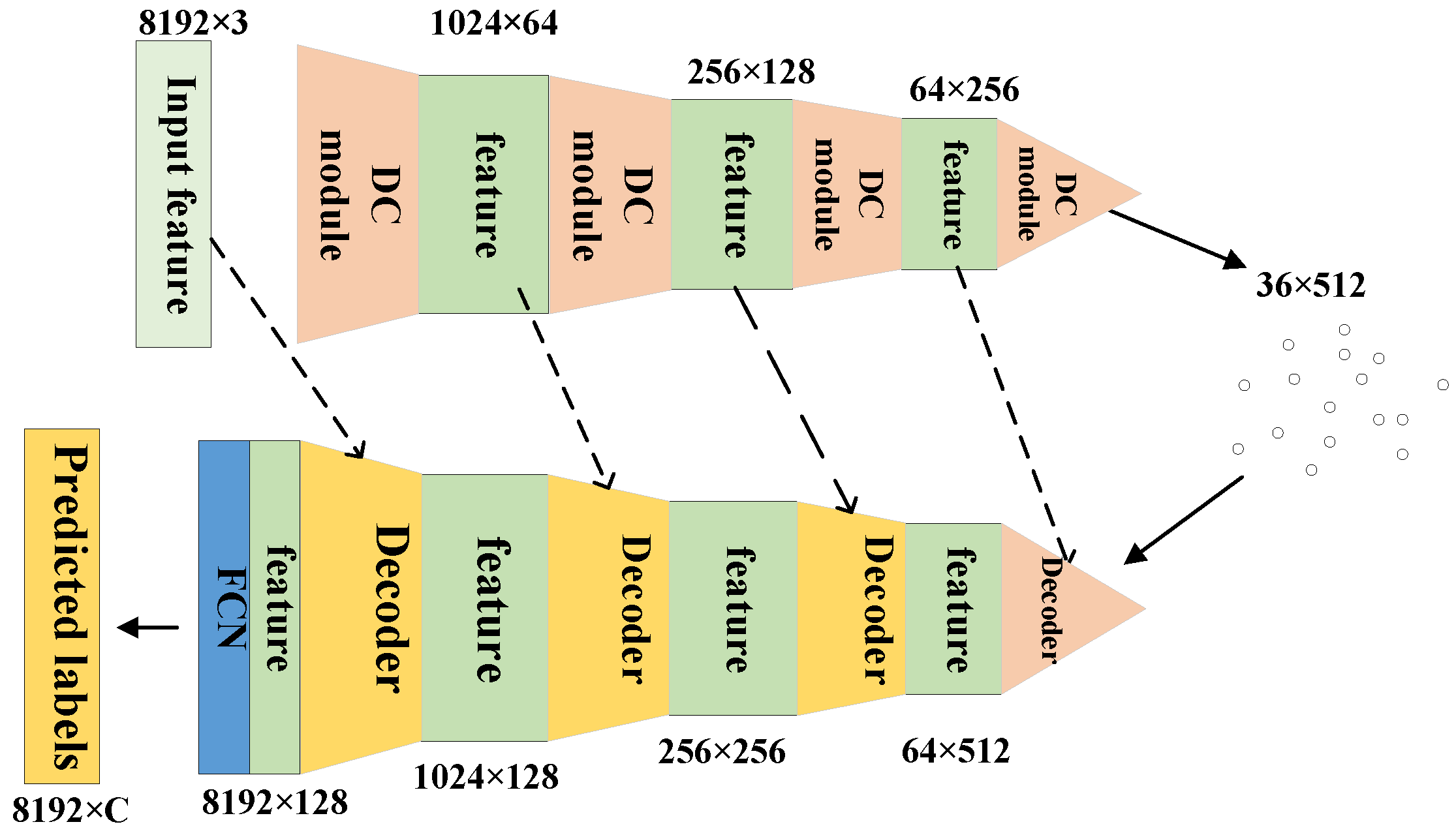
The improved PointConv network based on the DC module is shown in Figure 8. It uses the PointConv convolution method with the spatial eight-quadrant kernel convolution method to extract features from each local region of the point cloud, then cascades the two features which contains semantic information at different scales. Finally, the cascaded new features are fed into the MLP for training, and the point cloud features are extracted.
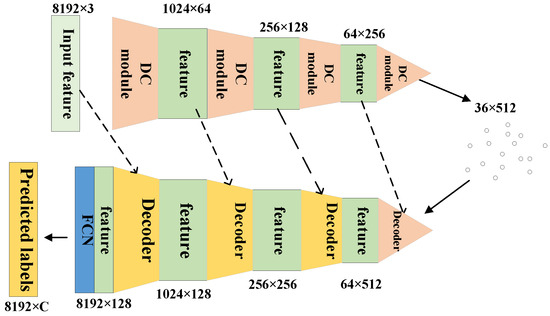
Figure 8.
The structure of SEQKC-PointConv network. The network consists of downsampling (DC module) and upsampling (Decoder module) procedures. The DC module is double convolution module mentioned above, and Decoder is the PointDeconv module in [15].
5. Experiment
To ensure the comparability of the experimental results, we evaluate our networks on the benchmark dataset ScanNet V2 [17] (Richly annotated 3D Reconstructions of Indoor Scenes). This dataset contains a large number of indoor scenes, obtained by camera scanning at different viewpoints and 3D reconstruction. The indoor scenes are rich in types and sizes, including not only large-scale indoor scenes such as apartments and libraries, but also many small indoor scenes such as storage rooms and bathrooms. Each scene may contain 19 different categories of objects such as doors, windows, chairs, tables, etc., and one unknown type. We used 1201 indoor scenes for training and the remaining 312 indoor scenes for testing. For a fair comparison, we follow we follow the PointNet++ [13], PointSIFT [14] and PointConv [15] to divide ScanNet dataset into the training set and the test set in the corresponding experiments. Note that the scenes of PointConv [15] in the training set and the test set are different from that of PointNet++ [13] and PointSIF [14], but the amount of data in the training set and the test set is the same. In all experiments, we implement the models with Tensorflow on a GTX 1080Ti GPU.
5.1. Hyperparameter Setting
Each training session uses non-uniform sampling to collect input points in each point cloud scene, and the input points size of the network is set to 8192. If the training platform does not have enough memory, the number of input points can be reduced to 4096, and the batch size is 12. The network uses Adam optimizer, the learning rate is set by exponential decay method, the initial learning rate is set to 0.001, decay step is 200,000 and decay rate is 0.7, max epoch is 1000.
5.2. Loss Function
To measure the degree of inconsistency between the predicted semantic labels of the model and the true semantic labels, we use the sparse cross entropy loss [30] function, and the formulas are shown in Equations (3) and (4).
where denotes the semantic label predicted by the network for any point, which is the probability score of each category, denotes the probability of the point on the jth category. The formula shows that P also has dimension, the natural logarithm of each dimension on p is obtained and multiplied with the actual semantic label y. The negative sum of all the dimensions is the desired loss.
5.3. Evaluation Criteria
In the experiments, we use the following evaluation metrics.
(1) Point calibrated average accuracy (caliacc). MPA treats each class equally and takes the average of all the accuracy of the classes. In fact, the proportion of each class in the point cloud is different, so that this method is flawed. As shown in Equation (5), the caliacc uses the proportion of each class in the point cloud points to weight the accuracy of each class, and sums them.
(2) Mean Intersection over Union (MIoU). The IoU refers to the ratio of intersection and union of two sets. For the prediction results of point cloud semantic labels, the more points that are predicted to be the right semantic labels, and the fewer points whose semantic labels are not of that class are predicted to be of that class. The IoU is more convincing than judging whether the semantic labels of only one class of points are predicted accurately without considering the PA values of other classes. As shown in Equation (6), the MIoU is obtained by summing the IoU for each class and taking the mean value.
5.4. The Experiments to Verify the Number of Kernel Point
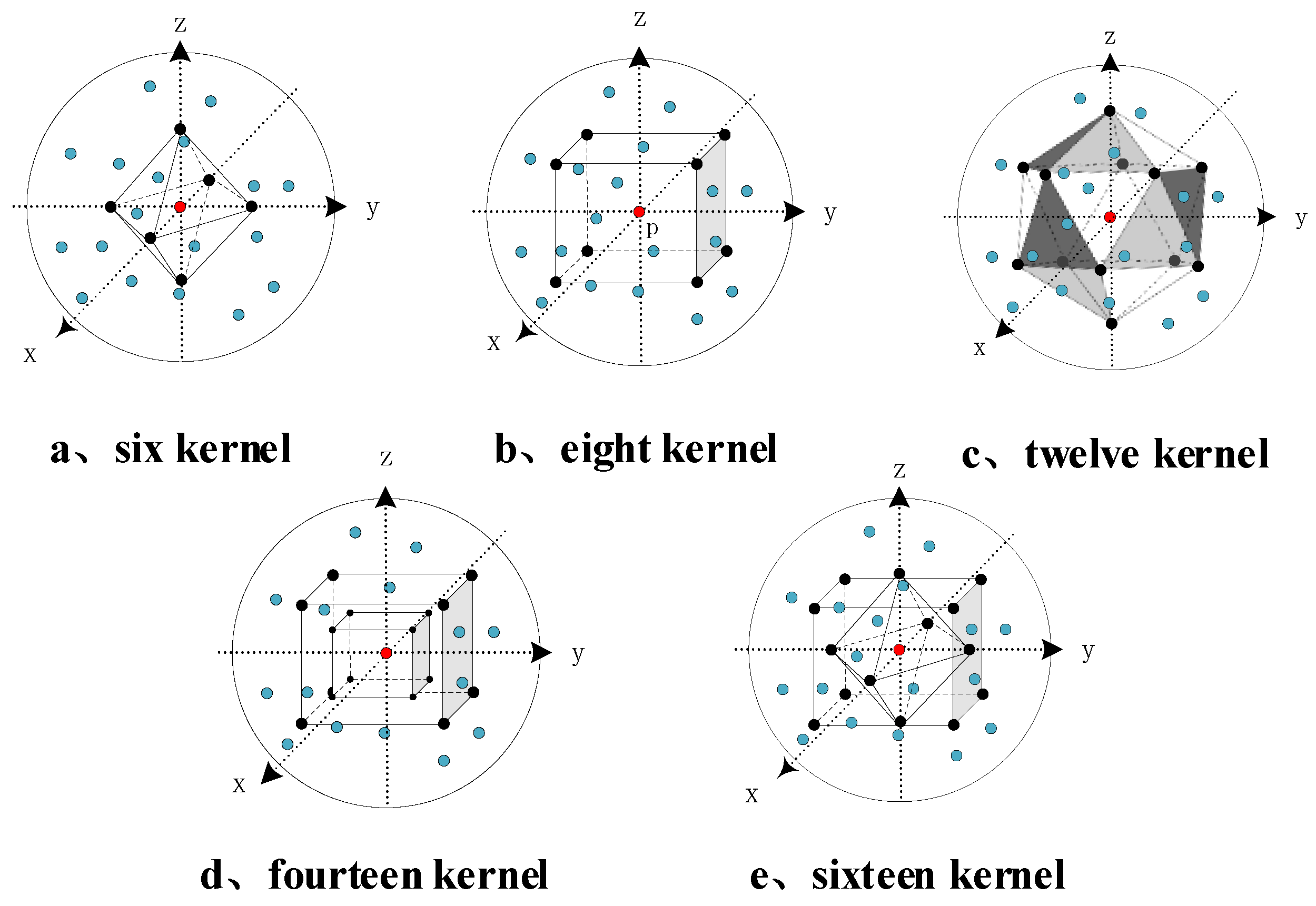
In order to find the optimal number of kernel points for the spatial kernel convolution algorithm, we distribute different numbers of kernel points uniformly in the spherical neighborhood, then conduct point cloud semantic segmentation experiments separately. The distribution of kernel points in the spherical neighborhood of the point cloud under each number is shown in Figure 9. The experiments are conducted based on the PointNet++ network, and the point cloud downsampling module of the PointNet++ network is replaced with SEQKC module, while the rest of the network structure remains unchanged. A comparison of the specific results is shown in Table 1, where denotes the original network.
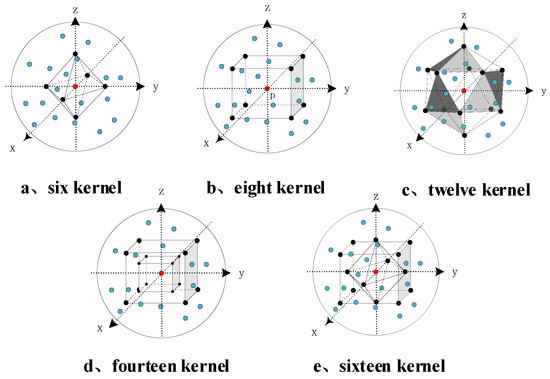
Figure 9.
The distribution of kernel in spatial for different kernel number.

Table 1.
The comparison results for different number of kernel point.
It can be seen that all PointNet++ networks using SEQKC module obtain an improvement in both MIoU and caliacc compared to the original network. As the number of kernel points increases, it reaches a maximum at 8 kernel points, and the network’s caliacc finally remains at about 84.74%. MIoU also reaches a maximum at 8 kernel points and then starts to decrease, so the spatial kernel convolution has the best semantic segmentation performance for 3D point clouds when 8 kernel points are used.
5.5. The Experiment to Verify Cascaded Seqkc Structure
Our proposed SA module with SEQKC fusion module is actually a residual structure of SEQKC module. In order to verify whether this residual structure is valid, experiments were conducted on the uncascaded SEQKC module and the cascaded SEQKC module with sampling and grouping operations, respectively. The experiments were based on PointNet++ network, and the results are shown in Table 2.

Table 2.
Experimental results of cascaded SEQKC module.
From Table 2, it can be seen that the SEQKC module can effectively improve the MIoU of point cloud semantic segmentation results with or without cascade, and the cascaded SEQKC module can improve the semantic segmentation caliacc of points. This indicates that the features extracted by the SEQKC method contain more detailed spatial scale and can imply the point-to-point connection information to improve the integrity of the object semantic segmentation results, thus improving the MIoU values.
In addition, in order to verify the importance of the kernel point coordinates, we cancel kernel point coordinates in SEQKC, and apply the eight weights without distance weighting to the input point cloud features. The results are shown in Table 3. The eight kernel points that lose the coordinates are convolved with the point cloud features without the distance weighting, and the network segmentation results are slightly lower in terms of caliacc than the network with the kernel point coordinates, and their MIoU is 2.52% lower than the network with the kernel point coordinates. This indicates that the coordinate positions of the kernel points can indeed help the network analyze the connection between points and help the network find the accurate location of the points in the final semantic segmentation results.

Table 3.
The comparison results for SEQKC with and without kernel point coordinates.
5.6. The Experiment of Semantic Segmentation-Based on Enhanced Networks
We embed the SEQKC module into classical semantic segmentation networks to evaluate the performance of the algorithm, and for the fairness of comparison, we ensure that the network parameters are the same as the original network except for the added module.
In order to better show the effectiveness and stability of our method, we did three repeated experiments on SEQKC-PointNet++, SEQKC-PointSIFT and SEQKC-PointConv with the same setting, and the results are shown in Table 4. It shows that the proposed method has stable improvement, although there is randomness in the training process. We compared the MIoU of the semantic segmentation results across all networks. From Table 4, we can see that the networks with the SEQKC module improve the MIoU compared to the original networsk, with a minimum improvement of 1.35%, indicating that our module can more accurately identify the points of small objects in indoor scenes, and has a stronger performance of the segmentation in visual.

Table 4.
The comparison results of the enhanced networks for semantic segmentation.
In order to analyze it in detail, Table 5 and Table 6 show the segmentation results of each category on the Scannet dataset under different networks. To make the comparison of experimental results more intuitive, we highlight the small objects in Table 5 and Table 6. As can be seen from the table, the semantic segmentation results of large objects are almost the same. However, the segmentation performance of our network is significantly better than that of the original network in terms of small objects, such as chair, shower curtain, sink, toilet, picture and so on.

Table 5.
Experimental results of all categories on Scannet dataset in terms of Caliacc (%).

Table 6.
IoU (%) comparison of various semantic segmentation results based on PointConv.
Compared to PiontNet++, the semantic segmentation accuracy of small objects (chair, desk, sink, bathtub, toilet, counter, shower curtain and picture) are improved by SEQKC-PointNet++. Especially, the semantic segmentation accuracy of SEQKC-PointNet++ significantly improved by 28.25% for shower curtains, 18.04% for sinks, 14.17% for doors, 13.93% for toilets, and 9.67% for picture. The reason why the “picture” is so difficult to segment is that most of them are hung on the wall, and they are almost integrated with the wall in the point cloud space, and the percentage of points in the whole Scannet dataset is only 0.04%. Therefore, the semantic segmentation of pictures requires the network to be able to extract fine-grained and discriminative features. It can be seen that our improved PointNet++ network based on SEQKC accomplishes this task well.
SEQKC-PointSIFT also has improved the semantic segmentation accuracy of small objects, such as chair, desk, bathtub, toilet, counter, curtain and picture. Among them, the semantic segmentation accuracy of curtain is improved by 14.80% and toilet is improved by 12.12%, and other objects also have small improvements, these objects have rich geometric structure, thanks to the SEQKC can carefully handle the relationship between the points in the point cloud space, the semantic segmentation accuracy of the small objects with the smallest percentage of points has improved.
Since the improvement of PointConv network for 3D point cloud semantic segmentation is more on the IoU, we compared the IoU for each category in the semantic segmentation results as shown in Table 6. As we can see from Table 6, the improved network with the SEQKC module has improved the IoU in 13 categories compared to the original network. The largest improvement is for doors, with a 11.38% increase in the IoU, the semantic segmentation IoU of shower curtain has also increased by 8.98%. This indicates that the embedded modules in the PointConv network substantially help the network to obtain more useful local features of the point cloud and strengthen the network’s ability to identify the structure of small scale objects in the point cloud space.
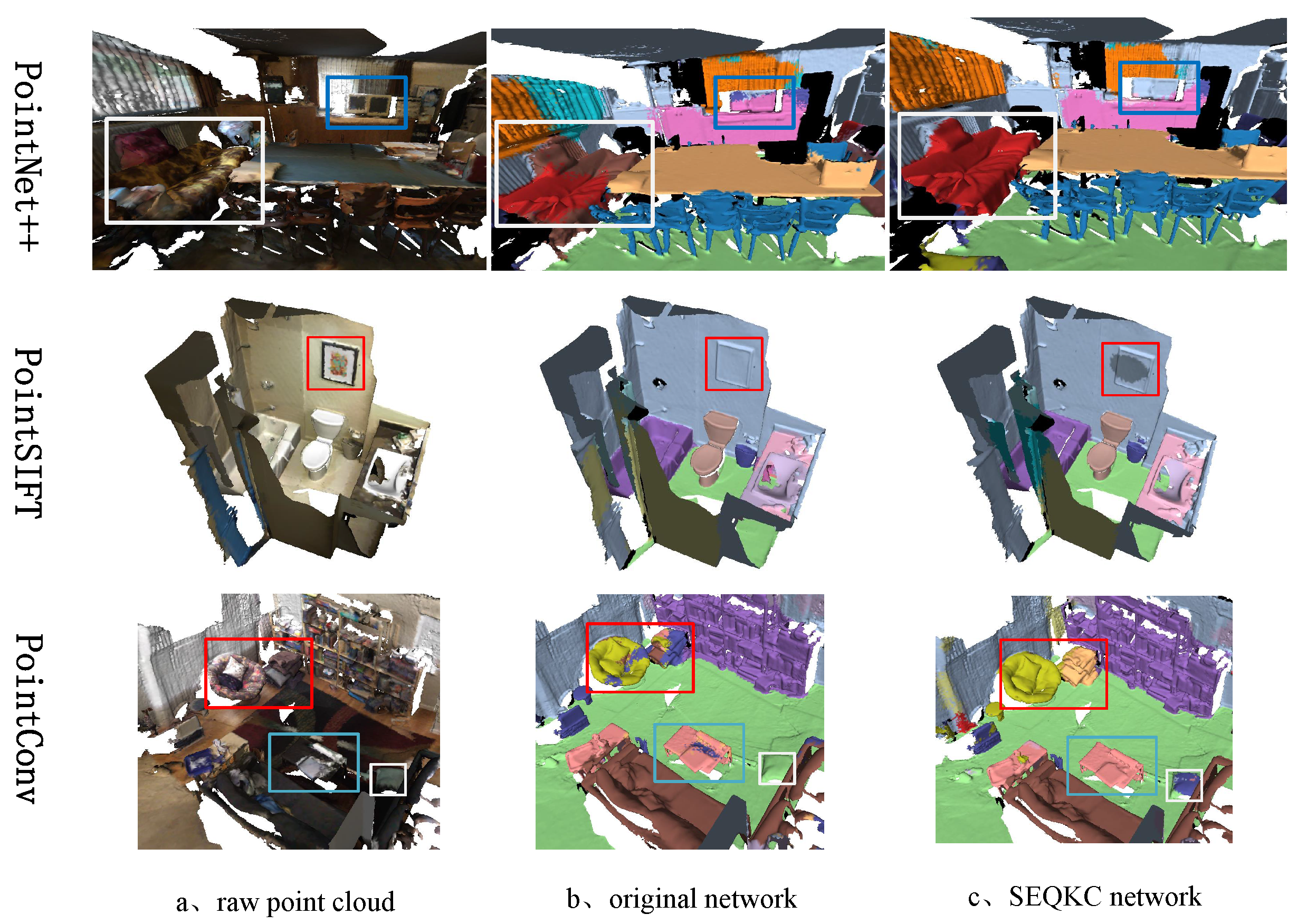
The results of the semantic segmentation were visualized using Meshlab software, and the results are shown in Figure 10. As shown in Figure 10, when the original network segment small objects in the 3D scene, the network sometimes could not recognize small objects surrounded by large objects and often confused them with the background or other large objects. Otherwise, the network was insensitive to the boundary information and produced irregular object boundaries after segmentation. The network combined with the SEQKC module is able to extract richer local semantic features, better segmentation of small objects and clearer segmentation boundaries due to the enhanced relationship between local points of the point cloud. The results show that the SEQKC algorithm can correctly analyze the detailed information of the local region of the point cloud, and using SEQKC module can effectively help the network extract more local feature information of the point cloud, improve the semantic segmentation accuracy of the network.
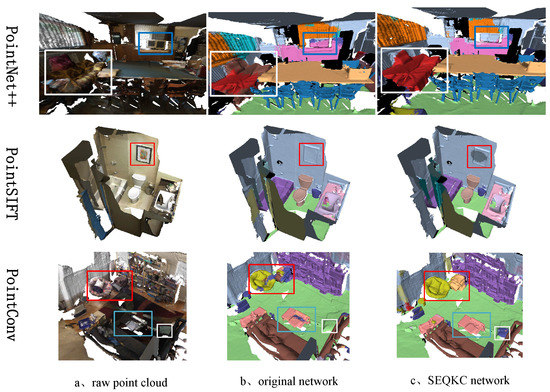
Figure 10.
Visualization of segmentation results on Scannet dataset.
5.7. Running Time
Table 7 illustrates a comparison of running time. For a fair comparison, we conduct all experiments on a single GTX 1080Ti GPU with the same environment. The training time is for training one epoch, and the test time is for evaluating 4 × 8192 points. As we can see, compare with the original networks, when segmenting the same scenes, our algorithms take about the same time, but our algorithms improve the segmentation accuracy, especially for small objects in the scenes.

Table 7.
The comparison results of running time.
6. Discussion
Each point in the point cloud space does not exist in isolation, the relationship of points between different objects or different parts of the same object are different. Such point-to-point relationships are important for the point cloud semantic segmentation task. To capture such relationships, we propose the spatial eight-quadrant kernel convolution algorithm, which captures point-to-point connections by constructing kernel points and weighting the neighborhood points with kernel point weights and distances, so that local fine-grained information of the point cloud can be extracted.
The proposed algorithm can be added to previous point cloud semantic segmentation network to improve the semantic segmentation performance. After incorporating the spatial eight-quadrant kernel convolution algorithm, the network is more sensitive to small objects and boundary features in point clouds, and the segmentation accuracy of the network is significantly improved.
7. Conclusions
In this paper, we propose a point cloud feature extraction algorithm, which called spatial eight-quadrant kernel convolution. The proposed algorithm models the relationship between points and extracts local fine-grained features from point clouds, so that it can improve the performance of semantic segmentation for small objects. We modified the downsampling module with the spatial eight-quadrant kernel convolution algorithm and apply it to classical point cloud semantic segmentation networks. The results show that small-scale objects in 3D point clouds are easily affected by large-scale objects, resulting in wrong semantic categories or partial boundary erosion by large-scale objects. The proposed SEQKC module can help the network to extract fine-grained feature information from the point cloud and improve the semantic segmentation ability of small-scale objects in complex and variable environments. Extensive experimental results on ScanNet v2 dataset show that The proposed model can help the network to improve the semantic segmentation.
Author Contributions
Methodology, L.L.; Software, J.Y. and L.T.; Validation, L.L., J.Y. and L.T.; Writing—original draft preparation, J.Y.; Writing—review and editing, W.S. and L.Z.; Visualization, J.Y. and L.T.; Supervision, W.T.; Funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant (61976227,61772213) and in part by the Natural Science Foundation of Hubei Province under Grant 2019CFB622.
Data Availability Statement
The ScanNet V2 Dataset used for this study can be accessed at http://www.scan-net.org/ accessed on 11 June 2018.
Acknowledgments
We would like to thank our colleagues for their helpful suggestions during the experiment, and thank the editor and the anonymous reviewers for their valuable comments and suggestions that greatly improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lamas, D.; Soilán, M.; Grandío, J.; Riveiro, B. Automatic Point Cloud Semantic Segmentation of Complex Railway Environments. Remote Sens. 2021, 13, 2332. [Google Scholar] [CrossRef]
- Luo, N.; Yu, H.; Huo, Z.; Liu, J.; Wang, Q.; Xu, Y.; Gao, Y. KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation. Remote Sens. 2021, 13, 1003. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar]
- Wang, J.; Zhu, M.; Wang, B.; Sun, D.; Wei, H.; Liu, C.; Nie, H. KDA3D: Key-Point Densification and Multi-Attention Guidance for 3D Object Detection. Remote Sens. 2020, 12, 1895. [Google Scholar] [CrossRef]
- Platt, C.; Young, S.; Austin, R.; Patterson, G.R.; Mitchell, D.; Miller, S.D. LIRAD Observations of Tropical Cirrus Clouds in MCTEX. Part I: Optical Properties and Detection of Small Particles in Cold Cirrus. J. Atmos. Sci. 2002, 59, 3145–3162. [Google Scholar] [CrossRef]
- Carmigniani, J.; Furht, B.; Anisetti, M.; Ceravolo, P.; Damiani, E.; Ivkovic, M. Augmented reality technologies, systems and applications. Multimed. Tools Appl. 2010, 51, 341–377. [Google Scholar] [CrossRef]
- Laskey, M.; Lee, J.; Chuck, C.; Gealy, D.V.; Hsieh, W.Y.S.; Pokorny, F.T.; Dragan, A.; Goldberg, K. Robot grasping in clutter: Using a hierarchy of supervisors for learning from demonstrations. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 827–834. [Google Scholar]
- Geng, X.; Ji, S.; Lu, M.; Zhao, L. Multi-Scale Attentive Aggregation for LiDAR Point Cloud Segmentation. Remote Sens. 2021, 13, 691. [Google Scholar] [CrossRef]
- Pierdicca, R.; Paolanti, M.; Matrone, F.; Martini, M.; Morbidoni, C.; Malinverni, E.S.; Frontoni, E.; Lingua, A.M. Point Cloud Semantic Segmentation Using a Deep Learning Framework for Cultural Heritage. Remote Sens. 2020, 12, 1005. [Google Scholar] [CrossRef] [Green Version]
- Kwak, J.; Sung, Y. DeepLabV3-Refiner-Based Semantic Segmentation Model for Dense 3D Point Clouds. Remote Sens. 2021, 13, 1565. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Gardner, M.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- Jiang, M.; Wu, Y.; Lu, C. PointSIFT: A SIFT-like Network Module for 3D Point Cloud Semantic Segmentation. arXiv 2018, arXiv:1807.00652. [Google Scholar]
- Wu, W.; Qi, Z.; Li, F. PointConv: Deep Convolutional Networks on 3D Point Clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9613–9622. [Google Scholar]
- Sheather, S.; Jones, M. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B-Methodol. 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-Annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2432–2443. [Google Scholar]
- Tatarchenko, M.; Park, J.; Koltun, V.; Zhou, Q.Y. Tangent Convolutions for Dense Prediction in 3D. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3887–3896. [Google Scholar]
- Lawin, F.J.; Danelljan, M.; Tosteberg, P.; Bhat, G.; Khan, F.S.; Felsberg, M. Deep projective 3D semantic segmentation. In Proceedings of the International Conference on Computer Analysis of Images and Patterns, Ystad, Sweden, 22–24 August 2017; pp. 95–107. [Google Scholar]
- Muresan, M.P.; Nedevschi, S. Multi-object tracking of 3D cuboids using aggregated features. In Proceedings of the 2019 IEEE 15th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 5–7 September 2019; pp. 11–18. [Google Scholar]
- Huang, J.; You, S. Point cloud labeling using 3D Convolutional Neural Network. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2670–2675. [Google Scholar]
- Tchapmi, L.; Choy, C.; Armeni, I.; Gwak, J.; Savarese, S. SEGCloud: Semantic Segmentation of 3D Point Clouds. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 537–547. [Google Scholar]
- Ibrahim, M.; Akhtar, N.; Wise, M.; Mian, A. Annotation Tool and Urban Dataset for 3D Point Cloud Semantic Segmentation. IEEE Access 2021, 9, 35984–35996. [Google Scholar] [CrossRef]
- Unal, O.; Van Gool, L.; Dai, D. Improving Point Cloud Semantic Segmentation by Learning 3D Object Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 2950–2959. [Google Scholar]
- Hua, B.S.; Tran, M.K.; Yeung, S.K. Pointwise Convolutional Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 984–993. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 6410–6419. [Google Scholar]
- Ye, X.; Li, J.; Huang, H.; Du, L.; Zhang, X. 3D Recurrent Neural Networks with Context Fusion for Point Cloud Semantic Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 403–417. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Hermans, A.; Leibe, B. Exploring Spatial Context for 3D Semantic Segmentation of Point Clouds. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 716–724. [Google Scholar]
- Raktrakulthum, P.A.; Netramai, C. Vehicle classification in congested traffic based on 3D point cloud using SVM and KNN. In Proceedings of the 2017 9th International Conference on Information Technology and Electrical Engineering (ICITEE), Phuket, Thailand, 12–13 October 2017; pp. 1–6. [Google Scholar]
- Rubinstein, R. Optimization of computer simulation models with rare events. Eur. J. Oper. Res. 1997, 99, 89–112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).